5.3. 葉の定義と性質
偽植物学の用語定義を続けよう。木が持つ葉を定義する:
\(T\) を木とする。次数が \(1\) である \(T\) の頂点を葉 (leaf) と呼ぶ。
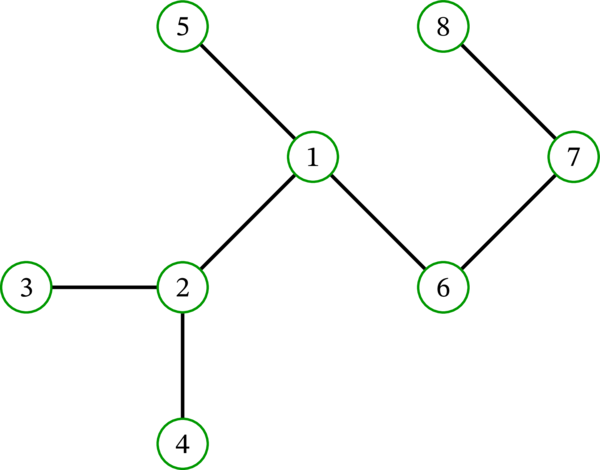
例えば、\(T\) を次の木とする:
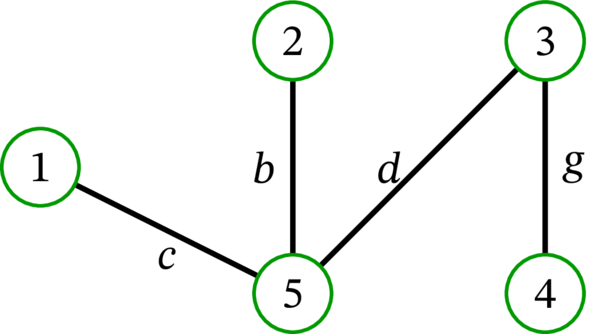
\(T\) は三つの葉 \(1\), \(2\), \(4\) を持つ。
頂点数が固定されたとき、どのような木が最も多くの葉を持つだろうか? \(n \geq 3\) のとき、単純グラフ
は (多重グラフとみなすとき) 木であり、\(n-1\) 個の葉を持つ。具体的には \(1,2,\ldots,n-1\) が葉となる。この木は \(n\) 頂点のスターグラフ (star graph) と呼ばれる。\(8\) 頂点のスターグラフを次に示す:
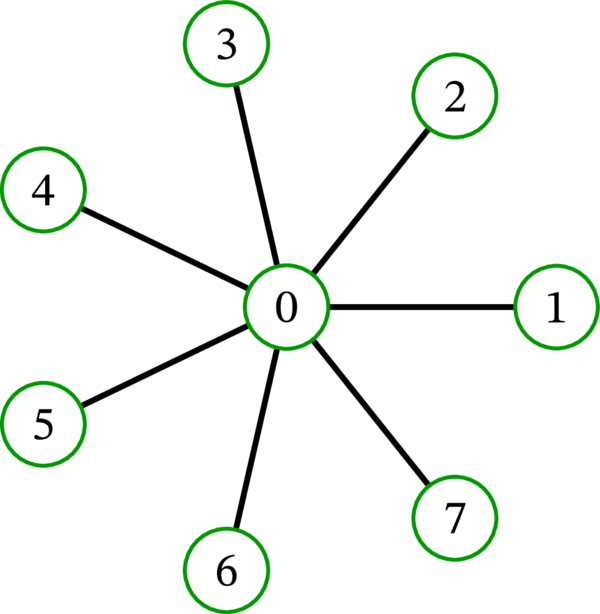
\(n\geq 3\) のとき木が持つ葉の個数が \(n-1\) より大きくならないことは容易に分かるので、スターグラフは葉の個数に関して最適である。なお、\(2\) 頂点のスターグラフが持つ葉の個数は \(1\) ではなく \(2\) である点に注意してほしい。
どのような木が最も少ない葉を持つだろうか? \(n \geq 2\) に対して、\(n\) 頂点の路グラフ

は葉を \(2\) 個 (\(1\) と \(n\)) しか持たない。これより葉が少ない木は存在するだろうか? \(n=1\) の場合には存在する: \(1\) 頂点の路グラフ \(P_{1}\) (頂点を一つだけ持ち辺を持たないグラフ) は葉を一つしか持たない。しかし \(n \geq 2\) の場合には、\(n\) 頂点の路グラフ \(P_{n}\) が最適である:
少なくとも \(2\) 個の頂点を持つ木を \(T\) とする。このとき:
-
\(T\) は少なくとも \(2\) 個の葉を持つ。
-
任意の \(T\) の頂点 \(v\) に対して、\(T\) の異なる葉 \(p\), \(q\) が存在して、\(p\) から \(q\) への路に \(v\) が含まれる。
木の同値性定理 (定理 5.2.4) の命題 T2 より、この定理における「\(p\) から \(q\) への路」は一意に定まることに注意してほしい。そのため英語では「a path」ではなく「the path」と書くことができる。
(b): 「最長路を使ったトリック」の一種を用いる。\(v\) を含む路の中で最長のものを \(\mathbf{w}\) とする。\(\mathbf{w}\) の始点と終点をそれぞれ \(p\), \(q\) とする。これから \(p\) と \(q\) が異なる頂点だと示す。
[念のため、\(\mathbf{w}\) の図を示す:

もちろん、木 \(T\) が \(\mathbf{w}\) に含まれない頂点と辺を持つ可能性はある。]
まず、\(T\) は木なので連結であり、\(T\) は少なくとも \(2\) 個の頂点を持つので \(v\) と異なる頂点 \(u\) を持つ。よって \(T\) は \(v\) から \(u\) への路 \(\mathbf{r}\) を持つ。\(u \neq v\) より、この路 \(\mathbf{r}\) は少なくとも \(1\) 個の辺を含む。よって \(\mathbf{r}\) は少なくとも \(1\) 個の辺と \(v\) を含む \(T\) の路である。従って、\(v\) を含む最長の路 \(\mathbf{w}\) も少なくとも \(1\) 個の辺を持つ。\(\mathbf{w}\) は \(p\) から \(q\) への路だから、\(p \neq q\) が分かる (\(1\) 個以上の辺を含む路の始点と終点は異なる)。
続いて、\(p\) が葉でないと仮定して矛盾を導く。このとき \(\deg p \neq 1\) が成り立つ。また、\(\mathbf{w}\) は \(p\) を含む辺を一つ (最初の辺として) 持つ。\(\deg p \neq 1\) より、\(T\) には \(p\) を含み \(\mathbf{w}\) に含まれない辺 \(f\) が存在する。この辺 \(f\) に注目する。\(f\) の \(p\) でない端点を \(p^{\prime}\) とする (\(f\) がループなら \(p^{\prime} = p\) とする)。\(f\) (および \(p^{\prime}\)) を \(\mathbf{w}\) の最初に追加すると、次のバックトラックフリー歩道 \(\mathbf{w^{\prime}}\) が得られる:
命題 5.1.2 によれば、バックトラック歩道は路であるか、そうでなければ閉路を含む。\(T\) は木であり閉路を持たないので、\(\mathbf{w^{\prime}}\) は路と結論できる。よって \(\mathbf{w^{\prime}}\) は \(\mathbf{w}\) より長く、かつ \(v\) を含む路である。これは \(v\) を含む最長の路が \(\mathbf{w}\) である事実と矛盾する。よって「\(p\) は葉でない」という仮定は間違いだと分かる。
従って \(p\) は葉である。同様の議論で \(q\) は葉だとも示せる (ここでは追加の辺と頂点を \(\mathbf{w}\) の最初ではなく最後に追加する必要がある)。まとめると、\(p\) と \(q\) は \(T\) の相異なる葉であり、\(p\) から \(q\) への唯一の路には \(v\) が含まれる (\(p\) から \(q\) への路 \(\mathbf{w}\) に \(v\) が含まれるため)。以上で定理 5.3.2 (b) は証明された。
(a): \(T\) の頂点 \(v\) を任意に取る。このとき、定理 5.3.2 (b) より \(T\) の相異なる葉 \(p\), \(q\) が存在して \(p\) から \(q\) への路に \(v\) に含まれる。特に、\(T\) には相異なる二つの葉 \(p\), \(q\) が存在する。つまり \(T\) は \(2\) 個以上の葉を持つ。これで定理 5.3.2 (a) は証明された。□
[Remark: (a) の別証明を示す。\(T=\left( V,E,\varphi\right) \) として、\(T\) に握手補題を適用すると次の等式を得る:
任意の \(v\in V\) で \(\deg v\geq1\) が成り立つ [なぜ?] ので、この等式からは少なくとも \(2\) 個の頂点で \(\deg v\leq1\) が成り立つこと分かる (そうでなければ \(\displaystyle \sum_{v\in V}\deg v \geq2\cdot\left\vert V\right\vert -1\) となってしまう)。よって少なくとも \(2\) 個の頂点は葉である。]
木に数学的帰納法を適用するとき葉は特に有用となる。その数学的な理由を示したのが次の定理である:
少なくとも \(2\) 個の頂点を持つ木を \(T\) とする。\(T\) の葉 \(v\) に対して、\(T\) から頂点 \(v\) と \(v\) を含む全ての辺 [\(v\) は葉なので、そのような辺は \(1\) 個しか存在しない] を除去した多重グラフを \(T \setminus v\) と表記する。このとき任意の葉 \(v\) に対する \(T \setminus v\) もまた木である。
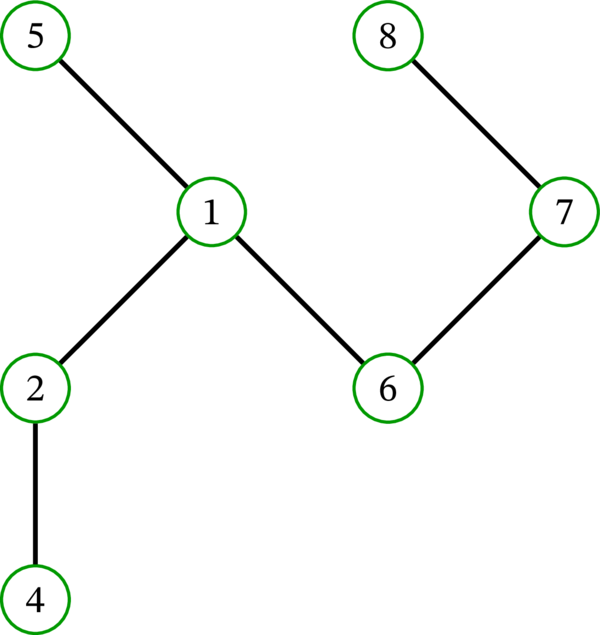
木 \(T\) と、\(T\) の葉 \(v\) を除去して得られる木 \(T \setminus v\) の例を次に示す。ここでは葉 \(3\) が除去されている:
\(T=\left( V,E,\varphi\right) \) とする。このとき \(T \setminus v\) は誘導部分グラフ \(T\left[ V\setminus\left\{ v\right\} \right] \) である。
グラフ \(T\) は木なので、閉路を持たない。よってグラフ \(T\setminus v\) も閉路を持たない。つまり \(T\setminus v\) は森である。
さらに、\(T\) は少なくとも \(2\) 個の頂点を持つので、\(T \setminus v\) は少なくとも \(1\) 個の頂点を持つ。
これから、\(T \setminus v\) の任意の二頂点 \(p\), \(q\) が \(T\setminus v\) で路連結なことを示す。
\(p\) と \(q\) を \(T \setminus v\) の任意の二頂点とする。\(T\) は連結なので、\(p\) と \(q\) は \(T\) で路連結である。よって \(T\) における \(p\) から \(q\) への路 \(\mathbf{w}\) が存在する。この \(\mathbf{w}\) に注目する。\(p\) と \(q\) は \(T\setminus v\) の頂点なので、どちらも \(v\) ではない。つまり \(\mathbf{w}\) の始点と終点はどちらも \(v\) でない。よって、もし \(v\) が \(\mathbf{w}\) に含まれるなら、\(v\) を含む \(2\) 個の辺が \(\mathbf{w}\) に存在しなければならない (具体的に言えば、そのような辺は \(\mathbf{w}\) において \(v\) の直前と直後に存在する)。しかし葉である \(v\) を含む \(T\) の辺は \(1\) 個しか存在しないので、これは不可能である。よって \(v\) は \(\mathbf{w}\) に含まれない。ここから \(\mathbf{w}\) は \(T\setminus v\) における路でもあることが分かる。つまり \(p\) と \(q\) は \(T\setminus v\) でも路連結である。
\(T \setminus v\) の任意の二頂点 \(p\), \(q\) が \(T \setminus v\) において路連結だと示せた。先述したように \(T \setminus v\) は少なくとも \(1\) 個の頂点を持つので、\(T \setminus v\) は連結だと分かる。\(T\setminus v\) は森でもあったから、\(T\setminus v\) は木である。□
定理 5.3.3 は逆も成り立つ:
\(G\) を多重グラフとする。「\(\deg v = 1\)」と「\(G \setminus v\) が木」を満たす \(G\) の頂点 \(v\) が存在するなら、\(G\) は木である。ここで \(G \setminus v\) は \(G\) から頂点 \(v\) と \(v\) を含む全ての辺を除去して得られる多重グラフを表す。
読者に任せる。\(G\) が閉路を持つとき \(v\) を選べないことを示す部分が主な障害となる。□
頂点の個数に関する帰納法を使って木の様々な性質を示すとき定理 5.3.3 は有用となる: 帰納ステップにおいて、適当な葉 \(v\) を除去したグラフ \(T\setminus v\) に帰納法の仮定を適用できる。
次の練習問題は本質的に定理 5.3.2 (a) の一般化である:
\(T\) を木、\(w\) を \(T\) の任意の頂点とする。\(T\) は \(\deg w\) 個以上の葉を持つことを示せ。
多重グラフ \(G\) の支配集合 (dominating set) は、台単純グラフ \(G^{\operatorname{simp}}\) の支配集合と定義される。
\(G\) が森のとき、次の等式を示せ:
\(T\) を少なくとも一つの頂点を持つ木、\(L\) を \(T\) の葉全体の集合とする。\(\left\vert L\right\vert -1\) 個の辺を新しく \(T\) に追加することで、ハミルトン閉路を持つ多重グラフに \(T\) を変形できることを示せ。