5.14. 行列木定理

5.14.1導入

前節の議論から、多重グラフの全域木を数える問題は多重有向グラフで (任意の頂点を終点とする) 全域有向木を数える問題の特殊ケースだと分かった。どちらの問題なら解けるだろうか？ 簡単な例から議論を始めよう:

例 5.14.1

完全グラフ \(K_{1}\) には全域木が \(1\) 個しか存在しない:

完全グラフ \(K_{2}\) にも全域木が \(1\) 個しか存在しない:

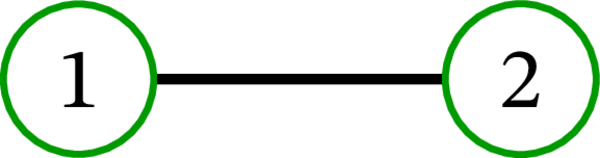
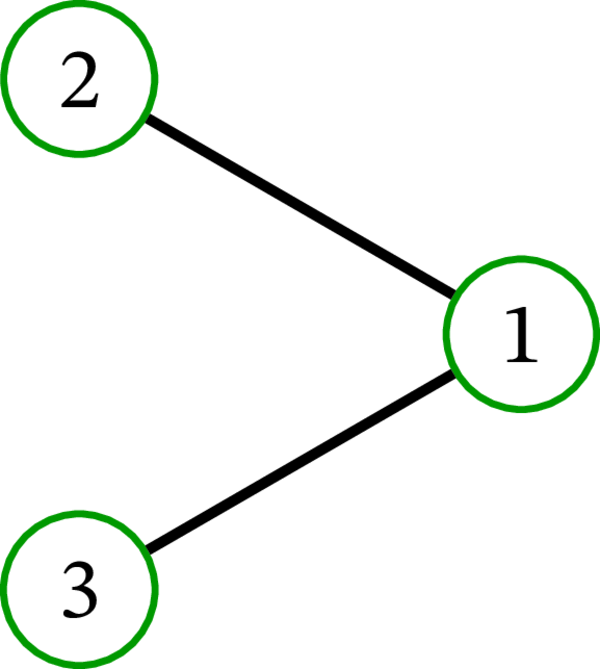
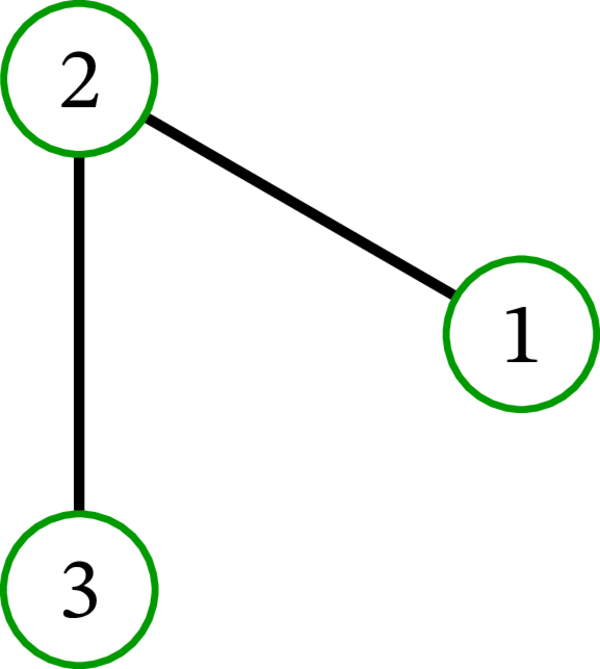
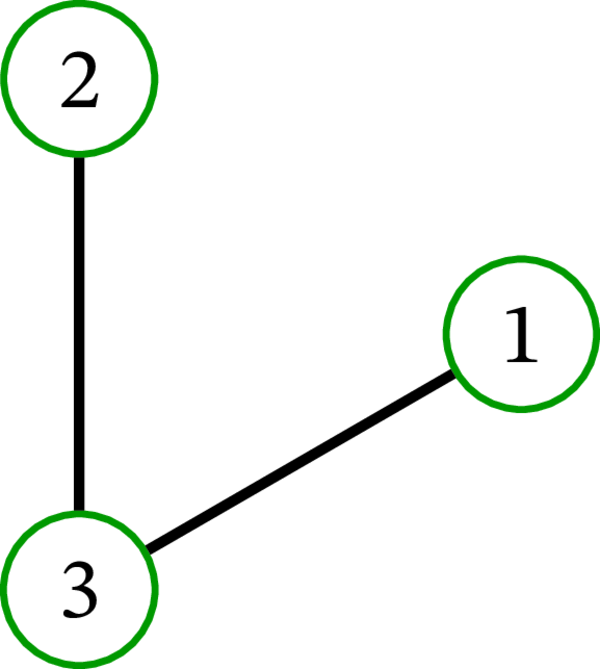
完全グラフ \(K_{3}\) には \(3\) 個の全域木が存在する:

[これらのグラフは同型であるものの、グラフとしては異なる。]

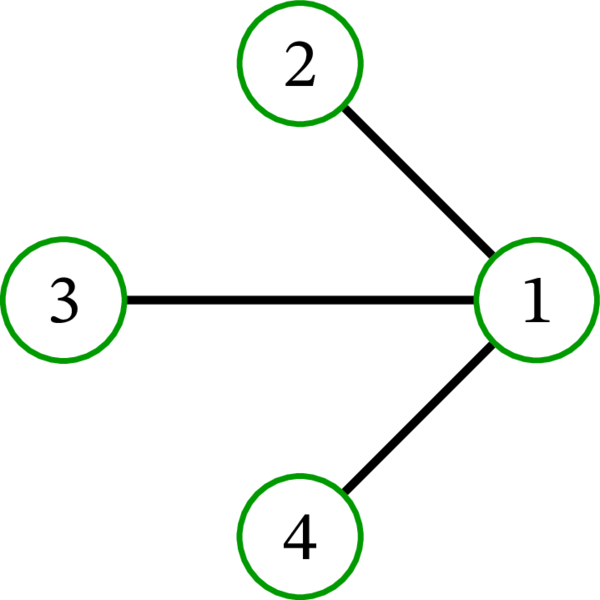
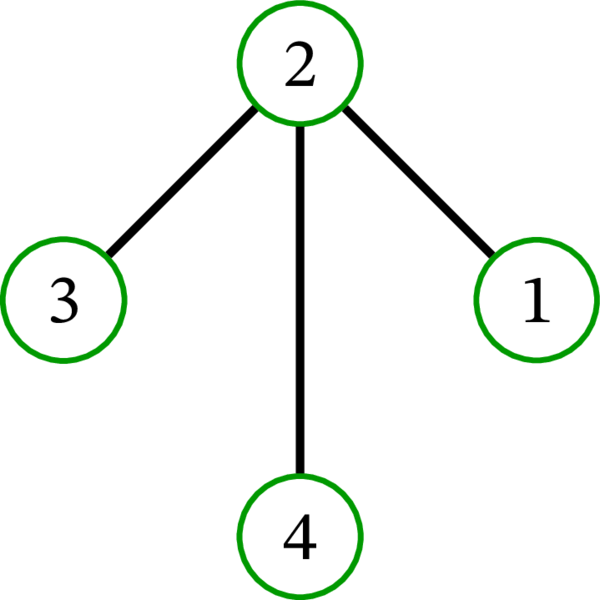
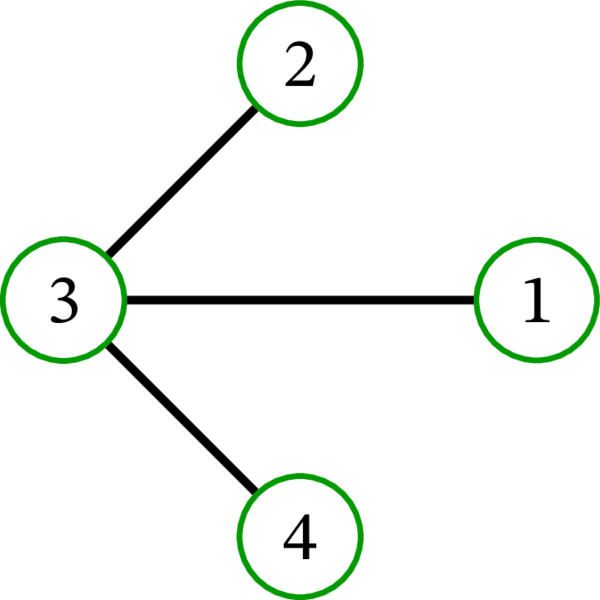
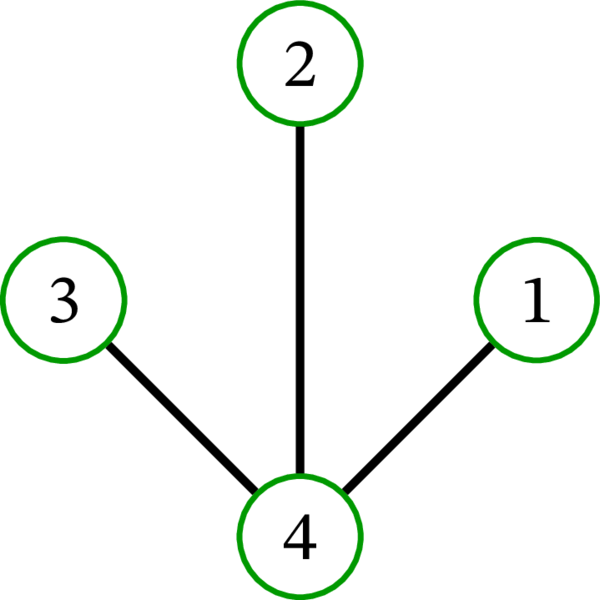
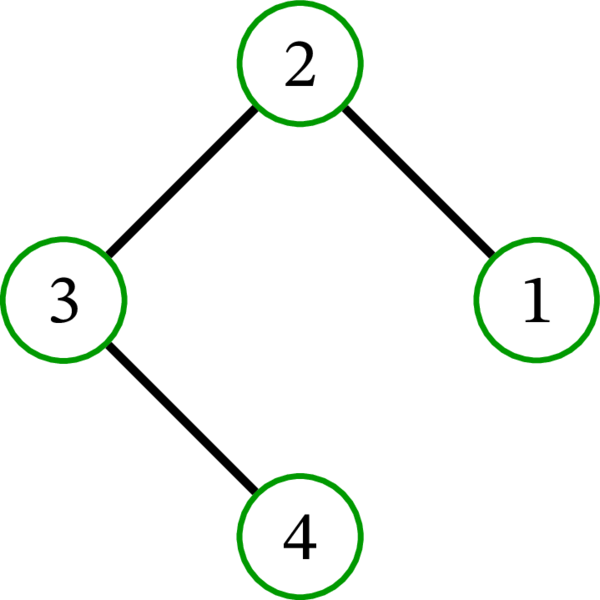
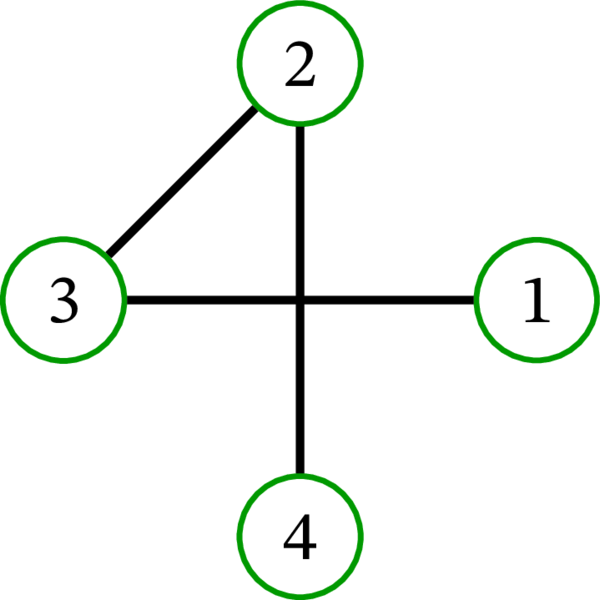
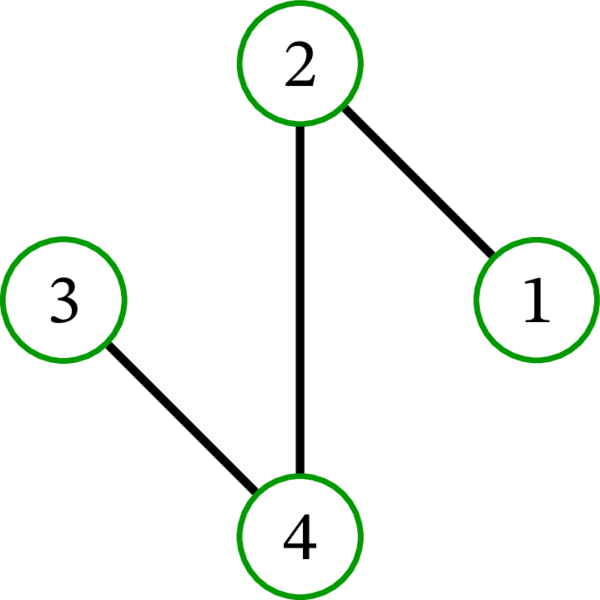
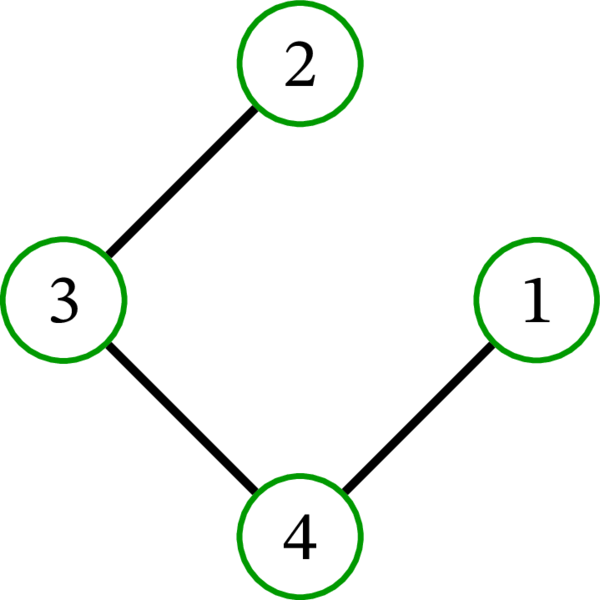
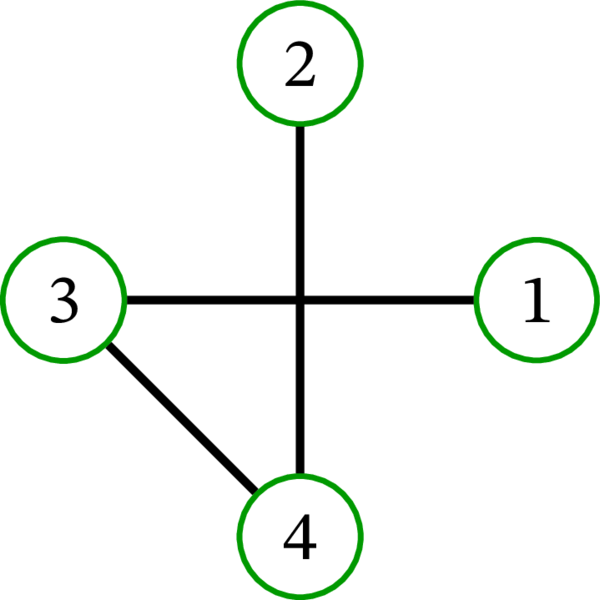
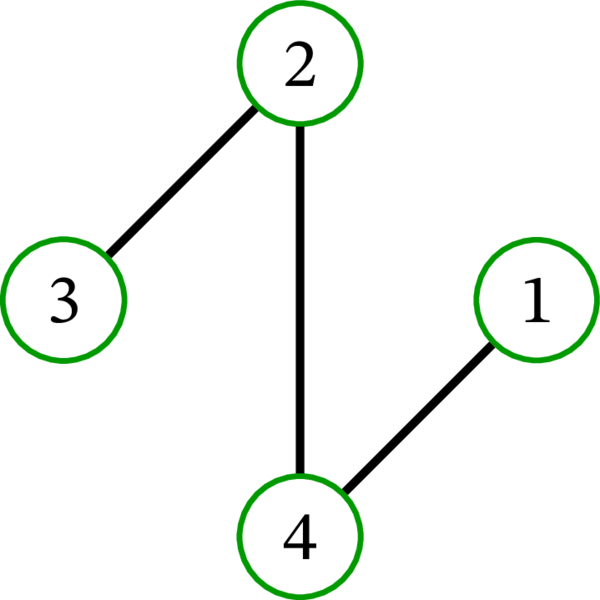
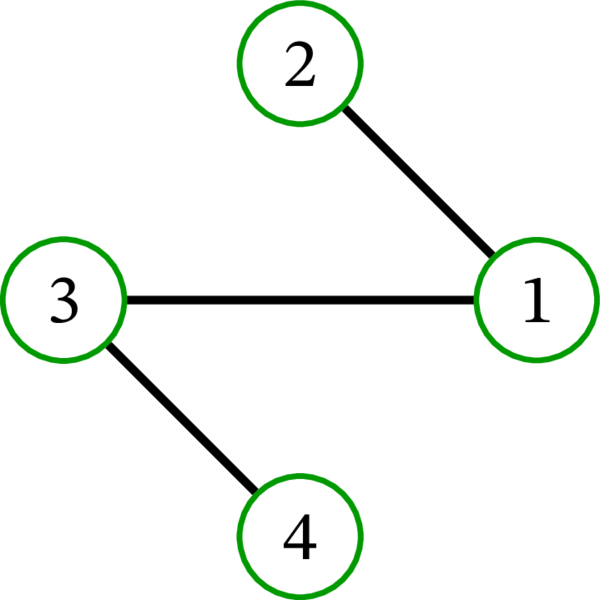
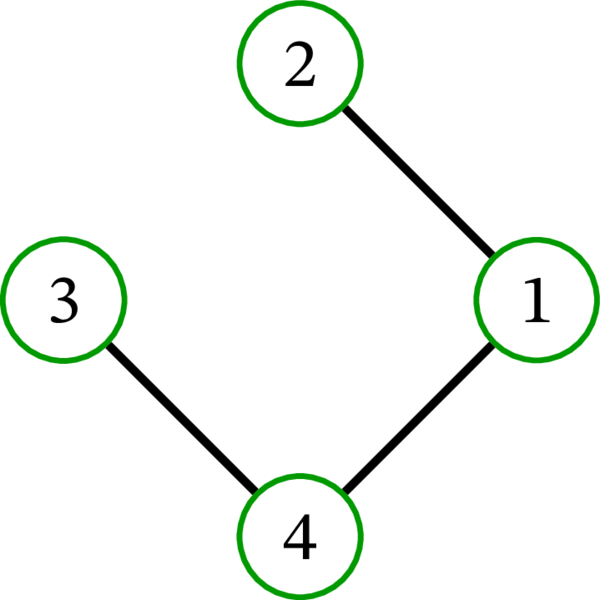
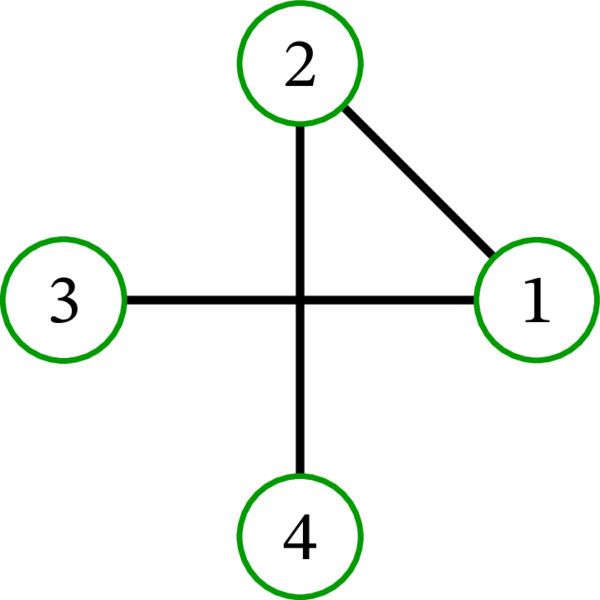
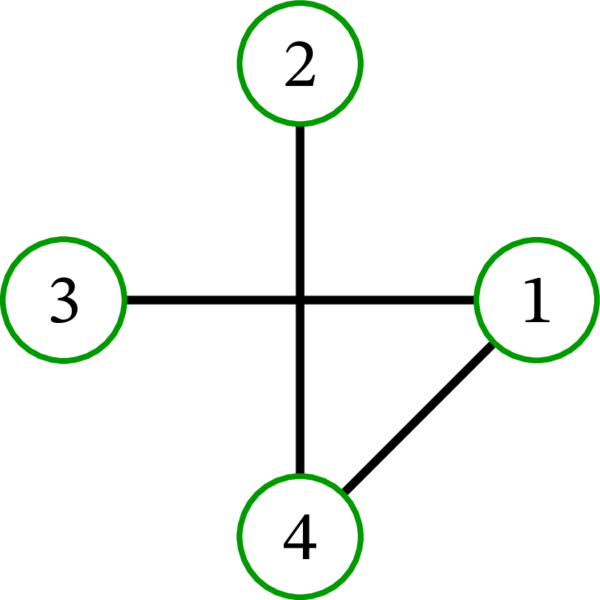
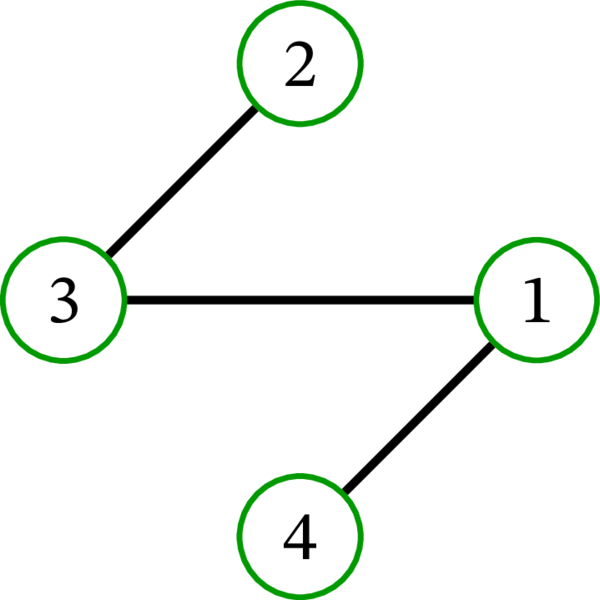
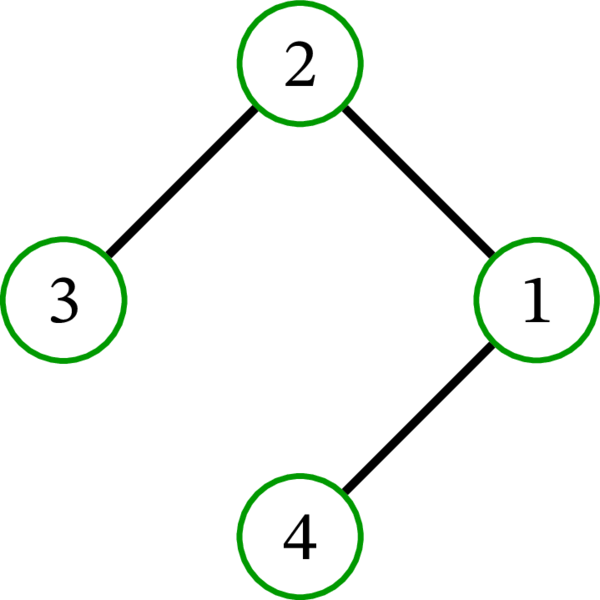
完全グラフ \(K_{4}\) には \(16\) 個の全域木が存在する:

[同型なグラフを同一視すると、全域木は二種類しかない。]

この例から、完全グラフ \(K_{n}\) の全域木の個数が \(n^{n-2}\) であることが示唆される。

この予想は正しく、後で証明もする。しかしまずは、任意の有向グラフ \(D\) が持つ全域有向木の個数を数える一般的な問題を考える。

5.14.2記法

最初に記法を導入する:

例えば \(\left[ K_{2}\text{ は木}\right] =1\) や \(\left[ K_{3}\text{ は木}\right] =0\) が成り立つ。

例えば次の等式が成り立つ:

5.14.3多重有向グラフのラプラシアン

次の定義は (ほぼ) 任意の多重有向グラフに行列を割り当てる:

例 5.14.5

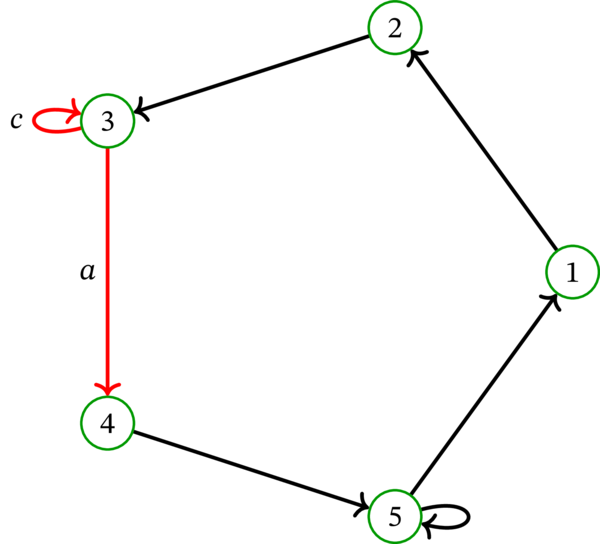
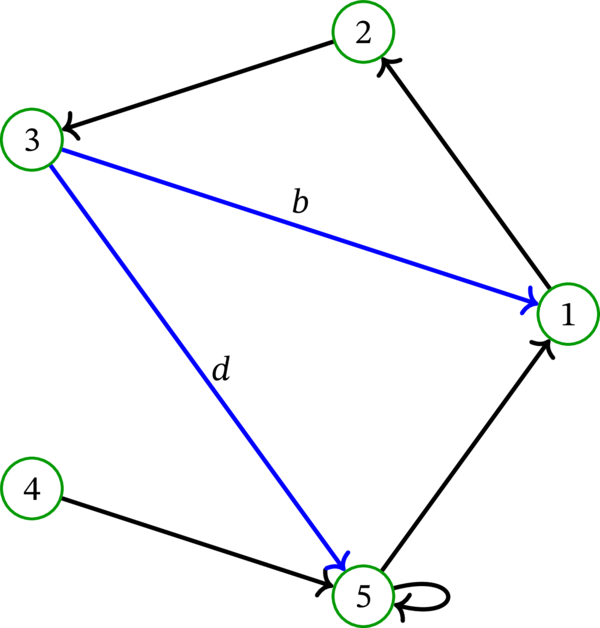
\(D\) を次の有向グラフとする:

\(D\) のラプラシアンは次の行列である:

\[ \left( \begin{array}{ccc} 2-1 & -1 & -0\\ -0 & 1-0 & -1\\ -0 & -0 & 1-1 \end{array} \right) =\left( \begin{array}{ccc} 1 & -1 & 0\\ 0 & 1 & -1\\ 0 & 0 & 0 \end{array} \right) \]

この例から分かる事実の一つとして、ループはラプラシアン \(L\) に影響しない。実際、始点 \(i\) と終点 \(i\) を持つループがあると \(\deg^{+}i\) と \(a_{i,i}\) の両方が \(1\) だけ増加するものの、二つの増加はラプラシアンの定義式で打ち消される。

ラプラシアンの簡単な性質を示す:

[証明] \(L\) の列を全て足すと零ベクトルとなる。実際、任意の \(i \in V\) で次の等式が成り立つ:

言い換えれば、ベクトル \(e\colonequals \left( 1,1,\ldots,1\right) ^{T}\) に対して \(Le=0\) が成り立つ。よって、このベクトル \(e\) は \(L\) の核 (零空間) に属する。つまり \(L\) は非正則である。□

[\(n\) が正である事実が使われていることに注意せよ！ \(0\) 要素のベクトルは必ず零ベクトルなので、\(n=0\) なら \(e\) は零ベクトルとなる。]

5.14.4行列木定理: 主張

命題 5.14.6 によれば、有向グラフのラプラシアンの行列式に興味深い点は無い。しかし行列式が \(0\) でも、\(0\) でない最大の小行列式 (最も大きな部分行列の行列式) が何らかの情報を持っている場合がよくある。この値は行列が持つ 「\(0\) でない行列式」に最も近い値と言える。ラプラシアンの場合には、この値が全域有向木の個数と関係する:

この定理に関する話題の前に、次の点を指摘しておく:

• 行列式 \(\det\left( L_{\sim r,\sim r}\right) \) は \(L\) の余因子行列の第 \((r,r)\) 要素である。

• \(V=\left\{ 1,2,\ldots,n\right\} \) という仮定は典型的な「一般性を失わない」仮定である: 任意の有向グラフ \(D\) を考える場合でも、頂点の名前を \(1,2,\ldots,n\) に変更すれば仮定は満たされる。このため、定理 5.14.7 は任意の有向グラフが持つ全域有向木の個数を数えるのに利用できる。行列の添え字に自然数ではなく任意の有限集合の要素を使う¹と定めれば、\(V=\left\{ 1,2,\ldots,n\right\} \) という仮定を除去することもできる。

5.14.5応用: \(K_n\) の全域木の数え上げ

行列木定理 (定理 5.14.7) を使って \(K_{n}\) の全域木を数えてみよう。この議論を理解しておけば、行列木定理の証明もいくらか理解しやすくなるはずである。

正整数 \(n\) を固定し、多重有向グラフ \(K_{n}^{\operatorname*{bidir}}\) のラプラシアンを \(L\) とする (\(K_{n}\) は以前と同様に集合 \(\left\{ 1,2,\ldots,n\right\} \) 上の完全グラフを表す)。このとき \(K_{n}^{\operatorname*{bidir}}\) の各頂点は \(n-1\) の出次数を持つので、次の等式が成り立つ:

[これは対角成分が \(n-1\) で、非対角成分が \(-1\) である \(n \times n\) 行列である。] 命題 5.13.1 (b) を \(G=K_{n}, r=1\) として適用すると、 \(\left\{ 1 \text{ を終根とする } K_{n}^{\operatorname*{bidir}} \text{ の全域有向木}\right\} \) と \(\left\{ K_{n} \text{ の全域木}\right\} \) の間に全単射が存在すると分かる。よって bijection principle より次の等式が分かる:

この行列式はどうすれば計算できるだろうか？ 次に三つの方法を示す:

• 最も初等的なアプローチは行変形を使うものである:

  \[ \begin{aligned} \small & \det\left( \begin{array}{cccc} n-1 & -1 & \cdots & -1\\ -1 & n-1 & \cdots & -1\\ \vdots & \vdots & \ddots & \vdots\\ -1 & -1 & \cdots & n-1 \end{array} \right) \\[30pt] &\quad =\det\left( \begin{array}{cccccc} n-1 & -1 & -1 & -1 & \cdots & -1\\ -n & n & 0 & 0 & \cdots & 0\\ -n & 0 & n & 0 & \cdots & 0\\ -n & 0 & 0 & n & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ -n & 0 & 0 & 0 & \cdots & n \end{array} \right) \quad \left( \begin{array}{c} \text{第 } 1 \text{ 行の} -1 \text{ 倍を}\\ \text{それ以外の行に足した } \end{array} \right) \\[40pt] &\quad =n^{n-2}\det\left( \begin{array}{cccccc} n-1 & -1 & -1 & -1 & \cdots & -1\\ -1 & 1 & 0 & 0 & \cdots & 0\\ -1 & 0 & 1 & 0 & \cdots & 0\\ -1 & 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ -1 & 0 & 0 & 0 & \cdots & 1 \end{array} \right) \quad \left( \begin{array}{c} \text{第 } 1 \text{ 行以外の行を}\\ n \text{ で割った} \end{array} \right) \\[40pt] & \quad =n^{n-2}\underbrace{\det\left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & \cdots & 0\\ -1 & 1 & 0 & 0 & \cdots & 0\\ -1 & 0 & 1 & 0 & \cdots & 0\\ -1 & 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ -1 & 0 & 0 & 0 & \cdots & 1 \end{array} \right) }_{\substack{\scriptsize =1\\[2pt] \scriptsize (\because\ \text{対角成分が } 1,1,\ldots,1 \text{ の三角行列であるため})}} \quad\left( \begin{array}{c} \text{第 } 1 \text{ 行以外の行を} \\ \text{第 } 1 \text{ 行に足した} \end{array} \right) \\[60pt] & \qquad =n^{n-2} \end{aligned} \]

• いわゆる行列式補題 (matrix determinant lemma) より、任意の \(m \times m\) 行列 \(A\in\mathbb{R}^{m\times m}\) と任意の列ベクトル \(u\in\mathbb{R}^{m\times1}\) と任意の行ベクトル \(v\in\mathbb{R}^{1\times m}\) に対して次の等式が成り立つ:

  \[ \det\left( A+uv\right) =\det A+v\left( \operatorname*{adj}A\right) u \]

  この補題を使うと考えている行列式を簡単に計算できる。具体的には、次のように \(A\), \(u\), \(v\) を設定すればよい:

  \[ \begin{aligned} & \left( \begin{array}{cccc} n-1 & -1 & \cdots & -1\\ -1 & n-1 & \cdots & -1\\ \vdots & \vdots & \ddots & \vdots\\ -1 & -1 & \cdots & n-1 \end{array} \right) \\[27pt] & \quad =\underbrace{\left( \begin{array}{cccc} n & 0 & \cdots & 0\\ 0 & n & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & n \end{array}\right) }_{=\,A}+\underbrace{\left( \begin{array}{c} -1\\ -1\\ \vdots\\ -1 \end{array} \right) }_{=\,u} \underbrace{\left( \begin{array}{cccc} 1 & 1 & \cdots & 1 \end{array} \right) }_{=\,v} \end{aligned} \]

• 線形代数 (固有ベクトルと固有値²) を利用するアプローチもある:

  \(\left( e_{1},e_{2},\ldots,e_{n-1}\right) \) を \(\mathbb{R}\) ベクトル空間 \(\mathbb{R}^{n-1}\) の標準基底とする。 [つまり、\(i\) 番目の要素が \(1\) で他の要素は \(0\) の列ベクトルを \(e_{i}\) とする。] このとき、考えている \(\left( n-1\right) \times\left( n-1\right) \) 行列

  \[ \left( \begin{array}{cccc} n-1 & -1 & \cdots & -1\\ -1 & n-1 & \cdots & -1\\ \vdots & \vdots & \ddots & \vdots\\ -1 & -1 & \cdots & n-1 \end{array} \right) \]

  の \(n-1\) 個の固有ベクトルと固有値は次の通りである:

  • 各 \(i\in\left\{ 2,3,\ldots,n-1\right\} \) に対する \(n-2\) 個の列ベクトル \(e_{1}-e_{i}\);\(\ \,\)対応する固有値は \(n\) [確認せよ！]

  • 固有ベクトル \(e_{1}+e_{2}+\cdots+e_{n-1}\);\(\ \,\)対応する固有値は \(1\) [確認せよ！]

  \(n-1\) 個の固有ベクトルは線形独立 [確認せよ！] なので、\(\mathbb{R}^{n-1}\) の基底である。よって ([Treil17, Chapter 4] より) 考えている行列は \(\underbrace{n,n,\ldots,n}_{n-2\text{ 個}},1\) を対角成分に持つ対角行列と相似であり、その行列式は \(\underbrace{nn\cdots n}_{n-2\text{ 個}}1=n^{n-2}\) だと分かる。

計算方法は他にもある。どの方法を使うにしても、結果は \(n^{n-2}\) となる。以上で次の事実が (まだ証明していない行列木定理を利用して) 証明された:

次のように言い換えることもできる:

[証明] 頂点集合が \(\left\{ 1,2,\ldots,n\right\} \) の単純グラフが木なら、それは \(K_{n}\) の全域木でもある。よって定理 5.14.8 から従う。□

Cayley の公式 (定理 5.14.8) には他にも様々な証明が知られている。私が特に気に入っているのは [Galvin21, § 2.4 and § 2.5] にある組合せ論的な二通りの証明と、[Leinst19] に概略が示されている Joyal の証明である。数え上げ組合せ論に関する教科書には Cayley の公式の証明がいくつか示されることが多い。例えば [Stanle18, Appendix to Chapter 9] には三つの証明がある。最も優れた数学の証明を集めた Aigner と Ziegler による書籍 [AigZie18, Chapter 33] では Cayley の公式の証明が四つ紹介されている。なお、行列木定理を無向グラフに対する命題として定式化する文献もある。これは本書で示す (有向グラフに対する) 行列木定理の特殊ケースである³。

しかし、証明を完了させるには行列木定理を証明する必要がある。

5.14.6証明の準備

行列木定理を証明する準備として、簡単な補題 (グラフが有向木かどうかを判定する、さらにもう一つの基準) を最初に示す:

この補題は弧の向きを反転させた練習問題 5.16 (b) である。以下に完全な証明を示す。

[補題 5.14.10 の証明] \(D\) の頂点を任意に取って \(u\) とする。\(u\) を始点とする最も長い \(D\) の路⁴を \(\mathbf{p}=\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) とする。このとき \(v_{0} = u\) である。

これから \(v_{k} = r\) を背理法で示す。\(v_{k} \neq r\) と仮定する。このとき \(v_{k}\in V\setminus\left\{ r\right\} \) が成り立つから、補題の仮定より \(v_{k}\) の出次数は \(1\) だと分かる。よって \(v_{k}\) を始点とする弧 \(b\) が \(D\) に存在する。弧 \(b\) の終点を \(w\) とする。弧 \(b\) と頂点 \(w\) を路 \(\mathbf{p}\) の末尾に加えると、次の歩道 \(\mathbf{w}\) が得られる:

この歩道 \(\mathbf{w}\) は \(v_{0}= u\) を始点に持つ。命題 4.5.9 より、\(\mathbf{w}\) は路であるか、そうでなければ閉路を含む。\(D\) は閉路を持たないから、\(\mathbf{w}\) は路だと分かる。つまり \(\mathbf{w}\) は \(u\) を始点とする \(D\) の路である。\(\mathbf{w}\) の長さは \(\mathbf{p}\) の長さより (\(1\) だけ) 大きいので、\(\mathbf{p}\) は \(u\) を始点とする最も長い \(D\) の路ではない。これは \(\mathbf{p}\) の定義と矛盾する。

この矛盾から仮定が偽だと分かる。以上で \(v_{k}=r\) が証明できた。よって \(\mathbf{p}\) は \(u\) から \(r\) への路である (\(v_{0}=0\) および \(v_{k}=r\) のため)。つまり、有向グラフ \(D\) は \(u\) から \(r\) への路を持つ。

\(u\) を固定したことを忘れる。\(D\) の任意の頂点 \(u\) に対して、\(D\) が \(u\) から \(r\) への路を持つことが以上で証明できた。言い換えれば、\(r\) は \(D\) の終根である。さらに、補題の仮定より \(\deg^{+}r=0\) が成り立ち、全ての \(v\in V\setminus\left\{ r\right\} \) が \(\deg^{+}v=1\) を満たすので、有向木の同値性定理の双対 (定理 5.10.5) の命題 A'6 を \(D\) は満たす。よって \(D\) は命題 A'1 も満たす (命題 A'1, A'2, ..., A'6 が同値であるため)。つまり \(D\) は \(r\) を終根とする有向木である。これで補題 5.14.10 は証明された。□

5.14.7行列木定理: 証明

いよいよ行列木定理 (定理 5.14.7) を証明する。我々の戦略は次の通りである:

1. まず、任意の頂点 \(v\in V\setminus\left\{ r\right\} \) の出次数が \(1\) のケースを証明する。このケースでは、\(r\) を始点とする弧 (\(r\) を終根とする全域有向木と \(D_{\sim r,\sim r}\) に影響しない弧) を \(D\) から除去することで、「\(D\) 自体が有向木」と「\(D\) が閉路を持つ」の二つの場合に議論を帰着できる。

2. その後、命題を少しだけ一般化して、任意の頂点 \(v\in V\setminus\left\{ r\right\} \) の出次数が \(1\) 以下のケースを証明する。ある頂点 \(v\in V\setminus\left\{ r\right\} \) の出次数が \(0\) のとき行列木定理は自明なので、この証明は易しい。

3. 最後に、一般的な行列木定理を証明する。この証明は \(D\) が持つ弧の個数に関する強い数学的帰納法で行われる。出次数が \(1\) より大きい頂点 \(v\in V\setminus\left\{ r\right\} \) を (存在するなら) 任意に取り、その頂点を始点とする弧に赤または青の色を (両方の色が少なくとも一度は使われるように) 塗る。このとき、青く塗られた弧を除去して得られる \(D\) の部分有向グラフ \(D^{\operatorname*{red}}\) と、赤く塗られた弧を除去して得られる \(D\) の部分有向グラフ \(D^{\operatorname*{blue}}\) を考えることができる。\(D^{\operatorname*{red}}\) と \(D^{\operatorname*{blue}}\) は両方とも弧の個数が \(D\) より少ないので、帰納法の仮定を適用できる。都合の良いことに、\(r\) を終根とする全域有向木の個数と行列式 \(\det\left( L_{\sim r,\sim r}\right) \) は「加法的」となる (その意味は後述される)。

というわけで一つ目のステップから証明を始める。最初に示すのは非常に特殊なケースである:

[証明] (a): 補題 5.14.10 より有向グラフ \(D\) は \(r\) を終根とする有向木だと分かる。よって、\(D\) 自体が \(r\) を終根とする \(D\) の全域有向木である。

よって有向木の同値性定理の双対 (定理 5.10.5) の命題 A'2 より⁵ \(\left\vert A\right\vert =\left\vert V\right\vert -1\) が成り立つ。ここから \(D\) の他に \(D\) の全域有向木は存在しないと分かる (弧を一つでも除去すると \(\left\vert A\right\vert =\left\vert V\right\vert -1\) が成り立たなくなるため)。よって \(r\) を終根とする \(D\) の全域有向木は \(D\) のみである。これで補題 5.14.11 (a) は証明された。

(b): 一般性を失うことなく \(r=n\) と仮定する (そうでなければ、\(r\) と \(n\) を交換して \(L_{\sim r,\sim r}\) ではなく \(L_{\sim n,\sim n}\) を考える)。

\(D\) の各頂点にループを一つ追加した多重有向グラフを \(D^{\prime}\) とする ── つまり、\(D\) に弧 \(\ell_{1},\ell _{2},\ldots,\ell_{n}\) (各 \(\ell_{i}\) は始点 \(i\) と終点 \(i\) を持つ) を加えた多重有向グラフを \(D^{\prime}\) とする。

次の集合の置換が構成する群を \(S_{n-1}\) とする:

\(r=n\) より、次の等式が成り立つ:

[行列式に対する Leibniz の公式を使った。] 最右辺の和で足されている項に注目し、積 \(\displaystyle \prod_{i=1}^{n-1}L_{i,\sigma\left( i\right) }\) が \(\sigma=\operatorname*{id}\) の場合を除いて \(0\) だと示す。

ある置換 \(\sigma\in S_{n-1}\) で \(\displaystyle \prod_{i=1}^{n-1}L_{i,\sigma\left( i\right) } \neq 0\) と仮定する。これから \(\sigma=\operatorname*{id}\) を示す。

任意に \(v\in\left\{ 1,2,\ldots,n-1\right\} \) を取る。このとき \(\displaystyle \prod_{i=1}^{n-1}L_{i,\sigma\left( i\right) } \neq 0\) より \(L_{v,\sigma\left( v\right) }\neq0\) が分かる。一方で \(L\) の定義からは \(L_{v,\sigma \left( v\right) }=\left( \deg^{+}v\right) \cdot\left[ v=\sigma\left( v\right) \right] -a_{v,\sigma\left( v\right) }\) を得る。よって次の等式が成り立つ:

つまり \(\left[ v=\sigma\left( v\right) \right] \) と \(a_{v,\sigma\left( v\right) }\) の少なくとも一方は \(0\) でない。それぞれ言い換えれば、「\(v=\sigma\left( v\right) \)」と「始点 \(v\) と終点 \(\sigma\left( v\right) \) を持つ弧が有向グラフ \(D\) に存在する」の少なくとも一方が成り立つ。いずれにせよ、有向グラフ \(D^{\prime}\) には始点 \(v\) と終点 \(\sigma\left( v\right)\) を持つ弧が存在する (\(v=\sigma\left( v\right) \) の場合には追加したループが条件を満たす)。\(v\) を \(\sigma\left( v\right) \) に置き換えて同様の議論をすれば、始点 \(\sigma\left( v\right) \) と終点 \(\sigma\left( \sigma\left( v\right) \right) \) を持つ弧が \(D^{\prime}\) に存在すると分かる。同様に始点 \(\sigma\left( \sigma\left( v\right) \right) \) と終点 \(\sigma\left( \sigma\left( \sigma\left( v\right) \right) \right) \) を持つ弧も \(D^{\prime}\) に存在する。この議論はどこまでも続けることができ、\(n\) 回続けると次に示す \(D^{\prime}\) における歩道 \(\mathbf{w}\) が得られる:

アスタリスクは何らかの弧を表す (以降で参照しないので名前を付けていない)。\(D^{\prime}\) は \(n\) 個の頂点を持つのに対して \(\mathbf{w}\) は \(n+1\) 個の頂点を持つので、\(\mathbf{w}\) は路でない。よって命題 4.5.9 より歩道 \(\mathbf{w}\) は閉路を持つ。\(D\) は閉路を持たないので、\(D^{\prime}\) の閉路はループだけからなる。特に、\(\mathbf{w}\) に含まれる閉路の最初の弧はループである。言い換えれば、ある \(i\in\left\{ 0,1,\ldots,n-1\right\} \) で \(\sigma ^{i}\left( v\right) =\sigma^{i+1}\left( v\right) \) が成り立つ。\(\sigma\) は単射だから、この等式の両辺に \(\sigma^{-i}\) を適用できる。\(\sigma^{-i}\) を適用すると \(v=\sigma \left( v\right) \) つまり \(\sigma\left( v\right) =v\) を得る。

\(v\) を固定したことを忘れる。任意の \(v\in\left\{ 1,2,\ldots,n-1\right\} \) で \(\sigma\left( v\right) =v\) となることが以上で証明できた。言い換えれば \(\sigma=\operatorname*{id}\) である。

\(\sigma\) を固定したことを忘れる。積 \(\displaystyle \prod_{i=1}^{n-1}L_{i,\sigma\left( i\right) }\) が \(0\) でない任意の置換 \(\sigma\in S_{n-1}\) は \(\sigma =\operatorname*{id}\) を満たすことが以上で証明できた。言い換えれば、積 \(\displaystyle \prod_{i=1}^{n-1}L_{i,\sigma\left( i\right) }\) が \(0\) でない置換 \(\sigma\in S_{n-1}\) は \(\operatorname*{id}\) のみである。

よって式 \((1)\) の最右辺の和で足されている項の中で \(0\) でないのは \(\sigma =\operatorname*{id}\) に対応する項だけと分かる。そのため式 \((1)\) は次のように単純化できる:

任意の \(i\in\left\{ 1,2,\ldots,n-1\right\} \) に対して、\(L_{i,\operatorname*{id}\left( i\right)}\) は次のように変形できる:

これを使えば \(\displaystyle \det\left( L_{\sim n,\sim n}\right) =\prod _{i=1}^{n-1}1=1\) が分かる。以上で 補題 5.14.11 (b) は証明された。□

続いて「\(D\) は閉路を持たない」の条件を落とす:

[証明] まず、\(r\) を終根とする \(D\) の全域有向木に始点が \(r\) の弧は含まれない (有向木の同値性定理の双対 (定理 5.10.5) の命題 A'6 より \(r\) を終根とする任意の有向木は \(\deg^{+}r = 0\) を満たす)。さらに、始点が \(r\) の弧はラプラシアン \(L\) において第 \(r\) 行だけに影響するので、そのような弧は行列 \(L_{\sim r,\sim r}\) (\(L\) の第 \(r\) 行と第 \(r\) 列を除去した行列) に影響しない。

つまり、行列木定理が注目する「\(r\) を終根とする \(D\) の全域有向木の個数」と「\(\det\left( L_{\sim r,\sim r}\right)\)」は始点が \(r\) の弧を \(D\) から除去しても変化しない。よって一般性を失うことなく \(D\) は始点が \(r\) の弧を持たないと仮定する (そうでなければ、そのような弧を除去する)。

さらに、一般性を失うことなく \(r=n\) と仮定する (そうでなければ、\(r\) と \(n\) を交換して \(L_{\sim r,\sim r}\) の代わりに \(L_{\sim n,\sim n}\) を考える)。

続いて、次の二つの場合を分けて考える:

• Case 1: 有向グラフ \(D\) が閉路を持つ。

• Case 2: 有向グラフ \(D\) が閉路を持たない。

Case 1 を考える。\(D\) が持つ閉路を閉路 \(\mathbf{v}=\left( v_{1},\ast,v_{2},\ast,\ldots,\ast,v_{m}\right) \) とする (アスタリスクは何らかの弧を表す)。\(D\) は始点が \(r\) の弧を持たないので、\(\mathbf{v}\) は \(r\) を含まない。つまり頂点 \(v_{1},v_{2},\ldots,v_{m}\) は全て \(V\setminus\left\{ r\right\} \) に属する。よって任意の \(i\in\left\{ 1,2,\ldots,m-1\right\} \) に対して \(v_{i}\) の出次数は \(1\) である (補題の仮定より任意の頂点 \(v\in V\setminus\left\{ r\right\} \) の出次数は \(1\) であるため)。ここから、任意の \(i\in\left\{ 1,2,\ldots,m-1\right\} \) に対して \(v_{i}\) を始点に持つ \(D\) の弧は \(\mathbf{v}\) に含まれる弧だけだと分かる。従って、行列 \(L\) の第 \(v_{i}\) 行は (\(\deg^{+}\left( v_{i}\right) =1\) より) 第 \(v_{i}\) 要素に \(1\) を持ち、(一つ前の文より) 第 \(v_{i+1}\) 要素に \(-1\) を持ち、他の要素は全て \(0\) である。\(r = n\) だから、同じことは行列 \(L_{\sim r,\sim r}\) に対しても言える。つまり、\(L_{\sim r,\sim r}\) の第 \(v_{i}\) 行は第 \(v_{i}\) 要素に \(1\) を持ち、\(v_{i+1}\) 要素に \(-1\) を持ち、他の要素は全て \(0\) である。よって \(L_{\sim r,\sim r}\) の第 \(v_{1}\) 行、第 \(v_{2}\) 行、…、第 \(v_{n}\) 行を全て足すと \(1\) と \(-1\) が打ち消し合って零ベクトルとなる⁶⁷。

和が零ベクトルであるような \(L_{\sim r,\sim r}\) の行の非空集合が見つかったので、\(L_{\sim r,\sim r}\) は非正則である (行列式の基礎的な性質より⁸)。よって \(\det\left( L_{\sim r,\sim r}\right) =0\) が分かる。一方、有向グラフ \(D\) は全域有向木を持たない (\(D\) の全域有向木を得るには閉路 \(\mathbf{v}\) に含まれる弧を除去しなければならないが、除去する弧の始点は出次数が \(0\) となり、その頂点から \(r\) への路が存在しなくなる)。言い換えれば、次の等式が成り立つ:

この等式と \(\det\left( L_{\sim r,\sim r}\right) =0\) より、Case 1 で行列木定理が成り立つと分かる。

次に Case 2 を考える。\(D\) が閉路を持たないので、補題 5.14.11 (b) より \(\det\left( L_{\sim r,\sim r}\right) =1\) を得る。さらに補題 5.14.11 (a) からは次の等式が分かる:

よって Case 2 でも行列木定理は成り立つ。

以上で補題 5.14.12 は証明された。□

続いて、少しだけ一般的なケースに足を踏み入れる:

[証明] もし全ての頂点の出次数が \(1\) なら、補題 5.14.12 から行列木定理の成立が言える。よって出次数が \(1\) でない頂点 \(v\in V\setminus\left\{ r\right\} \) が存在すると一般性を失うことなく仮定する。補題の仮定より \(v\) の出次数は \(1\) 以下でもあるので、\(0\) だと分かる。つまり \(v\) を始点とする弧は存在しない。

一般性を失うことなく \(r=n\) と仮定する (そうでなければ \(r\) と \(n\) を交換する)。\(v \neq r\) であり、\(v\) を始点とする弧が存在しないので、有向グラフ \(D\) は \(v\) から \(r\) への路を持たない。

よって \(D\) は \(r\) を終根とする全域有向木を持たない。言い換えれば、次の等式が成り立つ:

さらに、\(v\) を始点とする弧が存在しないので行列 \(L_{\sim r,\sim r}\) の第 \(v\) 行は零ベクトルであり、 \(\det\left( L_{\sim r,\sim r}\right) =0\) が成り立つ。つまり現在の仮定の下で行列木定理は成立する。よって補題 5.14.13 は証明された。□

これで一般的な行列木定理を証明する準備が整った。

[定理 5.14.7 の証明] まず、記法を一つ定義する:

例えば

のとき、\(M\overset{2}{\equiv}N\) が成り立つ。また、次の等式が成り立つ:

行列式のよく知られた性質 (多重線形性) より、二つの \(n \times n\) 行列 \(M\), \(N\) が何らかの \(j\in\left\{ 1,2,\ldots,n\right\} \) で \(M\overset{j}{\equiv}N\) を満たすとき、次の等式が成り立つ:

これでようやく行列木定理の証明に取り掛かれる。\(D\) が持つ弧の個数に関する強い数学的帰納法で示す。

帰納ステップ: \(m\in\mathbb{N}\) を任意に取る。弧の個数が \(m\) 未満の任意の有向グラフで行列木定理が成り立つと (帰納法の仮定として) 仮定する。この仮定を使って、\(m\) 個の弧を持つ有向グラフ \(D\) に対する行列木定理をこれから示す。

一般性を失うことなく \(r=n\) と仮定する (そうでなければ \(r\) と \(n\) を交換する)。

もし全ての頂点 \(v\in V\setminus\left\{ r\right\} \) が \(1\) 以下の出次数を持つなら、補題 5.14.13 より行列木定理の成立が言える。よって、ある頂点 \(v\in V\setminus\left\{ r\right\} \) の出次数が \(2\) 以上だと一般性を失うことなく仮定する。\(v\) を始点とする弧に赤または青の色を塗ることを考える。このとき、赤に塗られる弧と青に塗られる弧が両方とも少なくとも一つは存在するように色を塗る (\(v\) の出次数が \(2\) 以上なので、これは可能である)。始点が \(v\) でない弧には色を塗らない。

\(D\) から青い弧を全て除去して得られる部分有向グラフを \(D^{\operatorname*{red}}\) とする。このとき \(D^{\operatorname*{red}}\) の弧の個数は \(D\) より少ない。言い換えれば、\(D^{\operatorname*{red}}\) の弧の個数は \(m\) 未満である。よって帰納法の仮定より \(D^{\operatorname*{red}}\) で行列木定理は成立する。言い換えれば、次の等式が成り立つ:

ここで \(L^{\operatorname*{red}}\) は \(D^{\operatorname*{red}}\) のラプラシアンを表す。

同様に、\(D\) から赤い辺を全て除去して得られる部分有向グラフを \(D^{\operatorname*{blue}}\) とする。このとき \(D^{\operatorname*{blue}}\) の弧の個数は \(D\) より少ない。言い換えれば、\(D^{\operatorname*{blue}}\) の弧の個数は \(m\) 未満である。よって帰納法の仮定より \(D^{\operatorname*{blue}}\) で行列木定理は成立する。言い換えれば、次の等式が成り立つ:

ここで \(L^{\operatorname*{blue}}\) は \(D^{\operatorname*{blue}}\) のラプラシアンを表す。

例 5.14.14

\(D\) を次の多重有向グラフとする:

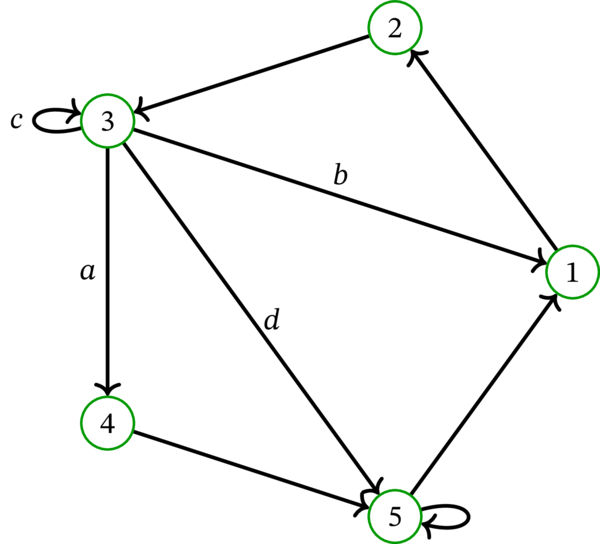
\(D\) は終根 \(1\) を持つ。\(D\) のラプラシアン \(L\) を次に示す:

\[ \small L=\left( \begin{array}{ccccc} 1 & -1 & 0 & 0 & 0\\ 0 & 1 & -1 & 0 & 0\\ -1 & 0 & 3 & -1 & -1\\ 0 & 0 & 0 & 1 & -1\\ -1 & 0 & 0 & 0 & 1 \end{array} \right) \]

出次数が \(2\) 以上の頂点 \(v\) として \(3\) を選択する。\(v=3\) を始点とする弧 \(a\), \(c\) を赤に、\(b\), \(d\) を青に塗ったとする。このときの \(D^{\operatorname*{red}}\) と \(D^{\operatorname*{blue}}\) (および \(L^{\operatorname*{red}}\) と \(L^{\operatorname*{blue}}\)) を次に示す:

\(\small D^{\operatorname*{red}}\) =

\[ \small L^{\operatorname*{red}}=\left( \begin{array}{ccccc} 1 & -1 & 0 & 0 & 0\\ 0 & 1 & -1 & 0 & 0\\ 0 & 0 & 1 & -1 & 0\\ 0 & 0 & 0 & 1 & -1\\ -1 & 0 & 0 & 0 & 1 \end{array} \right) \]

\(\small D^{\operatorname*{blue}}\) =

\[ \small L^{\operatorname*{blue}}=\left( \begin{array}{ccccc} 1 & -1 & 0 & 0 & 0\\ 0 & 1 & -1 & 0 & 0\\ -1 & 0 & 2 & 0 & -1\\ 0 & 0 & 0 & 1 & -1\\ -1 & 0 & 0 & 0 & 1 \end{array} \right) \]

有向グラフ \(D\), \(D^{\operatorname*{red}}\), \(D^{\operatorname*{blue}}\) は \(v\) を始点とする弧でのみ異なり、\(D\) が持つ \(v\) を始点とする各弧は \(D^{\operatorname*{red}}\) と \(D^{\operatorname*{blue}}\) のちょうど一方にだけ属する。よってラプラシアンの定義から次の等式が分かる:

\(r=n\) と \(v \neq r\) より、行列 \(L\) の第 \(r\) 行と第 \(r\) 列を除去しても第 \(v\) 行は第 \(v\) 行のままとなる。よって次の等式も成り立つ:

これと行列式の多重線形性を使えば、\(\det \left(L_{\sim r,\sim r}\right)\) を次のように変形できる:

一方、同様の等式は全域有向木の個数についても成り立つ。つまり、次の等式が成立する:

その理由は次の通りである: \(v\in V\setminus\left\{ r\right\} \) なので、有向木の同値性定理の双対 (定理 5.10.5) の命題 A'6 より、\(r\) を終根とする有向木では \(\deg ^{+}v=1\) が成り立つ。言い換えれば、\(r\) を終根とする有向木は始点が \(v\) の弧をちょうど一つ含む。よって特に、\(r\) を終根とする \(D\) の全域有向木が青い辺と赤い辺の両方を含むことはない。赤い辺を含む \(D\) の全域有向木は \(D^{\operatorname*{red}}\) の全域有向木であり、青い辺を含む \(D\) の全域有向木は \(D^{\operatorname*{blue}}\) の全域有向木である。また、\(D^{\operatorname*{red}}\) の全域有向木と \(D^{\operatorname*{red}}\) の全域有向木はどちらも \(D\) の全域有向木である。よって先ほど示した \(\det\left( L_{\sim r,\sim r}\right) =\det\left( L_{\sim r,\sim r}^{\operatorname*{red}}\right) +\det\left( L_{\sim r,\sim r}^{\operatorname*{blue}}\right) \) と合わせれば

を得る。つまり、今考えている有向グラフ \(D\) と頂点 \(r\) に対して行列木定理は成り立つ。これで帰納ステップが完了したので、行列木定理 (定理 5.14.7) は証明された。□

ここに示した定理 5.14.7 の証明は [Stanle18, Theorem 10.4] を参考にしている。他の文献を当たれば異なる証明を見つけられる: 例えば [VanEhr51, Theorem 7], [Margol10, Theorem 2.8], [DeLeen19, Theorem 1], [Holzer22, Theorem 2.5.3] などがある。 [より一般的な行列木定理が証明されている場合もある。紛らわしいことに、記法や仮定は文献によって微妙に異なる。しかし、たいていの場合は少し考えれば証明されている命題が本書の行列木定理と同値なことがすぐに分かる。]

5.14.8ラプラシアンに関する練習問題

次の二つの練習問題は chip-firing と呼ばれるゲーム、および chip-firing に関連する有向グラフ上の動的システムに関する理論の入門である (さらに詳しくは [CorPer18], [Klivan19], [JoyMel17] を参照してほしい)。ラプラシアンという言葉は直接登場しないものの、寄付の定義にラプラシアンが隠れている [どこに？]。

練習問題 5.19

\(D=\left( V,A,\psi\right) \) を強連結な多重有向グラフとする。

\(D\) 上の資産配分 (wealth distribution) とは、整数族 \(\left( k_{v}\right) _{v\in V}\) (各頂点に対する整数の割り当て) を意味する。\(k=\left( k_{v}\right) _{v\in V}\) が資産配分のとき、それぞれの値 \(k_{v}\) を頂点 \(v\) の資産 (wealth) と呼び、\(k\) の総資産 (total wealth) を和 \(\displaystyle \sum_{v\in V} k_{v}\) と定義する。資産配分 \(k=\left( k_{v}\right) _{v\in V}\) において頂点 \(v\) が借金を持つ (in debt) とは、\(v\) の資産 \(k_{v}\) が負であることを言う。

\(D\) の任意の頂点 \(v\), \(w\) に対して、始点 \(v\) と終点 \(w\) を持つ弧の個数を \(a_{v,w}\) と表記する。

頂点 \(v \in V\) による寄付 (donation) を、資産配分を改変する次の操作として定義する: 頂点 \(v\) の資産を出次数 \(\deg^{+}v\) だけ減少させ、加えて全ての頂点 \(w \in V\) (\(v\) 自身を含む) の資産を \(a_{v,w}\) だけ増加させる。 [始点が \(v\) の弧を通じて \(v\) が隣接頂点に資産を一単位ずつ渡す操作が寄付だと考えることができる。なお、寄付によって総資産は変化しない。]

総資産が \(\left\vert A\right\vert -\left\vert V\right\vert \) より大きい \(D\) 上の任意の資産配分を \(k\) とする。適切に選択された有限回の寄付を \(k\) に施すことで、借金を持つ頂点が存在しないようにできると示せ。

[例: 次の有向グラフを \(D\) とする:

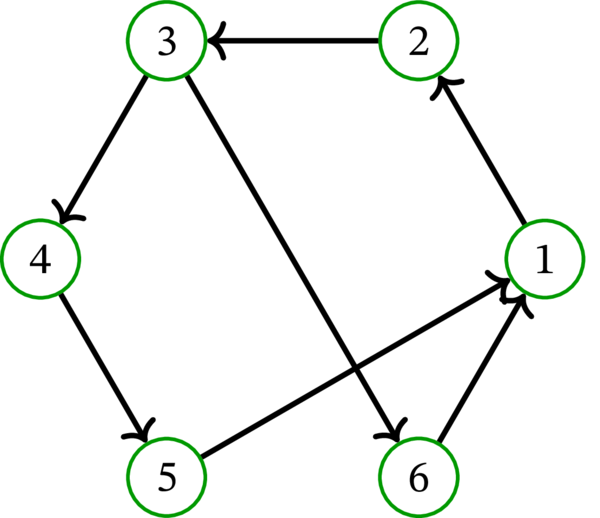
このとき \(\left( k_{1},k_{2},k_{3},k_{4},k_{5},k_{6}\right) =\left( -1,-1,1,2,0,1\right) \) は \(D\) 上の資産配分である。頂点 \(1\) と \(2\) は借金を持つものの、頂点 \(4,5,6,1\) がこの順番で寄付を行えば借金を持つ頂点が存在しなくなる (ただし容易に分かるように、寄付の順番は重要でない⁹)。]

[一つの頂点が寄付を複数回行っても構わないことに注意してほしい (上の例では複数回の寄付は必要なかった)。]

[ヒント: 資産分与 \(k\) において頂点 \(v\) が \(k_{v}\geq\deg^{+}v\) を満たすとき、\(v\) による寄付 (\(v\) が資産を失う寄付) を安全 (safe) と呼ぶことにする。まず、総資産が \(\left\vert A\right\vert -\left\vert V\right\vert \) より大きいなら、ある頂点 \(v\) で資産が \(\deg^{+}v\) 以上となる (つまり安全な寄付ができる) ことを示す。次に、資産配分 \(k\) に対して安全な寄付を有限回施すことで得られる資産配分が有限個しか存在しないことを示す。最後に、任意の頂点 \(v\) に対して定義される、\(v\) 以外の頂点が寄付を行ったときに増加する何らかの値を見つける。ここから、安全な寄付を十分に多い回数行うと全ての頂点が寄付する側になると結論付ける。安全な寄付で資産を失う頂点はその寄付の直前に借金を持たず、その後も借金を持たない。]

練習問題 5.20

練習問題 5.19 の設定と用語をここでも用いる。

頂点 \(v\in V\) による徴収 (clawback) を、資産配分を改変する次の操作として定義する: 頂点 \(v\) の資産を出次数 \(\deg^{+}v\) だけ増加させ、全ての頂点 \(w \in V\) (\(v\) 自身を含む) の資産を \(a_{v,w}\) だけ減少させる。 [徴収は寄付の逆である。]

総資産が \(\left\vert A\right\vert -\left\vert V\right\vert \) より大きい \(D\) 上の資産配分を \(k\) とする。適切に選択された有限回の徴収を \(k\) に施すことで、借金を持つ頂点が存在しないようにできると示せ。

[Remark: \(D\) が強連結だと仮定されていることに注意してほしい。この仮定がないと、示すべき命題は真にならない。例えば、次のグラフを \(D\) とする:

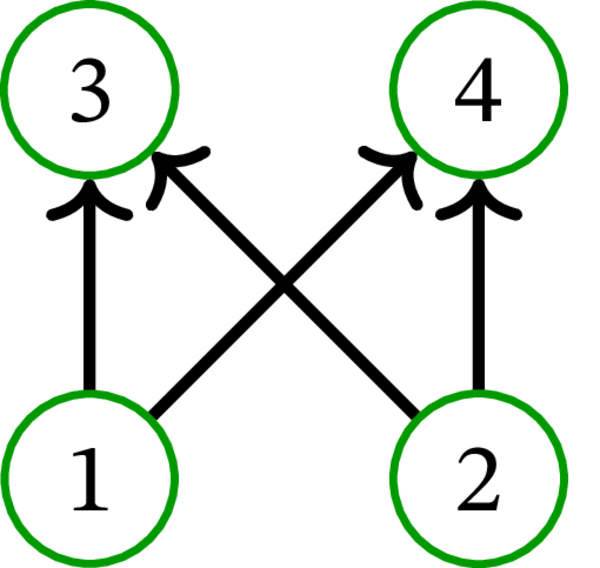
このとき、\(D\) 上の資産配分 \(\left( k_{1},k_{2},k_{3},k_{4}\right) =\left( 0,0,-1,2\right) \) に対してどのような寄付あるいは徴収を何度行ったとしても、借金を持つ頂点が必ず残る (寄付または徴収を行っても差 \(k_{4} - k_{3}\) は \(3\) で一定なので、総資産が \(1\) である限り \(k_{3}\) は必ず負になる)。]

[ヒント: 任意の寄付は適切に選択した有限回の徴収に等しいことを示す。ラプラシアンについて私たちが知っている事実が利用できるだろう。]

5.14.9応用: \(K_{n}^{\operatorname*{bidir}}\) が持つオイラー回路の数え上げ

行列木定理を使うと次の命題を証明できる:

[証明] 弧 \(a\) の始点を \(r\) とする。考えている多重有向グラフ \(K_{n}^{\operatorname*{bidir}}\) は平衡であり、各頂点は \(n-1\) の出次数を持つ。よって BEST' 定理 (定理 5.10.4) と第 5.14.5 項での議論より次が分かる:

以上で命題 5.14.15 は証明された。□

この命題と対称的に、無向グラフ \(K_{n}\) が持つオイラー回路の個数を計算する簡潔な式は知られていない。\(n\) が偶数ならオイラー回路は存在しない (\(K_{n}\) の各頂点の次数が奇数なため)。\(n\) が奇数ならオイラー回路の個数は非常に速く大きくなるものの、それ以外に知られている事実はほとんどない (既知の値は https://oeis.org/A135388 から確認できる)。練習問題 5.22 ではオイラー回路の個数が特定の数で割り切れることを見る。