5.8. 全域有向木
多重グラフの全域木に対応する概念として、多重有向グラフの全域有向グラフを定義する:
多重有向グラフ \(D=\left( V,A,\psi\right) \) の全域部分有向グラフ (spanning subdigraph) とは、\(A\) の部分集合 \(B\) を使って \(\left( V,B,\psi|_{B}\right) \) と書ける多重有向グラフを意味する。
言い換えれば、\(D\) と同じ頂点集合を持つ \(D\) の部分多重有向グラフを全域部分有向グラフと呼ぶ。
さらに言い換えれば、\(D\) の頂点を保持しながら弧をいくつか除去して得られる多重有向グラフを全域部分有向グラフと呼ぶ。
\(D\) を多重有向グラフ、\(r\) を \(D\) の頂点とする。\(r\) を根とする \(D\) の全域有向木 (spanning arborescence of \(D\) rooted from \(r\)) とは、\(D\) の全域部分有向グラフであって \(r\) を根とする有向木であるものを意味する。
\(D=\left( V,A,\psi\right) \) を次の多重有向グラフとする:
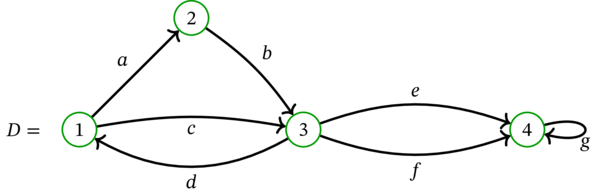
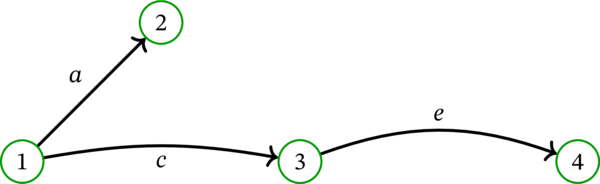
\(1\) を根とする \(D\) の全域有向木は存在するだろうか? 存在する。例えば次のグラフがそうである:
今後は記号を濫用し、全域部分有向グラフを弧の集合として表記する (弧が定まれば全域部分有向グラフは一意に定まる)。例えば、上に示した全域有向木は \(\left\{ a,c,e\right\} \) と表記する。\(1\) を根とする \(D\) の全域有向木は他にも \(\left\{ a,b,e\right\} \) や \(\left\{ a,b,f\right\} \) がある。これに対して \(\left\{ a,d,f\right\} \) は \(1\) を根とする全域有向木ではない (\(3\) を根とする全域有向木である)。
\(2\) を根とする \(D\) の全域有向木は存在するだろうか? 存在する。例えば \(\left\{ b,d,f\right\} \) がそうである。
\(4\) を根とする \(D\) の全域有向木は存在するだろうか? 存在しない。なぜなら、\(4\) は \(D\) の始根でないからである。
この例から全域有向木の存在に必要な条件が一つ分かる: 有向グラフ \(D\) で頂点 \(r\) が始根でない限り、\(r\) を根とする \(D\) の全域有向木は存在しない。この必要条件は十分条件でもある:
\(D\) を多重有向グラフ、\(r\) を \(D\) の始根とする。このとき \(D\) は \(r\) を根とする全域有向木を持つ。
以前に四通りの証明を示した「任意の連結な多重グラフは全域木を持つ」定理 (定理 5.4.6) の有向グラフバージョンがこの定理と言える。少なくとも一つ目の証明は有向グラフにも容易に適用できる:
\(r\) が始根であり続けるように \(D\) から弧を一つずつ除去する操作を考える。どの弧を除去しても \(r\) が始根でなくなる状態になったら、その時点で操作を終了する。
\(D\) の弧は有限個しか存在しないので、この操作はいずれ終了する。操作が終了した時点の多重有向グラフを \(D^{\prime}\) とする。このとき \(r\) は \(D^{\prime}\) の始根であり、\(D^{\prime}\) から任意の弧を除去すると \(r\) は始根でなくなる。つまり \(D^{\prime}\) は有向木の同値性定理 (定理 5.6.5) の命題 A5 を満たす。よって \(D^{\prime}\) は命題 A1 を満たす (六つの命題 A1, A2, ..., A6 は同値なため)。言い換えれば \(D^{\prime}\) は \(r\) を根とする全域有向木である。\(D^{\prime}\) は \(D\) の全域部分有向グラフでもあるから、\(D^{\prime}\) は \(r\) を根とする \(D\) の全域有向木である。□
\(n\) を正整数とする。頂点 \(1,2,\ldots,n\) と弧 \(12,\ 23,\ 34,\ \ldots,\ \left( n-1\right) n,\ n1\) を持つ単純有向グラフを \(n\) 頂点の有向閉路グラフ (\(n\)-cycle digraph) \(\overrightarrow{C}_{n}\) と呼ぶ。\(5\) 頂点の有向閉路グラフを次に示す:
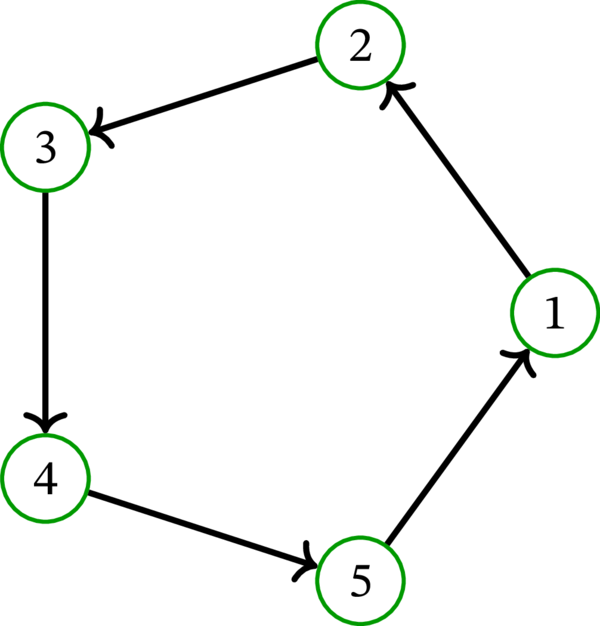
この有向グラフ \(\overrightarrow{C}_{n}\) は閉路グラフ \(C_{n}\) に対応する概念である。例 5.4.4 で示したように、閉路グラフ \(C_{n}\) は \(n\) 個の全域木を持つ。
これに対して、有向グラフ \(\overrightarrow{C}_{n}\) は \(1\) を根とする全域有向木を一つしか持たない。その全域有向木は \(\overrightarrow{C}_{n}\) から弧 \(n1\) を除去して得られる部分有向グラフである。
\(\overrightarrow{C}_{n}\) から弧 \(n1\) を除去すると、頂点 \(1,2,\ldots,n\) と弧 \(12,\ 23,\ \ldots ,\ \left( n-1\right) n\) を持つ単純有向グラフ \(E\) が得られる。\(E\) が \(1\) を根とする有向木であることは容易に分かる (実際、\(1\) は \(E\) の始根であり、台無向グラフ \(E^{\operatorname*{und}}=P_{n}\) は閉路を持たない)。よって \(E\) は \(1\) を根とする \(\overrightarrow{C}_{n}\) の全域有向木である。
続いて \(1\) を根とする \(\overrightarrow{C}_{n}\) の全域有向木が \(E\) 以外に存在しないことを示す。\(1\) を根とする \(\overrightarrow{C}_{n}\) の全域有向木を \(F\) とする。このとき任意の頂点 \(v\in\left\{ 2,3,\ldots ,n\right\} \) に対して有向グラフ \(F\) は \(1\) から \(v\) への路を持ち、その路には \(v\) を終点に持つ弧が (最後の弧として) 含まれる。つまり頂点 \(v\in\left\{ 2,3,\ldots ,n\right\} \) のそれぞれに対して有向グラフ \(F\) は弧 \(\left( v-1,v\right) \) を持つ。言い換えれば、有向グラフ \(F\) は \(n-1\) 個の弧 \(12\), \(23\), ..., \(\left( n-1\right) n\) を全て持つ。もし \(F\) が \(\overrightarrow{C}_{n}\) の残る一つの弧 \(n1\) を持っていると閉路が生じて \(F\) が有向木である事実と矛盾するので、\(F\) は弧 \(n1\) を持たない。言い換えれば \(F=E\) である。つまり \(1\) を根とする \(\overrightarrow{C}_{n}\) の全域有向木は \(E\) しか存在しない。□