5.13. 全域有向木と全域木

BEST 定理 (定理 5.9.1 と定理 5.10.4) は平衡な有向グラフが持つオイラー回路の個数と全域有向木の個数を関連付ける。続いて後者の値を計算する方法を考える。

例えば、何らかの多重グラフ \(G\) を使って \(G^{\operatorname*{bidir}}\) と書ける有向グラフが持つ全域有向木の個数を考えよう。実は、適当な頂点 \(r\) を終根とする \(G^{\operatorname*{bidir}}\) の全域有向木は \(G\) の全域木と本質的に等しいことが言える:

例 5.13.2

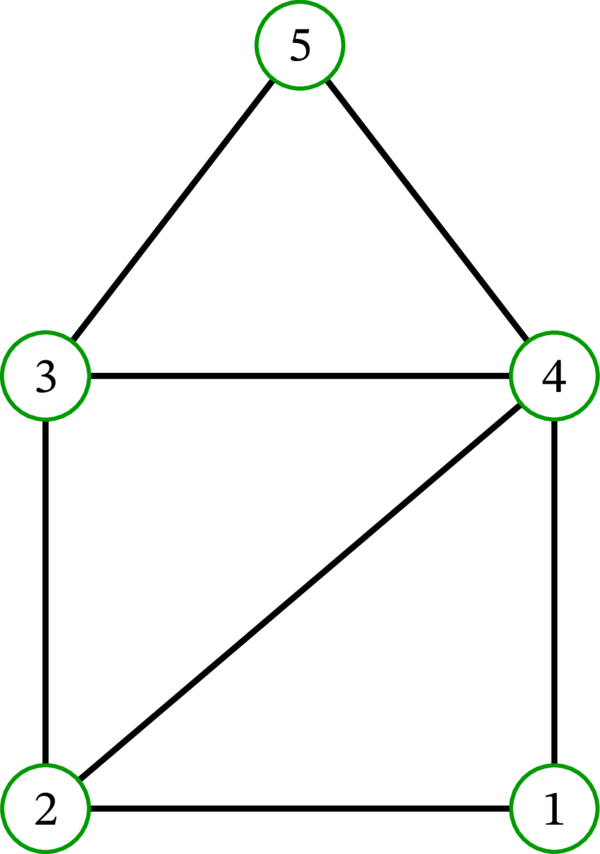
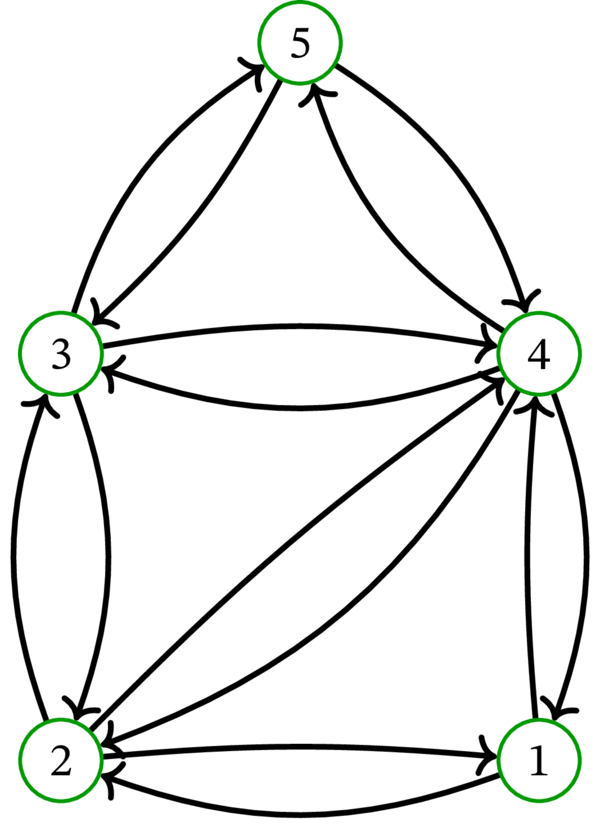
多重グラフ \(G\) と、それに対応する多重有向グラフ \(G^{\operatorname*{bidir}}\) の例を次に示す:

\(G = \hspace{5pt}\)

\(G^{\operatorname*{bidir}} = \hspace{5pt}\)

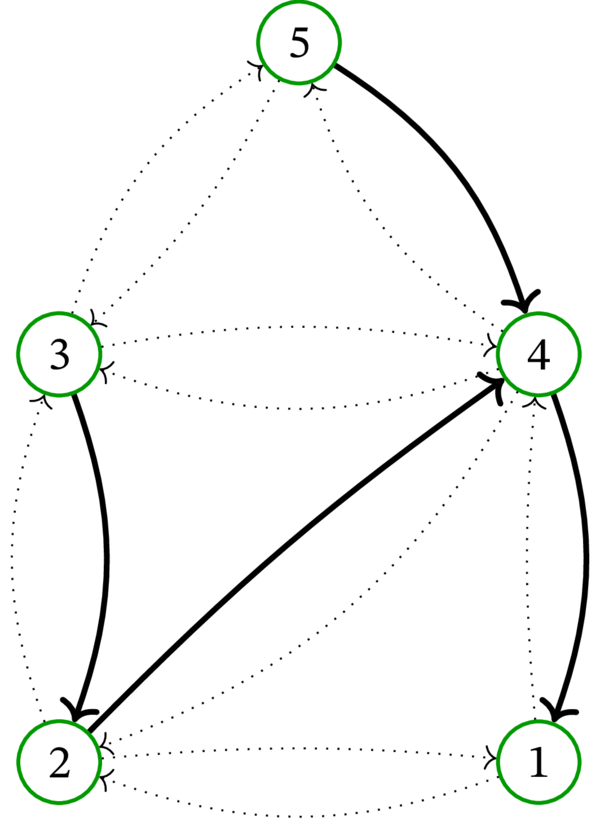
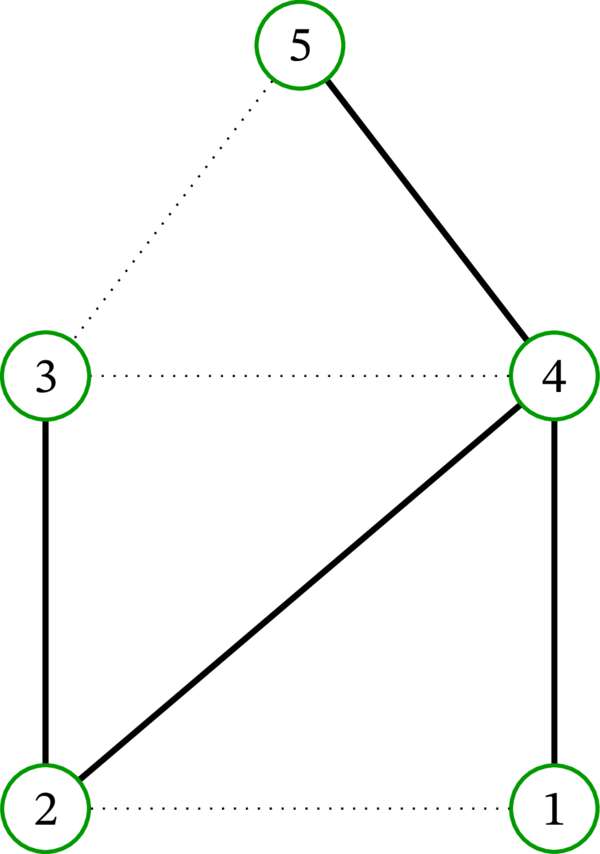
\(1\) を終根とする \(G^{\operatorname*{bidir}}\) の全域有向木 \(B\) と、それに対応する \(G\) の全域有向木 \(\overline{B}\) を次に示す:

\(B = \hspace{5pt}\)

\(\overline{B} = \hspace{5pt}\)

[\(B\) に属さない \(G^{\operatorname*{bidir}}\) の弧と \(\overline{B}\) に属さない \(G\) の辺は薄い点線で描かれている。] \(\overline{B}\) から \(B\) を構築する方法は簡単に理解できるだろう: \(\overline{B}\) の辺を適切な向きの付いた (頂点 \(1\) に向かう) 弧に置き換えればよい。

[命題 5.13.1 の証明] この命題の証明はヤクの毛刈り的な作業となる。非常によく似た毛刈りは第 5.7 節でも行った。今回は個別の木ではなく \(G\) の全域木を考える点が異なる。

(a): \(r\) を終根とする \(G^{\operatorname*{bidir}}\) の全域有向木を \(B\) とする。定理 5.10.5 の A'1 \(\Longrightarrow\) A'3 から、\(B^{\operatorname*{und}}\) は木だと分かる。容易に分かるように、多重グラフとして \(B^{\operatorname*{und}}\) と \(\overline{B}\) は同型である (実際、\(B^{\operatorname*{und}}\) の任意の頂点 \(v\) は \(\overline{B}\) の同じ頂点 \(v\) に対応し、\(B^{\operatorname*{und}}\) の任意の辺 \(\left( e,i\right) \) は \(\overline{B}\) の辺 \(e\) に対応する¹)。ここから \(\overline{B}\) が (\(B^{\operatorname*{und}}\) と同様に) 木だと分かる²。\(B^{\operatorname*{und}}\) は明らかに \(G\) の全域部分グラフなので、\(\overline{B}\) は \(G\) の全域木である。以上で命題 5.13.1 (a) が証明できた。

(b): \(\varphi\) が全射かつ単射だと示す必要がある。

全射性: \(T\) を \(G\) の全域木とする。このとき補題 5.7.7 より、多重有向グラフ \(T^{r\rightarrow}\) (定義 5.7.4) は \(r\) を根とする有向木である。よって \(T^{r\rightarrow}\) の全ての弧を反転させた多重有向グラフを \(T^{r\leftarrow}\) とすれば、\(T^{r\leftarrow}\) は \(r\) を終根とする有向木となる。ただ、\(T^{r\leftarrow}\) は \(G^{\operatorname*{bidir}}\) の部分有向グラフではない。これは次のつまらない理由による: \(T^{r\leftarrow}\) の弧は \(E\) の要素であるのに対して、\(G^{\operatorname*{bidir}}\) の弧は \(\left( e,i\right) \) の形をした組である (\(e\in E\), \(i\in\left\{ 1,2\right\} \))。

幸い、これは簡単に修正できる。\(T^{r\leftarrow}\) の各弧 \(e\) に対して、\(e\) と同じ始点を持つ \(G^{\operatorname*{bidir}}\) の弧 \(\left( e,i\right) \) を \(e^{\prime}\) と定める (このとき \(e^{\prime}\) の終点も \(e\) の終点と同じになる)。\(G^{\operatorname*{bidir}}\) の弧 \(\left( e,1\right) \) と \(\left( e,2\right) \) は異なる始点を持つ³ので、\(e^{\prime}\) は一意に決定する。\(T^{r\leftarrow}\) の弧 \(e\) をそれぞれ \(G^{\operatorname*{bidir}}\) の弧 \(e^{\prime}\) に置き換えると、\(G^{\operatorname*{bidir}}\) の全域部分有向グラフ \(S\) が得られる。その構成より、\(S\) は \(T^{r\leftarrow}\) と同様に \(r\) を終根とする有向木でもある。言い換えれば、\(S\) は \(r\) を終根とする \(G^{\operatorname*{bidir}}\) の全域有向木である。容易に分かるように \(\overline{S}=T\) なので、写像 \(\varphi\) は \(S\) を \(T\) に移す。つまり \(T\) は \(\varphi\) の値域に属する。\(G\) の任意の全域木 \(T\) が \(\varphi\) の値域に属することが示せたので、\(\varphi\) が全射だと分かる。

単射性: 「それぞれの辺を \(r\) へ向かう弧に置き換えることで全域木 \(\overline{B}\) から全域有向木 \(B\) を復元でき、異なる全域木からは異なる全域有向木が復元される」ことを示すのが基本的なアイデアとなる。証明の (うんざりするほど長い) 詳細は次の通りである:

\(B\), \(C\) を任意の sparb⁴ として、\(\overline{B}=\overline{C}\) が成り立つとする。\(B=C\) を示す必要がある。

背理法で示す。\(B \neq C\) だと仮定する。\(T\) を木 \(\overline {B}=\overline{C}\) とする。\(T = \overline{B}\) より、\(T\) の各辺 \(e\) は \(B\) で弧 \(\left( e,1\right) \) または弧 \(\left( e,2\right) \) に対応する。同様に \(T = \overline{C}\) より、\(T\) の各辺 \(e\) は \(C\) で弧 \(\left( e,1\right) \) または弧 \(\left( e,2\right) \) に対応する。\(B \neq C\) より、次の条件のどちらかを満たす \(T\) の辺 \(e\) が存在しなければならない:

• \(\left( e,1\right) \in B\) と \(\left( e,2\right) \in C\) が成り立つ。

• \(\left( e,1\right) \in C\) と \(\left( e,2\right) \in B\) が成り立つ。

この辺 \(e\) に注目する。一般性を失うことなく \(\left( e,1\right) \in B\) かつ \(\left( e,2\right) \in C\) だと仮定する (そうでなければ \(B\) と \(C\) を交換する)。\(G^{\operatorname*{bidir}}\) の弧 \(\left( e,1\right) \) が始点 \(s\) と終点 \(t\) を持つとする。このとき弧 \(\left( e,2\right) \) は始点 \(t\) と終点 \(s\) を持ち、辺 \(e\) は \(s\) と \(t\) を端点に持つ。

\(B\) が \(r\) を終根とする有向木なので、\(r\) は \(B\) の終根である。よって \(s\) から \(r\) への路 \(\mathbf{p}\) が \(B\) に存在する。\(\mathbf{p}\) の最初の弧は \(\left( e,1\right) \) である⁵。路 \(\mathbf{p}\) を \(T\) に射影することで、\(T\) における \(s\) から \(r\) への路 \(\overline{\mathbf{p}}\) が得られる (ここで「射影する」とは、路に含まれる弧 \(\left( e,i\right) \) を辺 \(e\) に置き換えることを言う。\(T = \overline{B}\) なので、この操作によって \(B\) の路は \(T\) の路に変換される)。路 \(\mathbf{p}\) の最初の弧は \(\left( e,1\right) \) なので、射影された路 \(\overline{\mathbf{p}}\) の最初の弧は \(e\) である。つまり木 \(T\) において \(s\) から \(r\) への路は辺 \(e\) で始まる (この路が \(\overline{\mathbf{p}}\) であるため)。\(e\) の端点は \(s\) と \(t\) なので、\(\mathbf{p}\) の二番目の頂点は \(t\) である。よって \(\mathbf{p}\) から最初の辺を除去すると \(t\) から \(r\) への路となる。ここから \(d\left( t,r\right) =d\left( s,r\right) -1\) を得る (\(d\) は木 \(T\) における距離を表す)。つまり \(d\left( t,r\right) < d\left( s,r\right) \) である。

\(B\) と \(C\), \(s\) と \(t\), \(\left( e,1\right) \) と \(\left( e,2\right) \) を入れ替えて同様の議論をすると \(d\left( s,r\right) < d\left( t,r\right) \) が示せる。しかし、これは \(d\left( t,r\right) < d\left( s,r\right) \) と矛盾する。

この矛盾から仮定が偽だと分かる。よって \(B=C\) が証明された。

\(B\) と \(C\) を固定したことを忘れる。以上の議論から、\(B\) と \(C\) が sparb で \(\overline{B}=\overline{C}\) なら \(B = C\) だと示せた。言い換えれば、写像 \(\varphi\) は単射である。

\(\varphi\) は全射かつ単射なので、全単射だと分かる。以上で命題 5.13.1 は証明された。□