5.4. 全域木

5.4.1全域部分グラフ

続いて非常に重要な木の応用に触れる。まず、任意の多重グラフに対して考えられる概念を定義する:

これを誘導部分グラフと比べてみてほしい:

• 誘導部分グラフを構築するには、グラフから頂点をいくつか除去した上で辺を可能な限り保持する。 [通常の数学における用法と同様に、「いくつか除去」には「一つも除去しない」と「全て除去」が含まれる。]

• これに対して、全域部分グラフを構築するには、頂点を全て保持した上で辺をいくつか除去する。

5.4.2全域木

全域部分グラフは木であるとき特に有用となる:

例 5.4.3

\(G\) を次の多重グラフとする:

\(G\) の全域木を示す:

\(G\) の異なる全域木を次に示す:

[\(\alpha\neq\beta\) なので、二つの全域木は異なる。]

次に示すのも \(G\) の全域木である:

[証明] \(n\) 個の頂点を持つ木は \(n-1\) 個の辺を持つ (定理 5.2.4 の T1 \(\Longrightarrow\) T4 より)。よって \(C_{n}\) の全域部分グラフは \(n-1\) 個の辺を持つときに限って、つまり辺を \(1\) 個だけ除去したときに限って全域木となれる (\(C_{n}\) は \(n\) 個の辺を持つため)。\(C_{n}\) から除去できる辺の選択肢は \(n\) 個あるので、\(C_{n}\) は最大で \(n\) 個の全域木を持つ。よって後は \(C_{n}\) から任意の一辺を除去した部分グラフが全域木だと示せばよい。しかし、これは易しい: そういった部分グラフは全て路グラフ \(P_{n}\) と同型なので、全域木だと分かる。□

練習問題 5.5

\(m\geq1\) に対して、\(G\) を \(3m + 2\) 個の頂点

\[ a,b,\ x_{1},x_{2},\ldots,x_{m},\ y_{1},y_{2},\ldots,y_{m},\ z_{1},z_{2},\ldots,z_{m} \]

と \(3m + 3\) 個の辺

\[ \begin{aligned} & ax_{1},\, ay_{1},\, az_{1} \\ & x_{i}x_{i+1},\, y_{i}y_{i+1},\, z_{i}z_{i+1}\qquad (\forall i\in\left\{ 1,2,\ldots,m-1\right\})\\ & x_{m}b,\, y_{m}b,\, z_{m}b \end{aligned} \]

を持つ単純グラフとする。\(G\) の全域木の個数を求めよ。

[\(G\) は二頂点 \(a\), \(b\) を三つの路で結んだグラフである。それぞれの路の長さは \(m+1\) であり、始点と終点を除いて頂点を共有しない。\(m=3\) の場合の \(G\) を示す:

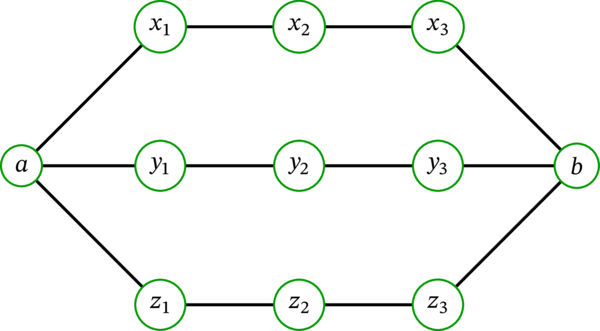
このグラフは \(11\) 個の頂点と \(12\) 個の辺を持つ。]

[解答が正しいことを示す議論は一行か二行の概略で構わない。完全に厳密な証明は必要ない。]

[解答: これは 2017 年春学期に開講された講義で出した homework set #3 の Exercise 2 (c) である。解答は講義ページに載っている。]

5.4.3全域森

\(G\) の全域木は \(G\) が持つ最小の「背骨」とみなせる ── つまり、\(G\) が連結でなくならないように辺を除去していくと、最終的に得られる部分グラフは全域木となる。当然 \(G\) が連結でなければこの操作は行えないので、そのとき全域木は存在しない。\(G\) が連結でないとき最も「背骨」に近い部分グラフは \(G\) の各成分に最小の辺が残された全域部分グラフである。これは全域森と呼ばれる:

\(G\) が連結な多重グラフのとき、\(G\) の全域森は全域木と同じ意味になる。

5.4.4全域木の存在と構築

次の定理は非常に重要なので、これから四つの異なる証明 (の概略) を示す:

[一つ目の証明 (概略)] \(G\) を連結な多重グラフとする。\(G\) の全域木を構築すればよい。\(G\) から辺を一つずつ除去していく操作を全域木が得られるまで繰り返すことを考える。この操作では、グラフを切断しない (連結のままにする) ことが求められる。定理 3.3.18 によれば、これは橋 (自身を含む閉路が存在しない辺) を除去しないようにすれば達成できる。よって非橋 (non-bridge, 橋でない辺) の除去を可能な限り (全ての辺が橋のグラフが得られるまで) 繰り返せばよい。

以上より次のアルゴリズムが分かる: \(G\) から始めて、非橋を一つずつ¹除去する。全ての辺が橋になったら終了し、その時点のグラフを出力する。この手続きは必ず停止する: \(G\) は有限個の辺しか持たないので、有限回の操作でグラフの全ての辺が橋となる。最終的に得られるグラフ \(G^{\prime}\) は閉路を持たない (閉路に含まれる辺は橋であるため)。また、\(G\) は連結であり、非橋を除去しても連結性は保たれるので、\(G^{\prime}\) は連結でもある。よって \(G^{\prime}\) は木である。さらに (その構成から) \(G^{\prime}\) は \(G\) の全域部分グラフでもあるので、\(G^{\prime}\) は \(G\) の全域木である。以上で定理 5.4.6 は証明された。□

[二つ目の証明 (概略)] 一つ目の証明では、\(G\) が木になるまで一つずつ辺を除去することで全域木を構成した。二つ目の証明では逆の方法を用いる: \(G\) と同じ頂点集合上の空グラフから始めて、連結なグラフが得られるまで \(G\) の辺を加えていく。

さらに詳細を詰めると次のようになる: まず、\(G\) と同じ頂点集合と空の辺集合を持つグラフを \(L\) とする。続いて、\(G\) の辺を任意の順序で一つずつ走査しながら「注目している辺を \(L\) に加えたとき閉路が生じないなら、その辺を \(L\) に加える」という処理を全ての辺に対して行う。\(u\) と \(v\) を端点に持つ辺 \(e\) を \(L\) に加えたとき閉路が生じるのは、\(e\) を加える前の \(L\) で \(u\) と \(v\) が同じ成分に属するとき、かつそのときに限る。よって \(L\) において異なる成分に属する頂点を結ぶ辺だけを \(L\) に加えることができる。この手続きを終えたとき、グラフ \(L\) は閉路を持たない (閉路ができないように辺を追加するため)。言い換えれば、最終的に得られるグラフは森である。

この手続きで最後的に得られる森を \(H\) とする。\(H\) が \(G\) の全域木だと示す。\(H\) は森だと分かっているので、\(H\) が連結だと示せばよい。背理法で示す。\(H\) が連結でないと仮定すると、\(H\) の異なる成分を接続する \(G\) の辺 \(e\) が存在する [なぜ？]。この辺 \(e\) は \(H\) の辺でないので、\(H\) の構築中に \(e\) は \(L\) に追加されていない。先述したように、これは \(H\) の構築中のある時点で \(e\) の両端点が \(L\) の同じ成分に属していたことを意味する。しかし、\(L\) に追加された辺は除去されないので、これは手続きが終了した時点でも \(e\) の両端点が \(L\) の同じ成分に属することを意味する。言い換えれば、\(e\) の両端点は \(H\) で同じ成分に属する。これは \(e\) が \(H\) の異なる成分を接続する仮定と矛盾するので、\(H\) は連結だと分かる。よって \(H\) は \(G\) の全域木であり、定理 5.4.6 の証明が完了した。□

[三つ目の証明] この証明は \(G\) の全域木を構築するさらに別のアプローチを利用する。\(G\) の適当な頂点 \(r\) を選び、そこから「噂」を段階的に広めていく。噂は頂点 \(r\) から始まり、一日ごとに噂を知っている頂点は自身が隣接する頂点に噂を広める。\(G\) は連結なので、噂はいずれグラフ全体に広まる。\(r\) を除く各頂点 \(v\) に「自分に噂を初めて伝えた頂点 \(v^{\prime}\) (複数の頂点から同時に伝えられたなら、一つを任意に選ぶ)」を記憶させておき、\(v\) と \(v^{\prime}\) を端点とする辺を \(e_{v}\) とする (\(r\) 以外の頂点 \(v\) は自身の隣接頂点から噂を伝えられるので、\(e_{v}\) は存在する)。\(G\) の頂点集合を \(V\) とするとき、全ての \(v\in V\setminus\left\{ r\right\} \) に対応する \(e_{v}\) は \(G\) の全域木を構成する。つまり、頂点集合が \(V\) で辺集合が \(\left\{ e_{v}\mid v\in V\setminus\left\{ r\right\} \right\} \) のグラフ \(H\) は \(G\) の全域木となる。なぜだろうか？

直感的に納得するのは難しくない: \(H\) は (タイムループが起きない限り) 閉路を持たず、連結でもある (任意の頂点 \(v\) から \(e_{v}\) を経由することで \(r\) に到達できる)。これを厳密な証明とするために、\(H\) の構築を数学的に定式化する:

\(G=\left( V,E,\varphi\right) \) とする。\(G\) の頂点を任意に一つ取って \(r\) とする。

これから、次に示す \(G\) の部分グラフの列を再帰的に定義する:

基本的なアイデアは「各 \(i \in \mathbb{N}\) に対して、集合 \(V_{i}\) は第 \(i\) 日目の時点で「噂」を知っている頂点から構成され、集合 \(E_{i}\) は各 \(v \in V_{i}\) に対応する \(e_{v}\) から構成される」となる。写像 \(\varphi_{i}\) は当然 \(\varphi\) の \(E_{i}\) への制限である。

部分グラフの列は次のように定義される:

• ベースケース: \(V_{0}\colonequals \left\{ r\right\} \) および \(E_{0}\colonequals \varnothing\) と定める。\(\varphi_{0}\) は \(\varphi\) の (空) 集合 \(E_{0}\) への制限とする。

• 再帰ステップ: \(i \in \mathbb{N}\) に対して \(G\) の部分グラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) が定義されていると仮定する。このとき \(V_{i+1}\) を次のように定める:

  \[ V_{i+1}\colonequals V_{i}\cup\left\{ v\in V\mid v\text{ は }V_{i} \text{ に属する頂点と } G \text{ で隣接する} \right\} \]

  各 \(v\in V_{i+1}\setminus V_{i}\) に対して、\(V_{i}\) に属する頂点と \(v\) を接続する²辺を一つ選んで \(e_{v}\) とする (そのような辺は \(v\in V_{i+1}\) より存在する)。そして \(E_{i+1}\) を次のように定める:

  \[ E_{i+1}\colonequals E_{i}\cup\left\{ e_{v}\mid v\in V_{i+1}\setminus V_{i}\right\} \]

  最後に、\(\varphi_{i+1}\) を写像 \(\varphi\) の集合 \(E_{i+1}\) への制限とする。このとき \(\varphi_{i+1}\) は \(E_{i+1}\) から \(\mathcal{P}_{1,2}\left( V_{i+1}\right) \) への写像である (任意の \(v\in V_{i+1}\setminus V_{i}\) に対する辺 \(e_{v}\) の端点は、一つが \(V_{i+1}\setminus V_{i}\subseteq V_{i+1}\) に属する \(v\) で、もう一つが \(V_{i}\subseteq V_{i+1}\) に属する頂点であるため)。よって \(\left( V_{i+1},E_{i+1},\varphi_{i+1}\right) \) は well-defined な \(G\) の部分グラフである。

この構築からは、各 \(i \in \mathbb{N}\) に対する \(\left( V_{i},E_{i},\varphi_{i}\right) \) が \(\left( V_{i+1},E_{i+1},\varphi_{i+1}\right) \) の部分グラフであることも分かる。よって \(V_{0}\subseteq V_{1}\subseteq V_{2}\subseteq\cdots\) であり、\(\left\vert V_{0}\right\vert \leq\left\vert V_{1}\right\vert \leq\left\vert V_{2}\right\vert \leq\cdots\) を得る。\(\left\vert V\right\vert \) という上界を持つ整数列 \(\left\{\left\vert V_{i}\right\vert\right\} \) が大きくなり続けることはなく、ある \(i \in \mathbb{N}\) で \(\left\vert V_{i}\right\vert =\left\vert V_{i+1}\right\vert \) が成り立つ。この \(i\) に注目する。\(\left\vert V_{i}\right\vert =\left\vert V_{i+1}\right\vert \) と \(V_{i}\subseteq V_{i+1}\) より \(\left\vert V_{i}\right\vert =\left\vert V_{i+1}\right\vert \) が分かる。

先述の口語的な説明において、\(V_{i}=V_{i+1}\) は第 \(i+ 1\) 日目に新しく噂を知らされた頂点が存在しないことを意味する。つまり、この時点で全ての頂点が噂を知っている。数学的に言い換えれば、\(V_{i}=V\) が成り立つと予想できる。この等式の厳密な証明は \(G\) が連結な事実を使えば容易に行える³。

続いて、部分グラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) が \(G\) の全域木だと示す。このためには、この部分グラフが連結な森だと示せばよい (\(V_{i}=V\) より全域部分グラフであることは分かっている)。証明を始める前に、一つ例を示しておく:

例 5.4.7

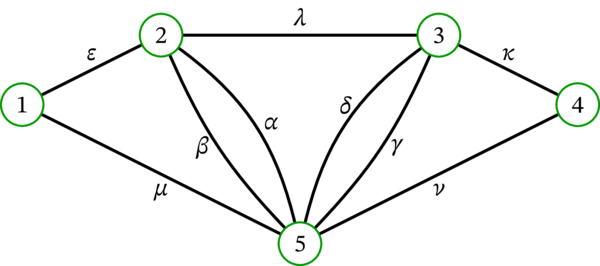
\(G\) を次の多重グラフとする:

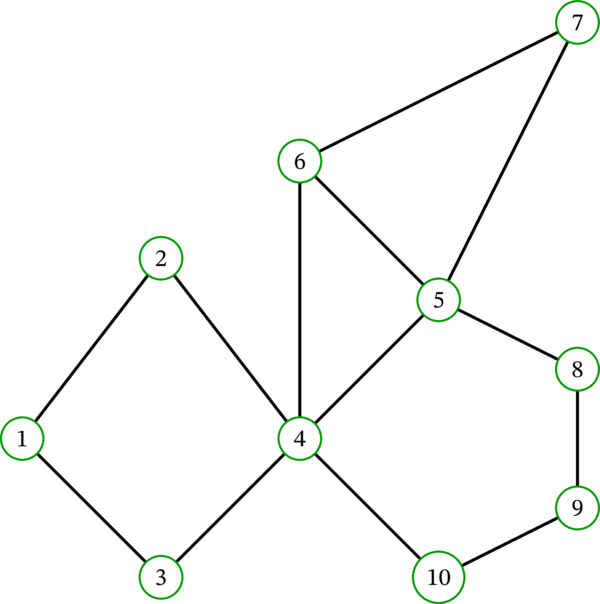
\(r = 3\) として \(V_{i}\) を構築すると、\(i = 3\) で \(V_{i} = V\) となる:

\[ \begin{aligned} V_{0} & =\left\{ 3\right\} ,\\ V_{1} & =\left\{ 3,1,4\right\} ,\\ V_{2} & =\left\{ 3,1,4,2,5,6,10\right\} ,\\ V_{3} & =\left\{ 3,1,4,2,5,6,10,8,9,7\right\} =V \end{aligned} \]

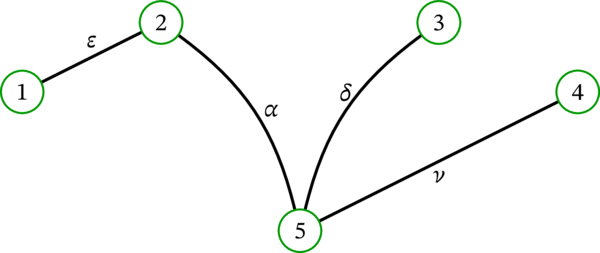
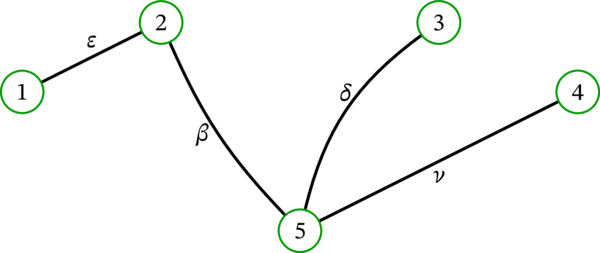
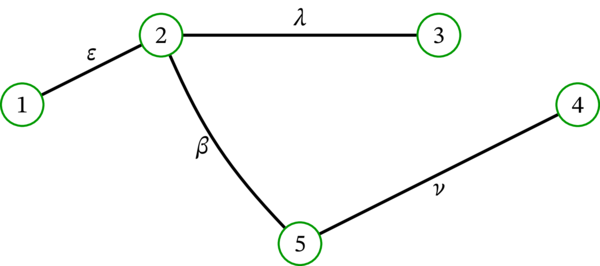
任意の \(k \geq 3\) で \(V_{k} = V\) が成り立つので、\(i = 3\) の場合だけを考えればよい。\(V_{k}\) が段階的に大きくなる様子を次の図に示す:

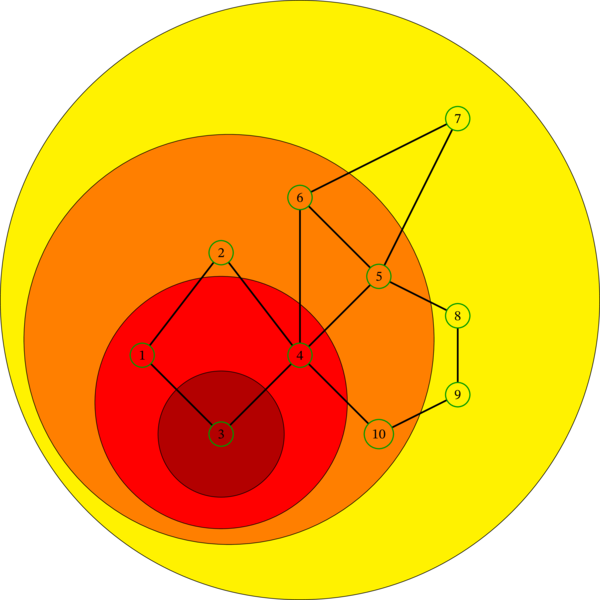
[一番暗い円が \(V_{0}\) を表し、\(i\) が大きくなるにつれて \(V_{i}\) を表す円は明るくなる。黄色い円が \(V_{3}=V_{4}=V_{5}=\cdots=V\) を表す。] 最後に、選択される \(e_{v}\) の一例を次の図に示す:

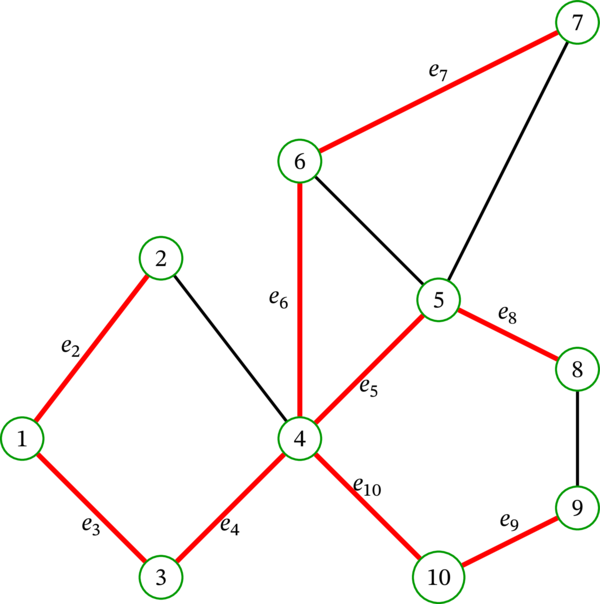
このグラフでは、\(e_{v}\) の選択肢が複数ある場面が二つある: 辺 \(e_{2}\) としては \(12\) と \(42\) のどちらか、辺 \(e_{7}\) としては \(67\) と \(57\) のどちらかを選択できる。この図では両方の場面で前者を選択している。もう一方の辺を選択しても問題はない。

一般的なグラフにおける証明に戻る。まずは次の命題を示す:

Claim 1 の証明: \(j\) に関する数学的帰納法を用いる:

ベースケース: \(j = 0\) のとき命題は明らかに成り立つ (\(V_{0}=\left\{ r\right\} \) であり頂点が \(r\) しか存在しないため)。

再帰ステップ: 正整数 \(k\) を固定する。\(j = k - 1\) のとき Claim 1 が成り立つと (帰納法の仮定として) 仮定する。このとき、\(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) の各頂点は \(r\) と路連結である。

グラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) の頂点を任意に一つ取って \(v\) とする。このグラフで \(v\) と \(r\) が路連結だと証明する必要がある。\(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) は \(\left( V_{k},E_{k},\varphi_{k}\right) \) の部分グラフなので、帰納法の仮定より \(v \in V_{k-1}\) なら \(r\) と \(v\) は \(\left( V_{k},E_{k},\varphi_{k}\right) \) で路連結である。よって一般性を失うことなく \(v \notin V_{k-1}\) と仮定する。このとき \(v\in V_{k}\setminus V_{k-1}\) であり、\(E_{k}\) の再帰的な定義によれば \(V_{k-1}\) に属する頂点と \(v\) を接続する辺 \(e_{v} \in E_{k}\) が存在する。前者の頂点を \(u\) とすれば、\(e_{v}\) が長さ \(1\) の \(v\) から \(u\) への路を提供するので、\(u\) と \(v\) は路連結である。一方で \(u\in V_{k-1}\) だから、帰納法の仮定より \(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) で \(u\) と \(r\) は路連結と分かる。さらに \(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) は \(\left( V_{k},E_{k},\varphi_{k}\right) \) の部分グラフなので、\(u\) と \(r\) は \(\left( V_{k},E_{k},\varphi _{k}\right) \) でも路連結だと分かる。路連結性は推移的な関係なので、\(\left( V_{k},E_{k},\varphi _{k}\right) \) で \(v\) と \(r\) は路連結だと結論できる。

つまり、グラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) の任意の頂点 \(v\) は (このグラフで) \(r\) と路連結である。言い換えれば、Claim 1 は \(j = k\) でも成り立つ。以上で再帰ステップが完了したので、Claim 1 は証明された。

Claim 1 で \(j = i\) と置き換えると、\(\left( V_{i},E_{i},\varphi_{i}\right) \) の各頂点がこのグラフで \(r\) と路連結だと分かる。路連結性は同値関係なので、これは任意の二頂点が路連結であることを意味する。よってグラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) は (少なくとも一つの頂点を持つので) 連結である。後はグラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) が森だと示せれば証明が完了する。

ここでも補助的な命題を利用する:

Claim 2 の証明: \(j\) に関する数学的帰納法を用いる。

ベースケース: \(E_{0}=\varnothing\) よりグラフ \(\left( V_{0},E_{0},\varphi_{0}\right) \) は辺を持たないので閉路も持たない。よって Claim 2 は \(j = 0\) のとき成り立つ。

再帰ステップ: 正整数 \(k\) を固定する。Claim 2 が \(j = k - 1\) のとき成り立つと (帰納法の仮定として) 仮定する。このときグラフ \(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) は閉路を持たない。

グラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) が閉路を持たないことを背理法で示す。グラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) が閉路 \(C\) を持つと仮定する。グラフ \(\left( V_{k-1},E_{k-1},\varphi_{k-1}\right) \) は閉路を持たないので、\(C\) は \(E_{k}\setminus E_{k-1}\) に属する辺を少なくとも一つ持つ。一方 \(E_{k}\) の定義からは、\(E_{k}\setminus E_{k-1}\) に属する各辺は何らかの \(v\in V_{k}\setminus V_{k-1}\) に対応する \(e_{v}\) だと分かる。そこで、閉路 \(C\) に含まれ \(E_{k}\setminus E_{k-1}\) に属する辺を任意に一つ選び、それを \(e_{v}\) (\(v\in V_{k}\setminus V_{k-1}\)) とする。\(C\) は \(e_{v}\) を含むので、\(e_{v}\) の端点 \(v\) も含む。しかし (ここでも \(E_{k}\) の定義より) \(e_{v}\) は \(E_{k}\) の中で頂点 \(v\) を含む唯一の辺でなければならない。ここから頂点 \(v\) は \(\left( V_{k},E_{k},\varphi_{k}\right) \) の任意の閉路に含まれないことが分かる (何らかの閉路に \(e_{v}\) が含まれる場合、\(v\) を含む辺が \(e_{v}\) 以外に少なくとも一つ存在するため)。これは閉路 \(C\) が \(v\) を含む事実と矛盾する。

\(C\) を固定したことを忘れる。以上の議論でグラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) が閉路 \(C\) を持つと矛盾が起こることが示せたので、グラフ \(\left( V_{k},E_{k},\varphi_{k}\right) \) は閉路を持たない。言い換えれば、Claim 2 は \(j=k\) でも成り立つ。以上で Claim 2 が証明された。

Claim 2 で \(j = i\) と置き換えると、グラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) が閉路を持たないと分かる。つまり、このグラフは森である。連結であることは前に示したから、グラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) は木である。さらに、このグラフは \(G\) の全域部分グラフでもあるから、グラフ \(\left( V_{i},E_{i},\varphi_{i}\right) \) は全域木だと分かる。□

この証明で構築したグラフに関する重要な性質を指摘しておく:

証明は \(k\) に関する数学的帰納法を使えば難しくない。この結果から、三つ目の証明で構築される全域木 \(\left( V_{i},E_{i},\varphi_{i}\right) \) が次の性質を持つと分かる: 各頂点 \(v \in V\) に対して、この全域木における \(r\) から \(v\) への路は \(G\) における \(r\) から \(v\) への最短路に等しい。なお、この全域木には幅優先探索木 (breadth-first search tree, BFS tree) という名前が付いている。根となる頂点 \(r\) の選択が意味を持つことに注意してほしい: 幅優先探索木における任意の頂点 \(u\) から任意の頂点 \(v\) への路が \(G\) における最短路であるとは限らない。というより、この特徴を持った \(G\) の全域木は \(G\) 自体が「ほぼ」木 (\(G^{\operatorname*{simp}}\) が木) であるときを除けば存在しない！

[四つ目の証明 (概略)] \(G\) の辺をつたって移動しながら \(G\) の頂点を全て食べようとしているヘビを想像してほしい。このヘビは頂点 \(r\) を出発し、すぐに \(r\) を食べ、各時刻で次の行動を取る:

• \(v\) の隣接頂点の中にまだ食べていないものがあるなら、ヘビはその中から一つを選んで \(w\) として、\(w\) と \(v\) を接続する辺 \(f\) を適当に選ぶ。そしてヘビは辺 \(f\) を伝って \(w\) へ移動し、頂点 \(w\) を食べ、辺 \(f\) に印を付ける。

• もし頂点 \(v\) の隣接頂点を全て食べているなら、ヘビは \(v\) に探索が終了したことを表す印を付け、探索が終了した印がついていない以前に訪れた頂点に (印の付いた辺をつたって) 戻る。

この手続きは戻る辺が無くなった時点で終了する。この手続きが終了した時点で未探索の頂点は存在せず、印が付いている辺が \(G\) の全域木となる。

この事実を詳細に証明することはせず、簡単なヒントを示すだけとする。ただ、最初に例を示す:

例 5.4.8

\(G\) を次の連結な多重グラフとする:

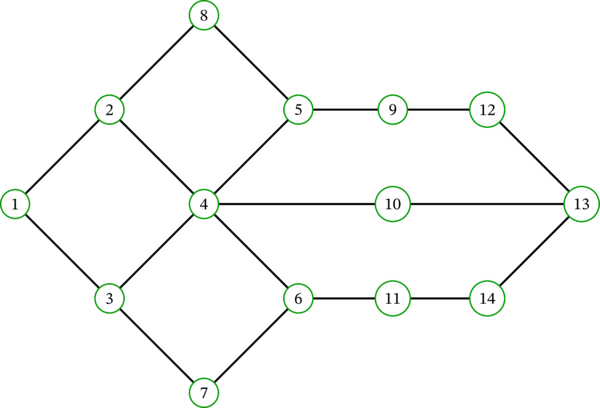
\(r=3\) をスタートしたヘビの動きの一例を示す。ヘビは最初に頂点 \(3\) を食べた後、頂点 \(1\) を次の獲物として選択したとする (このとき \(4\) あるいは \(7\) も選択できる)。このときヘビは頂点 \(1\) に移動し、そのとき辺 \(31\) に印をつけ、頂点 \(1\) を食べる。ヘビが頂点 \(1\) の次に選択できる頂点は \(2\) しかない (頂点 \(3\) は既に食べているため)。ヘビは辺 \(12\) に印を付けつつ頂点 \(2\) に移動し、頂点 \(2\) を食べる。この次にヘビは頂点 \(4\) を選択したとする (これ以外の選択肢としては頂点 \(8\) がある)。ヘビは辺 \(24\) に印を付けつつ頂点 \(4\) に移動し、頂点 \(4\) を食べる。続いてヘビが頂点 \(5\), \(8\) の順に移動したとする。このときヘビは頂点 \(8\) の隣接頂点は全て食べているので、どこにも移動できない。そこでヘビは頂点 \(8\) に探索済みの印を付け、最後の頂点 \(5\) に戻る。頂点 \(5\) からヘビは頂点 \(9\) に進み、同様の処理を繰り返す。以上の動きの軌跡を次の図に示す。食べる頂点の選択肢がいくつか存在する場面が何度かあるので、この図が示すのは動きの一例でしかない:

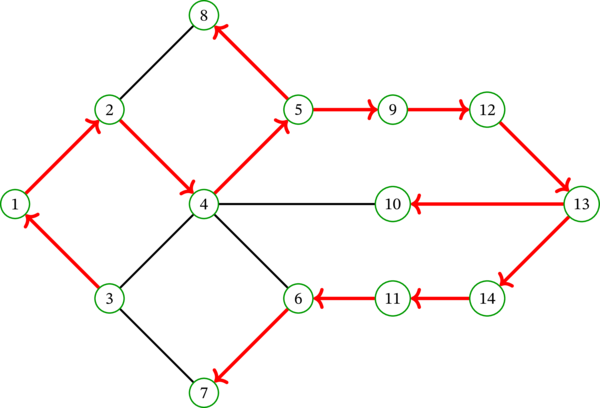
ここで太い赤い線が印の付いた辺を表し、辺に付いた矢印がその辺をつたって最初に移動した方向を表す。例えば \(2\) と \(4\) を結ぶ辺は \(4\) に向かう矢印を持っているので、ヘビは最初 \(2\) から \(4\) に移動したのだと分かる。

続いて先ほど予告した通り、命題「印の付いた辺が \(G\) の全域木を構成する」の証明の概略を示す。具体的には、次の四つの命題を (理想的にはこの順に) 示していくと証明できる:

1. 各ステップにおいて、印の付いた辺はヘビがこれまで移動してきた辺にちょうど等しい。

2. 各ステップにおいて、ヘビの食べた頂点と印の付いた辺からなるネットワークは木を構成する。

3. 十分に多くのステップが経過した後、ヘビが食べた全ての頂点には探索済みの印が付く。

4. その時点で、ヘビが食べた頂点と印の付いた辺のネットワークが全域木を構成する (探索済みの印が付いた頂点の隣接頂点は全て食べられており、さらに三つ目の命題より探索済みの印が付いているため)。

詳細は読者に任せる。

これで定理 5.4.6 がまた証明された。しかし、この証明からは全域木に関する定理以上のものが得られる。ヘビが印を付ける辺を辺集合に持つ \(G\) の全域木 \(T\) は深さ優先探索木 (depth-first search tree, DFS tree) と呼ばれる。深さ優先探索木は次の性質を持つ: \(G\) で隣接する任意の二頂点 \(u\), \(v\) に対して、\(T\) における \(r\) から \(v\) への路に \(u\) が含まれるか、そうでなければ \(T\) における \(r\) から \(u\) への路に \(v\) が含まれる。 [この性質を持つ全域木は直系全域木 (lineal spanning tree) と呼ばれる。詳しい解説が [BenWil06, § 6.1] にある。]

5.4.5応用

全域木は様々な応用を持つ:

• グラフの全域木はグラフの「背骨」であり、任意の二頂点間の「正準な」路を定めると解釈できる。これは例えば異なる路が選択されると問題が発生するネットワーク分野における応用で有用となる (Spanning Tree Protocol などで利用される)。

• \(w\)-最小全域木 (練習問題 5.8) は大局的な最小コスト路問題を解く。クラスターの検出にも利用できる。

• 深さ優先探索 (定理 5.4.6 の四つ目の証明で使ったアルゴリズム) はグラフの全ての頂点を通過して開始地点に戻る方法を定める。特に、深さ優先探索は迷路を解くアルゴリズムを与える (迷路の「部屋」を頂点に、「ドア」を辺に対応させれば、グラフで迷路をモデル化できる)。これは十九世紀に Trémaux が深さ優先探索を考案した動機だったようである。

全域木の理論的な応用も存在する:

[証明] \(G\) の全域木を \(T\) とする (定理 5.4.6 より \(G\) の全域木は存在する)。定理 5.3.2 (a) より、\(T\) は少なくとも \(2\) 個の葉を持つ。そして \(T\) の葉は \(G\) の切断頂点でない [なぜ？]。 □

5.4.6練習問題

練習問題 5.7

\(G\) を連結な多重グラフとする。単純グラフ \(\mathcal{S}\) を次のように定める: \(\mathcal{S}\) の頂点は \(G\) の全域木であり、二つの全域木 \(T_{1}\), \(T_{2}\) は \(T_{1}\) から辺を一つ除去して別の辺を一つ追加することで \(T_{2}\) が得られるとき、かつそのときに限って (\(e_{2} \neq e_{1}\) と \(T_{2} \setminus e_{2} = T_{1} \setminus e_{1}\) が成り立つような \(T_{1}\) の辺 \(e_{1}\) と \(T_{2}\) の \(e_{2}\) が存在するとき、かつそのときに限って) \(\mathcal{S}\) で隣接する。

単純グラフ \(\mathcal{S}\) が連結だと示せ。 [簡単な言葉で言えば: \(G\) の任意の全域木は、合法な「辺を一つ除去して別の辺を一つ追加する」操作を何度か繰り返すことで \(G\) の任意の全域木に変形できることを示せ。ここで操作が合法とは、変形後のグラフが全域木であることを言う。]

[例: \(G\) を次の多重グラフとする:

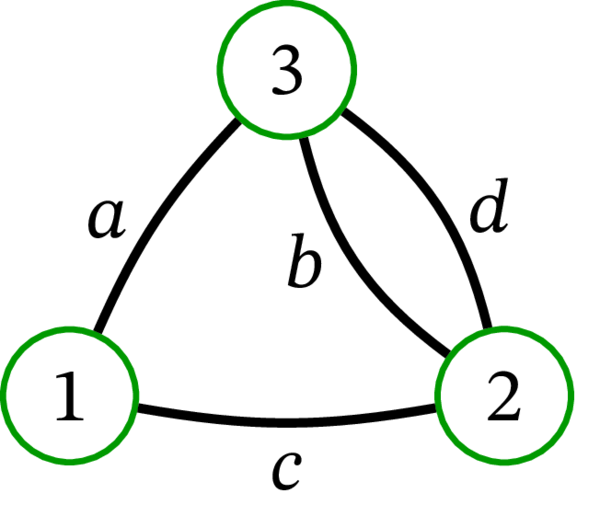
\(G\) に対応するグラフ \(\mathcal{S}\) を次に示す:

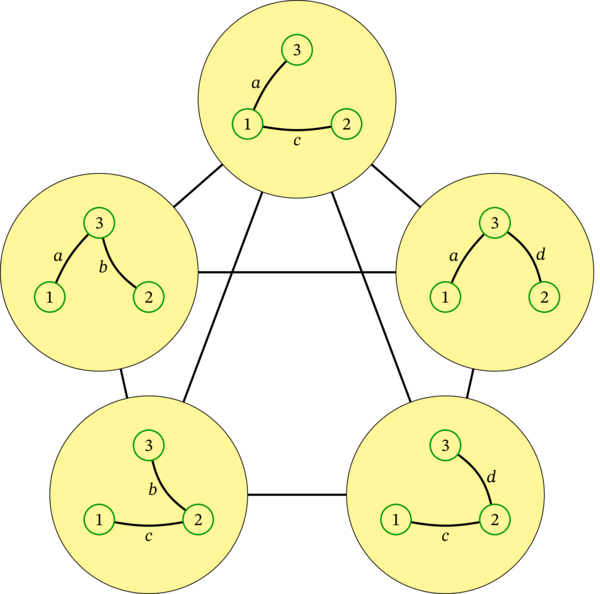
ここから分かるように、\(G\) の全域木が \(\mathcal{S}\) の頂点となる。]

5.4.7全域森の存在と構築

連結なグラフが全域木を持つことは分かった。非連結なグラフに対しては何が言えるだろうか？

[証明] 定理 5.4.6 を多重グラフの各成分に適用し、各成分の全域木を一つにまとめれば全域森が得られる。□