5.15. 無向グラフに対する行列木定理

5.15.1定理

行列木定理は \(G^{\operatorname*{bidir}}\) の形をした有向グラフに適用すると単純になる:

[証明] (a): \(G\) の頂点を任意に取って \(r\) とする。命題 5.13.1 (b) より、次の全単射の存在が分かる:

よって bijection principle と行列木定理 (定理 5.14.7) より、次が分かる:

以上で定理 5.15.1 (a) は証明された。

(b): これから次の等式を示す:

この等式は純粋に線形代数的な議論で証明でき、\(L\) が有向グラフのラプラシアンである事実は利用されないことに注意してほしい。\(L\) が任意の正方行列だとしても式 \((1)\) は証明できる。

式 \((1)\) が証明できれば、定理 5.15.1 (b) は次の変形によって簡単に示せる:

よって式 \((1)\) を示せばよい。

厳密な証明は [21s, Proposition 6.4.29] または https://math.stackexchange.com/a/3989575/ を参照してほしい (どちらも多項式 \(\det\left( tI_{n}+L\right) \) の \(t^1\) の係数 \(c_{1}\) だけではなく全ての係数 \(c_{0},c_{1},\ldots,c_{n}\) を陽に記述している)。ここでは簡単な例を使って式 \((1)\) の証明の概略を示す。

計算したいのは \(c_{1}\) である。言い換えれば、多項式 \(\det\left( tI_{n}+L\right) \) の \(t^1\) の係数を求めたい。例えば \(n=4\) なら、\(L\) は次の形をしている:

よって \(\det\left( tI_{n}+L\right)\) は次のように書ける:

右辺を Leibniz の公式で展開し、そこから生じる積をさらに展開することを考える。例えば積 \(\left( t+a\right) \left( t+b^{\prime}\right) d^{\prime\prime} c^{\prime\prime\prime}\) を展開すると

となる。注目しているのは多項式 \(\det\left( tI_{n}+L\right) \) の \(t^1\) の係数なので、展開後の式の \(t\) を一つだけ含む項だけを考えればよい。そういった項はどのように生まれるだろうか？ \(\left( t+a\right) \left( t+b^{\prime}\right) d^{\prime\prime} c^{\prime\prime\prime}\) といった積を展開した項が \(t^{1}\) を含むには、\(L\) の対角成分が少なくとも一つ必要になる (例えば \(cd^{\prime}b^{\prime\prime}a^{\prime\prime\prime}\) のような積は \(t^{1}\) の項を持たない)。積に含まれる \(L\) の \(r\) 番目の対角成分に注目すると、積の残りの部分は \(\det\left( L_{\sim r,\sim r}\right) \) の展開の一部となる (\(t^{1}\) を考えているので、積の残りの部分に含まれる \(t\) は無視できる)。全て合わせると、多項式 \(\det\left( tI_{n}+L\right) \) の \(t^{1}\) の係数は \(\displaystyle \sum_{r=1}^{n}\det\left( L_{\sim r,\sim r}\right) \) だと分かる。以上で式 \((1)\) が示せたので、定理 5.15.1 (b) も証明された。

(c): (b) で考えた多項式 \(\det\left( tI_{n}+L\right) \) の \(t^1\) の係数 \(c_{1}\) にここでも注目する。

\(L\) の特性多項式 \(\det\left( tI_{n}-L\right) \) は最高次の係数が \(1\) の \(n\) 次多項式であり、その根は \(L\) の固有値 \(\lambda_{1},\lambda_{2},\ldots,\lambda_{n}\) であることが知られている。よって特性多項式は次のように因数分解できる:

両辺の \(t\) を \(-1\) に置き換えると次の等式を得る:

両辺に \(\left( -1\right) ^{n}\) を乗じると次の等式を得る:

最後の式に注目すると、多項式 \(\det\left( tI_{n}+L\right) \) の \(t^{1}\) の係数が \(\lambda_{1}\lambda_{2}\cdots\lambda_{n-1}\) だと分かる。この値は \(c_{1}\) の定義そのものだから、\(c_{1}=\lambda_{1}\lambda_{2}\cdots\lambda_{n-1}\) を得る。よって定理 5.15.1 (b) より次の等式を得る:

以上で定理 5.15.1 (c) は証明された。□

5.15.2応用: \(K_{n,m}\) の全域木の数え上げ

有向グラフのラプラシアンが計算可能な固有値を持つことも多いので、定理 5.15.1 (c) は非常に実用性が高い。ラプラシアンの固有値を通して全域木の個数を計算できるグラフの意外な例として \(n\) 次元超立方体グラフ \(Q_{n}\) (以前に第 2.14.4 項で触れた) を練習問題 5.26 で見る。

ただ、まずは単純な例を見る。次の問題では定理 5.15.1 (a) で十分となる:

練習問題 5.23

正整数 \(n\), \(m\) に対して、単純グラフ \(K_{n,m}\) を次のように定義する: まず、\(K_{n,m}\) は次の \(n+m\) 個の頂点を持つ:

\[ 1,2,\ldots,n, \qquad -1,-2,\ldots,-m \]

そして、\(K_{n,m}\) の任意の頂点 \(i\), \(j\) は両者が逆の符号を持つとき、かつそのときに限って隣接する (任意の正の頂点は全ての負の頂点と隣接し、同じ符号の頂点同士は隣接しない)。

例えば、\(K_{5,2}\) は次のグラフである:

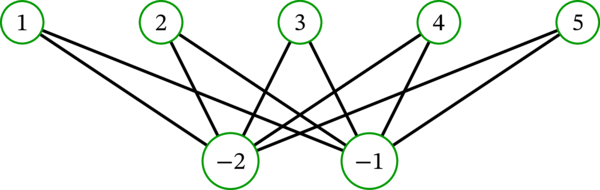
\(K_{n,m}\) の全域木はいくつあるだろうか？

[解答] 負の頂点 \(-1,-2,\ldots,-m\) を \(n+1,n+2,\ldots,n+m\) と改名すれば、有向グラフ \(K_{n,m}^{\operatorname*{bidir}}\) のラプラシアン \(L\) はブロック行列として次のように書ける:

ここで \(A\), \(B\), \(C\), \(D\) は次のように定義される:

• \(A\) は \(n\times n\) の対角行列であり、対角成分は全て \(m\) に等しい (正の頂点同士を結ぶ辺は存在せず、任意の正の頂点は次数 \(m\) を持つため)。

• \(B\) は \(n\times m\) 行列であり、全ての要素が \(-1\) に等しい。

• \(C\) は \(m \times n\) 行列であり、全ての要素が \(-1\) に等しい。

• \(D\) は \(m\times m\) の対角行列であり、対角成分は全て \(n\) に等しい。

例えば \(n=3\), \(m=2\) なら、ラプラシアン \(L\) は次のようになる:

定理 5.15.1 (a) より、\(K_{n,m}\) の任意の頂点 \(r\) に対して次の等式が成り立つ:

よって、何らかの頂点 \(r\) に対して \(\det\left( L_{\sim r,\sim r}\right) \) を計算すればよい。\(r=1\) とする。このとき \(L\) の小行列 \(L_{\sim r,\sim r}=L_{\sim 1,\sim1}\) はブロック行列として次のように書ける:

ここで:

• \(\widetilde{A}\) は \(\left(n - 1\right) \times \left(n - 1\right)\) の対角行列であり、対角成分は全て \(m\) に等しい。

• \(\widetilde{B}\) は \(\left( n-1\right) \times m\) 行列であり、全ての要素が \(-1\) に等しい。

• \(\widetilde{C}\) は \(m \times \left( n-1\right)\) 行列であり、全ての要素が \(-1\) に等しい。

• \(D\) は \(m\times m\) の対角行列であり、対角成分は全て \(n\) に等しい。

幸い、ブロック行列の行列式は (少なくともブロックの一部が可逆であれば) 簡単に計算できる場合が多い。例えば Schur 補行列は便利な公式を与える。しかし、今解くべき問題では \(\widetilde{A}\) と \(D\) が恒等行列の定数倍 (具体的には \(\widetilde{A}=mI_{n-1}\) および \(D=nI_{m}\)) なので、行列式はさらに簡単に計算できる: \(L_{\sim r,\sim r}=\left( \begin{array}{cc}\widetilde{A} & \widetilde{B}\\ \widetilde{C} & D \end{array}\right)\) に対して、「第 \(1\) ブロック行」\(\left(\begin{array}{cc}\widetilde{A} & \widetilde{B} \end{array}\right)\) の \(\widetilde{C}\widetilde{A}^{-1}\) 倍を「第 \(2\) ブロック行」\(\left(\begin{array}{cc}\widetilde{C} & D \end{array} \right)\)から引く「ブロック単位の行変形」を施せばよい (この変形は行列式を変化させない ── 行列式が \(1\) の行列 \(\left( \begin{array}{cc}I_{n-1} & 0\\ -\widetilde{C}\widetilde{A}^{-1} & I_{m} \end{array}\right)\) を左から乗じるのに等しい)。つまり、考えている行列式は次のように変形できる:

最後の行列は「ブロック上三角行列」なので、その行列は次のように計算できる¹:

\(\widetilde{A}\) は対角成分が全て \(m\) の \(n\times n\) 対角行列なので、\(\det\widetilde{A}=m^{n-1}\) が分かる。\(\det\left( D-\widetilde{C}\widetilde{A}^{-1}\widetilde{B}\right) \) の計算はこれより面倒にはなるものの、不可能ではない: 行列 \(\widetilde{A}^{-1}\) は対角成分が全て \(m^{-1}\) の対角行列なので、\(\widetilde{C}\widetilde{A}^{-1}\widetilde{B}=m^{-1}\widetilde{C}\widetilde{B}\) が成り立つ。\(\widetilde{C}\) と \(\widetilde{B}\) の要素は全て \(-1\) なので、\(\widetilde{C}\widetilde{B}\) の要素は全て \(n-1\) となる。よって、\(D-\widetilde{C}\widetilde{A}^{-1}\widetilde{B}\) は対角成分が全て \(n-m^{-1}\left( n-1\right) \) で非対角成分が全て \(-m^{-1}\left( n-1\right) \) の \(n\times n\) 行列と分かる。これに非常によく似た形をした行列の行列式は Cayley の公式 (第 5.14.5 項) を示すときに計算した。一般的な命題として書き換えると次のようになる:

この命題は第 5.14.5 項と同様の議論で証明できる; この命題については後でもう一度触れる。今考えている行列式では \(n=m\), \(\ x=n-m^{-1}\left( n-1\right)\), \(\ a=-m^{-1}\left( n-1\right)\) だから、次の等式を得る:

これまでに示してきた等式と 定理 5.15.1 (a) より次が分かる:

よって、次の定理が証明された:

この定理の組合せ論的な証明は [AbuSbe88] から確認できる。

練習問題 5.24

正整数 \(n\) に対して、単純グラフ \(K_{n,2}\) を次のように定める: \(K_{n,2}\) の頂点集合は \(\left\{ 1,2,\ldots,n\right\} \cup\left\{ -1,-2\right\} \) であり、\(K_{n,2}\) の任意の二頂点は符号が異なるとき、かつそのときに限って隣接する (任意の正の頂点は全ての負の頂点と隣接し、同じ符号の頂点同士は隣接しない)。この \(K_{n,2}\) を通常通りの方法で多重グラフとみなす。

1. 行列木定理を使わずに、\(K_{n, 2}\) の全域木の個数が \(n \cdot2^{n-1}\) だと示せ。

2. \(K_{n,2}\) に辺 \(\left\{ -1,-2\right\} \) を追加して得られるグラフを \(K_{n,2}^{\prime}\) とする。\(K_{n,2}^{\prime}\) に全域木はいくつあるか？

[例: \(n=5\) に対する \(K_{n,2}\) を次に示す:

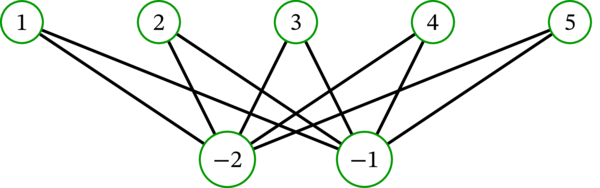
\(K_{n,2}^{\prime}\) を次に示す:

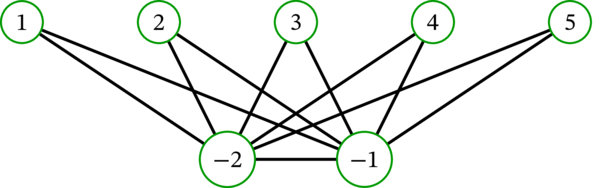
\(K_{n,2}\) に辺 \(\left\{ -1,-2\right\} \) を追加したグラフが \(K_{n,2}^{\prime}\) である。]

練習問題 5.26

\(n\) を正整数、\(Q_{n}\) を \(n\) 次元超立方体グラフ (定義 2.14.7) とする。復習しておくと、\(Q_{n}\) の頂点集合は長さ \(n\) のビット文字列であり、任意の二頂点はビット文字列として \(1\) ビットだけ異なるとき、かつそのときに限って隣接する。\(Q_{n}\) の全域木の個数を計算しよう。

有向グラフ \(Q_{n}^{\operatorname*{bidir}}\) のラプラシアンを \(L\) とする。これから \(L\) を \(V\times V\) 行列 (行と列が \(V\) に属するビット文字列で特定される \(2^{n}\times2^{n}\) 行列) として扱う。

ビット文字列 \(a\) の \(i\) 番目のビットを \(a_{i}\) と表す。例えば、任意のビット文字列 \(a \in V\) に対して \(a = \left( a_{1}, a_{2}, \ldots, a_{n} \right) \) が成り立つ (この列を \(a_{1} a_{2} \cdots a_{n}\) と省略する記法は積と混同する可能性があるので使用しない)。

任意の二つのビット文字列 \(a,b \in V\) に対して、整数 \(a_{1}b_{1}+a_{2}b_{2}+\cdots+a_{n}b_{n}\) を \(\left\langle a,b\right\rangle \) と定める。

1. 全てのビット文字列 \(a \in V\) が次の等式を満たすと示せ:

   \[ \sum_{b\in V}\left( -1\right) ^{\left\langle a,b\right\rangle }= \begin{cases} 2^{n} & (a=\mathbf{0} \text{ のとき}) \\ 0 & (\text{それ以外のとき}) \end{cases} \]

   ここで \(\mathbf{0}\) はビット文字列 \(\left( 0,0,\ldots,0\right) \in V\) を表す。

続いて、\(\left( a,b\right) \) 要素が次の等式を満たす \(V \times V\) 行列を \(G\) と定める:

\[ G_{a,b}=\left( -1\right) ^{\left\langle a,b\right\rangle }\qquad (\forall a,b\in V) \]

さらに、\(V \times V\) の対角行列 \(D\) を次の等式で定義する:

\[ \begin{aligned} D_{a,a} & =2\cdot\left(\text{\# } \text{\(a_{i}=1\) が成り立つ \(i\in\left\{ 1,2,\ldots,n\right\} \) }\right) \\ & =2\cdot\left(\text{\(a\) に含まれる \(1\) の個数}\right) \qquad (\forall a\in V) \end{aligned} \]

(\(D\) の非対角成分は \(0\) である。)

次の命題を示せ:

2. \(G^{2} = 2^{n} \cdot I\) が成り立つ (\(I\) は \(V \times V\) の恒等行列を表す)。

3. \(GLG^{-1} = D\) が成り立つ。

4. \(L\) の固有値は \(k \in\left\{ 0, 1, \ldots, n \right\} \) を使って \(2k\) と書ける。固有値 \(2k\) の重複度は \(\dbinom{n}{k}\) である。

5. \(Q_{n}\) の全域木の個数は

   \[ \dfrac{1}{2^{n}}\prod_{k=1}^{n}\left( 2k\right) ^{\binom{n}{k}} \]

   である。

[例: \(n=3\) とした場合の例を示す。このとき \(Q_{n}\) は次のグラフとなる:

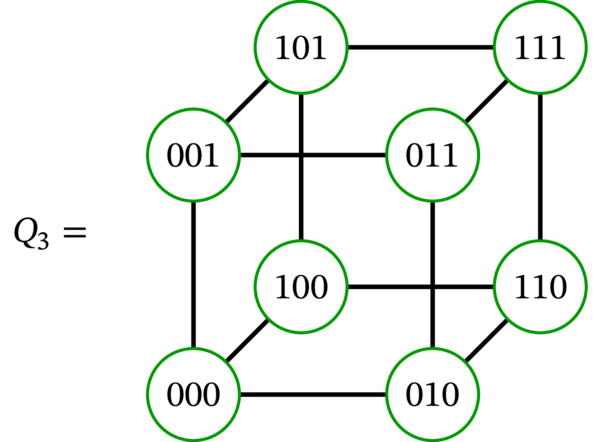
行列 \(L\), \(G\), \(D\) は次の通りである:

\[ \begin{aligned} \small L & = \begin{pmatrix} 3 & -1 & -1 & 0 & -1 & 0 & 0 & 0\\ -1 & 3 & 0 & -1 & 0 & -1 & 0 & 0\\ -1 & 0 & 3 & -1 & 0 & 0 & -1 & 0\\ 0 & -1 & -1 & 3 & 0 & 0 & 0 & -1\\ -1 & 0 & 0 & 0 & 3 & -1 & -1 & 0\\ 0 & -1 & 0 & 0 & -1 & 3 & 0 & -1\\ 0 & 0 & -1 & 0 & -1 & 0 & 3 & -1\\ 0 & 0 & 0 & -1 & 0 & -1 & -1 & 3 \end{pmatrix} \\[55pt] G & = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{pmatrix} \\[55pt] D & = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 6 \end{pmatrix} \end{aligned} \]

ここで、行列の各行と各列は順にビット文字列 \(000\), \(001\), \(010\), \(011\), \(100\), \(101\), \(110\), \(111\) に対応する。]

続いて先ほど予告したように、もう一度命題 5.15.2 に触れる。この命題は行変換を使えば簡単に証明できる (第 \(1\) 行を他の全ての行から引き、第 \(1\) 行以外の行から \((x-a)\) をくくり出す。その後、第 \(1\) 行以外の行の \(a\) 倍をそれぞれ第 \(1\) 行から引くと三角行列が得られる )。一方で、命題 5.15.2 は次に示す行列式に関する等式の特殊化とみなすこともできる:

どちらも行列式の計算の良い練習問題となるだろう。命題 5.15.4 の証明は [Grinbe20, Exercise 6.21] から、命題 5.14.5 の証明は https://math.stackexchange.com/a/2112473/ から確認できる。

行列木定理の応用については [KleSta19] や [Rubey00] を、行列木定理に関連する様々な結果については [Holzer22] を参照してほしい。