5.19. 重み付き行列木定理

5.19.1定義

ここまでは有向木の数え上げ (counting) を考えてきた。数え上げの自然な一般化として重み付き数え上げ (weighted counting) がある ── つまり、有向木のそれぞれに何らかの重み (weight) を割り振り、全ての有向木の重みの和を求める問題である。任意の有向木の重みを \(1\) とすれば重み付き数え上げで有向木の個数を求められるので、重み付き数え上げは確かに数え上げの一般化と言える。

有向木の重みを適当に割り振ったのでは、重み付き和に特別な意味は生まれない。しかし、良い性質を持った重みの付け方は存在する。例えば、有向グラフの弧に重みを割り当て、有向木の重みを有向木に含まれる全ての弧の積として定義したとき、何が言えるかを考えてみよう。

これらの定義は「重み無し」の定義を一般化したものである。実際、全ての弧の重みを \(1\) とすれば、頂点 \(i\) の重み付き出次数 \(\deg^{+w}i\) は通常の出次数 \(\deg i\) に、重み付きラプラシアン \(L^{w}\) は通常のラプラシアン \(L\) に、部分有向グラフ \(B\) の重み \(w\left( B\right) \) は \(1\) に等しくなる。

5.19.2重み付き行列木定理

行列木定理 (定理 5.14.7) は次のように一般化できる:

例 5.19.3

\(D\) を次の多重有向グラフとする:

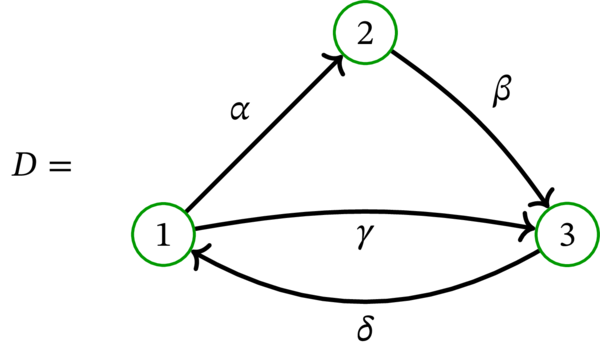
そして \(r = 3\) とする。このとき \(r\) を終根とする \(D\) の全域有向木は二つ存在する: 弧 \(\alpha\), \(\beta\) を持つものと、弧 \(\gamma\), \(\beta\) を持つものである。前者の重みは \(w_{\alpha}w_{\beta}\) で、後者の重みは \(w_{\gamma}w_{\beta}\) だから、次の等式が成り立つ:

\[ \sum_{\substack{B:\, r \text{ を終根とする } \\ D \text{ の全域有向木}}}w\left( B\right) =w_{\alpha}w_{\beta}+w_{\gamma}w_{\beta} \qquad (9) \]

一方、\(D\) の重み付きラプラシアン \(L^{w}\) は次の通りである:

\[ L^{w}=\left( \begin{array}{ccc} w_{\alpha}+w_{\gamma} & -w_{\alpha} & -w_{\gamma}\\ 0 & w_{\beta} & -w_{\beta}\\ -w_{\delta} & 0 & w_{\delta} \end{array} \right) \]

[定義より \(\deg^{+w}1=w_{\alpha}+w_{\gamma}\), \(\,a_{1,1}^{w}=0\), \(\,a_{1,2}^{w}=w_{\alpha}\) などが成り立つため。] ここから次の等式を得る:

\[ \begin{aligned} L_{\sim3,\sim3}^{w} & =\left(\begin{array}{cc}w_{\alpha}+w_{\gamma} & -w_{\alpha}\\ 0 & w_{\beta} \end{array}\right) \\ \therefore\ \det\left( L_{\sim3,\sim3}^{w}\right) & =\left( w_{\alpha}+w_{\gamma }\right) w_{\beta}=w_{\alpha}w_{\beta}+w_{\gamma}w_{\beta} \end{aligned} \]

この式の右辺は式 \((9)\) の右辺と一致する。つまり、ここで考えた \(D\) と \(r\) に対して重み付き行列木定理は成り立つ。

先述した通り、重み付き行列木定理で弧の重み \(w_{a}\) を全て \(1\) にすると通常の行列木定理が得られるので、重み付き行列木定理は通常の行列木定理の一般化である。

しかし、逆方向の議論もできる: 通常の行列木定理を使った重み付き行列木定理の証明が存在する。これを示そう。

5.19.3多項式等価性の永続原理

まず、多項式等価性の永続原理 (principle of permanence of polynomial identities) や多項式等価性のトリック (polynomial identity trick) などと呼ばれる代数学における基礎的な結果を復習しておく。これは次のように表現できる:

定理 5.19.4 は「二つの多項式が等しいと示すには、非負整数点で等しいと示せば十分である」と表現されることもある (ここで非負整数点とは非負整数だけからなる点 ── 多項式への入力 ── を意味する)。さらに短く「多項式の等価性 (二つの多項式間の等式) に必要なのは非負整数における確認だけ」と言うこともできる。例えば、次の等式を示したいとする:

このとき、\(x\), \(y\) が任意の非負整数と仮定して等式が証明できれば、多項式としての等式が証明できたことになる。つまり \(x\) と \(y\) が任意の可換環の要素であるときも等式は成り立つ。

任意の非負整数で成り立つことが分かっている多項式の等価性が任意の入力に対しても成り立つと示すことが定理 5.19.4 の典型的な応用である。そういった議論は [19fco, § 2.6.3 and § 2.6.4] などから確認できる。また、[Conrad21, Theorem 2.6] は定理 5.19.4 の変種である。実際、[Conrad21, Theorem 2.6] の証明は自明に定理 5.19.4 にも適用できる (「\(\mathbb{C}^{k}\) 上の非空開集合」を「\(\mathbb{N}^{k}\)」に置き換えればよい)。本当のことを言えば、定理 5.19.4 の「非負整数」や 「\(\mathbb{N}^{m}\)」 に特別な意味は無く、この部分は任意の無限集合に置き換えても定理は成り立つ (さらに、十分に大きな有限集合で置き換えることもできる ── ここで「十分に大きい」は「要素数が \(\max\left\{ \deg P,\deg Q\right\} \) より大きい」を意味する)。そういった事実を考慮した非常に一般化なバージョンの定理 5.19.4 は [Alon02, Lemma 2.1] から確認できる¹。

5.19.4重み付き行列木定理の証明

通常の行列木定理から重み付き行列木定理を導く準備がこれで整った:

[定理 5.19.2 の証明] \(D\) と \(r\) を固定するとき、定理 5.19.2 の主張は弧の重み \(w_{a}\) の多項式に関する等式の成立である。 [例えば例 5.19.3 では \(w_{\alpha}w_{\beta}+w_{\gamma}w_{\beta}=\det {\begin{pmatrix} w_{\alpha}+w_{\gamma} & -w_{\alpha}\\ 0 & w_{\beta} \end{pmatrix}}\) という等式の成立を確認した。]

よって定理 5.19.4 より、全ての重み \(w_{a}\) が非負整数という仮定の下で等式が成り立つと示せれば十分となる。そこで一般性を失うことなく全ての重み \(w_{a}\) が非負整数だと仮定する。

\(D\) の各弧 \(a\) を、\(w_{a}\) 個の \(a\) のコピー (\(a\) と同じ始点と終点を持つ弧) で置き換えたグラフ \(D^{\prime}\) を考える。この例を示す:

例 5.19.5

次の有向グラフを \(D\) とする:

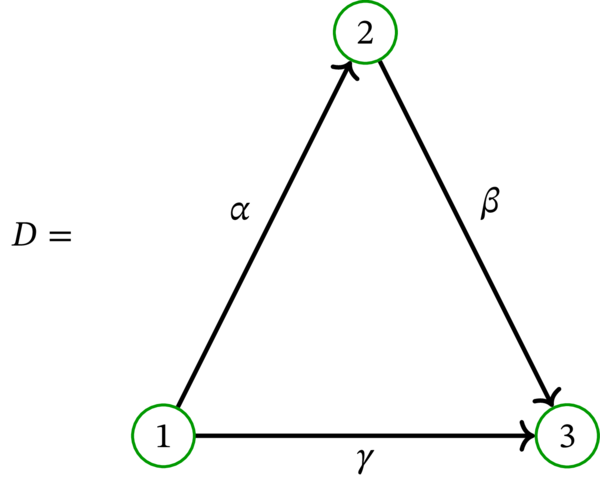
\(D\) の弧の重みを \(w_{\alpha}=2\), \(w_{\beta}=3\), \(w_{\gamma}=2\) と定める。このとき \(D^{\prime}\) は次の有向グラフである:

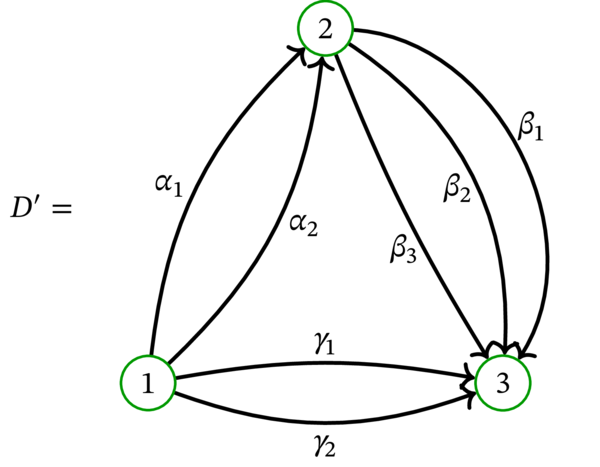
ここで \(\alpha_{1}\), \(\alpha_{2}\) は \(\alpha\) から得られた弧を表し、他の記号についても同様となる。

こうして得られる有向グラフ \(D^{\prime}\) は \(D\) と同じ頂点を持つものの、\(D\) の各弧 \(a\) は \(D^{\prime}\) で \(w_{a}\) 個の弧に変換される。つまり、\(D\) の頂点 \(i\) が重み付き出次数 \(\deg^{+w}i\) を持つとき、\(D^{\prime}\) の頂点 \(i\) は (通常の、重みを考えない) 出次数 \(\deg^{+}i\) を持つ。よって \(D\) の重み付きラプラシアン \(L^{w}\) は \(D^{\prime}\) の (通常の、重みを考えない) ラプラシアンに等しい。

繰り返しになるが、有向グラフ \(D^{\prime}\) は \(D\) と同じ頂点を持つものの、\(D\) の各弧 \(a\) は \(D^{\prime}\) で \(w_{a}\) 個の弧に変換される。よって \(D\) の任意の部分有向グラフ \(B\) に対して、\(B\) と同じ頂点を持ち \(B\) と同型な \(D^{\prime}\) の部分有向グラフは \(w\left( B\right) \) 個存在する (\(B\) の各弧 \(a\) に対応する弧の選択肢が \(a_{w}\) 個あるため)。さらに、この対応関係において \(D\) の全域有向木は \(D^{\prime}\) の全域有向木に関連付き²、\(D^{\prime}\) の任意の全域有向木はちょうど一つの \(B\) に対応する。よって次の等式が分かる:

よって通常の行列木定理 (定理 5.14.7) を \(D^{\prime}\) に適用すれば、\(D\) に対する重み付き行列木定理が得られる (\(D\) の重み付きラプラシアンが \(D^{\prime}\) のラプラシアンに等しいため)。以上で定理 5.19.2 は証明された。□

[Remark: 本書で示した通常の行列木定理の証明と同様の議論で重み付き行列木定理を証明することも難しくない。]

5.19.5応用: 次数を考慮した木の数え上げ

重み付き行列木定理を使うと、通常の行列木定理からは明らかでない結果が得られる。その一つを示す:

[解答] \(n\)-木は完全グラフ \(K_{n}\) の全域木に等しい。

これから条件 \(\deg i=d_{i}\) を考慮した数え上げを行うために、生成関数を利用する。そこで \(d_{1},d_{2},\ldots,d_{n}\) を固定して議論する代わりに、次の多項式を考える:

この多項式は \(n\) 個の不定元 \(x_{1},x_{2},\ldots,x_{n}\) を持ち、\(\deg i\) は \(T\) における \(i\) の次数を意味する。全ての頂点 \(i\) が条件 \(\deg i = d_{i}\) を満たすような \(n\)-木の個数は、この多項式の \(x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{n}^{d_{n}}\) の係数に等しい。 [条件を満たす任意の \(n\)-木は右辺の和で単項式 \(x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{n}^{d_{n}}\) となり、他の任意の \(n\)-木は異なる単項式となるため。]

\(K_{n}\) の任意の辺 \(ij\) に重み \(w_{ij}\colonequals x_{i}x_{j}\) を割り当てる。このとき \(P\left( x_{1},x_{2},\ldots,x_{n}\right) \) の定義は次のように書き換えられる:

ここで \(w\left( T\right) \) は \(T\) が持つ辺の重みの積を表す。 [実際、\(K_{n}\) の任意の部分グラフ \(T\) に対して、その重み \(w\left(T\right)\) は \(x_{1}^{\deg1}x_{2}^{\deg2}\cdots x_{n}^{\deg n}\) に等しい (\(\deg i\) は \(T\) における頂点 \(i\) の次数を表す)。]

続いて、前段落でグラフ \(K_{n}\) の辺に割り当てたのと「同じ」重みを有向グラフ \(K_{n}^{\operatorname*{bidir}}\) の辺に割り当てる。つまり、\(K_{n}\) の辺 \(ij\) に対応する二つの弧 \(\left( ij,1\right) \) と \(\left( ij,2\right) \) に重み \(x_{i}x_{j}\) を割り当てる。このとき次の等式が成り立つ:

命題 5.13.1 より、\(K_{n}\) の全域木と \(1\) を終根とする \(K_{n}^{\operatorname*{bidir}}\) の全域有向木の間には全単射が存在する。よって次の等式が成り立つ:

さらに、この全単射は (式 \((12)\) より) 重みを保存するので、次の等式も成り立つ:

\(K_{n}\) の全域木は \(n\)-木そのものなので、この等式は次のように書き換えられる:

右辺の計算では重み付き行列木定理が利用できる。上で定義した重みに対する \(K_{n}^{\operatorname*{bidir}}\) の重み付きラプラシアンを \(L^{w}\) とする。\(L^{w}\) は \(n\times n\) 行列であり、その要素は次の式で与えられる:

ここから小行列式 \(\det\left( L_{\sim1,\sim1}^{w}\right) \) を計算するのは難しくない (例えば、Cayley の公式 (定理 5.14.8) の証明で見たような行変形を使う³)。実際に計算すると次の値が得られる:

これまでに分かったことをまとめる:

求めたいのは多項式 \(P\left( x_{1},x_{2},\ldots,x_{n}\right)\) の \(x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{n}^{d_{n}}\) の係数だった。上式より次の等式が分かる:

多項式 \(\left( x_{1}+x_{2}+\cdots +x_{n}\right) ^{n-2}\) の係数、一般には多項式 \(\left( x_{1}+x_{2}+\cdots+x_{n}\right) ^{m}\) (\(m\in\mathbb{N}\)) の係数はどうすれば表現できるだろうか？ この値には多項係数 (multinomial coefficients) という名前が付いている。その定義を次に示す: 非負整数 \(p_{1},p_{2},\ldots,p_{n},q\) が \(q=p_{1}+p_{2}+\cdots+p_{n}\) を満たすとき、多項係数 \(\dbinom{q}{p_{1},p_{2},\ldots,p_{n}}\) は \(\dfrac{q!}{p_{1}!p_{2}!\cdots p_{n}!}\) と定義される (\(n=2\) のとき多項係数は二項係数に等しい)。\(q=p_{1}+p_{2}+\cdots+p_{n}\) が満たされないときの多項係数は \(0\) と定義される。いずれの場合でも、多項係数が整数であることは容易に分かる⁴。多項定理 (multinomial theorem) によると、任意の \(k \in \mathbb{N}\) で次の等式が成り立つ:

[条件 \(i_{1}+i_{2}+\cdots+i_{n}=k\) が成り立たないとき \(\dbinom{k}{i_{1},i_{2},\ldots,i_{n}} = 0\) と定義されるので、この条件を和から除去しても問題ない。] ここから次の等式が分かる:

今までの結果をまとめると、次の等式を得る:

一方で先述したように、\(P\left( x_{1},x_{2},\ldots,x_{n}\right) \) の \(x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{n}^{d_{n}}\) の係数は全ての \(i \in \left\{1,2,\ldots,n\right\}\) が \(\deg i = d_{i}\) を満たす \(n\)-木の個数に等しい。つまり、以上で次の定理が証明された:

5.19.6重み付き調和ベクトル定理

ラプラシアンに対する調和ベクトル定理 (定理 5.18.1) にも重み付きバージョンが存在する:

[証明] 重みの無いケースと同様に示せる。□

本書における全域木と全域木の数え上げに関する話題はここで終了となる。興味のある読者は [Rubey00], [Holzer22], [Moon70], [GrSaSu14] などを使って学習を続けることができる。