第 14 章適応フィルタ

ここまでに考えた問題では、追跡する物体がプロセスモデルに従って行儀良く振る舞っていた。例えば直線的に移動する物体を追跡するなら、定常速度フィルタ (定常速度モデルを仮定するカルマンフィルタ) を使うことができる。物体が直線上をそれなりに等しい速度で移動する限り、あるいは速度や進行方向を非常に少しずつ変化させる限り、このフィルタは優れた推定値を出力する。しかし追跡するのが機動 (maneuver) する目標、例えば曲がりくねった道路を進む車や風にもまれながら飛行する航空機だったらどうなるだろうか？こういった状況でフィルタの性能は大きく悪化する。あるいは海に浮かぶ帆船の追跡を考えてほしい。制御入力をモデルに組み込むことはできても、風や海流をモデル化する方法は存在しない。

この問題に対する最初のアプローチとして、プロセスノイズ行列 \(\mathbf{Q}\) を大きくして系のダイナミクスの予測不可能性をフィルタに伝えるというのがある。これはフィルタが発散しなくなるという意味で間違ってはいないが、こうすると結果は最適から遠く離れたものになる。\(\mathbf{Q}\) を大きくすると観測値に含まれるノイズが重視された結果となるためだ。この例はすぐ後で見る。

本章では適応フィルタ (adaptive filter) という考え方を議論する。適応フィルタはプロセスノイズで捉えられないダイナミクスを検出すると、自身をそれに適応させる。これから問題の例を示し、適応フィルタをいくつか説明する。

14.1 軌道する目標の追跡

まず機動する目標のシミュレーションが必要になる。途中で速度や旋回方向を設定できる簡単な二次元モデルを次に実装した。新しい速度や旋回方向を指定すると、目標は自身の状態を少しずつ新しい状態に変化させる:

In [3]

from math import sin, cos, radians

def angle_between(x, y):
    return min(y-x, y-x+360, y-x-360, key=abs)

class ManeuveringTarget(object):
    def __init__(self, x0, y0, v0, heading):
        self.x = x0
        self.y = y0
        self.vel = v0
        self.hdg = heading

        self.cmd_vel = v0
        self.cmd_hdg = heading
        self.vel_step = 0
        self.hdg_step = 0
        self.vel_delta = 0
        self.hdg_delta = 0

    def update(self):
        vx = self.vel * cos(radians(90-self.hdg))
        vy = self.vel * sin(radians(90-self.hdg))
        self.x += vx
        self.y += vy

        if self.hdg_step > 0:
            self.hdg_step -= 1
            self.hdg += self.hdg_delta

        if self.vel_step > 0:
            self.vel_step -= 1
            self.vel += self.vel_delta
        return (self.x, self.y)

    def set_commanded_heading(self, hdg_degrees, steps):
        self.cmd_hdg = hdg_degrees
        self.hdg_delta = angle_between(self.cmd_hdg,
                                       self.hdg) / steps
        if abs(self.hdg_delta) > 0:
            self.hdg_step = steps
        else:
            self.hdg_step = 0

    def set_commanded_speed(self, speed, steps):
        self.cmd_vel = speed
        self.vel_delta = (self.cmd_vel - self.vel) / steps
        if abs(self.vel_delta) > 0:
            self.vel_step = steps
        else:
            self.vel_step = 0

続いてノイズを持ったセンサーのシミュレーションを実装しよう:

In [4]

from numpy.random import randn

class NoisySensor(object):
    def __init__(self, std_noise=1.):
        self.std = std_noise

    def sense(self, pos):
        """
        実際の位置 (x,y) を受け取り、ノイズを加えた (x',y') を返す。
        """
        return (pos[0] + (randn() * self.std),
                pos[1] + (randn() * self.std))

次は移動経路を生成・プロットして、全てが正しく動いていることをテストする。データの生成は関数にして、異なる経路を試せるようにしておく (理由はすぐに明らかになる):

In [5]

import kf_book.book_plots as bp
import numpy as np
import matplotlib.pyplot as plt

def generate_data(steady_count, std):
    t = ManeuveringTarget(x0=0, y0=0, v0=0.3, heading=0)
    xs, ys = [], []

    for i in range(30):
        x, y = t.update()
        xs.append(x)
        ys.append(y)

    t.set_commanded_heading(310, 25)
    t.set_commanded_speed(1, 15)

    for i in range(steady_count):
        x, y = t.update()
        xs.append(x)
        ys.append(y)

    ns = NoisySensor(std)
    pos = np.array(list(zip(xs, ys)))
    zs = np.array([ns.sense(p) for p in pos])
    return pos, zs

sensor_std = 2.
track, zs = generate_data(50, sensor_std)
plt.figure()
bp.plot_measurements(*zip(*zs), alpha=0.1)
plt.plot(*zip(*track), color='b', label='track')
plt.axis('equal')
plt.legend(loc=4)
bp.set_labels(title='Track vs Measurements', x='X', y='Y')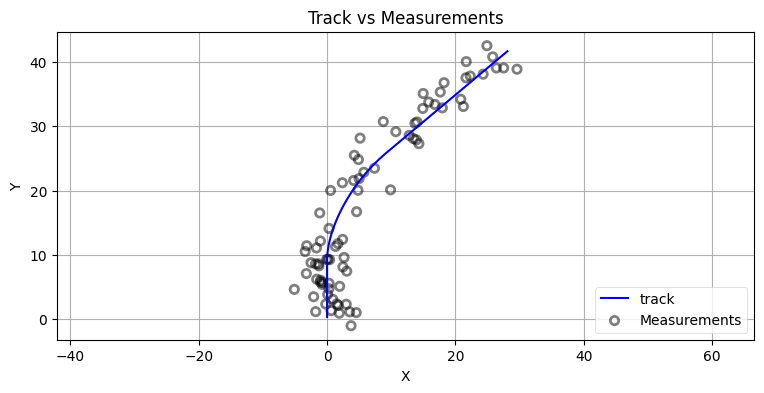

これだけ大きなノイズを加えておけば、様々な設計の選択肢が持つ効果が分かりやすくなる。

この物体を追跡するカルマンフィルタがこれで実装できる。ただ一点だけ単純化しておく。\(x\) 座標と \(y\) 座標は独立だから、別々に追跡できる。そこで本章ではコードと行列を可能な限り小さくするために、これ以降は \(x\) 座標だけを考えることにする。

最初は定常速度フィルタを実装しよう:

In [6]

from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise

def make_cv_filter(dt, std):
    cvfilter = KalmanFilter(dim_x = 2, dim_z=1)
    cvfilter.x = np.array([0., 0.])
    cvfilter.P *= 3
    cvfilter.R *= std**2
    cvfilter.F = np.array([[1, dt],
                           [0,  1]], dtype=float)
    cvfilter.H = np.array([[1, 0]], dtype=float)
    cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.02)
    return cvfilter

def initialize_filter(kf, std_R=None):
    """ ヘルパー関数: このフィルタは何度も初期化することになる。 """
    kf.x.fill(0.)
    kf.P = np.eye(kf.dim_x) * .1
    if std_R is not None:
        kf.R = np.eye(kf.dim_z) * std_R

実行する:

In [7]

sensor_std = 2.
dt = 0.1

# フィルタの初期化
cvfilter = make_cv_filter(dt, sensor_std)
initialize_filter(cvfilter)

track, zs = generate_data(50, sensor_std)

# フィルタの実行
z_xs = zs[:, 0]
kxs, _, _, _ = cvfilter.batch_filter(z_xs)

# plot results
bp.plot_track(track[:, 0], dt=dt)
bp.plot_filter(kxs[:, 0], dt=dt, label='KF')
bp.set_labels(title='Track vs KF', x='time (sec)', y='X');
plt.legend(loc=4);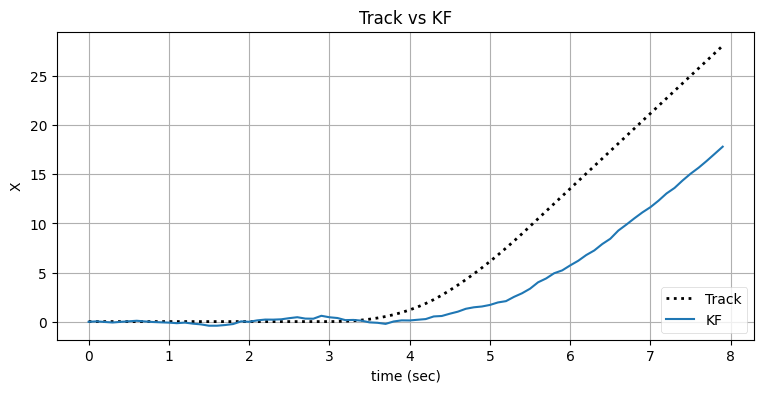

このカルマンフィルタは進行方向の変化を追跡できていない。g-h フィルタの章を思い出せば、こうなる原因は加速をモデルに含めていないためにフィルタが必ず入力に遅れるためである。ただ入力がこの後安定すれば、フィルタはそれに追いつけるはずだ。これを確認しておく:

In [8]

# フィルタをもう一度初期化する。
dt = 0.1
initialize_filter(cvfilter)

track2, zs2 = generate_data(150, sensor_std)
xs2 = track2[:, 0]
z_xs2 = zs2[:, 0]

kxs2, _, _, _ = cvfilter.batch_filter(z_xs2)

bp.plot_track(xs2, dt=dt)
bp.plot_filter(kxs2[:, 0], dt=dt, label='KF')
plt.legend(loc=4)
bp.set_labels(title='Effects of Acceleration',
              x='time (sec)', y='X')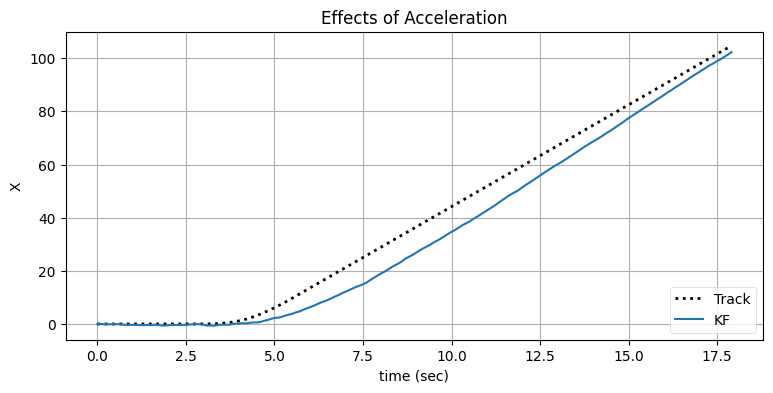

このフィルタに内在する問題は、入力の安定する間はプロセスモデルが正しいものの、物体が機動するときは正しくないことである。\(\mathbf{Q}\) を大きくすればこの問題に対処できる:

In [9]

# フィルタをもう一度初期化する。
dt = 0.1
initialize_filter(cvfilter)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=2.0)
track, zs = generate_data(50, sensor_std)

# もう一度追跡を行う。
kxs2, _, _, _ = cvfilter.batch_filter(z_xs2)
bp.plot_track(xs2, dt=dt)
bp.plot_filter(kxs2[:, 0], dt=dt, label='KF')
plt.legend(loc=4)
bp.set_labels(title='Large Q (var=2.0)', x='time (sec)', y='X')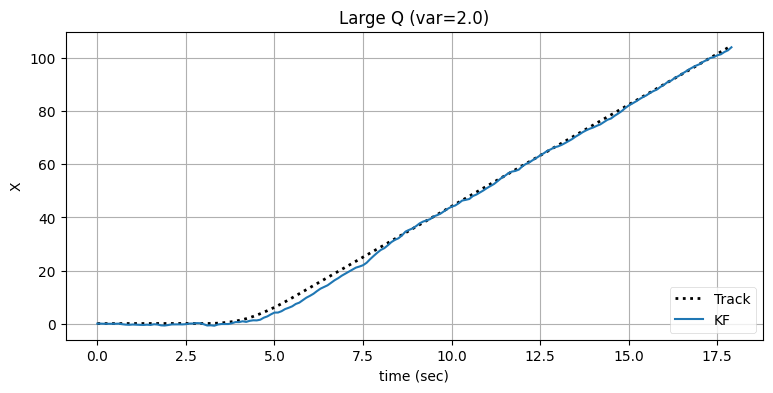

フィルタが正しい軌道に戻るまでの時間が短縮され、その代わり出力のノイズが増加したのが確認できる。ただ多くの追跡問題では、追跡開始から \(4\) 秒後から \(8\) 秒後の間にある遅延が許されない状況になる場合が多い。出力のノイズをさらに大きくしても構わないなら、\(\mathbf{Q}\) をさらに大きくすることで遅延をさらに小さくできる:

In [10]

# フィルタをもう一度初期化する。
dt = 0.1
initialize_filter(cvfilter)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=50.0)
track, zs = generate_data(50, sensor_std)

# もう一度追跡を行う。
cvfilter.x.fill(0.)
kxs2, _, _, _ = cvfilter.batch_filter(z_xs2)

bp.plot_track(xs2, dt=dt)
bp.plot_filter(kxs2[:, 0], dt=dt, label='KF')
plt.legend(loc=4)
bp.set_labels(title='Huge Q (var=50.0)', x='time (sec)', y='X')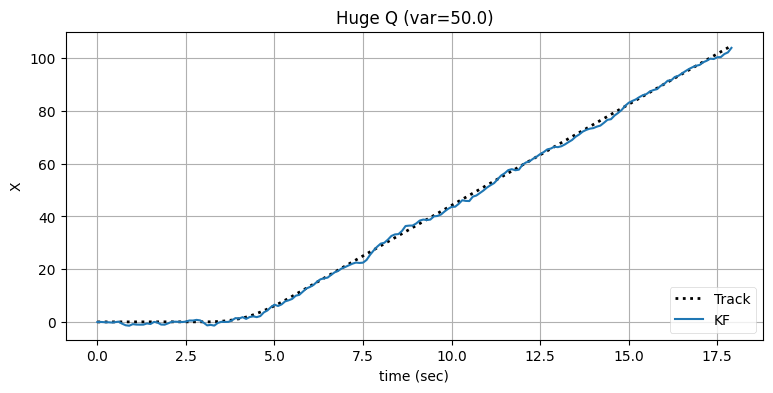

Out [10]\(\mathbf{Q}\) を極端に大きくしたときのフィルタの出力

機動は加速度を意味する。そこで定常加速度フィルタ (定常加速度モデルを仮定するカルマンフィルタ) を実装して、同じデータに対してどう振る舞うかを確認しよう:

In [11]

def make_ca_filter(dt, std):
    cafilter = KalmanFilter(dim_x=3, dim_z=1)
    cafilter.x = np.array([0., 0., 0.])
    cafilter.P *= 3
    cafilter.R *= std
    cafilter.Q = Q_discrete_white_noise(dim=3, dt=dt, var=0.02)
    cafilter.F = np.array([[1, dt, 0.5*dt*dt],
                           [0, 1,         dt],
                           [0, 0,          1]])
    cafilter.H = np.array([[1., 0, 0]])
    return cafilter

def initialize_const_accel(f):
    f.x = np.array([0., 0., 0.])
    f.P = np.eye(3) * 3

In [12]

dt = 0.1
cafilter = make_ca_filter(dt, sensor_std)
initialize_const_accel(cafilter)

kxs2, _, _, _ = cafilter.batch_filter(z_xs2)

bp.plot_track(xs2, dt=dt)
bp.plot_filter(kxs2[:, 0], dt=dt, label='KF')
plt.legend(loc=4)
bp.set_labels(title='Constant Acceleration Kalman Filter',
              x='time (sec)', y='X')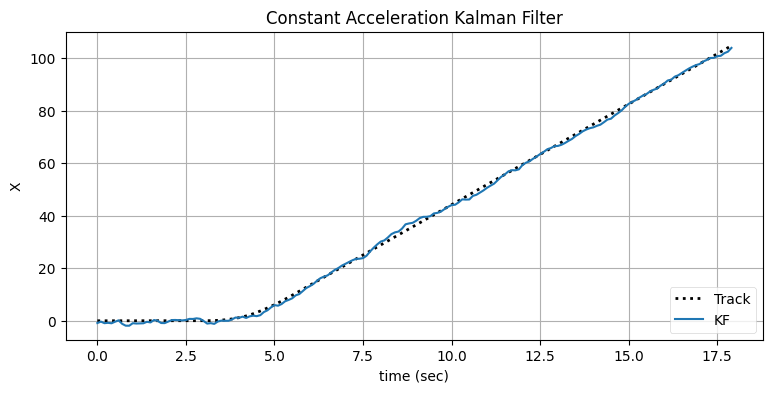

定常加速度フィルタは機動を遅延なく追跡できている。ただ、状態が安定しているときの出力に含まれるノイズが非常に大きいのが分かる。ノイズの多い出力が得られるのは、入力に含まれるノイズと機動の開始をフィルタが区別できていないためである。入力に加わるノイズによって加速度が発生し、フィルタの加速度項がそれを追跡してしまう。

どうしようもないように思える。定常速度モデルを使うと対象が加速するとき素早く反応できず、定常加速度モデルを使うと加速度が加わっていないときにノイズを加速度と誤解してしまう。

しかし、私たちを解決法に導く重要な洞察が一つある。対象が機動していないとき (加速度がゼロのとき) は定常速度フィルタが最適に振る舞う。また対象が機動するときは定常加速度フィルタ (およびプロセスノイズ行列 \(\mathbf{Q}\) を非常に大きくした定常速度フィルタ) が優れた振る舞いを見せる。フィルタが自身を追跡対象の振る舞いに適応させることができれば、二つのフィルタのいいとこどりができるかもしれない。

14.2 機動の検出

適応フィルタの作り方を議論する前に、まずは目標の機動を検出する方法を考えよう。機動しているかどうかが分からなければ、機動に対応することは当然できない。

これまでは機動 (maneuver) という言葉を物体の加速と同じ意味で使ってきた。ただ一般には、カルマンフィルタが用いるプロセスモデルと異なる振る舞いを物体がしているとき、物体はそのカルマンフィルタから見て機動していると言う。

追跡中の物体が機動しているとき、フィルタに関して数学的に何が言えるだろうか？物体はフィルタの予測と異なる振る舞いをするから、残差が大きくなるはずである。残差は現在時刻におけるフィルタの予測値と観測値の差だったことを思い出そう。

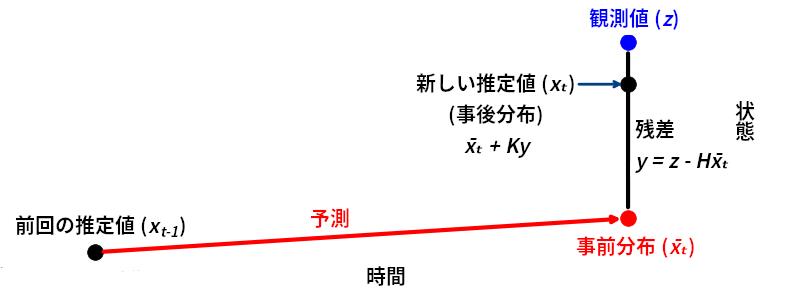
これを確かめるために、機動している間の残差を確認してみる。残差を見やすくするためにノイズの量を少なくしている:

In [13]

from kf_book.adaptive_internal import plot_track_and_residuals

def show_residual_chart():
    dt = 0.1
    sensor_std = 0.2
    pos2, zs2 = generate_data(150, sensor_std)
    xs2 = pos2[:, 0]
    z_xs2 = zs2[:, 0]

    cvfilter = make_cv_filter(dt, sensor_std)
    initialize_filter(cvfilter)
    cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.02)
    xs, res = [], []
    for z in z_xs2:
        cvfilter.predict()
        cvfilter.update([z])
        xs.append(cvfilter.x[0])
        res.append(cvfilter.y[0])

    xs = np.asarray(xs)
    plot_track_and_residuals(dt, xs, z_xs2, res)

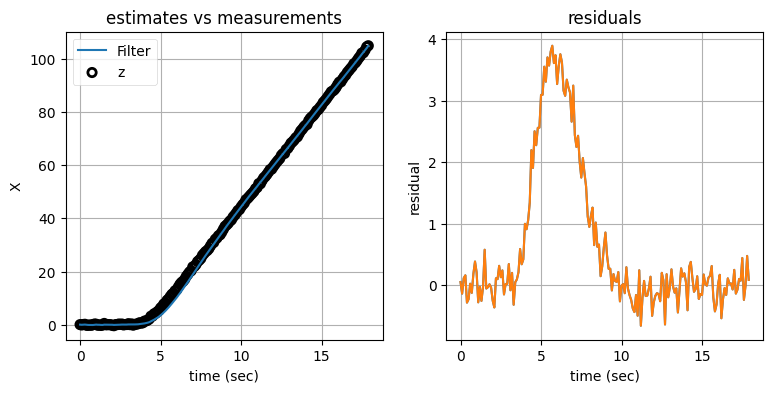
show_residual_chart();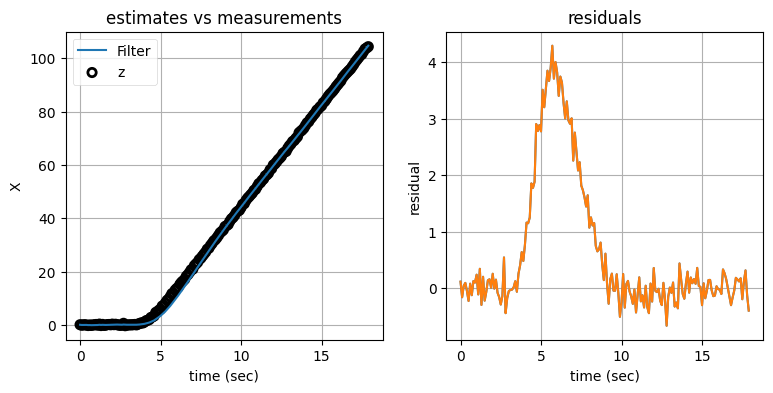

左のグラフにはノイズの含まれる観測値とカルマンフィルタの出力をプロットしてあり、右のグラフにはフィルタが計算する残差──観測値とフィルタが計算する予測値の差──をプロットしてある。次の点は重要なので強調しておく: 右のグラフに示されているのは、左のグラフにある二つの曲線の差ではない。左のグラフが示すのは観測値とカルマンフィルタの出力であり、これに対して右のグラフは観測値とプロセスモデルによる予測値の差を示している。

大したことのない違いに思えるかもしれないが、グラフを見ると大違いだと分かる。機動が始まった直後の値のずれは左のグラフだとあまり大きくないように見えるのに対して、右のグラフだと値のずれは非常に大きい。もし追跡している物体がプロセスモデルに従って動いていたとしたら、残差は \(0.0\) に近い値を取るはずである。なぜなら、このとき観測値は次の式を満たすからだ:

\[ \text{観測値} = \text{プロセスモデル}(t) + \text{ノイズ}(t) \]

目標が機動を始めると、フィルタによる予測は実際の振る舞いと一致しなくなる。これは式が次のように変化するためである:

\[ \text{観測値} = \text{プロセスモデル}(t) + \text{機動による差分}(t) + \text{ノイズ}(t) \]

よって残差の平均が \(0.0\) から離れていたら、機動が始まったのだと分かる。

ただ、私たちには厄介な仕事が残っている。残差のグラフを見れば機動が起こっているかどうかは分かるものの、入力に含まれるノイズのせいで機動がいつ始まったかが分かりにくい。これは入力からノイズを取り除くという、私たちがずっと考えてきた問題である。

14.3 調整可能なプロセスノイズ行列

私たちが考える一つ目のアプローチは、次数の低いモデルを使っておいて、機動の有無に応じてプロセスノイズ行列を調整するというものだ。残差が (何らかの意味で) "大きく" なったらプロセスノイズ行列を大きくする。こうすればフィルタはプロセスモデルによる予測より観測値を優先するようになり、入力をより正確に追跡できるようになる。そして残差が小さくなったらプロセスノイズ行列を元の小さな値に戻す。

専門的な文献にはこれを行う様々な方法が載っている。ここではいくつかの選択肢を示す。

連続的な調整

一つ目の方法は Bar-Shalom ら著 Estimation with Applications to Tracking and Navigation¹ にあるもので、残差の二乗を次の式で正規化する:

\[ \varepsilon = \mathbf{y^\mathsf{T}S}^{-1}\mathbf{y} \]

ここで \(\mathbf{y}\) は残差であり、\(\mathbf{S}\) は次の式で表される系不確実性 (系共分散行列) を表す:

\[ \mathbf{S} = \mathbf{HPH^\mathsf{T}} + \mathbf{R} \]

線形代数があってよく分からないと感じたら、逆行列を取る操作は逆数を取るのと似ていることを思い出してほしい。つまり \(\varepsilon = \mathbf{y^\mathsf{T}S}^{-1}\mathbf{y}\) は次のように解釈できる:

\[ \varepsilon\approx\frac{\mathbf{y}^2}{\mathbf{S}} \]

\(\mathbf{y}\) と \(\mathbf{S}\) は両方とも filterpy.KalmanFilter の属性なので、この手法は簡単に実装できる。時刻と \(\varepsilon\) をプロットしてみよう:

In [14]

from numpy.linalg import inv
dt = 0.1
sensor_std = 0.2
cvfilter= make_cv_filter(dt, sensor_std)
_, zs2 = generate_data(150, sensor_std)

epss = []
for z in zs2[:, 0]:
    cvfilter.predict()
    cvfilter.update([z])
    y, S = cvfilter.y, cvfilter.S
    eps = y.T @ inv(S) @ y
    epss.append(eps)

t = np.arange(0, len(epss) * dt, dt)
plt.plot(t, epss)
bp.set_labels(title='Epsilon vs time',
              x='time (sec)', y='$\\varepsilon$')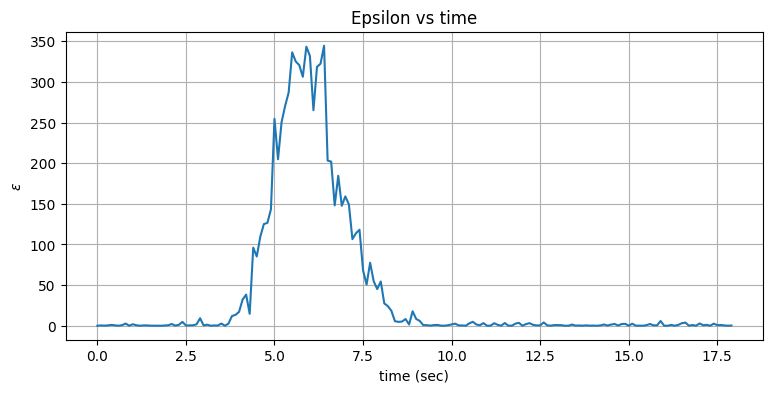

正規化された残差の効果はこのグラフから明らかなはずだ。残差を二乗することで正であることが保証され、さらに系不確実性で正規化することで残差が観測値と比べたときに大きくなった瞬間が分かりやすくなる。機動は \(3\) 秒に始まり、\(\varepsilon\) もそれからすぐに大きくなっている。

続いて \(\varepsilon\) が何らかの閾値を超えたら \(\mathbf{Q}\) を大きくして、閾値より下に戻ったら \(\mathbf{Q}\) を戻すようにしたい。\(\mathbf{Q}\) の調整はスケーリング係数を乗じることで行う。このスケーリング係数を解析的に求める方法も文献を探せば見つかるとは思うが、ここでは実験的に求めることにする。\(\varepsilon\) の閾値 (\(\varepsilon_{max}\) と呼ぶ) の選択ではもう少し解析的になれる: 一般に残差が \(3\sigma\) より大きくなったら、それはノイズではない大きな変更が起こっているのだと考えられる。ただセンサーの観測値が完璧なガウス分布になることはまずないので、実際のデータで使うときは \(5\sigma\) や \(6\sigma\) といった大きな値が使われる。

\(\mathbf{Q}\) のスケーリング係数と \(\varepsilon_{max}\) に適切な値を設定した実装を次に示す:

In [15]

# フィルタをもう一度初期化する。
dt = 0.1
sensor_std = 0.2
cvfilter = make_cv_filter(dt, sensor_std)
_, zs2 = generate_data(180, sensor_std)

Q_scale_factor = 1000.
eps_max = 4.

xs, epss = [], []

count = 0
for i, z in zip(t, zs2[:, 0]):
    cvfilter.predict()
    cvfilter.update([z])
    y, S = cvfilter.y, cvfilter.S
    eps = y.T @ inv(S) @ y
    epss.append(eps)
    xs.append(cvfilter.x[0])

    if eps > eps_max:
        cvfilter.Q *= Q_scale_factor
        count += 1
    elif count > 0:
        cvfilter.Q /= Q_scale_factor
        count -= 1

bp.plot_measurements(zs2[:,0], dt=dt, label='z', alpha=0.1)
bp.plot_filter(t, xs, label='filter')
plt.legend(loc=4)
bp.set_labels(title='epsilon=4', x='time (sec)', y='$\\varepsilon$')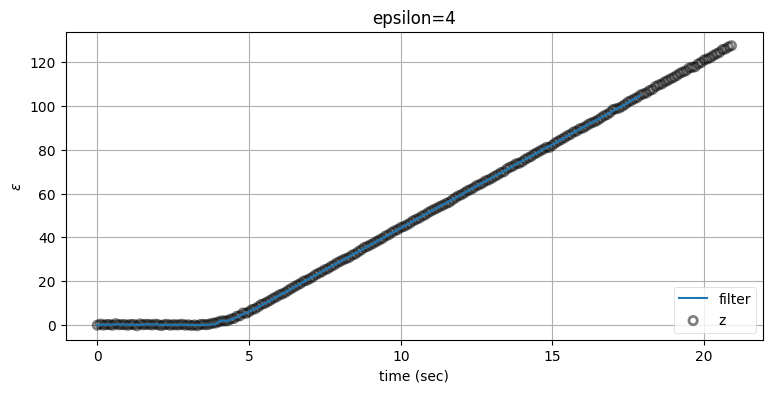

この適応フィルタの性能は定常速度フィルタより明らかに向上している。定常速度フィルタは機動が始まってから出力が追いつくまでに約 \(10\) 秒かかっていたのに対して、適応フィルタは \(1\) 秒もかかっていない。

連続的な調整──標準偏差を使うバージョン

一つ目と非常に似たこの手法は Zarchan ら著 Fundamentals of Kalman Filtering: A Practical Approach² にあるもので、次の式で表される系不確実性の標準偏差を利用する:

\[ \begin{aligned} std &= \sqrt{\mathbf{HPH}^\mathsf{T} + \mathbf{R}} \\ &= \sqrt{\mathbf{S}} \end{aligned} \]

この標準偏差を何倍かした値より残差の絶対値が大きくなっていたら、仮定するプロセスノイズの大きさを増加させ、\(\mathbf{Q}\) を再計算し、フィルタの実行を続ける:

In [16]

from math import sqrt

def zarchan_adaptive_filter(Q_scale_factor, std_scale,
                            std_title=False, Q_title=False):
    cvfilter = make_cv_filter(dt, std=0.2)
    pos2, zs2 = generate_data(180-30, std=0.2)
    xs2 = pos2[:,0]
    z_xs2 = zs2[:,0]
    # フィルタをもう一度初期化する。
    initialize_filter(cvfilter)
    cvfilter.R = np.eye(1)*0.2

    phi = 0.02
    cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=phi)
    xs, ys = [], []
    count = 0
    for z in z_xs2:
        cvfilter.predict()
        cvfilter.update([z])
        y = cvfilter.y
        S = cvfilter.S
        std = sqrt(S)

        xs.append(cvfilter.x)
        ys.append(y)

        if abs(y[0]) > std_scale*std:
            phi += Q_scale_factor; count += 1
            cvfilter.Q = Q_discrete_white_noise(2, dt, phi)
        elif count > 0:
            phi -= Q_scale_factor; count -= 1
            cvfilter.Q = Q_discrete_white_noise(2, dt, phi)

    xs = np.asarray(xs)
    plt.subplot(121)
    bp.plot_measurements(z_xs2, dt=dt, label='z', alpha=0.1)
    bp.plot_filter(xs[:, 0], dt=dt, lw=1.5)
    bp.set_labels(x='time (sec)', y='$\\varepsilon$')
    plt.legend(loc=2)
    if std_title: plt.title(f'position(std={std_scale})')
    elif Q_title: plt.title(f'position(Q scale={Q_scale_factor})')
    else: plt.title('position')

    plt.subplot(122)
    plt.plot(np.arange(0, len(xs)*dt, dt), xs[:, 1], lw=1.5)
    plt.xlabel('time (sec)')
    if std_title: plt.title(f'velocity(std={std_scale})')
    elif Q_title: plt.title(f'velocity(Q scale={Q_scale_factor})')
    else: plt.title('velocity')
    plt.show()

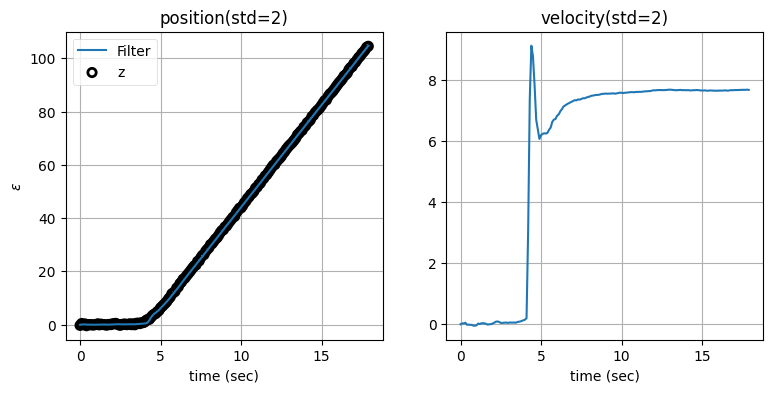
zarchan_adaptive_filter(1000, 2, std_title=True)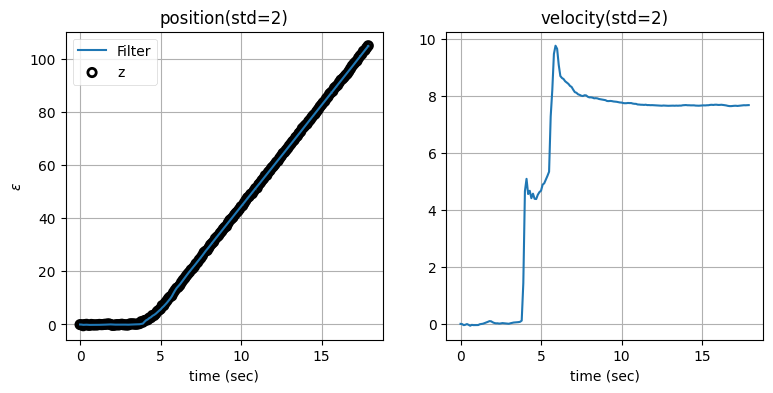

ノイズのスケーリング係数は \(1000\) として、残差の閾値は標準偏差の二倍としている。この値を選んだ理由は何か？ ... まぁまずは、残差の閾値を標準偏差の二倍および三倍としたときに何が変わるかを見てみよう:

標準偏差の二倍としたとき

In [17]

zarchan_adaptive_filter(1000, 2, std_title=True)

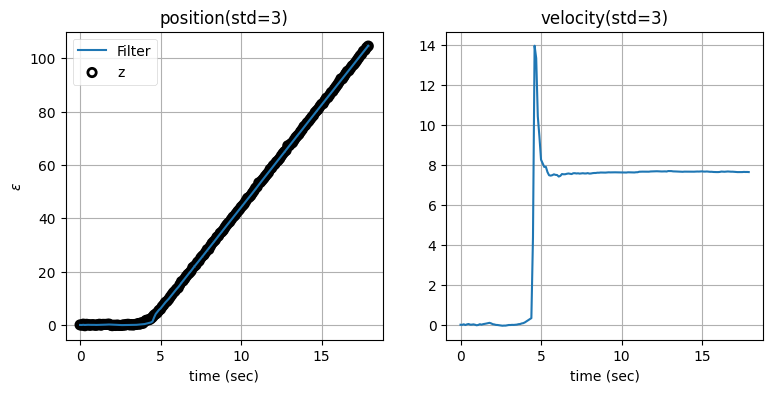
標準偏差の三倍としたとき

In [18]

zarchan_adaptive_filter(1000, 3, std_title=True)

どちらの値を閾値に採用しても、フィルタから出力される位置はあまり変わらないことが分かる。これに対して、速度ではグラフの形が異なる。これに関してさらに調べよう。まず閾値を非常に小さくしたときの振る舞いを示す:

In [19]

zarchan_adaptive_filter(1000, .1, std_title=True)
zarchan_adaptive_filter(1000, 1, std_title=True)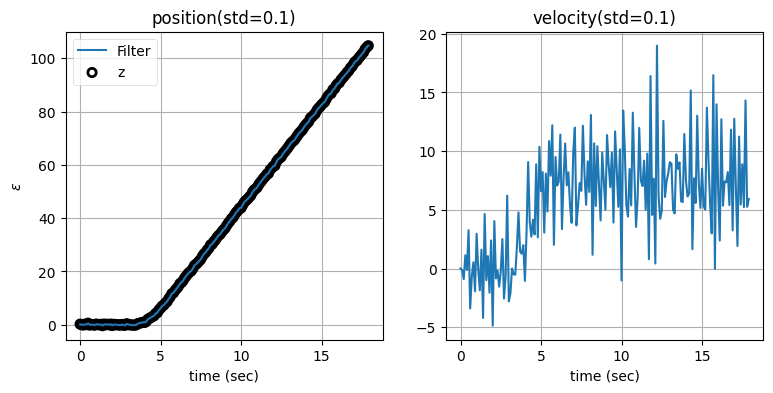

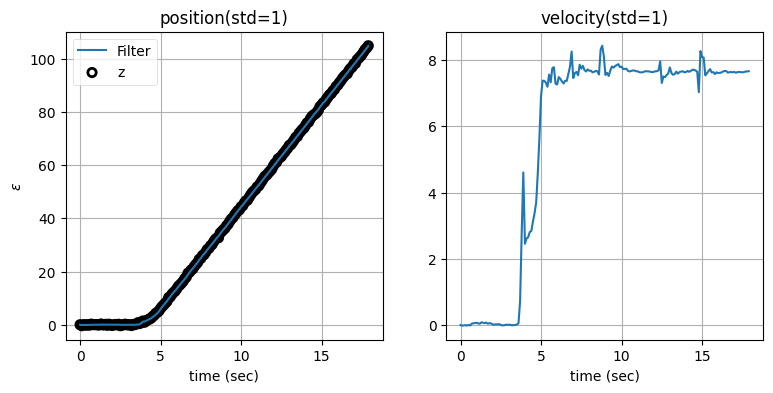
閾値が小さくなると速度の推定値は悪くなる。なぜこうなるのかを考えてみてほしい。閾値を小さくするとフィルタが少しでも予測から外れると観測値が予測値より優先され、すぐにほぼ全ての重みが観測値に割り当てられるようになる。予測に重みが割り当てられないと、隠れ変数である速度を作成するための情報が失われてしまう。そのため閾値が標準偏差の十分の一だと、速度は観測値に含まれるノイズによって大きく振り回される。一方で観測値が優先されるので、位置の出力は観測値をほぼ完全に追跡できている。

次はプロセスノイズ行列 \(\mathbf{Q}\) のスケーリング係数を変えたときに何が起こるかを見よう。残差の閾値を標準偏差の二倍に固定し、\(\mathbf{Q}\) のスケーリング係数を \(1\) から \(10,000\) にしたときの結果を示す:

In [20]

zarchan_adaptive_filter(1, 2, Q_title=True)
zarchan_adaptive_filter(10, 2, Q_title=True)
zarchan_adaptive_filter(100, 2, Q_title=True)
zarchan_adaptive_filter(1000, 2, Q_title=True)
zarchan_adaptive_filter(10000, 2, Q_title=True)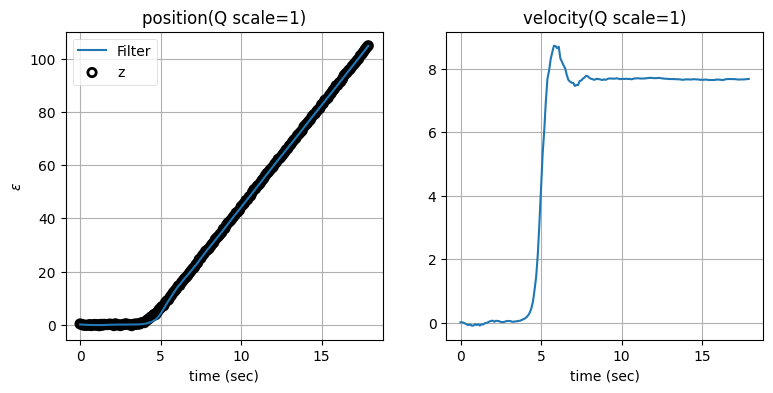

Out [20]\(\mathbf{Q}\) のスケーリング係数を \(1\) にしたときの出力

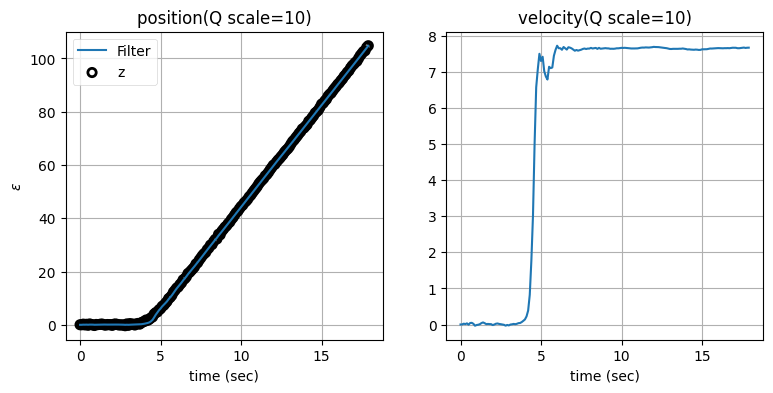
Out [20]\(\mathbf{Q}\) のスケーリング係数を \(10\) にしたときの出力

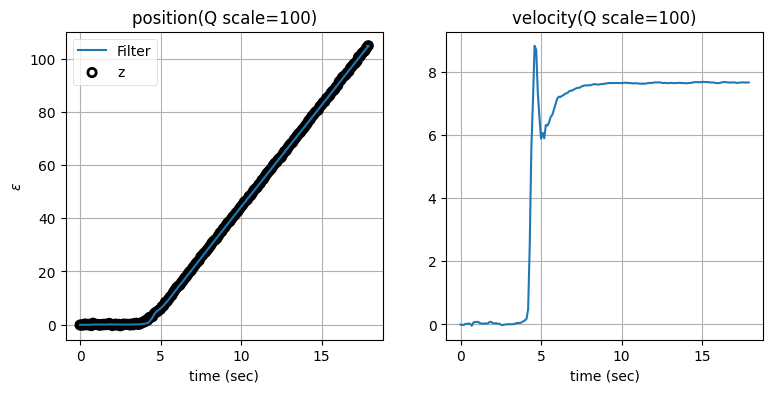
Out [20]\(\mathbf{Q}\) のスケーリング係数を \(100\) にしたときの出力

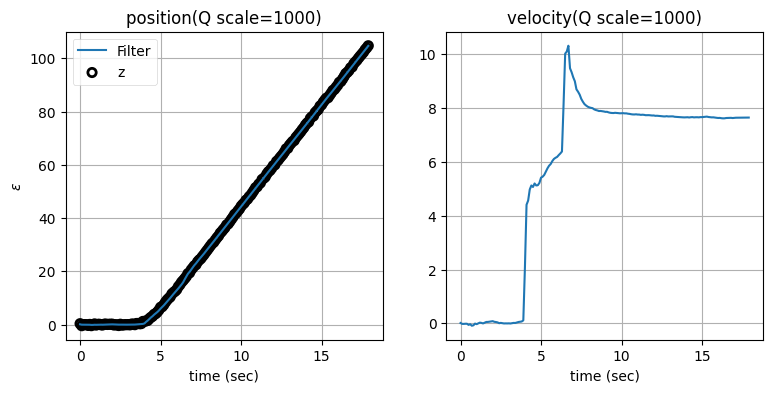
Out [20]\(\mathbf{Q}\) のスケーリング係数を \(1000\) にしたときの出力

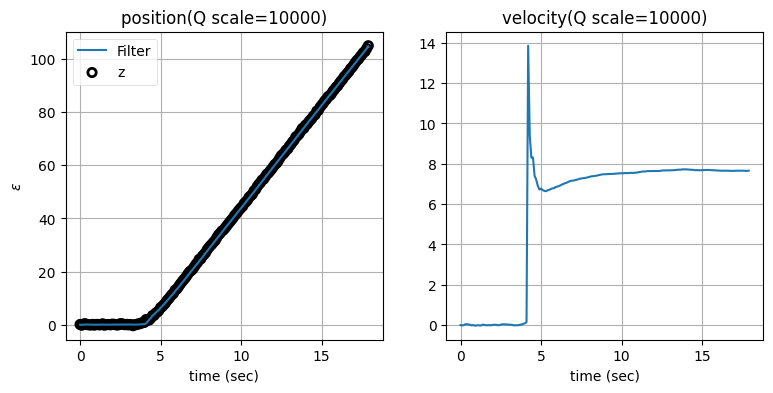
Out [20]\(\mathbf{Q}\) のスケーリング係数を \(10000\) にしたときの出力

\(\mathbf{Q}\) のスケーリング係数を大きくすると位置の推定値は正確になるものの、速度の推定値に大きなオーバーシュートが生じることが分かる。

どの値が「正しい」かを私が決めることはできない。現実のデータとシミュレートされたデータの両方でフィルタの性能をテストし、それぞれの状態変数が必要とする正確さと最もよく合致する値を選ぶ必要がある。

14.4 減衰記憶フィルタ

減衰記憶フィルタ (fading memory filter) は通常適応フィルタに分類される。入力に適応するわけではないものの、機動する目標に対して優れた性能を持つためだ。また一次・二次・三次のキネマティックフィルタ (本章で考えているフィルタ) に対しては計算が非常に簡単な形になるという利点もある。この簡単な形ではカルマンゲインの計算にリッカチ方程式が必要にならず、計算が大きく削減される。ただし本章では適応フィルタに焦点を当てているので、ここでは標準的なカルマンフィルタに対して動作する形の減衰記憶フィルタを紹介する。FilterPy では両方の形の減衰記憶フィルタが実装されている。

カルマンフィルタは再帰的ではあるものの、各反復におけるカルマンゲインの計算では間接的にこれまでの観測値が全て考慮される。観測対象の振る舞いがプロセスモデルと一致するなら、全ての観測値を取り入れることでカルマンフィルタは最適な推定値を計算できる。大気中を自由落下するボールを考えれば、これまでの観測値を一つ残らず考えに入れれば時刻 \(t\) におけるボールの位置を正確に予測できるのは明らかだ。観測値の一部しか使わないと現在位置の確実性は小さくなり、推定値は観測値のノイズからの影響を受けやすくなる。まだ何を言いたいかが分からなかったら、最悪の場合を考えてみてほしい: 最新の観測値だけを考えて、他の観測値は全て忘れるとしたらどうなるだろうか？このときボールの位置や放物線に関して自信を持つことはできず、現在の観測値を重視するしかない。よって観測値のノイズが大きければ、推定値のノイズも大きくなる。この現象はカルマンフィルタを初期化した直後に必ず見られる: カルマンフィルタが出力する推定値は最初ノイズが大きいものの、観測値を取得するにつれ推定値は落ち着いていく。

しかし追跡対象の物体が機動するなら、その物体はプロセスモデルが予測する通りに振る舞わない。このとき過去の観測値は記憶しても推定を改善しないという意味で負債と言える。この事実は上のグラフを見ても分かる: 対象が旋回を始めても、カルマンフィルタは直線的な運動を予測し続けている。これはフィルタが対象の移動履歴を取り入れており、そこから計算した向きと速度で対象が直線的に移動することに (誤って) 自信を持っているためである。

減衰記憶フィルタは古い観測値の重みを小さく、最近の観測値の重みを大きくすることでこの問題に対処する。

減衰記憶フィルタには様々な定式化が存在する。ここでは Dan Simon 著 Optimal State Estimation³ にある定式化を示す。導出は省略して、結果だけを説明する。

カルマンフィルタで推定誤差の共分散行列は次の式で表される:

\[ \bar{\mathbf P} = \mathbf{FPF}^\mathsf T + \mathbf Q \]

次のように \(\alpha^2\) を乗じると、フィルタに過去の観測値を忘れさせることができる:

\[ \tilde{\mathbf P} = \alpha^2\mathbf{FPF}^\mathsf T + \mathbf Q \]

ここで \(\alpha > 1.0\) である。\(\alpha = 1\) なら通常のカルマンフィルタと同一になる。FilterPy では \(\alpha\) が KalmanFilter クラスの属性となっている。\(\alpha\) のデフォルト値は \(1\) なので、明示的に \(1\) でない値を設定しない限り KalmanFilter は通常のカルマンフィルタとして振る舞う。\(\alpha\) の選択に関して厳密な規則は存在しないものの、通常は \(1.01\) のような非常に \(1\) に近い値が使われる。シミュレートされたデータや現実のデータを使って多くのテストを行い、機動に反応できつつも観測値を必要以上に重視して推定値にノイズが含まれることがない値を見つける必要があるだろう。

なぜこれは正しく動作するのだろうか？推定誤差の共分散行列が大きくなることで、フィルタが推定値に関して抱く確信の度合いは小さくなる。そのため観測値がより重視されるのである。

注意事項が一つある──\(\alpha\) に値を設定すると \(\mathbf{P}\) ではなく \(\tilde{\mathbf P}\) が計算される。言い換えれば、KalmanFilter.P は事前分布の共分散行列と等しくなくなるので、そうであるかのように扱ってはいけない。

減衰記憶フィルタを使って考えていたデータをフィルタリングして結果を確認しよう。いくつかのアプローチを比較できるよう系には大きなノイズを加えている:

In [21]

pos2, zs2 = generate_data(70, std=1.2)
xs2 = pos2[:, 0]
z_xs2 = zs2[:, 0]

cvfilter = make_cv_filter(dt, std=1.2)
cvfilter.x.fill(0.)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.02)
cvfilter.alpha = 1.00

xs, res = [], []
for z in z_xs2:
    cvfilter.predict()
    cvfilter.update([z])
    xs.append(cvfilter.x[0])
    res.append(cvfilter.y[0])
xs = np.asarray(xs)
plt.subplot(221)
bp.plot_measurements(z_xs2, dt=dt, label='z', alpha=0.1)
plt.plot(t[0:100], xs, label='filter')
plt.legend(loc=2)
plt.title('Standard Kalman Filter')

cvfilter.x.fill(0.)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=20.)
cvfilter.alpha = 1.00

xs, res = [], []
for z in z_xs2:
    cvfilter.predict()
    cvfilter.update([z])
    xs.append(cvfilter.x[0])
    res.append(cvfilter.y[0])

xs = np.asarray(xs)

plt.subplot(222)
bp.plot_measurements(z_xs2, dt=dt, label='z', alpha=0.1)
plt.plot(t[0:100], xs, label='filter')
plt.legend(loc=2)
plt.title('$\mathbf{Q}=20$')

cvfilter.x.fill(0.)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.02)
cvfilter.alpha = 1.02

xs, res = [], []
for z in z_xs2:
    cvfilter.predict()
    cvfilter.update([z])
    xs.append(cvfilter.x[0])
    res.append(cvfilter.y[0])
xs = np.asarray(xs)
plt.subplot(223)
bp.plot_measurements(z_xs2, dt=dt, label='z', alpha=0.1)
plt.plot(t[0:100], xs, label='filter')
plt.legend(loc=2)
plt.title('Fading Memory ($\\alpha$ = 1.02)')

cvfilter.x.fill(0.)
cvfilter.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.02)
cvfilter.alpha = 1.05

xs, res = [], []
for z in z_xs2:
    cvfilter.predict()
    cvfilter.update([z])
    xs.append(cvfilter.x[0])
    res.append(cvfilter.y[0])
xs = np.asarray(xs)
plt.subplot(224)
bp.plot_measurements(z_xs2, dt=dt, label='z', alpha=0.1)
plt.plot(t[0:100], xs, label='filter')
plt.legend(loc=2)
plt.title('Fading Memory ($\\alpha$ = 1.05)')
plt.tight_layout();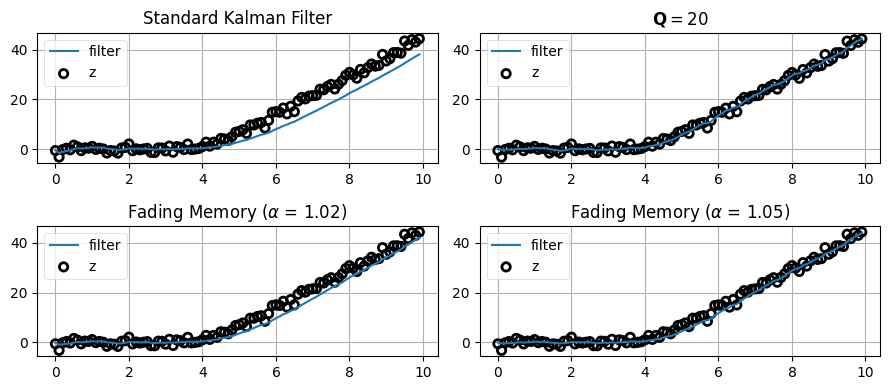

上の二つのグラフはカルマンフィルタの出力を示す。左上のグラフでは目標の機動が始まってからフィルタの出力が入力信号に追いつくまでに \(10\) 秒程度かかっている。その後プロセスノイズ行列を大きくした結果が右上のグラフであり、ここでは旋回を素早く追跡できているものの、代わりにノイズを含んだ観測値を過度に重視するために出力のノイズも大きくなっている。左下のグラフは \(\alpha=1.02\) とした減衰記憶フィルタの結果を示す。フィルタから出力される推定値は非常に滑らかで、対象が状態を安定させてからフィルタが落ち着くまでには数秒かかっている。この時間はゼロではないものの、カルマンフィルタよりずっと短い。つまり減衰記憶フィルタでは遅延が小さく、推定値はカルマンフィルタより正確に対象を追跡する。最後に、\(\alpha\) を \(1.05\) まで大きくしたのが右下のグラフである。ここではフィルタが機動にほぼ瞬時に反応しているのが分かる。ただフィルタが過去の観測値を早く忘れるために、系が安定している間の推定値は綺麗な直線から離れる。

非常に少ないコードの変更でかなり大きな性能向上が得られた！なお "正しい" \(\alpha\) の値は存在しない。観測ノイズ行列、プロセスノイズ行列、目標が行う機動の振る舞い、自分が必要とする推定値の精度に合わせて自分で \(\alpha\) を設定する必要がある。

14.5 多重モデル推定 (MME)

本章で使ってきた例では、安定した状態で移動する目標が機動を行い、その後は安定した状態に戻っていた。私たちはこれを二つのモデルを使って考えている──定常速度モデルと、定常加速度モデルである。系をいくつかのモデルのいずれかに従うとして記述できるとき、多重モデル推定 (multiple model estimation, MME) が利用できる。同じ系を記述する異なるプロセスモデルを使う複数のフィルタを用意して、追跡している物体のダイナミクスに応じてフィルタを切り替えたり混ぜたりするのが多重モデル推定である。

想像できると思うが、MME は広大なトピックであり、設計と実装には様々な選択肢が存在する。本章ではここまでに追ってきた問題に対する簡単なアプローチを説明する。ここでのアイデアは、定常速度フィルタと定常加速度フィルタを同時に実行し、残差から機動が検出されたら使うフィルタを切り替えるというものだ。しかしこの方法にさえ多くの選択肢がある: 旋回を行う車のダイナミクスを考えよう。例えば車は車軸を利用して旋回する。これは非線形なプロセスだから、追跡には何らかの非線形フィルタ (EKF や UKF など) が必要になる。一方で系の状態が安定している間は線形な定常速度フィルタでも正確な推定が行えるだろう。よって旋回する車に対する MME では線形カルマンフィルタと (例えば) EKF が必要になる。しかし一方で、この二つのフィルタはどちらも加速と減速のような振る舞いを上手くモデル化できない。このように、正確な MME を行うには追跡する物体の特定の性能限界を考慮して設計されたフィルタを数多く用意しなければならない。

それから当然、フィルタの差異はモデルの次数だけではない。ノイズモデルやパラメータを変化させることもできる。例えば本章ではこれまでに、パラメータを変化させると速度と位置の推定値がどう変化するかを示すプロットを多く示した。パラメータのある値は位置の推定に優れ、異なる値は速度の推定値に優れるという場合があるかもしれない。このとき両方のフィルタを使う MME を行えば、片方のフィルタからは位置の推定値を取り、もう片方のフィルタからは速度の推定値を取るといったことができる。

二フィルタ適応フィルタ

最良の性能を得るために複数のフィルタの間で利用するものを切り替えるというアイデアは理解できたと思う。では、このアイデアを実装するときに利用すべき数学的基礎は何だろうか？私たちが直面している問題は、ノイズの含まれる観測値から系の振る舞いの根本的な変化を検出する問題である。カルマンフィルタにおいて観測値と予測値の差はなんと言っただろうか？そう、残差だ。

一次のカルマンフィルタ (定常速度フィルタ) があるとしよう。目標が機動しない限りこのフィルタは目標を正確に追跡し、観測値の約 68% は \(1\sigma\) に収まる。加えて、残差は \(0\) の周りを変動するはずである: センサーの誤差がガウス分布に従うなら、誤差が正になる確率と負になる確率が等しいためだ。もし残差の絶対値が大きくなり、予測される期間より長い間そこにとどまったなら、目標は状態モデルが予測する通りに振る舞っていない。この例は本章で前に見た: 次のグラフで残差は最初 \(0\) の周りを変動しているものの、追跡している物体が機動を開始すると残差は突然正の大きな値に跳ね上がってしばらくそのままとなる。

In [22]

show_residual_chart()

前に見たように、この問題では物体が安定した状態にある間は定常速度フィルタの方が定常加速度フィルタより優れた推定値を計算し、物体が機動している間は逆になる。上のグラフでは \(4\) 秒地点でその遷移が起こっている。

というわけで二つのフィルタを使うアルゴリズムは簡単に書ける。定常速度フィルタと定常加速度フィルタの両方を初期化し、予測/更新のループで一緒に実行する。更新のたびに定常速度フィルタの残差を確認し、もし残差が理論的な範囲に収まっていれば定常速度フィルタの推定値を、そうでなければ定常加速度フィルタの推定値を採用するというものだ。この実装を示す:

In [23]

def run_filter_bank(threshold, show_zs=True):
    dt = 0.1
    cvfilter= make_cv_filter(dt, std=0.8)
    cafilter = make_ca_filter(dt, std=0.8)
    pos, zs = generate_data(120, std=0.8)
    z_xs = zs[:, 0]
    xs, res = [], []

    for z in z_xs:
        cvfilter.predict()
        cafilter.predict()
        cvfilter.update([z])
        cafilter.update([z])

        std = np.sqrt(cvfilter.R[0,0])
        if abs(cvfilter.y[0]) < 2 * std:
            xs.append(cvfilter.x[0])
        else:
            xs.append(cafilter.x[0])
        res.append(cvfilter.y[0])
    xs = np.asarray(xs)
    if show_zs:
        plot_track_and_residuals(dt, xs, z_xs, res)
    else:
        plot_track_and_residuals(dt, xs, None, res)

run_filter_bank(threshold=1.4)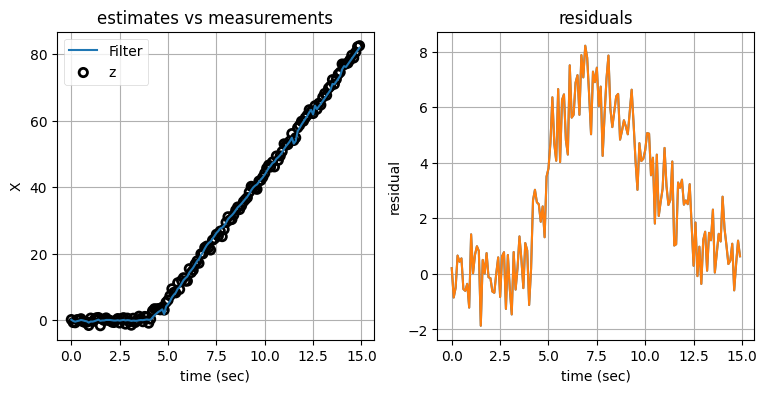

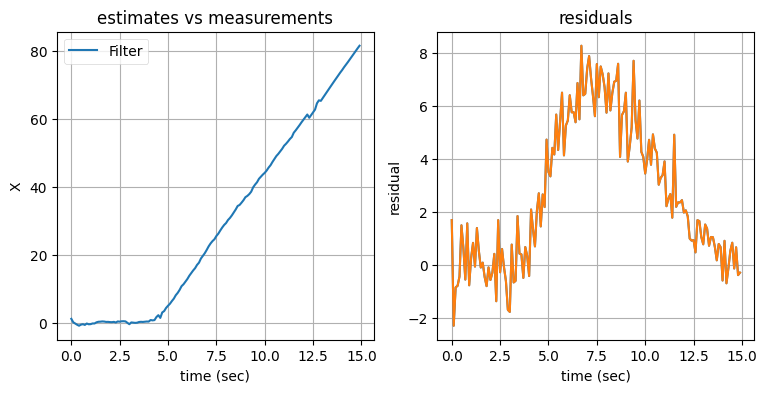
このフィルタは機動を正確に追跡できている。目標が機動しないときはノイズがほとんどなく、機動があると素早く検出して定常加速度フィルタへ切り替わる。ただ、出力が理想的とは言えない。フィルタの出力だけをプロットしたグラフを示す:

In [24]

run_filter_bank(threshold=1.4, show_zs=False)

出力が大きく変動している箇所がいくつかあるのが分かる。この大きな変動は利用するフィルタが切り替わったときに発生する。私はこのフィルタをプロダクションのシステムで使おうとは思わない。次の節ではこの問題を解決するフィルタの実装手法を説明する。

14.6 多重モデル適応推定 (MMAE)

複数のフィルタを使って機動を検出するというアイデア自体に問題はないものの、あるフィルタから別のフィルタへ一気に切り替えると推定値が大きく変動してしまう。そもそも「フィルタが二つあるときに片方だけを選んで使う」というのは本書でずっと使ってきた考え方を真っ向から否定している。その考え方とは、確率論を使って観測値や予測値の尤度を計算するというものだ。私たちは観測値または予測値から可能性の高い方を選択するのではなく、尤度を使って二つの値を混ぜ合わせる処理を行ってきた。ここでも同じことを行う。このアプローチは多重モデル適応推定 (multiple model adaptive estimation, MMAE) と呼ばれる。

カルマンフィルタの設計の章で尤度関数を学んだ:

\[ \mathcal{L} = \frac{1}{\sqrt{2\pi S}}\exp \left[-\frac{1}{2}\mathbf{y}^\mathsf{T}\mathbf{S}^{-1}\mathbf{y} \right] \]

ここで \(\mathbf{y}\) は残差、\(\mathbf{S}\) は系不確実性 (観測空間における共分散行列) を表す。つまり \(\mathcal{L}\) は残差と系不確実性を使って計算したガウス分布の確率密度関数の値である。この値は入力を受け取ったフィルタが最適に振る舞っている可能性を示す。例えば残差が大きければ不確実性が大きくなり、尤度、つまり観測値がフィルタの現在状態と適合している可能性は低くなる。

尤度を使えば、各フィルタがデータにフィットする確率を計算できる。\(N\) 個のフィルタがあると仮定し、時刻 \(k\) における \(i\) 番目のフィルタの尤度を \(\mathcal{L}^i_k\) と表す。このとき時刻 \(k\) において他のフィルタと比べたときに \(i\) 番目のフィルタが正しい相対的確率 \(p^i_k\) は次のように計算できる:

\[ p_k^i = \frac{\mathcal{L}_k^ip_{k-1}^i}{\sum\limits_{j=1}^N \mathcal{L}_k^jp_{k-1}^j} \]

見た目は複雑に見えるが、意味を考えれば難しくはない。分子は現在のタイムステップにおける尤度を一つ前のタイムステップにおいてフィルタが正しい確率に乗じた値であり、分母は全てのフィルタに関する確率の和 \(\sum p^j_k\) を \(1\) にするための正規化係数である。

これは再帰的な定義なので、各フィルタに対して初期確率を割り当てる必要がある。特に情報がない場合は \(1/N\) を使う。この確率を計算したら、各フィルタからの出力にフィルタが正しい確率を乗じた値の和を最終的な状態の推定値とする。

完全な実装を示す:

In [25]

def run_filter_bank():
    dt = 0.1
    cvfilter = make_cv_filter(dt, std=0.2)
    cafilter = make_ca_filter(dt, std=0.2)

    _, zs = generate_data(120, std=0.2)
    z_xs = zs[:, 0]
    xs, probs = [], []

    pv, pa = 0.8, 0.2
    pvsum, pasum = 0., 0.

    for z in z_xs:
        cvfilter.predict()
        cafilter.predict()
        cvfilter.update([z])
        cafilter.update([z])

        cv_likelihood = cvfilter.likelihood * pv
        ca_likelihood = cafilter.likelihood * pa

        pv = (cv_likelihood) / (cv_likelihood + ca_likelihood)
        pa = (ca_likelihood) / (cv_likelihood + ca_likelihood)

        x = (pv * cvfilter.x[0]) + (pa*cafilter.x[0])
        xs.append(x)
        probs.append(pv / pa)

    xs = np.asarray(xs)
    t = np.arange(0, len(xs) * dt, dt)
    plt.subplot(121)
    plt.plot(t, xs)
    plt.subplot(122)
    plt.plot(t, xs)
    plt.plot(t, z_xs)
    return xs, probs

xs, probs = run_filter_bank()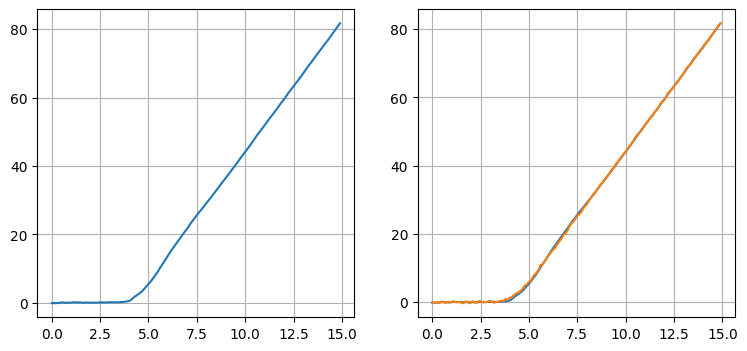

左のグラフには結果の滑らかさが分かるようにフィルタが出力する推定値だけをプロットし、右のグラフにはフィルタが機動を追跡できていることが分かるように推定値と観測値の両方をプロットした。

これが本書を通じて利用してきたベイズ的なアルゴリズムにほかならないことをもう一度強調しておきたい。二つ (あるいはもっと多く) の観測値あるいは推定値があり、それらの正しい確率が得られているなら、推定値は正しい確率に比例する値を重みとした重み付き平均として計算できる。また各ステップで行われる確率の計算は次の式で表される:

\[ \frac{\text{P(観測値 | 状態)} \times\text{事前分布}}{\text{正規化定数}} \]

これはまさにベイズの定理である。

現実の問題では二つより多いフィルタを考えることが多い。私は仕事でコンピュータービジョンを利用して複数の物体を追跡する問題に取り組んでいる。私が追跡するのはホッケーのパックである。パックは滑ったり、跳ね返ったり、壁をこすりながら進んだり、跳ね飛んだり、誰かが手に持って運んだり、選手が素早く "ドリブル" したりする。人間 (ホッケー選手) も追跡するのだが、彼らが行える非線形な振る舞いには限度というものがほとんどない。こういった状況では二つのフィルタを使うだけでは正確な推定値は得られないので、プロセスモデルとノイズモデルを数多く用意しなければならない。ただ、ここに示した例で核となるアイデアはつかめたはずだ。

MMAE の欠点

上で説明した MMAE は一つ重大な問題を抱えている。定常速度フィルタの確率と定常加速度フィルタの確率の比をプロットした次のグラフを見てほしい (値の変化を分かりやすくするため \(y\) 軸を対数目盛にしている):

In [26]

plt.plot(t[0:len(probs)], np.log(1.0 + np.array(probs)))
plt.title('probability ratio p(cv)/p(ca) (log scale)')
plt.xlabel('time (sec)');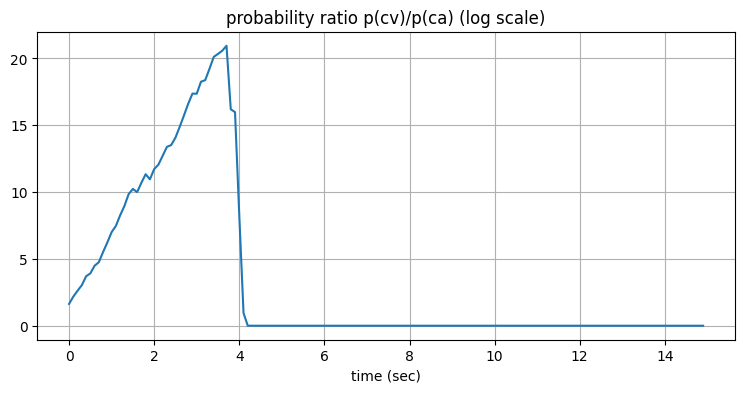

追跡している物体が直線上を移動する最初の三秒間では、定常速度フィルタが定常化速度フィルタよりずっと大きな確率を持っている。そして機動が開始されると、すぐに定常加速度フィルタの確率が大きくなる (プロットした値はゼロに近くなる)。ここまでは予想通りである。それから機動が \(6\) 秒地点で終了すると、定常速度フィルタの確率がまた大きくなると予想される。しかし確率の比率はゼロのまま大きくなっていない。

この原因は確率の再帰的な計算にある:

\[ p_k = \frac{\mathcal{L}_{k-1}p_{k-1}}{\sum \mathcal{L}_{k-1}p_{k-1}} \]

この式を使って更新を行うと一度非常に小さくなった確率は戻ってこられなくなり、MMAE は最も可能性の高いフィルタにすぐに収束してしまう。よってフィルタをロバストにするには各フィルタの確率を監視し、非常に確率が低くなったフィルタを取り除いて正確な推定値を出力している確率の高いフィルタで取り換える処理が必要になる。この機能は既存のフィルタの集合を分割して小集合ごとに優れたフィルタを選ぶようにすると実装できる。またフィルタが発散する最悪のケースに備えて、現在の観測値に近い値でフィルタを完全に初期化する機能を付けることもできる。

14.7 相互干渉多重モデル (IMM)

多重モデル推定を別の視点で考えよう。シナリオは前と同じで、機動する目標を追跡したいとする。モデルに関する仮定を変更すれば、いくつかのカルマンフィルタをまとめて設計できる。例えばフィルタの次数やプロセスモデルのノイズ量を変えればよい。新しい観測値を受け取ったとき、それぞれのフィルタはモデルが正しい確率を計算できる。

ナイーブなアプローチだと組み合わせ爆発が起こる。ステップ 1 で \(N\) 個 (それぞれのフィルタから一つずつ) の仮説を作ったとしよう。このときステップ 2 で \(N\) 個の仮説のそれぞれから \(N\) 個の仮説がさらに生まれるので、仮説は全体で \(N^2\) 個になる。可能性の低い仮説を刈り取ったり似た仮説を統合したりする手法が数多く提案されてきたものの、どのアルゴリズムも計算量の増加や低性能に悩まされている。こういったアルゴリズムを本書では扱わないが、専門的な文献で圧倒的によく使われるのは一般化疑似ベイズ (generalized pseudo Bayes, GPB) アルゴリズムである。

相互干渉多重モデル (interacting multiple models, IMM) アルゴリズムは多重モデル推定で組み合わせ爆発が起こる問題を解決するために Blom⁴ によって考案された。これに続く Blom と Bar-Shalom の論文⁵が最もよく引用される。そのアイデアは、系の振る舞いのモードにつき一つのフィルタを用意して、確率の高いフィルタの推定値で確率の低いフィルタの推定値を修正するというものだ。この修正は確率的に行われるので、確率の低いフィルタもわずかではあるが確率の高いフィルタを修正する。

例えば、系の振る舞いについて「直進」と「旋回」の二つのモードを考えているとしよう。「直進」のモードは一次のカルマンフィルタで、「旋回」のモードは二次のカルマンフィルタで表されると仮定する。目標が旋回しているとき二次のフィルタは優れた推定値を出力し、一次のフィルタは信号に遅れるだろう。このときフィルタが計算する尤度を見れば正しい可能性が高いフィルタが分かる。一次のフィルタは尤度が低いだろうから、その推定値は二次のフィルタの出力を使って大きく修正される。逆に二次のフィルタは尤度が高いだろうから、その推定値は一次のフィルタの出力を使って少しだけ修正される。

続いて目標が旋回を止めたとする。一次のフィルタの推定値は二次のフィルタの推定値で常に修正されているから、その時点でも信号から大きく遅れてはいない。そのため数エポックもすれば、一次のフィルタは優れた (高い尤度の) 推定値を生成するようになる。すると一次のフィルタは二次のフィルタより正しい確率が高くなり、二次のフィルタの推定値に大きな影響を及ぼすようになる。二次のフィルタは観測ノイズを加速と誤認することを思い出してほしい。一次のフィルタからの修正により、この誤認による影響が大きく緩和される。

モード確率

系が持つ全てのモードからなる集合を \(m\) として、目標は必ず \(m\) に含まれるモードのいずれかにあるとする。例えば上で説明した例では「直進」と「旋回」のモードがあるから、\(m=\{\text{直進},\ \text{旋回}\}\) となる。

続いて目標がそれぞれのモードにある確率を割り当てることで、モード確率 (mode probability) を表すベクトル \(\mu\) を構築する。今の例では \(m\) が二つのモードから構成されるから、\(\mu\) は二つの確率からなるベクトルとなる。例えば目標が直進する確率が 70% と考えているとき、\(\mu\) は次のように書ける:

\[ \mu = \begin{bmatrix} 0.7 & 0.3\end{bmatrix} \]

「旋回」モードの確率 \(0.3\) は確率の和が \(1\) であることから計算される。\(\mu\) はモード確率を表すのによく使われる記号なのでここでも使った (必ず \(\mu\) が使われるわけではない)。平均と混同しないように注意する必要がある。

Python では次のように実装できる:

In [27]

mu = np.array([0.7, 0.3])
mu

Out [27]

array([0.7, 0.3])

きちんと定義すれば次のようになる: 観測値 \(Z\) が与えられたとき、\(m_i\) が正しい (追跡している物体がモード \(i\) にある) 事前確率を

\[ \mu_i = P(m_i|Z) \]

と表記する。

モードの遷移

続いて、追跡しているのが機動する目標である事実を考えに入れなければならない。目標は最初直進し、それから旋回し、また直進する。このモードの遷移はマルコフ連鎖 (Markov chain) でモデル化される。マルコフ連鎖の例を次の図に示す:

In [28]

import kf_book.adaptive_internal as adaptive_internal
adaptive_internal.plot_markov_chain()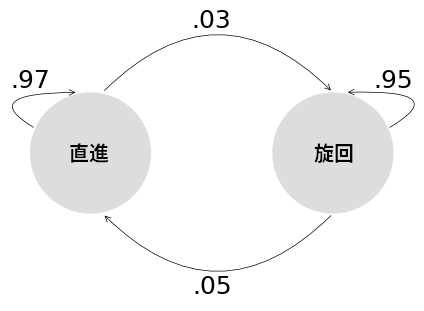

これは追跡対称の物体が持つ二つのモード (「直進」と「旋回」) に対する遷移の例を示す。この図によると、対象が現在「直進」のモードにあるとき、対象は 97% の確率で直進を続け、3% の確率で旋回を開始する。そして対象が一度旋回を始めると、対象は 95% の確率で旋回を続け、5% の確率で直進に戻る。

IMM のアルゴリズムは具体的な確率の値にかかわらず動作し、通常は適切な値を決定するためにシミュレーションや実験が必要になる。ただ上に示した値は十分適切な値である。

マルコフ連鎖は遷移確率行列 (transition probability matrix) \(\mathbf{M}\) で表す。上の図に示したマルコフ連鎖に対する \(\mathbf{M}\) は次のように書ける:

\[ \mathbf M = \begin{bmatrix}.97 & .03\\.05 & .95\end{bmatrix} \]

言葉で説明すれば、\(\mathbf{M}[i,j]\) は一つ前の時刻でモード \(i\) にあった系が現在モード \(j\) にある確率を表す。今考えている例で言えば、対象が一つ前の時刻で旋回していた (\(i=1\)) ときに現在時刻で直進している (\(j=0\)) 確率は \(\mathbf M[1,\ 0] = 0.05\) となる。Python では次のように書ける:

In [29]

M = np.array([[.97, .03], [.05, .95]])
print(M)
print('旋回から直進になる確率:', M[1, 0])

Out [29]

[[0.97 0.03]
 [0.05 0.95]]
旋回から直進になる確率: 0.05

遷移確率行列を使えば新しいモード確率を計算できる。前に示したモード確率 \(\mu = \Big[0.7 \ \ 0.3\Big]\) を使うとき、遷移後に対象が「直進」モードにある確率を求めてみよう。遷移後に対象が「直進」モードになる可能性は二つある: 一つ前の時刻で直進していて引き続き直進する可能性と、一つ前の時刻で旋回していて直進するようになった可能性である。前者の確率は \(0.7\times 0.97\) と計算でき、後者の確率は \(0.3\times 0.05\) と計算できる。この計算ではモード確率と対応する線確率行列の要素を利用している。全確率は二つ確率の和だから、\(0.7 \times 0.97 + 0.3 \times 0.05 = 0.694\) となる。

第 3 章で説明した全確率の定理を思い出してほしい。この定理によると、いくつかの独立した事象を通じてのみ実現される事象 \(A\) の確率は次のように計算できる:

\[ P(A) = \sum_B P(A\mid B)\, P(B) \]

今考えている問題では \(P(A)\) が考えているモードの確率、\(P(A \mid B)\) が遷移確率行列 \(\mathbf{M}\) の要素、\(P(B)\) が \(\mu\) の要素に対応する。\(\mathbf{M}\) と \(\mu\) はそれぞれ行列と配列を使って表していたから、ベクトルと行列の乗算で要素の積の和が計算できる事実を利用できる:

\[ \begin{bmatrix}\mu_1 & \mu_2 \end{bmatrix}\begin{bmatrix}m_{11} & m_{12}\\m_{21} & m_{22}\end{bmatrix} = \begin{bmatrix}\mu_1 m_{11} + \mu_2 m_{21} & \mu_1 m_{12} + \mu_2 m_{22}\end{bmatrix} \]

これは IMM を扱う文献で次のように表される:

\[ \bar c_j = \sum\limits_{i=1}^{N} \mu_i M_{ij} \]

Python では NumPy の dot 関数でこの計算を行える。行列乗算演算子の @ でも同じ計算ができるものの、dot の方が分かりやすいと感じるので dot を使うことにする:

In [30]

cbar = np.dot(mu, M)
cbar

Out [30]

array([0.694, 0.306])

モード確率の計算

新しいモード確率はベイズの定理を使って計算できる。ベイズの定理の式は次の通りだった:

\[ \text{事後分布} = \frac{\text{尤度} \cdot \text{事前分布}}{\text{正規化定数}} \]

今考えているモード確率の計算では前節で計算した全確率が事前分布となる。また尤度はカルマンフィルタが計算する値であり、現在状態における観測値の確からしさを表す。復習しておくと、尤度は次のように計算される:

\[ \mathcal{L} = \frac{1}{\sqrt{2\pi \mathbf S}}\exp \left[-\frac{1}{2}\mathbf y^\mathsf T\mathbf S^{-1}\mathbf y \right] \]

数学的な記法を使えば、更新後のモード確率 \(\mu_i\) は次のように表せる:

\[ \mu_i = \| \mathcal{L}_i {\bar c}_{i}\| \]

言葉で説明すれば、それぞれのカルマンフィルタ (モード) に対して「一つ前の時刻におけるモード確率を遷移確率行列で遷移させた確率」と「モードの尤度」の積に比例する値としてモード確率が計算される。最後の正規化は和を \(1\) にするためにある。

この計算は Python で簡単に行える。以下のコードでは尤度を格納する変数 L を導入している。尤度は更新ステップ KalmanFilter.update で計算され KalmanFilter.L と参照できるようになるのだが、まだカルマンフィルタを作っていないので L の値はハードコードしている:

In [31]

# L = [kf0.L, kf1.L]  # カルマンフィルタから尤度を取得する。
L = [0.000134, 0.0000748]
mu = cbar * L
mu /= sum(mu) # 正規化する。
mu

Out [31]

array([0.802, 0.198])

比較的大きい定常速度フィルタの尤度が「直進」モードの確率を 70% から 80.2% に押し上げたのが分かる。

混合確率

ここまでの式を使えば、モードの遷移を使って可能性のある選択肢とその確率を計算していくことができる。例えば \(\mu = \Big[ 0.63 \ \ 0.27\Big]\) だとしよう。このとき「直進」モードの確率 (\(0.63\)) は遷移によって直進または旋回が起きて二つの可能性に分かれる。同様に「旋回」モードの確率 (\(0.27\)) も二つに分かれるから、次のタイムステップでは全部で四つの可能性が生まれる。さらに次のタイムステップでは四つの可能性が八つになり、以下同様となる。この手法は正確であるものの、計算負荷が大きすぎて実際の問題では手に負えない。

というわけで、計算量の小さい近似的な手法が必要になる。IMM はこの問題の解決に混合確率 (mixing probability) を利用する。そのアイデアは単純である。現在一つ目のモード (「直進」モード) の確率が高く、二つ目のモード (「旋回」モード) の確率が低いとしよう。このとき IMM は一つ目のモードのカルマンフィルタだけを使うのではなく (可能性のある推定値を全て考えるのでもなく)、全てのフィルタの推定値の重み付き平均として推定値を計算する。そのとき重みは確率の高いフィルタに大きく、確率の低いフィルタに小さくなるように割り当てる。こうすることで、確率の高いフィルタが持つ情報を使った確率の低いフィルタの改善が可能になる。以上が IMM で最も重要な部分である。

行うべきことは決して難しくない。まず各カルマンフィルタで更新ステップを実行してそれぞれのフィルタの新しい平均と共分散行列を計算し、それから混合確率 \(\omega\) を使った重み付き平均として最終的な平均と共分散行列 (混合平均と混合共分散行列) を計算する。\(\omega\) は行列であり、\(\omega_{ij}\) は \(i\) 番目のフィルタがどれだけ \(j\) 番目のフィルタに影響するかを表す。混合確率を使った重み付き平均の計算によって正しい確率が高いフィルタはそうでないフィルタによって少しだけ修正され、正しい確率が低いフィルタはそうでないフィルタによって大きく修正される。専門的な文献ではこうして修正された平均と共分散行列を混合条件 (mixed condition) あるいは混合初期条件 (mixed initial condition) と呼ぶ。\(j\) 番目のフィルタの混合状態 \(\mathbf x^m_j\) と混合共分散行列 \(\mathbf{P^m_j}\) は次の式で計算できる:

\[ \begin{aligned} \mathbf x^m_j &= \sum_{i=1}^N \omega_{ij} \mathbf x_i \\ \mathbf P^m_j &= \sum_{i=1}^N \omega_{ij}\left[(\mathbf x^i - \mathbf x^m_i) (\mathbf x^i - \mathbf x^m_i)^\mathsf T + \mathbf P_i\right] \end{aligned} \]

下付き添え字は配列にアクセスするときの添え字だと考えればよい。この式を実装する Python 風の疑似コードを示す:

for j in N:
    x0[j] = sum_over_i(w[i,j] * x[i])
    P0[j] = sum_over_i(w[i,j] * (P[i] + np.outer(x[i] - x0[j])))

数式の見た目に惑わされないことだ。ここでのアイデアは単純で、確率の高いフィルタが計算した推定値を確率の低いフィルタの推定値に組み込むことで、全てのフィルタが優れた推定値を持つことを保証している。

混合確率はどう計算できるだろうか？読み進める前に納得できる解答を見つけてみてほしい。私たちが手にしているのは現時点における各モードの確率を記述するモード確率と、モードの遷移を記述する遷移確率行列である。どうすれば新しい確率を計算できるだろうか？

もちろん、ベイズの定理だ！事前分布と尤度を乗じて、正規化すればいい。事前分布はモード確率であり、尤度はモードの遷移を表すマルコフ連鎖 (つまり遷移確率行列 \(\mathbf{M}\)) から分かる:

\[ \omega_{ij} = \| \mu_i \cdot \mathbf M_{ij}\| \]

これは次のように計算できる。コードの実行順序の都合で正規化係数 cbar を再計算している:

In [32]

cbar = np.dot(mu, M) # cbar[j] = 対象がモード j にある全確率

omega = np.zeros((2, 2))
for i in range(2):
    for j in range(2):
        omega[i, j] = (M[i, j] * mu[i]) / cbar[j]
omega

Out [32]

array([[0.987, 0.114],
       [0.013, 0.886]])

新しい事前分布を計算するには、カルマンフィルタの予測ステップを実行しなければならない。\(j\) 番目のフィルタの予測ステップは混合推定値を使って次の式を計算する:

\[ \begin{aligned} \bar{\mathbf x}_j &= \mathbf F_j\mathbf x^m_j\\ \bar{\mathbf P}_j &= \mathbf F_j\mathbf P^m_j\mathbf F_j^\mathsf T + \mathbf Q_j \end{aligned} \]

IMM アルゴリズムの推定値

最後に、IMM の出力として推定値を計算する処理が必要になる。どうすればよいだろうか？混合推定値の重み付け平均を求めるだけで済む:

\[ \begin{aligned} \mathbf x &= \sum_{j=1}^N \mu_j{\bar{\mathbf x}}_j\\ \mathbf P &= \sum_{j=1}^N \mu_j\left[(\bar{{\mathbf x}}_j - \bar{\mathbf x})({\bar{\mathbf x}}_j - \bar{\mathbf x})^\mathsf T + \bar{\mathbf P_j}\right] \end{aligned} \]

14.8 機動する目標の IMM を使った追跡

一つ例を見せよう。Crassidis ら著 Optimal estimation of dynamic systems⁶ は物体追跡の完全な例が載っている数少ない書籍の一つであり、これから説明する例はこの書籍から取ったものである。この例では移動する目標を 600 秒にわたって追跡する。目標は最初の 400 秒間直進して、400 秒後から加えられる制御入力によって 90 度の旋回を行う。Crassidis らは二つの定常加速度フィルタを使ってこの問題を解いている。一つのフィルタはプロセスノイズを持たず、もう一つのフィルタはスペクトル密度が \(10^{-3}\mathbf I\) のプロセスノイズを持つ。両方のフィルタで優れた初期値を設定し、\(\mathbf P =10^{-12}\) としている。私の実装を次に示す:

In [33]

import copy
from scipy.linalg import block_diag
from filterpy.kalman import IMMEstimator
from filterpy.common import Saver

N = 600
dt = 1.
imm_track = adaptive_internal.turning_target(N)

# ノイズの入った観測値を作成する。
zs = np.zeros((N, 2))
r = 1
for i in range(N):
    zs[i, 0] = imm_track[i, 0] + randn()*r
    zs[i, 1] = imm_track[i, 2] + randn()*r

ca = KalmanFilter(6, 2)
dt2 = (dt**2)/2
F = np.array([[1, dt, dt2],
              [0,  1,  dt],
              [0,  0,   1]])

ca.F = block_diag(F, F)
ca.x = np.array([[2000., 0, 0, 10000, -15, 0]]).T
ca.P *= 1.e-12
ca.R *= r**2
q = np.array([[.05, .125, 1/6],
              [.125, 1/3, .5],
              [1/6, .5, 1]])*1.e-3
ca.Q = block_diag(q, q)
ca.H = np.array([[1, 0, 0, 0, 0, 0],
                 [0, 0, 0, 1, 0, 0]])

# プロセスノイズを持たない同じフィルタを作成する。
cano = copy.deepcopy(ca)
cano.Q *= 0
filters = [ca, cano]

M = np.array([[0.97, 0.03],
              [0.03, 0.97]])
mu = np.array([0.5, 0.5])
bank = IMMEstimator(filters, mu, M)

xs, probs = [], []
for i, z in enumerate(zs):
    z = np.array([z]).T
    bank.predict()
    bank.update(z)

    xs.append(bank.x.copy())
    probs.append(bank.mu.copy())

xs = np.array(xs)
probs = np.array(probs)
plt.subplot(121)
plt.plot(xs[:, 0], xs[:, 3], 'k')
plt.scatter(zs[:, 0], zs[:, 1], alpha=0.1)

plt.subplot(122)
plt.plot(probs[:, 0])
plt.plot(probs[:, 1])
plt.ylim(-1.5, 1.5)
plt.title('probability ratio p(cv)/p(ca)');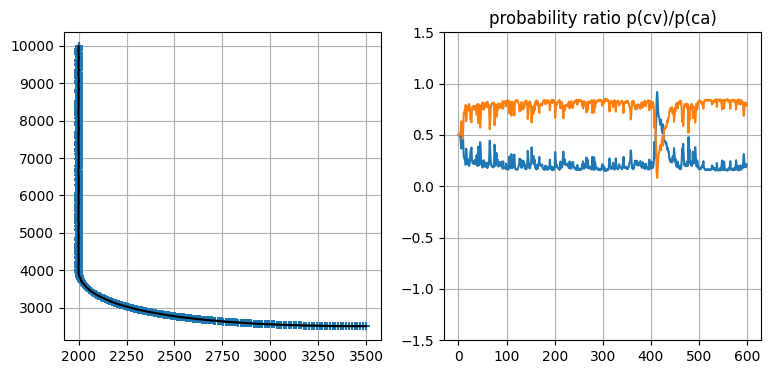

このグラフだとフィルタの性能が確認しにくいので、対象が旋回を開始したときの推定値を確認してみよう。見やすくするため \(x\) 軸と \(y\) 軸を入れ替えた上で拡大したグラフを次に示す。旋回は \(Y=4000\) で始まる。目を凝らして見ると、旋回が始まってから推定値が少し上下に振れているのが分かる。ただフィルタが観測値に遅れることはなく、推定値はすぐに滑らかになる。

In [34]

plt.plot(xs[390:450, 3], xs[390:450, 0], 'k')
plt.scatter(zs[390:450, 1], zs[390:450, 0], marker='+', s=100);
plt.xlabel('Y'); plt.ylabel('X')
plt.gca().invert_xaxis()
plt.axis('equal');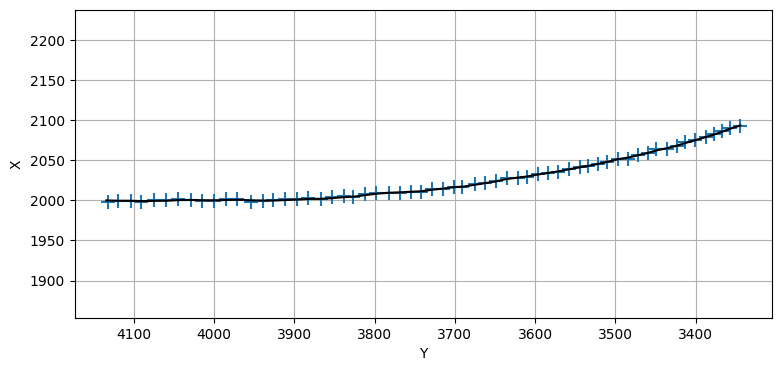

IMM の欠点

私は IMM をあまり使ったことがないので、その欠点に自分が思うほど上手くは対処できない。ただ IMM は機動する航空機を追跡するために航空交通管制の分野で開発されており、どの報告を見てもこの分野では素晴らしく振る舞うようである。

航空交通管制のユースケースにはいくつか仮定がある。最も大きな仮定が、IMM が内部に持つ全てのフィルタの状態が同じ次元であることだ。その理由は数式を追えば分かる。IMM が混合推定値を計算するときは次の式が使われる:

\[ \mathbf x = \sum_{j=1}^N \mu_j{\bar{\mathbf x}}_j \]

これは各フィルタの状態 \(\mathbf{x}\) が同じ次元を持つとき、かつそのときに限って計算可能になる。加えて、各フィルタにおける \(\mathbf{x}[i]\) の解釈も一致しなければならない。

例えば定常速度モデルを使うフィルタと定常加速度モデルを使うフィルタから IMM を作ろうとしても、状態 \(\mathbf{x}\) の次元が異なってしまうので上手く行かない。FilterPy でこれを試すと ValueError が送出される:

In [35]

ca = KalmanFilter(3, 1)
cv = KalmanFilter(2, 1)

trans = np.array([[0.97, 0.03],
                  [0.03, 0.97]])

try:
    imm = IMMEstimator([ca, cv], (0.5, 0.5), trans)
except ValueError:
    print("ValueError!")

Out [29]

ValueError!

この点に関してメールやバグ報告をもらうことがある。以前は定常速度フィルタを三次元で設計し、F を次のようにして加速度を無視することを推奨していた:

F = np.array([[1, dt, 0],
              [0, 1,  0],
              [0, 0,  0]])

しかし今考えると、これが適切かどうかは疑わしい。こうすれば IMM を動作させることはできるものの、明らかに加速度の推定値は不正確になる。片方のフィルタは正確な加速度の推定値を持つのに対して、もう一方のフィルタは加速度が常に \(0\) だと推定するためだ。この不正確な加速度は次の予測ステップで使われることになる。

もっと極端な例を考えることもできる。あるフィルタは x[2] を加速度と解釈し、別のフィルタは x[2] を回転角と解釈していたとしよう。加速度と回転角は当然足せないので、このとき混合推定値の x[2] は意味のない値になる。

繰り返すが、私は IMM についてあまり詳しくない。おそらく専門的な文献にはこういった状況に対処する方法も載っているだろう。私に言えるのは FilterPy が実装する IMM はそういったケースに対応していないということだけだ。

航空交通管制向けに設計される IMM はプロセスに関して異なる仮定を持ったフィルタを利用する。航空機は水平飛行するかもしれないし、加速や減速、あるいは釣り合い旋回や不釣り合い旋回をするかもしれない。それぞれのフィルタで F と Q は異なるものの、状態推定値 x は同一になる。

14.9 まとめ

本章には本書の他の部分と比べてかなり難しい話題が含まれる。ただ本章の内容は現実的なカルマンフィルタを実装する上で避けては通れない。ロボットを制御しているならプロセスモデルが既知なので、カルマンフィルタは簡単に構築できる。しかし現実には時系列データを渡されて「なんとかしてね」と言われることの方がずっと多い。その場合プロセスモデルはほとんど分からないので、本章に示した手法を使ってモデルをパラメータ化する方法を (機械学習的な意味で) "学ぶ" ことになる。モデルは対象の機動に応じて変化するから、フィルタもモデルの変化に適応できなければならない。

最適解を求めようとすると組み合わせ爆発が起こる。そのため現実のデータに対して最適解を求める手法は使えない。IMM が標準的なアルゴリズムになったのは、その性能が優れていて、かつ計算量的に扱いやすかったためである。

IMM が現実で使われるときは通常二つより多いフィルタが利用される。たくさんのフィルタが利用される場合も多い。目標の振る舞いが根本的に変化すると、一部のフィルタの確率は存在しないに等しくなる。多くの適応フィルタは確率の極端に低いフィルタを取り除いて現在の振る舞いを追跡できているフィルタで置き換えるアルゴリズムを実装する。詳細は問題空間によって大きく異なり、非常にアドホックである。フィルタの除去と作成に関する手法は自分で考案し、シミュレートしたデータと現実のデータを使ってその手法をテストする必要があるだろう。

アルゴリズム全体は複雑であるものの、土台にある考え方は非常に単純である事実をあなたが理解できたことを願っている。使っているのは第 2 章で学んだベイズの定理と全確率の定理だけである。ベイズの定理で新しい情報を取り入れ、全確率の定理でプロセスモデルの影響を計算する。

カルマンフィルタのベイズ的な定式化の美しさは本章で強調されるように私は思う。IMM アルゴリズムの細かい部分をあなたが覚えていなくても私は気にしないが、このアルゴリズムを導いた非常に易しい確率的な考え方をあなたが理解してくれたことは願っている。カルマン博士はカルマンフィルタの式を導くとき、直交射影 (orthogonal projection) という線形代数的な考え方を使った。直交射影には独特の美しさがあるので、カルマン博士の論文はぜひ読むべきである。ただ、この考え方は直感的とは言えないように思える。また IMM のような新しい非最適フィルタを直交射影の観点から説明する方法は全く明らかでない。ベイズの定理を使うと、そういった問題を簡単に扱うことができる。

Yaakov Bar-Shalom, X. Rong Li, and Thia Kirubarajan, Estimation with Applications to Tracking and Navigation, John Wiley & Sons, 2001, 424.^[return]
Paul Zarchan and Howard Musoff, Fundamentals of Kalman Filtering: A Practical Approach, American Institute of Aeronautics and Astronautics, 2000.^[return]
Dan Simon, Optimal State Estimation, John Wiley & Sons, 2006, 208-212.^[return]
H. A. P. Blom, "An efficient filter for abruptly changing systems," The 23rd IEEE Conference on Decision and Control, pp. 656-658, 1984.^[return]
H. A. P. Blom and Y. Bar-Shalom, "The interacting multiple model algorithm for systems with Markovian switching coefficients," IEEE Transactions on Automatic Control, vol. 33, no. 8, pp. 780-783, 1988.^[return]
John L. Crassidis and John L. Junkins, Optimal estimation of dynamic systems. CRC press, 2011.^[return]

第 14 章 適応フィルタ