第 8 章 カルマンフィルタの設計
多変量カルマンフィルタの章では "教科書的な" 問題に取り組んだ。ああいった問題は問題として記述するのが簡単で、数行のコードでプログラムにできて、さらに教えやすい。しかし現実世界の問題があれほど簡単なことはほとんどない。本章ではより現実的な例に取り組み、フィルタの性能の評価方法を学ぶ。
二次元空間を動くロボットを追跡する問題から始める。二次元空間とは例えば広場や倉庫を想像してほしい。最初は単純なノイズ付きセンサーから出力されるノイズの含まれた \((x, y)\) 座標をフィルタリングして二次元の軌跡を生成する問題を考える。この問題を理解できたら、次はセンサーの個数を増やしたり制御入力を加えたりすることで問題を大きく拡張する。
その後は非線形な問題に進む。世界は非線形だが、カルマンフィルタは線形である。少しだけ非線形な問題ならカルマンフィルタを使っても平気なこともあるが、そうでない場合もある。本章で両方の例を示す。これは非線形な問題に対する手法を学ぶ本書後半の準備になるだろう。
8.1 ロボットの追跡
最初に考えるロボット追跡問題はこれまでに考えた一次元空間を移動する犬の追跡問題と非常によく似ている。ここでは廊下における位置を観測するセンサーではなく、二次元空間の位置を観測するセンサーがある。各時刻 \(t\) において、センサーは広場における自身の位置を表すノイズ付き観測値として二次元座標 \((x,y)\) を出力する。
実際のセンサーと対話するコードの実装は本書の範囲を超えるので、これまでと同様に簡単なセンサーのシミュレーションを書くことになる。本章では様々な条件を追加するごとにシミュレーションを書く必要がある。
というわけで、最初は非常に簡単なシミュレーションから始めよう。次の PosSensor クラスは直進する物体に取り付けられたセンサーをシミュレートする。初期位置、速度、そしてノイズの標準偏差で初期化され、read メソッドが位置をタイムステップ一つ分だけ更新して新しい観測値を返す:
from numpy.random import randn
class PosSensor(object):
def __init__(self, pos=(0, 0), vel=(0, 0), noise_std=1.):
self.vel = vel
self.noise_std = noise_std
self.pos = [pos[0], pos[1]]
def read(self):
self.pos[0] += self.vel[0]
self.pos[1] += self.vel[1]
return [self.pos[0] + randn() * self.noise_std,
self.pos[1] + randn() * self.noise_std]期待通りに動くことは簡単なテストで確かめられる:
import matplotlib.pyplot as plt
import numpy as np
from kf_book.book_plots import plot_measurements
pos, vel = (4, 3), (2, 1)
sensor = PosSensor(pos, vel, noise_std=1)
ps = np.array([sensor.read() for _ in range(50)])
plot_measurements(ps[:, 0], ps[:, 1]);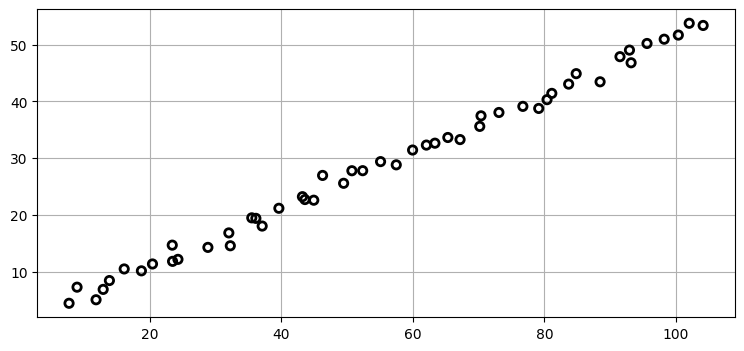
これは正しく見える。直線の傾きが \(\frac{1}{2}\) となっているが、速度を \((2,1)\) にしたので期待通りだ。またデータは \((6,4)\) の近くから始まっているように見える。この動きは現実的とは言えず、いまだに "教科書的な" 問題でしかない。以降で現実的における振る舞いを考慮した様々な条件を加えていく。
状態変数の選択
いつも通り、状態変数の選択がカルマンフィルタ設計の最初のステップとなる。物体を二次元で追跡していてセンサーは二つの次元のそれぞれに関する観測値を出力するので、\(x\) と \(y\) という二つの観測変数が存在することが分かる。この二つだけを状態変数としてカルマンフィルタを作ったとしたら、速度の情報を無視しているために正確な結果は得られないだろう。カルマンフィルタには速度も取り入れる必要がある。位置と速度は次のように表す:
この並べ方に特別な意味はない。\(\Big[x \ \ y \ \ \dot x \ \ \dot y\Big]^\mathsf T\) やその他の論理的でない並べ方も使うこともできる: 以降で使う行列が変わるだけだ。私が位置と速度を上のように並べたのは、こうすると位置と速度の共分散が共分散行列で分散と同じブロックになるためである。例えば私が使った並べ方だと P[1,0] が \(x\) と \(\dot x\) の共分散になり、\(x\) の分散の横に並ぶ。他の並べ方だとこの共分散は P[2,0] などとなり、次元数が増えると共分散がさらに散らばってしまう。
少し話を止めて、隠れ変数を見つける方法を考えよう。今の例では一次元の場合を前に考えたことがあるので隠れ変数はすぐに分かるものの、すぐには隠れ変数が分からない場合もある。この問題に簡単な答えはない。ただ、センサーからのデータの一階微分と二階微分の解釈を最初に自問してみるとよい。なぜなら、センサーの出力が固定されたタイムステップで取得されるとき一階微分と二階微分は数学的にとても簡単に計算できるからだ。例えば一階微分は隣り合う時刻における観測値をタイムステップで割るだけで済む。今考えている追跡問題では一階微分に明らかな物理的解釈が存在する: 隣り合う時刻における位置からは速度が分かる。
これに加えて、二つ以上の異なるセンサーからのデータを組み合わせることでより多く情報を生成する方法を考えることもできる。これはセンサー統合 (sensor fusion) と呼ばれる考え方であり、本章の後半で例を示す。ここでは、適切な状態変数の選択がフィルタの性能を可能な限り高めるために最も重要な要素であることを認識してほしい。隠れ変数を選んだら、たくさんのテストを実行して現実的な結果が得られることを確認しなければならない。カルマンフィルタはどんなモデルを与えても動作するものの、与えたモデルが隠れ変数に関する優れた情報を生成できないとカルマンフィルタの出力は無意味なものになってしまう。
状態遷移関数の設計
次のステップは状態遷移関数の設計である。カルマンフィルタでは状態遷移関数が行列 \(\mathbf{F}\) として実装され、\(\mathbf{F}\) に状態を乗じることで次の状態 (の予測値) を計算することを思い出してほしい。これを表した式を示す:
状態遷移の式は次のようになる。多変量カルマンフィルタの章で考えた一次元の場合とよく似ているので、説明は省略する:
このように書くと、\(\mathbf{F}\) の形状と値がはっきりする。行列とベクトルを使った形式で書くとこうなる:
では、これを Python で書いてみよう。とても簡単に書ける: 新しいのは dim_z を 2 に設定する点だけだ:
from filterpy.kalman import KalmanFilter
tracker = KalmanFilter(dim_x=4, dim_z=2)
dt = 1. # タイムステップは 1 秒
tracker.F = np.array([[1, dt, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, dt],
[0, 0, 0, 1]])プロセスノイズ行列の設計
\(\mathbf{Q}\) は FilterPy が計算してくれる。話を簡単にするため、ノイズは離散白色ノイズ (離散化した時刻の間で定数) だと仮定する。この仮定があると、ステップごとにモデルがどの程度変化するかを分散で指定できるようになる。この説明が理解できなかったらプロセスノイズ行列の設計の節を読み直してほしい:
from scipy.linalg import block_diag
from filterpy.common import Q_discrete_white_noise
q = Q_discrete_white_noise(dim=2, dt=dt, var=0.001)
tracker.Q = block_diag(q, q)
print(tracker.Q)[[0. 0.001 0. 0. ]
[0.001 0.001 0. 0. ]
[0. 0. 0. 0.001]
[0. 0. 0.001 0.001]]ここで \(x\) 軸方向の位置/速度のノイズと \(y\) 軸方向の位置/速度のノイズは独立と仮定しており、対応する共分散は全てゼロとなっている。このため最初に一つの次元に対する \(\mathbf{Q}\) を計算してから block_diag 関数で二つの次元に対する \(\mathbf{Q}\) を組み立てている。
制御関数の設計
ロボットに制御入力は与えていないので、このステップで行うべきことはない。デフォルトで KalmanFilter クラスは制御入力がないことを仮定して B を零行列に初期化する。
つまり書くべきコードはない。書きたければ tracker.B を明示的に 0 にしておいてもいいだろう。ただ次に示すように、何もしなくても零行列を表す None が代入されている:
tracker.B観測関数の設計
カルマンフィルタの観測関数 \(\mathbf{H}\) は状態変数 \(\mathbf{x}\) から観測値 \(\mathbf{z}\) を \(\mathbf{z} = \mathbf{Hx}\) と計算する方法を与える。今考えている例では観測値が \((x,y)\) だから、\(\mathbf{z}\) は \(\Big[x \ \ y\Big]^\mathsf T\) という \(2{\times}1\) 行列となる。状態変数 \(\mathbf{x}\) のサイズは \(4{\times}1\) だった。\(M{\times}N\) 行列と \(N{\times}P\) 行列の積は \(M{\times}P\) 行列であることを思い出せば、
より \(\mathbf{H}\) は \(2{\times}4\) 行列と分かる。
\(\mathbf{H}\) の値を埋めるのは難しくない。観測値はロボットの位置であり、これは状態 \(\mathbf{x}\) に含まれる \(x\) と \(y\) そのものだからだ。ここでは問題を少しだけ面白くするために、単位の変換が必要だとしてみよう。観測値はフィートで出力され、カルマンフィルタではメートルで処理を行いたいとする。\(\mathbf{H}\) は状態を観測値に変換するのだから、そこで起こる変換は「\(\text{フィート} = \text{メートル} / 0.3048\)」である。よって次が分かる:
この \(\mathbf{H}\) は次の線形方程式に対応する:
観測関数の設計は簡単であり、途中の次元解析も行わずに直接求ることもできただろう。ただカルマンフィルタの式は全ての行列の次元を特定することは覚えておいたほうがいい。何を設計すればいいのか分からなくなったときは、行列の次元に注目すると見通しが良くなることが多い。
\(\mathbf{H}\) の実装を示す:
tracker.H = np.array([[1/0.3048, 0, 0, 0],
[0, 0, 1/0.3048, 0]])観測ノイズ行列の設計
変数 \(x\), \(y\) は独立な白色ガウス過程であると仮定する。つまり、\(x\) のノイズと \(y\) のノイズは互いに全く影響を及ぼさず、平均 \(0\) の正規分布に従うとする。今は \(x\) と \(y\) の分散として \(5~\text{ft²}\) を採用しておく。また \(x\) と \(y\) は独立だから、共分散はない。つまり共分散行列の非対角成分は \(0\) である。以上より \(\mathbf{R}\) が分かる:
一般に \(n\) 個の変数があるとき共分散行列は \(n{\times}n\) 行列となるので、センサーから入力が二つあるとき \(\mathbf{R}\) は \(2{\times}2\) 行列となる。Python では次のように書ける:
tracker.R = np.array([[5., 0],
[0, 5]])
tracker.Rarray([[5., 0.],
[0., 5.]])初期条件
今考えている問題は簡単なので、初期位置は \((0,0)\) に、初期速度は \((0,0)\) に設定する。これは完全な当てずっぽうであることを考慮して、推定値の共分散行列 \(\mathbf{P}\) は大きな値に設定する:
Python 実装はこうなる:
tracker.x = np.array([[0, 0, 0, 0]]).T
tracker.P = np.eye(4) * 500.フィルタの実装
これでフィルタの設計は完了したので、後はフィルタを実行して結果を出力するコードを書くだけだ。結果の出力には好きなフォーマットを利用できる。フィルタを 30 反復するコードを書くことにする (グラフが見やすいようノイズを調整してある):
from filterpy.stats import plot_covariance_ellipse
from kf_book.book_plots import plot_filter
R_std = 0.35
Q_std = 0.04
def tracker1():
tracker = KalmanFilter(dim_x=4, dim_z=2)
dt = 1.0 # time step
tracker.F = np.array([[1, dt, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, dt],
[0, 0, 0, 1]])
tracker.u = 0.
tracker.H = np.array([[1/0.3048, 0, 0, 0],
[0, 0, 1/0.3048, 0]])
tracker.R = np.eye(2) * R_std**2
q = Q_discrete_white_noise(dim=2, dt=dt, var=Q_std**2)
tracker.Q = block_diag(q, q)
tracker.x = np.array([[0, 0, 0, 0]]).T
tracker.P = np.eye(4) * 500.
return tracker
# ロボットの移動のシミュレート
N = 30
sensor = PosSensor((0, 0), (2, .2), noise_std=R_std)
zs = np.array([sensor.read() for _ in range(N)])
# フィルタの実行
robot_tracker = tracker1()
mu, cov, _, _ = robot_tracker.batch_filter(zs)
for x, P in zip(mu, cov):
# x と y の共分散
cov = np.array([[P[0, 0], P[2, 0]],
[P[0, 2], P[2, 2]]])
mean = (x[0, 0], x[2, 0])
plot_covariance_ellipse(mean, cov=cov, fc='g', std=3, alpha=0.5)
# 結果のプロット
zs *= .3048 # メートルへの変換
plot_filter(mu[:, 0], mu[:, 2])
plot_measurements(zs[:, 0], zs[:, 1])
plt.legend(loc=2)
plt.xlim(0, 20);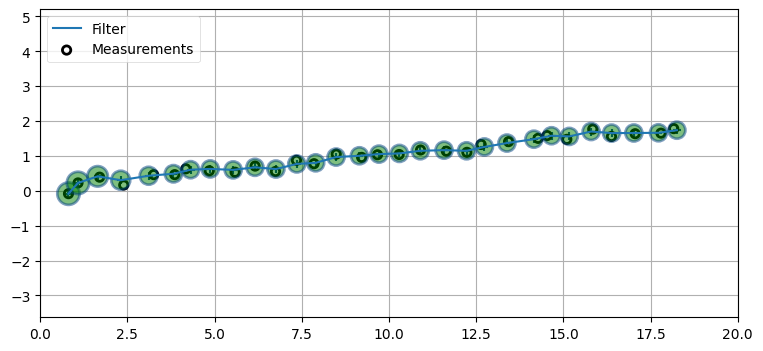
\(\mathbf{Q}\) と \(\mathbf{R}\) を様々な値に変更してみることを勧める。ただそういったことはこれまでの章でかなり行ったので、そして私たちには学ばなければならないことが多くあるので、さらに複雑なケースへこのまま進むことにする。そこでも値を変化させる経験はできるだろう。
上のグラフでは \(x\) と \(y\) に対する \(3\sigma\) の共分散楕円をプロットしている。その形を説明できるだろうか? 多変量カルマンフィルタの章で見たような傾いた楕円を期待したかもしれない。しかし、そこでは \(x\) と \(y\) ではなく \(x\) と \(\dot{x}\) をプロットしたことを思い出してほしい。\(x\) と \(\dot{x}\) には相関があるのに対して、\(x\) と \(y\) には相関がない (独立である)。よって今回楕円は傾かない。加えて \(x\) と \(y\) のノイズは同じ標準偏差を持つとしていた。例えば \(\mathbf{R}\) を
と設定したら、\(x\) に \(y\) より大きなノイズが含まれることがカルマンフィルタに伝わるので、共分散楕円は縦に長くなるだろう。
\(\mathbf{P}\) の最後の値は状態変数の相関について私たちが知りたいことの全てを伝える。対角要素を見れば各変数の分散が分かる。つまり \(\mathbf{P}_{0,0}\) は \(x\) の分散、\(\mathbf{P}_{1,1}\) は \(\dot x\) の分散、\(\mathbf{P}_{2,2}\) は \(y\) の分散、\(\mathbf{P}_{3,3}\) は \(\dot y\) の分散をそれぞれ表す。対角要素は numpy.diag() で取り出せる:
print(np.diag(robot_tracker.P))[0.007 0.003 0.007 0.003]今考えている共分散行列は \(2{\times}2\) 行列を四つ持つとみなせる。どこで区切るかは簡単に分かるはずだ。これは \(x\) と \(\dot x\) の相関および \(y\) と \(\dot y\) の相関が存在するためである。左上の \(2{\times}2\) ブロックは \(x\) と \(\dot x\) の共分散行列となっている:
c = robot_tracker.P[0:2, 0:2]
print(c)
plot_covariance_ellipse((0, 0), cov=c, fc='g', alpha=0.2)[[0.007 0.003]
[0.003 0.003]]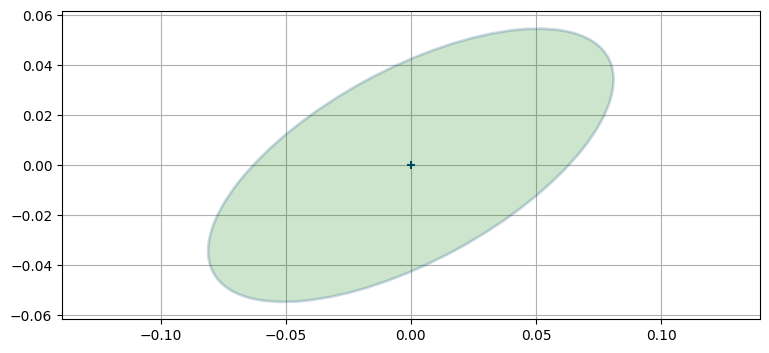
\(x\) と \(\dot x\) の共分散行列が \(\mathbf P\) の左上にあるのは、状態変数をそのように並べたからである。\(\mathbf{P}_{i,j}\) と \(\mathbf{P}_{j,i}\) には \(\sigma_{ij}\) が含まれるのを思い出してほしい。
最後に \(\mathbf{P}\) の左下を見ると、この部分は全て \(0\) になっている。なぜだろうか? \(\mathbf{P}_{3,0}\) を考えよう。ここには \(\sigma_{30}\) つまり \(\dot y\) と \(x\) の共分散が格納される。この二つの変数は独立だから、\(\mathbf{P}_{3,0}\) は \(0\) となる。他の項についても同様に変数の独立性から \(0\) になると分かる。
robot_tracker.P[2:4, 0:2]array([[0., 0.],
[0., 0.]])8.2 フィルタの次数
これまでに考えたのは位置と速度を追跡するフィルタだった。このフィルタは上手く動作したものの、それは私が適切な問題を選んでいたからだ。カルマンフィルタの経験は十分に積めたと思うので、カルマンフィルタを一般的に論じてみよう。
次数 (order) とは何か? 系のモデル化を考える文脈において、次数は系を正確にモデル化するのに必要になる最大の微分の回数を指す。例えば建物の高さのように変わらない系を考えると、変わらないのだから微分を取る必要はない。よってそういった系の次数は \(0\) であり、\(x = 312\) のような方程式で表すことができる。フィルタの次数とはフィルタが考えている系の次数を言う。
一次の系のモデルには一次の微分が含まれる。例えば位置の変化率は速度だから、次のように書ける:
これを積分するとニュートンの運動方程式となる:
これは一次の系のモデルの例である。速度が一定なことを仮定しているので、定常速度モデル (constant velocity model) と呼ばれる。
二次の系のモデルには二次微分が含まれる。例えば位置の二次微分は加速度だから、
と書ける。これを積分すれば次を得る:
これは二次の系のモデルの例であり、定常加速度モデル (constant acceleration model) と呼ばれる。
系の次数は多項式の次数を考えても確認できる。二次微分を持つ定常加速度モデルが表す系は二次なのと同様に、このモデルを表す式 \(x = \frac{1}{2}at^2 +v_0t + x_0\) も二次の多項式となっている。
状態変数とプロセスモデルの設計では、モデル化する系の次数を選択しなければならない。物体の追跡で一次の系を仮定し、定常速度モデルを使うとしよう。現実世界の現象は完璧でないから、短い時間の間に速度は少し変化する。このとき速度の小さな変化を捉えるために二次のフィルタ (二次の系を仮定するフィルタ) を使うべきだと思うかもしれない。
しかし実際には二次のフィルタを使っても優れた結果は得られないことが多い。この問題を深く理解するために、フィルタリングする系と次数が異なるプロセスモデルを使ったときに何が起こるかを確認してみよう。
まずフィルタリングする系からの観測値データが必要になる。そこで等速で移動する物体をシミュレートする ConstantVelocityObject クラスを書く。現実世界の物理系で物体が完全に等速で移動することは原理的にあり得ないので、更新のたびに速度を少しだけ変化させる。またセンサーはガウス分布に従うノイズを持つものとしてシミュレートする。次にコードを示す。動作が正しいことを確認するために一度実行して結果をプロットしている:
from kf_book.book_plots import plot_track
class ConstantVelocityObject(object):
def __init__(self, x0=0, vel=1., noise_scale=0.06):
self.x = x0
self.vel = vel
self.noise_scale = noise_scale
def update(self):
self.vel += randn() * self.noise_scale
self.x += self.vel
return (self.x, self.vel)
def sense(x, noise_scale=1.):
return x[0] + randn()*noise_scale
np.random.seed(124)
obj = ConstantVelocityObject()
xs, zs = [], []
for i in range(50):
x = obj.update()
z = sense(x)
xs.append(x)
zs.append(z)
xs = np.asarray(xs)
plot_track(xs[:, 0])
plot_measurements(range(len(zs)), zs)
plt.legend(loc='best');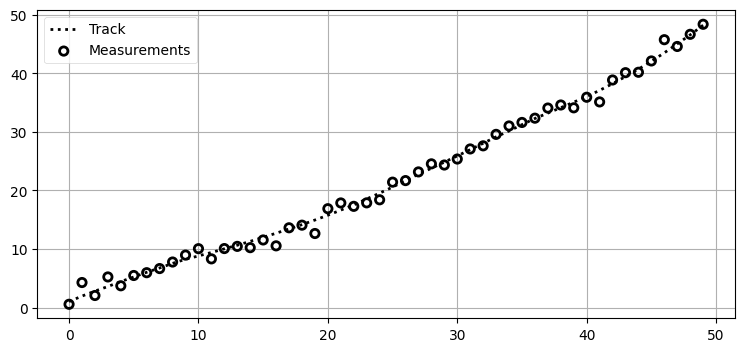
満足いくプロットが得られた。系にノイズを追加したために、軌跡は完璧な直線にはなっていない──これは道を歩く人の軌跡かもしれないし、あるいは様々な方向から風にもまれる航空機の軌跡かもしれない。このモデルは意図的に加えられる加速度を持たないので定常速度モデルと呼ばれる。ここでも、小さな加速があるのだから二次のカルマンフィルタを使えばいいのではないかと思うことだろう。本当にそうなのかを確かめよう。
零次、一次、二次のカルマンフィルタはどのように設計すればいいだろうか? 実はこの設計は本書でこれまでに「次数」という言葉を使わずに行ったことがある。読むのは少し面倒かもしれないが、ここではそれぞれの設計を完全に説明する──もし分かっているなら飛ばしても構わない。
零次のカルマンフィルタ
零次のカルマンフィルタは微分を使わずに追跡を行う。今は位置を追跡しているから、これは状態変数に位置だけが含まれ (速度と加速度は含まれず)、遷移関数は位置だけを考えることを意味する。状態変数をベクトルで表すと次のようになる:
状態遷移関数は非常に簡単になる。位置は変化しないのだから、モデルは \(x=x\) となる。言い換えれば、時刻 \(t+1\) における \(x\) は時刻 \(t\) における \(x\) から変化しない。行列で表せば次のようになる:
観測関数も非常に簡単になる。状態変数 \(\mathbf{x}\) を観測値に変換する方法を観測関数で定義する必要があったことを思い出してほしい。観測値は位置と仮定すれば、状態は位置だけからなるので次が分かる:
この零次のカルマンフィルタを構築して返す関数を書こう:
def ZeroOrderKF(R, Q, P=20):
"""
零次のカルマンフィルタを作成する。
R と Q には float を指定する。
"""
kf = KalmanFilter(dim_x=1, dim_z=1)
kf.x = np.array([0.])
kf.R *= R
kf.Q *= Q
kf.P *= P
kf.F = np.eye(1)
kf.H = np.eye(1)
return kf一次のカルマンフィルタ
一次のカルマンフィルタは一次の系を追跡する。例えば位置と速度からなる系は一次の系である。本書で犬の追跡問題を通して設計したのは一次のカルマンフィルタだから、どんなものかは分かっているはずだ。ただここではもう一度フィルタを設計してみよう。
一次の系は位置と速度を持つので、状態変数も位置と速度からなる必要がある。これをベクトルで表せば次のようになる:
続いて状態遷移を設計する。ニュートンの運動方程式を考えると、時刻 \(t-1\) および時刻 \(t\) における位置と速度には次の関係がある:
これを次の形の線形方程式に変換しなければならないのだった:
\(\mathbf{F}\) を
とすれば、上述の方程式が得られる。
最後に観測関数を設計する。観測関数 \(\mathbf{H}\) は次の等式を実装する必要がある:
今考えているセンサーは位置だけを出力するので、\(\mathbf{H}\) は状態から位置を取り出し、速度を捨てる。これは次のようにすれば行える:
この一次のカルマンフィルタを構築して返す関数を示す:
def FirstOrderKF(R, Q, dt):
"""
一次のカルマンフィルタを作成する。
R と Q には float を指定する。
"""
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.x = np.zeros(2)
kf.P *= np.array([[100, 0], [0, 1]])
kf.R *= R
kf.Q = Q_discrete_white_noise(2, dt, Q)
kf.F = np.array([[1., dt],
[0., 1]])
kf.H = np.array([[1., 0]])
return kf二次のカルマンフィルタ
二次のカルマンフィルタは二次の系を追跡する。例えば位置、速度、加速度からなる系は二次の系である。状態変数は次のようになる:
続いて状態遷移を設計しなければならない。時刻 \(t-1\) および時刻 \(t\) における位置・速度・加速度には次の関係がある:
これを次の形の線形方程式に変換しなければならないのだった:
\(\mathbf{F}\) を
とすれば上述の方程式が得られる。
最後に観測関数を設計する。観測関数 \(\mathbf{H}\) は次の等式を実装する必要がある:
センサーの出力はここでも位置だけだから、\(\mathbf{H}\) は状態から位置だけを取り出して速度と加速度を捨てる。これは次のようにすれば行える:
この二次のカルマンフィルタを構築して返す関数を示す:
def SecondOrderKF(R_std, Q, dt, P=100):
"""
二次のカルマンフィルタを作成する。
R と Q には float を指定する。
"""
kf = KalmanFilter(dim_x=3, dim_z=1)
kf.x = np.zeros(3)
kf.P[0, 0] = P
kf.P[1, 1] = 1
kf.P[2, 2] = 1
kf.R *= R_std**2
kf.Q = Q_discrete_white_noise(3, dt, Q)
kf.F = np.array([[1., dt, .5*dt*dt],
[0., 1., dt],
[0., 0., 1.]])
kf.H = np.array([[1., 0., 0.]])
return kf8.3 フィルタの次数の評価
それでは、それぞれのカルマンフィルタをシミュレーションに対して実行して結果を見てみよう。
結果はどうすれば評価できるだろうか? 結果をプロットして目で判断すれば定性的な評価はできるものの、厳密なアプローチでは数学が使われる。推定値の共分散行列 \(\mathbf{P}\) には分散と共分散が状態変数 (の組) ごとに格納されることを思い出そう。対角要素が分散となる。またノイズがガウス分布なら全ての観測値の 99% が平均から \(3\sigma\) の範囲に収まることも思い出そう。これは大事なポイントなので、もし分からなかったら確率・ガウス分布・ベイズの定理の章を読み直してから進んでほしい。
よってフィルタを評価するには、推定された状態と実際の状態の残差を求め、それを \(\mathbf{P}\) から導かれる標準偏差と比較すればよい。もしフィルタが正しく動作しているなら、計算された残差の 99% は \(3\sigma\) に収まるはずである。これは位置だけではない全ての状態変数に対して成り立つ。
このフィルタの評価方法はシミュレートされた系でのみ正しいと言っておかなければならない。現実世界のセンサーからのデータは完璧なガウス分布ではないので、この基準を (例えば \(5\sigma\) まで) 広げる必要があるかもしれない。
では、一次の系に対して一次のカルマンフィルタを実行して性能を確認しよう。おそらく性能は良いはずだと予想できると思うが、標準偏差を使ってそのことを確認してみる。
最初に、ノイズが入った観測値を生成する関数を書く:
def simulate_system(Q, count):
obj = ConstantVelocityObject(x0=.0, vel=0.5, noise_scale=Q)
xs, zs = [], []
for i in range(count):
x = obj.update()
z = sense(x)
xs.append(x)
zs.append(z)
return np.array(xs), np.array(zs)続いて、フィルタリングを実行して出力を Saver オブジェクトに書き込む関数を書く:
from filterpy.common import Saver
def filter_data(kf, zs):
s = Saver(kf)
kf.batch_filter(zs, saver=s)
s.to_array()
return sこれでフィルタを実行して結果を確認する準備が整った:
from kf_book.book_plots import plot_kf_output
R, Q = 1, 0.03
xs, zs = simulate_system(Q=Q, count=50)
kf = FirstOrderKF(R, Q, dt=1)
data1 = filter_data(kf, zs)
plot_kf_output(xs, data1.x, data1.z)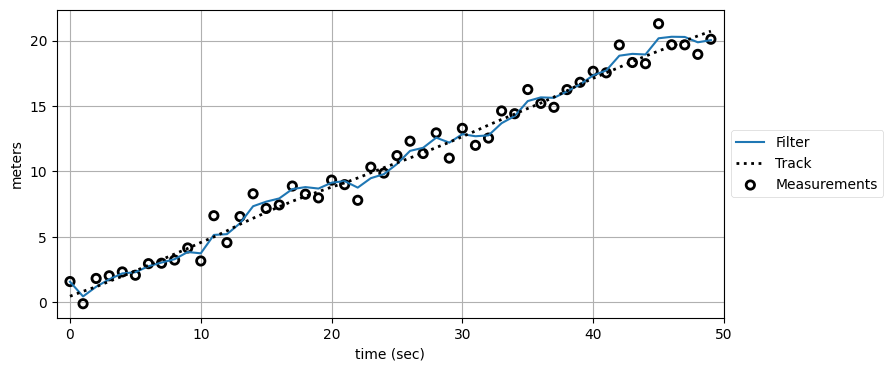
フィルタは正しく振る舞っているようだ。ただ振る舞いが正確にどれくらい正しいのかは分からない。残差をプロットして何か分からないかを見よう。残差のプロットは何度も行うので、関数を作っておく:
from kf_book.book_plots import plot_residual_limits, set_labels
def plot_residuals(xs, data, col, title, y_label, stds=1):
res = xs - data.x[:, col]
plt.plot(res)
plot_residual_limits(data.P[:, col, col], stds)
set_labels(title, 'time (sec)', y_label)plot_residuals(xs[:, 0], data1, 0,
title='First Order Position Residuals(1$\sigma$)',
y_label='meters')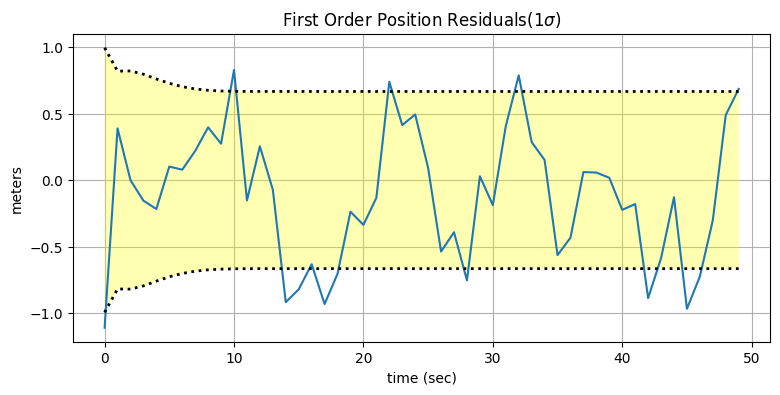
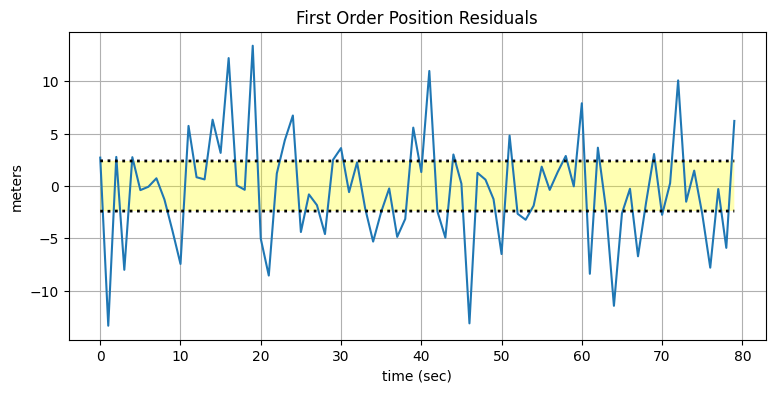
このグラフはどう解釈できるだろうか? 折れ線は残差──観測値と推定値の差──を表す。もし観測ノイズが全く存在せずカルマンフィルタの予測が常に完璧だったら、残差も常にゼロとなる。つまり理想的な出力は \(x\) 軸に沿った水平な直線である。実際のプロットでは残差がゼロを中心として上下しており (さらに残差より上の値と残差より下の値が同じ程度存在するので)、ノイズがガウス分布に従っていることに自信が持てる。破線に囲まれた黄色い領域は \(1\sigma\) であり、フィルタの理論的性能を示す。残差はこの領域にほぼ収まっているので、フィルタは正しく動作しており、発散はしていないことが分かる。
次は速度の残差を見てみよう:
plot_residuals(xs[:, 1], data1, 1,
title='First Order Velocity Residuals(1$\sigma$)',
y_label='meters/sec')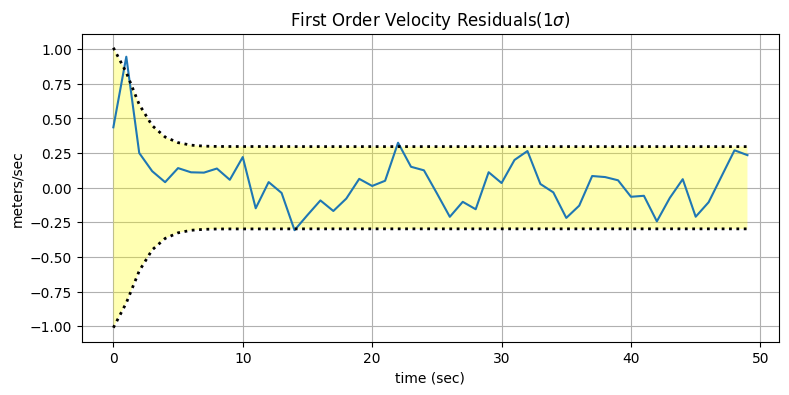
ここでも期待通り、残差はフィルタの理論的性能が示す領域の内側に収まっている。よって私たちはフィルタがこの系に対して正しく設計されていることに自信が持てる。
では零次のカルマンフィルタで同じことをしてみよう。コードと数式はほぼ同じなので、実装はあまり説明せずに結果だけを見ていく:
kf0 = ZeroOrderKF(R, Q)
data0 = filter_data(kf0, zs)
plot_kf_output(xs, data0.x, data0.z)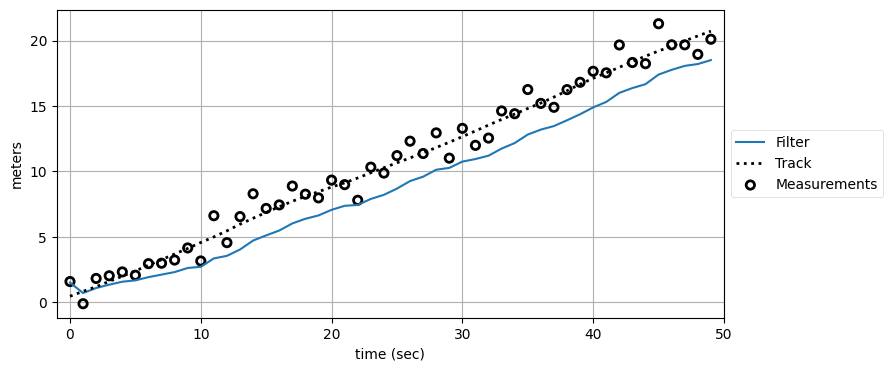
予想した通り、このフィルタには問題がある。g-h フィルタの章で入力データに加速度を加えたときのことを思い出してほしい。速度の変化に十分早く反応するための項がフィルタに存在しないために、g-h フィルタの出力は必ず入力から遅れていた。この例でカルマンフィルタは全ての予測ステップで位置が変わらないという予測を立てる──現在の位置が \(4.3\) なら次の時刻における位置も \(4.3\) と予測する。もちろん次の時刻における実際の位置は \(5.3\) の近くで、観測値は \(5.4\) のような値になる。これを受けてフィルタは \(4.3\) と \(5.4\) の間にある値を推定値として選択するので、実際の値 \(5.3\) からは大きく遅れてしまう。同じことは以降ステップでも延々に続き、フィルタの出力が実際の値に追いつくことはない。
グラフからはこれとは別の非常に重要なポイントも分かる: 「定数」の仮定は離散的なサンプルの間で状態が定数であるという仮定であり、フィルタの出力は時間の経過とともに変化できる。
では残差を見てみよう。速度は追跡していないから、確認できるのは位置の残差だけだ:
plot_residuals(xs[:, 0], data0, 0,
title='Zero Order Position Residuals(3$\sigma$)',
y_label='meters',
stds=3)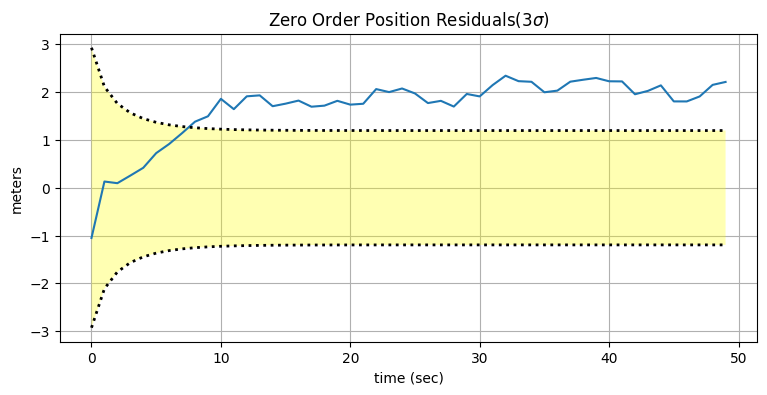
フィルタの出力がすぐに発散しているのが分かる。十秒もしないうちに残差は \(3\sigma\) の領域を外れてしまう。ここでは共分散行列 \(\mathbf{P}\) が報告するのは全ての入力が正しいと仮定したときの理論的なフィルタの性能であることを理解するのが重要である。言い換えれば、実際には出力が発散しているにもかかわらず、\(\mathbf{P}\) は推定値の分散が小さくなっていることを示しているので、このカルマンフィルタは自身の推定値が時間の経過とともに正確になっていると思っている。フィルタはあなたが系に関して嘘を教えたとは知る由もない。こういったフィルタは独善的 (smug) と呼ばれる──自身の性能に自信過剰になっている。
この系では発散がすぐに起こり、非常に分かりやすい。しかし多くの系では発散がゆっくりと、小さく起こる。自分が考えている系で上のようなグラフをプロットして、フィルタの性能が理論的性能に収まることを確かめるのが重要である。
続いて二次の系を試そう。二次の系を使うのは良いことだと思うかもしれない。結局、シミュレートされた物体の移動にはノイズが存在するのだから、加速が存在するはずだ。なら二次の系で加速度をモデル化すればいい、加速度を系に含めないとゼロに推定されるだけじゃないか! さて、フィルタはどう振る舞うだろうか? 考えてから読み進めてほしい。
kf2 = SecondOrderKF(R, Q, dt=1)
data2 = filter_data(kf2, zs)
plot_kf_output(xs, data2.x, data2.z)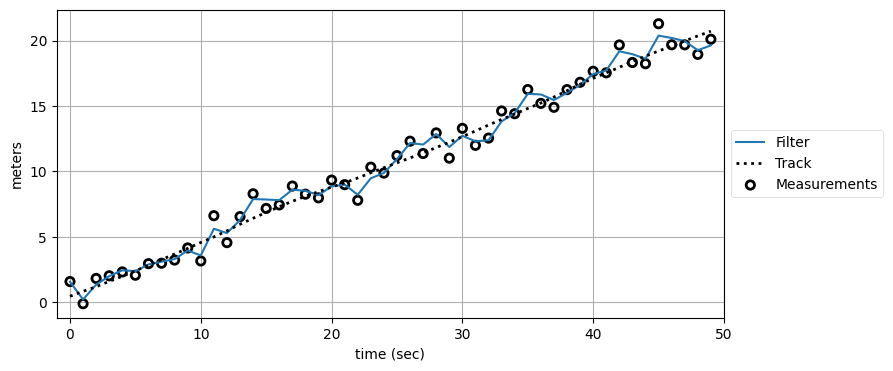
フィルタは予想通りの性能となっただろうか?
二次のフィルタは一次のフィルタより性能が悪いことが分かる。なぜだろうか? このフィルタは加速をモデル化しているために、観測値の大きな変化の原因はノイズではなく加速だと解釈する。そのためフィルタはノイズを忠実に追跡してしまう。それだけではなく、だんだん大きくなる (あるいはだんだん小さくなる) ように見えるノイズが連続した場合にはフィルタがノイズをオーバーシュートする可能性さえある。そのときフィルタは存在しない加速度を存在すると誤って思い込み、観測値ごとに正しい軌道から離れていく。これは良い状況ではない。
ただ、どうしようもない出力であるわけでもない。残差を見て何が分かるかを確認しよう。小さな問題がここから分かる。二次の系を使ったときの残差は発散もしていないし、\(3\sigma\) の領域から飛び出しているわけでもない。ただ一次のフィルタと二次のフィルタの残差を比較すると興味深いことが分かるので、同じグラフにプロットする:
res2 = xs[:, 0] - data2.x[:, 0]
res1 = xs[:, 0] - data1.x[:, 0]
plt.plot(res1, ls="--", label='order 1')
plt.plot(res2, label='order 2')
plot_residual_limits(data2.P[:, 0, 0])
set_labels('Second Order Position Residuals',
'meters', 'time (sec)')
plt.legend();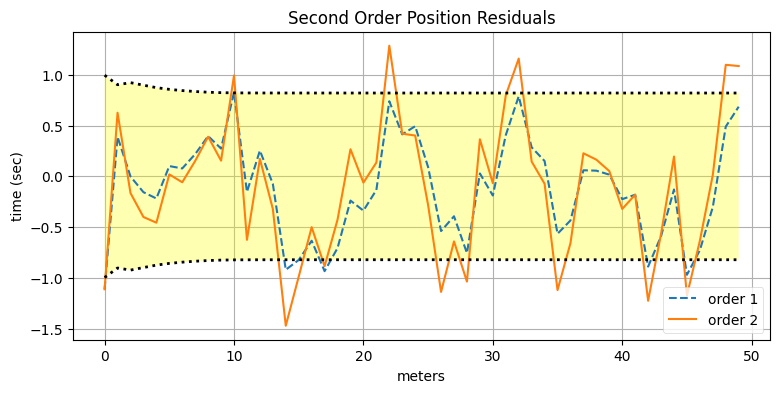
二次のフィルタにおける位置の残差は一次のフィルタより少しだけ悪いのが分かる。ただどちらも理論的性能を表す領域に収まっている。ここには特に警戒すべき点はない。
次は速度の残差を見てみよう:
res2 = xs[:, 1] - data2.x[:, 1]
res1 = xs[:, 1] - data1.x[:, 1]
plt.plot(res2, label='order 2')
plt.plot(res1, ls='--', label='order 1')
plot_residual_limits(data2.P[:, 1, 1])
set_labels('Second Order Velocity Residuals',
'meters/sec', 'time (sec)')
plt.legend();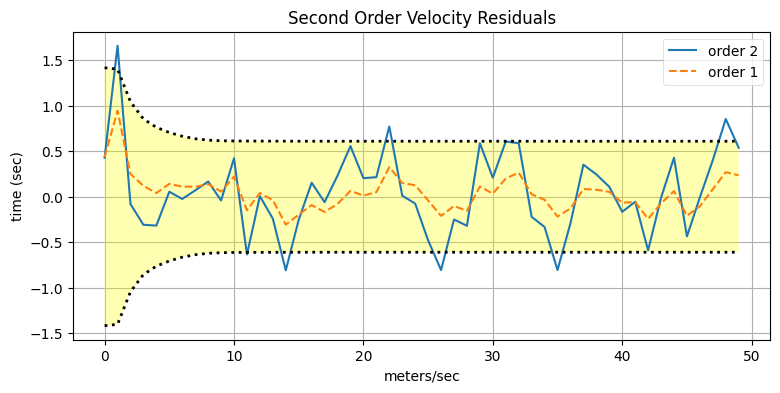
ここでは話がずいぶん変わってくる。二次の系を使ったときの速度の残差は理論的なフィルタ性能の範囲に収まってはいるものの、その残差は一次の系を使ったときの残差より格段に大きい。これは今考えているようなシナリオでよく得られる結果である。フィルタは存在しない加速度を存在するものと考えており、観測値に含まれるノイズから検出された加速度が予測ステップごとに速度の推定値に加算される。もちろん実際には加速度は存在しないから、このとき速度の残差は最適よりもずっと大きくなる。
実はまだ使っていない秘策が一つある。私たちがフィルタリングしようとしているのは一次の系であり、速度はほぼ変化しない。現実世界の系は必ず完璧でないから、速度が時刻をまたいで完全に同じであることは絶対にない。一次のフィルタを使うときは、この速度の微小な変化をプロセスノイズとして処理していた。プロセスノイズ行列 \(\mathbf{Q}\) を設定したのは位置の微小な変化を考えに入れるためである。二次のフィルタでは速度の変化が状態変数として処理されるのだから、プロセスノイズは考えなくても、つまり \(\mathbf{Q}\) を \(\mathbf{0}\) にしても問題ないかもしれない!
kf2 = SecondOrderKF(R, 0, dt=1)
data2 = filter_data(kf2, zs)
plot_kf_output(xs, data2.x, data2.z)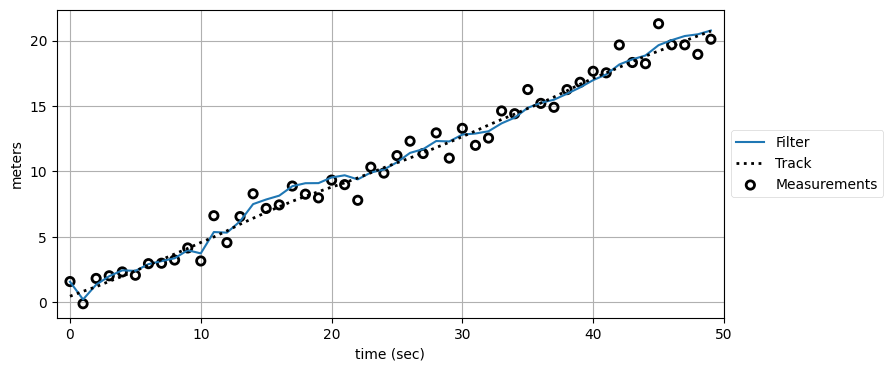
私の目には、こちらの方が早く本当の軌道に収束しているように見える。成功だ!
... 本当だろうか? プロセスノイズ行列を \(\mathbf{0}\) に設定するのはプロセスモデルが完璧だとフィルタに伝えるのに等しい。もっと長い間フィルタを実行したときの性能を確認しよう:
np.random.seed(25944)
xs500, zs500 = simulate_system(Q=Q, count=500)
kf2 = SecondOrderKF(R, 0, dt=1)
data500 = filter_data(kf2, zs500)
plot_kf_output(xs500, data500.x, data500.z)
plot_residuals(xs500[:, 0], data500, 0,
'Second Order Position Residuals',
'meters')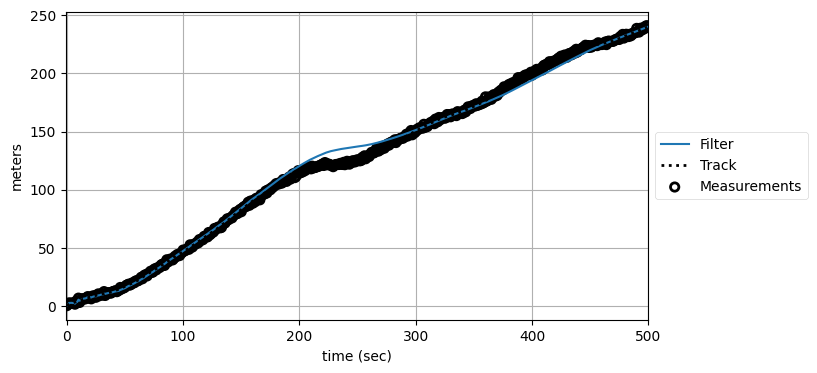
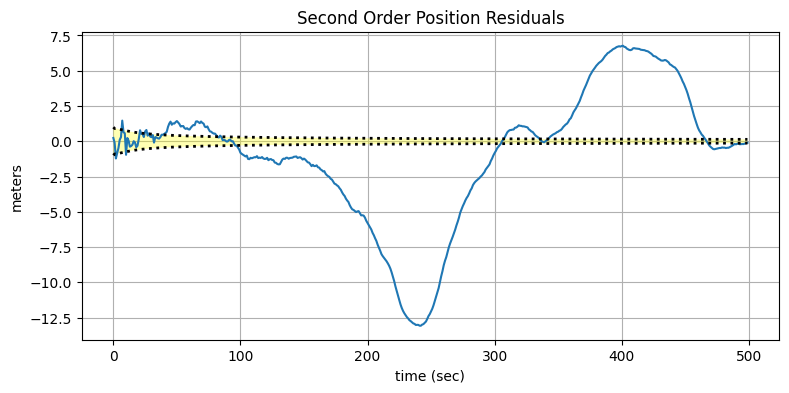
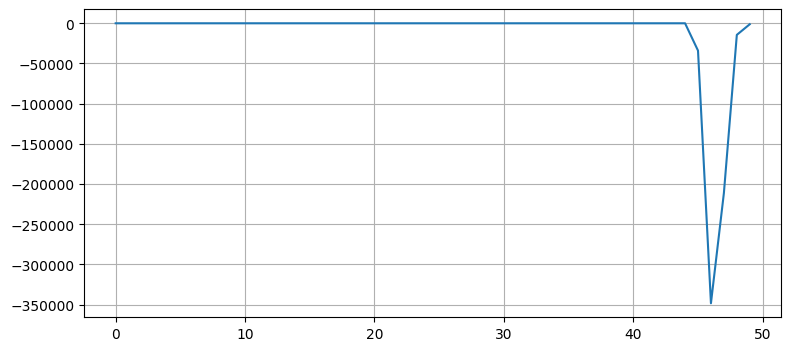
絶望的なフィルタの性能が確認できる。一つ目のグラフからはフィルタの出力が正しい軌道から長い間離れているのが分かり、二つ目のグラフだとその問題がさらに明確になる。100 回目の更新あたりを境にフィルタの出力は理論的性能から大きく離れていっている。もしかしたら最終的には正しい値に戻ってくるかもしれないが、可能性は低そうだ。一方で、全期間を通じてフィルタは分散が小さくなっていると報告している。ここから重要な教訓が得られる: フィルタの性能を判断するのにフィルタの共分散行列を使ってはいけない!
なぜこのようなことが起こるのだろうか? プロセスノイズ行列を \(\mathbf{0}\) に設定するのは、プロセスモデルだけを使うようフィルタに伝えるのに等しい。よって観測値は最終的には無視される。物理系は完璧ではなく、その完璧でない振る舞いにフィルタは適応できない。
ではプロセスノイズ行列を非常に小さくしたら? 試してみよう:
np.random.seed(32594)
xs2000, zs2000 = simulate_system(Q=0.0001, count=2000)
kf2 = SecondOrderKF(R, 0, dt=1)
data2000 = filter_data(kf2, zs2000)
plot_kf_output(xs2000, data2000.x, data2000.z)
plot_residuals(xs2000[:, 0], data2000, 0,
'Second Order Position Residuals',
'meters')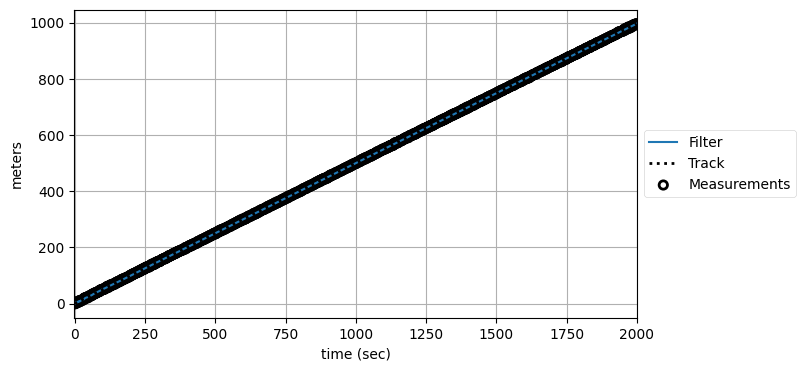
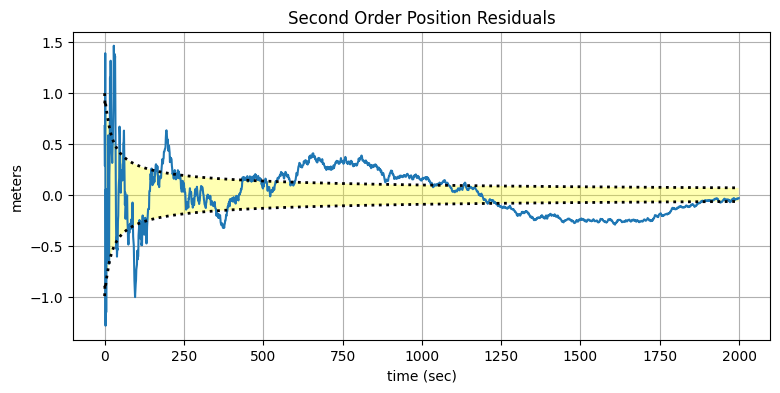
ここでも、残差のグラフが重要な事実を伝える。一つ目のグラフの軌跡は良さそうに見えるものの、残差のグラフからはフィルタが理論的性能から長い間離れていることが分かる。
こういった事実をどう受け止めるべきだろうか? アプリケーションによっては最後の設定で "十分" かもしれない。しかし、理論的性能から離れたフィルタが元に戻らない場合もある点に注意しなければならない。異なるデータセットや振る舞いの異なる物理系では、観測値と異なる方向に突き進むフィルタとなる可能性もある。
また、この問題はデータのフィッティングの観点から考えることもできる。与えられた二つの点を直線で結ぶよう言われたとする。
可能な解答は図にある直線だけであり、加えてこの解答は最適である。点が増えた場合でも最小二乗フィッティングで最良の直線を見つけることができ、そのときの解答も最小二乗の意味で最適となる。
続いて、二つの点をもっと次数の高い多項式でフィッティングするよう言われたと考えてほしい。この問題への解答は無限に存在する。例えば考えている二つの点を通る二次の放物線は無限に存在する。同様にカルマンフィルタが考えている物理系より高次だと、選択できるフィルタが無限に存在することになる。そういったフィルタは最適でない上に、出力が理論的性能から離れて戻ってこないこともよくある。
最良の性能を得るには、系と同じ次数を持つフィルタが必要となる。多くの場合、次数の選択は簡単に行える──冷蔵庫に付いている温度計に対するカルマンフィルタを設計しているなら、零次のフィルタが正しい選択肢なのは明らかに思える。しかし車を追跡するときはどの次数を使うべきだろうか? 一次のフィルタは車が直線上を動くなら優れた性能を発揮する。しかし車は進行方向や速度を変更するので、そういったことを考えれば二次のフィルタの方が優れていると言える。この問題は適応フィルタの章で考える。そこでは追跡するオブジェクトの振る舞いの次数が変わったときにも適応できるフィルタの設計方法を学ぶ。
そうは言っても、プロセスノイズ行列を十分大きくして細かい離散化を行えば、低い次数のフィルタでも高次の系を追跡できる (普通は一秒間に百サンプルも取れば系は局所的に線形になる)。結果は最適でないものの非常に優れており、私は必ず適応フィルタを試す前にこの方法を使ってみるようにしている。系に加速度がある例で試してみよう。まずシミュレーションを書く:
class ConstantAccelerationObject(object):
def __init__(self, x0=0, vel=1., acc=0.1, acc_noise=.1):
self.x = x0
self.vel = vel
self.acc = acc
self.acc_noise_scale = acc_noise
def update(self):
self.acc += randn() * self.acc_noise_scale
self.vel += self.acc
self.x += self.vel
return (self.x, self.vel, self.acc)
R, Q = 6., 0.02
def simulate_acc_system(R, Q, count):
obj = ConstantAccelerationObject(acc_noise=Q)
zs = []
xs = []
for i in range(count):
x = obj.update()
z = sense(x, R)
xs.append(x)
zs.append(z)
return np.asarray(xs), zs
np.random.seed(124)
xs, zs = simulate_acc_system(R=R, Q=Q, count=80)
plt.plot(xs[:, 0]);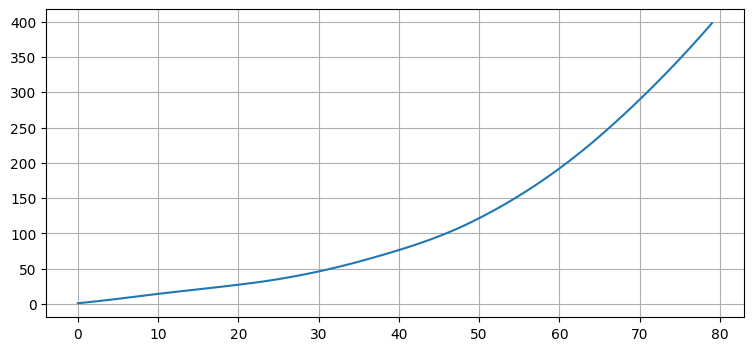
まず、このデータを二次のフィルタでフィルタリングする:
np.random.seed(124)
xs, zs = simulate_acc_system(R=R, Q=Q, count=80)
kf2 = SecondOrderKF(R, Q, dt=1)
data2 = filter_data(kf2, zs)
plot_kf_output(xs, data2.x, data2.z, aspect_equal=False)
plot_residuals(xs[:, 0], data2, 0, 'Second Order Position Residuals', 'meters')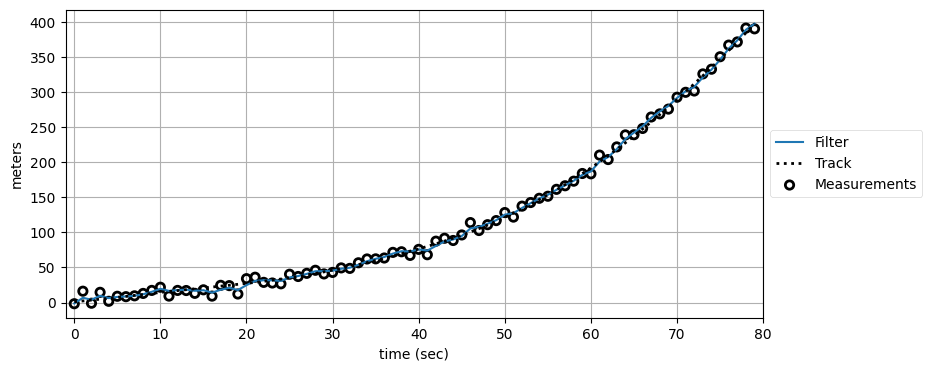
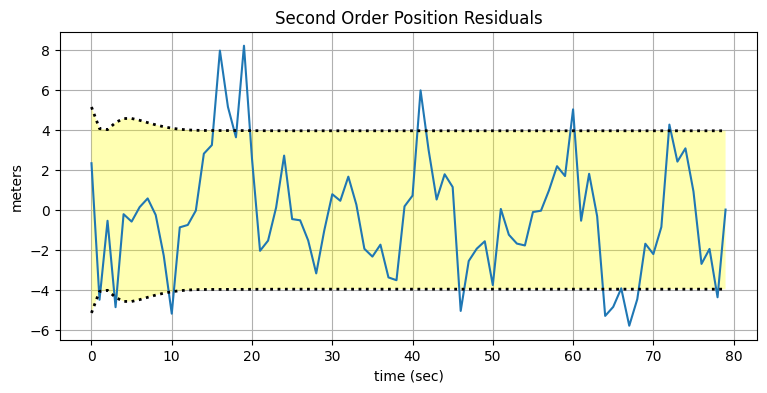
フィルタが理論的な性能を示す領域に収まっているのが分かる。
続いて低い次数のフィルタを使ってみよう。前に示したように、低い次数のフィルタは加速度をモデル化しないので信号から遅れる。しかしプロセスノイズ行列を大きくすれば加速度によるデータのずれを (ある程度) モデルに組み込むことができる。こうするとフィルタは加速度をプロセスモデルに含まれるノイズとして扱う。結果は最適ではないものの、フィルタを上手く設計すれば実際の値から離れることはない。プロセスノイズ行列の大きさを選ぶのは完全な科学ではない。サンプルデータを使って実験する必要があるだろう。今のデータでは \(\mathbf{Q}\) を十倍にすると優れた結果が得られた:
kf3 = FirstOrderKF(R, Q * 10, dt=1)
data3= filter_data(kf3, zs)
plot_kf_output(xs, data3.x, data3.z, aspect_equal=False)
plot_residuals(xs[:, 0], data3, 0, 'First Order Position Residuals', 'meters')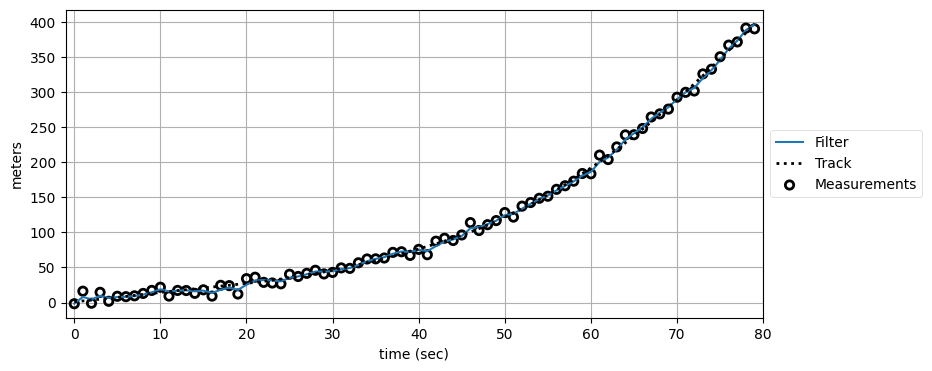
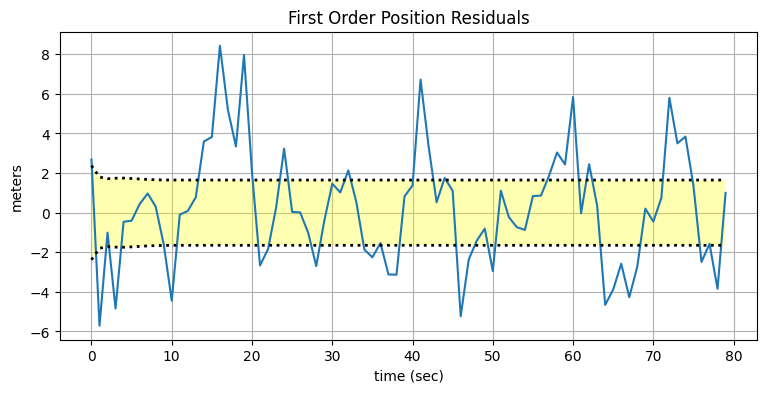
プロセスノイズ行列を必要よりはるかに大きくしたとき何が起こるかを考えてみてほしい。大きなプロセスノイズが設定されたフィルタは観測値を重視するから、観測値のノイズをぴったり追跡するはずである。確認しよう:
kf4 = FirstOrderKF(R, Q * 10000, dt=1)
data4 = filter_data(kf4, zs)
plot_kf_output(xs, data4.x, data4.z, aspect_equal=False)
plot_residuals(xs[:, 0], data4, 0,
'First Order Position Residuals',
'meters')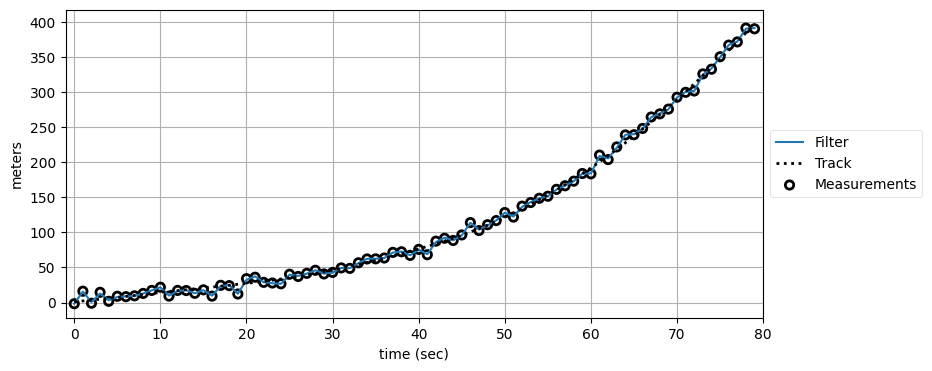
8.4 練習問題: 状態変数の設計
前述したように、\(\mathbf{x}\) に含まれる変数は好きな順番で並べることができる。例えば一次元の定常加速度モデルの状態を \(\mathbf x = \Big[\ddot x \ \ x \ \ \dot x\Big]^\mathsf T\) と定義しても構わない。そうする理由は無いように思えるが、可能である。
もう少し理にかなったことをしてみよう。二次元空間を動くロボットに対する二次のフィルタを設計で \(\mathbf x = \Big[x \ \ y \ \ \dot x \ \ \dot y \Big]^\mathsf T\) を使うとする。本章ではここまで \(\mathbf x = \Big[x \ \ \dot x \ \ y \ \ \dot y \Big]^\mathsf T\) を使っていた。
なぜ異なる順序を選ぶのだろうか? これから見るように、\(\mathbf{x}\) に含まれる変数の順序を変えるとフィルタで使われるほぼ全ての行列の行や列が組み変わる。調べたいデータ (例えば \(\mathbf{P}\) に含まれる相関) によっては、\(\mathbf{x}\) の順序を変えることでデータの調査が簡単にも難しくもなる。
順序を変える方法を考えよう。何を変えるべきだろうか? 明らかに、カルマンフィルタの行列をこの新しい設計を反映するように変更すればよい。
次のボイラープレートコードを使って順序を変えたカルマンフィルタを実装せよ:
N = 30 # 反復回数
dt = 1.0 # タイムステップ
R_std = 0.35
Q_std = 0.04
sensor = PosSensor((0, 0), (2, .5), noise_std=R_std)
zs = np.array([sensor.read() for _ in range(N)])
tracker = KalmanFilter(dim_x=4, dim_z=2)
# ここで状態変数を変数を代入する
xs, ys = [], []
for z in zs:
tracker.predict()
tracker.update(z)
xs.append(tracker.x[0])
ys.append(tracker.x[1])
plt.plot(xs, ys);
解答
\(\mathbf{F}\) から始めよう。少し練習すれば、この行列はすぐに書けるようになるはずだ。それはまだ難しいと感じたら、\(\mathbf{F}\) が表す方程式の集合を状態変数と同じ順序で変数を並べながら書くと分かりやすくなる:
係数を取り出せば、次を得る:
プロセスノイズ行列も調整する必要がある。まず状態変数の順序に合わせるにはどうすればいいかを考えよう。行列の外側に状態変数を縦および横に並べると添え字がどう組み合わせが分かりやすくなる。ただこれは Jupyter Notebook では難しいので、結果だけを示す:
\(x\) と \(y\) に相関はないから、対応する項も \(0\) になる:
こうするとパターンが分かりやすいので、\(\mathbf{Q}\) の設計も素早く行えるだろう。
Q_discrete_white_noise 関数は今考えているのとは異なる順序の行列を返すので、項を入れ替える必要がある。この処理のコードは以下で示す。
続いて観測関数 \(\mathbf{H}\) を設計しよう。\(\mathbf{H}\) は状態 \(\Big[x \ \ y \ \ \dot x \ \ \dot y \Big]^\mathsf T\) を観測値 \(\mathbf z = \Big[z_x \ \ z_y\Big]^\mathsf T\) に変換する:
この行列の要素は簡単に埋められるはずだ:
観測値 \(\mathbf z = \Big[z_x \ \ z_y\Big]^\mathsf T\) は変化していないので、\(\mathbf{R}\) は変化しない。
最後に \(\mathbf{P}\) がある。\(\mathbf{P}\) の要素は \(\mathbf{Q}\) と同じ順序で並ぶので、特別な設計は必要にならない。
以上で設計が完了した。後はコードにするだけだ:
N = 30 # 反復回数
dt = 1.0 # タイムステップ
R_std = 0.35
Q_std = 0.04
M_TO_FT = 1 / 0.3048
sensor = PosSensor((0, 0), (2, .5), noise_std=R_std)
zs = np.array([sensor.read() for _ in range(N)])
tracker = KalmanFilter(dim_x=4, dim_z=2)
tracker.F = np.array([[1, 0, dt, 0],
[0, 1, 0, dt],
[0, 0, 1, 0],
[0, 0, 0, 1]])
tracker.H = np.array([[M_TO_FT, 0, 0, 0],
[0, M_TO_FT, 0, 0]])
tracker.R = np.eye(2) * R_std**2
q = Q_discrete_white_noise(dim=2, dt=dt, var=Q_std**2)
tracker.Q[0,0] = q[0,0]
tracker.Q[1,1] = q[0,0]
tracker.Q[2,2] = q[1,1]
tracker.Q[3,3] = q[1,1]
tracker.Q[0,2] = q[0,1]
tracker.Q[2,0] = q[0,1]
tracker.Q[1,3] = q[0,1]
tracker.Q[3,1] = q[0,1]
tracker.x = np.array([[0, 0, 0, 0]]).T
tracker.P = np.eye(4) * 500.
xs, ys = [], []
for z in zs:
tracker.predict()
tracker.update(z)
xs.append(tracker.x[0])
ys.append(tracker.x[1])
plt.plot(xs, ys);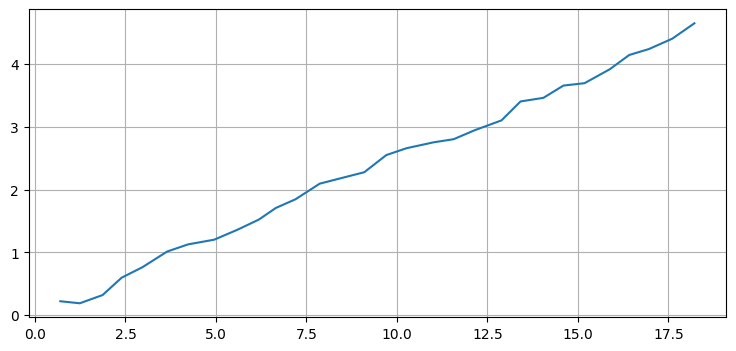
8.5 悪い観測値の検出と破棄
カルマンフィルタは悪い観測値を検出・破棄する手立てを持たない。航空機を追跡していて、航空機の現在位置から \(100~\text{km}\) 離れた場所を指す観測値が得られたとしよう。この観測値を使って更新を行うと、新しい推定値はその観測値に大きく引っ張られてしまう。
具体的な例としてシミュレーションを実行しよう。100 エポックの後に現在位置の 2 倍の位置で更新を行ってみる。以下の実装ではコードを短くするために、指定した次元と次数を持つ線形キネマティックフィルタを作成する関数 filterpy.common.kinematic_kf を使っている。本書でこの関数が使われるのはここだけであり、他の場所ではフィルタの設計を練習するために使っていない:
from filterpy.common import kinematic_kf
kf = kinematic_kf(dim=2, order=1, dt=1.0, order_by_dim=False)
kf.Q = np.diag([0, 0, .003, .003])
kf.x = np.array([[1., 1., 0., 0.]]).T
kf.R = np.diag([0.03, 0.21]) # 異なる誤差を使う
for i in range(101):
kf.predict()
kf.update(np.array([[i*.05, i*.05]])) # 時速約 200 キロ
p0 = kf.x[0:2]
kf.predict()
prior = kf.x
z = kf.x[0:2]*2
kf.update(z)
p1 = kf.x[0:2]
# 事前分布から観測値の誤差を計算する
y = np.abs(z - kf.H @ prior)
dist = np.linalg.norm(y)
np.set_printoptions(precision=2, suppress=True)
print(f'悪い観測値 : {z.T} km')
print(f'悪い観測値の前 : {p0.T} km')
print(f'悪い観測値の後 : {p1.T} km')
print(f'推定値の移動 : {np.linalg.norm(p1 - prior[:2]):.1f} km')
print(f'事前分布からの距離 : {dist:.1f} km')悪い観測値 : [[10.1 10.1]] km
悪い観測値の前 : [[5. 5.]] km
悪い観測値の後 : [[7.84 7.01]] km
推定値の移動 : 3.4 km
事前分布からの距離 : 7.1 km悪い観測値によって推定値が \(3.4~\text{km}\) だけ飛び、予測値 (事前分布) と観測値の差は \(7~\text{km}\) を超えているのが分かる。
どうすればこれを避けられるだろうか? 事前分布と観測値の差 (残差) が巨大になっていないかを確認するという方法がまず考えられる。このとき比較対象に事前分布を使って現在の推定値を使わないのは、更新を行うと推定値が悪い観測値にとても近くなってしまう可能性があるためだ (今の例ではそれほど近くなっていない)。
上のコードで残差を計算するときに \(\mathbf z - \mathbf{Hx}\) を使っていることに注目してほしい。同じ計算は prior[0:2] - z でもできるが、数学的に正しい式を使っている。なお、この計算を行ったのは説明のためであり、KalmanFilter クラスは y に残差を自動的に格納する。この値を使うとこう書ける:
print(f'残差 = {np.linalg.norm(kf.y):.1f} km (時速 {dist*3600:.0f} kph)')残差 = 7.1 km (時速 25710 kph)この例では予測された位置から \(7~\text{km}\) 離れた場所に観測値がある。これは「遠い」と言えるのではないだろうか? 観測値単位がキロメートルで、更新の頻度が一秒おきなら遠いと言える: この観測値が正しいとき追跡している航空機は時速 \(25000~\text{km}\) で飛ぶことになるが、そんな速さで飛べる航空機は存在しない。ただ観測値の単位がセンチメートルで更新の頻度が一分毎なら、\(7.1\) はあきれるほど小さな値となる。
航空機の限界性能を考慮したテストを入れてもいいかもしれない:
vel = y / dt
if vel >= MIN_AC_VELOCITY and vel <= MAX_AC_VELOCITY:
kf.update()
これが適切でロバストな手法だと思うだろうか? 読み進める前に反論をできるだけ多く考えてみてほしい。
私はこの手法にあまり満足できない。例えばフィルタを適当に推測した位置で初期化したとき、この手法だと良い観測値を捨てることになってフィルタリングがいつまでたっても始まらないかもしれない。また、この手法はセンサーとプロセスに関する誤差の知識を全く無視している。カルマンフィルタは現在の推定値の正確さを \(\mathbf{P}\) に保持するので、例えば \(\mathbf{P}\) が \(\sigma = 10\,\text{m}\) を示すときに残差が \(1~\text{km}\) なら、その観測値は事前分布から \(100\sigma\) も離れていると判断できる。
\(\mathbf{P}\) をプロットしてみよう。\(1\sigma\), \(2\sigma\), \(3\sigma\) を示す:
x, P = kf.x[0:2], kf.P[0:2, 0:2]
plot_covariance_ellipse(x, P, std=[1,2,3])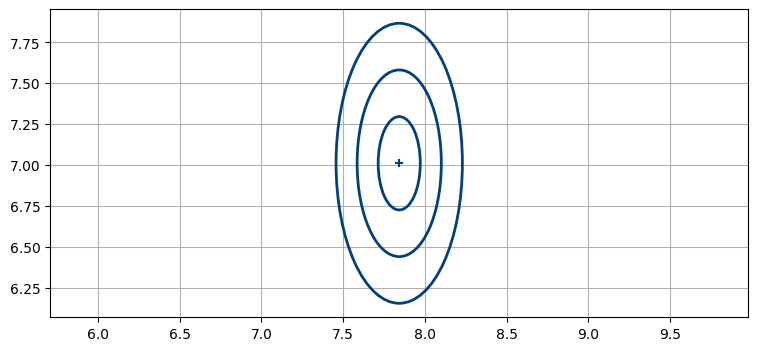
前節では \(\mathbf{P}\) の表す図形が円だったが、ここでは楕円になっている。今使っているフィルタでは \(\mathbf R = \bigl[ \begin{smallmatrix}0.03 & 0 \\ 0 & 0.15\end{smallmatrix}\bigl ]\) なので、\(y\) の観測値が \(x\) の観測値と比べて五倍の誤差を持つとしている。この仮定はいくらか人工的だが、以降の章で考える問題では、ほとんど全ての共分散楕円が自然な理由で楕円になる。
共分散楕円が意味することを考える。統計学によると、全ての観測値の 99% は \(3\sigma\) に収まる。これは観測値を同じグラフにプロットすると、\(3\sigma\) の楕円の中に 99% が収まることを意味する。問題の観測値を同じグラフにプロットしてみよう:
plot_covariance_ellipse(x, P, std=[1,2,3])
plt.scatter(z[0], z[1], marker='x');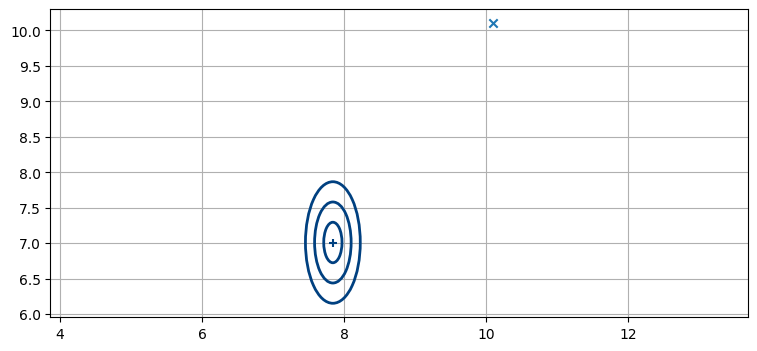
明らかに、この観測値は事前分布を示す共分散楕円から遠く離れている。これは悪い観測値とみなして使わない方がよさそうだ。どうすればこの判定を一般的に行えるだろうか?
一つ目のアイデアとして、\(x\) と \(y\) の標準偏差を取り出して簡単な if 文で判定するというものがある。この実装では KalmanFilter クラスの新しい機能を使う: 事前分布と観測値の残差を計算する residual_of メソッドである。今は update 関数で kf.y が計算されているために residual_of を使う必要はないものの、実際のループで観測値を破棄するかどうかを判定するときは update 関数を呼ぶ前に残差を計算するので、その段階だと kf.y には前回の残差が含まれている。
それから新しい用語を二つ導入する。ゲート (gate) とは観測値が良いか悪いかを判定する式あるいはアルゴリズムを言う。ゲートを使って良い観測値だけを通過させる処理をゲーティング (gating) と呼ぶ。
実際の観測値は純粋なガウス分布に従わないので、\(3\sigma\) を使ったゲートだと良い観測値も破棄してしまう可能性が高い。ここでは \(4\sigma\) を使っておく。詳しい理由は後で説明する:
GATE_LIMIT = 4.
std_x = np.sqrt(P[0,0])
std_y = np.sqrt(P[1,1])
y = kf.residual_of(z)[:,0]
if y[0] > GATE_LIMIT * std_x or y[1] > GATE_LIMIT * std_y:
print(f'観測値を破棄します。残差は {y[0]/std_x:.0f}σ, {y[1]/std_y:.0f}σ です。')
print('y =', y)
print(f'std = {std_x:.2f} {std_y:.2f}')観測値を破棄します。残差は 39σ, 18σ です。
y = [5.05 5.05]
std = 0.13 0.29問題の観測値は破棄され、\(x\) 方向と \(y\) 方向の残差がそれぞれ \(39\sigma\) と \(18\sigma\) だと分かる。さて、この手法で十分だろうか?
おそらくは十分である。ただ、if 文の条件が判定するのは楕円を囲む長方形の領域に観測値が収まっているかどうかであることに注目してほしい。そのため、例えば次の図でオレンジ色の観測値は明らかに \(3\sigma\) の楕円の外側にあるにもかかわらず、ゲートはこの観測値を (もう一つの青い観測値と同様に) 通過させる:
plot_covariance_ellipse(x, P, std=[1,2,3])
plt.scatter(8.08, 7.7, marker='x')
plt.scatter(8.2, 7.65, marker='x');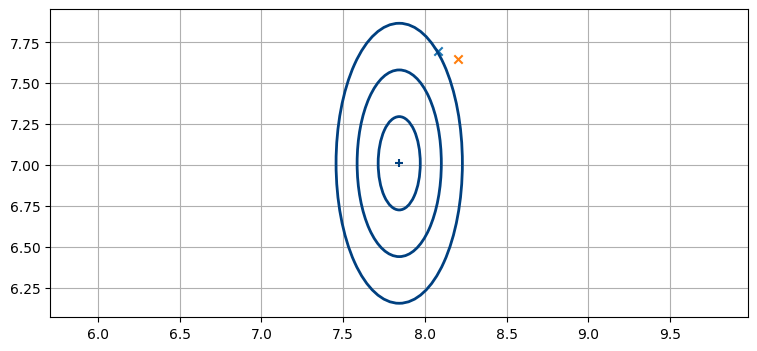
これとは別の方法でゲートを定義することもできる。今から考えるゲートはマハラノビス距離 (Mahalanobis distance) と呼ばれる分布と点の距離の指標を利用する。定義と数式を示す前に、いくつかの点に対するマハラノビス距離の計算を示す。filterpy.stats が mahalanobis 関数を実装している:
from filterpy.stats import mahalanobis
m = mahalanobis(x=z, mean=x, cov=P)
print(f'マハラノビス距離 = {m:.1f}')マハラノビス距離 = 20.6単位を知らなくても、以前に計算した \(x\) 方向および \(y\) 方向の誤差 \(39\sigma\) と \(18\sigma\) との比較はできる。マハラノビス距離は \(20.6\) であり、\(39\) と \(18\) に近い値が求められている。上でプロットした二つの点に対してもマハラノビス距離を計算してみよう:
print(f'マハラノビス距離 = {mahalanobis(x=[8.08, 7.7], mean=x, cov=P):.1f}')
print(f'マハラノビス距離 = {mahalanobis(x=[8.2, 7.65], mean=x, cov=P):.1f}')マハラノビス距離 = 3.0
マハラノビス距離 = 3.6これから見るように、マハラノビス距離は標準偏差を一単位として計算した点と分布の距離を表すスカラーである。ユークリッド距離が二つの点の距離を表す距離であったのとよく似ている。
上の実行例からもマハラノビス距離が標準偏差を一単位としていることが分かる。\(3\sigma\) の境界線に乗っている点のマハラノビス距離は \(3.0\) であり、\(3\sigma\) の楕円から少し離れた点では \(3.6\) となっている。
マハラノビス距離はどのように計算されるのだろうか? 平均 \(\mu\) で共分散行列 \(\mathbf{S}\) の分布と点 \(\mathbf{x}\) のマハラノビス距離 \(D_m\) は次のように定義される:
これがユークリッド距離の式と似ていることに注意してほしい。ユークリッド距離 \(D_e\) は次の式で計算できる:
実は共分散行列 \(\mathbf{S}\) が単位行列ならマハラノビス距離とユークリッド距離は一致する。線形代数の知識を使えば理由が分かる: 単位行列の逆行列は単位行列だから、\(\mathbf{S}^{-1}\) の乗算が \(1\) の乗算に等しくなる。また直感的にも理解できる: 各次元の標準偏差が全て \(1\) なら、半径 \(1\) の円上の点は分布の平均から \(1\sigma\) 離れ、かつユークリッド距離でも \(1\) 単位離れている。
ここからもう一つの解釈も分かる。もし共分散行列が対角行列なら、マハラノビス距離はスケールされたユークリッド距離となる。どのようにスケールされるかというと、各項が共分散行列の対応する対角要素で割られる:
二次元の場合にはこうなる:
これでマハラノビス距離の式が簡単に理解できたと思う。ベクトルを行列で割ることはできないが、逆行列の乗算が除算と事実上同じとみなせる (もちろん数学的に厳密な議論ではない)。\(\mathbf{S}^{-1}\) の左右に残差 \(\mathbf y = \mathbf x - \mu\) を乗じると共分散行列でスケールした二乗ノルム \(\mathbf y^\mathsf T \mathbf S^{-1}\mathbf y\) が得られる。この式は二乗されているから、最後に平方根を取れば共分散行列でスケールしたユークリッド距離を表すスカラーが得られる。
ゲーティングとデータ対応付け
専門的な文献では、これら二つのゲートをその形からそれぞれ長方形ゲート (rectangular gate) および楕円ゲート (ellipsoidal gate) と呼ぶことがある。ここで紹介していないゲートも多くある。例えば機動ゲート (maneuver gate) は機動する物体を追跡するためのゲートであり、物体の現在速度と機動能力を考慮する。例えば戦闘機の機動ゲートは現在位置から進行方向に向かって前方に広がる円錐のような形になるだろうし、自動者の機動ゲートは現在位置から前方に広がる二次元のパイの形になるだろう。また船は旋回や加速の性能が最低限だから、機動ゲートは非常に小さくなるに違いない。
どのゲートを使うべきだろうか? 万能な解答はない。使うべきゲートは問題の次元と利用できる計算資源によって大きく変化する。長方形ゲートはとても簡単に計算でき、機動ゲートもそれほど時間はかからない。しかし楕円ゲートは次元が大きいと高価になる場合がある。ただ一方で、次元を増やすと楕円ゲートと長方形ゲートの相対的な体積の差は非常に大きくなる。
これは、あなたが想像するよりも大きな問題になる。全ての観測値にはノイズが含まれる。悪い観測値がゲートの内側に入ると、それはフィルタに入力されてしまう。長方形の面積が楕円の面積よりも大きければそれだけ、楕円ゲートが破棄する悪い観測値を長方形ゲートが通過させる可能性が高まる。ここで計算はしないが、五次元では単位立方体の体積がその内部に収まる球の六倍に、十次元では四百倍にもなる。
計算時間が問題になっていて破棄する観測値が多い場合は、二つのゲートを利用するアプローチを使うこともできる。一つ目のゲートとして明らかに悪いと分かる観測値を破棄するための大きい長方形ゲートを利用し、一つ目のゲートを通過した数少ない観測値に対してのみ二つ目の楕円ゲートで高価なマハラノビス距離の計算を行うというものだ。モダンなデスクトップコンピューターでカルマンフィルタを実行するときはマハラノビス距離の計算に必要な行列の乗算は問題にならないものの、限られた浮動小数点数性能しか持たない組み込みチップで実行するときは問題になる可能性がある。
データ対応付け (data association) は広大なトピックであり、深く論じるには本が一冊必要になる。データ対応付けの典型的な例にレーダーを使った航空機の追跡がある。レーダーの観測値から航空機の軌跡を構築し、そのときノイズの多い観測値は破棄しなければならないという、非常に難しい問題である。例えば最初のスイープ (レーダーが一周すること) で五つの観測値が手に入ったら、可能性のある軌道が 5 個作成される。そして次のスイープで六つの観測値が手に入ったとしたら、一つ目の観測値のそれぞれが二つ目の観測値のどれとも対応付く可能性があるので、可能性のある軌道が 30 個になる。しかし二回目のスイープで観測されたのが全て新しい航空機である可能性もあるので、可能性がさらに 6 個増える。その後わずか数エポックで、可能性のある軌跡の個数は数百万から数十億に達する。
データ対応付けでは、この数十億個の軌跡の可能性それぞれに対してスコアが計算される。数式は次節で示すので、ここでは定性的に説明する。例えば 3 エポックの間で Z の形を描く軌跡を想像してほしい。そんな形に飛ぶ航空機は存在しないから、その軌跡には非常に低いスコアが付けられる。また形は直線であるものの、速度が \(10000~\text{km/h}\) の軌跡はどうだろうか? これも可能性はほとんどないから、スコアは低い。一方で軌跡が \(200~\text{km/h}\) で緩く曲がっていたら、可能性が高そうなのでスコアは高くなる。
航空機の追跡にはゲーティングとデータ対応付けの他にも、枝刈り (pruning) と呼ばれる不必要なデータを捨てる操作も関わってくる。例えば、レーダーによる二度目のスイープがちょうど起こったとしよう。このとき考えられる点の組み合わせの全てを可能性のある軌跡として考えに入れるべきだろうか? おそらく入れるべきではない。一度目のスイープにおける点 1 と二度目のスイープにおける点 2 を結んだ軌跡の速度が \(200~\text{km/h}\) なら、そこからの軌跡は考える必要がある。一方で速度が \(5000~\text{km/h}\) になる軌跡は不可能と言っていいほどに可能性が低いので捨てても構わないだろう。しばらくして軌跡が成長すると楕円ゲートや軌道ゲートが適切な大きさで定義されるので、観測値を軌道に対応付けるときの選択肢は少なくなる。
データ対応付けの方法はいくつかある。一つの観測値を一つの軌道だけに関連付けることもできるし、観測値が属する軌道に関する正確な知識の欠如を反映して一つの観測値を複数の軌道に関連付けることもできる。例えば、レーダーからの視点で二機の軌道が交差するとしよう。二機が接近すると、二つの観測値をいずれかの軌道に関連付けるのは難しくなる。そのため短い間は一つの観測値を二つの軌道に割り当て、もっと観測値が集まってから確率の高い方の軌道に戻すということが行われる。
"数十億" という数字は組み合わせ爆発の規模を少しも捉えられていない。可能性のある軌道を全て表現するためのデータは数秒もすればコンピューターのメモリに乗りきらない量になり、それから少しすれば宇宙の全ての原子を使っても足らなくなる。実際のアルゴリズムでは軌道を積極的に枝刈りする必要がある。この枝刈りも計算能力を追加で必要とする。
本書の後半では、この問題に対する現代的な解答が提示される。それは粒子フィルタ (particle filter) と呼ばれ、組み合わせ爆発を統計的サンプリングで解決する。これは私のお気に入りのアプローチなので、この節よりも詳しく一つの章を使って解説する。私はこの領域の最新研究に精通しているわけではないから、追跡する物体が複数ある場合や問題のある観測値が複数ある場合に関しては自分で調べてほしい。粒子フィルタにも固有の難点や制限がある。
本や研究者をいくつか紹介しておく。私が読んだ物体追跡に関する本の中で最も分かりやすかったのは Samuel S. Blackman 著 Multiple-Target Tracking with Radar Application1 だが、1986 年出版なので最新の情報は書かれていない。Yaakov Bar-Shalom は物体追跡に関して非常に詳しい著作がある。Subhash Challa ら著 Fundamentals of Object Tracking2 は非常に現代的な著作であり、様々なアプローチが解説される。この本は数学的に非常に厳密な形で書かれている: 積分を含んだベイズ統計の様々な式を大量に使ってフィルタが記述され、実際のアルゴリズムへ変換する作業は読者に任せられている。本書の数学を全て理解しておけば読めるとは思うが、簡単ではないだろう。Lawrence D. Stone ら著 Bayesian Multiple Target Tracking3 はフィルタリングをベイズ推論の問題として扱っている。このアプローチは本書と同様だが、この書籍は非常に理論的であり、実際には粒子フィルタを使って解くような複雑な積分の最大値問題を軽率に読者へ提示していたりする。
私たちが考えている簡単な問題に戻ろう──たまに悪い観測値が混じる単一物体の追跡問題である。この問題はどのような実装で解くべきだろうか? 実装はとても簡単に書ける: 観測値が悪かったらその時点で破棄して、更新ステップを実行しなければいい。こうすると観測値を破棄する前後で予測ステップが連続で二度呼ばれることになるが、そこに問題はない。不確実性は大きくなるものの、普通は何回か更新を逃すだけでは大きな不都合は起こらない。
ゲートのカットオフ値はいくつに設定すべきだろうか? 私には分からない。理論的には \(3\sigma\) だが、実際に使うときは他の値にした方がいいかもしれない。データを集め、そのデータに様々なゲートを設定したフィルタを実行し、どれが最良の結果を与えるかを確認するべきである。次節ではフィルタの性能を評価するための式を示す。\(4.5\sigma\) より内側にある観測値を全て受け入れるべきだと判明するかもしれないし、\(5\sigma\) や \(6\sigma\) のゲートを使うべきとしている NASA の動画を見たこともある。使うべき値は問題とデータによって異なる。
8.6 フィルタの性能の評価
シミュレートされた状況に対するカルマンフィルタは簡単に設計できる。プロセスモデルに加えたノイズの量を知っているのだから、プロセスノイズ行列 \(\mathbf{Q}\) に同じ値を指定するだけだ。観測値のシミュレーションで加えたノイズも分かっているから、観測ノイズ行列 \(\mathbf{R}\) も同じように自明に定義できる。
実際のフィルタの設計はもっとアドホックになる。現実のセンサーはまず仕様通りに振る舞わず、観測値やノイズがガウス分布に従うこともほとんどない。また環境的なノイズからも簡単に影響を受ける。例えば回路ノイズが引き起こす電圧変動がセンサーの出力に影響する可能性がある。プロセスモデルとプロセスノイズの設計はさらに難しい。例えば自動車のノイズは非常に難易度が高い: ハンドルを切れば非線形な振る舞いが起こり、旋回・アクセル・ブレーキでタイヤはスリップし、風に押された車は進行方向を変える。このためカルマンフィルタが仮定するモデルは系の不正確なモデルとなる。モデルが不正確であるために振る舞いは最適でなくなり、最悪の場合にはフィルタの出力が完全に発散してしまう。
未知の情報があるためにフィルタの行列に対する正確な値を解析的に求められないことがある。そのときは考えられる中で最も良い推定値から始めて、様々なシミュレーションデータや実際のデータを使ってそのフィルタをテストすることになる。性能の評価結果が行列をどのように変化させるべきかを伝える。同じことはこれまでにも行った──\(\mathbf{Q}\) を大きくあるいは小さくしたときの効果を見せた。
フィルタの性能を確認する解析的な方法を考えよう。もしカルマンフィルタが最適に動作しているなら、推定誤差 (実際の状態と推定された状態の差) は次の性質を持つはずである:
- 推定誤差の平均は \(0\) に等しい。
- 推定誤差の共分散行列はカルマンフィルタの共分散行列に等しい。
二乗正規化推定誤差 (NEES)
この最初に紹介する手法は最も強力だが、シミュレーションでしか使えない。シミュレーションを行っていて状態の真の値が分かるなら、任意のステップにおける推定誤差 \(\tilde{\mathbf x}\) を、フィルタが推定した状態 \(\hat{\mathbf{x}}\) と真の値 \(\mathbf{x}\) の差として自明に計算できる:
これを使って二乗正規化推定誤差 (normalized estimated error squared, NEES) を次のように定義する:
この式を理解するために、状態が一次元のときにどうなるかを確認しよう。このとき \(\mathbf{x},\ \mathbf{P}\) はスカラー \(x,\ P\) であり、次を得る:
なぜこうなるのか分からなかったら、スカラー \(a\) に対して \(a^\mathsf T = a\) と \(\displaystyle a^{-1} =\frac{1}{a}\) が成り立つことに注意してほしい。
つまり誤差を固定して共分散行列を小さくすると NEES は大きくなる。共分散行列はフィルタによる自身の誤差の推定値だから、推定誤差に比べて共分散行列が小さいときフィルタの性能は低い。
この式で計算される \(\varepsilon\) は \(\mathbf{x},\ \mathbf{P}\) の形状に関わらず必ずスカラーとなる。実際 \(\mathbf{x}\) が \(n{\times}1\) だとすれば、この式は \((1{\times}n) \cdot (n{\times}n) \cdot (n{\times}1)\) という計算であり、結果は \(1{\times}1\) になると分かる。
\(\varepsilon\) は何を表すのだろうか? 数学的な議論は本書の範囲を超えるが、確率変数 \(\tilde{\mathbf x}^\mathsf T\mathbf P^{-1}\tilde{\mathbf x}\) は 自由度 \(n\) のカイ二乗分布 (chi-squared distributed with \(n\) degrees of freedom) と呼ばれる分布に従い、期待値が \(n\) になる。Bar-Shalom ら著 Estimation with Applications to Tracking and Navigation4にこの話題に関する素晴らしい議論がある。
ごく簡単に言えば、各ステップにおける NEES の平均が \(\mathbf{x}\) の次元より小さいならフィルタの誤差は十分小さいと言える。本章の最初で使った例で確認してみよう:
from scipy.linalg import inv
def NEES(xs, est_xs, Ps):
est_err = xs - est_xs
err = []
for x, p in zip(est_err, Ps):
err.append(x.T @ inv(p) @ x)
return errR, Q = 6., 0.02
xs, zs = simulate_acc_system(R=R, Q=Q, count=80)
kf2 = SecondOrderKF(R, Q, dt=1)
est_xs, ps, _, _ = kf2.batch_filter(zs)
nees = NEES(xs, est_xs, ps)
eps = np.mean(nees)
print(f'NEES の平均: {eps:.4f}')
if eps < kf2.dim_x:
print('passed')
else:
print('failed')NEES の平均: 0.8893
passedNEES は FilterPy に実装されている。次のように使う:
from filterpy.stats import NEES
NEES はフィルタの性能の素晴らしい指標であり、プロダクションのコードでフィルタの性能を実行中に評価する必要があるときはどんなときでも使われるべきである5。ただフィルタの設計している間は残差をプロットした方がフィルタの振る舞いが分かりやすいので、私は残差をプロットすることが多い。
しかし、シミュレーションの忠実度が低いときは別のアプローチが必要になる。
尤度関数
統計学において尤度 (likelihood) は確率 (probability) と非常によく似た概念であり、その小さな違いが今の私たちにとって重要になる。確率とは何らかの事象の起こりやすさを表す値であり、「公平なサイコロを六回振って 6 が三回出る確率は?」のように使われる。尤度は逆のことを質問する──「サイコロを六回振って 6 が三回出たとき、このサイコロが公平である尤度は?」のように使われる。
尤度関数は離散ベイズフィルタの章で初めて議論した。こういったフィルタの文脈において、尤度は与えられた現在状態における観測値のもっともらしさを表す指標である。
フィルタの性能測定において尤度は重要になる。なぜなら、ガウス分布に従うノイズと線形な振る舞いという仮定があるときにフィルタが最適に振る舞っている尤度を私たちが手にしているフィルタの出力から計算できれば、それがフィルタの性能の指標になるからだ。もし尤度が低ければ、仮定のいずれかが間違っていると分かる。適応フィルタの章では尤度の情報を使ってフィルタを改善する方法を学ぶが、ここでは観測値の悪さを判定する方法だけを学ぶ。
フィルタの残差 \(\mathbf{y}\) と系不確実性 \(\mathbf{S}\) は次のように定義される:
ここから尤度関数 \(\mathcal{L}\) は
と計算できる (\(n\) は状態の次元数)。複雑に見えるかもしれないが、よく見れば多変量ガウス分布の確率密度関数と同じなので、次のように実装できる:
from scipy.stats import multivariate_normal
hx = (H @ x).flatten()
S = H @ P @ H.T + R
likelihood = multivariate_normal.pdf(z.flatten(), mean=hx, cov=S)
ただ実際に尤度を使うときは少し違う使い方をする。尤度は数学的に扱いが難しいので、代わりに対数尤度 (log-likelihood) を計算することが多い。対数尤度とは文字通り尤度の対数を取った値であり、いくつか利点がある。例えば狭義単調増加である対数関数は引数に与えられた関数が最大となる点で最大になる。また尤度を考えるときは \(\prod_i f_i(x)\) の形をした式を最大化することが良くあるが、これは対数 \(\sum_i \log f_i(x)\) を考えると簡単に行える。こういった性質は本書では使わないものの、フィルタの解析で非常に重要となる。
尤度と対数尤度は update 関数を呼ぶたびに計算され、フィルタオブジェクトの likelihood 属性および log_likelihood 属性としてアクセスできる。これを確認してみよう。最初フィルタに期待される範囲の観測値を入力し、最後に期待される値から遠く離れた観測値を入力する:
R, Q = .05, 0.02
xs, zs = simulate_acc_system(R=R, Q=Q, count=50)
zs[-5:-1] = [100, 200, 200, 200] # 非常に悪い観測値
kf = SecondOrderKF(R, Q, dt=1, P=1)
s = Saver(kf)
kf.batch_filter(zs, saver=s)
plt.plot(s.likelihood);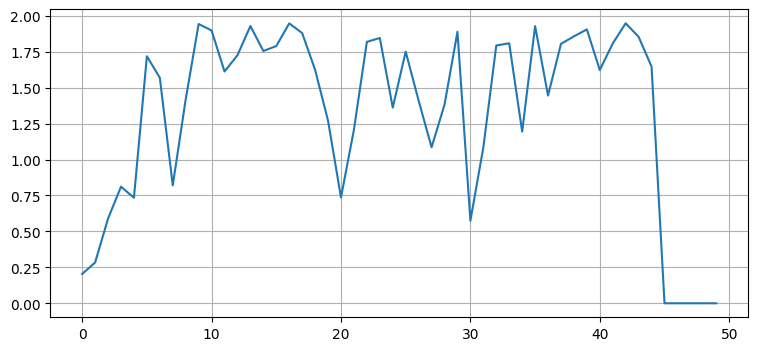
フィルタが落ち着くまでの最初の数反復で尤度は大きくなる。それから尤度は上下し、悪い観測値が入力されると一気にほぼゼロになる。これは、もし観測値が正当ならフィルタが最適であることはまずあり得ないことを示す。
対数尤度を見ると、フィルタが "悪く" なっている部分がすぐに分かる:
最後のいくつかの観測値で対数尤度が \(0\) に戻っているのはどうしてだろうか? 答えを読む前に考えてみてほしい。これは、フィルタが新しい観測値に適応して状態を観測値の近くに変化させたためである。加えて最悪の対数尤度が極端に小さいので、まだ \(0\) に近い尤度も大きく改善されたような見た目になる。
8.7 制御入力
離散ベイズフィルタの章ではフィルタの性能を改善するために制御入力という概念を導入した。物体がこれまでと同様に移動すると仮定するのではなく、制御入力に関して私たちが持つ知識を使って物体の位置を予測するのである。一次元カルマンフィルタの章でも同じアイデアを使った。カルマンフィルタの予測は次のような計算を行う:
def predict(pos, movement):
return (pos[0] + movement[0], pos[1] + movement[1])
多変量カルマンフィルタの章で状態の予測で使われる式を学んだ:
状態はベクトルなので、制御入力もベクトルとして表現しなければならない。上の式で \(\mathbf{u}\) が制御入力であり、\(\mathbf{B}\) は制御入力を状態 \(\mathbf{x}\) の変化に変換する行列である。簡単な例を考えよう。私たちが制御しているロボットの状態が \(x = \Big[ x \ \ \dot x \Big]^\textsf{T}\) で、制御入力はロボットの速度を変化させるコマンドであるとする。このとき制御入力は
と表せる。簡単のためロボットはこの入力へ瞬時に応答できると仮定すると、\(\Delta t\) 秒後の新しい位置と速度は次のようになる:
この式の集合を \(\bar{\mathbf x} = \mathbf{Fx} + \mathbf{Bu}\) の形に表す必要がある。
記号の対応を考えれば、\(\mathbf{Fx}\) は上の式の \(x\) となり、残りの部分は \(\mathbf{Bu}\) が担当することが分かる:
これは単純な例である。典型的にはステアリング角の変化や加速度の変化などが制御入力となり、状態は非線形に変化する。非線形な制御入力の扱いは後半の章で学ぶ。
カルマンフィルタの制御入力以外の部分は通常通りに設計できる。ここまでに何度も見てきているのでコメントは省略する:
dt = 1.
R = 3.
kf = KalmanFilter(dim_x=2, dim_z=1, dim_u = 1)
kf.P *= 10
kf.R *= R
kf.Q = Q_discrete_white_noise(2, dt, 0.1)
kf.F = np.array([[1., 0], [0., 0.]])
kf.B = np.array([[dt], [ 1.]])
kf.H = np.array([[1., 0]])
print(kf.P)
zs = [i + randn()*R for i in range(1, 100)]
xs = []
cmd_velocity = np.array([1.])
for z in zs:
kf.predict(u=cmd_velocity)
kf.update(z)
xs.append(kf.x[0])
plt.plot(xs, label='Kalman Filter')
plot_measurements(zs)
plt.xlabel('time')
plt.legend(loc=4)
plt.ylabel('distance');[[10. 0.]
[ 0. 10.]]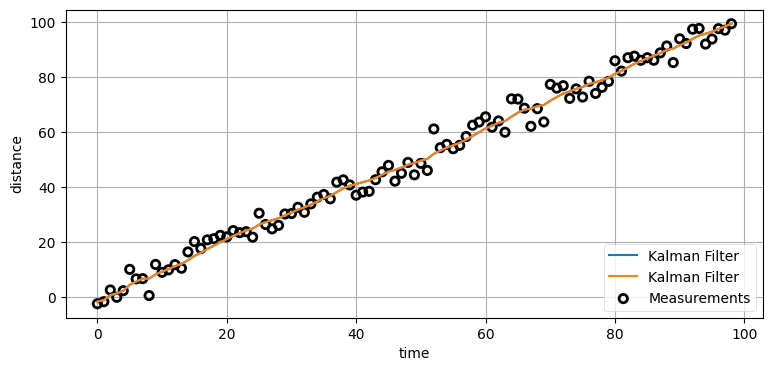
8.8 センサー統合
g-h フィルタの章の最初で、正確な体重計からの観測値と不正確な体重計からの観測値を受け取るフィルタの設計を考えた。そこでは不正確な体重計からの観測値を必ず取り入れるべきだと結論付けた──どんな情報も捨てるべきではない。系を観測する二つのセンサーが二つある同じような状況を考えよう。それぞれのセンサーからの観測値をどのようにカルマンフィルタに取り入れるべきだろうか?
線路を走る車両を考えよう。車輪に回転数を測定するセンサー (以降「車輪センサー」と呼ぶ) が付いていて、回転数を線路に沿った距離に変換できるとする。また GPS のようなセンサー (以降「位置センサー」と呼ぶ) が胴体に付いていて、そこからも位置が分かるとする。単に GPS としない理由は次節で説明する。つまり観測値が二つあり、両方から線路に沿った位置が報告されている。さらに車輪センサーの正確さは位置センサーの十倍だとしたら、どうすれば二つの観測値を組み合わせて一つのフィルタに入力できるだろうか? わざとらしい例だと思うかもしれないが、例えば航空機は GPS・INS・ドップラーレーダー・VOR・対気速度計といったセンサーからの観測値を組み合わせるのにセンサー統合を利用する。
慣性装置に対するカルマンフィルタは非常に難しいものの、同じ状態変数 (例えば位置) の観測値を与える複数のセンサーからのデータの統合は非常に簡単に行える。ここで関係する行列は観測行列 \(\mathbf{H}\) である。この行列はカルマンフィルタの状態 \(\mathbf{x}\) を観測値 \(\mathbf{z}\) に変換する方法を示す行列だったことを思い出そう。カルマンフィルタの状態 \(\mathbf{x}\) が車両の位置と速度からなるとすれば
と書ける。位置の観測値は二つあるから、観測値ベクトル \(\mathbf{z}\) を車輪センサーと位置センサーの観測値を並べたものとして定義する:
続いて状態 \(\mathbf{x}\) を観測値 \(\mathbf{z}\) に変換する観測行列 \(\mathbf{H}\) を設計しなければならない。観測値 \(\mathbf{z}\) はどちらも位置だから、変換は \(1\) を乗じるだけで済む:
理解を深めるために、車輪センサーから報告されるのは位置ではなく車輪の回転数で、車輪が一回転するごとに \(2~\text{m}\) 移動するとした場合を考えてみよう。このときは次のように書ける:
次は観測ノイズ行列 \(\mathbf{R}\) を設計する必要がある。車輪センサーからの観測値の標準偏差が \(1.5~\text{m}\) で、位置センサーからの観測値の分散が車輪センサーからの観測値の分散の倍だと仮定すれば、
となる。カルマンフィルタの設計はこれでほぼ終わった。\(\mathbf{Q}\) も設計しなければならないが、これはセンサー統合の有無と関係がない (以下のコードでは適当な値を選んでいる)。
こうして設計されたカルマンフィルタをシミュレートしてみよう。速度は \(10~\text{m/s}\)、更新は 0.1 秒ごとに設定した:
from numpy import array, asarray
import numpy.random as random
def fusion_test(wheel_sigma, ps_sigma, do_plot=True):
dt = 0.1
kf = KalmanFilter(dim_x=2, dim_z=2)
kf.F = array([[1., dt], [0., 1.]])
kf.H = array([[1., 0.], [1., 0.]])
kf.x = array([[0.], [1.]])
kf.Q *= array([[(dt**3)/3, (dt**2)/2],
[(dt**2)/2, dt ]]) * 0.02
kf.P *= 100
kf.R[0, 0] = wheel_sigma**2
kf.R[1, 1] = ps_sigma**2
s = Saver(kf)
random.seed(1123)
for i in range(1, 100):
m0 = i + randn()*wheel_sigma
m1 = i + randn()*ps_sigma
kf.predict()
kf.update(array([[m0], [m1]]))
s.save()
s.to_array()
if do_plot:
ts = np.arange(0.1, 10, .1)
plot_measurements(ts, s.z[:, 0], label='Wheel')
plt.plot(ts, s.z[:, 1], ls='--', label='Pos Sensor')
plot_filter(ts, s.x[:, 0], label='Kalman filter')
plt.legend(loc=4)
plt.ylim(0, 100)
set_labels(x='time (sec)', y='meters')
return s
fusion_test(1.5, 3.0);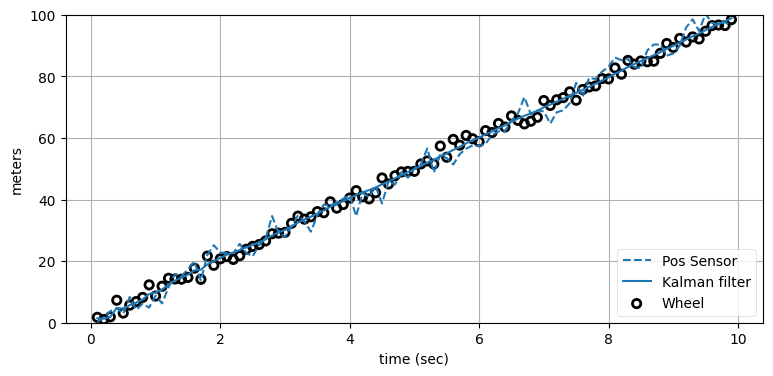
カルマンフィルタの出力は青い実線で表されている。
この例を直感的に理解するのは少し難しいかもしれないので、別の問題も考えてみよう。二次元空間を移動する物体を追跡していて、異なる位置にある二つの基地に配備されたレーダーから観測を行っているとする。それぞれのレーダーが距離と方位を報告するとき、二つの観測値はどう結果に影響するだろうか?
距離と方位から位置を計算するには三角関数が必要なので、これは非線形な問題である。カルマンフィルタで非線形な問題を解く方法を私たちは知らないから、ここではコードの出力を示す図だけに集中してコード自体は気にかけないことにする。以降の章でもう一度この問題を考え、ここにあるコードの書き方を学ぶ。
目標の物体は最初 \((100,\ 100)\) にあり、一つ目のレーダーは \((50,\ 50)\)、二つ目のレーダーは \((150,\ 50)\) にあるとする。このとき最初の観測値で一つ目のレーダーでは \(45^\circ\) の方位、二つ目のレーダーでは \(135^\circ\) の方位が観測される。
次のコードはカルマンフィルタを作成し、共分散行列の初期値をプロットする。ここでは以降の章で説明する無香料カルマンフィルタを使っている:
from kf_book.kf_design_internal import sensor_fusion_kf
kf = sensor_fusion_kf()
x0, p0 = kf.x.copy(), kf.P.copy()
plot_covariance_ellipse(x0, p0, fc='y', ec=None, alpha=0.6)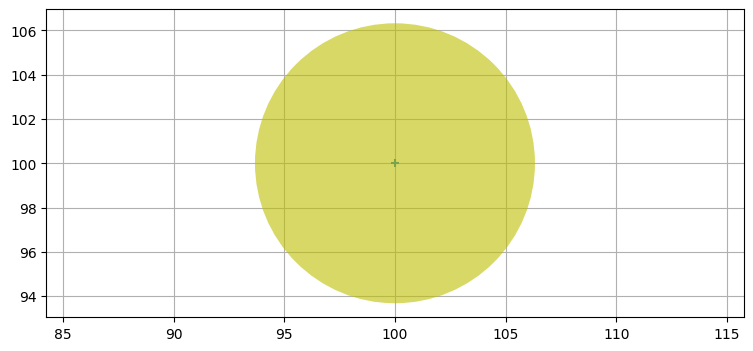
\(x\) 方向の不確実性と \(y\) 方向の不確実性は等しいから、共分散楕円は円になる。
まずカルマンフィルタを一つ目のレーダーからの観測値で更新する。方位および距離の誤差を表す標準偏差はそれぞれ \(0.5^\circ\) と \(3\, \text{m}\) に設定してある:
from math import radians
from kf_book.kf_design_internal import sensor_fusion_kf, set_radar_pos
# レーダーが報告する方位と距離に含まれる誤差を設定する。
kf.R[0, 0] = radians(.5)**2
kf.R[1, 1] = 3.**2
# 一つ目のレーダーからの観測値を使って位置と共分散行列を更新する。
set_radar_pos((50, 50))
dist = (50**2 + 50**2) ** 0.5
kf.predict()
kf.update([radians(45), dist])
# 結果をプロットする。
x1, p1 = kf.x.copy(), kf.P.copy()
plot_covariance_ellipse(x0, p0, fc='y', ec=None, alpha=0.6)
plot_covariance_ellipse(x1, p1, fc='g', ec='k', alpha=0.6)
plt.scatter([100], [100], c='y', label='Initial')
plt.scatter([100], [100], c='g', label='1st station')
plt.legend(scatterpoints=1, markerscale=3)
plt.plot([92, 100], [92, 100], c='g', lw=2, ls='--');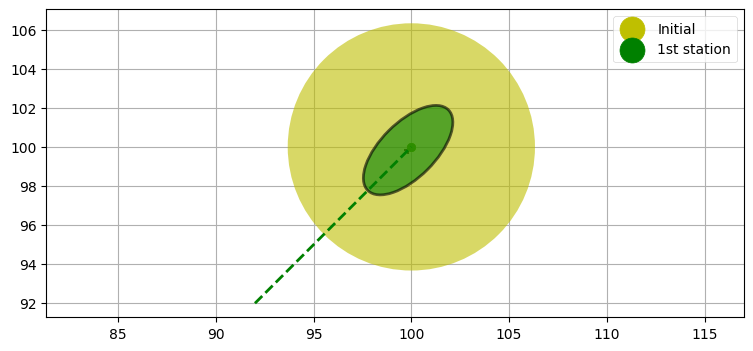
観測値に含まれる誤差の影響を図から確認できる。レーダーは目標の左下にある。方位の観測値は \(\sigma=0.5^\circ\) と非常に正確なのに対して、距離の誤差は \(\sigma=3~\text{m}\) で非常に大きい。正確な方位と不正確な距離の影響は共分散楕円の形に分かりやすく表れている。
続いて二つ目のレーダーからの観測値を取り入れよう。二つ目のレーダーは目標の右下 \((150,\ 50)\) にある。読み進める前に、この新しい観測値を取り入れた後に共分散楕円がどうなるかを考えてみてほしい。
# 二つ目のレーダーからの観測値を使って位置と共分散行列を更新する。
set_radar_pos((150, 50))
kf.predict()
kf.update([radians(135), dist])
plot_covariance_ellipse(x0, p0, fc='y', ec='k', alpha=0.6)
plot_covariance_ellipse(x1, p1, fc='g', ec='k', alpha=0.6)
plot_covariance_ellipse(kf.x, kf.P, fc='b', ec='k', alpha=0.6)
plt.scatter([100], [100], c='y', label='Initial')
plt.scatter([100], [100], c='g', label='1st station')
plt.scatter([100], [100], c='b', label='2nd station')
plt.legend(scatterpoints=1, markerscale=3)
plt.plot([92, 100], [92, 100], c='g', lw=2, ls='--')
plt.plot([108, 100], [92, 100], c='b', lw=2, ls='--');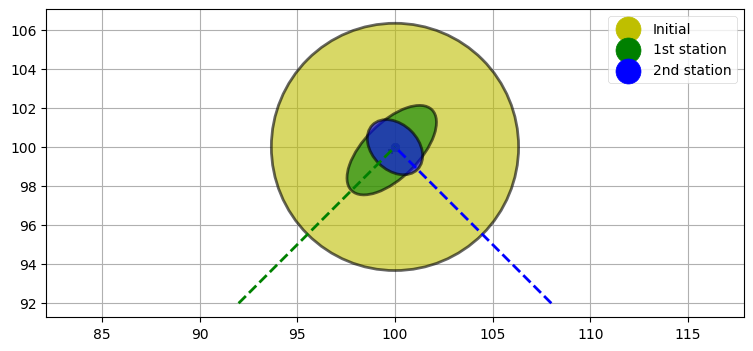
新しい観測値が共分散行列を変化させたことが分かる。二つ目のレーダーと目標を結んだ直線は一つ目のレーダーと目標を結んだ直線と直角だから、距離と方位の誤差の関係が反転して共分散楕円の方向が二つ目のレーダーを向くように変化する。方向が変化しただけではなく、共分散行列の大きさがずっと小さくもなっていることも重要である。
フィルタは必ず利用可能な情報を全て取り入れる。この例では取り入れる情報に問題の幾何学的構成が含まれ、これによって何が起きているかが格段に分かりやすくなる。しかし同じことは一つのセンサーが位置を報告し、もう一つのセンサーが速度を報告するとき、あるいは二つのセンサーが位置を報告するときにも起こる。
次に進む前に最後に一つ: センサー統合は広大なトピックであり、ここでは誤解を生じさせかねないほど単純なことしか説明していない。例えば GPS は人工衛星から報告される疑似距離 (pseudorange) の集合に対して反復最小二乗法を使って位置を決定しており、カルマンフィルタは使われていない。この話題は補遺の反復最小二乗法によるセンサー統合で触れている。
GPS 受信機のデータ統合では反復最小二乗法がよく使われるが、手法は他にもある。あなたがホビイストなら私の説明を読めばプログラムを書いて遊べるかもしれない。しかし商用グレードのフィルタでは統合プロセスの非常に注意深い設計が必要となる。これは本が数冊書けるトピックであり、考えている領域をカバーする文献を見つけてさらに学ぶ必要があるだろう。
8.9 練習問題: GPS の出力をフィルタリングできるか?
前節では「GPS のような」センサーに対してカルマンフィルタを適用した。では商用 GPS デバイスに内蔵されたカルマンフィルタ (正確には反復最小二乗法) の出力に自分で書いたカルマンフィルタを適用できるだろうか? 言い換えると、新しく追加した二つ目のフィルタの出力は元の GPS からの出力と比べて良くなるだろうか、悪くなるだろうか、そのままだろうか?
解答
商用 GPS にはカルマンフィルタが組み込まれており、そのフィルタによる推定値が出力される。GPS からの安定した出力列を持っていて、その出力は位置と位置誤差からなるとする。その二つのデータを自分で書いたフィルタに通すことができるではないか!
さて、二つのデータ列の特徴は何だろうか? より重要なこととして、カルマンフィルタが入力に要求する基礎的な要件は何だろうか?
カルマンフィルタへの入力はガウス分布に従い、時間に関して独立でなければならない。これはマルコフ性が要件として課されるためである: 現在状態は一つ前の時刻における状態と現在時刻における入力だけに依存することが仮定される。これがあるからこそ、再帰的なフィルタが可能になる。しかし GPS の出力は時間に依存する: GPS に搭載されたカルマンフィルタが推定値を計算するときに使う一つ前の時刻における状態は、一つ前の時刻における観測値と二つ前の時刻における状態 (つまり再帰的に全ての観測値) に依存している。したがって信号は白色ノイズを持たず、時間に関して独立ではない。よって答えは No である。商用 GPS の出力をカルマンフィルタに通しても良い推定値が得られることはない。
カルマンフィルタが最小二乗の意味で最適である事実からも同じ結論を得られる。最適な解をどんなフィルタに通したとしても、そのフィルタから "より最適な" 解を得ることはできない。それは論理的に不可能である。二つ目のフィルタで信号が変化しないときに限って最適であり、少しでも変化すれば最適でない。
これはホビイストが GPS や IMU といった既製品のセンサーを使おうとしたときに直面する難しい問題である。
何が起こるかを見てみよう。商用 GPS は位置と推定された誤差の範囲を報告する。推定された誤差とはカルマンフィルタの行列 \(\mathbf{P}\) のことだ。そこで、これからノイズの含まれたデータにフィルタリングを行い、その結果をもう一度フィルタに入力したときの結果を確認してみる。言い換えれば、一つ目のフィルタが推定した状態 \(\mathbf{x}\) が二つ目のフィルタに入力される観測値 \(\mathbf{z}\) となり、同様に状態共分散行列 \(\mathbf{P}\) は観測値共分散行列 \(\mathbf{R}\) となる。影響を際立たせるために、同じことを二度行ったとき (観測値を全部で三つのフィルタに通したとき) の結果もプロットしてみよう。フィルタを三つも使う意味はない (誰もしないだろう) が、要点は分かりやすくなる。まずコードとプロットを示す:
np.random.seed(124)
R = 5.
xs, zs = simulate_acc_system(R=R, Q=Q, count=30)
kf0 = SecondOrderKF(R, Q, dt=1)
kf1 = SecondOrderKF(R, Q, dt=1)
kf2 = SecondOrderKF(R, Q, dt=1)
# 観測値にフィルタリングを行う。
fxs0, ps0, _, _ = kf0.batch_filter(zs)
# 状態を入力としたフィルタリングを二度行う。
fxs1, ps1, _, _ = kf1.batch_filter(fxs0[:, 0])
fxs2, _, _, _ = kf2.batch_filter(fxs1[:, 0])
plot_kf_output(xs, fxs0, zs, 'KF', False)
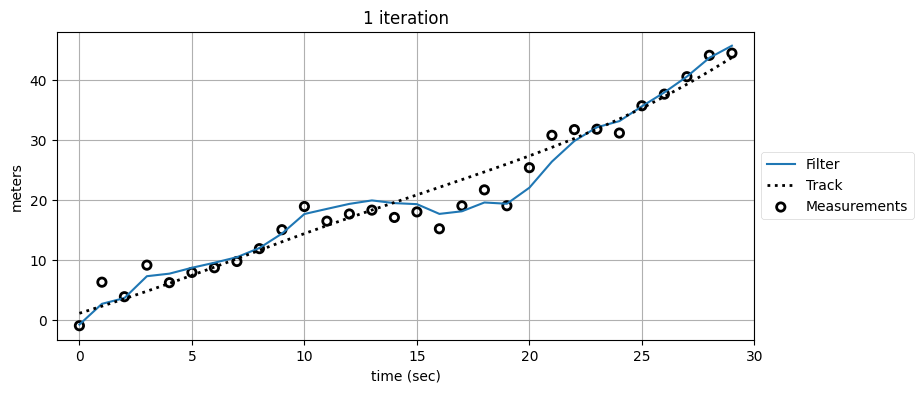
plot_kf_output(xs, fxs1, zs, '1 iteration', False)
plot_kf_output(xs, fxs2, zs, '2 iterations', False)
R,Q(5.0, 0.02)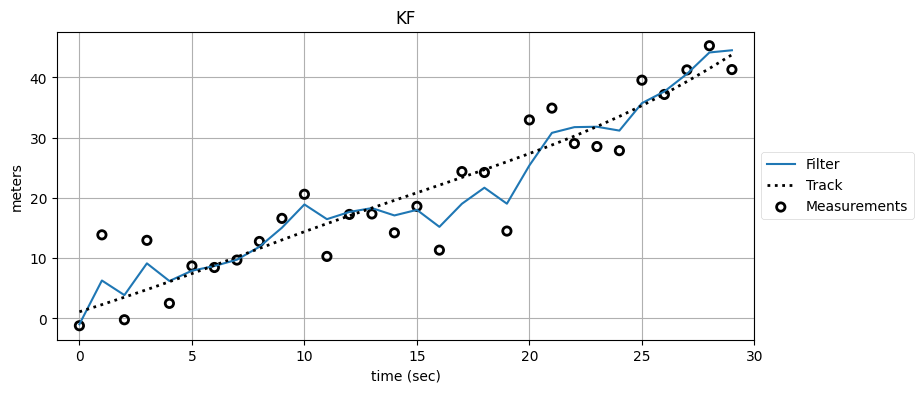
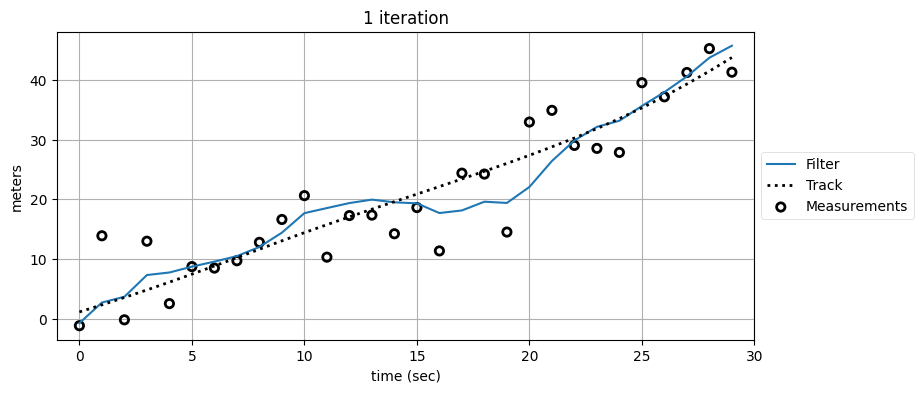
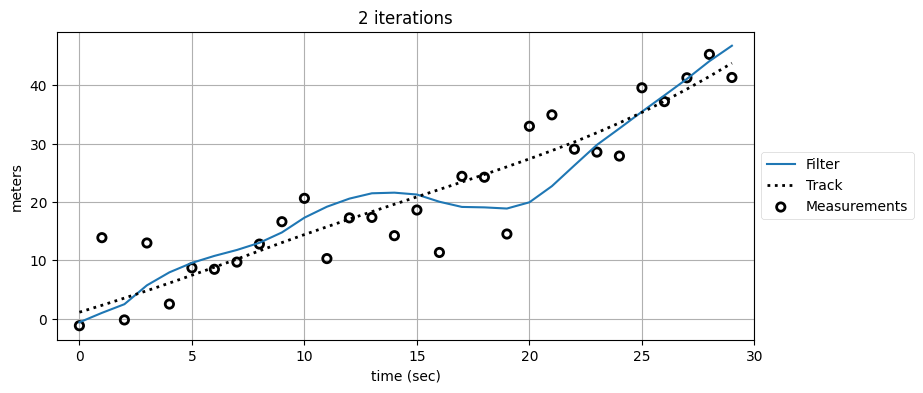
複数のフィルタを通すと出力が滑らかになって、正しい軌道から離れるのが分かる。何が起きているのだろうか? カルマンフィルタは信号が時間に関して相関を持たないことを要求するのだった。しかしカルマンフィルタは状態の推定値をそれまでの観測値を全て取り入れて計算するので、その出力は時間に関して相関を持つ。観測値を三つのフィルタに通した最後のグラフを見ると、正しい軌道よりも上にある最初の方の観測値をフィルタが "記憶" しており、13 秒あたりまで推定値が正しい軌道より上にあるのが分かる (数学的な議論を避けるために曖昧な言葉を使っている)。それから観測値はたまたま軌道の下になっている。このこともフィルタは "記憶" し、複数回フィルタを適用した出力は下に引っ張られる。
これを違う方法で見てみよう。二回目と三回目のフィルタは観測値として \(\mathbf{z}\) ではなく前回のフィルタの推定値を使っているから、今度はフィルタの出力とそのフィルタに入力された値をプロットしてみる:
plot_kf_output(xs, fxs0, zs, title='KF', aspect_equal=False)
plot_kf_output(xs, fxs1, fxs0[:, 0], '1 iteration', False)
plot_kf_output(xs, fxs2, fxs1[:, 0], '2 iterations', False)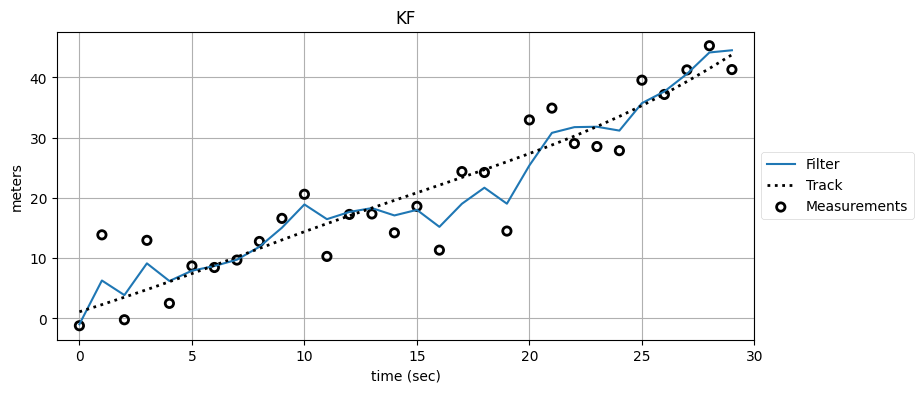
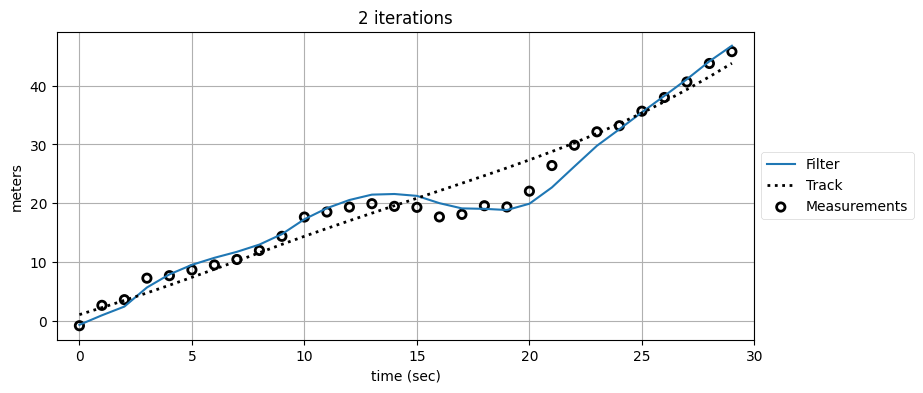
このアプローチの問題がこれで明らかになったことを願う。最後のグラフを見ると、カルマンフィルタが前回のフィルタの不完全な推定値を追跡しており、以前の観測値の "記憶" が入力信号に組み込まれるために遅延が生まれているのが分かる。
8.10 練習問題: 位置センサーがフィルタを改善することの証明
位置センサーと車輪センサーの観測値を統合すると車輪センサーだけの観測値より正確な結果が得られることの証明 (あるいは確認方法) を考えよ。
s1 = fusion_test(1.5, 1.0, do_plot=False)
s2 = fusion_test(1.5, 1e40, do_plot=False)
nom = range(1, 100)
res1 = nom - s1.x[:, 0, 0]
res2 = nom - s2.x[:, 0, 0]
print(f'残差の標準偏差 (位置センサーあり): {np.std(res1):.3f}')
print(f'残差の標準偏差 (位置センサーなし): {np.std(res2):.3f}')残差の標準偏差 (位置センサーあり): 0.306
残差の標準偏差 (位置センサーなし): 0.438実行結果から、位置センサーをほぼ完全に無視したときフィルタの誤差が大きくなるのが分かる。fusion_test は random.seed を呼ぶので、二つの fusion_test では同じデータが使われることに注意してほしい。
dt = 0.1
wheel_sigma = 1.5
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = array([[1., dt], [0., 1.]])
kf.H = array([[1., 0.]])
kf.x = array([[0.], [1.]])
kf.Q *= 0.01
kf.P *= 100
kf.R[0, 0] = wheel_sigma**2
random.seed(1123)
nom = range(1, 100)
zs = np.array([i + randn()*wheel_sigma for i in nom])
xs, _, _, _ = kf.batch_filter(zs)
ts = np.arange(0.1, 10, .1)
res = nom - xs[:, 0, 0]
print(f'標準偏差 (車輪センサーのみ): {np.std(res):.3f}')
plot_filter(ts, xs[:, 0], label='Kalman filter')
plot_measurements(ts, zs, label='Wheel')
set_labels(x='time (sec)', y='meters')
plt.legend(loc=4);
s_fused = fusion_test(1.5, 1.5, do_plot=False)
res_fused = nom - s_fused.x[:, 0, 0]
print(f'標準偏差 (統合センサー) : {np.std(res_fused):.3f}')標準偏差 (車輪センサーのみ): 0.523
標準偏差 (統合センサー) : 0.351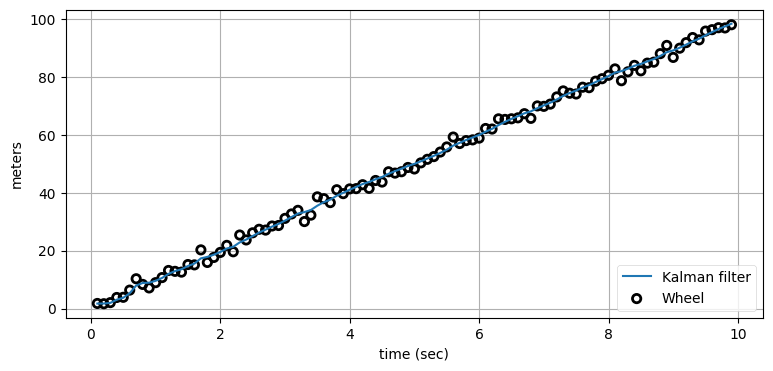
センサーを統合すると標準偏差が \(0.523\) から \(0.351\) に減少しており、正確な推定値が得られているのが分かる。
8.11 非定常プロセス
ここまではカルマンフィルタの様々な行列が定常 (stationary) だと仮定してきた──時間が経過しても、最初に設定した値が変わることはない。例えばロボットの追跡を考えたときは \(\Delta t = 1.0\, \text{s}\) と仮定し、状態遷移行列を次のように設計した:
しかし、もしデータの生成頻度 (データレート) が予測できない形で変化したらどうするべきだろうか? あるいはセンサーが二つあって、データレートが異なっていたら? 観測値の誤差が変化したら?
データレートの変化
これは簡単に処理できる: カルマンフィルタの行列を現在の状況に合うように入れ替えるだけだ。犬の追跡問題をもう一度考えよう。ここではセンサーからのデータの報告が散発的だと仮定する。この問題では
であり、KalmanFilter の F を次のように初期化していた:
dt = 0.1
kf.F = np.array([[1, dt],
[0, 1]])
観測値ごとに \(\Delta t\) が変わる場合でも、対応は簡単に行える──\(\Delta t\) が関係する行列を変更すればいい。\(\mathbf{F}\) は \(\Delta t\) が変わったとき変化するから、更新/予測のループで F を変更する必要がある。また \(\mathbf{Q}\) も \(\Delta t\) に依存するから、Q にもループごとに値の割り当てが必要になる。これを実装したコード例を示す:
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.x = array([0., 1.])
kf.H = array([[1, 0]])
kf.P = np.eye(2) * 50
kf.R = np.eye(1)
q_var = 0.02
# 観測値を表すタプル: (観測値, 経過時間)
zs = [(1., 1.), (2., 1.1), (3., 0.9), (4.1, 1.23), (5.01, 0.97)]
for z, dt in zs:
kf.F = array([[1, dt],
[0, 1]])
kf.Q = Q_discrete_white_noise(dim=2, dt=dt, var=q_var)
kf.predict()
kf.update(z)
print(kf.x)[1. 1.]
[2. 0.92]
[2.96 1. ]
[4.12 0.97]
[5.03 0.96]異なるデータレートを持つセンサーの統合
種類の異なるセンサーが同じ頻度でデータを出力することはまずない。位置センサーが \(3~\text{Hz}\) で新しいデータを生成し、車輪センサーは \(7~\text{Hz}\) で生成するとしよう。さらにデータが報告されるタイミングは正確でないと仮定する──センサーには揺らぎがあって、観測値が手に入るのは予測される時刻から多少前後する。さらに状況を複雑にするために、車輪センサーは位置ではなく速度の推定値を出力するものとさせてほしい。
この二つのセンサーを統合するには、次のようにする。まず、いずれかのセンサーから観測値が手に入るまで待機する。手に入ったら最後の更新からの経過時刻を求め、影響を受ける行列を変更する。今の例では \(\mathbf{F}\) と \(\mathbf{Q}\) が \(\Delta t\) の項を含むから、この二つの行列を発展のたびに調整しなければならない。
観測値がどちらのセンサーから手に入ったかに応じて \(\mathbf{H}\) と \(\mathbf{R}\) も変化させる必要がある。位置センサーは \(\mathbf{x}\) の位置要素を変化させるので、次の値を代入する:
車輪センサーは \(\mathbf{x}\) の速度要素を変化させるので、次の値を代入する:
以上の処理を実装したコードを示す:
def gen_sensor_data(t, ps_std, wheel_std):
# シミュレートされたセンサーデータを生成する。
pos_data, vel_data = [], []
dt = 0.
for i in range(t*3):
dt += 1/3.
t_i = dt + randn() * .01 # 観測値取得タイミングの揺らぎ
pos_data.append([t_i, t_i + randn()*ps_std])
dt = 0.
for i in range(t*7):
dt += 1/7.
t_i = dt + randn() * .006 # 観測値取得タイミングの揺らぎ
vel_data.append([t_i, 1. + randn()*wheel_std])
return pos_data, vel_data
def plot_fusion(xs, ts, zs_ps, zs_wheel):
xs = np.array(xs)
plt.subplot(211)
plt.plot(zs_ps[:, 0], zs_ps[:, 1], ls='--', label='Pos Sensor')
plot_filter(xs=ts, ys=xs[:, 0], label='Kalman filter')
set_labels(title='Position', y='meters',)
plt.subplot(212)
plot_measurements(zs_wheel[:, 0], zs_wheel[:, 1], label='Wheel')
plot_filter(xs=ts, ys=xs[:, 1], label='Kalman filter')
set_labels('Velocity', 'time (sec)', 'meters/sec')
def fusion_test(pos_data, vel_data, wheel_std, ps_std):
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = array([[1., 1.], [0., 1.]])
kf.H = array([[1., 0.], [1., 0.]])
kf.x = array([[0.], [1.]])
kf.P *= 100
xs, ts = [], []
# プロットのためデータをコピーする。
zs_wheel = np.array(vel_data)
zs_ps = np.array(pos_data)
last_t = 0
while len(pos_data) > 0 and len(vel_data) > 0:
if pos_data[0][0] < vel_data[0][0]:
t, z = pos_data.pop(0)
dt = t - last_t
last_t = t
kf.H = np.array([[1., 0.]])
kf.R[0,0] = ps_std**2
else:
t, z = vel_data.pop(0)
dt = t - last_t
last_t = t
kf.H = np.array([[0., 1.]])
kf.R[0,0] = wheel_std**2
kf.F[0,1] = dt
kf.Q = Q_discrete_white_noise(2, dt=dt, var=.02)
kf.predict()
kf.update(np.array([z]))
xs.append(kf.x.T[0])
ts.append(t)
plot_fusion(xs, ts, zs_ps, zs_wheel)
random.seed(1123)
pos_data, vel_data = gen_sensor_data(25, 1.5, 3.0)
fusion_test(pos_data, vel_data, 1.5, 3.0);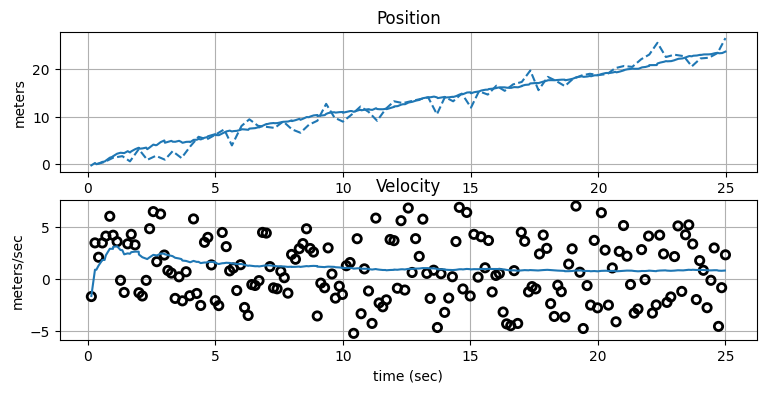
8.12 ボールの追跡
続いて、追跡している物体の物理的挙動に関する知識が限られている状況を考えよう。真空中に投げられたボールはニュートンの運動方程式に従って運動し、場の重力が一定であれば放物線を描く。この放物線を示す式を読者は知っているものと仮定する:
ここで \(g\) は重力加速度、\(t\) は時間、\(v_{x0}\) と \(v_{y0}\) はそれぞれ \(x\) 方向および \(y\) 方向の初期速度を表す。もしボールが速度 \(v\) で \(\theta\) の角度に投げられたなら、\(v_{x0}\) と \(v_{y0}\) は次のように計算できる:
現実のデータは持っていないので、ボールのシミュレーターを書くことにする。いつも通り、センサーに含まれるノイズをシミュレートするために時間に関して独立なノイズを加えている:
from math import radians, sin, cos
import math
def rk4(y, x, dx, f):
"""
dy/dx に対する四次のルンゲ=クッタ法を計算する。
x は x の初期値。
y は y の初期値。
dx は次の x との差 (タイムステップ)。
f は dy/dx を計算する関数。f(y, x) と呼び出される。
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2*k2 + 2*k3 + k4) / 6.
def fx(x,t):
return fx.vel
def fy(y,t):
return fy.vel - 9.8*t
class BallTrajectory2D(object):
def __init__(self, x0, y0, velocity,
theta_deg=0.,
g=9.8,
noise=[0.0, 0.0]):
self.x = x0
self.y = y0
self.t = 0
theta = math.radians(theta_deg)
fx.vel = math.cos(theta) * velocity
fy.vel = math.sin(theta) * velocity
self.g = g
self.noise = noise
def step(self, dt):
self.x = rk4(self.x, self.t, dt, fx)
self.y = rk4(self.y, self.t, dt, fy)
self.t += dt
return (self.x + randn()*self.noise[0],
self.y + randn()*self.noise[1])例えば、点 \((0,15)\) から始まる速度 \(100\,\text{m/s}\) で角度 \(60^\circ\) の軌道は次のように作成できる:
traj = BallTrajectory2D(x0=0, y0=15, velocity=100, theta_deg=60)
後はタイムステップごとに traj.step(t) を呼べばシミュレーションが行える。試してみよう:
def test_ball_vacuum(noise):
y = 15
x = 0
ball = BallTrajectory2D(x0=x, y0=y,
theta_deg=60., velocity=100.,
noise=noise)
t = 0
dt = 0.25
while y >= 0:
x, y = ball.step(dt)
t += dt
if y >= 0:
plt.scatter(x, y, color='r', marker='.', s=75, alpha=0.5)
plt.axis('equal');
# test_ball_vacuum([0, 0]) # 理想的なボールの軌道
test_ball_vacuum([1, 1]) # ノイズ入りのボールの軌道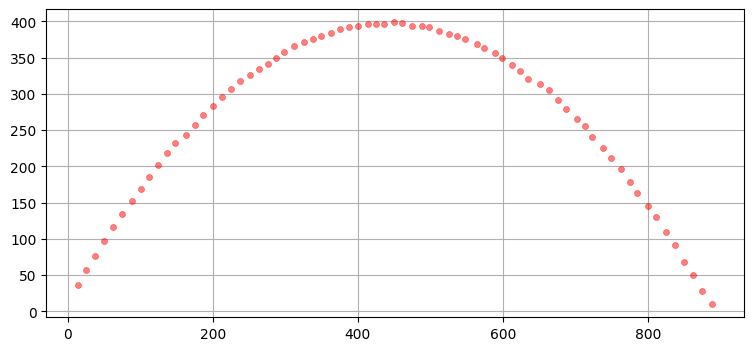
よさげな見た目をしている。次に進もう (読者への練習問題: シミュレーションの正しさをロバストに検証してみよ)。
状態変数を選ぶ
犬の追跡で使ったのと同じ状態変数を使えばいいと思うかもしれないが、それでは上手く行かない。カルマンフィルタの状態遷移は \(\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu}\) と表され、これは現在の状態が直前の状態から計算できることを意味するのだった。私たちはボールが真空中を飛んでいくと仮定しているので、\(x\) 方向の速度は一定で、\(y\) 方向の速度は重力定数 \(g\) にだけ影響を受ける。よく知られたオイラー法 (Euler's method) を使って \(\Delta t\) に関してニュートンの運動方程式を離散化すると、次の式を得る:
補足: オイラー法は微分方程式をステップごとに積分する方法であり、時刻 \(t\) から \(t+\Delta t\) の間で \(x\) の傾き (微分係数) が一定であることを仮定する。今考えている問題では位置 \(x\) の微分が速度だから、オイラー法は \(\Delta t\) のタイムステップで速度を一定だと仮定して新しい位置を計算し、速度を次のタイムステップで使う値に更新する。オイラー法より正確な手法 (例えば本書でも使ったルンゲ=クッタ法) も存在するものの、各ステップで観測値による状態の更新があるので、オイラー法でも十分正確な結果が得られる。ルンゲ=クッタ法を使うときは、状態遷移を計算する
predict関数を自分で書く必要がある。共分散行列は通常のカルマンフィルタの式 \(\mathbf{\bar P}=\mathbf{FPF}^\mathsf T + \mathbf Q\) で更新できる。
ここから \(y\) 方向の加速度をカルマンフィルタに組み込む必要があることが示唆される (\(x\) 方向の加速度は必要ない)。このとき状態変数は次のようになる:
しかし \(y\) 方向の加速度は重力によるものであり、定数である。カルマンフィルタに定数を追跡するよう伝えなくても、重力の値をそのまま──制御入力として──扱うこともできる。言い換えると、重力は系の振る舞いを変化させる外力であり、どう変化させるかは既知であり、ボールが運動するとき常に存在すると考えるということだ。
このとき状態の予測 (遷移) は \(\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu}\) という式で行われる。行列 \(\mathbf{F}\) はお馴染みの状態遷移関数であり、ボールの位置と速度をモデル化する。ベクトル \(\mathbf{u}\) はフィルタへの制御入力であり、例えば車ではアクセルやブレーキを押す強さやハンドルの回転などが制御入力になる。今考えているボールの運動では重力が制御入力になる。行列 \(\mathbf{B}\) は制御入力が系の振る舞いにどのような影響を及ぼすかをモデル化する。もう一度車を考えると、\(\mathbf{B}\) はアクセルやブレーキが押される強さを速度の変化に、ハンドルの回転を位置や進行方向の変化に変換する。ボールを追跡する問題では \(\mathbf{B}\) が重力に起因する速度の変化を計算する。詳細は後で説明するので、今は重力を制御入力とみなすとき状態が次のようになることを納得してほしい:
状態遷移関数の設計
次のステップは状態遷移関数の設計である。カルマンフィルタで状態遷移関数は行列 \(\mathbf{F}\) として実装され、\(\mathbf{F}\) を一つ前の状態に乗じると次の状態 (事前分布) \(\bar{\mathbf{x}} = \mathbf{Fx}\) が得られることを思い出してほしい。
ボールの追跡問題は多変量カルマンフィルタの章で考えた犬を追跡する一次元の問題とよく似ているので、細かい説明はしない。位置と速度の状態方程式は次のようになる:
この式に重力加速度 \(g\) が含まれていないことに注目してほしい。先ほど説明したように、重力は系に対する制御入力として処理する。
これを行列形式で書けばこうなる:
制御関数の設計
重力は系に加わる制御入力とみなされるので、\(\mathbf{\bar x} = \mathbf{Fx}\) に加えられる \(\mathbf{Bu}\) が重力による \(\mathbf{\bar x}\) の変化をモデル化する。\(\mathbf{Bu}\) には \(\Big[\Delta x_g \ \ \Delta \dot{x_g} \ \ \Delta y_g \ \ \Delta \dot{y_g}\Big]^\mathsf T\) が含まれると言える。
離散化された式を見ると、重力は \(y\) 方向の速度だけに影響を及ぼすのが分かる:
よって制御関数と制御入力の積 \(\mathbf{Bu}\) は \(\Big[0 \ \ 0 \ \ 0 \ \ -g \Delta t \Big]^\mathsf T\) になるべきである。ある意味では、\(\mathbf{Bu}\) がこの値になる限り \(\mathbf{B}\) と \(\mathbf{u}\) をどのように定義しても構わない。例えば \(\mathbf{B}=1\) および \(\mathbf{u} = \Big[0 \ \ 0 \ \ 0 \ \ -g \Delta t \Big]^\mathsf T\) としても問題はない。しかしこの定義は \(\mathbf{u}\) が制御入力で \(\mathbf{B}\) が制御関数だとした私たちの考え方と噛み合わない。今考えている制御入力は \(y\) 方向の速度に対する \(-g\) なので、例えば次の定義だと私たちの考え方と合致する:
私の目には、この定義は少し大きすぎるように思える。\(x\) 方向と \(y\) 方向の速度に対する制御入力だけを考えることもでき、そうすると次の定義が得られる:
あるいは存在する制御入力だけを与えることもできる。\(x\) 方向の速度に対する制御入力は存在しないから、次の定義となる:
次の定義が使われているのも見たことがある:
こうしても正しい結果は得られるものの、私は \(\mathbf{u}\) に時間を入れようとは思わない。\(\Delta t\) は制御入力そのものではなく制御入力を状態の変化に変換する値であり、その役目は \(\mathbf{B}\) が担うからだ。
観測関数の設計
観測関数は状態変数から観測値を得る方法を定義する。カルマンフィルタにおいて観測関数は行列 \(\mathbf{H}\) であり、\(\mathbf z = \mathbf{Hx}\) で状態から観測値が計算される。ここではセンサーがボールの位置 \((x,y)\) を報告し、速度と加速度は観測できないものとする。このとき観測関数の式は
となる。つまり次の通りである:
観測ノイズ行列の設計
ロボットの例と同じように、\(x\) 方向と \(y\) 方向の誤差は独立だと仮定する。そして観測誤差の分散はそれぞれの方向に \(0.5~\text{m²}\) だとする。このとき観測ノイズ行列 \(\mathbf{R}\) は次のようになる:
プロセスノイズ行列の設計
ボールは真空中を運動すると仮定していたので、プロセスノイズは存在しないはずである。状態変数は四つの要素を持つから、プロセスノイズ行列 \(\mathbf{Q}\) は \(4{\times}4\) の零行列となる:
初期条件の設計
このステップは状態遷移関数を考えたときに終わっている。\(x\) 方向および \(y\) 方向の初期速度を三角関数で計算し、それを \(\mathbf{x}\) の初期値としていた:
omega = radians(omega)
vx = cos(omega) * v0
vy = sin(omega) * v0
f1.x = np.array([[x, vx, y, vy]]).T
以上のステップが終われば、フィルタを実装してテストする準備が整う。まず実装を示す:
from math import sin, cos, radians
def ball_kf(x, y, omega, v0, dt, r=0.5, q=0.):
kf = KalmanFilter(dim_x=4, dim_z=2, dim_u=1)
kf.F = np.array([[1., dt, 0., 0.], # x = x0 + dx*dt
[0., 1., 0., 0.], # dx = dx0
[0., 0., 1., dt], # y = y0 + dy*dt
[0., 0., 0., 1.]]) # dy = dy0
kf.H = np.array([[1., 0., 0., 0.],
[0., 0., 1., 0.]])
kf.B = np.array([[0., 0., 0., dt]]).T
kf.R *= r
kf.Q *= q
omega = radians(omega)
vx = cos(omega) * v0
vy = sin(omega) * v0
kf.x = np.array([[x, vx, y, vy]]).T
return kf続いて BallTrajectory2D クラスを使ってボールの観測値を生成し、フィルタをテストする:
def track_ball_vacuum(dt):
global kf
x, y = 0., 1.
theta = 35. # 射出角度
v0 = 80.
g = np.array([[-9.8]]) # 重力定数
ball = BallTrajectory2D(x0=x, y0=y, theta_deg=theta, velocity=v0,
noise=[.2, .2])
kf = ball_kf(x, y, theta, v0, dt)
t = 0
xs, ys = [], []
while kf.x[2] > 0:
t += dt
x, y = ball.step(dt)
z = np.array([[x, y]]).T
kf.update(z)
xs.append(kf.x[0])
ys.append(kf.x[2])
kf.predict(u=g)
p1 = plt.scatter(x, y, color='r', marker='.', s=75, alpha=0.5)
p2, = plt.plot(xs, ys, lw=2)
plt.legend([p2, p1], ['Kalman filter', 'Measurements'],
scatterpoints=1)
track_ball_vacuum(dt=1./10)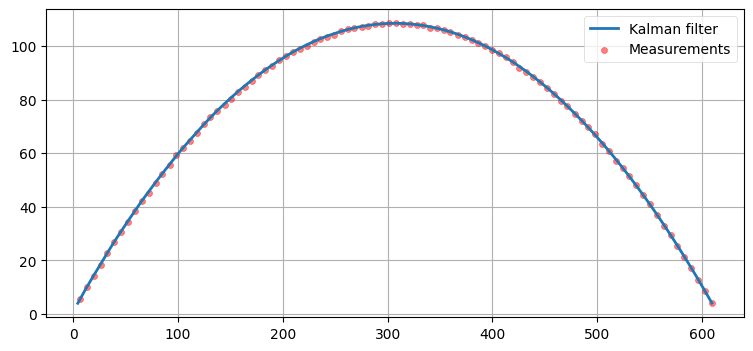
カルマンフィルタは正しくボールを追えているのが分かる。ただし先述したように、これはプロセスノイズが存在しないとした自明な例である。真空中を運動するボールの軌跡は任意の精度で予測できる: この例でカルマンフィルタは話を複雑にしているだけだ。全く同一の結果は最小二乗法を使った曲線フィッティングでも得られる。
8.13 大気中を運動するボールの追跡
次の問題では地球の大気中を運動するボールの追跡を行う。このときボールの軌跡は風や空気抵抗、あるいはボールの回転に影響を受ける。センサーはカメラだと仮定し、ボールの位置を検出する画像処理アルゴリズムによって位置が分かるとする。画像に含まれる物体の位置を計算するこの処理をコンピュータービジョンの用語でブロブ検出 (blob detection) と呼ぶ。ブロブ検出のアルゴリズムは完璧でないので、ブロブが検出されなかったり誤ったブロブが検出されたりする可能性がどのフレームにも存在する。最後に、ボールが運動を開始した時点での位置・角度・回転は分からないと仮定する。追跡を行うコードは与えられる観測値に基づいて追跡処理を初期化しなければならない。この問題での主な単純化は二次元の運動を考えていることだ: ボールは必ずカメラのセンサーに対して垂直に運動することが仮定される。カメラが提供する二次元のデータから三次元のデータを取り出す方法は議論していないので、この単純化が必要になる。
空気抵抗の実装
最初のステップとして、大気中におけるボールの運動を記述する式を求める。利用できる定式化はいくつかある。ロバストな解はボールの粗さ (速度に応じて非線形な形で空気抗力に影響する) やマグヌス効果 (回転によってボールの片側で大気との相対速度が反対側より速くなり、空気抗力が変化する)、あるいは揚力・湿度・空気密度といった要素を全て考えに入れたものである。読者はボールの物理学に興味がないだろうから、ここではスピンのない野球ボールに加わる空気抗力の効果だけを考えることにする。今から説明する定式化は Nicholas Giordano と Hisao Nakanishi 著 Computational Physics6 にあるものを参考にしており、全ての要因を考えに入れているわけではない。Alan Nathan による最も詳細な定式化は彼のウェブサイトから確認できる。私が取り組んだコンピュータービジョンの課題では彼の数式を使ったことがあるものの、ここで複雑なモデルを使って説明が長くなるのは避けたい。
重要: 先に進む前に、これから説明する物理学的な背景を理解しなくても後のカルマンフィルタに関する議論には付いていけることを強調しておく。ここでの目標は現実世界における野球ボールの振る舞いをそれなりの正確さで再現するモデルを作り、その現実的な振る舞いに対してカルマンフィルタがどう振る舞うかを確認することである。現実世界での応用においては系の物理的振る舞いを完全にモデル化できないことが多く、そのときは巨視的な振る舞いだけを取り入れたプロセスモデルでどうにかしなければならない。さらに手にしているデータで上手く振る舞うよう観測ノイズ行列とプロセスノイズ行列にも調整が必要になる。ここには深刻なリスクがある: テストデータに対して完璧に動作するまでカルマンフィルタを細かく調整しても、微妙に異なるデータに対しては性能が優れないという状況はよくある。これはおそらくカルマンフィルタの設計で最も難しい部分であり、カルマンフィルタが「黒魔術」などと呼ばれる理由でもある。
説明をせずに式を実装する本は好きでないので、これから大気中を運動するボールの物理学を考える。興味が無いならシミュレーションの実装まで飛ばして構わない。
大気中を運動するボールは風の抵抗を受ける。風邪の抵抗によりボールの表面に抗力 (drag) と呼ばれる力が加わり、軌道が変化する。Giordano らの著作では抗力が
と表される。ここで \(B_2\) は実験的に導かれる係数、\(v\) は物体の速度を表す。\(F_{drag}\) を \(x\) 方向と \(y\) 方向に分けると次を得る:
\(m\) をボールの質量とすれば、\(F=ma\) から加速度を求められる:
Giordano は \(\displaystyle \frac{B_2}{m}\) に対して次の関数を与えている。この式は野球ボールの断面積、粗さ、空気密度を考えに入れている。これは風洞実験やいくつかの単純化のための仮定に基づいた近似であることを理解してほしい。この式は SI 単位系を使っており、速度はメートル毎秒、時間は秒で表される:
真空中を運動するボールの軌跡をオイラー法で離散化した式から定式化を始めよう:
空気抗力 (による加速度) は \(a \Delta t\) を速度の更新式に付け足せば取り入れることができる。抗力は速度を低下させるから、この項は引くべきである。抗力を \(x\) 要素と \(y\) 要素に分けるだけだから、このコードは非常に簡単に書ける。
計算物理学は本書の範囲を超えるので、この問題を物理学的に考えるのはここまでとする。忠実度の高いシミュレーションは高度・温度・ボールのスピンといった要因を取り入れることは知っておいてほしい。興味があるなら、前述した Alan Nathan による研究がこの話題に触れている。ここでの私の意図は、現実的な振る舞いを加えたシミュレーションを与えたときに、それより単純なモデルを使ったカルマンフィルタがどう反応するかを確認することだ。プロセスモデルが現実世界を正確に記述できることは決してない。優れたカルマンフィルタを設計する上で重要な要素の一つは現実のデータを使った振る舞いのテストである。
次のコードは高度 \(0~\text{m}\) から大気中に発射され風の影響を受けながら運動するボールの振る舞いを計算する。同じ初期条件で風が吹いていない場合と \(10~\text{mph}\)7 の風が吹いている場合のボールの軌道をプロットしている。野球の統計はヤード・ポンド法で記録されるので、ここでもヤード・ポンド法を用いる。このコードで使っている初期速度 \(110~\text{mph}\) は典型的なホームランの打球速度である:
from math import sqrt, exp
# 訳注: mph は「マイル毎時」
# mps は「メートル毎秒」
def mph_to_mps(x):
return x * .447
def drag_force(velocity):
"""
指定された速度で運動する野球ボールに加わる空気抗力からの力を返す。
引数は SI 単位で表される。
"""
return velocity * (0.0039 + 0.0058 /
(1. + exp((velocity-35.)/5.)))
v = mph_to_mps(110.)
x, y = 0., 1.
dt = .1
theta = radians(35)
def solve(x, y, vel, v_wind, launch_angle):
xs = []
ys = []
v_x = vel*cos(launch_angle)
v_y = vel*sin(launch_angle)
while y >= 0:
# オイラー法で求めた x と y に対する式
x += v_x*dt
y += v_y*dt
# 空気抗力による力
velocity = sqrt((v_x-v_wind)**2 + v_y**2)
F = drag_force(velocity)
# オイラー法で求めた vx と vy に対する式
v_x = v_x - F*(v_x-v_wind)*dt
v_y = v_y - 9.8*dt - F*v_y*dt
xs.append(x)
ys.append(y)
return xs, ys
x, y = solve(x=0, y=1, vel=v, v_wind=0, launch_angle=theta)
p1 = plt.scatter(x, y, color='blue', label='no wind')
wind = mph_to_mps(10)
x, y = solve(x=0, y=1, vel=v, v_wind=wind, launch_angle=theta)
p2 = plt.scatter(x, y, color='green', marker="v",
label='10mph wind')
plt.legend(scatterpoints=1);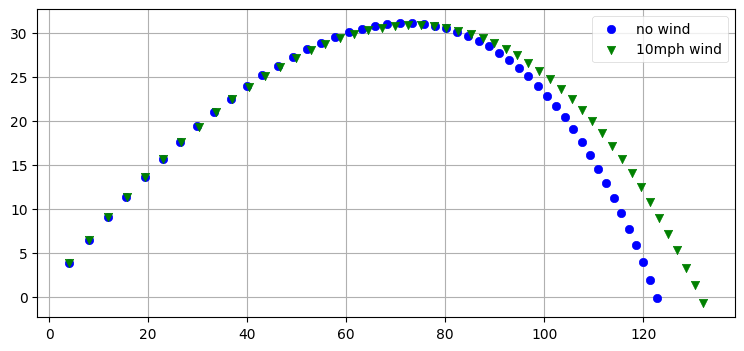
真空中の軌道と大気中の軌道の違いが簡単に確認できる。ここでは初期速度と初期角度を前節の真空中におけるシミュレーションと同じに設定している。真空中ではボールが約 \(240~\text{m}\) 飛ぶと計算されていたのに対して、ここでは大気中だとボールの飛距離は \(120~\text{m}\) 程度と計算されている。\(120~\text{m}\) はホームランの飛距離として妥当な値だから、シミュレーションがそれなりに正確であるようだと自信が持てる。
難しい話はこれくらいにして、上述の数式を使ったより現実的なボールのシミュレーションを行うクラスを実装しよう。空気抗力が非線形であるために任意の時刻におけるボールの位置を求める解析解は存在せず、位置はステップごとに計算しなければならないことに注意してほしい。解の伝播にはオイラー法を使っている: より正確なルンゲ=クッタ法などを使うのは読者への練習問題とする。ここで設定するタイムステップに対しては異なる手法を使っても正確さの変化は小さいので、コードを複雑にする必要はない:
class BaseballPath:
def __init__(self, x0, y0, launch_angle_deg, velocity_ms,
noise=(1.0, 1.0)):
"""
野球ボールの二次元軌跡オブジェクトを作る。
(x 座標 = 地面と平行に測った開始地点からの距離
y 座標 = 地面からの高さ)
x0, y0 初期位置
launch_angle_deg 射出角度 (水平線進行方向が 0 度)
velocity_ms 初期速度 (メートル毎秒)
noise それぞれの位置に加えるノイズ (x, y)
"""
omega = radians(launch_angle_deg)
self.v_x = velocity_ms * cos(omega)
self.v_y = velocity_ms * sin(omega)
self.x = x0
self.y = y0
self.noise = noise
def drag_force(self, velocity):
"""
指定された速度で運動する野球ボールに加わる空気抗力からの力を返す。
引数は SI 単位で表される。
"""
B_m = 0.0039 + 0.0058 / (1. + exp((velocity-35.)/5.))
return B_m * velocity
def update(self, dt, vel_wind=0.):
"""
指定したタイムステップと風の速度を使って野球ボールの位置を計算する。
位置を表すタプル (x, y) を返す。
"""
# オイラー法で求めた x と y に対する式
self.x += self.v_x*dt
self.y += self.v_y*dt
# 空気抗力による力
v_x_wind = self.v_x - vel_wind
v = sqrt(v_x_wind**2 + self.v_y**2)
F = self.drag_force(v)
# オイラー法で求めた vx と vy に対する式
self.v_x = self.v_x - F*v_x_wind*dt
self.v_y = self.v_y - 9.81*dt - F*self.v_y*dt
return (self.x + randn()*self.noise[0],
self.y + randn()*self.noise[1])このモデルで作成した観測値に対してカルマンフィルタを動作させてみよう:
x, y = 0, 1.
theta = 35. # 射出角度
v0 = 50.
dt = 1/10. # タイムステップ
g = np.array([[-9.8]])
plt.figure()
ball = BaseballPath(x0=x, y0=y, launch_angle_deg=theta,
velocity_ms=v0, noise=[.3,.3])
f1 = ball_kf(x, y, theta, v0, dt, r=1.)
f2 = ball_kf(x, y, theta, v0, dt, r=10.)
t = 0
xs, ys = [], []
xs2, ys2 = [], []
while f1.x[2] > 0:
t += dt
x, y = ball.update(dt)
z = np.array([[x, y]]).T
f1.update(z)
f2.update(z)
xs.append(f1.x[0])
ys.append(f1.x[2])
xs2.append(f2.x[0])
ys2.append(f2.x[2])
f1.predict(u=g)
f2.predict(u=g)
p1 = plt.scatter(x, y, color='r', marker='.', s=75, alpha=0.5)
p2, = plt.plot(xs, ys, lw=2)
p3, = plt.plot(xs2, ys2, lw=4)
plt.legend([p1, p2, p3],
['Measurements', 'Filter(R=0.5)', 'Filter(R=10)'],
loc='best', scatterpoints=1);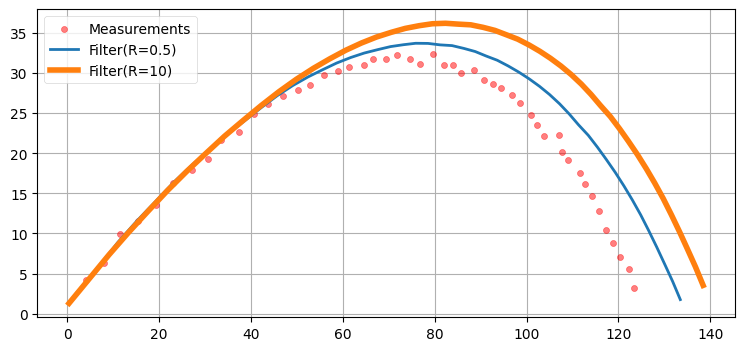
二つの異なる設定におけるカルマンフィルタの出力をプロットしている。ピンク色の点が観測値、青い直線が R=0.5 としたカルマンフィルタの出力、青い実線が R=10 としたカルマンフィルタの出力を表す。R は観測ノイズの出力への影響を見せるために選んでおり、この値が正しい設計であるわけではない。
どちらのフィルタもボールを上手く追跡できていないのが分かる。最初は両方とも観測値を追えているものの、時間が経過すると発散してしまう。発散が起こるのは、空気抗力の状態モデルが非線形であるにもかかわらずカルマンフィルタが線形モデルを仮定するためである。g-h フィルタの章の非線形性に関する議論を思い出そう: g-h フィルタは系の加速に必ず遅れて付いていくことを説明した。同じことがここでも起こる──系に加わる加速度は負だから、カルマンフィルタは一貫してボールの位置をオーバーシュートする。加速が続く限りフィルタがボールに追い付く方法は存在せず、フィルタは発散し続ける。
どうすればフィルタの性能を改善できるだろうか? 最も優れたアプローチは非線形カルマンフィルタであり、これは次章以降で触れる。しかし、「エンジニアリング」(と私なら呼ぶ手法) による解決法も存在する。今考えているカルマンフィルタはボールが真空中を運動するものと仮定するので、プロセスノイズが存在しないとしている。しかし実際のボールは大気中を運動し、大気からは力が加わる。この力をプロセスノイズと考えることができる。これは厳密な考え方とは言えない: まず、ボールに加わる力は決してガウス分布に従わない。次に、この力は計算できるので、両手を挙げて「力はランダムだよ」と言っても最適な解は得られない。しかし、この考え方を採用するとどうなるかを見てみよう。
次のコードはこれまでと同じカルマンフィルタを実装するが、プロセスノイズ行列を \(\mathbf{0}\) でない値に設定できるようにしてある。Q=0.1 とした場合と Q=0.01 とした場合の結果をプロットした:
def plot_ball_with_q(q, r=1., noise=0.3):
x, y = 0., 1.
theta = 35. # 射出角度
v0 = 50.
dt = 1/10. # time step
g = np.array([[-9.8]])
ball = BaseballPath(x0=x,
y0=y,
launch_angle_deg=theta,
velocity_ms=v0,
noise=[noise,noise])
f1 = ball_kf(x, y, theta, v0, dt, r=r, q=q)
t = 0
xs, ys = [], []
while f1.x[2] > 0:
t += dt
x, y = ball.update(dt)
z = np.array([[x, y]]).T
f1.update(z)
xs.append(f1.x[0])
ys.append(f1.x[2])
f1.predict(u=g)
p1 = plt.scatter(x, y, c='r', marker='.', s=75, alpha=0.5)
p2, = plt.plot(xs, ys, lw=2, color='b')
plt.legend([p1, p2], ['Measurements', 'Kalman filter'])
plt.show()
plot_ball_with_q(0.01)
plot_ball_with_q(0.1)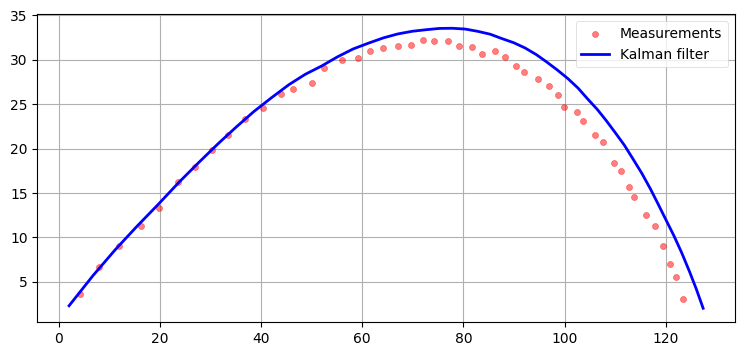
Q=0.01 としたフィルタリング
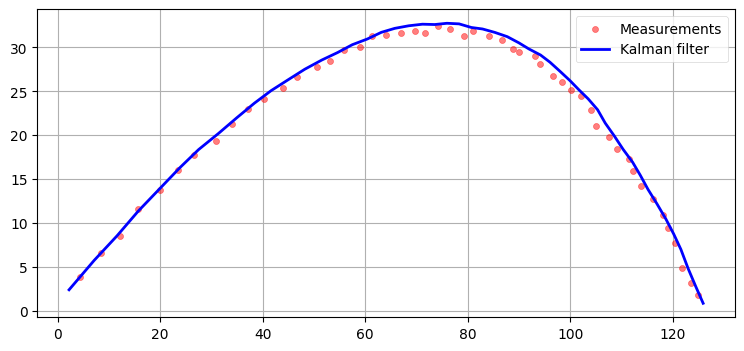
Q=0.1 としたフィルタリング
二つ目のフィルタは観測値をかなり正確に追跡できている。少し遅れても見えるが、ほんの少しだけだ。
これは優れたテクニックなのだろうか? 普通はそうでないものの、場合によっては有用なこともある。今の例ではボールに加わる力の非線形性がほぼ一定で定常的だった。車を追跡するとしたら、車が速度や方向を変えるたびにプロセスモデル以外の加速度は変化するだろう。プロセスノイズ行列を系に含まれる実際のノイズより大きく設定するとき、フィルタは観測値をより重視するようになる。観測値にノイズが少なければそれでも問題ないかもしれないが、観測値のノイズを増やしたときの次のプロットを見てみてほしい:
plot_ball_with_q(0.01, r=3, noise=3.)
plot_ball_with_q(0.1, r=3, noise=3.)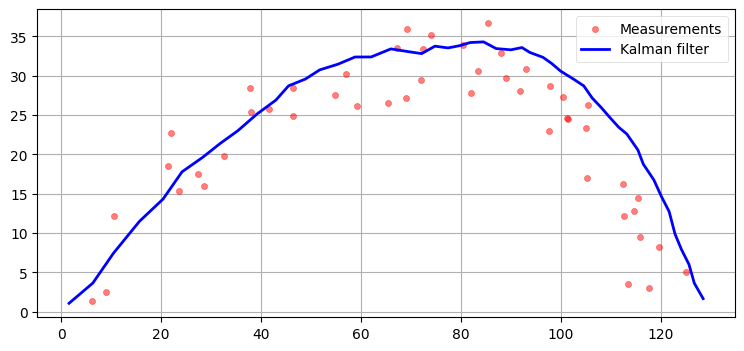
Q=0.01)
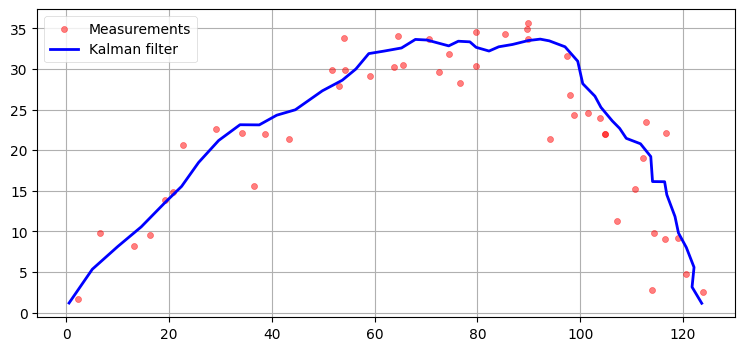
Q=0.1)
出力はめちゃくちゃだ。フィルタはプロセス (予測ステップ) ではなく観測値を重視する以外の選択肢を持たないにもかかわらず観測値のノイズが大きいので、フィルタはノイズを追跡してしまう。こういった制限が線形カルマンフィルタに内在するために、非線形なバージョンのカルマンフィルタの開発が行われた。
ただそうは言っても、考えている系の小さな非線形性にプロセスノイズで対処することも間違いなく可能である。これはカルマンフィルタの「黒魔術」と言える。センサーと系のモデルが完璧なことは決してない: センサーはガウス分布で表せず、プロセスモデルは正確でない。これは観測ノイズ行列とプロセスノイズ行列を理論的に正しい値よりも大きく設定すれば埋め合わせができるものの、代わりに解は最適でなくなる。フィルタが発散するよりは最適でない解の方が優れているものの、上のグラフに示したように、そのときフィルタの出力は容易にとても悪くなってしまう。また大量に行ったシミュレーションやテストでは非常に良い性能が得られるにもかかわらず、現実世界のデータで条件が少しだけ変わっただけでフィルタの振る舞いが大幅に悪化することも本当によくある。
この例ではカルマンフィルタを明らかに誤った問題に適用しているので、今はこの問題をこれ以上は考えない。この問題は次章以降でまた考えて、様々な非線形のテクニックの効果を見ることにする。非線形な問題を線形カルマンフィルタでどうにかできる領域も存在するものの、普通は本書の残りの部分で学ぶ手法のいずれかを使わなければならないはずだ。
-
Samuel S. Blackman, Multiple-Target Tracking with Radar Application, Artech House, 1986.[return]
-
Subhash Challa, Mark R. Morelande, Darko Mušicki, and Robin J. Evans, Fundamentals of Object Tracking, Cambridge University Press, 2011.[return]
-
Lawrence D. Stone, Roy L. Streit, Thomas L. Corwin, and Kristine L. Bell, Bayesian Multiple Target Tracking, Artech House, 2013.[return]
-
Yaakov Bar-Shalom, X. Rong Li, and Thia Kirubarajan, Estimation with Applications to Tracking and Navigation, John Wiley & Sons, 2001.[return]
-
訳注: NEES は真の値を知らないと計算できないので、現実世界の観測値を取得しながらフィルタを実行するときには計算できない。その場合は系不確実性 \(\mathbf{S}\) と残差 \(\mathbf{y}\) を使って \(\mathbf{y}^\mathsf T \mathbf{S}^{-1} \mathbf{y}\) と定義される二乗正規化イノベーション (normalized innovation squared, NIS) を使うと同様の議論でフィルタの性能を評価できる。[return]
-
Nicholas Giordano, and Hisao Nakanishi, Computational Physics, Benjamin Cummings, 2005.[return]
-
訳注: mph は「マイル毎時」のこと。\(1\) マイルは約 \(1.6\) キロメートル。[return]