第 9 章非線形フィルタリング

これまでに考えたカルマンフィルタは線形の方程式を仮定しているので、線形の問題しか扱えない。しかし世界は非線形であり、本書で学んできた古典的なフィルタを適用できる問題は非常に限られる。

プロセスモデルに非線形性が存在する場合もある。例えば大気中を落下する物体を追跡したいとしよう。その物体の加速度は大気から受ける抗力によって変化する。抗力は空気密度に依存し、空気密度は高度が上がると減少する。一次元の落下は次の非線形微分方程式でモデル化できることが知られている:

\[ \ddot x = \frac{0.0034ge^{-x/22000}\dot x^2}{2\beta} - g \]

観測値からも非線形性が発生する。例えばレーダーは航空機と自身を結んだ斜め方向の距離 (直距離, slant distance) を観測するが、私たちが知りたいのは航空機の地上における座標である。よってピタゴラスの定理が必要になり、式が非線形になる:

\[ x = \sqrt{\text{直距離}^2 - \text{高度}^2} \]

こういった事実はカルマンフィルタのアーリーアダプターによって見過ごされたわけではなかった。カルマン博士が論文を発表してすぐに、カルマンフィルタを非線形の問題に拡張する研究が始まっている。

人類が解法を知っている方程式は \(\mathbf{Ax} = \mathbf{b}\) だけと言っても過言ではない。私たちは線形代数ならよく知っている。どんな線形方程式系を見せられても、解が存在すれば解を求められるし、解が存在しなければそれを証明できる。

数学や物理学の正式な教育を受けた者なら誰でも、数年をかけて積分や微分方程式の解析解の求め方を学ぶ。しかし非常に簡単な物理系でさえ解析的には解けない方程式を生むことがある。あるいは積分できる式であっても、被積分関数の最初に \(\log\) を付ければまず積分できなくなる。これは「物理学者『牛を真空中の摩擦のない表面に置かれた球だと仮定すると...』」といったジョークが作られる理由でもある。極端な単純化をしない限り、ほとんどの物理の問題は解析解を持たない。

では、コンピューターで航空機の周りの空気の流れをモデル化したり、気象を予測したり、カルマンフィルタを使ってミサイルを追跡したりするにはどうすればいいだろうか？自分たちが知っていることまで退却することになる: つまり \(\mathbf{Ax} = \mathbf{b}\) だ。どうにかして問題を線形化して線形方程式系に変形し、線形代数のソフトウェアパッケージを使って解を近似すればいい。

非線形な問題を線形化すると不正確な答えが得られる。そのためカルマンフィルタや気象追跡システムといった再帰的なアルゴリズムでは、小さな誤差がステップごとに大きくなり、アルゴリズムの出力がすぐに意味のない値になる可能性がある。

今ここで私たちが取り組み始めたのは難しい問題である。簡単かつ正確で、数学的に最適な解はもはや存在しない。式には近似が使われ、計算には誤差が含まれ、フィルタの発散との戦いが止むことはない: フィルタの数値的誤差が解を圧倒する可能性が常にある。

この短い章の残りの部分では、非線形カルマンフィルタが直面する様々な問題を説明する。非線形フィルタを設計するには、あなたが取り組む問題に含まれる非線形性が具体的にどのような問題を引き起こすかを理解しなければならない。次章以降では様々な種類の非線形フィルタを設計・実装する方法を学ぶ。

9.1 非線形が引き起こす問題

カルマンフィルタの数式が美しい理由の一つはガウス分布の確率密度関数が特別な特徴を持つことだ。ガウス分布の確率密度関数は非線形ではあるものの、和や積が別のガウス分布となる。この特徴は非常に稀であり、例えば \(\sin{x} \cdot \sin{y}\) は \(\sin\) にならない。

「線形性」という言葉の意味することは明らかかもしれないが、細かい注意を要する点がある。線形性に必要な数学的条件は次の二つだ:

加法性: \(f(x+y) = f(x) + f(y)\)
斉次性: \(f(ax) = af(x)\)

この定義から、入力に線形比例する値の和が出力となるような系が線形な系だと言える。さらにここから、入力が全てゼロなら出力もゼロだと分かる。マイクに付いたアンプを考えよう──私がマイクに向かって歌い、あなたが同じマイクに向かって話すとき、マイクが線形だと仮定すれば、その出力は二人の声の和をアンプのゲインでスケールした音となる。しかしアンプに何も入力しないときに何らかの音 (例えばプーンという音) が出力されたとしたら、その時点で線形性は成り立たない。これは線形性が \(amp(voice) = amp(voice + 0)\) を要求するためである。この式の両辺は明らかに同じであるべきだが、\(amp(0)\) がゼロでないと次の等式が成り立ってしまう:

\[ \begin{aligned} amp(voice) &= amp(voice + 0) \\ &= amp(voice) + amp(0) \\ &= amp(voice) + \text{ゼロでない値} \end{aligned} \]

もちろんこれはおかしい。よって、一見すると線形に見える式

\[ L(f(t)) = f(t) + 1 \]

は \(L(0) = 1\) となるので線形ではない。注意してほしい！

9.2 非線形な問題の直感的な考え方

これから説明するのは非線形な問題の捉え方で私が特に気に入っているものである。これは Dan Simon 著 Optimal State Estimation¹ から取った。物体の距離と方位が観測される状況で、物体の位置を追跡したいとしよう。実際の距離は \(50~\text{km}\) で、実際の方位は \(90^\circ\) とする。距離と方位の誤差はガウス分布に従うと仮定したとき、無限個の観測値を取得したときの位置の期待値はどの点になるだろうか？

本書では直感的な理解を推奨してきた。この問題ではどうなるかを考えてみよう。距離の平均は \(50~\text{km}\) で方位の平均は \(90^\circ\) だと思うかもしれない。このとき位置の期待値は \(x=0~\text{km}\) および \(y=50~\text{km}\) となる。

プロットして考えよう。距離は標準偏差 \(0.4~\text{km}\) の正規分布、方位は標準偏差 \(0.35~\text{rad}\) の正規分布に従うとして \(3000\) 個の点を生成し、その平均を求めてみる。計算された平均を赤い星で、直感的に考える平均を黒い点で示す:

In [3]

import numpy as np
from numpy.random import randn
import matplotlib.pyplot as plt

N = 5000
a = np.pi/2. + (randn(N) * 0.35)
r = 50.0     + (randn(N) * 0.4)
xs = r * np.cos(a); ys = r * np.sin(a)

plt.scatter(xs, ys, label='Sensor', color='k', alpha=0.4, marker='.', s=1)
xmean, ymean = sum(xs) / N, sum(ys) / N
plt.scatter(0, 50, c='k', marker='o', s=200, label='Intuition')
plt.scatter(xmean, ymean, c='r', marker='*', s=200, label='Mean')
plt.axis('equal')
plt.legend();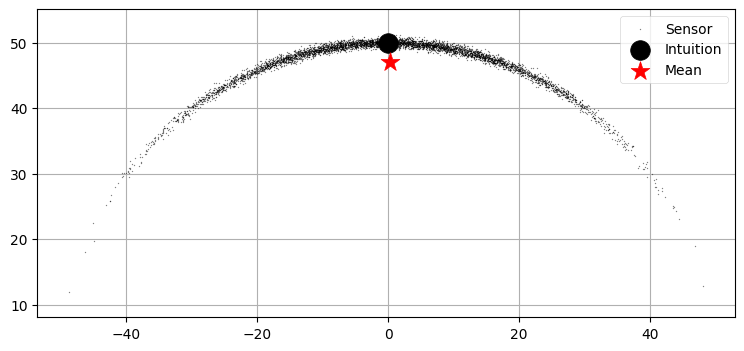

グラフからは直感が間違っているのが分かる。これは誤差が一方向 (この例では下方向) に偏る (バイアスがある) ためであり、問題が非線形であるときにだけ起こる。このバイアスは反復とともにカルマンフィルタを発散させる可能性があり、発散が起こらなくてもフィルタの出力は最適でなくなる。非線形な問題に対する線形近似は不正確な結果をもたらす。

9.3 ガウス分布に非線形関数を適用したときの影響

ガウス分布は任意の非線形関数に関しては閉じていない。カルマンフィルタの式を思い出そう──各時刻の発展で、一つ前の時刻における状態を表すガウス分布を一連のプロセス関数に渡して次の時刻における状態を表すガウス分布を計算していた。カルマンフィルタのプロセス関数は必ず線形だから、出力も必ずガウス分布になる。これをグラフに表してみよう。適当なガウス分布を取って、それを \(f(x) = 2x + 1\) に通して結果をプロットしてみる。これは解析的にも行えるが、ここではサンプリングを利用する: 正規分布に従う 500,000 個の点を生成し、\(f(x)\) に通し、その結果をプロットする。ここでサンプリングを使うのは、次に考える非線形な関数では結果を解析的に計算できないためだ:

In [4]

from numpy.random import normal
data = normal(loc=0., scale=1., size=500000)
plt.hist(2*data + 1, 1000);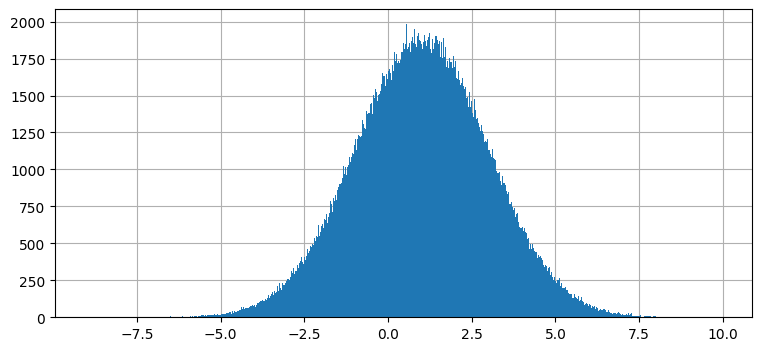

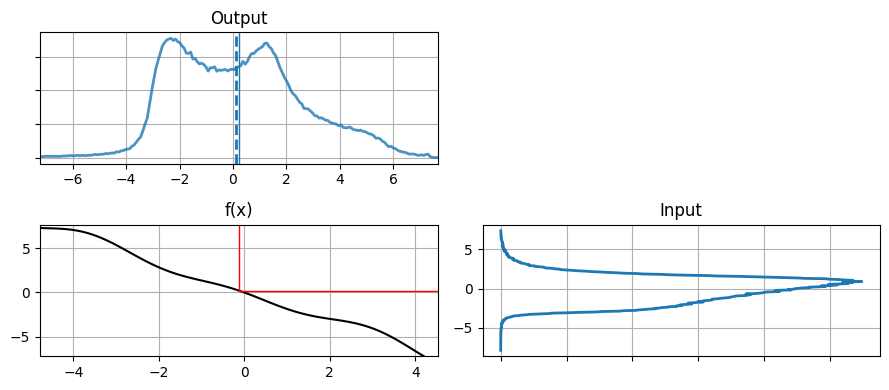
これは驚くような結果ではない。ガウス分布を \(f(x)=2x+1\) に通した結果は \(1\) を中心とする別のガウス分布である。入力、非線形関数、出力を一度に見てみよう:

In [5]

from kf_book.nonlinear_plots import plot_nonlinear_func

def g1(x):
    return 2*x+1

plot_nonlinear_func(data, g1)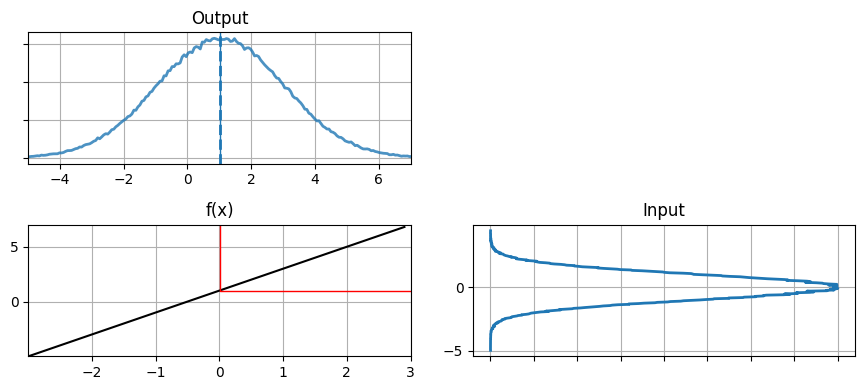

補遺 C にこういったグラフのプロット方法などを説明してある。

"Input" とラベルが付いているのがオリジナルのデータを表すヒストグラムである。このデータが左下のグラフに示された関数 \(f(x)=2x+1\) に入力される。赤い線は \(x=0\) という一つの値が \(f(x)\) によってどの値に移るかを示す。これと同じ処理を右下のヒストグラムにプロットされた全ての点に対して行ったのが左上の "Output" とラベルの付いたヒストグラムである。左上のヒストグラムの平均が計算された点の平均として計算され、青い破線で示されている。加えて平均 \(x=0\) の変換先を表す青い実線も引かれている。

出力はガウス分布らしい見た目をしており、実際ガウス分布だと示せる。出力の分散が入力の分散より大きく、平均が \(0\) から \(1\) に移動したのが分かる。これはデータを移す関数 \(f(x)=2x+1\) を考えれば納得できる: \(2x\) が分散を大きくし、\(+1\) が平均をスライドさせる。計算された平均 (青い破線) は実際の平均とほぼ同じになっており、サンプルを多くすれば実際の平均にいくらでも近づけることができる。

次は非線形関数を使ったときに確率分布がどう変化するかを確認しよう:

In [6]

def g2(x):
    return (np.cos(3*(x/2 + 0.7))) * np.sin(0.3*x) - 1.6*x

plot_nonlinear_func(data, g2)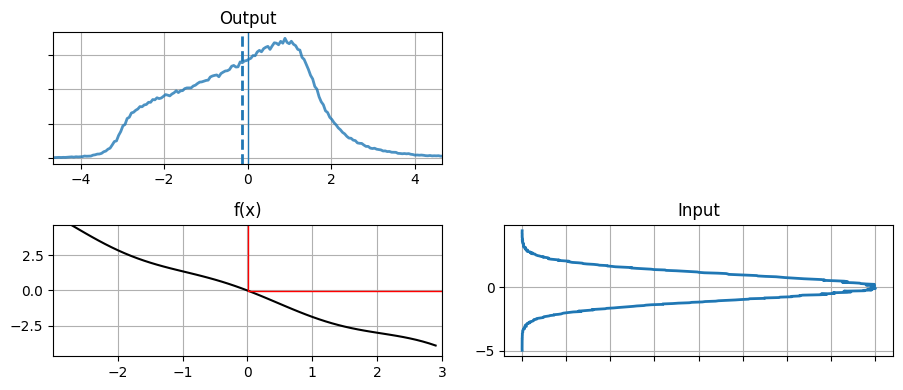

この結果を見て驚くかもしれない。関数 g2 のグラフはかなり線形に見えるにもかかわらず、出力される確率分布はガウス分布とは大きく異なっている。二つの単変量ガウス分布の確率密度関数を乗じるときは次の式を使った:

\[ \begin{aligned} \mu &=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2} \\ \sigma &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \end{aligned} \]

この式はガウス分布以外の分布では成り立たない。もちろん上の "Output" にある確率分布でも成り立たない。

同じデータは散布図としてもプロットできる:

In [7]

N = 30000
plt.subplot(121)
plt.scatter(data[:N], range(N), alpha=.1, s=1.5)
plt.title('Input')
plt.subplot(122)
plt.title('Output')
plt.scatter(g2(data[:N]), range(N), alpha=.1, s=1.5);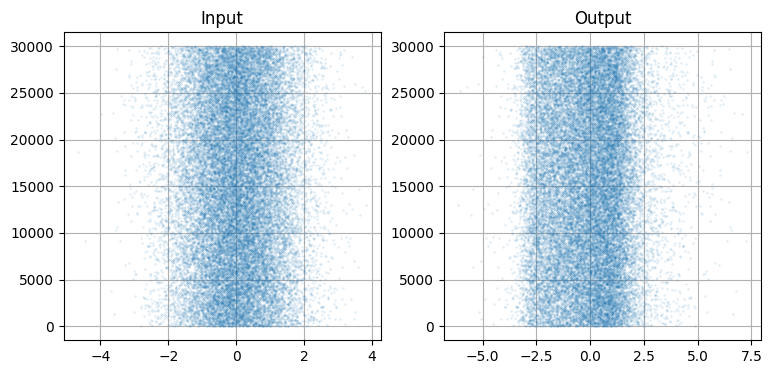

左に示した元のデータは明らかにガウス分布のような見た目をしているのに対して、それを g2(x) を通した右のデータはそうなっていない。\(-3\) のあたりに壁があり、それより左にはほとんどデータが存在していない。右のグラフを一つ前の "Output" のグラフと比べれば、PDF の形が g(data) の散らばり具合いと一致することが分かるだろう。

前章までに考えたカルマンフィルタのアルゴリズムにおいてこの現象が何を意味するかを考えてみてほしい。カルマンフィルタのアルゴリズムはプロセス関数を通過したガウス分布がガウス分布のままであることを仮定していた。この仮定が成り立たないと、カルマンフィルタが保証する性質はどれも成り立たない。g2 の出力をもう一度 g2 に通して、カルマンフィルタの次のタイムステップで行われる計算をシミュレートしてみよう:

In [8]

y = g2(data)
plot_nonlinear_func(y, g2)

グラフから分かるように、確率分布は最初のガウス分布からさらに離れる。ただグラフは \(x=0\) に関して対称であるように見える。平均と分散を計算してみよう:

In [9]

print('入力の平均と分散: %.4f, %.4f' % (np.mean(data), np.var(data)))
print('出力の平均と分散: %.4f, %.4f' % (np.mean(y), np.var(y)))

Out [9]

入力の平均と分散:  0.0021, 1.0008
出力の平均と分散: -0.1282, 2.4064

非線形関数 g2 による変換結果を g2 に似た線形関数による変換結果と比べてみよう。g2 に似た線形関数として \((-2,3)\) と \((2,-3)\) を通る直線を表す関数を採用する。この直線の傾きは次のように求められる:

\[ \text{傾き}=\frac{-3-3}{2-(-2)}=-1.5 \]

よって:

In [10]

def g3(x):
    return -1.5 * x

plot_nonlinear_func(data, g3)
out = g3(data)
print('出力の平均と分散: %.4f, %.4f' % (np.mean(out), np.var(out)))

Out [10]

出力の平均と分散: -0.0032, 2.2518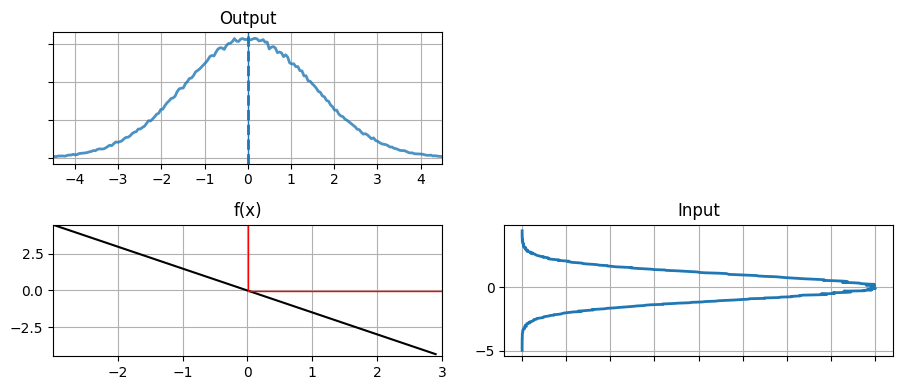

出力の形は大きく異なるにもかかわらず、平均と分散はほぼ同じ値となった。ここから非線形な関数が "ほぼ" 線形なら問題を無視しても構わないのではないかというアイデアが生まれる。これが正しいかどうかを確認するために、何度か反復した結果を確認してみよう:

In [11]

out = g3(data)
out2 = g2(data)

for i in range(10):
    out = g3(out)
    out2 = g2(out2)
print('線形    出力の平均と分散: %.4f, %.4f' %
      (np.average(out), np.std(out)**2))
print('非線形  出力の平均と分散: %.4f, %.4f' %
      (np.average(out2), np.std(out2)**2))

Out [11]

線形    出力の平均と分散: -0.1820, 7487.9650
非線形  出力の平均と分散: -9.5179, 30515.4481

残念ながら非線形関数 g2 を何度も適用すると結果が大きくずれてしまう。平均は \(0\) から大きく離れ、分散は線形関数を使った場合の四倍近くになっている。

これまでに使った非線形関数は直線に非常に近く、問題は最小化されていた。\(y(x)=-x^2\) のような直線とかけ離れた関数を使ったらどうなるだろうか？

In [12]

def g3(x):
    return -x*x

data = normal(loc=1, scale=1, size=500000)
plot_nonlinear_func(data, g3)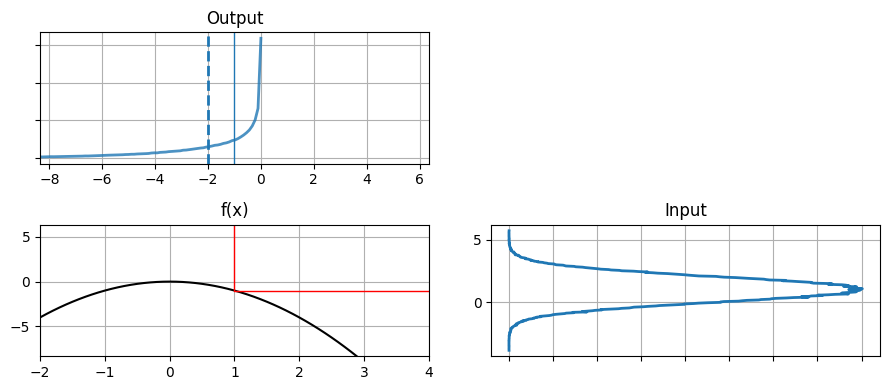

y=x^2 による変換 — Out [12]\(y(x)=-x^2\) による変換

曲線 \(y(x) = -x^2\) は滑らかであり、特に \(x=1\) の近くでは直線に近いと言える。しかし出力は決してガウス分布に見えず、出力の平均は平均の出力と一致していない。この関数が特別なわけではない──ボールを放れば放物線になるので、これはフィルタで扱える必要のある種類の非線形性である。前章で行ったボールの追跡を思い出せば、あの追跡は大きな失敗だった。このグラフを見れば、フィルタの性能があれほど落ちた理由が納得できるだろう。

9.4 二次元の例

確率分布を見てフィルタで何が起こるかを考えるのは難易度が高い。そこでレーダーで航空機を追跡する問題を考えよう。推定値は次のような位置と共分散行列を持つかもしれない:

In [13]

import kf_book.nonlinear_internal as nonlinear_internal

nonlinear_internal.plot1()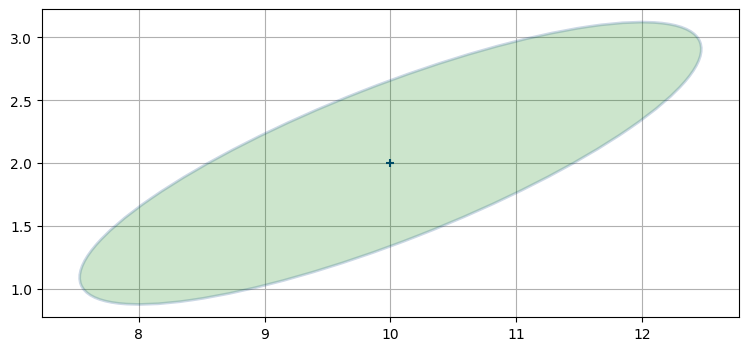

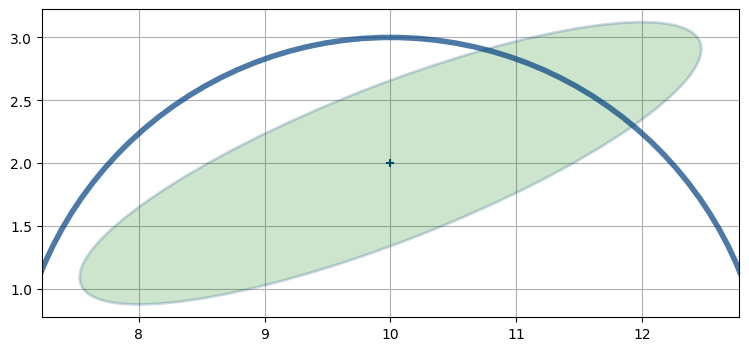
レーダーは航空機との距離を観測すると仮定する。レーダーが航空機の真下 \((10, 0)\) にあって、次の観測値が「三マイル」だとしたら、その観測値に合う位置は半径三マイルの円となる:

In [14]

nonlinear_internal.plot2()

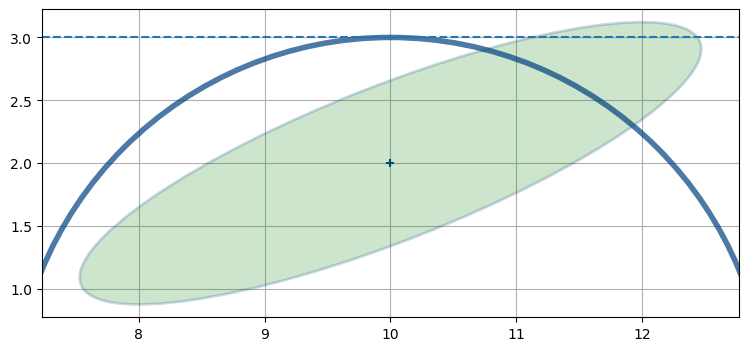
このとき航空機の位置を推定したい。この問題はどうすれば線形化できるだろうか？グラフから考えると、航空機の位置として可能性が高いのは \((11.4,2.7)\) の近くだと分かる。この点で共分散楕円と観測値を表す円が交わるためだ。しかし距離の観測値は非線形だから、線形化しなければならない。まだ説明はしていないものの、拡張カルマンフィルタは一つ前の時刻における航空機の位置 \((10,2)\) で観測値の線形化を行う。\(x=10\) のとき距離の観測値からは \(y=3\) が分かるので、そこで線形化を行う:

In [15]

nonlinear_internal.plot3()

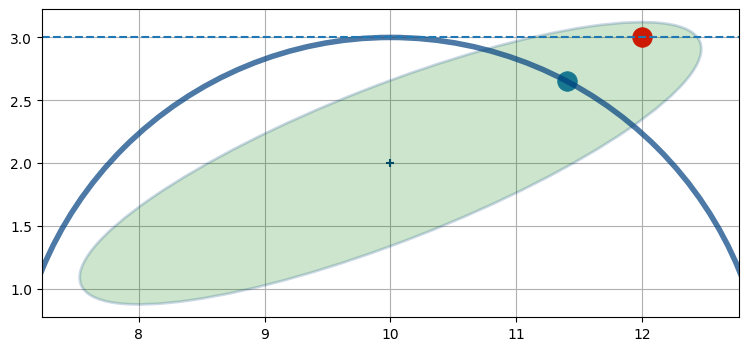
これで問題の線形な表現 (水平な直線を使った表現) が得られた。これなら解くことができる。しかし残念ながら、この直線と共分散楕円の交点 (赤点) は実際の航空機の位置 (青点) から離れている:

In [16]

nonlinear_internal.plot4()

こういった種類の誤差が悲惨な結果を招くことはよくある。この例で推定値の誤差は現時点でさえ大きいものの、次の発展でフィルタは非常に悪い推定値を使ってレーダーからの観測値を線形化するので、次の推定値はさらに悪くなることが予想される。これを数回も反復すればカルマンフィルタは発散し、現実と全く対応の取れない結果を生成するようになってしまう。

ここで考えた共分散楕円は数マイルの大きさを持つ。大きな非線形性を持つ系の難しさを強調するために私は誇張したサイズを使った。実際のレーダー追跡問題では非線形性がそこまで悪いことは少ない。ただし、それでも誤差は積もっていくし、この例と同程度の非線形性を持つ系に取り組むことになるかもしれない──誇張したのは説明のためだけではない。非線形な系の問題を考えるときは、常に発散と格闘することになる。

9.5 アルゴリズム

特定の問題を早く解きたいと思っていて、どのフィルタを使うべきか悩んでいる読者もいるかもしれない。次章以降の章はある程度独立しているので、飛ばして読んでも大きな問題はない。ただ全ての事項をきちんと習得したいなら順番通りに読むのを勧める。

非線形フィルタにおける馬車馬は線形化カルマンフィルタ (linearized Kalman filter) と拡張カルマンフィルタ (extended Kalman filter, EKF) である。この二つの手法はカルマン博士がカルマンフィルタの論文を発表した後すぐに考案されており、それから非線形な問題に対する主な手法として使われてきた。航空機に搭載されるフライトソフトウェアや車・携帯に搭載される GPS ではまず間違いなくどちらかの手法が使われている。

しかし、この二つの手法は要求するものが非常に大きい。EKF は微分方程式を一点で線形化するので、微分係数からなる行列 (ヤコビ行列) を求めなければならない。解析的にこれを行うのは困難あるいは不可能になることもある。仮に可能だったとしてもヤコビ行列を求めるには数値的手法が必須であり、これは計算量が大きい上に系に誤差が加わる。最後に、問題の非線形性が大きいと線形化によって各ステップで大きな誤差が生まれるので、フィルタが頻繁に発散する。式を適当なソルバに突っ込めば優れた結果が得られると期待することはできない。非線形フィルタリングはプロにとっても難しい領域である。また EKF は現実世界の応用で最もよく使われる手法であるにもかかわらず、多くのカルマンフィルタの教科書は EKF にほんの少ししか触れないことも記しておく。

近年、非線形フィルタリングは面白い方向へ進化している。まず、コンピューターの性能が向上したために以前はスーパーコンピューターでさえ手に負えなかった手法が可能になった。この手法はモンテカルロ法 (Monte Carlo method) と呼ばれる──コンピューターで数千から数万のランダムな点 (粒子) を生成し、それら全てに対して観測値とマッチするかどうかをテストする。そしてテスト結果に応じて確率的に粒子を捨てるか分裂させるかするという手法である。観測値から離れた粒子が保持される可能性は低く、観測値に近い粒子は高い確率で保持される。これを何度か繰り返すと考えている物体を追跡する粒子の密な集まりが得られ、物体の存在しない場所には粒子の薄い集まりが残る。モンテカルロ法を使うこのフィルタを粒子フィルタ (particle filter) と呼ぶ。

粒子フィルタには二つの利点がある。第一に、このアルゴリズムはロバストであり、極端な非線形性を持つ問題に対してさえ動作する。第二に、このアルゴリズムは任意の個数のオブジェクトを一度に追跡できる──例えば一部の粒子がある物体とマッチし、別の粒子がそれとは別の物体にマッチしても問題はない。そのため粒子フィルタは往来する車や人を追跡するのによく使われる。

粒子フィルタのコストは明らかなはずだ。フィルタの各ステップで数千あるいは数万の点をテストするのは計算量的に大きなコストである。ただ現代の CPU は非常に高速であり、またモンテカルロ法のアルゴリズムは一部が並列化可能なので GPU と相性が良い。モンテカルロ法の解答が数学的でないというのもコストになる。カルマンフィルタでは共分散行列が推定値に含まれる誤差の量について重要な情報を持っていたのに対して、粒子フィルタでは推定値の誤差を計算する厳密な方法が存在しない。最後に、粒子フィルタの出力は粒子の集まりとなる: その解釈は自分で行わなければならない。普通は平均と標準偏差などを計算すればいいのだが、これは難しい問題になる。追跡している物体に「属さない」点が多くあるので、物体を追跡していると思われる点の集合をクラスタリングアルゴリズムなどで最初に計算し、さらにその集合から別のアルゴリズムを使って状態の推定値を取り出さなければならない。手に負えないほどではないものの、こういった処理は計算量的なコストが非常に大きい。

最後に、無香料カルマンフィルタ (unscented Kalman filter, UKF) と呼ばれる新しいアルゴリズムがある。UKF では非線形な式の解析解を求める必要がないにもかかわらず、ほとんどの場合で EKF を上回る性能が得られる。EKF が非常に苦手とするタイプの非線形な問題も UKF は問題なく扱える。さらに UKF は非常に簡単に設計できる。UKF の評価はまだ定まっていないと言う人もいるが、UKF はほぼ全ての点で EKF に勝っているように私には思える。どんな問題であれフィルタを実装するなら UKF を最初に試すべきだと私は言いたい。あなたが制御理論で修士号を取ったカルマンフィルタのプロでないならなおさらである。UKF の主な欠点は EKF より数倍遅くなる場合があるというものだ。しかしそれは EKF がヤコビ行列を解析的に求めるか数値的に求めるかに依存する。もし EKF が数値的にヤコビ行列を求めるなら、まず間違いなく UKF の方が高速になる。UKF が必ず EKF より正確な結果を出力することは証明されていない (おそらく証明はできないだろう)。ただ実際に使うと、ほとんど常に UKF は EKF より正確な結果を生成し、はるかに正確であることも多い。UKF は理解・実装が簡単なので、このフィルタを最初に試すのを強く勧める。

9.6 まとめ

世界は非線形であるにもかかわらず、私たちは線形の問題しか完全に解くことができない。このためカルマンフィルタは大きな困難に直面する。本章では非線形性がフィルタリングに与える影響を三つの異なる (しかし等価な) 方法で確認して、非線形フィルタリングの主要な手法を簡単に説明した: 線形化カルマンフィルタ、拡張カルマンフィルタ、無香料カルマンフィルタ、粒子フィルタである。

最近まで線形化カルマンフィルタと EKF が非線形な問題を扱う標準的な方法だった。この二つは理解して使うのが非常に難しく、実装が非常に不安定になる可能性もある。

近年の研究の進展により、(私が思うに) これらより優れた手法が考案された。UKF は偏微分方程式の解を求める必要がなく、それでいて普通は EKF より正確になる。さらに理解するのも使うのも簡単であり、私なら FilterPy を使えば基本的な UKF を数分で実行できる。粒子フィルタは数学的モデル化を完全に取り去り、代わりに数千個の点からなる雲を生成するモンテカルロ法を使用する。実行は遅いものの、これ以外の方法では手に負えない問題を比較的簡単に解くことができる。

私が受け取るメールは EKF に関するものが最も多い。これは書籍や論文、インターネット上の資料のほとんどが EKF を使っているためだと思う。フィルタリングの分野を習得するのが目的なら当然 EKF について学ばなければならない。しかし、もし優れた結果を得ようとしているだけなら、UKF と粒子フィルタを先に試すことを勧める。この二つの手法の方が理解するのも、実装するのも、利用するのも格段に簡単であり、さらに EKF よりずっと安定することが多い。

このアドバイスに文句を言いたくなる人もいるだろう。最近の文献の中には特定の問題に対して EKF と UKF あるいは他の手法を比較したものが数多く存在する。そういった比較を行うべきでは？もしあなたがロケットを火星に飛ばそうとしているなら、もちろん比較をしなければならない。そして正確性、切り捨て誤差、発散、正しさの数学的な証明の有無、そして必要となる計算量のバランスを取ることになるだろう。そういった問題に取り組む人が EKF を深く理解していないなどあり得ない。

一方で UKF はとてつもなく良く動作する！私は仕事で取り組む現実の問題で UKF を使っている。UKF で十分なことが検証できるので、そういった問題の多くでは EKF を実装しようともしない。EKF を使えば 0.2% の改善が得られる状況もあるのではないかって？もちろんあるだろう！では私はそれを気にするか？いや気にしない！私は UKF の実装を完全に理解しているし、動作は簡単にテスト・検証できる。他の人にコードを渡したとしても、渡された人はすぐに実装を理解して改変できると自信を持って言える。それに、私は正しく動作する解法を既に持っているときでも難しい数式と格闘せずにはいられないマゾヒストではない。何らかの問題に対して UKF と粒子フィルタの性能が悪ければ他の手法を試すかもしれないが、それも性能が悪いことを確認してからの話だ。さらに、広い範囲の問題と条件において UKF が EKF より格段に高い性能を達成するのが現実である。もし「とてもよい」が十分優れているなら、私は他の問題に取り組むのに時間を使いたい。

この点を長々と語っているのは、ほとんどの教科書が EKF を主役にしているからだ。UKF は全く説明されないか二ページ程度で簡単に説明されるだけであり、それだけではフィルタを使う準備は全く整わない。UKF は比較的まだ新しく、そして書籍の新版が出るのには時間がかかる。多くの本が書かれたころ、UKF はまだ存在していないか、性能の評価が定まっていない (しかし興味深い) 新手法に過ぎなかった。しかし本書が執筆されるまでの間に UKF は圧倒的な成功を収めたので、あなたの道具箱に入れておく必要がある。これ以降の本書は UKF の説明が多くの部分を占める。

Dan Simon, Optimal State Estimation, John Wiley & Sons, 2006.^[return]

第 9 章 非線形フィルタリング