第 5 章多変量ガウス分布

前章で説明した手法は非常に強力であるものの、一つの変数 (次元) にしか適用できず、広場を動き回る犬の位置と速度といった多次元のデータを表現する方法は提供されない。位置と速度は互いに影響する関係にあるので、g-h フィルタの章で学んだようにこの情報は絶対に捨ててはいけない。本章ではこの関係を確率的に記述する方法を学ぶ。この重要な洞察があるとフィルタの性能が大きく向上する。

5.1 多変量正規分布

ここまでは確率密度関数が \(\mathcal{N}(\mu, \sigma^2)\) と表される単一の確率変数に対するガウス分布を使ってきた。この分布を正式な用語で単変量正規分布 (univariate normal distribution) と呼ぶ。「単変量」とは変数が一つあることを意味する。

では 多変量正規分布 (multivariate normal distribution) はどんなものになるだろうか？「多変量」とは複数の変数が存在することを意味する。ここでの目標は複数の次元を持った正規分布を表現することである。次元といっても空間的な次元であるとは限らない: 例えば三次元座標 \((x,\ y,\ z)\) で表される航空機の位置・速度・加速度の追跡は九次元の問題である。二次元のケースを考えよう。二次元の正規分布が表すのはロボットの \(x\) 座標と \(y\) 座標かもしれないし、\(x\) 軸上を動く犬の位置と加速度かもしれないし、牛乳の生産量と乳牛にやる餌の量かもしれない。何を考えても構わない。少し考えれば分かるように、\(N\) 次元の正規分布には \(N\) 個の平均が必要になる。この \(N\) 個の平均は列行列 (列ベクトル) として次のように表す:

\[ \mu = \begin{bmatrix}\mu_1\\\mu_2\\ \vdots \\\mu_n\end{bmatrix} \]

例えば私たちが \(x = 2\) および \(y = 17\) を信じているとすれば、私たちの信念を表す二次元正規分布で次が成り立つ:

\[ \mu = \begin{bmatrix}2\\17\end{bmatrix} \]

続いて分散の表現が必要である。一見すると、平均と同じく \(N\) 次元の正規分布には \(N\) 個の分散が必要だと思うかもしれない。つまり \(x\) と \(y\) の分散がそれぞれ \(10\) と \(4\) のとき、次のように分散を表すということだ:

\[ \sigma^2 = \begin{bmatrix}10\\4\end{bmatrix} \]

しかし、この方法はより一般的な場合を考えていないために不完全である。確率・ガウス分布・ベイズの定理の章では学生の身長の分散を計算した。これは学生の身長が互いにどれくらいに離れているかを表す指標であり、全員の身長が同じなら \(0\) に、身長が大きくバラついているなら大きな値になる。

ただ身長と体重の間にも関係性は存在する。一般に、背の高い学生は背の低い学生より重い傾向がある。このような状況を指して「身長と体重には相関 (correlation) がある」と言う。多変量正規分布の分散は身長と体重の散らばり度合いを表現できるだけではなく、身長と体重の相関の度合いも表現できるのが望ましい。つまり、私たちは身長が変化したときに体重がどれくらい変化するかを表現したい。この指標は共分散 (covariance) と呼ばれる。

多変量正規分布を理解する前に、まず相関と共分散の裏にある数学を理解する必要がある。

5.2 相関と共分散

共分散 (covariance) の値は二つの変数がどれくらい同時に変動するかを表す。言い換えると、分散は考えている集団の中で値がどれくらい変動するかを表す指標であったのに対して、共分散は変数が二つあるときにそれぞれがもう一方の変動に応じてどれくらい変動するかを表す指標である。

例えば身長が高くなると一般に体重も増えるから、二つの変数は相関する。身長と体重のように一つの変数が大きくなるともう一方も大きくなる関係があるとき、二つの変数に正の相関 (positive correlation) があると言う。また戸外の気温が低くなると暖房費は高くなる。このように一つの変数が大きくなるともう一方は小さくなる関係があるとき、二つの変数に逆の相関 (inverse correlation) あるいは負の相関 (negative correlation) があると言う。紅茶の値段と私の犬がしっぽを振る回数は関係がない。このようなとき二つの変数は無相関 (uncorrelated) である、あるいは独立 (independent) であると言う。

相関があると予測が可能になる。あなたが私よりずっと背が高いなら体重も私より重いだろうし、冬が近づけば暖房費は増えるだろう。一方で私の犬がしっぽをいつもより多く振っていたとしても、紅茶の値段が変わっているかどうかは分からない。

例として、とある学校の陸上チームの身長と体重を考えよう (下図)。データの近くを通るように引かれた直線によると、学生の身長が (例えば) 68 インチなら体重は大体 160 ポンドだろうと予測できる。相関関係は完璧ではないから、この予測も同様に完璧ではない。

In [3]

from kf_book.gaussian_internal import plot_correlated_data

height = [60, 62, 63, 65, 65.1, 68, 69, 70, 72, 74]
weight = [95, 120, 127, 119, 151, 143, 173, 171, 180, 210]
plot_correlated_data(height, weight, 'Height (in)', 'Weight (lbs)', False)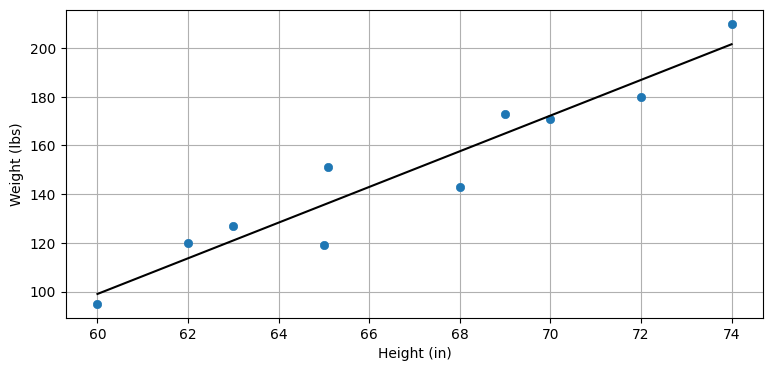

本書では線形の相関だけを考え、変数の間の関係は線形だとする。つまりデータが直線に上手くフィットすることを仮定する。上のグラフではデータに対して直線をフィットさせている。非線形相関 (nonlinear correlation) という概念も存在するが、本書では使わない。

\(X\) と \(Y\) の間の共分散は次の式で定義される:

\[ COV(X, Y) = \sigma_{xy} = \mathbb E\big[(X-\mu_x)(Y-\mu_y)\big] \]

ここで \(\mathbb E[X]\) は \(X\) の期待値であり、次のように定義される:

\[ \mathbb E[X] = \begin{cases} \displaystyle \sum_{i=1}^n p_ix_i & \text{(離散分布)}\\[15pt] \displaystyle \int_{-\infty}^\infty f(x)\, x & \text{(連続分布)}\end{cases} \]

これから考える離散確率で全てのデータが平等に確からしいと仮定すれば、各データの確率は \(\frac{1}{N}\) となる。このとき次の関係が成り立つ:

\[ \mathbb E[X] = \frac{1}{N}\sum_{i=1}^n x_i \]

共分散の定義を分散の定義と比べると、よく似ていることが分かる:

\[ \begin{aligned}VAR(X) = \sigma_x^2 &= \mathbb E[(X - \mu)^2]\\ COV(X, Y) = \sigma_{xy} &= \mathbb E\big[(X-\mu_x)(Y-\mu_y)\big]\end{aligned} \]

特に、\(COV(X, X)\) は \(VAR(X)\) に等しくなる。分散は考えている集団の中で値がどれくらい変動するかの指標であると言ったが、この関係からもそれが分かる。

多変量正規分布の分散と共分散は共分散行列 (covariance matrix) で表される。共分散行列は次の形している:

\[ \Sigma = \begin{bmatrix} \sigma_1^2 & \sigma_{12} & \cdots & \sigma_{1n} \\ \sigma_{21} &\sigma_2^2 & \cdots & \sigma_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_n^2 \end{bmatrix} \]

対角要素に各変数の分散が収まり、非対角要素 \(\sigma_{ij}\ (i \neq j)\) に \(i\) 番目の変数と \(j\) 番目の変数の共分散が収まる。例えば \(\sigma_3^2\) は三番目の変数の分散、\(\sigma_{13}\) は一番目の変数と三番目の変数の共分散となる。

共分散が \(0\) なら、それは相関がないことを意味する。もし \(x\) と \(y\) の分散それぞれ \(10\) と \(4\) で、\(x\) と \(y\) に相関がないなら、共分散行列はこう書ける:

\[ \Sigma = \begin{bmatrix}10&0\\0&4\end{bmatrix} \]

もし \(x\) と \(y\) に小さな正の相関があるなら、共分散行列は次のような値になる:

\[ \Sigma = \begin{bmatrix}10&1.2\\1.2&4\end{bmatrix} \]

ここで \(1.2\) が \(x\) と \(y\) の共分散である。相関が「小さい」と言ったのは、共分散 \(1.2\) が分散 \(10\) や \(4\) に比べると小さいためだ。

\(x\) と \(y\) に強い負の相関があるなら、次の共分散行列となるかもしれない:

\[ \Sigma = \begin{bmatrix}10&-9.7\\-9.7&4\end{bmatrix} \]

共分散行列は対称である。\(x\) と \(y\) の共分散が \(y\) と \(x\) の共分散に等しい、つまり \(\sigma_{xy}=\sigma_{yx}\) が任意の \(x\) と \(y\) に対して成り立つためだ。

あなたが説明に付いて来れているかが心配なので、一つ例を考えてみよう。確率・ガウス分布・ベイズの定理の章で学生の身長が \(H=[1.8,\ 2.0,\ 1.7,\ 1.9,\ 1.6]\) となるクラスを考えた。このとき分散は次のように計算できる:

\[ \begin{aligned} \mathit{VAR}(H) &= E[(H - \mu_H)^2] \\ &= \frac{1}{N}\sum_{i=1}^n (H_i - \mu_H)^2 \\ &= \frac{1}{5} [(1.8-1.8)^2 + (2-1.8)^2 \\ & \qquad \qquad + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2] \\ &= 0.02 \end{aligned} \]

簡単だ。同じ学生の体重を量ったところ \(W = [70.1,\ 91.2,\ 59.5,\ 93.2,\ 53.5]\) になったとしよう。共分散行列を作るのに必要な要素を計算できるだろうか？もちろんできる。求めたい共分散行列は

\[ \Sigma = \begin{bmatrix}\sigma_H^2 & \sigma_{H,W} \\ \sigma_{W,H} & \sigma_{W}^2\end{bmatrix} \]

である。左上にある身長の分散 \(\sigma_H^{2}\) はちょうど先ほど計算した。右下の \(\sigma_W^2\) は重みの分散だから、同じ式で計算できる:

\[ \begin{aligned} \mu_W &= \frac{1}{5}(70.1 + 91.2 + 59.5 + 93.2 + 53.5) = 73.5 \\ \sigma_W^2 &= \frac{1}{5} [(70.1-73.5)^2 + (91.2-73.5)^2 \\ &\qquad\qquad + (59.5-73.5)^2 + (93.2-73.5)^2 + (53.5-73.5)^2 ] \\ &= 261.8 \end{aligned} \]

次は共分散だ。上述の定義を使って計算する:

\[ \begin{aligned} \sigma_{H,W} &= \mathbb E\big[(H-\mu_H)(W-\mu_W)\big] \\ &= \frac{1}{N}\sum_{i=1}^n (H_i-\mu_H)(W_i-\mu_W) \\ &= \frac{1}{5}[(1.8-1.8)(70.1-73.5) + (2-1.8)(91.2-73.5) \\ &\qquad\qquad + (1.7-1.8)(59.5-73.5) + (1.9-1.8)(93.2-73.5) \\ &\qquad\qquad + (1.6-1.8)(53.5-73.5)] \\ &= 2.18 \end{aligned} \]

計算は面倒だが、難しくはない。今後このように手で共分散行列を計算することはない。なぜなら、もちろん、NumPy が計算してくれるからだ:

In [4]

import numpy as np

W = [70.1, 91.2, 59.5, 93.2, 53.5]
H = [1.8, 2.0, 1.7, 1.9, 1.6]
np.cov(H, W)

Out [4]

array([[  0.025,   2.727],
       [  2.727, 327.235]])

おっと計算が合っていない！どこかで間違えたのだろうか？実は NumPy はサンプルサイズが小さいときのための修正を自動的に行っている: デフォルトの設定だと、NumPy では正規化項として \(\frac{1}{N}\) ではなく \(\frac{1}{N-1}\) を利用する。

この修正が必要な理由は本書の範囲を超えるが、簡単に説明しておこう。クラスに大勢の学生がいて、全員の体重は測れないためにサンプルとして 5 人を選んで体重を測ったとする。このとき、証明はしないが、平均との差の二乗和を \(N=5\) で割って求める分散だと期待値がクラス全員の分散と一致せず、\(N-1=4\) で割る分散だと期待値がクラス全員の分散と一致することが示せる。通常プログラムが扱うのは大きな集合から取ったデータサンプルだから、NumPy ではデフォルトで \(N-1\) で割る方の分散が使われる。\(N\) で割る分散は np.cov にキーワード引数 bias=1 を渡すと計算できる:

In [5]

np.cov(H, W, bias=1)

Out [5]

array([[  0.02 ,   2.182],
       [  2.182, 261.788]])

こうすると手計算と一致する。なお、私たちが考える確率変数は無限の要素を持つ集合 (例えば追跡する物体の可能な位置の集合) から値を取得するので、これから本書では bias=1 を使わない。今の例では考えている集合全体に関する分散と共分散を計算しているので、bias=1 とするのが正しい。

計算された共分散行列から何が分かるだろうか？まず身長の分散が \(0.02~\text{m²}\) で体重の分散が \(261.788~\text{kg²}\) だと分かる。さらに体重と身長に正の相関があることも読み取れる──身長が伸びると体重も増えるようだ。

完璧に相関するデータを作ってみよう。「完璧に相関する」とは完全に直線に乗ることを意味する──直線から離れることはない:

In [6]

X = np.linspace(1, 10, 100)
Y = np.linspace(1, 10, 100)
np.cov(X, Y)

Out [6]

array([[6.956, 6.956],
       [6.956, 6.956]])

共分散行列からは、共分散が X と Y の分散に等しいことが分かる。

続いて片方の変数にノイズを加えて完璧には相関しないようにしてみよう。加えて負の相関の例を示すために Y の符号を反転させる:

In [7]

X = np.linspace(1, 10, 100)
Y = -(np.linspace(1, 5, 100) + np.sin(X)*.2)
plot_correlated_data(X, Y)
print(np.cov(X, Y))

Out [7]

[[ 6.956 -3.084]
 [-3.084  1.387]]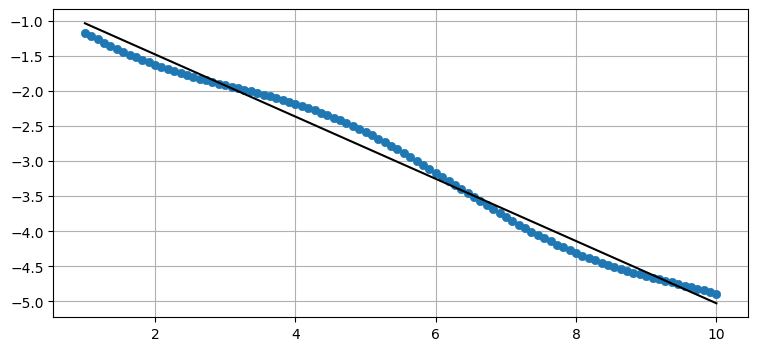

データ (青丸) は直線にならない。ただ共分散 \(\sigma_{xy}=-3.08\) は \(\sigma_x^2\) や \(\sigma_y^2\) と比べて絶対値が同程度なので、高い相関があると分かる。これはグラフを見ても分かる: データは直線に非常に近い。

次は直線に大きなノイズを加えてみよう:

In [8]

from numpy.random import randn
X = np.linspace(1, 10, 1000) + randn(1000)*2
Y = np.linspace(1, 5, 1000) + randn(1000)
plot_correlated_data(X, Y)
print(np.cov(X, Y))

Out [8]

[[10.527  2.929]
 [ 2.929  2.362]]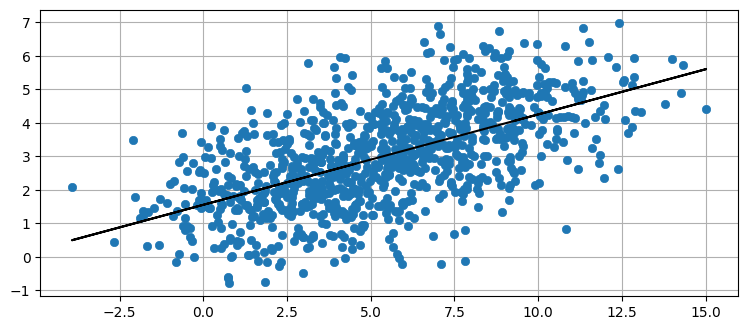

\(X\) と \(Y\) の相関が弱くなったために、共分散が分散と比較して小さくなったのが分かる。データにフィットする直線は引けるものの、データの変動はずっと大きくなった。

最後に、完全にランダムなデータの共分散楕円を示す:

In [9]

X = randn(100000)
Y = randn(100000)
plot_correlated_data(X, Y)
print(np.cov(X, Y))

Out [9]

[[ 1.001 -0.005]
 [-0.005  0.997]]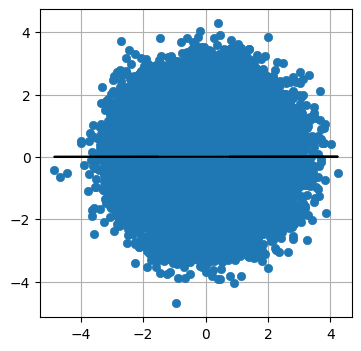

このとき共分散はほぼゼロになる。グラフから分かるように、データにきちんとフィットする直線を引くことはできない。グラフでは水平な線が引かれているが、垂直な線を引いたとしても説得力は (低いままで) 同じだろう。

5.3 多変量正規分布の定義

第 3 章で示した正規分布の定義を思い出そう:

\[ f(x, \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left [{-\frac{1}{2}}{(x-\mu)^2}/\sigma^2 \right ] \]

\(n\) 次元の多変量正規分布の定義を示す:

\[ f(\mathbf{x},\, \mu,\,\Sigma) = \frac{1}{\sqrt{(2\pi)^n|\Sigma|}}\, \exp \left[{ -\frac{1}{2}(\mathbf{x}-\mu)^\mathsf{T}\Sigma^{-1}(\mathbf{x}-\mu) }\right] \]

多変量のバージョンは単変量正規分布の定義に含まれるスカラーを行列で置き換えただけだ。線形代数をよく知っているなら、この定義は非常に扱いやすく思えるだろう。線形代数を知らなくても心配しないでほしい: 多変量正規分布を計算する関数は FilterPy と SciPy の両方から提供される。計算方法は気にしないで、値をプロットして形を確認してみよう:

In [10]

import kf_book.mkf_internal as mkf_internal

mean = [2., 17.]
cov = [[10., 0.],
       [0., 4.]]

mkf_internal.plot_3d_covariance(mean, cov)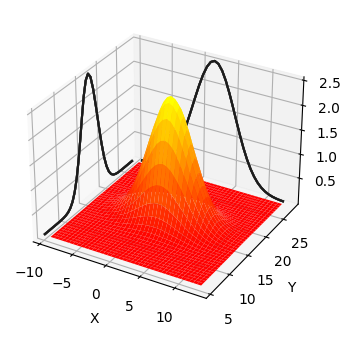

これは平均 \(\mu=\Big[\begin{smallmatrix}2\\17\end{smallmatrix}\Big]\) と共分散行列 \(\Sigma=\Big[\begin{smallmatrix}10&0\\0&4\end{smallmatrix}\Big]\) を持つ多変量正規分布のプロットである。三次元の形状が任意の \((X, Y)\) の組に対する確率密度を \(z\) 軸方向の高さとして表す。グラフの側面には \(X\) または \(Y\) だけを考えたときの確率分布が投影してあり、その曲線はガウス分布の釣鐘曲線になっているのが分かる。\(X\) だけを考えた曲線の幅が \(Y\) だけを考えた曲線より広いのは \(\sigma_x^2=10\) と \(\sigma_y^2=4\) によって説明できる。三次元曲面が最も高くなるのは \(X\) と \(Y\) が平均となる点である。

全ての多変量ガウス分布はこの形を持つ。犬の位置が多変量ガウス分布で表されるとすれば、それぞれの位置 \((X, Y)\) における \(z\) の値は犬がその位置にいる確率密度を表す。正確に言えばこのグラフが表すのは同時確率密度関数である。この言葉の意味はすぐに定義する。例えば犬は \((2,\ 17)\) の近くにいる確率が最も高く、\((5,\ 14)\) の近くにいる確率は中ぐらいで、\((10,\ 10)\) の近くにいる確率は非常に低い。単変量の場合と同じく、このグラフが表すのは確率密度であって確率ではない。連続分布には可能な値が無限に存在するので、犬がちょうど \((2,\ 17)\) (あるいは他の任意の一点) にいる確率は 0% となる。犬が特定の領域にいる確率は、その領域と曲面が囲む領域の体積を積分で計算することで求められる。

FilterPy は filterpy.stats モジュールの multivariate_gaussian 関数で多変量ガウス分布を実装し、SciPy は stats モジュールの multivariate_normal 関数で実装する。SciPy は平均と共分散行列を設定して "固まった" オブジェクトを最初に作り、そのオブジェクトを使って任意の位置に対する確率密度を何度も計算するという形式を取っている。SciPy の関数と混同しないよう FilterPy の関数には multivariate_gaussian という名前を付けてある。

分布の "固め方" やその他の便利な機能については scipy.stats モジュールのチュートリアル http://docs.scipy.org/doc/scipy/reference/tutorial/stats.html に説明がある。

In [11]

from filterpy.stats import gaussian, multivariate_gaussian

面白い話題に移る前に、まずはこの関数の使い方を示そう。

まず、私たちは犬が \((2,\ 7)\) にいると信じていて、\(x\) 軸方向および \(y\) 軸方向における信念の分散がそれぞれ \(8\), \(3\) だとする。このとき犬が \((2.5,\ 7.3)\) にいる確率密度はいくつだろうか？

まず x を \((2.5,\ 7.3)\) に設定する。タプル・リスト・NumPy 配列のどれを使っても構わない:

In [12]

x = [2.5, 7.3]

続いて私たちが持つ信念の平均を設定する:

In [13]

mu = [2.0, 7.0]

最後に共分散行列を定義しなければならない。問題の設定では \(x\) 座標と \(y\) 座標の相関関係について何も言及がないから、相関していないものとして話を進める。この仮定は自然である: 広場を動き回る犬は \(x\) 軸方向の移動量と \(y\) 軸方向の移動量を独立に選ぶことができ、両者は互いに影響しない。共分散行列は P で表す。カルマンフィルタは \(\textbf{P}\) で共分散行列を表すので、私たちもこの表記に慣れておく必要がある。

In [14]

P = [[8., 0.],
     [0., 3.]]

では関数を呼び出そう:

In [15]

%precision 4
multivariate_gaussian(x, mu, P)

Out [15]

0.0315

scipy.statis モジュールからも同じ結果が得られる:

In [16]

import scipy
from scipy.stats import multivariate_normal
print(f'{multivariate_normal(mu, P).pdf(x):.4f}')

Out [16]

0.0315

ここで用語をいくつか定義する。同時確率 (joint probability) \(P(x,y)\) とは \(x\) と \(y\) の両方が起きる確率を言う。例えば二つのサイコロを振るとき、\(P(2,5)\) は一つ目のサイコロの目が 2 で二つ目のサイコロの目が 5 となる確率を表す。サイコロが六面で公平だと仮定すれば、この確率は \(P(2,5) = \frac{1}{6}\times \frac{1}{6}=\frac{1}{36}\) と計算できる。上に示した 3D グラフは同時確率密度関数 (joint probability density function) を表す。

周辺確率 (marginal probability) とは他の事象を考えに入れずに計算した特定の事象が起こる確率を言う。上のグラフでは左側の壁に書かれているのが \(Y\) の周辺確率であり、これは犬の \(X\) 座標を無視したときに犬が \(Y\) の任意の位置にいる確率密度を表す。前に「グラフの側面には \(X\) または \(Y\) だけを考えたときの確率分布が投影してあり...」と書いたことからも分かるように、\(X\) と \(Y\) のそれぞれに周辺確率が存在する。ガウス分布が計算量的に有利なもう一つの理由が、多変量ガウス分布の周辺確率がガウス分布となることである！

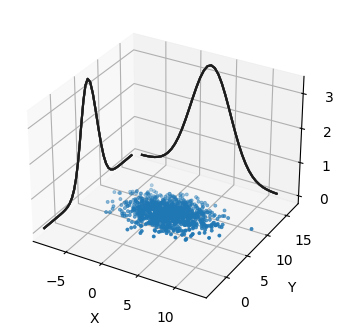
これを少し違う視点から見てみよう。確率分布を示す曲面をプロットするのではなく、\(\mu = [\begin{smallmatrix}2\\17\end{smallmatrix}]\), \(P=[\begin{smallmatrix}8&0\\0&3\end{smallmatrix}]\) の多変量ガウス分布から 1,000 個の点を生成してプロットする:

In [17]

mkf_internal.plot_3d_sampled_covariance(mu, P)

サンプルされた点は設定した平均と共分散行列における犬の位置として可能な値とみなせる。側面にある曲線は \(X\) および \(Y\) の周辺確率を表す。グラフで点が集まっている \((2,\ 7)\) の近くに真の値がある確率は、点がほとんどない \((-5,\ 10)\) の近くにいる確率よりずっと高い。

このプロットの見た目は美しいが、ここから有用な情報を引き出すのは難しい。例えば \(X\) と \(Y\) の分散が同じかどうか、あるいは \(X\) と \(Y\) に相関があるかどうかをこのプロットから判定するのは難しい。そのため本書では基本的に多変量ガウス分布を等高線のプロットで図示する。

ガウス分布の等高線をプロットしたときに表れるのは、特定の標準偏差を考えたときに多変量ガウス分布が取る値の領域である。これは 3D グラフを水平に切ったときの断面と言える。

標準偏差三つ分の高さで切ったスライスと共分散行列の関係を次に示す:

In [18]

mkf_internal.plot_3_covariances()

本書をオンラインあるいは Jupyter Notebook で読んでいる読者に向けて、分散を固定したまま共分散を変化させたときの等高線のアニメーションを次に示す:

こういった等高線のプロットは円や楕円に見える。実は、多変量ガウス分布の任意のスライスは楕円となることが示せる。そのため統計学ではこういった図を「ガウス分布の等高線のプロット」とは呼ばず、誤差楕円 (error ellipse)、信頼楕円 (confidence ellipse)、共分散楕円 (covariance ellipse) などと呼ぶ。どの用語も同じ意味である。

ここまでのコードは filterpy.stats モジュールの plot_covariance_ellipse 関数を使っている。この関数はデフォルトで標準偏差一つ分のスライスを示すが、キーワード引数 variance あるいは std を指定することで図を調整できる。例えば variance=3**2 または std=3 を指定すると標準偏差三つ分のスライスが表示され、variance=[1,4,9] または std=[1,2,3] と指定すると標準偏差一つ、二つ、三つ分のスライスが異なる色で表示される。この機能の使用例を示す:

In [19]

from filterpy.stats import plot_covariance_ellipse
import matplotlib.pyplot as plt

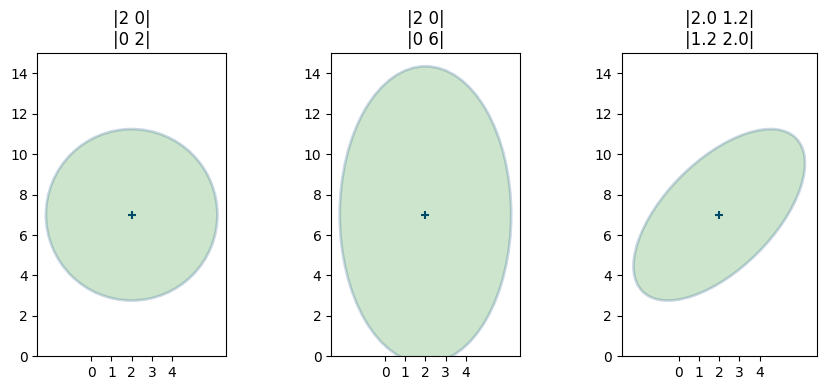
P = [[2, 0], [0, 6]]
plot_covariance_ellipse((2, 7), P, fc='g', alpha=0.2, std=[1, 2, 3],
                        title='|2 0|\n|0 6|')
plt.gca().grid(False);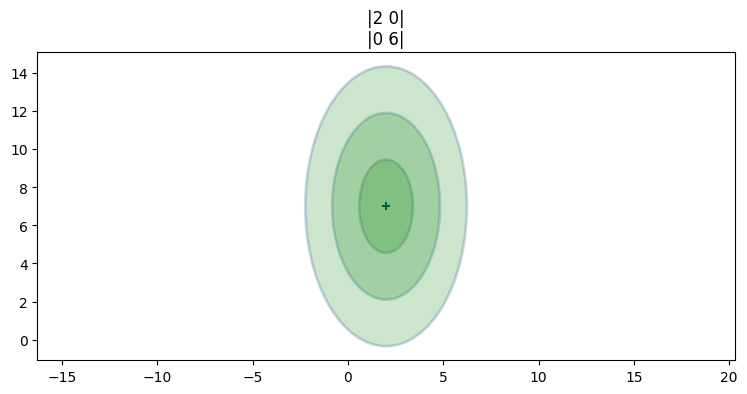

<code>plot_covariance_ellipse</code> にキーワード引数を渡す — Out [19]`plot_covariance_ellipse` にキーワード引数を渡す

単色で塗られている部分では確率密度が一定なのかと思ってしまうかもしれないが、それは正しくない。ガウス分布の 3D プロットを見れば確率密度が一定でないことが確認できる。共分散行列が \((\begin{smallmatrix}2&1.2\\1.2&1.3\end{smallmatrix})\) の多変量ガウス分布を陰影として二次元でプロットした図を次に示す。影が濃いほど確率密度が高い:

In [20]

from kf_book.nonlinear_plots import plot_cov_ellipse_colormap
plot_cov_ellipse_colormap(cov=[[2, 1.2], [1.2, 1.3]]);

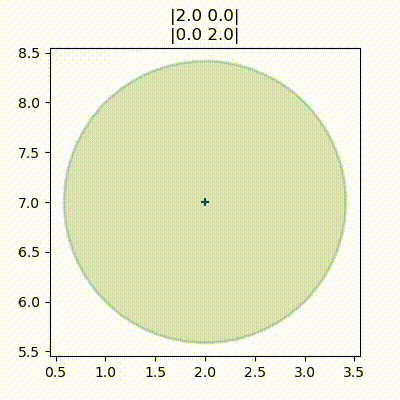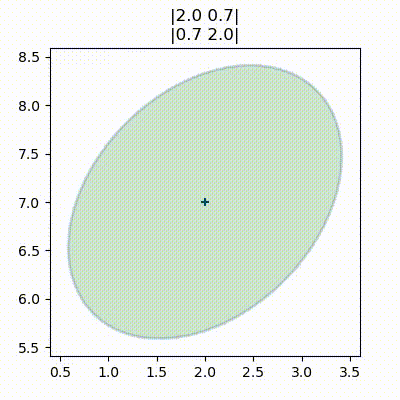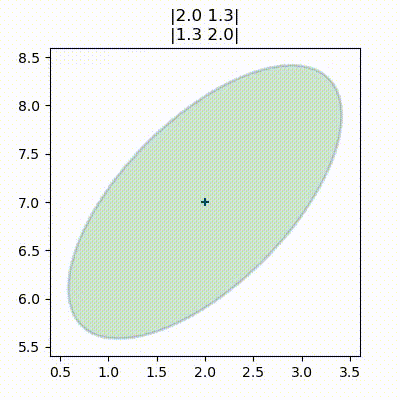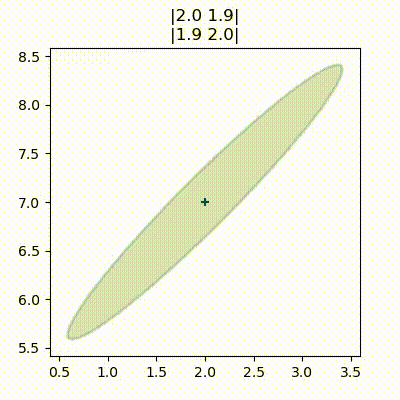
こういったプロットの物理的な解釈を考えると意味が明確になる。三つのプロットが載っている図の一つ目のプロットでは、平均と共分散行列は次の値だった:

\[ \mu =\begin{bmatrix}2\\7\end{bmatrix},\, \, \Sigma = \begin{bmatrix}2&0\\0&2 \end{bmatrix} \]

In [21]

x = [2, 7]
P = [[2, 0], [0, 2]]
plot_covariance_ellipse(x, P, fc='g', alpha=0.2, title='|2 0|\n|0 2|')
plt.gca().grid(False)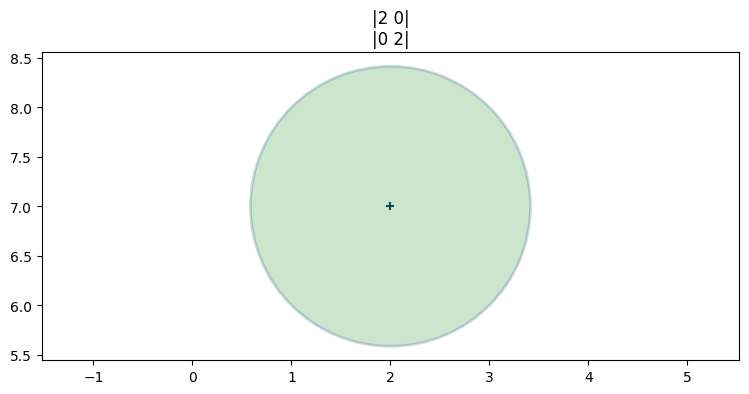

ベイズ的な考え方だと、多変量ガウス分布をスライスして得られる楕円は信念の不確実性を示す。楕円が小さいと不確実性は小さく、楕円が大きいと不確実性は大きい。また楕円の形は二つの変数が持つ不確実性の関係を幾何学的に示す。このプロットでは楕円が円だから、二つの変数には同程度の不確実性があると私たちは信じている。

二つ目のプロットでは平均と共分散行列が次の値だった:

\[ \mu =\begin{bmatrix}2\\7\end{bmatrix}, \, \, \, \Sigma = \begin{bmatrix}2&0\\0&6\end{bmatrix} \]

In [22]

x = [2, 7]
P = [[2, 0], [0, 6]]
plot_covariance_ellipse(x, P, fc='g', alpha=0.2, title='|2 0|\n|0 6|')
plt.gca().grid(False)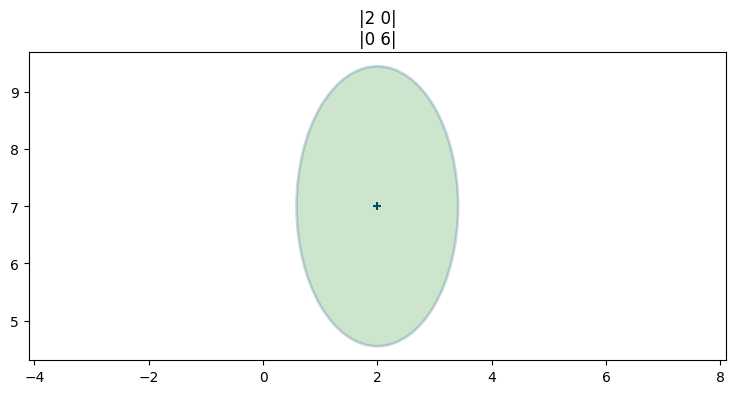

ここでは \(X\) の分散 (\(\sigma_x^2=2\)) と \(Y\) の分散 (\(\sigma_y^2=6\)) が異なっており、縦に細長い楕円が手に入る。つまり \(Y\) の値は \(X\) の値より不確実性が大きい。この分布も一つ前の分布も犬が \((2,\ 7)\) にいると信じてはいるものの、二つの分布の間で位置の不確実性が異なる。

三つ目のプロットでは平均と共分散行列が次の値だった:

\[ \mu =\begin{bmatrix}2\\7\end{bmatrix}, \, \, \, \Sigma = \begin{bmatrix}2&1.2\\1.2&2\end{bmatrix} \]

In [23]

x = [2, 7]
P = [[2, 1.2], [1.2, 2]]
plot_covariance_ellipse(x, P, fc='g', alpha=0.2,
                    title='|2 1.2|\n|1.2 2|')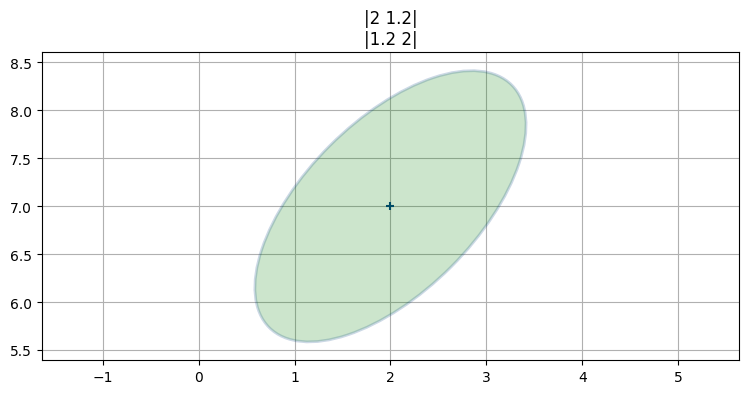

これは共分散行列の非対角要素がゼロでない値を持つときの等高線であり、プロットされる楕円は斜めに傾く。これは偶然ではなく、二つの事実は同じことを言っている。傾いた楕円は \(X\) と \(Y\) がいくらか相関していることを示し、共分散行列のゼロでない非対角要素も \(X\) と \(Y\) に相関が存在することを示す。

身長と体重をプロットしたときのことを思い出そう。そこではプロットされた点が斜めになったグループを形成していた。NumPy の numpy.cov 関数を使うと二次元配列に格納した二つ以上の変数の共分散行列を計算できる。これを計算して、\(2\sigma\) に対応する楕円をデータの上にプロットしてみよう。今は計算に使うデータがサンプルではなく考えている集団全体を表すので、bias=1 を使う必要がある:

In [24]

cov_hw = np.cov(np.vstack((height, weight)), bias=1)
cov_hw

Out [24]

array([[  18.5249,  135.701 ],
       [ 135.701 , 1092.29  ]])

In [25]

plt.scatter(height, weight, s=120, marker='s')
plt.title('Track Team Height vs. Weight')
plt.xlabel('Height (in)'); plt.ylabel('Weight (lbs)')
plot_covariance_ellipse((np.mean(height), np.mean(weight)), cov_hw, fc='g',
                        alpha=0.2, axis_equal=False, std=2)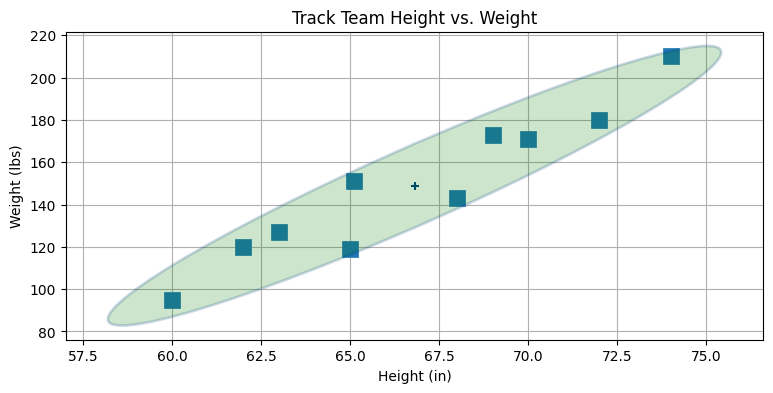

これを見ると共分散行列の意味と使い道が直感的によく理解できるはずだ。共分散行列を示す楕円の形を見ると、二つのデータがどのように散らばっているかが分かる。今回のように傾いた細長い楕円はデータが強く相関していることを示す。身長が定まると、体重の値として可能性の高い値は狭い区間しか存在しない。また楕円は右上を向いているので、正の相関があることも分かる──身長が大きくなると体重は増える。楕円が左下を向いていれば負の相関が存在する──片方が大きくなるともう一方は小さくなる。次のプロットに負の相関があるデータを示す:

In [26]

max_temp = [200, 250, 300, 400, 450, 500] # エンジンの温度
lifespan = [10, 9.7, 5, 5.4, 4.3, 0.3]    # 寿命

plt.scatter(max_temp, lifespan, s=80)
cov = np.cov(np.vstack((max_temp, lifespan)))
plot_covariance_ellipse((np.mean(max_temp), np.mean(lifespan)), cov, fc='g',
            alpha=0.2, axis_equal=False, std=2)
plt.title('Engine Temperature vs Lifespan')
plt.xlabel('Temperature (C)'); plt.ylabel('Years');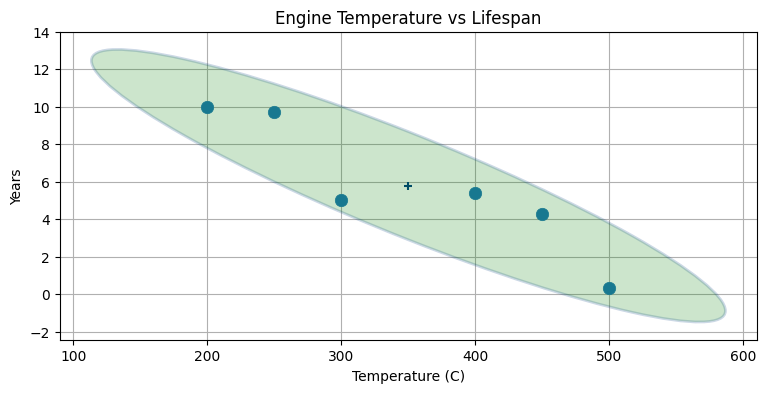

分散と共分散の関係は頭の中で考えるだけだと分かりにくいかもしれないので、対話的なプロットを次に示す。

In [27]

from ipywidgets import interact
from kf_book.book_plots import figsize, FloatSlider

fig = None
def plot_covariance(var_x, var_y, cov_xy):
    global fig
    if fig: plt.close(fig)
    fig = plt.figure(figsize=(4,4))
    P1 = [[var_x, cov_xy], [cov_xy, var_y]]

    plot_covariance_ellipse((10, 10), P1, axis_equal=False,
                            show_semiaxis=True)

    plt.xlim(4, 16)
    plt.gca().set_aspect('equal')
    plt.ylim(4, 16)
    plt.show()

with figsize(y=6):
    interact (plot_covariance,
          var_x=FloatSlider(5, min=0, max=20),
          var_y=FloatSlider(5, min=0, max=20),
          cov_xy=FloatSlider(1.5, min=0, max=50, step=.2));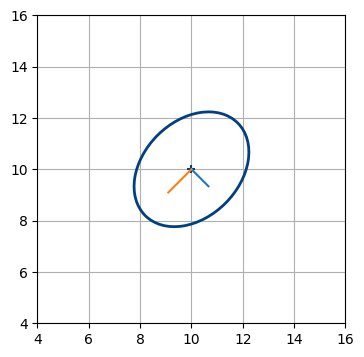

Out [27]対話的な共分散行列のプロット (Jupyter Notebook でのみ実行可能)

ピアソンの相関係数

この相関係数は本書で使わないが、他の場所で見たことがある人もいるかもしれないので触れておく。興味がないなら飛ばしても構わない。

二つの確率変数 \(X,\ Y\) の相関の度合いはピアソンの相関係数 (Pearson's correlation coefficient) で数値として表すことができる。この値は次のように定義される:

\[ \rho_{xy} = \frac{COV(X, Y)}{\sigma_x \sigma_y} \]

この値は \(-1\) から \(1\) までの値を取る。共分散が \(0\) なら \(\rho_{xy}=0\) となり、正の \(\rho_{xy}\) は \(X\) と \(Y\) の関係が正の相関であることを、負の \(\rho\) は \(X\) と \(Y\) の関係が負の相関であることを表す。\(\rho_{xy}\) が \(-1\) または \(1\) に近いときは強い相関が存在し、\(0\) に近いときは弱い相関が存在する。

相関係数と共分散は非常に密接な関係を持つ。ただ共分散は単位を持つのに対して、相関係数は単位を持たない比となる点は異なる。例えば動き回る犬の位置データに対する \(\sigma_{xy}\) はメートル二乗の単位を持つ。

ピアソンの相関係数は scipy.stats.pearsonr で計算できる。この関数は二つの数値が入ったタプルを返し、その第一要素がピアソンの相関係数である。第二要素は本書では使わない。次のコードは学生アスリートの身長と体重に対する \(\rho\) を計算する:

In [28]

from scipy.stats import pearsonr
pearsonr(height, weight)[0]

Out [28]

0.9539731096080192

次のコードはエンジン温度と寿命の相関係数を計算する:

In [29]

pearsonr(max_temp, lifespan)[0]

Out [29]

-0.9178223453527254

5.4 相関を使った推定値の改善

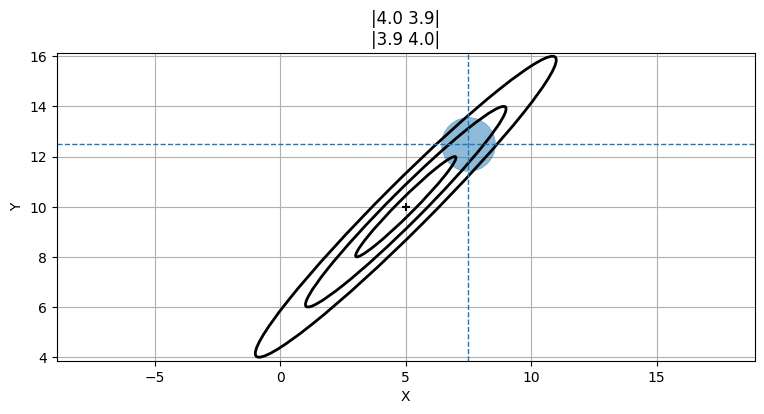
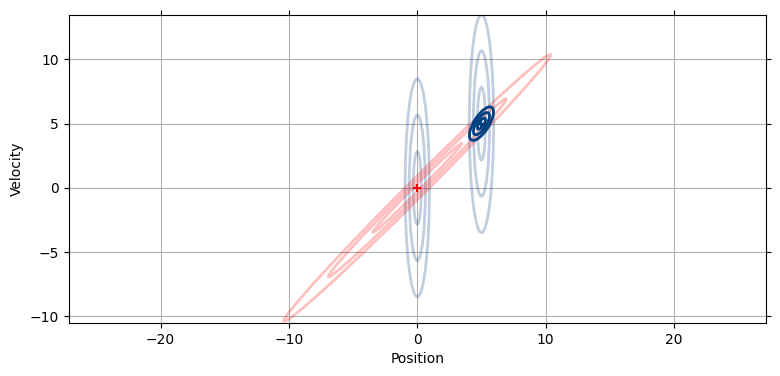
犬の現在位置が \((5,\ 10)\) だと信じているとする。この信念の標準偏差が \(x\) 軸方向と \(y\) 軸方向にそれぞれ \(2~\text{m}\) だったとしても、二つの値が強い相関を持つとしたら、共分散行列を示す等高線は次のような形となる:

In [30]

P = [[4, 3.9], [3.9, 4]]

plot_covariance_ellipse((5, 10), P, ec='k', std=[1, 2, 3])
plt.xlabel('X')
plt.ylabel('Y');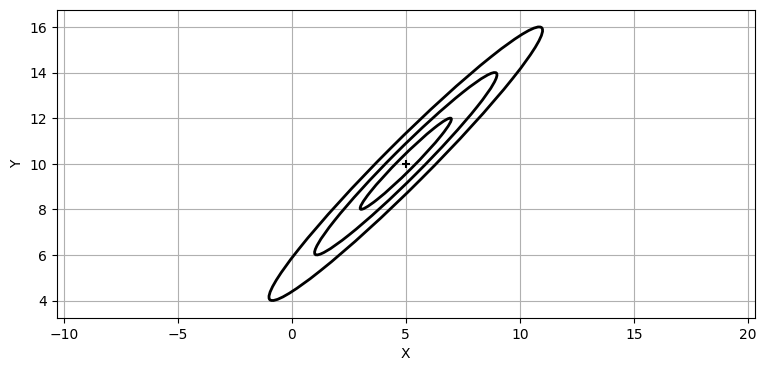

ここで \(x=7.5\) だと分かったと仮定する。ここから \(y\) の値について何が分かるだろうか？犬の位置は非常に高い確率で共分散行列の \(3\sigma\) を示す楕円の中に入るから、\(X\) と \(Y\) に相関が存在するとき共分散行列を使って \(y\) の位置を推論できる。\(y\) の値として可能性の高い区間を次の図に青い円で示した:

In [31]

mkf_internal.plot_correlation_covariance()

この円は数学的には正しくないのだが、考え方は伝わるだろう。数学的な考え方は次の節で説明する。今は \(y\) が \(12\) の近くになると予測できることを納得してほしい。\(y=6\) などはまずあり得ない。

相関と独立について少し説明する。いくつかの変数が独立 (independent) だと、それらは自由に値を変えられる。あなたが開けた野原を歩くとき、あなたは \(x\) 軸方向にも \(y\) 軸方向にも、二つの方向を組み合わせた方向にも自由に動くことができる。このとき \(x\) 軸方向の移動量と \(y\) 軸方向の移動量は独立である。独立な変数は必ず無相関 (uncorrelated) にもなる。特殊な場合を除けば、この逆は成り立たない: 相関のない変数が従属である (独立でない) ことはあり得る。例えば \(y=x^2\) がある。相関は線形な関係を表す指標なので \(x\) と \(y\) は相関を持たないと計算されるものの、\(x\) と \(y\) は独立していない (\(y\) が \(x\) に従属している)。

5.5 多変量ガウス分布の積

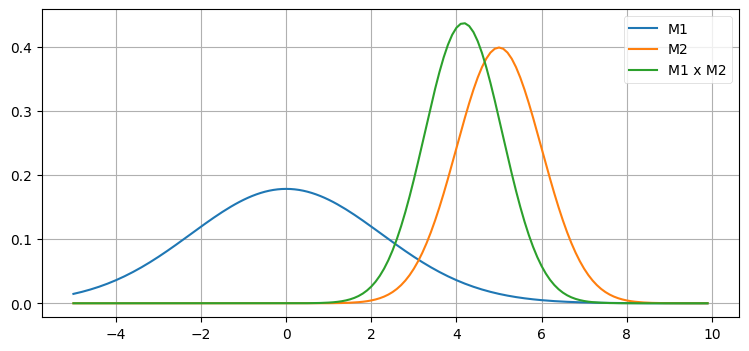
前章ではガウス分布の積を計算することで不正確な観測値と不正確な推定値を組み合わせた。ガウス分布の確率密度関数を二つ乗じて正規化を行うと、小さい分散を持つガウス分布の確率密度関数が手に入る。不正確な二つの情報を組み合わせて得られる結論は、組み合わせる前の情報より高い正確さを持つはずだ。これを次のグラフに示す:

In [32]

mkf_internal.plot_gaussian_multiply()

二つの観測値を組み合わせると正確さが増すので、新しいガウス分布は背が伸びて幅が狭く (分散が小さく) なる。同じことは多次元の多変量ガウス分布でも起こる。

多変量ガウス分布の積を求める式を示す。大文字のシグマ \(\Sigma\) はスカラーではなく行列 (共分散行列) を表す:

\[ \begin{aligned} \mu &= \Sigma_2(\Sigma_1 + \Sigma_2)^{-1}\mu_1 + \Sigma_1(\Sigma_1 + \Sigma_2)^{-1}\mu_2 \\ \Sigma &= \Sigma_1(\Sigma_1+\Sigma_2)^{-1}\Sigma_2 \end{aligned} \]

この関係はベイズの定理の式に多変量ガウス分布として表された事前分布と観測値を代入すると得られる。単変量の場合における導出は第 3 章で示した。

この公式はすぐに説明するカルマンフィルタの式で計算されるので、覚える必要はない。この計算は FilterPy の filterpy.stats モジュールにある multivariate_multiply 関数で行える。

この式をよく理解するために、単変量ガウス分布の積を求める式を思い出そう:

\[ \begin{aligned} \mu &=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2} \\ \sigma^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{aligned} \]

これは多変量の式と同じような見た目をしている。\(AA^{-1} = I\) が成り立つから、\(-1\) 乗として表記される逆行列の計算は逆数の計算のようなものだと考えれば、似ていることがさらに分かりやすくなる。逆行列を除算として書き直してみよう──行列による除算は定義されないので数学的には間違った式だが、等式を見比べるには都合がいい:

\[ \begin{aligned} \mu &\approx \frac{\Sigma_2\mu_1 + \Sigma_1\mu_2}{\Sigma_1 + \Sigma_2} \\ \Sigma &\approx \frac{\Sigma_1\Sigma_2}{\Sigma_1+\Sigma_2} \end{aligned} \]

こう書くと単変量と多変量の式の関係が明らかになる。

次は具体例を使って多変量ガウス分布の積を見ていこう。二つのレーダーを使って航空機を追跡しているとする。高度は無視して二次元座標だけを考え、レーダーはターゲットの距離と方位を報告すると仮定する。航空機の初期位置は分からないので、共分散行列 (つまり位置の不確実性) は例えば次のようになるだろう。ベイズ統計の用語を使えば、これが事前確率である:

In [33]

P0 = [[6, 0], [0, 6]]
plot_covariance_ellipse((10, 10), P0, fc='y', alpha=0.6)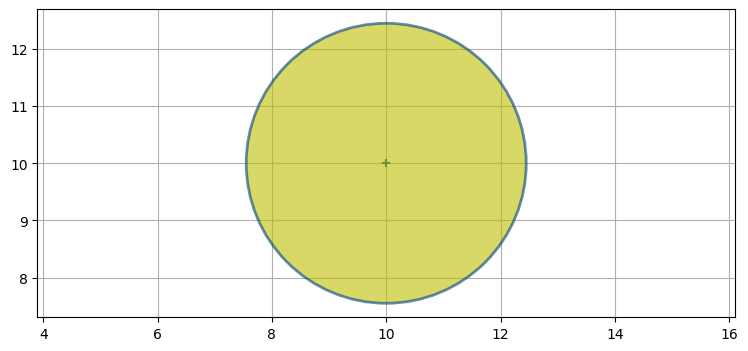

航空機の左下にレーダーがあると仮定し、さらに方位の観測値は正確で、距離の観測値は不正確とする。このとき観測値に含まれる誤差の共分散行列は次のような形になる (黄色の上に緑色でプロットしている)。ベイズ統計ではこれを証拠と呼んでいた:

In [34]

P1 = [[2, 1.9], [1.9, 2]]
plot_covariance_ellipse((10, 10), P0, fc='y', alpha=0.6)
plot_covariance_ellipse((10, 10), P1, fc='g', alpha=0.9)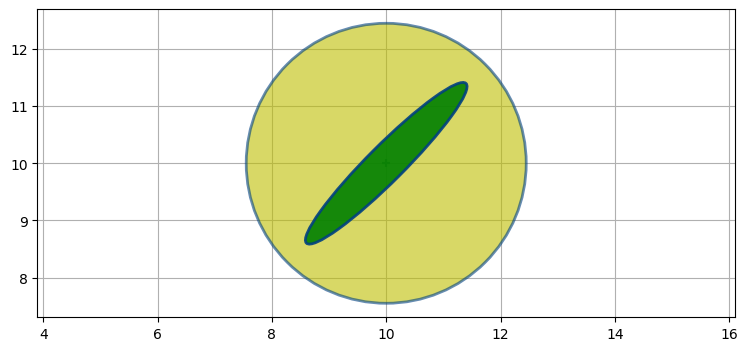

この楕円はレーダーに向かって細長くなっている。楕円が長いのは距離の観測値が不正確なために航空機の位置として可能性の高い区間がレーダーと航空機を結んだ方向に非常に長いからであり、楕円が細いのは方位の観測値が正確なために航空機の方位の真の値が観測値と非常に近いからだ。

これらから事後分布、つまり証拠を事後分布に組み込んで得られる平均と分散を求めたい。ここまでの全ての章と同じように、証拠は乗算で組み込むことができる:

In [35]

from filterpy.stats import multivariate_multiply

P2 = multivariate_multiply((10, 10), P0, (10, 10), P1)[1]
plot_covariance_ellipse((10, 10), P0, ec='k', fc='y', alpha=0.2)
plot_covariance_ellipse((10, 10), P1, ec='k', fc='g', alpha=0.9)
plot_covariance_ellipse((10, 10), P2, ec='k', fc='b')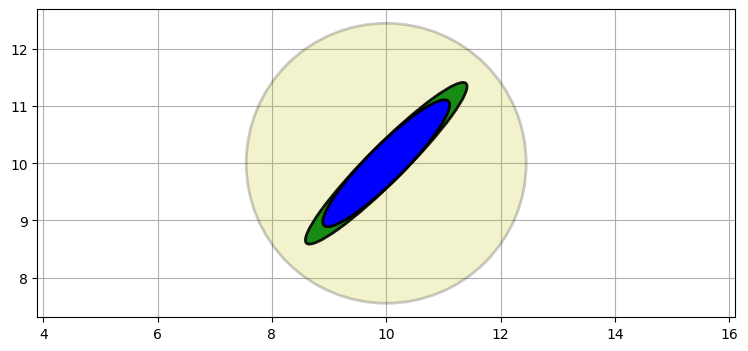

最初の推定値 (事前分布) は薄い黄色で、レーダーの観測値 (証拠) は緑色で、最終的な推定値 (事後分布) は青でプロットしてある。

事後分布はレーダーの観測値と同じ位置と形状を保持しつつも小さくなっている。これは一次元のガウス分布でも見られた現象である。二つのガウス分布を乗じるのは二つの情報を組み合わせることに等しいので、不確実性が減少して分散は小さくなる。それからもう一つ、共分散行列の形が航空機とレーダーの物理的な位置関係を反映していることにも注目してほしい。この位置関係の重要性は次のステップで明らかになる。

続いて航空機の右下に存在する二つ目のレーダーからの観測値が手に入ったとしよう。これまでのステップの事後分布が新しい事前分布となる。次の図に新しい事前分布は黄色で、新しい観測値は緑色でプロットした:

In [36]

P3 = [[2, -1.9], [-1.9, 2.2]]
plot_covariance_ellipse((10, 10), P2, ec='k', fc='y', alpha=0.6)
plot_covariance_ellipse((10, 10), P3, ec='k', fc='g', alpha=0.6)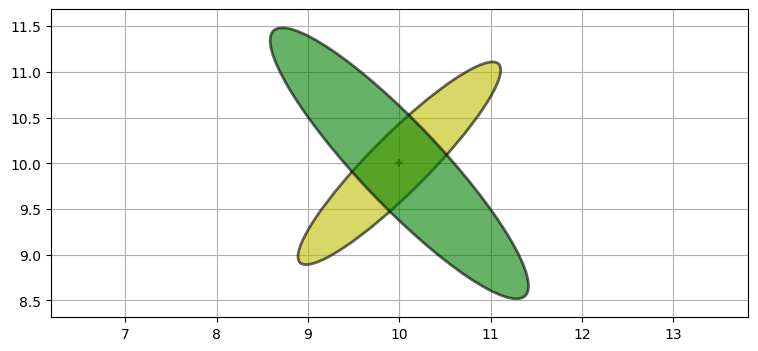

この情報はガウス分布を乗じることで取り入れることができる:

In [37]

P4 = multivariate_multiply((10, 10), P2, (10, 10), P3)[1]
plot_covariance_ellipse((10, 10), P2, ec='k', fc='y', alpha=0.6)
plot_covariance_ellipse((10, 10), P3, ec='k', fc='g', alpha=0.6)
plot_covariance_ellipse((10, 10), P4, ec='k', fc='b')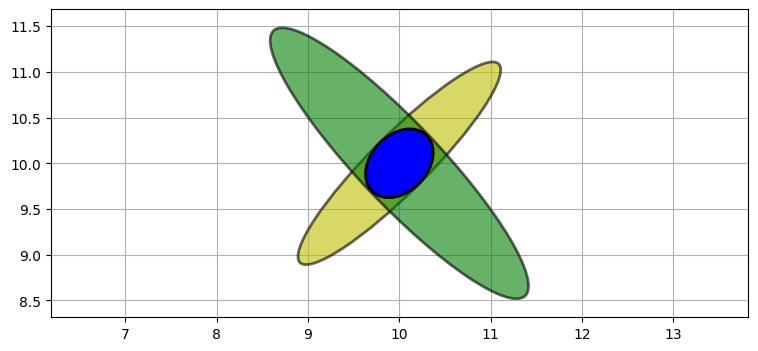

航空機の位置として可能性があるのは二つの楕円が交わる領域だけだ。この交わる領域は事前分布と観測値の積として計算される新しいガウス分布である。楕円の形は問題の設定の幾何学的特徴を表す。ここでは二つの観測値を使って航空機の位置を三角測量しているのに等しく、非常に正確な推定位置が得られる。三角測量を明示的に行うコードは書いていない: これは観測値を表すガウス分布を乗じると起こる自然な結果である。

g-h フィルタの章で二つの体重計からの観測値とそのエラーバーを図示したときのことを思い出そう。推定値はエラーバーが重なる部分に存在しなければならなかった。例えば次の例では 161 ポンドから 163 ポンドである:

In [38]

import kf_book.book_plots as book_plots
book_plots.plot_errorbars([(160, 8, 'A'), (170, 8, 'B')], xlims=(150, 180))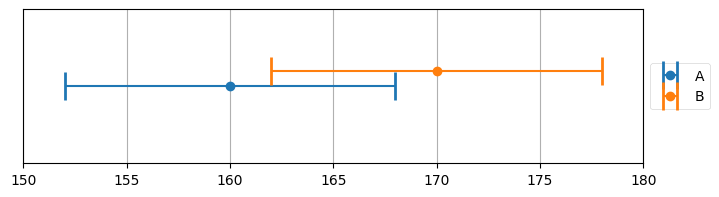

今はガウス分布を使って同じことをしていると言える。

次は異なる位置関係を考えよう。一つ目のレーダーが航空機のちょうど左にあるとする。この観測誤差は次の共分散行列でモデル化できる:

\[ \Sigma = \begin{bmatrix}2&0\\0&0.2\end{bmatrix} \]

事前分布と観測値の積を次に示す:

In [39]

P1 = [[2, 0], [0, .2]]
P2 = multivariate_multiply((10, 10), P0, (10, 10), P1)[1]
plot_covariance_ellipse((10, 10), P0, ec='k', fc='y', alpha=0.2)
plot_covariance_ellipse((10, 10), P1, ec='k', fc='g', alpha=0.6)
plot_covariance_ellipse((10, 10), P2, ec='k', fc='b')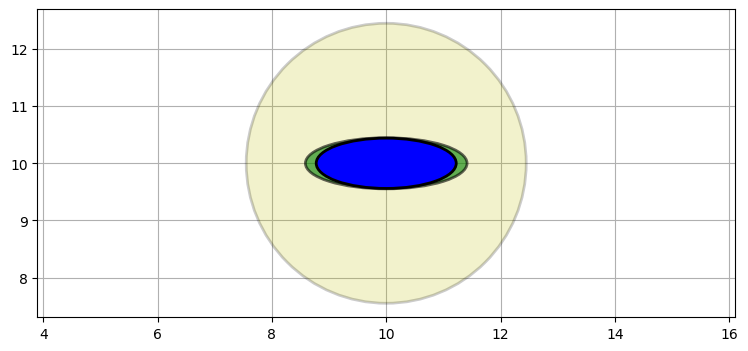

続いて二つ目のレーダーからの観測値を取り入れる。このレーダーの位置は前と同じとする:

In [40]

P3 = [[2, -1.9], [-1.9, 2.2]]
P4 = multivariate_multiply((10, 10), P2, (10, 10), P3)[1]
plot_covariance_ellipse((10, 10), P2, ec='k', fc='y', alpha=0.2)
plot_covariance_ellipse((10, 10), P3, ec='k', fc='g', alpha=0.6)
plot_covariance_ellipse((10, 10), P4, ec='k', fc='b')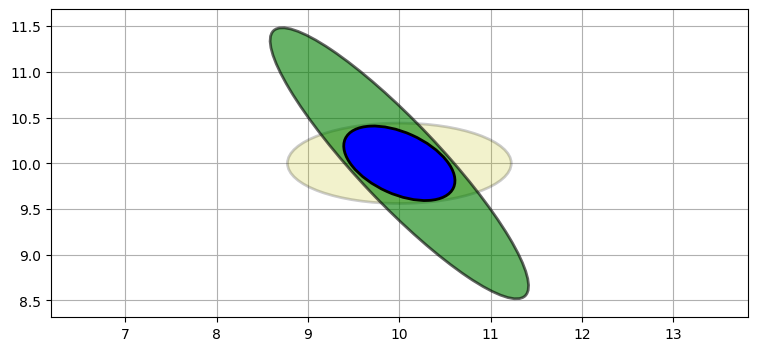

得られた推定値は一つ前の例ほど正確ではない。二つのレーダー基地が航空機から見て直交する位置にないので、三角測量は最適な形で行えていない。

最後の例として、二つの観測値を同じレーダーから短い間隔で取得した場合を考える。このとき共分散行列を表す二つの楕円がほぼ重なるので、最終的な推定値に大きな誤差が残る:

In [41]

P5 = multivariate_multiply((10,10), P2, (10.1, 9.97), P2)
plot_covariance_ellipse((10, 10), P2, ec='k', fc='y', alpha=0.2)
plot_covariance_ellipse((10.1, 9.97), P2, ec='k', fc='g', alpha=0.6)
plot_covariance_ellipse(P5[0], P5[1], ec='k', fc='b')
plt.xlim(6, 14);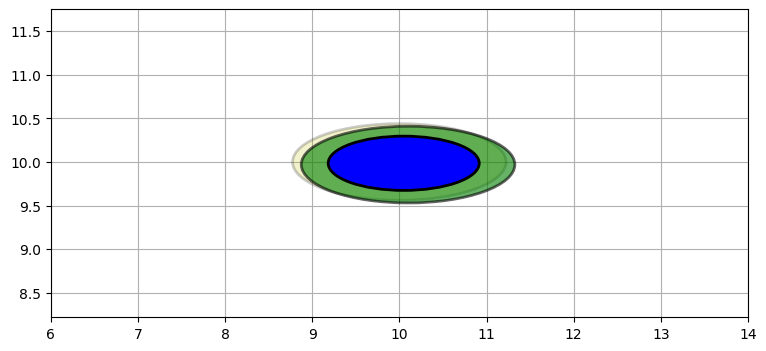

5.6 隠れ変数

多変量ガウス分布カルマンフィルタが単変量のものより優れた性能を持つ理由が見えてきた。変数の間に相関があると、推定値が大きく向上する。この事実はさらに利用できる。本章で鍵となる考え方がこの節で説明されるので、注意深く読むこと。

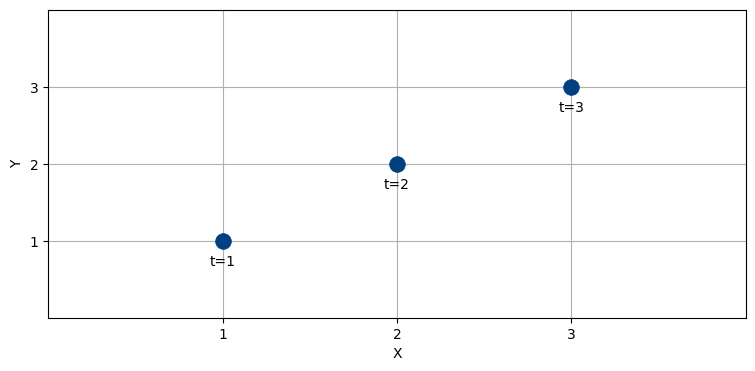
航空機を追跡していて、時刻 \(t=1,\ 2,\ 3\) 秒で \(x\) 座標と \(y\) 座標が次の通りだったとする。このとき \(t=4\) 秒における \(x\)の値はいくつになると直感的に考えるだろうか？

In [42]

mkf_internal.show_position_chart()

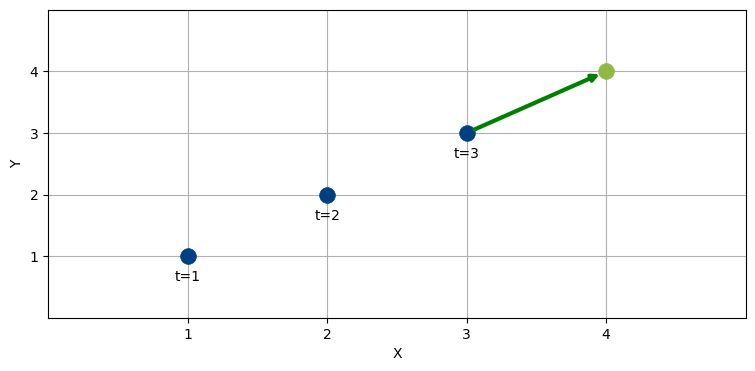
航空機は直線的に飛行しているように見え、そして航空機は急に進行方向を変えられないことを私たちは知っている。よって最も理にかなった推定は \(t=4\) で航空機が \((4,\ 4)\) にいるというものだ。次の図に緑色の矢印で示す:

In [43]

mkf_internal.show_position_prediction_chart()

このように考えたのは、航空機の速度が一定だとあなたが推論したからである。この観測値を手にしたときは、航空機が \(x\) 軸方向と \(y\) 軸方向に一単位ずつ移動するというのが理にかなった仮定になる。

g-h フィルタでノイズが含まれる体重計からの観測値を使って体重の予測を改善しようとしたときに何をしたかを思い出そう。私たちは体重のゲインを等式に追加することで、翌日の体重予測を正確にしていた。g-h フィルタではパラメータ \(g\) が体重の観測値をどれくらい重視するかを制御し、パラメータ \(h\) が体重のゲインをどれくらい重視するかを制御する。

カルマンフィルタでも同じことを行う。突き詰めればカルマンフィルタも g-h フィルタの一種に過ぎない。今考えている例では航空機を追跡しているので、体重と体重のゲインではなく位置と速度を追跡する必要がある。体重のゲインは体重の微分係数であり、速度はもちろん位置の微分係数である。\(x\) 軸方向と \(y\) 軸方向に関する位置と速度を同時に考えると四次元座標が必要になってグラフで表せないので、まずは \(x\) 軸方向についてだけ考えよう。ここで説明する数式は高次元に一般化できる。

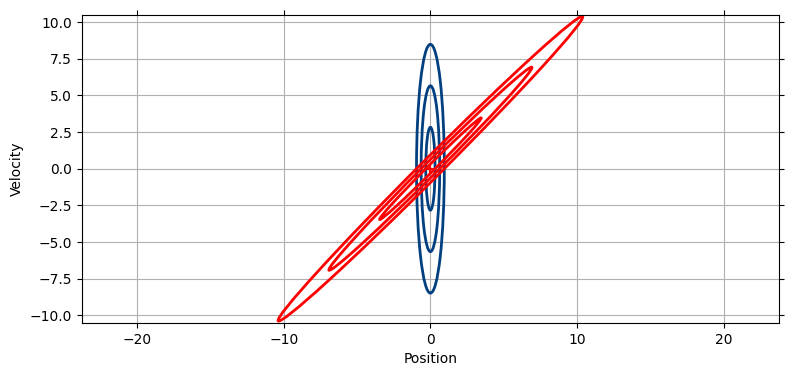
最初の時刻において私たちは位置に関して \(x=0\) だとかなり正確に知っていて、速度に関してはほとんど何も知らないと仮定する。この信念を共分散行列と共に次の図に示す。横方向の幅が狭いのは位置に関する確かさが比較的高いことを表し、縦に長いのは速度に関する知識が欠けていることを表す:

In [44]

mkf_internal.show_x_error_chart(1)

しかし位置と速度には相関がある。もし速度が \(5~\text{m/s}\) なら 1 秒後の位置は \(5~\text{m}\) になり、速度が \(-10~\text{m/s}\) なら 1 秒後に \(-10~\text{m}\) になる。この事実により、一秒後における位置と速度の予測を図示すると、その予測を表す楕円は斜めに傾く:

In [45]

mkf_internal.show_x_error_chart(2)

今から説明することを計算する方法は次の章を読むまで明らかにならないので、計算方法は気にせずに論理展開だけを理解してほしい。追跡している物体の 1 秒後における本当の位置は速度が不正確なので正確に分からない。よって予測を表す赤い楕円は \(x\) 軸方向に大きく伸びる。また速度が不正確なので、この楕円は \(y\) 軸方向にも大きく伸びる。しかし一つ前の段落で指摘したように、位置と速度には相関がある。もし速度が \(5~\text{m/s}\) なら 1 秒後の位置は \(5~\text{m}\) 地点の近くになり、速度が \(-10~\text{m/s}\) なら 1 秒後に \(-10~\text{m}\) 地点の近くになる。相関は非常に強いので、この楕円は非常に細くなる。

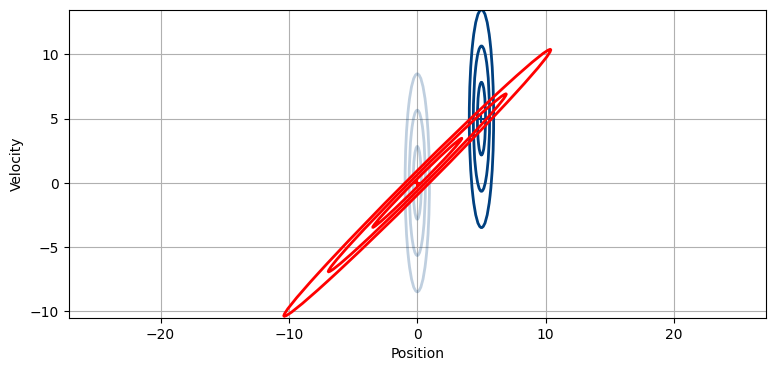
予測によって速度の分散から新しい情報が得られるわけではない。速度については情報が少ないので、新しい位置の予測も不確かなままだ。しかし一秒後には位置が更新される。新しい観測値は \(x=5\) だったとしよう:

In [46]

mkf_internal.show_x_error_chart(3)

二つの楕円が交わる部分で魔法は起こる。この時刻 (位置 5 が観測された時刻) における推定値として考えられるのは予測値の楕円と観測値の楕円が重なる領域しかあり得ない！より正確に言うと、その領域は二つの共分散行列が表すガウス分布の積として前節で示した式で計算できる。ベイズ的な視点で言えば、事前分布と証拠の確率 (尤度) を乗じることで事後分布を計算できる。予測値の共分散行列と観測値の共分散行列をベイズの式で乗じた結果を示す:

In [47]

mkf_internal.show_x_error_chart(4)

新しい (事後分布の) 共分散行列は予測値の共分散行列と観測値の共分散行列が交わる領域に収まる。少しだけ傾いており、位置と速度に相関があるのが分かる。それよりずっと重要なのは、この楕円が予測値および観測値のいずれよりも小さくなっていることである。前章の update 関数では予測値を表すガウス分布に新しい観測値を表すガウス分布を乗じるたびに分散が減少していた。ここでも同じことが起こるのだが、分散の改善は目に見えて大きい。こうなるのは、異なりながらも相関する二つの情報を使っているためである。つまり相関関係があるために、大まかな速度と大まかな位置からでも非常に正確な推定が可能になる。この図からは分かりにくいが、新しい共分散行列が \(x\) 軸方向に観測値ほど広がっておらず、位置の不確実性も小さくなっているのが確認できる。つまり位置の他に速度を考えに入れると、速度が正確になるだけではなく位置も正確になる！

ここが要点だから、注意して読んでほしい！レーダーは航空機の位置だけを観測する。この位置のような変数を観測変数 (observed variable) と呼ぶ。位置があると速度が計算できる。この速度のような変数を隠れ変数 (hidden variable) と呼ぶ。隠れ変数は文字通りのことを意味する──速度を観測するセンサーは存在せず、その値は私たちから隠されている。ただ位置と速度の相関を使えば速度の値を非常に正確に導ける。

観測変数と隠れ変数の他に観測不能変数 (unobserved variable) という用語もある。例えば航空機の状態には方向、エンジンの RPM、重量、色、パイロットのファーストネームといったものを含めても構わないが、位置センサーはこういった値を直接計測できない。よってこれらは観測変数ではない。一方でこれらの値はセンサーの観測値から相関関係を使って導くこともできないから、隠れ変数でもない。こういった変数を観測不能変数と呼ぶ。観測不能変数をフィルタの状態に加えても、その変数に対する推定値はでたらめな値にしかならない。

以上の論理展開はなぜ可能なのだろうか？追跡している航空機の位置と別の飛行機の速度を同時にグラフにプロットしたところを想像してほしい。二つの値は明らかに相関していないから、組み合わせても新しい情報は手に入らない。しかし追跡している航空機の速度からは重要なことが分かる──航空機の運動方向と運動速度である。そして航空機が速度を変えない限り、その情報から次の位置を予測できる。ただ予測した位置が観測値と一致する確率は速度に比較的小さな誤差があるだけで非常に小さくなる。考えてみてほしい──航空機が進行方向を変えると、次の時刻における位置は大きく変化する。しかし位置と速度には相関があるから、速度が変動したとき位置も変動し、その位置の変動は予測が可能である。

速度と位置に相関が存在する事実をここで利用していることをぜひ理解してほしい。二つの観測値から距離と時間が求まれば速度を大まかに推定でき、加えてベイズの定理を使えば数回の観測で非常に正確な推定値が得られる。少しでも分からない部分があるなら、この節を読み直すべきだ。ここが理解できないと、以降の章で学ぶことを理解するのは不可能に近い。

速度を考えに入れることで生まれる効果は位置だけに注目すると小さく見える。しかしこの例で示したのは一度の更新だけだ。次章では更新を何度か行うと正確さが格段に向上する様子を見る。観測値の分散が大きくても、推定された位置の分散は小さくなる。予測値の共分散行列と観測値の共分散行列の交差を取るたびに楕円は上図の \(x\) 軸方向に小さくなり、位置の分散も小さくなる。

5.7 高次元の場合

ここまでに示したのは二次元のガウス分布だったが、ガウス分布の数式は三次元以上にも適用できる。以降の章では九次元あるいは十二次元さえ考える。また気象予測のような分野では数千次元を扱うこともある。

高次元のガウス分布はどんな見た目だろうか？二次元のガウス分布は誤差を表す楕円で図示できたから、三次元のガウス分布は誤差を表す三次元の楕円体で図示できると考えるのが自然だろう。ここで数学的なことを掘り下げはしないが、この考えは正しいと示せる。FilterPy はこの楕円体をプロットする関数を提供する。

まず、適当な共分散行列を使ってノイズの含まれるデータを生成しよう。これは楕円体と共にプロットされる:

In [48]

from filterpy.stats import plot_3d_covariance

mu = [0.3, 5., 10.]
C = np.array([[1.0, .03, .2],
              [.03,  4.0, .0],
              [.2,  .0, 16.1]])

sample = np.random.multivariate_normal(mu, C, size=1000)

続いて FilterPy の plot_3d_covariance 関数で楕円体を描画し、sample もプロットする:

In [49]

ax = plot_3d_covariance(mu, C, alpha=.4, std=3, limit_xyz=True)
ax.scatter(sample[:, 0], sample[:, 1], zs=sample[:, 2],);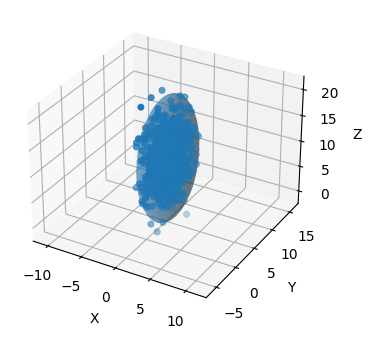

理論的には分布の 99% が標準偏差三つ分に含まれるが、グラフでもそれは正しいように見える。

では九次元では？九次元の楕円を二次元の画面にプロットする方法を私は知らないから、グラフは書けない。それでも考え方は同じである: 分布の平均から標準偏差いくつか分だけ離れた領域は九次元の楕円で記述できる。

5.8 まとめ

系が持つ幾何学的関係や相関関係を利用することで非常に正確な推定値を得ることができた。数式は考えているのが二つの位置なのか、位置と速度なのか、それとも空間的な寸法なのかを気にかけない。部屋の面積と家の値段に相関があるなら家の値段を追跡するカルマンフィルタが書けるし、年齢と疾病の発生に相関があるなら疾病の発生を追跡するカルマンフィルタが書ける。あるいはゾンビの数とショットガンの個数に負の相関があるなら、ゾンビの数を追跡するカルマンフィルタが書ける。本章では相関を利用するという考え方を幾何学的に説明して三角測量についても話したが、これは分かりやすくするためにそうしただけである。幾何学的表現を全く持たない状態変数に対してもカルマンフィルタは書ける。例えば株価にも適用できるし、牛の出すミルクの量にだって適用できる (ミルクの生産量を追跡している人物からメールをもらったことがある！)。こういった値をガウス分布と相関関係を使って表現する考え方に慣れておいてほしい。私たちが抱いている不確実性を多変量ガウス分布として表すことができれば、事前分布と尤度の積を計算することでずっと正確な結果が得られる。

第 5 章 多変量ガウス分布