第 1 章 g-h フィルタ
本題に入る前に、Jupyter Notebook の使い方を確認して、SciPy, NumPy, Matplotlib に慣れておいてほしい。これらのパッケージは本書で絶え間なく使われる。はじめにの章に使い方を簡単に示してある。
1.1 直感をつかむための思考実験
体重計が存在しない世界を想像してほしい。ある日、同僚が駆け寄ってきて言うには、彼女は "体重計" を発明したらしい。彼女の説明を聞いたあなたは、さっそくその機械に乗ってみた: 結果は「172 ポンド」。あなたは有頂天になった──生まれて初めて自分の体重を知れたのもそうだが、この機械を世界中の減量クリニックに売ることを想像するだけでドル記号が目の中で踊る! この発明は素晴らしい!
別の同僚が騒ぎを聞きつけ、あなたが何にそんなに興奮しているのかを見に来た。あなたは発明品を説明してから体重計にもう一度乗り、意気揚々と結果を読み上げる: 結果は「161 ポンド」 ... あなたは声を詰まらせ、困惑した。
「数秒前には 172 ポンドだったのに」とあなたは体重計を発明した同僚に文句を言う。
すると「体重を正確に計測できるなんて言ってないけど」と彼女は応えた。
センサーは不正確である。これはフィルタリングに関する数多くの研究を動機付けるモチベーションであり、この問題を解決する方法が本書のトピックとなる。過去半世紀をかけて開発された様々な手法をただ示すこともできるのだが、そういった手法は私たちが持っている知識と私たちが行う予測に関する非常に簡単で基礎的な疑問を深堀りすることで考案された。数式を並べる前に、その発見の旅をたどってみよう。そうすればフィルタリングに関する直感がつかめるかもしれない。
体重計を二つ使う
この結果を改善する方法はあるだろうか? 明らかに、より正確なセンサーを手に入れるのが最初の選択肢である。残念ながら同僚によると、彼女が作った十個のスケールはほぼ同じ正確さを持つとのことだ。そこであなたは彼女に別の体重計を持ってこさせ、それで自分の体重を測ってみた。すると一つ目の体重計 (A) は「160 ポンド」、二つ目の体重計 (B) は「170 ポンド」を報告した。このとき、体重の推定値として採用すべき値はいくつだろうか?
さて、推定値の選択肢は次の通りだ:
- A だけを信じることにして、体重の推定値として 160 ポンドを採用する。
- B だけを信じることにして、170 ポンドを採用する。
- A と B の両方より小さい値を採用する。
- A と B の両方より大きい値を採用する。
- A と B の間にある値を採用する。
最初の二つの選択肢はもっともらしいが、いずれかの体重計をもう片方より信用する理由がない。B ではなく A を選んで信じるのはなぜ? そうする理由など存在しない。三つ目と四つ目の選択肢は不合理である。たしかに体重計はあまり正確ではないものの、 観測された二つの値を結んだ範囲の外側にある値を選択する理由は全くない。よって最後の選択肢が唯一の合理的な選択肢となる。体重計が二つとも正確でないなら、そして体重計で真の値より大きい値が観測される確率と真の値より小さい値が観測される確率が同じなら、真の値は A と B の間にあることが多いはずだ。
これは数学で期待値 (expected value) として定式化される考え方であり、本書でも後で触れる。ここでは同じ二度の測定を百万回行ったときについてさらに考えよう。このとき "普通" 何が起こるだろうか? 二つの観測値が両方とも真の値より小さい場合もあれば、両方とも大きい場合もあるだろう。それ以外の全ての場合では、二つの観測値が真の値をまたぐことになる。もし A と B が真の値をまたぐなら、A と B の間にある値を選ぶべきである。またがなかったとしても、A と B がどちらも真の値より小さいのか大きいのか分からないから、A と B の間にある値を選ぶことで悪い方の観測値の影響を和らげることができる。例えば真の体重が 180 ポンドだとしよう。このとき 160 ポンドの観測値には大きな誤差が含まれるが、160 ポンドと 170 ポンドの間の値を選ぶことで 160 ポンドより優れた推定値が得られる。同じ議論は二つの観測値が両方とも真の体重より大きいときでも成り立つ。
後できちんと扱うが、最良の推定値が A と B の平均値であることは今の段階でも理解できると思う:
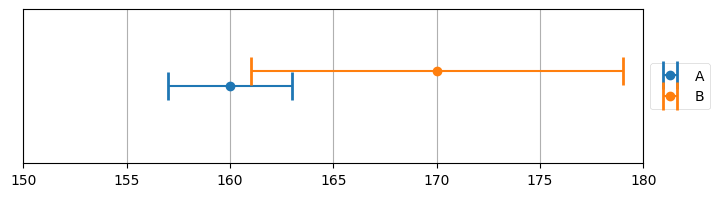
以上の議論はグラフを使っても行える。体重計の誤差1を ±8 ポンドと仮定して A と B の観測値をプロットしたグラフを次に示す。観測値が 160 ポンドと 170 ポンドなら、推定値として理にかなった値は 160 ポンドと 170 ポンドの間にある値しかあり得ないことが分かる:
import kf_book.book_plots as book_plots
from kf_book.book_plots import plot_errorbars
plot_errorbars([(160, 8, 'A'), (170, 8, 'B')], xlims=(150, 180))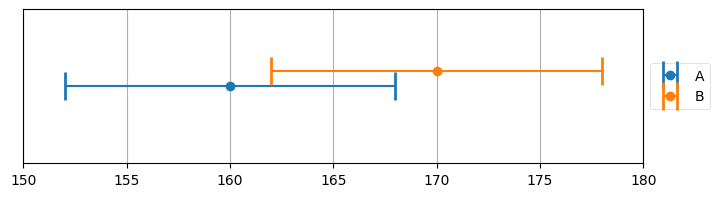
このグラフの作成方法について少し。ここでは kf_book ディレクトリの book_plots モジュールをインポートしている。グラフのプロットには退屈なボイラープレートがたくさん必要になるので、この本ではプロット処理を別モジュールの関数にして省略することが多い。このセルを実行すると plot_errorbars 関数が呼び出され、グラフがページに挿入される。
Jupyter Notebook を初めて使う人に向けて説明しておくと、上のコードはセルの中に入っている。セルに付いている In というラベルはこのセルにコードを入力できることを表し、[3] という数字はこのセルが三番目に実行されたことを表す。マウスでセルをクリックしてからキーボードで CTRL+Enter を押すとセルを実行できる。160, 170, 8 の部分を他の値に変えてセルを実行してみるとよい。値に応じて異なる値が表示される。
plot_errorbars のコードを見たいときはエディタでソースを開いても構わないが、新しくセルを作って関数の名前の後にクエスチョンマークを二つ付けてから CTRL+Enter を押すとソースコードが表示されたウィンドウを開くことができる。これは Jupyter Notebook の機能で、クエスチョンマークを一つにすると関数のドキュメントだけを閲覧できる。つまり
plot_errorbars??
または
plot_errorbars?
と打ち込めばいい。
というわけで 165 ポンドが理にかなった推定値のようだ。ただ二つのエラーバーからはこれ以外のことも分かる: 真の体重としては A と B のエラーバーが交わる領域の値しかあり得ない。例えば真の体重が 161 ポンドであることはあり得ない: 最大の誤差が 8 ポンドなのだから、真の体重が 161 ポンドのとき体重計 B で 170 ポンドが観測されることはない。同様に 169 ポンドもあり得ない: そのとき体重計 A で 160 ポンドが観測されることはない。この例では 162 ポンドから 168 ポンドの間だけが真の値としてあり得る値となる。
正確さの異なる二つの体重計を使う
続いて別のシナリオを考えよう。もし A が B より三倍正確だと伝えられたら、どうすべきだろうか? 前に示した五つの選択肢をもう一度見てみる。A から B の区間の外側にある値を推定値として採用するのはここでも理にかなってないから、これらは選択肢から外れる。今回の仮定の下では A の値を推定値として採用する選択肢の説得力が増したように思えるかもしれない──A の方が正確なのだから、B は無視すればいい。B が存在することで、A だけを使った推定値がさらに正確になるのだろうか?
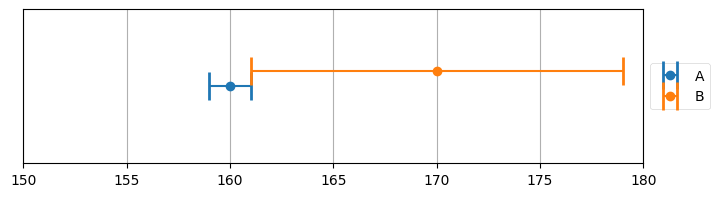
この質問の答えは、おそらく直感に反して、「さらに正確になる」である。二つの体重計 A, B からの観測値がそれぞれ 160 ポンドと 170 ポンドで、A の誤差が ±3 ポンド、B の誤差がその 3 倍の ±9 ポンドだとしよう。このときグラフは次のようになる:
A のエラーバーと B のエラーバーが交わる部分のどこかに真の値は存在する。二つのエラーバーの交わりは A 単体のエラーバーより小さい。さらに重要なこととして、この場合は交わりに 160 ポンドも 165 ポンドも含まれない。A の方が正確だからと言って A の観測値をそのまま使ったとしたら 160 ポンドが推定値となり、A と B の平均を取ったとしたら 165 ポンドが推定値となる。しかし体重計の正確さに関する知識を考えに入れると、この二つの値はどちらもあり得ないと分かる。B の観測値を取り入れると、推定値は二つのエラーバーの交差する 161 ポンドと 163 ポンドの間の値になる。
この例を極端にしてみよう。体重計 A の正確さが ±1 ポンドだとする。言い換えると、真の値が 170 ポンドのとき観測値が 169, 170, 171 ポンドのいずれかとなるような正確さを持つとする。体重計 B の正確さは ±9 ポンドだとしよう。そして二つの体重計で体重を測ったところ、A=160 と B=170 を得たとする。体重の推定値はいくつとするべきだろうか? グラフを描いて確認してみる:
このグラフからは可能な体重の値が 161 ポンドだけだと分かる。これは重要な結果である: 比較的不正確な二つのセンサーを使うことで、非常に正確な結果を導くことができた。
つまり二つのセンサーあると、たとえ片方のセンサーがあまり正確でなくても、一つのセンサーより推定値は正確になる。この事実は本書で繰り返し登場する。どれだけ弱い情報であっても、私たちはそれを捨てたりはしない。これから開発していくのは全ての情報を取り入れて最良の推定値を計算するための数式とアルゴリズムである。
しかし、ここまでの議論は私たちが解きたい問題と少し異なる問題を考えている。体重計を複数購入する顧客などいないし、さらに全ての体重計が同じ程度に (不) 正確であるという仮定を最初に置いていた。ただ正確さがどんなものであれ全ての観測値を使うという洞察は後で重要な役割を果たすので、忘れないでほしい。
同じ体重計を何度も使う
持っている体重計が一つで、それで何度も体重を測った場合はどうなるだろうか? 正確さが同じ体重計が二つあるときはそれぞれの観測値の平均を取るべきであることを前に説明した。では一つの体重計で体重を 10,000 回測ったら? 一回の測定で真の値より大きい値が観測される確率と真の値より小さい値が観測される確率は同じだと仮定しているので、観測値の平均が真の値と非常に近いことを示すのは難しくない。ここではシミュレーションを書いてみよう。数値計算エコシステム SciPy に含まれるパッケージ NumPy を使う:
import numpy as np
measurements = np.random.uniform(160, 170, size=10000)
mean = measurements.mean()
print(f'観測値の平均は {mean:.4f}')観測値の平均は 164.9827出力される数値は乱数生成器の状態によって変化するが、165 に非常に近いはずだ。
このコードはおそらく正しくない仮定を一つ置いている──可能な値が全て同じ確率で観測される、例えば真の値が 165 ポンドのとき観測値が 160 ポンドになる確率と 165 ポンドになる確率が等しいという仮定である。この仮定が成り立つことはまずない。現実のセンサーは真の値に近い値を観測する確率が高く、真の値から遠い値を観測する確率は真の値からの距離が大きくなるに従って小さくなるはずだ。この話題は第 3 章で詳しく触れる。ここでは説明を飛ばして numpy.random.normal 関数を使用する。この関数は真の値 (ここでは 165 ポンド) に近い値を多く生成し、遠い値を少なく生成する。現実世界の体重計による観測値と似た値が得られるのだと思ってほしい。numpy.random.normal を使ってシミュレーションをしてみよう:
mean = np.random.normal(165, 5, size=10000).mean()
print(f'観測値の平均は {mean:.4f}')観測値の平均は 164.9170ここでも答えは 165 に非常に近い。
なるほど素晴らしい、これでセンサーに関する問題が片付いた! ただこれは現実的な答えではない。自分の体重を 10,000 回も測る忍耐力を持つ人はいないし、そもそも 10 回測るのだって誰もしないだろう。
体重を三日間計測する
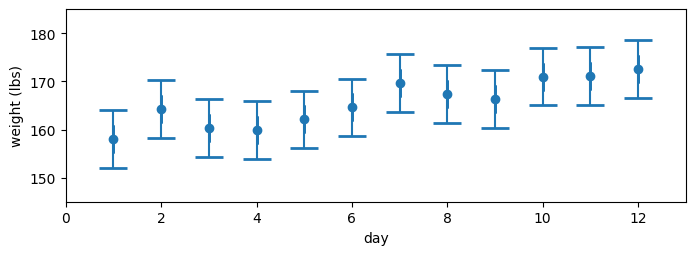
というわけで、また別のシナリオを考えよう。自分の体重を一日に一度測定して、観測値が 170 ポンド、161 ポンド、169 ポンドだったとする。このとき体重は減っているのか、増えているのか、それともノイズによって観測値が変化しただけか?
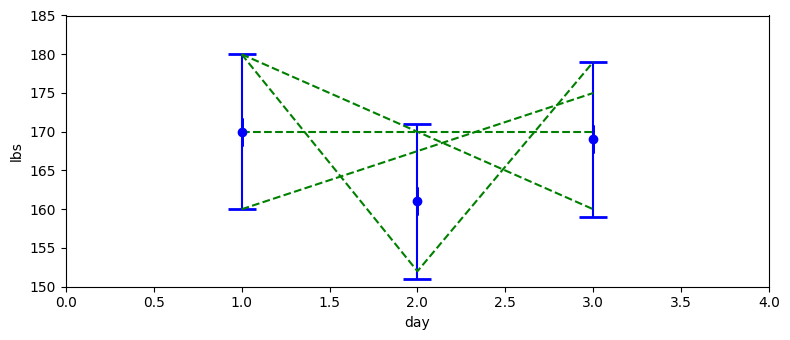
確かなことは分からない。最初の観測値が 170 ポンドで最後の観測値が 169 ポンドだから、1 ポンド減ったともいえるかもしれない。しかし体重計の誤差が ±10 ポンドなら、この差はノイズで説明できる。体重が増えている可能性さえある: 真の体重は初日に 165 ポンドで、三日目は 172 ポンドかもしれない。この場合でも 170 ポンドと 169 ポンドという観測値が得られる可能性はある。体重計は体重が減ったと言っているのに、本当は体重が増えているなんて! これをグラフにしてみよう。エラーバー付きの観測値の他に、これらの観測値で説明できる三種類の体重の推移を示す緑色の破線を付けてある:
このグラフからは、考えている三つの観測値で説明できる体重の推移には非常に様々な種類があることが分かる。実は、考えられる推移の選択肢は無限に存在する。では諦めようか? 私は諦めない! 私たちが観測しているのは人間の体重であることを思い出そう。一日目に 180 ポンドだった人物が三日目に 160 ポンドになる、あるいは一日で 30 ポンド体重が減って次の日に減少した分の体重が戻る、といった推移が人間の体重で起こることはまずあり得ない (体の一部を失うなどの事故があれば別だが、そのようなことはないと仮定しよう)。
私たちが観測している物理系の振る舞いは観測の解釈に影響を与えるべきである。石の重さを毎日観測するなら、重さの変化は全てノイズによると結論付けるだろう。しかし雨水を貯める貯水槽の重さを観測していて、その水が日常の家事にも使われているなら、重さは実際に変化したと思うはずだ。
体重を十日間計測する
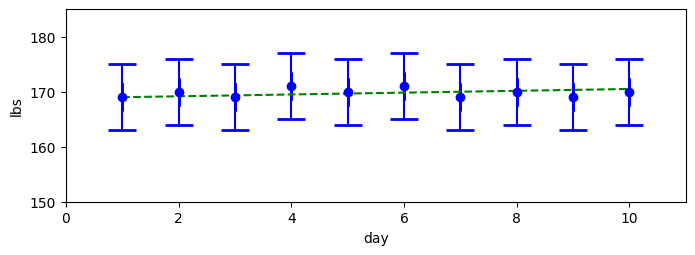
今までとは異なる体重計を使って毎日体重を測定したところ、169, 170, 169, 171, 170, 171, 169, 170, 169, 170 という観測値が得られたとしよう。直感的にどう思うだろうか? 例えば「毎日 1 ポンドずつ体重が増えていて、ノイズにより同じ体重が観測された」可能性もあるし、逆に「毎日 1 ポンドずつ体重が減っていて、ノイズにより同じような体重が観測された」可能性もある。しかし、そういった可能性が高いとは思えない。コインを投げて十回連続で表が出る確率を考えれば、これは非常に低い。この十個の観測値だけでは確かなことは証明できないが、体重はほとんど変わらなかった可能性が非常に高く思える。次のグラフにエラーバーを付けた十個の観測値を示す。緑の破線はあり得そうに見える真の体重を表す。緑の破線が示すのは考えている問題への "本当の" 答えではなく、観測値で説明できる理にかなった推定値の一つである:
体重を十日間計測する──体重が増加するように見えるケース
さらに別のシナリオを考える: 観測値が 158.0, 164.2, 160.3, 159.9, 162.1, 164.6, 169.6, 167.4, 166.4, 171.0 だったら? 観測値をグラフにして、何か分からないかを考えよう:
本当は体重が減っていて、ノイズのせいでこの観測値となるのはどれくらいあり得そうに "見える" だろうか? あまりあり得そうには見えない。では体重が変わらないというのは? それもなさそうだ。このデータは時とともに大きくなっている: 同じペースではないが、明らかに体重は上向きである。確かなことは言えないものの、体重の増加は間違いなさそうだ。グラフを作ってこの仮説を確認しよう。データは表で見るよりグラフにして "目で" 確認した方が状況を理解しやすい場合が多い。
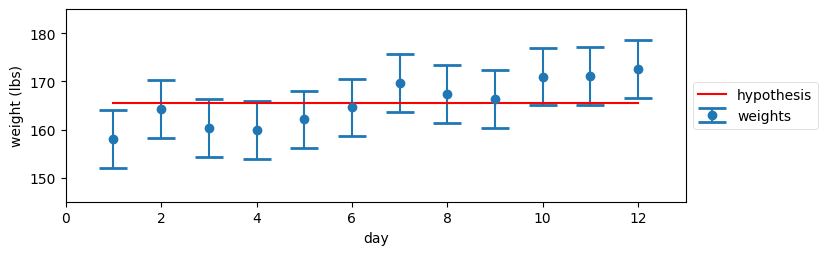
これから二つの仮説を見ていく。まず、体重が変わっていないとしてみよう。このとき推定値は観測値の平均だと前に納得したから、平均値をグラフに加えてみる:
この仮説にはあまり説得力がない。よく見ると、全ての観測値のエラーバーを横切る水平な線を書くことはできないのが分かる。
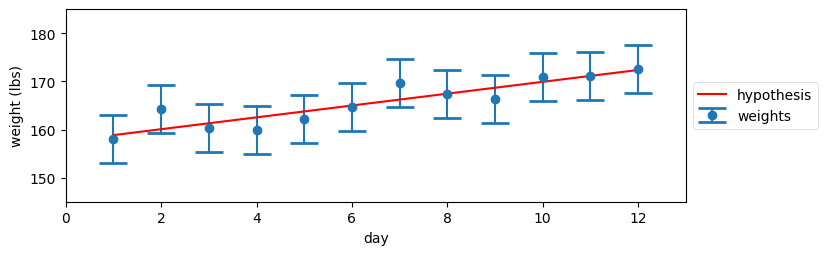
では、体重が増加したとしてみよう。どれくらいの増加だろうか? 私には分からないが、NumPy は知っている! ここで行いたいのは観測値に近い値を通る正しそうな直線が引くという処理であり、NumPy には「最小二乗フィッティング」と呼ばれる規則でこれを行う関数が存在する。計算の詳細は気にしないことにして (もし気になるなら、ここでは numpy.polyfit 関数を使っている)、結果を見てみよう:
少なくとも私の目には、こちらのグラフの方がずっとましに見える。一つ目の仮説と異なり、ここでは仮説の直線が観測値に非常に近い値を通っていることに注目してほしい。「体重が増加した」は「体重が増加しなかった」よりはるかに可能性が高そうだ。では本当に体重は 13 ポンド増加したのだろうか? そんなことが分かるのか? これに答えるのは不可能に思える。
「本当に不可能なの?」と同僚が声を上げる。
体重の予測を行う
もっとおかしなことをやってみよう。一日に約 1 ポンド体重が増すと知っている状況を仮定する。どうしてそれが分かるのかはここで重要でない。とにかく一日におよそ 1 ポンド太ると知っているとする: 一日に 6000 キロカロリーぐらいの食事をしているのかもしれない。何でもいい。この情報が利用できるとき、これを活用する方法を考える。
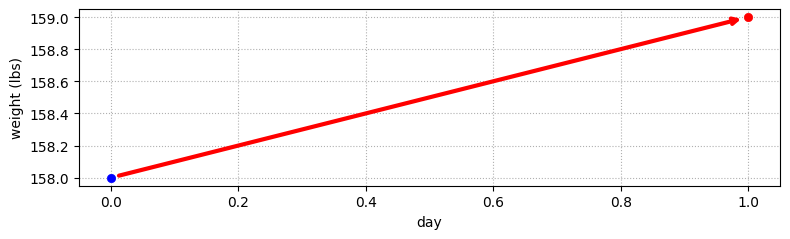
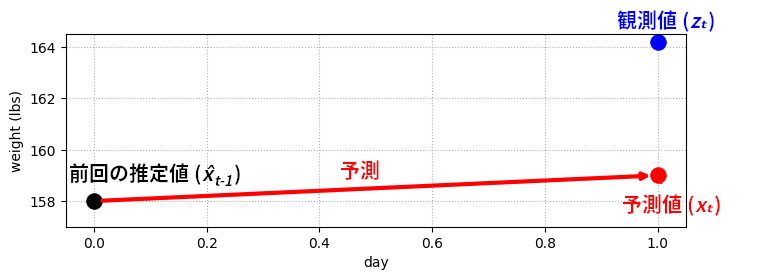
初日の観測値は 158 ポンドだった。最初はこれ以外に何も情報がないから、この値を推定値として受け入れよう。ある日の体重が 158 ポンドなら、次の日の体重は? 一日に 1 ポンド太ると思っているのだったから、次の日の体重は 159 ポンドと予測できる。これを次のグラフに示す:
さて、この予測はどれくらい正しいだろうか? 「一日に 1 ポンド太る」のが絶対に正しいと決め込んで十日間の予測値を計算することもできるが、体重計を使っておいて観測値を捨てるのは馬鹿な真似に思える。そこで次の観測値を見てみよう。次の日に体重計に乗ると、目盛りは 164.2 ポンドを指した:
このグラフから分かる問題がある: 予測値と観測値が合っていない! しかしこれは驚くようなことでもないはずだ: 予測値が必ず観測値と一致するなら、測定がフィルタに新しい情報を追加することはない。そもそも、予測が完璧なら測定を行う意味がない。
本書で最も重要な考え方が次の段落で説明される。注意深く読むこと!
ではどうするか? 観測値だけから推定値を計算すると、予測値が結果に影響しない。予測値だけから推定値を計算すると、観測値が無視される。よって二つの値を活用するには、予測値と観測値を何らかの方法で混ぜ合わせる必要がある (重要な部分を太字にした)。
二つの値を混ぜ合わせる──これは前に触れた二つの体重計を使う状況とよく似ている。そのときと同じ議論を使えば、予測値と観測値の間にある値を推定値として選ぶのが理にかなった唯一の選択肢だと分かる。例えば 165 ポンドを推定値に選ぶのはおかしいし、157 ポンドもおかしい。推定値は 159 ポンド (予測値) と 164.2 ポンド (観測値) の間にあるべきだ。
繰り返すが、これは非常に重要である。誤差を含む二つの値が与えられたなら、その二つの値の中間にある値を選ぶべきだと前に見た。その値がどのように生成されたかは問題ではない。本章の最初に示した例では二つの観測値が与えられたが、今は観測値と予測値が与えられている。中間の値を選ぶ理由は同じであり、よってそのときの数式も同じになる。私たちは絶対に情報を捨てない。絶対だ。ノイズが多いデータをそのまま捨てる商用ソフトウェアを私はいくつも見たことがあるが、あんなことはしてはいけない! 私たちが行った体重の予測はあまり正確でないかもしれないが、少しでも情報が含まれるなら使うべきである。
このことについて一度立ち止まって深く考えるよう読者に強く言っておかなければならない。ここでは前の例における体重計からの不正確な観測値が人間の生理学的側面を使った不正確な予測値に置き換えられてはいるものの、予測値もデータに変わりはない。数式は代入される値が体重計から来たのか予測から来たのかを気に留めない。本書の残りの部分ではこの「いくらかのノイズが入ったデータが二つ受け取って、それをどうにかして組み合わせる」という処理を行う非常に複雑な数式を開発する。そのとき数式にとってデータの来歴は重要でない: 数式は値とその正確さに基づいて計算を行うだけだ。
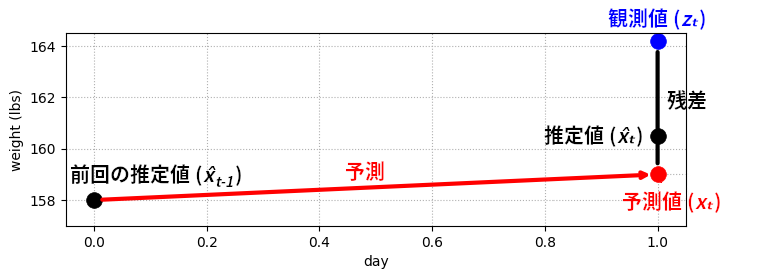
推定値は観測値と予測値の中央にすべきだろうか? そうするのも一理あるが、一般には観測値よりも予測値の方がある程度正確であることを知っている場合が多いように思える。おそらく予測値の正確さは体重計の正確さと異なるだろう。体重計 A が体重計 B より正確だった状況を思い出そう──そのとき推定値を B から離して A に近づけていたから、予測値が観測値より正確な今の状況では推定値を予測値に近づけるべきだ。この考え方を次のグラフに示す:
推定値をスケールする値を適当に選ぼう: ここでは \(\frac{4}{10}\) とする。新しい推定値は \(\frac{4}{10}\) が観測値で、残りの \(\frac{6}{10}\) は予測値とする。言い換えれば、「観測値より予測値の方がある程度正しいはずだ」という信念 (belief) を、私たちは \(\frac{4}{10}\) という数字の選択によって表現している。このとき推定値は次の式で計算できる:
観測値と予測値の違いは残差 (residual) と呼ばれる。上の図で残差は黒い垂直な直線として描かれている。この値は観測値とフィルタの出力の差から求まる正確な値なので、後で重要になる。小さい残差は予測が正確であることを意味する。
以上の手続きをコードにして、上述した観測結果に対して適用したとき何が起こるかを見よう。コードではもう一つ定めなければならない係数がある: 予測で使う体重のゲイン (増分) の単位は「重さ/時間」なので、タイムステップを追加する必要がある。ここではタイムステップを 1 日とする。
体重のデータは真の値が 160 ポンドから始まってゲインが 1 ポンド/日となるように生成した。つまり初日 (第 0 日) の真の体重は 160 ポンドであり、次の日 (第 1 日、体重が変化する最初の日) に真の体重は 161 ポンドとなり、以降同様である。
初日の体重も推測しなければならないが、初期値の選び方を説明するにはまだ早い。ここでは初期値を 160 ポンドに設定してある:
from kf_book.book_plots import figsize
import matplotlib.pyplot as plt
weights = [158.0, 164.2, 160.3, 159.9, 162.1, 164.6,
169.6, 167.4, 166.4, 171.0, 171.2, 172.6]
time_step = 1.0 # 単位は日
scale_factor = 4.0/10
def predict_using_gain_guess(estimated_weight, gain_rate, do_print=False):
# フィルタリング結果の格納場所
estimates, predictions = [estimated_weight], []
# フィルタリングの文献では観測値に z を使うことが多い
for z in weights:
# 新しい位置を予測する
predicted_weight = estimated_weight + gain_rate * time_step
# フィルタを更新する
estimated_weight = predicted_weight + scale_factor * (z - predicted_weight)
# 結果を保存して、必要ならログを出力する
estimates.append(estimated_weight)
predictions.append(predicted_weight)
if do_print:
gh.print_results(estimates, predicted_weight, estimated_weight)
return estimates, predictions
initial_estimate = 160.
estimates, predictions = predict_using_gain_guess(
estimated_weight=initial_estimate, gain_rate=1, do_print=True)前回の推定値: 160.00, 予測値: 161.00, 推定値 159.80
前回の推定値: 159.80, 予測値: 160.80, 推定値 162.16
前回の推定値: 162.16, 予測値: 163.16, 推定値 162.02
前回の推定値: 162.02, 予測値: 163.02, 推定値 161.77
前回の推定値: 161.77, 予測値: 162.77, 推定値 162.50
前回の推定値: 162.50, 予測値: 163.50, 推定値 163.94
前回の推定値: 163.94, 予測値: 164.94, 推定値 166.80
前回の推定値: 166.80, 予測値: 167.80, 推定値 167.64
前回の推定値: 167.64, 予測値: 168.64, 推定値 167.75
前回の推定値: 167.75, 予測値: 168.75, 推定値 169.65
前回の推定値: 169.65, 予測値: 170.65, 推定値 170.87
前回の推定値: 170.87, 予測値: 171.87, 推定値 172.16# 結果のプロット
book_plots.set_figsize(10)
gh.plot_gh_results(weights, estimates, predictions, [160, 172])
weights[158.0,
164.2,
160.3,
159.9,
162.1,
164.6,
169.6,
167.4,
166.4,
171.0,
171.2,
172.6]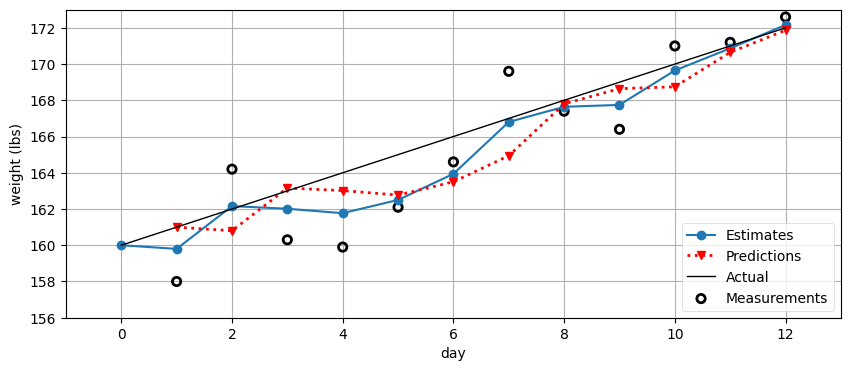
かなりよさそうだ! この図にはデータが多く含まれるから、何を意味するかを一つずつ説明しよう。青い実線はフィルタからが出力する推定値を表し、第 0 日の初期推測値 160 ポンドから始まっている。赤い破線は前日の結果から計算した予測値を表す。例えば第 1 日では前日の推測値が 160 ポンド、体重のゲインが 1 ポンドだから、予測値は 161 ポンドとなっている。第 1 日の推測値は予測値と観測値から 159.8 ポンドと計算される。また黒い実線が真の体重の増分を示す。グラフの上に並ぶ数字は計算された推定値である。
同じことを全ての日に対して考えて、予測値と推定値がどのように計算されているかを確認するとよい。特に、推定値は必ず観測値と予測値の中間にある。
計算される推定値を結んでも直線にはならないが、観測値を結んだものよりは振れ幅が小さく、観測値を生成するのに使った値に近くなっている。また時間が進むにつれ推測値が正確になっているようにも見える。
このフィルタリング結果が馬鹿げて見えるかもしれない: 体重のゲインが 1 ポンド/日であるという正しい仮定をしたのだから、結果が正しくなるのは当然だ! では最初の推測を悪くしてみよう。体重が一日に 1 ポンド減ると推測したらどうなるだろうか?
e, p = predict_using_gain_guess(initial_estimate, -1.)
gh.plot_gh_results(weights, e, p, [160, 172])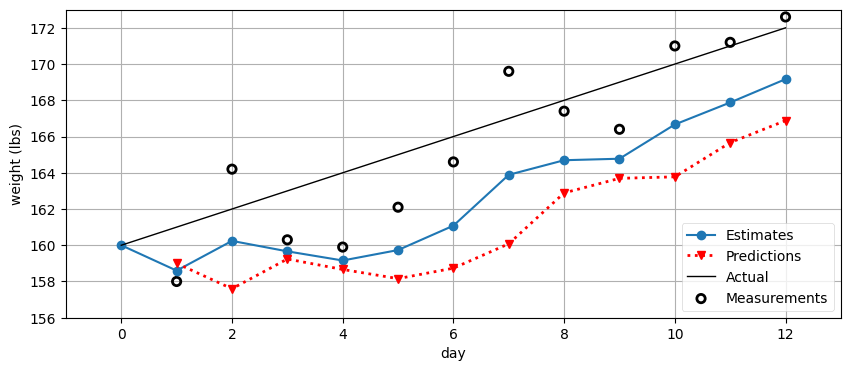
これは褒められたものではない。推定値は観測値からすぐに離れていっている。データの変化率を正しく推測しなければならないフィルタというのは、明らかに役に立たない。さらに、たとえ最初の推測が正しかったとしても、変化率が変わればフィルタは値の推定に失敗してしまう。もし私が暴食をやめたら、フィルタはそれに上手く適応できない。ただ適応自体は起きていることに注意してほしい! 「体重は一日に 1 ポンド減るぞ」とフィルタに伝えたにもかかわらず、推定値は大きくなっている。フィルタが十分速く適応できていないというだけだ。
では、こうしたらどうだろうか: 予測で使う体重のゲインを初期推測値 1 ポンドのままにするのではなく、既存の観測値と推定値から計算した値に置き換えるというのは? 第 1 日の推定値は次のように計算された:
翌日の観測値は 164.2 ポンドだから、体重のゲインは (1 ポンドではなく) 164.2 - 159.8 = 4.4 ポンドとなる。この情報も利用できないだろうか? できそうに思える: 結局、体重の観測値も現実世界の体重に基づいているのだから、その値にも役立つ情報が含まれるはずだ。体重のゲインを推定しても完璧な値は得られないかもしれないが、「ゲインは一ポンド/日だろう」と特に理由もなく推測するよりは明らかに優れている。データは、たとえノイズを含んでいたとしても、推測より優れる。
ここで戸惑う人が多いので、よく納得しておいてほしい。ノイズを含んだ二つの観測値があると、体重のゲイン (またはロス) の推定値が計算できる。観測値が不正確なときゲイン (またはロス) の推定値は非常に不正確になるが、そこにも情報は含まれる。例えば一ポンドの正確さを持つ体重計で牛の体重を測定したところを想像してほしい。その観測値が 10 ポンド増加したなら、牛の真の体重は 8 ポンドから 12 ポンド増加している。正確な増加量は観測値に含まれる誤差によって異なるものの、牛の体重が増加したことは分かるし、その増加がどれくらいかも大まかに知ることができる。
私の食生活の話に戻ろう。新しいゲインは 4.4 ポンド/日とするべきだろうか? 昨日の時点ではゲインは 1 ポンド/日と考えていて、今日は 4.4 ポンド/日と考えている。二つの数字を持っていて、それをどうにかして混ぜ合わせたい。ふーむ、さっきと同じ問題に思える。同じ手法を使ってみよう──といっても今の私たちは「二つの値の中間の値を選ぶ」という手法しか知らないのだが。今回は適当に選んだ値 \(\frac{1}{3}\) を使う。数式はほぼ同じだが、ゲインは「率」で単位が「重さ/時間」なために残差を時間 (タイムステップ) で割る必要がある点が異なる:
この数式を追加したフィルタを実装しよう:
weight = 160.0 # 初期推測値
gain_rate = -1.0 # 初期推測値
time_step = 1.
weight_scale = 4./10
gain_scale = 1./3
estimates = [weight]
predictions = []
for z in weights:
# 予測ステップ
weight = weight + gain_rate*time_step
gain_rate = gain_rate
predictions.append(weight)
# 更新ステップ
residual = z - weight
gain_rate = gain_rate + gain_scale * (residual/time_step)
weight = weight + weight_scale * residual
estimates.append(weight)
gh.plot_gh_results(weights, estimates, predictions, [160, 172])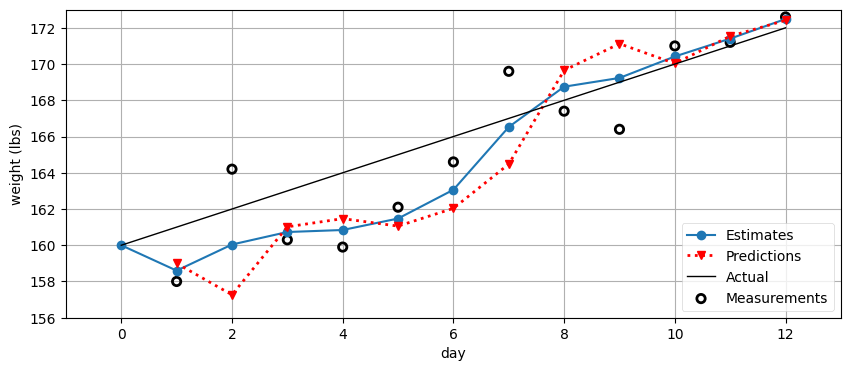
非常に良くなってきたように思える。体重のゲインは -1 という不正確な推測値から始まるので、正しい推定値が計算されるまでにフィルタは数日を要しているものの、ゲインが一度正しく計算された後は正しく体重を追跡できている。スケーリングに使った係数 \(\frac{4}{10}\) と \(\frac{1}{3}\) を選んだ理由は特に存在しない (実は値を調整すればもっと優れた結果も得られる) が、それ以外の数式は理にかなった仮定から導かれていることに注目してほしい。
次の話題に進む前に、一つ言っておきたいことがある。予測ステップに
gain_rate = gain_rate
という行がある。もちろんこの行に意味はなく、削除することもできる。これを書いたのは、予測ステップでは全ての変数 (ここでは weight と gain_rate) に対する次の値を予測する必要があるためだ。今考えた例でゲインは変化しないものとしているが、この仮定はアルゴリズムを一般化するときに取り払われる。
1.2 g-h フィルタ
以上のアルゴリズムは g-h フィルタ と呼ばれる。\(g\) と \(h\) はこれまでの例で出てきた二つのスケーリング係数 (weight_scale と gain_scale) を表す。\(g\) は観測値 (今までの例では体重) に対するスケーリング係数で、\(h\) は観測値の変化 (今までの例では日ごとの体重の変化) に対するスケーリング係数である。\(g\) と \(h\) ではなく \(\alpha\) と \(\beta\) が使われることもあり、そのときは \(\alpha\)-\(\beta\) フィルタ と呼ばれる。
g-h フィルタは膨大な種類のフィルタの土台になっており、そこにはカルマンフィルタも含まれる。つまりカルマンフィルタは g-h フィルタの亜種である (この事実は後で証明する)。他に最小二乗フィルタもそうだし、ベネディクト-ボードナーフィルタもそうだ (前者は聞いたことがあるかもしれないが、後者はないだろう)。異なるフィルタは \(g\) と \(h\) に異なる方法で値を割り当てるものの、その点を除けばアルゴリズムは変わらない。例えばベネディクト-ボードナーフィルタは \(g\) と \(h\) に特定の範囲に収まる定数を割り当てる。またカルマンフィルタのように \(g\) と \(h\) を各ステップで変化させるフィルタも存在する。
非常に重要なので、要点をもう一度繰り返させてほしい。これが理解できないと、本書の残りの部分も理解できない。理解できれば、本書の残りの部分の議論も「もし ... なら \(g\) と \(h\) はどうなる?」という質問に対する数学的な解答として自然に理解できるだろう。数式の見た目は大きく異なるかもしれないが、次の基本的なアルゴリズムは全く同じである:
- 単一のデータ点を使うより複数のデータ点を使う方が正確なので、どんなに不正確であってもデータ点を捨てない。
- データ点が二つあるなら、必ずその中間にある値を推定値として選択して正確さを向上させる。
- 現在の推定値と変化率の推定から、次の観測値と変化率を予測する。
- 予測値と次の観測値をそれぞれの正確さでスケールして混ぜ合わせ、新しい推定値を計算する。
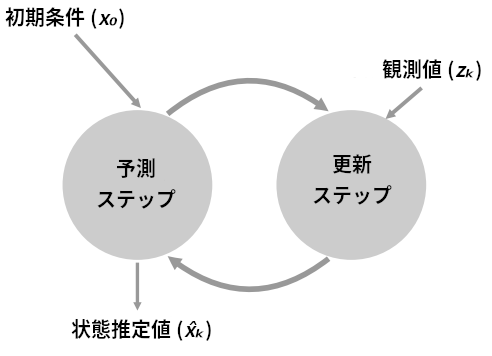
このアルゴリズムを表す図を示す:
正式な用語をいくつか導入しよう。推定対象のオブジェクトを系 (system) と呼ぶ。本章では重さを測ろうとしているもの (人間や牛) が系となる。系をプラント (plant) と呼ぶ文献もある。これは制御理論の用語である。
系の状態 (state) とは、その系に関連付く値であって私たちが注目するものを言う。本章で私たちは体重にしか注目していないから、状態は体重を表す値だけからなる。例えば \(100~\text{kg}\) の重りを体重計の上に乗せたなら、\(100~\text{kg}\) という値が状態になる。状態には私たちに関係のある値だけが含まれる。例えば体重計の色は今考えている問題と関係がないので、この問題では状態に含まれない。これに対して体重計を生産する会社の品質管理エンジニアであれば、生産プロセスを追跡・制御するために体重計の色を状態に入れるかもしれない。
観測値 (measurement) とは系を観測して得られる値を言う。観測は不正確である可能性があるので、状態と観測値が同じ値を持たない可能性がある。
状態推定値 (state estimate) とはフィルタを使って推定した状態の値を言う。例えば \(100~\text{kg}\) の重りを体重計に乗せたときの状態推定値は、センサーに誤差があるために \(99.327~\text{kg}\) になるかもしれない。状態推定値は省略して推定値 (estimate) と呼ばれることも多い (本章ではそうしてきた)。
言い換えると、状態は系の実際の値として理解されるべきである。ただし、系を表すこの真の値は隠れている (hidden) 場合が多い。例えば私が体重計に乗ったときに得られるのは観測値であって、真の体重ではない。観測値のように直接観測できる値は観察可能 (observable) であると呼ばれる。これに対して、私の体重を表す真の値を直接取得することはできない。体重は測定できるだけだ。
この「隠れている」と「観測可能である」という概念は重要である。どんな推定問題も、観測可能な観測値を通して隠れた状態の推定値を計算する処理を持つ。推定問題を扱う文献では問題を定義するときにこういった用語を使うので、慣れておく必要がある。
数学的に系をモデル化するときは何らかのプロセスモデル (process model) が仮定される。本章の例では「今日の私の体重は昨日の体重に昨日のゲインを足すと得られる」という仮定がプロセスモデルに当たる。プロセスモデルにはセンサーをモデル化しないし、センサーがプロセスモデルに組み込まれることもない。もう一つ例を出しておくと、自動車では「移動距離は速度と時間の積に等しい」というプロセスモデルが使われるかもしれない。もちろん、このモデルは完璧ではない: 自動車の速度はどんなに小さい時間でも変化するし、タイヤがスリップするかもしれない。このモデルにおける誤差を系誤差 (system error) あるいはプロセス誤差 (process error) と呼ぶ。この値が正確に分かることはない: もし正確に分かったら、それをモデルに取り入れることで誤差の無いモデルが得られてしまう! 文献によってはプラントモデル (plant model) と プラント誤差 (plant error) という言葉が使われることもある。またプロセスモデルがシステムモデル (system model) と呼ばれる場合もある。意味はどれも変わらない。
予測ステップは系伝播 (system propagation) とも呼ばれる。プロセスモデルを使って新しい状態推定値を作る処理が系伝播である。プロセス誤差が存在するために、こうして計算される状態推定値は完璧ではない。時とともに変化するデータを追跡しているときは「状態を未来へ伝播させる」などと表現する場合もある。伝播を発展 (evolution) と呼ぶ文献もある。
更新ステップは観測更新 (measurement update) とも呼ばれる。系伝播と観測更新の反復一度分をまとめてエポック (epoch) と呼ぶ。
このアルゴリズムをさらに理解するために、異なる問題ドメインをいくつか見てみよう。まず線路を走る車両を追跡する問題を考える。車両の位置は線路によって非常に小さな領域に制限される。また、車両は大きくて動きが遅い: 速度を大きく上げたり下げたりするには数分単位の時間がかかる。そのため、例えばもし車両が時刻 \(t\) (秒) においてキロポスト \(23~\text{km}\) 地点を時速 \(18~\text{km}\) で通過したと知っていれば、時刻 \(t + 1\) における車両の位置は大きな自信を持って答えられる。どうしてこれが重要なのだろうか? 車両の位置を \(±250~\text{m}\) の精度でしか観測できないとしよう。車両が時速 \(18~\text{km}\) (秒速 \(5~\text{m}\)) で移動しているとすれば、時刻 \(t + 1\) で車両は \(23.005~\text{km}\) 地点に移動するが、観測値は \(22.505~\text{km}\) から \(23.505~\text{km}\) の間の値となる。よって例えば次の観測値が \(23.4~\text{km}\) だったら、観測値と予測値の差異は誤差によるものだろうと推定できる: 時刻 \(t\) で運転士がブレーキを入れたとしても、車両が一秒で速度を大きく落とすことはないので、車両の位置は \(23.005~\text{km}\) に非常に近くなるためだ。そのためこの問題に対するフィルタを設計する (この章でも後で行う!) ときは、観測ではなく予測に大きな重みを割り当てるフィルタを設計することになる。
次は放り投げられたボールを追跡する問題を考えよう。重力が作用する真空中を運動する物体が放物線を描くことはよく知られているが、地球上で投げられたボールには空気抵抗が働くので完全な放物線にはならない。野球のピッチャーは遅いカーブを投げるときにこの事実を利用する。球場でマウンドから投げられたボールをコンピュータービジョンで追跡したいとしよう (私が仕事で取り組む種類の問題だ)。コンピュータービジョンによる追跡はあまり正確でない。一方で未来の時点におけるボールの位置をボールが放物線を描くとして予測するのも非常に正確とは言えない。そのためこの問題では、観測値と予測値に同程度の重みを与えるフィルタを設計することになる。
続いてハリケーンに巻き込まれた風船を追跡する問題を考えよう。この風船の振る舞いを予測できる正当なモデルは存在せず、非常に短いタイムスケールにおける予測 (例えば「風船が一秒で \(100~\text{km}\) 吹き飛ぶことはない」など) しか行えない。よってこの問題では、予測値ではなく観測値に大きな重みを与えるフィルタを設計することになる。
本書の大部分は、ここまでの三つの段落の内容を数学的に表現することに費やされる。数学的な表現があれば (特定の数学的な意味で) 最適な解が求められるようになる。本章では直感的にそれらしい値を \(g\) と \(h\) に割り当てただけなので、手に入るフィルタが最適とは言えない。しかし土台にあるアイデアは同じである: 系の振る舞いを記述するモデルを使ったいくらか不正確な予測値といくらか不正確な観測値を組み合わせた推定値をフィルタリング結果とすれば、片方だけよりも正確な値が手に入る。
以上の考え方はアルゴリズムとして次のように表せる:
初期化
- フィルタの状態を初期化する。
- 状態に関する信念を初期化する。
予測
- 系の振る舞いのモデルを使って次のステップにおける状態を予測する。
- 予測の不確実性に応じて信念を調整する。
更新
- 観測値とその正確さに関する信念を取得する。
- 予測値と観測値の残差を計算する。
- 残差を表す直線上にある値を新しい推定値として採用する。
本書ではこのアルゴリズムを少しずつ改変しながらずっと使っていく。
1.3 記号
フィルタリングの文献で使われる標準的な記号や変数名をここで紹介する。一部は本書のグラフでも使ってきた。観測値は普通 \(z\) で表されるので、私たちも \(z\) で表す (\(y\) を使う文献もある)。添え字の \(k\) はタイムステップを表し、例えば \(z_k\) は \(k\) 番目の時刻における観測値を表す。ボールドフォントはベクトルまたは行列を表す。これまでは一つのセンサーだけを考えてきたのでセンサーからの観測値も一つだけだったが、一般には \(n\) 個のセンサーからの \(n\) 個の観測値が存在する。状態はベクトルであることを考慮して \(\mathbf{x}\) と表される。体重計の例で言えば、状態 \(\mathbf{x}\) には体重 \(x\) とその変化率 \(\dot{x}\) の両方が含まれる:
ここでは変数の上にドットを付けて変化率を表すニュートンの記法を使っている。正確に言うと、\(x\) にドットを付けると時間に関する \(x\) の微分が表される。微分とはもちろん変化率のことだ。例えば体重が \(62~\text{kg}\) の人の体重が一日に \(0.3~\text{kg}\) のペースで増えているなら、その状態は次のように書ける:
記号が定義されれば、先述のアルゴリズムは簡単に記述できる。最初に状態を初期推測値 \(\mathbf{x}_0\) で初期化してからメインループに入る。メインループでは時刻 \(k-1\) における値から時刻 \(k\) の状態を予測し、観測値 \(\mathbf{z}_k\) を取得し、予測値と観測値の中間にある値を推定値 \(\mathbf{x}_k\) として採用する。
1.4 練習問題: アルゴリズムの一般的な実装
上で示した例では、本章で考えてきた体重計の問題を解くために g-h フィルタのアルゴリズムを明示的にコードにした。そのため例えば weight_scale や gain といった変数が存在する。こうしたのはアルゴリズムを理解しやすくするためだ──正しく実装されていることはステップごとに簡単に確認できる。しかし、そのコードは一つの問題のためだけに書かれている。g-h フィルタのアルゴリズムは任意の問題に適用できる。そこでコードを一般的に──どんな問題に対しても使えるように──書き直してほしい。次の関数シグネチャを使うこと:
def g_h_filter(data, x0, dx, g, h, dt):
"""
固定された g と h を使った g-h フィルタを単一の状態変数に対して適用する
'data': フィルタリングを行うデータ
'x0': 状態変数の初期値
'dx': 状態変数の変化率の初期値
'g': g-h フィルタの g 係数
'h': g-h フィルタの h 係数
'dt': タイムステップの間隔
"""
返り値はリストではなく NumPy 配列とすること。以前の例と同じデータを入力し、結果をプロットして正しさを視覚的に確認せよ。
from kf_book.gh_internal import plot_g_h_results
def g_h_filter(data, x0, dx, g, h, dt):
pass # 解答をここに書く
# コメントを解除するとフィルタを実行して結果をプロットできる
# book_plots.plot_track([0, 11], [160, 172], label='Actual weight')
# data = g_h_filter(data=weights, x0=160., dx=1., g=6./10, h=2./3, dt=1.)
# plot_g_h_results(weights, data)import matplotlib.pylab as pylab
def g_h_filter(data, x0, dx, g, h, dt=1.):
x_est = x0
results = []
for z in data:
# 予測ステップ
x_pred = x_est + (dx*dt)
dx = dx
# 更新ステップ
residual = z - x_pred
dx = dx + h * (residual) / dt
x_est = x_pred + g * residual
results.append(x_est)
return np.array(results)
book_plots.plot_track([0, 11], [160, 172], label='Actual weight')
data = g_h_filter(data=weights, x0=160., dx=1., g=6./10, h=2./3, dt=1.)
plot_g_h_results(weights, data)
print(weights)
print(data)[158.0, 164.2, 160.3, 159.9, 162.1, 164.6, 169.6, 167.4, 166.4, 171.0, 171.2, 172.6]
[159.2 161.8 162.1 160.78 160.985 163.311 168.1 169.696
168.204 169.164 170.892 172.629]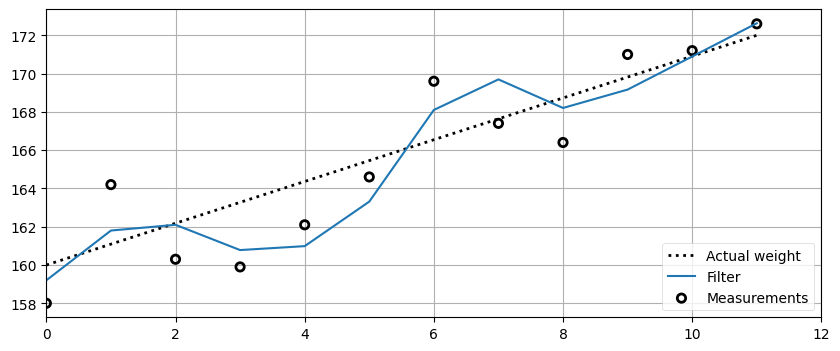
難しいところはないはずだ。体重の問題に対するコードに含まれる変数の名前を x0 や dx にしただけで、他の部分は変わっていない。
1.5 \(g\) と \(h\) の選び方
g-h フィルタは一つのフィルタではない──複数のフィルタを含む族の分類である。Eli Brookner は Tracking and Kalman Filtering Made Easy2 で g-h フィルタに分類される 11 種類のフィルタを示しているが、もっとあることは間違いない。それだけではなく、g-h フィルタに含まれる各フィルタには様々な小分類が存在する。g-h フィルタは \(g\) と \(h\) の選び方によって分類される。\(g\) と \(h\) に定数を設定するフィルタもあれば、動的に値を設定するフィルタもある。カルマンフィルタは各ステップで \(g\) と \(h\) を変更するし、他にも \(g\) と \(h\) を特定の範囲から自由に選べたり、あるいは片方をもう一方から \(g = f(h)\) と求められるような制約が存在したりする。
本書の目的は g-h フィルタの族を全て説明することではない。もっと重要なこととして、私たちの興味はこういったフィルタのベイズ的な側面にある (まだ説明できていないが)。そのため \(g\) と \(h\) の選び方は詳しく説明しない。もし気になるなら、Tracking and Kalman Filtering Made Easy はこの話題に関する素晴らしい資料である。変な説明の順序だと思ったかもしれないが、数学的に g-h フィルタと同じアルゴリズムに帰着されるカルマンフィルタは g-h フィルタの一種であるにもかかわらず、典型的なカルマンフィルタの定式化では \(g\) と \(h\) が全く使われない。カルマンフィルタを設計するときに設定する値は数学的に \(g\) と \(h\) に帰着できるものの、カルマンフィルタが使う定式化の方が問題を考える上でずっと便利なことが多い。この意味が現時点で分からなくても気にすることはない。カルマンフィルタの理論を詳しく説明するとき明らかになる。
そうは言っても \(g\) と \(h\) を変えたときにどのような影響があるかは確認しておくべきだと思うので、いくつか例を示す。この種のフィルタが持つ本来的な強みと弱みがよく理解できるだろう。より洗練されたカルマンフィルタの振る舞いも理解しやすくなるはずだ。
1.6 練習問題: データを生成する関数の作成
まずはノイズの入ったデータを生成する関数を書こう。本書ではノイズを白色ノイズとしてモデル化する。白色ノイズの定義を完全に理解するのに必要な統計の用語は説明できていない。簡単に言うと、白色ノイズは正の値と負の値を同じ確率で、何のパターンも持たずに生成する。これを統計の言葉で「逐次相関性を持たない、分散が有限で平均がゼロの乱数」と言う。今この意味が分からなくても、第 3 章の終わりまで読めば理解できる。この練習問題は統計を知らないと難しいかもしれないので、もし分からないなら解答と考察を見て構わない。
白色ノイズは numpy.random.randn 関数で生成できる。私たちに必要なのは引数に開始値、ステップごとの変化量、ステップ数、そして加えたいノイズの量を受け取り、生成されたデータからなるリストを返す関数である。この関数を実装し、それを使って 30 個のデータ点を生成し、g_h_filter 関数でフィルタリングを行い、plot_g_h_results 関数で結果をプロットせよ。
# 解答をここに書くfrom numpy.random import randn
def gen_data(x0, dx, count, noise_factor):
return [x0 + dx*i + randn()*noise_factor for i in range(count)]
measurements = gen_data(0, 1, 30, 1)
data = g_h_filter(data=measurements, x0=0., dx=1., dt=1., g=.2, h=0.02)
plot_g_h_results(measurements, data)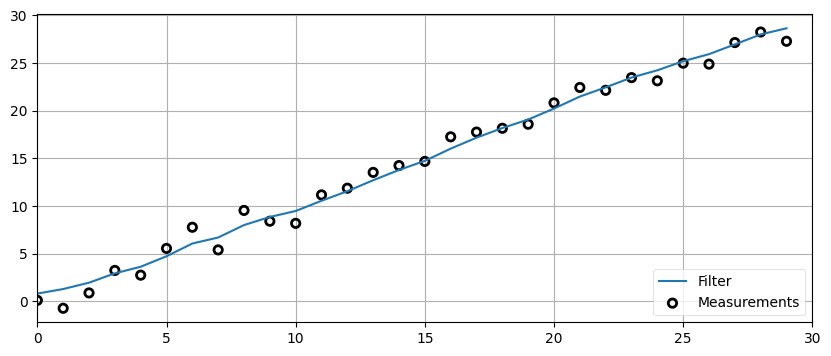
考察
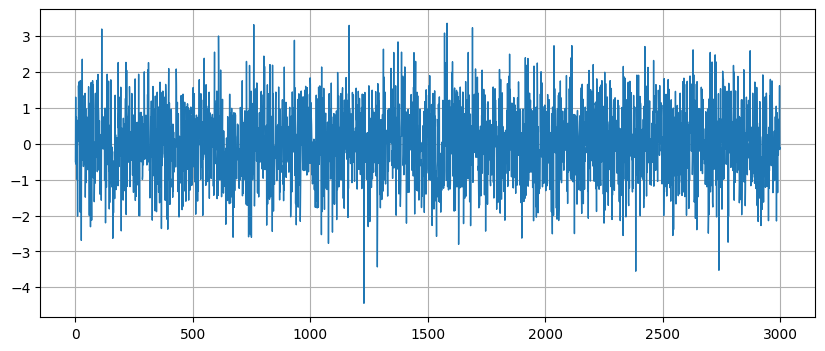
randn は \(0\) を中心とした乱数を返す──そのとき \(0\) より大きい値と \(0\) より小さい値は同じ確率で選択される。また randn の返り値は標準偏差が \(1\) となるように広がる──この言葉の意味が分からなくても今は気にする必要はない。randn 3,000 回分のプロットを次に示す。生成されるデータは \(0\) の近くに多く、小数の例外を除けば \(-2\) の少し下から \(+2\) の少し上までの間 (平均から標準偏差二つ分だけ離れた領域) にほぼ収まっていることが分かる:
1.7 練習問題: 初期条件が悪いときの振る舞い
gen_data と g_h_filter を使って 100 個のデータ点をフィルタリングするコードを書け。データの開始値は 5, 変化率は 2, ノイズのスケーリング係数は 10, g は 0.2, h は 0.02 に設定し、x と dx の初期値はそれぞれ 100 および 2 とすること。
# 解答をここに書くzs = gen_data(x0=5., dx=2., count=100, noise_factor=10)
data = g_h_filter(data=zs, x0=100., dx=2., dt=1., g=0.2, h=0.02)
plot_g_h_results(measurements=zs, filtered_data=data)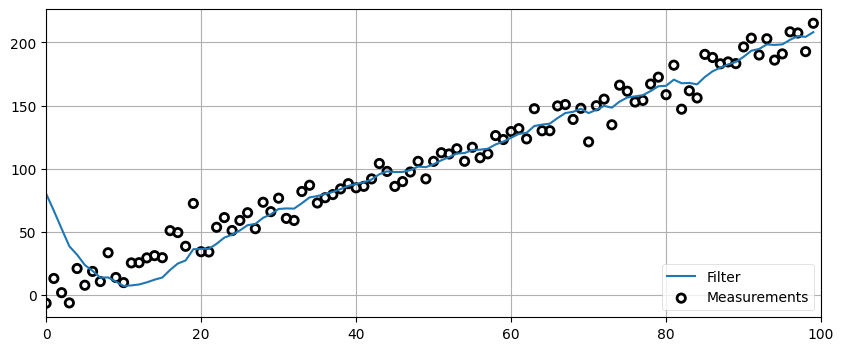
初期推測値 100 が真の値と大きく異なるために、最初フィルタが出力する推定値は観測値から遠く離れた場所にある。またフィルタの出力が観測値とほぼ同じになるまでの間に「リンギング」が起きているのも確認できる。「リンギング (ringing)」とは信号が実際のデータより大きくなったり小さくなったりすること (オーバーシュートとアンダーシュート) を正弦波のように繰り返す現象のことを言う。フィルタリングで非常によく起こる現象であり、フィルタの設計ではリンギングを最小化するために多くの手間が掛けられる。現段階ではこの種の問題を解決することはできないが、知っておいてほしいので言及した。
1.8 練習問題: ノイズが極端に大きいときの振る舞い
前問と同じテストを、ノイズのスケーリング係数を 100 として行え。初期値によるリンギングを抑えるために、初期条件を 100 ではなく 5 とすること。
# 解答をここに書くzs = gen_data(x0=5., dx=2., count=100, noise_factor=100)
data = g_h_filter(data=zs, x0=5., dx=2., g=0.2, h=0.02)
plot_g_h_results(measurements=zs, filtered_data=data)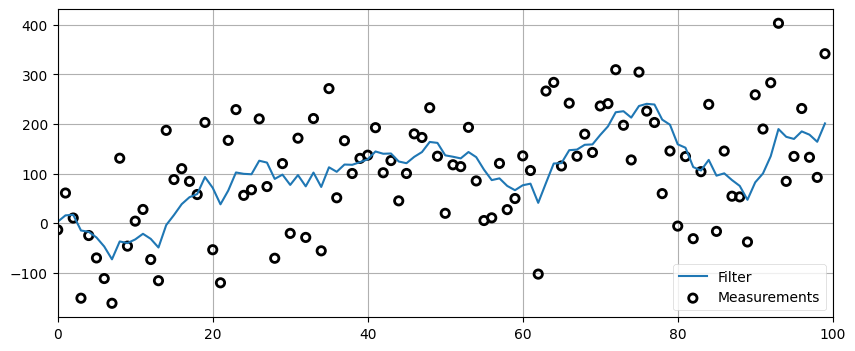
この結果は満足いくものではない。フィルタリング後の信号はノイズの多い入力信号と比べれば変動が小さいものの、直線からは程遠い。フィルタリング後の結果だけをプロットしたら、入力信号が \(5\) から始まってタイムステップごとに \(2\) ずつ増加するとは誰も思わないだろう。フィルタによってノイズが減っている部分もあるが、他の場所ではオーバーシュートやアンダーシュートが起こっている。
この結果が優れているのかどうかは現時点の私たちには判断できない。ノイズを山ほど加えたから、どうフィルタリングしてもこれより上手くできないかもしれない。ただ、本書がまだ始まったばかりであるという事実は、ずっと上手くできることを示唆しているはずだ。
1.9 練習問題: 加速の影響
定数の加速係数を組み込んだデータ生成関数を書け。言い換えると、データ点を計算するたびに dx に定数を加えることで、速度 (dx) が時間の経過とともに大きくなるようにせよ。その関数でノイズを 0 にして生成したデータに対して \(g\) を 0.2、\(h\) を 0.02 に設定した g-h フィルタを適用し、plot_g_h_results (あるいは自分で書いた関数) を使って結果をプロットせよ。異なる加速度とタイムステップをいくつか試し、結果を説明せよ。
# 解答をここに書くdef gen_data(x0, dx, count, noise_factor, accel=0.):
zs = []
for i in range(count):
zs.append(x0 + accel * (i**2) / 2 + dx*i + randn()*noise_factor)
return zs
predictions = []
zs = gen_data(x0=10., dx=0., count=20, noise_factor=0, accel=9.)
data = g_h_filter(data=zs, x0=10., dx=0., g=0.2, h=0.02)
plot_g_h_results(measurements=zs, filtered_data=data)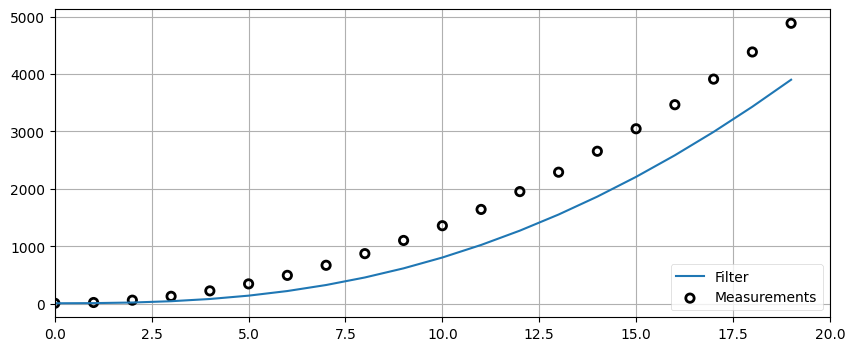
予測値は全て信号に後れを取っている。何が起きているかを考えればこうなる理由を理解できるはずだ。私たちのモデルでは速度が一定であると仮定していた。g-h フィルタは \(x\) の一次微分 \(\dot{x}\) を計算するが、二次微分 \(\ddot{x}\) は計算しない。つまり \(\ddot{x} = 0\) が仮定されており、予測ステップで新しい値は \(x + \dot{x} \cdot dt\) として計算される。しかしこの問題の入力では加速があるので、この予測値は必ず実際の値より小さくなる。その後 \(\dot{x}\) は新しく計算されるものの、\(h\) が存在するために \(\dot{x}\) は部分的にしか調整されない。そのため次の反復ではまた値を実際より小さく予測することになる。
\(g\) と \(h\) をどんな値に設定しようとこの問題は修正できないことに注意してほしい。これは遅延誤差 (lag error) あるいは系統誤差 (systematic error) などと呼ばれる g-h フィルタの基礎的な特徴である。読者の頭にはこの問題の解決法やワークアラウンドが既に浮かんでいるかもしれない。推察の通り、この誤差を小さくするために多くの研究が行われてきた。本書でも様々な手法を紹介する。
家に帰っても覚えておいてほしいポイントはこれだ: フィルタは系を記述するのに使われる数学的モデルと同程度の正確さしか持てない。
1.10 練習問題: \(g\) の変化させたときの影響
\(g\) を変化させたときの影響を見よう。この練習問題を解く前に、\(g\) は観測値と予測値の間から推定値を選ぶときに使われるスケーリング係数であることを思い出してほしい。\(g\) が大きいとき何が起こるだろうか? 小さかったら?
noise_factor=50 および dx=5 としてデータを生成して、g を 0.1, 0.4, 0.8 としたときのフィルタリング結果をそれぞれプロットせよ。
# 解答をここに書くnp.random.seed(100)
zs = gen_data(x0=5., dx=5., count=50, noise_factor=50)
data1 = g_h_filter(data=zs, x0=0., dx=5., dt=1., g=0.1, h=0.01)
data2 = g_h_filter(data=zs, x0=0., dx=5., dt=1., g=0.4, h=0.01)
data3 = g_h_filter(data=zs, x0=0., dx=5., dt=1., g=0.8, h=0.01)
with book_plots.figsize(y=4):
book_plots.plot_measurements(zs, color='k')
book_plots.plot_filter(data1, label='g=0.1', marker='s', c='C0')
book_plots.plot_filter(data2, label='g=0.4', marker='v', c='C1')
book_plots.plot_filter(data3, label='g=0.8', c='C2')
plt.legend(loc=4)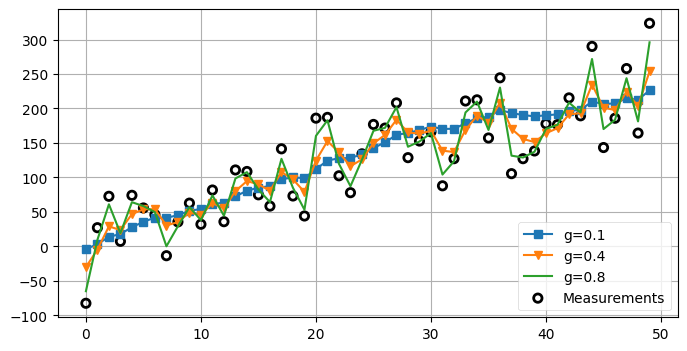
\(g\) を大きくすると出力が予測値から離れて観測値に近づくのが明らかに分かる。\(g=0.8\) のときは入力信号をそのまま出力しているのに近く、ノイズはほとんど減っていない。ここから、ノイズの削減を最大化するにはどんなときでも \(g\) を非常に小さく設定すべきだと考えてしまうかもしれない。しかし、小さい \(g\) は予測値を優先して観測値をほぼ無視することを意味する。入力信号がノイズで変動したのではなく、本当に状態が変わっていたら? 試してみよう。最初の 9 ステップで \(\dot{x}=1\) として、その後は \(\dot{x}=0\) としてデータを作成する:
zs = [5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
for i in range(50):
zs.append(14)
data1 = g_h_filter(data=zs, x0=4., dx=1., dt=1., g=0.1, h=0.01)
data2 = g_h_filter(data=zs, x0=4., dx=1., dt=1., g=0.5, h=0.01)
data3 = g_h_filter(data=zs, x0=4., dx=1., dt=1., g=0.9, h=0.01)
book_plots.plot_measurements(zs)
book_plots.plot_filter(data1, label='g=0.1', marker='s', c='C0')
book_plots.plot_filter(data2, label='g=0.5', marker='v', c='C1')
book_plots.plot_filter(data3, label='g=0.9', c='C3')
plt.legend(loc=4)
plt.ylim([6, 20]);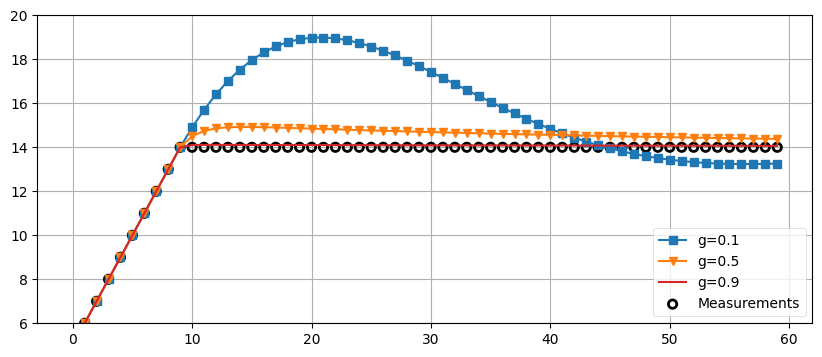
このグラフからは入力信号を無視することの影響が分かる。ノイズをフィルタリングするだけでは不十分で、入力信号の変化も考慮しなければならない。
では私たちに必要なのは "ゴルディロックス" のフィルタなのだろうか? \(g\) が大きすぎず小さすぎない、ちょうどよい値にあるフィルタなら万事解決? 残念ながら、そういうわけでもない。先ほど少し触れたように、\(g\) と \(h\) の値は問題の数学的な特徴を考えて選択しなければならない。例えばベネディクト-ボードナーフィルタは \(\dot{x}\) が定数から定数へジャンプするときの過渡状態における誤差 (transient error, 過渡誤差) を最小化するフィルタとして考案されている。本書ではベネディクト-ボードナーフィルタを説明しないが、このフィルタで許される \(g\) と \(h\) の値の組を使ったフィルタリングを次に示す。\(\dot{x}\) が定数から定数へジャンプするときの過渡誤差は小さくなるが、その代わり他の種類の \(\dot{x}\) の変化に対しては最適ではない。
zs = [5,6,7,8,9,9,9,9,9,10,11,12,13,14,
15,16,16,16,16,16,16,16,16,16,16,16]
data1 = g_h_filter(data=zs, x0=4., dx=1., dt=1., g=.302, h=.054)
data2 = g_h_filter(data=zs, x0=4., dx=1., dt=1., g=.546, h=.205)
book_plots.plot_measurements(zs)
book_plots.plot_filter(data2, label='g=0.546, h=0.205', marker='s', c='C0')
book_plots.plot_filter(data1, label='g=0.302, h=0.054', marker='v', c='C1')
plt.legend(loc=4)
plt.ylim([6, 18]);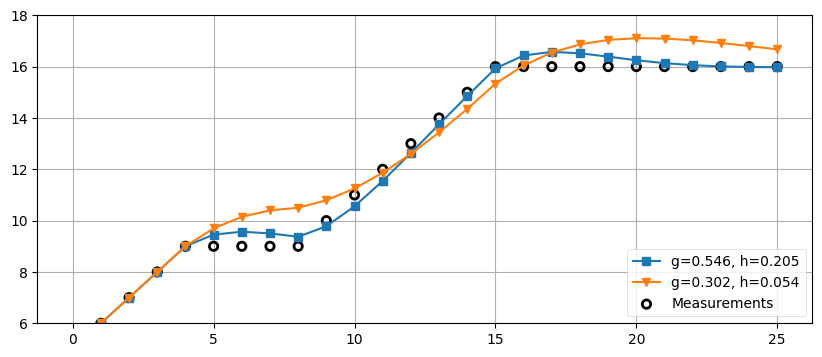
1.11 \(h\) の変化させたときの影響
次は \(g\) を固定して、\(h\) を変化させたときの影響を調べよう。\(h\) は観測された \(\dot{x}\) の値と予測された \(\dot{x}\) の値のどちらを優先するかを定めるのだった。これは何を意味するのだろうか? 入力信号が大きく (フィルタのタイムステップと比べて素早く) 変化するとき、\(h\) が大きいと過渡的変化に素早く反応できる。逆に \(h\) が小さいと反応が遅れる。
次に三つの例を示す。入力にノイズはなく、0 から 1 へ 50 ステップをかけて変化する。一つ目のフィルタはほぼ正しい初期推測値と小さい \(h\) を持つ。このときフィルタの出力は入力信号に非常に近いことがグラフから分かる。二つ目のフィルタは全く間違った初期推測値 \(\dot{x} = 2\) を使っており、ここではフィルタが正しい値に落ち着くまでに「リンギング」を起こしているのが確認できる。三つ目のフィルタは二つ目と同じ初期値を持つが、\(h\) を \(0.5\) まで大きくしている。よく見ると、リンギングの振幅は二つ目のフィルタよりも小さく、周波数は大きくなっている。またリンギングが落ち着くのも少し早いのも分かる。
zs = np.linspace(0, 1, 50)
data1 = g_h_filter(data=zs, x0=0, dx=0., dt=1., g=.2, h=0.05)
data2 = g_h_filter(data=zs, x0=0, dx=2., dt=1., g=.2, h=0.05)
data3 = g_h_filter(data=zs, x0=0, dx=2., dt=1., g=.2, h=0.5)
book_plots.plot_measurements(zs)
book_plots.plot_filter(data1, label='dx=0, h=0.05', c='C0')
book_plots.plot_filter(data2, label='dx=2, h=0.05', marker='v', c='C1')
book_plots.plot_filter(data3, label='dx=2, h=0.5', marker='s', c='C2')
plt.legend(loc=1);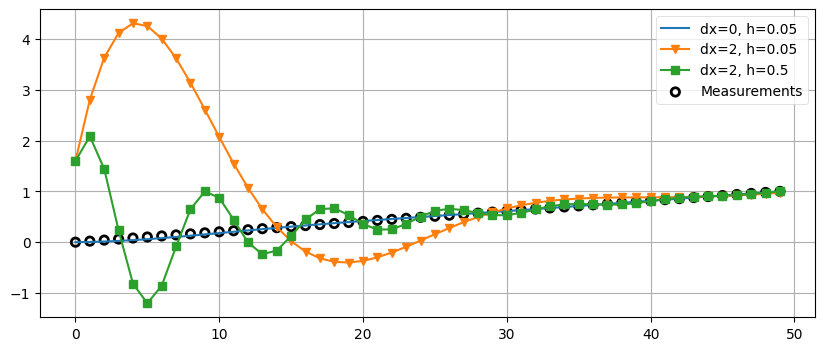
1.12 対話的な例
本書を Jupyter Notebook で読んでいる人に向けて対話的なフィルタを示す。\(\dot{x}\), \(g\), \(h\) を変化させたときのフィルタの振る舞いをリアルタイムで確認できるようになっており、\(\dot{x}\), \(g\), \(h\) に対するスライダーを移動させると入力データに対する再フィルタリングとプロットがその場で行われる。
自分の理解を確認したいなら、次の段落を読んで実際に試す前に何が起こるかを考えるとよい。
まず \(g\) と \(h\) を一番小さくしてみよ。このときフィルタは完璧な出力を生成する! これは初期推測値が完全に正しいためである。その後 \(\dot{x}\) を 5 でない値に設定すると、フィルタの出力は入力データから離れて戻ってこない (発散する)。\(g\) または \(h\) の値を大きくすれば、フィルタの出力がデータを追うようになる。\(g\) だけもしくは \(h\) だけを大きくしたとき、出力の変化はどう違うか? その違いはどう説明できるか? さらに \(g\) を 1 より大きくしてみよ。結果をどう説明できるか? \(g\) を常識的な値 (0.1 など) に戻し、\(h\) を非常に大きくしてみよ。結果をどう説明できるか? \(g\) と \(h\) の両方を最大値にしたらどうなるか?
このコードでさらに実験したいなら、配列 zs の値をこれまでの練習問題や例で使った値に入れ替えてからセルを再実行するとよい。
from ipywidgets import interact
# FloatSlider が返す ipywidgets.FloatSlider では
# continuous_update=False となっている。フィルタリングの実行には
# 時間がかかるので、スライダーの値が変化するたびに再計算を行うのは無理。
from kf_book.book_plots import FloatSlider
zs1 = gen_data(x0=5, dx=5., count=100, noise_factor=50)
def interactive_gh(x, dx, g, h):
data = g_h_filter(data=zs1, x0=x, dx=dx, g=g, h=h)
plt.scatter(range(len(zs1)), zs1, edgecolor='k',
facecolors='none', marker='o', lw=1)
plt.plot(data, color='b')
plt.show()
interact(interactive_gh,
x=FloatSlider(value=0, min=-200, max=200),
dx=FloatSlider(value=5, min=-50, max=50),
g=FloatSlider(value=.1, min=.01, max=2, step=.02),
h=FloatSlider(value=.02, min=.0, max=.5, step=.01));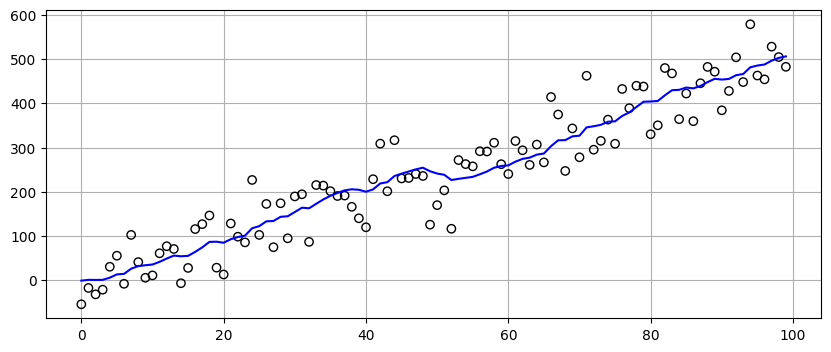
zs = gen_data(x0=5., dx=.2, count=100, noise_factor=100)
data = g_h_filter(data=zs, x0=5., dx=.2, dt=1., g=0., h=0.)
book_plots.plot_measurements(zs)
book_plots.plot_filter(data, label='filter')
plt.legend(loc=1);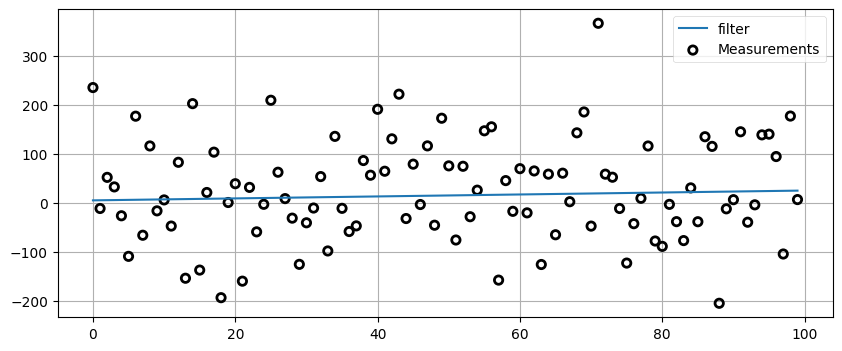
ノイズが大量に入ったデータから直線を鮮やかに取り出した! ただフィールズメダルを受け取る準備をするのはまだ早そうだ。このフィルタは \(g\) と \(h\) を両方とも 0 に設定している。このとき何が起きているのかと言えば、フィルタは観測値を全く考慮せず、新しい位置を常に \(x + dx \cdot dt\) と計算しているのである。観測値を無視すれば直線が手に入るのは当たり前だ。
観測値を無視するフィルタは役に立たない。私だけが持つ超能力を持たない読者は \(g\) と \(h\) を両方 0 に設定することはないと信じているが、気を抜いているときに \(g\) と \(h\) を本来あるべき値より小さく設定してしまうことは間違いなくある。そのとき特定のテストデータに対しては素晴らしい見た目の結果が出力されるのだが、定数をそのデータに対して調整してあるために、異なるデータを試すと残念な結果となる。\(g\) と \(h\) に反映させるべきはフィルタリング対象の系の現実世界における振る舞いであり、特定のデータセットの振る舞いではない。ここで私は注意せよと言うことしかできない。用心しておかないとテストデータでだけ完璧な結果となり、現実のデータではこんな結果になる:
zs = gen_data(x0=5, dx=-2, count=100, noise_factor=5)
data = g_h_filter(data=zs, x0=5., dx=2., dt=1., g=.005, h=0.001)
book_plots.plot_measurements(zs)
book_plots.plot_filter(data, label='filter')
plt.legend(loc=1);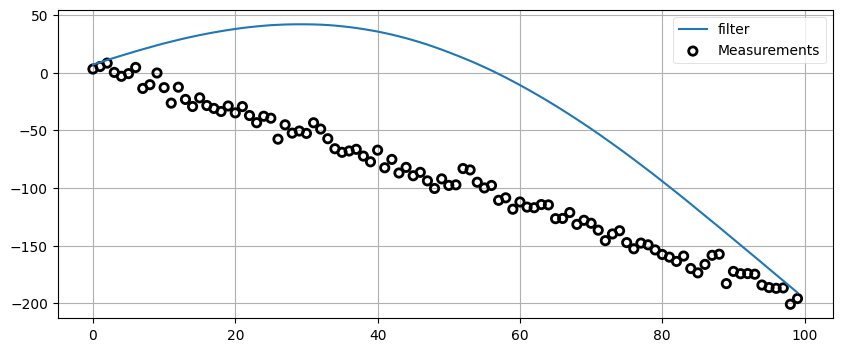
1.14 列車の追跡
以上で実践的な例を見ていく準備が整った。本章の最初の方で車両を追跡する問題について話をした。車両は重くて鈍感なので、速度を素早く変えることができない。また線路の上を走るので、完全に止まってから逆方向に進まない限り方向を変えられない。よって車両の位置と速度の近似値を知ることができれば、近い将来の位置を非常に正確に予測できる。列車の速度が一秒か二秒で大きく変わることはないからだ。
では車両用のフィルタを書いてみよう。車両の位置は線路上のどこかに固定された点からの距離として表されるとする。その固定された点が位置 \(0~\text{km}\) で、そこから線路を \(1~\text{km}\) 進んだ点が位置 \(1~\text{km}\) となる。速度はメートル毎秒で表す。位置の観測を一秒に一度行っていて、その正確さが \(±500~\text{m}\) であるとき、どのようにフィルタを実装するべきだろうか?
まずフィルタは考えずに状況をシミュレートしよう。車両は現在 \(23~\text{km}\) 地点を速度 \(15~\text{m/s}\) で走行中とする。これはコードで次のように書ける:
pos = 23*1000
vel = 15
続いて近い将来における車両の位置を計算する関数を書く。ここでは dt の間に速度が変化しないと仮定している:
def compute_new_position(pos, vel, dt=1):
return pos + (vel * dt)
計算された位置にランダムなノイズを加えることで位置の観測をシミュレートできる。誤差は \(±500~\text{m}\) だったから、コードは次のようになる:
def measure_position(pos):
return pos + random.randn()*500
以上のコードをセルにまとめて、100 秒間のシミュレーションを行おう。次のコードでは NumPy の asarray 関数を使ってデータを NumPy 配列に変換することで、各要素を / でまとめて割れるようにしている:
from numpy.random import randn
def compute_new_position(pos, vel, dt=1.):
""" dt は時間差分 (単位は秒) """
return pos + (vel * dt)
def measure_position(pos):
return pos + randn()*500
def gen_train_data(pos, vel, count):
zs = []
for t in range(count):
pos = compute_new_position(pos, vel)
zs.append(measure_position(pos))
return np.asarray(zs)
pos, vel = 23.*1000, 15.
zs = gen_train_data(pos, vel, 100)
plt.plot(zs / 1000.) # キロメートルに変換する
book_plots.set_labels('Train Position', 'time(sec)', 'km')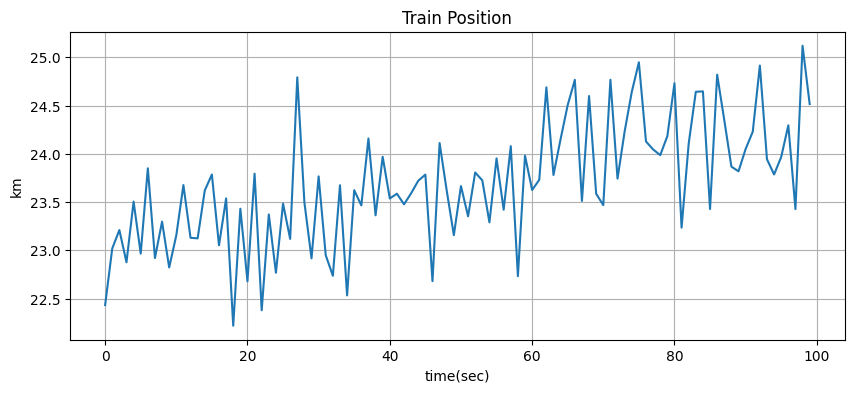
グラフからは観測値が全く正確でないことが分かる。車両はこのように動かない。
このデータのフィルタリングでは \(g\) と \(h\) をどのような値に設定すべきだろうか? このための理論を私たちは知らないから、経験と勘で理にかなった値を選んでみよう。観測値が非常に不正確なことを知っているから、観測値には大きな重みを与えたくない。こうするには \(g\) を非常に小さい値にする必要がある。また車両が大きく加速・減速することもないから、\(h\) の値も非常に小さくていい。例を示す:
zs = gen_train_data(pos=pos, vel=15., count=100)
data = g_h_filter(data=zs, x0=pos, dx=15., dt=1., g=.01, h=0.0001)
plot_g_h_results(zs/1000., data/1000., 'g=0.01, h=0.0001')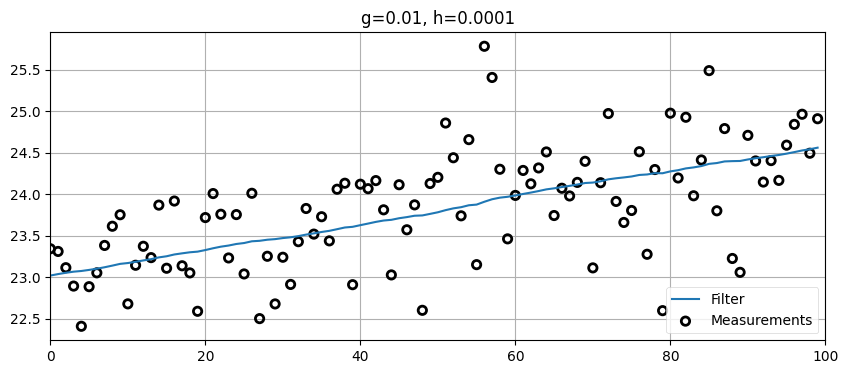
最初に設定した値にしてはかなりいい見た目をしている。\(g\) を大きくするとどうなるかを見よう:
zs = gen_train_data(pos=pos, vel=15., count=100)
data = g_h_filter(data=zs, x0=pos, dx=15., dt=1., g=.2, h=0.0001)
plot_g_h_results(zs/1000., data/1000., 'g=0.2, h=0.0001')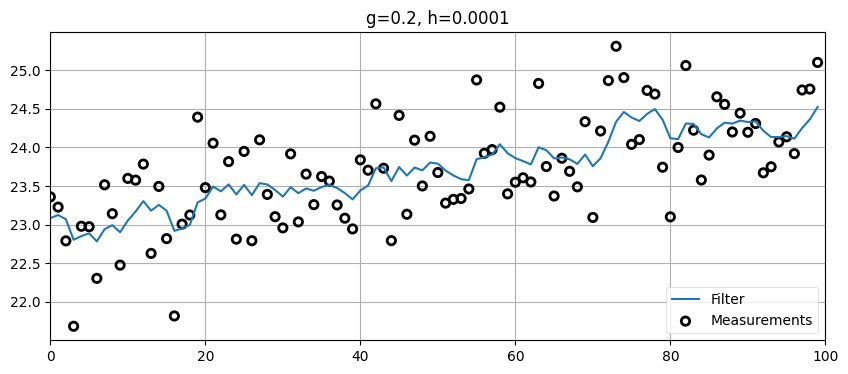
g=0.2 にすると、出力は入力より多少滑らかになっているものの、推定される位置 (および速度) が短い時間間隔で大きく変動しており、全く現実の車両らしくないことが分かる。ここから g << 0.2 が望ましいのだろうと経験的に分かる。
\(h\) に悪い値を設定したらどうなるかも確認しておく:
zs = gen_train_data(pos=pos, vel=15., count=100)
data = g_h_filter(data=zs, x0=pos, dx=15., dt=1., g=0.01, h=0.1)
plot_g_h_results(zs/1000., data/1000., 'g=0.01, h=0.1')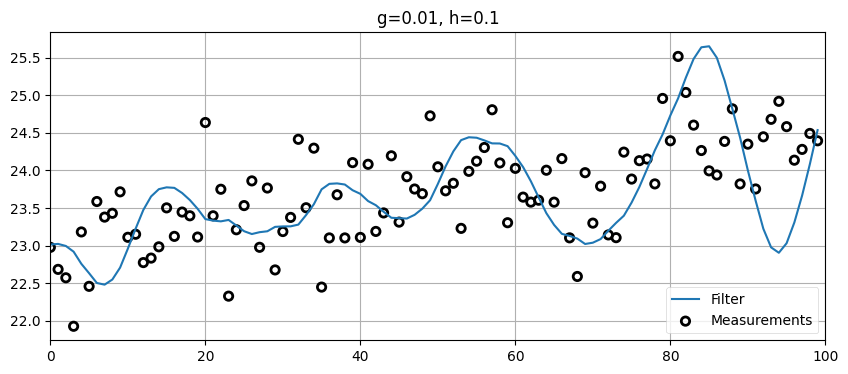
\(g\) が小さいために位置の変化は滑らかだが、\(h\) が大きいのでフィルタは観測値に大きく影響を受ける。これが起こるのは数秒間で起こる急激な観測値の変化が大きな速度変化とみなされ、\(h\) が大きいためにその速度変化が素早くフィルタに反映されるためである。現実の車両は速度を機敏に変えられないので、このフィルタは正しくデータをフィルタリングできていない──フィルタの出力が示す速度は現実の車両が行えるよりも激しく変化している。
最後に、車両に加速を加えてみよう。現実の車両の加速度を私は知らないが、ここでは \(0.2~\text{m/s²}\) で加速しているとする:
def gen_train_data_with_acc(pos, vel, count):
zs = []
for t in range(count):
pos = compute_new_position(pos, vel)
vel += 0.2
zs.append(measure_position(pos))
return np.asarray(zs)zs = gen_train_data_with_acc(pos=pos, vel=15., count=100)
data = g_h_filter(data=zs, x0=pos, dx=15., dt=1., g=.01, h=0.0001)
plot_g_h_results(zs/1000., data/1000., 'g=0.01, h=0.0001')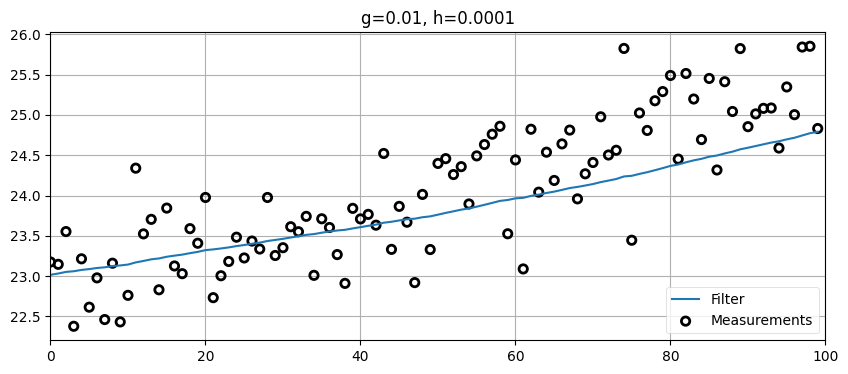
車両が加速するために、フィルタがもはや車両を正確に追跡できなくなる。\(h\) を調整すれば改善できるが、そうすると推定値は滑らかでなくなる:
zs = gen_train_data_with_acc(pos=pos, vel=15., count=100)
data = g_h_filter(data=zs, x0=pos, dx=15., dt=1., g=.01, h=0.001)
plot_g_h_results(zs/1000., data/1000., 'g=0.01, h=0.001')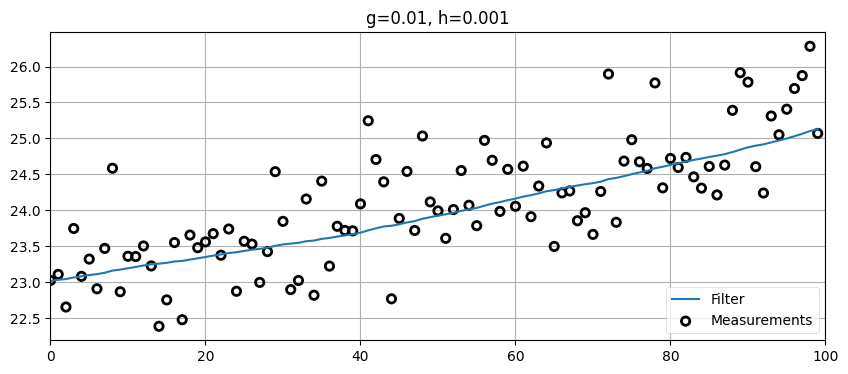
ここからは二つの教訓が学べる。一つ目の教訓は \(h\) を大きくするとモデルに含まれない速度の変化に素早く反応できるようになること。そしてより重要なもう一つの教訓は、入力の変化に対する素早い正確な反応とモデルが想定する定常状態を反映した理想的な出力の生成の間にトレードオフが存在することである。もし車両が速度を決して変えないなら、\(h\) を極端に小さくしてフィルタが出力する推定値が観測値のノイズに過度に影響されないようにするべきだ。しかし私たちが興味のあるデータではまず間違いなく状態が変化し、その変化には素早く反応できるのが望ましい。一方で反応を素早くすると、それだけフィルタの出力はセンサーが持つノイズに影響されやすくなる。
さらに踏み込んだ話もできるかもしれないが、ここでの狙いは g-h フィルタの理論を細かく解説することではなく、観測値と予測値を組み合わせてフィルタリング後の推定値を計算する処理を深く理解することである。こういった問題における \(g\) と \(h\) の選び方を論じた文献は大量に存在し、様々な目標を達成するために最適な \(g\) と \(h\) の選び方も示されている。前述したように、こういったテストデータで実験しているときは簡単にフィルタへ "嘘" をつける。以降の章ではカルマンフィルタがこの問題をどのように解決するのかを見ていく。土台にある考え方は同じだが、ずっと高度な数学が使われる。
1.15 FilterPy による g-h フィルタ
FilterPy は私が開発したオープンソースのフィルタリングライブラリである。本書で登場するフィルタが全て実装されており、他のフィルタもいくつか実装されている。g-h フィルタを自分でプログラムをするのは非常に簡単だが、本書を読み進めると FilterPy に頼ることが増える。簡単な紹介として、ここで FilterPy の g-h フィルタに触れておく。
FilterPy がインストールされていないなら、最初に次のコマンドをコマンドラインから実行する:
pip install filterpy
FilterPy を GitHub からインストール・ダウンロードする方法について詳しくは 補遺 A を参照してほしい。
g-h フィルタを使うには、GHFilter クラスをインポートしてインスタンスを作成する:
from filterpy.gh import GHFilter
f = GHFilter(x=0., dx=0., dt=1., g=.8, h=.2)インスタンスを構築するときは、入力信号の初期値 x, 初期変化率 dx, 更新ごとのタイムステップ dt, そして二つのフィルタパラメータ g と h を指定する。dx は x/dt と同じ単位を持つ必要がある──例えば x がメートルで dt が秒なら、dx はメートル毎秒でなければならない。
フィルタを実行するには update を呼び出す。そのときパラメータ z に観測値を渡す。\(z\) は様々な文献で観測値を表すのに使われる標準的な名前である:
f.update(z=1.2)(0.96, 0.24)update は新しい x と dx の値からなるタプルを返す。この二つの値はフィルタオブジェクトからもアクセスできる:
print(f.x, f.dx)0.96 0.24g と h は途中で変更できる:
print(f.update(z=2.1, g=.85, h=.15))(1.965, 0.375)観測値の列をバッチとして渡すこともできる:
print(f.batch_filter([3., 4., 5.]))[[1.965 0.375]
[2.868 0.507]
[3.875 0.632]
[4.901 0.731]]複数の独立変数をフィルタリングすることもできる。例えば航空機を追跡するときは三次元空間で追跡しなければならないはずだ。これは x, dx と観測値に対して NumPy 配列を使うと行える:
x_0 = np.array([1., 10., 100.])
dx_0 = np.array([10., 12., .2])
f_air = GHFilter(x=x_0, dx=dx_0, dt=1., g=.8, h=.2)
f_air.update(z=np.array((2., 11., 102.)))
print(' x =', f_air.x)
print('dx =', f_air.dx) x = [ 3.8 13.2 101.64]
dx = [8.2 9.8 0.56]GHFilterOrder クラスを使うと、次数が 0, 1, 2 のフィルタを作成できる。g-h フィルタの次数は 1 である。g-h-k フィルタという、本書では説明していない次数が 2 のフィルタを使うと加速度も追跡できる。GHFilter と GHFilterOrder はどちらも分散低減係数 (variance reduction factor, VRF) の計算といった現実のアプリケーションで必要となる機能を持つ。この本の残りを g-h フィルタの理論と応用だけで埋めることもできるが、私たちは他にも目標がある。もし興味があるなら、FilterPy のコードや他の文献に目を通してみるとよい。
FilterPy のドキュメントは https://filterpy.readthedocs.org/ にある。
1.16 まとめ
g-h フィルタで実験を行い、フィルタの反応をよく理解しておくことを勧める。少し試せば、\(g\) と \(h\) をアドホックに選ぶだけでは優れた結果が得られないことが分かるはずだ。ある値の組が特定の状況で上手く動作しても、他の状況には全く対応できなかったりする。\(g\) と \(h\) の影響をきちんと理解したとしても、適切な値を選ぶのは難しい場合がある。実を言えば、選択した \(g\) と \(h\) が与えられた適当な問題に対して最適になる可能性はほぼ存在しない。フィルタは設計されるべきであり、アドホックに選択されるべきではない。
\(g\) と \(h\) の選択については話題がたくさんあるので、ここで章を終えたくない気持ちもある。しかし、この形の g-h フィルタは本書の本題ではない。カルマンフィルタの設計では様々なパラメータの指定が必要になる──これは \(g\) と \(h\) を間接的に選ぶことに近いのだが、カルマンフィルタを設計するときに \(g\) と \(h\) が直接登場することはない。さらに \(g\) と \(h\) はステップごとにかなり非自明な形で値を変える。
こういったフィルタに関連する話題で私たちがほとんど触れていないものがもう一つある──ベイズ統計だ。本書のタイトルに「ベイズ」という言葉があるが、これは偶然ではない! \(g\) と \(h\) は詳しく調べないまま脇において、次章ではフィルタリングに関する確率的推論を非常に強力な形式で解説する。解説を進めると突然 g-h フィルタと同じアルゴリズムが登場する。そのときに手にしている数学体系を使うと、同じアルゴリズムで複数のセンサーからの入力を受け取れるフィルタを作ったり、解に含まれる誤差を正確に推定したり、ロボットを制御したりできるようになる。
-
訳注: ここで「体重計の誤差が \(\pm X\) ポンド」とは、「真の体重が \(x\) ポンドのとき、観測値は \(x-X\) から \(x+X\) までの任意の値を同じ確率で取る」を意味する。この仮定の下では、\(x-X\) より小さい値と \(x+X\) より大きい値は一切観測されない。[return]
-
Eli Brookner, Tracking and Kalman Filtering Made Easy, Wiley-Interscience, 1998.[return]