第 4 章一次元カルマンフィルタ

これで離散ベイズフィルタとガウス分布が理解できたので、カルマンフィルタを実装する準備が整った。カルマンフィルタの実装は離散ベイズフィルタと同じように行う──数式から始めるのではなく、問題について考えることで段階を踏んでコードを書いていく。

「一次元」フィルタとは追跡する状態変数が一つだけ (例えば \(x\) 軸上における位置だけ) であることを意味する。複数の状態変数 (例えば位置・速度・加速度など) を同時に追跡できる一般的な多次元フィルタは以降の章で学ぶ。g-h フィルタでは位置だけではなく速度も追跡することで優れた結果が得られていたことを思い出してほしい。同じことはカルマンフィルタでも起こる。

では最初から多次元のフィルタを説明しないのはなぜか？正直に言うと、説明に必要な数学が難しいために、直感的にフィルタを開発していく私のアプローチが上手く行かなくなるからだ。難しい数学によってカルマンフィルタを支えるごく簡単な考え方が分かりにくくなってしまう。

というわけで、本章ではガウス分布を使ってベイズフィルタを実装する方法を学ぶ。これが──ガウス分布を使うベイズフィルタが──まさにカルマンフィルタである。次章でそのフィルタを多次元の形式に書き換えると、カルマンフィルタの完全な力が解き放たれる！

4.1 問題の説明

離散ベイズフィルタの章と同様に、職場にある長い廊下を動き回る物体 (犬) を追跡する問題を考える。犬の位置をそれなりに正確に報告する RFID トラッカーをこの前のハッカソンで誰かが作成し、このセンサーは廊下の左端から犬までの距離 (単位はメートル) を報告するとしよう。例えばセンサーが \(23.4\) を報告したら、それは廊下の左端から \(23.4~\text{m}\) の地点に犬がいることを意味する。

しかしこのセンサーは完璧ではない。センサーからの出力が \(23.4\) だったとしても、犬は \(23.7~\text{m}\) あるいは \(23.0~\text{m}\) の地点にいる可能性がある。ただ \(47.6~\text{m}\) 地点にいる確率は非常に低いだろう。ハッカソン中に行ったテストでもこの結果が確認されている──センサーは "それなりに" 正確であり、誤差があるものの小さい。加えて、誤差は真の値から両方向に同じ確率で現れることも分かった。例えば犬が \(23~\text{m}\) 地点にいるなら、\(22.9\) と \(23.1\) は同じ確率で観測される。おそらくこの誤差はガウス分布でモデル化できるだろう。

犬は動いていると予測する。この予測は完璧ではなく、オーバーシュートすることもあればアンダーシュートすることもあるだろう。ただ大きいオーバーシュート/アンダーシュートよりも小さいオーバーシュート/アンダーシュートの方が起こりやすい。これもガウス分布でモデル化できそうだ。

4.2 信念をガウス分布で表す

犬の位置に関する信念はガウス分布を使って表現できる。追跡している犬が \(10~\text{m}\) 地点にいると信じていて、その信念の分散は \(1~\text{m²}\) だとしよう。このとき犬の位置に関する信念は \(\mathcal{N}(10,\, 1)\) で表現できる。このガウス分布の PDF をプロットすると次のようになる:

In [3]

import filterpy.stats as stats
stats.plot_gaussian_pdf(mean=10., variance=1., xlim=(4, 16), ylim=(0, .5));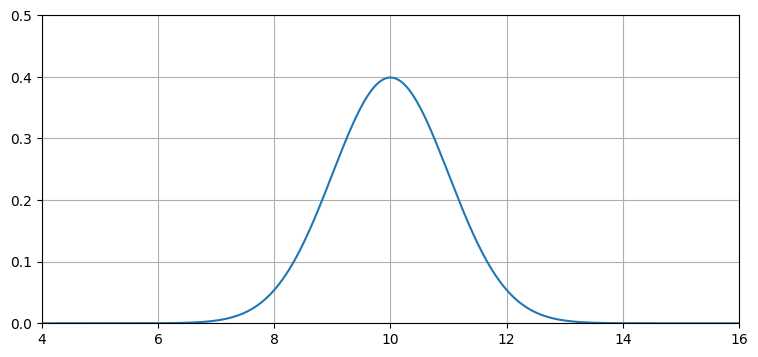

このグラフは犬の位置が正確には分からないことを示している。このガウス分布が表すのはかなり不正確な信念と言える: 私たちは犬が \(10~\text{m}\) 地点にいる可能性が最も高いと信じてはいるものの、\(9~\text{m}\) と \(11~\text{m}\) の間の任意の位置も十分あり得ると思っている。さて、もう一度センサーから値を取得したところ、\(10.2~\text{m}\) だったとする。まだ犬は動いていないとして、この新しい情報は推定値を改善するだろうか？

直感的には改善しそうに思える。例えばセンサーから値を 500 回取得したとして、その全てが \(8\) と \(12\) の間にあり、\(10\) の周りの値が多かったとすれば、犬が \(10~\text{m}\) 地点にいることに大きな自信を持てる。もちろん違う解釈もできる: 「犬はランダムに左右に動いており、その動きの観測値がたまたま正規分布のように見えたのだ」と主張できるかもしれない。しかしその可能性は非常に低く思える──そんな動きをする犬は見たことがない。\(\mathcal N(10, 1)\) から 500 個の値を取得してプロットしてみよう:

In [4]

import numpy as np
from numpy.random import randn
import matplotlib.pyplot as plt

xs = range(500)
ys = randn(500)*1. + 10.
plt.plot(xs, ys)
print(f'出力の平均は {np.mean(ys):.3f}')

Out [4]

出力の平均は 9.941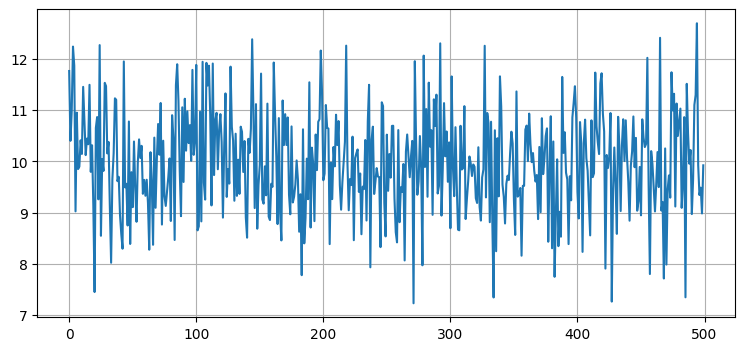

これを見れば直感が正しいと分かる──こんな動きをする犬は存在しない。しかしノイズの含まれるセンサーデータならこのような値を示す。計算された出力値の平均はほぼ \(10\) に等しい。犬がじっとしていると仮定すれば、犬は位置 \(10\) にいて観測値の分散は \(1\) だと言える。

4.3 ガウス分布を使った追跡

離散ベイズフィルタでは確率のヒストグラムを使って犬を追跡した。ヒストグラムの縦棒のそれぞれが位置を表し、縦棒の高さで犬がその位置にいる確率を表す。

追跡は予測と更新のサイクルを繰り返すことで行われ、新しい確率分布の計算には次の等式が使われた:

\[ \begin{aligned} \bar {\mathbf x} &= \mathbf x \ast f_{\mathbf x}(\bullet)\, \, &\text{予測} \\ \mathbf x &= \mathcal L \cdot \bar{\mathbf x}\, \, &\text{更新} \end{aligned} \]

\(\bar{\mathbf x}\) は事前分布、\(\mathcal L\) は事前分布 \(\bar{\mathbf x}\) を仮定したときの観測値の尤度、\(f_{\mathbf x}(\bullet)\) はプロセスモデル、\(\ast\) は畳み込みを表す。\(\mathbf x\) は数値のヒストグラム (つまりはベクトル) であることを示すために太字になっている。

この方法で追跡は行えるものの、犬が複数の場所に同時に存在することを示唆するヒストグラムが得られてしまう。また大規模な問題に対しては計算が遅くなる。

ヒストグラム \(\mathbf x\) をガウス分布 \(\mathcal N(x, \sigma^2)\) に置き換えられないだろうか？もちろんできる！信念をガウス分布で表す方法は学んだから、二つの数値の組で表されるガウス分布 \(\mathcal N(\mu, \sigma^2)\) で確率を表すヒストグラムを丸ごと置き換えることができる:

In [5]

import kf_book.kf_internal as kf_internal
kf_internal.gaussian_vs_histogram()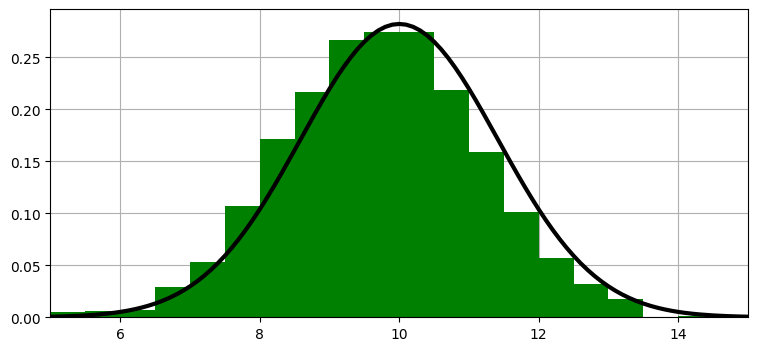

読者がガウス分布の力を感じられていることを願う。ガウス分布を使えば、数十万個に達する可能性のある数値をわずか二つの数値に置き換えられる。

ガウス分布の裾は両側に無限に伸びるから、ガウス分布を使えばヒストグラムに含まれる縦棒をいくらでも考えに入れることができる。ガウス分布で廊下にいる犬の位置を表すとしたら、一つのガウス分布で廊下全体 (さらにはその軸上にある実数全体) をカバーできる。私たちの考えでは犬が位置 \(10\) にいる可能性が最も高いものの、\(8\) や \(10\) にいる可能性もあるし、\(10^{80}\) にいる可能性も (限りなく \(0\) に近いが) 存在する。

本章では次のようにしてヒストグラムをガウス分布に取り換える:

\[ \begin{array}{l|l|c} \text{離散ベイズ} & \text{ガウス分布} & \text{ステップ} \\ \hline \bar {\mathbf x} = \mathbf x \ast f(\mathbf x) & \bar{x}_{\mathcal{N}} = x_{\mathcal{N}} \, \oplus \, f_{x_{\mathcal{N}}}(\bullet) & \text{予測} \\ \mathbf x = \|\mathcal L \bar{\mathbf x}\| & x_{\mathcal{N}} = L \, \otimes \, \bar{x}_{\mathcal{N}} & \text{更新} \end{array} \]

\(\oplus\) と \(\otimes\) は私たちがまだ知らないガウス分布に対する演算を意味する。\(x_{\mathcal{N}}\) に付いている添え字の \(\mathcal{N}\) は変数がガウス分布に従うことを示す (分かりやすいように付けているだけで、これ以降この添え字を使うことはない)。

離散ベイズフィルタは予測で畳み込みを行う。この畳み込みが全確率の定理の等式を和として計算することに等しいと前章で示したから、同様にガウス分布も足せるかもしれない。また観測値を事前分布に組み入れるときは乗算を使ったから、ここでもガウス分布を乗じればいいかもしれない。もしそうなら簡単だ:

\[ \begin{aligned} \bar x &\stackrel{?}{=} x + f_x(\bullet) \\ x &\stackrel{?}{=} \mathcal L \cdot \bar x \end{aligned} \]

これはガウス分布の和と積がガウス分布になるときにだけ正しい。そうでなければ最初のエポックの後に \(x\) がガウス分布ではなくなり、この手法は上手く動かなくなる。

4.4 ガウス分布を使った予測

現在の速度と前回の位置があれば、ニュートンの運動方程式から現在の位置が計算できる:

\[ \begin{aligned}\bar{x}_k &= x_{k-1} + v_k \Delta t \\ &= x_{k-1} + f_x\end{aligned} \]

式を簡単にするために \(f_x(\bullet)\) を \(f_x\) と表記している。

犬が \(10~\text{m}\) 地点にいて、速度が \(15~\text{m/s}\) とする。エポックが二秒間隔だとすれば、

\[ \begin{aligned} f_x &= v\Delta t = 15\cdot 2\\ \bar{x}_k &= 10 + (15\cdot 2) = 40 \end{aligned} \]

が成り立つ。しかし犬の位置と速度は正確には分からないから、いま行いたいのはこの計算ではない。ガウス分布を使って不確実性を表す必要がある。

位置については簡単で、\(x\) をガウス分布として定義すればいい。例えば犬が \(10~\text{m}\) 地点にいると思っていて、その信念の不確実性を標準偏差で表すと \(0.2~\text{m}\) だとすれば、\(x=\mathcal N(10, 0.2^2)\) となる。

移動量の不確実性はどう表現すればよいだろうか？ \(f_x\) をガウス分布として定義することになる。犬の速度が \(15~\text{m/s}\) でエポックが 1 秒ごと、移動量の不確実性が標準偏差で表すと \(0.7~\text{m/s}\) だとすれば、\(f_x = \mathcal N (15, 0.7^2)\) となる。

このとき事前分布を計算する方程式は

\[ \bar x = x + f_x \]

となる。ガウス分布に従う二つの独立な確率変数があるとき、それらの和はどのような分布に従うだろうか？前章で証明したように和も正規分布となり、平均と分散は次の関係を満たす:

\[ \begin{aligned} \mu &= \mu_1 + \mu_2 \\ \sigma^2 &= \sigma^2_1 + \sigma^2_2 \end{aligned} \]

これは素晴らしいニュースだ: ガウス分布に従う変数を足すとまたガウス分布が現れる！

以上が数学的な説明だが、直感的に理解できただろうか？この抽象的な方程式を具体的に考えてみよう。先ほど考えた例では

\[ \begin{aligned} x &= \mathcal N(10, 0.2^2)\\ f_x &= \mathcal N(15, 0.7^2) \end{aligned} \]

だったから、二つのガウス分布を足すと次を得る:

\[ \begin{aligned} \bar x &= \mu_x + \mu_{f_x} = 10 + 15 = 25 \\ \bar\sigma^2 &= \sigma_x^2 + \sigma_{f_x}^2 = 0.2^2 + 0.7^2 = 0.53 \end{aligned} \]

予測された位置が前回の位置に移動量を足したものであることに不思議はない。しかし分散についてはどうだろうか？こちらは直感的に理解するのが難しい。ただ離散ベイズフィルタで predict 関数を呼ぶたびに必ず情報が失われていたことを思い出してほしい。犬の移動量が正確には分からないから、犬の位置に関する自信は小さく (分散は大きく) なる。\(\sigma_{f_x}^2\) は移動の予測が不完全なために系へ追加される不確実性の量であり、これが元の不確実性に足されている。

Python の collection モジュールにある namedtuple クラスを利用して、ガウス分布を表すオブジェクトを実装してみよう。もう一つの選択肢としては普通のタプルを使って \(\mathcal N(10, 0.04)\) を g = (10., 0.04) などと表す方法がある。このとき平均には g[0] とアクセスでき、分散には g[1] とアクセスできる。

namedtuple は基本的にはタプルと同様に動作するが、型とフィールドに名前を付けられる点が異なる。理解しなくても構わないが、次のコードでは作成したオブジェクトの __repr__ メソッドを改変することで print を使ったときに本章と同じ記法で表示されるようにしている:

In [6]

from collections import namedtuple
gaussian = namedtuple('Gaussian', ['mean', 'var'])
gaussian.__repr__ = lambda s: '𝒩(μ={:.3f}, 𝜎²={:.3f})'.format(s[0], s[1])

このときガウス分布を表すオブジェクトは次のように作成できる:

In [7]

g1 = gaussian(3.4, 10.1)
g2 = gaussian(mean=4.5, var=0.2**2)
print(g1)
print(g2)

Out [7]

𝒩(μ=3.400, 𝜎²=10.100)
𝒩(μ=4.500, 𝜎²=0.040)

平均と分散には添え字もしくはフィールドの名前を使ってアクセスできる:

In [8]

g1.mean, g1[0], g1[1], g1.var

Out [8]

(3.4, 3.4, 10.1, 10.1)

predict 関数の完全な実装を次に示す。pos と movement はガウス分布を表す \((\mu,\ \sigma^2)\) という形をした名前付きタプルである:

In [9]

def predict(pos, movement):
    return gaussian(pos.mean + movement.mean, pos.var + movement.var)

テストしてみよう。初期位置がガウス分布 \(\mathcal N(10, 0.2^2)\) で移動量がガウス分布 \(\mathcal N (15, 0.7^2)\) のとき、事前分布を求めるとこうなる:

In [10]

pos = gaussian(10., .2**2)
move = gaussian(15., .7**2)
predict(pos, move)

Out [10]

𝒩(μ=25.000, 𝜎²=0.530)

計算された事前分布は犬が \(25~\text{m}\) 地点にいて分散が \(0.53~\text{m²}\) と主張しており、手で計算した値と一致する。

4.5 ガウス分布を使った更新

離散ベイズフィルタは犬の位置に関する信念を確率が並んだヒストグラムとして表す。離散ベイズフィルタが使う確率分布は離散的かつ多峰性なので、位置は離散的に表現され、二つの位置に対して高い信念が同時に割り当てられることもある。

私たちは現在ヒストグラムをガウス分布で置き換えることを提案している。離散ベイズフィルタでは事後分布の計算を次のコードで行った:

def update(likelihood, prior):
    posterior = likelihood * prior
    return normalize(posterior)

これは次の等式を実装する:

\[ x = \| \mathcal L\bar x \| \]

事前分布をガウス分布として表せることはちょうど先ほど証明した。尤度についてはどうだろうか？尤度とは現在の状態における観測値の確率である。観測値をガウス分布として表現する方法はこれまでに学んだ。例えば犬が \(23~\text{m}\) 地点にいて標準偏差が \(0.4~\text{m}\) だとセンサーが報告したなら、観測値は尤度として \(z = \mathcal N (23, 0.16)\) と表せる。

以上で尤度と事前分布の両方がガウス分布として表せた。ガウス分布の確率密度関数の積を考えることはできるだろうか？これもガウス分布の確率密度関数だろうか？

一つ目の質問の答えは「できる」で、二つ目の質問の答えは「ほぼそうなる」である。前章で示したように、ガウス分布の確率密度関数を二つ乗じるとガウス関数となる。そのとき積の平均 \(\mu\) と分散 \(\sigma\) は次の関係を満たす:

\[ \begin{aligned} \mu &= \frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2} \\ \sigma^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{aligned} \]

ここから分かることがいくつかある。まず、この積を正規化すればガウス分布の確率密度関数となる。次に、一つのガウス分布が尤度を、もう一つのガウス分布が事前分布を表すとすれば、積の平均は事前分布と観測値の重み付き和となっている。また、積の分散は事前分布の分散と観測値の分散を組み合わせた値である。最後に、積の分散は平均から全く影響を受けない！

これをベイズ的な考え方で書き直すと、次のようになる:

\[ \begin{aligned} \mathcal N(\mu, \sigma^2) &= \| \text{事前分布} \cdot \text{尤度} \|\\ &= \| \mathcal{N}(\bar\mu, \bar\sigma^2)\cdot \mathcal{N}(\mu_z, \sigma_z^2) \|\\ &= \mathcal N \left(\frac{\bar\sigma^2 \mu_z + \sigma_z^2 \bar\mu}{\bar\sigma^2 + \sigma_z^2},\ \frac{\bar\sigma^2\sigma_z^2}{\bar\sigma^2 + \sigma_z^2} \right) \end{aligned} \]

これを gaussian_multiply 関数として実装すれば、フィルタの更新ステップはこう書ける:

In [11]

def gaussian_multiply(g1, g2):
    mean = (g1.var * g2.mean + g2.var * g1.mean) / (g1.var + g2.var)
    variance = (g1.var * g2.var) / (g1.var + g2.var)
    return gaussian(mean, variance)

def update(prior, likelihood):
    posterior = gaussian_multiply(likelihood, prior)
    return posterior

# update 関数のテスト
predicted_pos = gaussian(10., .2**2)
measured_pos = gaussian(11., .1**2)
estimated_pos = update(predicted_pos, measured_pos)
estimated_pos

Out [11]

𝒩(μ=10.800, 𝜎²=0.008)

具体的な名前を付けるともっと分かりやすいかもしれない:

def update_dog(dog_pos, measurement):
    estimated_pos = gaussian_multiply(measurement, dog_pos)
    return estimated_pos

こうすれば抽象的でなくなって (おそらくは) 理解しやすくなるものの、コードの書き方として褒められたものではない。私たちが書いているのは廊下にいる犬の追跡だけではなく任意の問題に対して適用できるカルマンフィルタなのだから、変数名に dog は入れない方がいい。さらに更新ステップで事前分布と尤度を乗じているという事実も見えにくくなってしまう。

これでフィルタは大部分が実装できたが、この更新ステップが分かりにくいのではないかと私は心配している。二つのガウス分布を乗じると正しく更新ステップが計算できると説明したが、それが正しいのはなぜだろうか？少し回り道をして、ガウス分布の積について考えよう。

ガウス分布の積を理解する

確率密度関数の積 \(\mathcal{N}(10,\, 1) \times \mathcal{N}(10,\, 1)\) のグラフを次に示す。結果を見ずにグラフの形を予想できるだろうか？新しい平均はいくつだろうか？曲線の幅は \(\mathcal{N}(10,\, 1)\) と比べて狭くなるだろうか、広くなるだろうか、それとも同じだろうか？

In [12]

z = gaussian(10., 1.)  # ガウス分布 N(10, 1)

product = gaussian_multiply(z, z)

xs = np.arange(5, 15, 0.1)
ys = [stats.gaussian(x, z.mean, z.var) for x in xs]
plt.plot(xs, ys, label='$\mathcal{N}(10,1)$')

ys = [stats.gaussian(x, product.mean, product.var) for x in xs]
plt.plot(xs, ys, label='$\mathcal{N}(10,1) \\times \mathcal{N}(10,1)$', ls='--')
plt.legend()
print(product)

Out [12]

𝒩(μ=10.000, 𝜎²=0.500)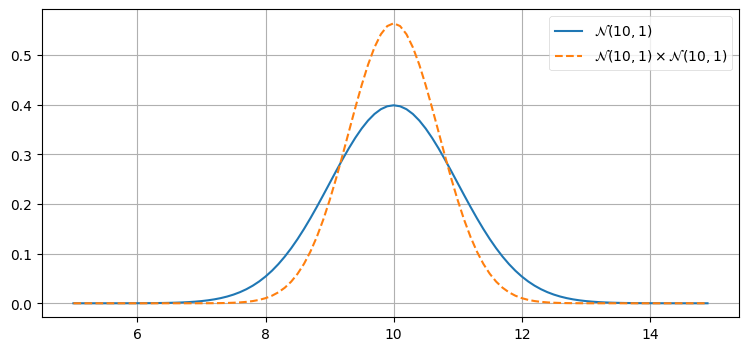

乗算の結果は元のガウス分布よりも高く、幅が狭くなっていて、平均は変わっていない。あなたの直感と一致するだろうか？

ガウス分布を二つの観測値だと考えよう。観測を二度行い、両方で観測値 \(10~\text{m}\) が得られたとすれば、実際の長さは \(10~\text{m}\) に近いのだと結論するべきである。このとき長さが \(11~\text{m}\) あるいは \(9.5~\text{m}\) であると結論するのは理にかなっていない。また観測値が二つあるときは観測値が一つだけのときより自信が持てるので、結果の分散も小さくなる。

「二度測り、一度切れ」という有名なことわざがあるが、ガウス分布の積はこの現実世界における教訓を数学的に表していると言える。

観測値が二度続けて同じ値になるのは考えにくい。今度は \(\mathcal{N}(10.2,\, 1) \times \mathcal{N}(9.7,\, 1)\) をプロットしてみよう。どのような結果になるだろうか？考えてからグラフを見てほしい:

In [13]

def plot_products(g1, g2):
    plt.figure()
    product = gaussian_multiply(g1, g2)

    xs = np.arange(5, 15, 0.1)
    ys = [stats.gaussian(x, g1.mean, g1.var) for x in xs]
    plt.plot(xs, ys, label='$\mathcal{N}$'+'$({},{})$'.format(g1.mean, g1.var))

    ys = [stats.gaussian(x, g2.mean, g2.var) for x in xs]
    plt.plot(xs, ys, label='$\mathcal{N}$'+'$({},{})$'.format(g2.mean, g2.var))

    ys = [stats.gaussian(x, product.mean, product.var) for x in xs]
    plt.plot(xs, ys, label='product', ls='--')
    plt.legend();

z1 = gaussian(10.2, 1)
z2 = gaussian(9.7, 1)

plot_products(z1, z2)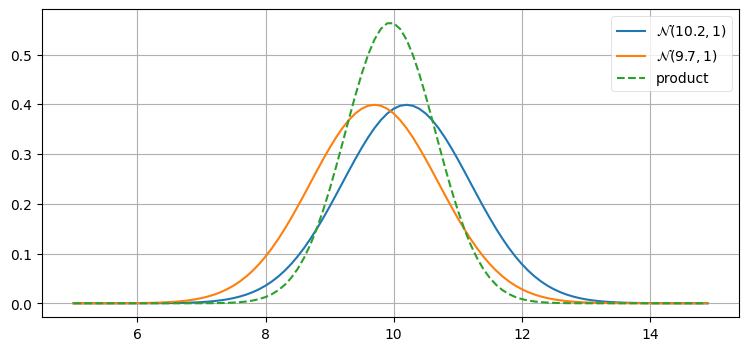

テーブルと壁の距離を測ってほしいと誰か二人に頼んだとして、一人は \(10.2~\text{m}\)、もう一人は \(9.7~\text{m}\) を報告したとする。このとき二人の測定スキルが同じだと信じるなら、平均 \(9.95~\text{m}\) を推定値とするのが最も優れている。

g-h フィルタの章を思い出そう。自分の体重を二度測って、一度目は 160 ポンド、二度目は 170 ポンドだったとする。このとき両方の測定が同じ正確さを持つとすれば、最も優れた推定値は 165 ポンドであると私たちは納得した。さらに、165 ポンドには 160 ポンドや 170 ポンドよりも多少自信が持てていた: 両方の観測値が大外れである可能性は低いから、二つの観測値の中間にある値を選んでおけば安心できる。

複雑な状況では直感に反するような結果となるので、さらに別のシナリオを考えよう: より現実的な仮定として、測定を頼んだ一人がミスをしていたとする。このとき正確な観測値は \(10.2~\text{m}\) と \(9.7~\text{m}\) のどちらかであり、\(9.95~\text{m}\) では確実にない。これは十分あり得る仮定である。しかし観測値にノイズが含まれると知っていたとしても、正確な方の観測値にノイズが全く含まれないとは考えられず、さらにノイズの含まれる方の観測値の誤差が観測値を破棄できるほど大きいとみなすこともできない。よって利用できる情報を全て取り入れると、ここでも \(9.95~\text{m}\) が最も優れた推定値となる。

カルマンフィルタの更新ステップで組み合わせるのは二つの観測値ではなく一つの観測値と事前分布 (観測値を取り入れる前の推定値) である。この考え方は g-h フィルタでも利用した: 二つの観測値からの情報を組み合わせる場合でも、観測値と予測からの情報を組み合わせる場合でも、数式は変わらない。

このことを確認してみよう。次の一つ目のプロットでは、あまり正確でない事前分布 \(\mathcal N(8.5, 1.5)\) とそれより正確な観測値 \(\mathcal N(10.2, 0.5)\) を作成している。ここで「正確な」とはセンサーの分散が事前分布の分散より小さいことを意味しており、犬の位置が \(10.2~\text{m}\) より \(8.5~\text{8}\) に近いと私が知っていることを意味しているわけではない。二つ目のプロットでは正確さの関係を逆点させており、正確な事前分布 \(\mathcal N(8.5, 0.5)\) と不正確な観測値 \(\mathcal N(10.2, 1.5)\) を使っている:

In [14]

prior, z = gaussian(8.5, 1.5), gaussian(10.2, 0.5)
plot_products(prior, z)

prior, z = gaussian(8.5, 0.5), gaussian(10.2, 1.5)
plot_products(prior, z)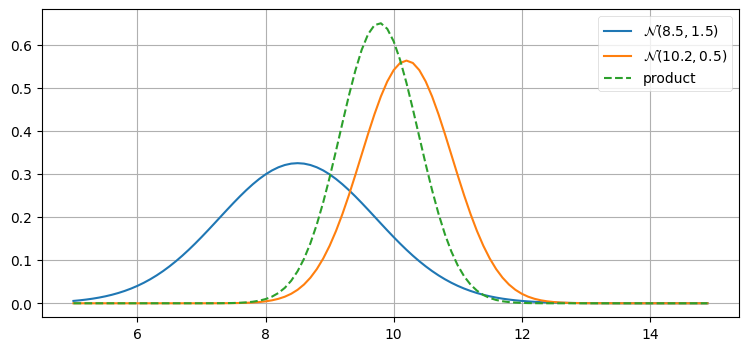

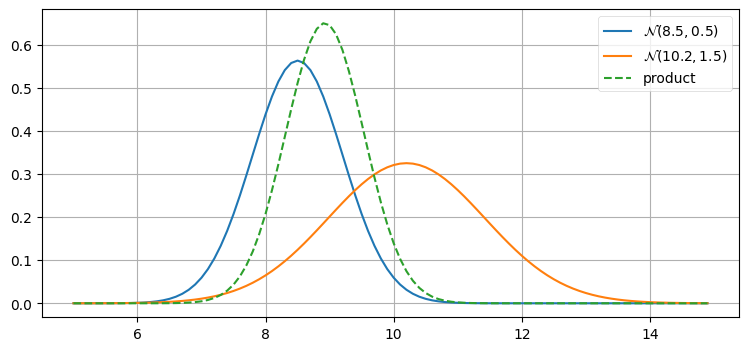
乗算の結果はいずれの入力よりも背の高いガウス分布となっている。これはおかしなことではない──情報を取り入れたのだから、分散は小さくなるはずだ。また乗算の結果が小さい分散を持つ入力に近いことにも注目してほしい。分散が小さい分布には大きな自信を持っているのだから、その分布の重みを大きくするのが理にかなっている。

以上の考え方は正しいように見えるが、本当にそうだろうか？この話題に関して言うべきことはもっとあるものの、まずは実際に動くフィルタを作って読者が具体的なデータで実験を行えるようにしよう。その後にガウス分布の積をもう一度考えて、これが正しい理由を明らかにする。

対話的な例

次の対話的なコードには乗じられる二つのガウス分布の平均と分散を変化させるためのスライダーが付いており、スライダーを動かすとプロットが再描画される。Jupyter Notebook で開いてからカーソルをコードセルの中に移動させ、CTRL+Enter を押すと実行できる。

In [15]

from ipywidgets import interact

def interactive_gaussian(m1, m2, v1, v2):
    g1 = gaussian(m1, v1)
    g2 = gaussian(m2, v2)
    plot_products(g1, g2)
    plt.show()

interact(interactive_gaussian,
         m1=(5, 10., .5), m2=(10, 15, .5),
         v1=(.1, 2, .1), v2=(.1, 2, .1));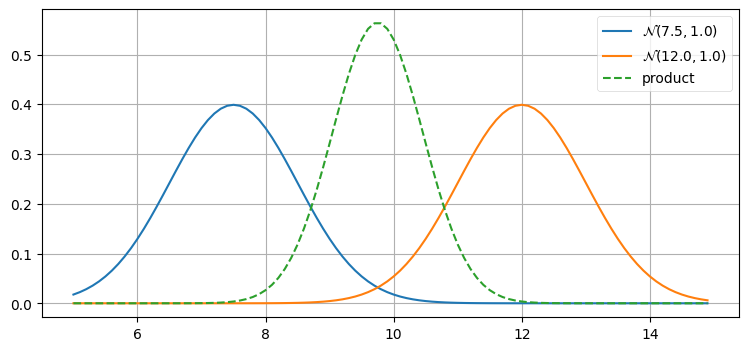

Out [15]ガウス分布の積の対話的なプロット (Jupyter Notebook でのみ実行可能)

4.6 初めてのカルマンフィルタ

具体的な例に戻って、カルマンフィルタを実装しよう。update 関数と predict 関数は実装したから、後は犬の動きとセンサーをシミュレートするボイラープレートコードを書くだけだ。このタスクが読者の注意をそらさないように、この部分は kf_internal モジュールの DogSimulation クラスに実装してある。

次に示すのは平均と分散を定義して犬の動きのシミュレートを行い、観測値を作成することで問題をセットアップするボイラープレートコードである:

In [16]

import kf_book.kf_internal as kf_internal
from kf_book.kf_internal import DogSimulation

np.random.seed(13)

process_var = 1. # 犬の動きの分散
sensor_var = 2.  # センサーの分散

x = gaussian(0., 20.**2)  # 犬の位置 = N(0, 20**2)
velocity = 1
dt = 1. # タイムステップ (単位は秒)
process_model = gaussian(velocity*dt, process_var) # 移動量が x に加算される

# 犬をシミュレートして観測値を得る
dog = DogSimulation(
    x0=x.mean,
    velocity=process_model.mean,
    measurement_var=sensor_var,
    process_var=process_model.var)

# 観測値のリストを作成する
zs = [dog.move_and_sense() for _ in range(10)]

そしてカルマンフィルタはこうなる:

In [17]

print('予測\t\t\t更新')
print('     x      var\t\t  z\t    x      var')

# 観測値 z に対してカルマンフィルタを実行する
for z in zs:
    prior = predict(x, process_model)
    likelihood = gaussian(z, sensor_var)
    x = update(prior, likelihood)

    kf_internal.print_gh(prior, x, z)

print()
print('最後の推定値:     {:10.3f}'.format(x.mean))
print('実際の最後の位置: {:10.3f}'.format(dog.x))

Out [17]

予測                    更新
     x      var                 z         x      var
  1.000  401.000      1.354     1.352   1.990
  2.352    2.990      1.882     2.070   1.198
  3.070    2.198      4.341     3.736   1.047
  4.736    2.047      7.156     5.960   1.012
  6.960    2.012      6.939     6.949   1.003
  7.949    2.003      6.844     7.396   1.001
  8.396    2.001      9.847     9.122   1.000
 10.122    2.000      12.553   11.338   1.000
 12.338    2.000      16.273   14.305   1.000
 15.305    2.000      14.800   15.053   1.000

最後の推定値:      15.053
実際の最後の位置:  14.838

フィルタのアニメーションを次に示す。赤い三角形が予測値を表す。予測ステップの後フィルタは黒い円で示される次の観測値を受け取り、予測値と観測値の間にある値を推定値として採用する:

In [18]

from kf_book import book_plots as book_plots
from ipywidgets.widgets import IntSlider

# プロットするために、出力をこれらのリストに保存する
xs, predictions = [], []

process_model = gaussian(velocity, process_var)

# カルマンフィルタを実行する
x = gaussian(0., 20.**2)
for z in zs:
    prior = predict(x, process_model)
    likelihood = gaussian(z, sensor_var)
    x = update(prior, likelihood)

    # 結果を保存する
    predictions.append(prior.mean)
    xs.append(x.mean)

def plot_filter(step):
    plt.cla()
    step -= 1
    i = step // 3 + 1

    book_plots.plot_predictions(predictions[:i])
    if step % 3 == 0:
        book_plots.plot_measurements(zs[:i-1])
        book_plots.plot_filter(xs[:i-1])
    elif step % 3 == 1:
        book_plots.plot_measurements(zs[:i])
        book_plots.plot_filter(xs[:i-1])
    else:
        book_plots.plot_measurements(zs[:i])
        book_plots.plot_filter(xs[:i])

    plt.xlim(-1, 10)
    plt.ylim(0, 20)
    plt.legend(loc=2)
    plt.show()
interact(plot_filter,
         step=IntSlider(value=len(predictions)*3, min=1, max=len(predictions)*3));

Out [18]カルマンフィルタのアニメーション (Jupyter Notebook でのみ実行可能)

事前分布 (ラベルでは prediction)、観測値、フィルタの出力をプロットしてある。反復ごとに事前分布の計算、観測値の取得、観測値からの尤度の計算、事前分布への尤度の組み込みが行われる。

グラフを見ると、フィルタの出力する推定値が必ず観測値と予測値の間にあることが分かる。g-h フィルタで観測値と予測値の間にある値を推定値として選ばなければならないという議論をしていたことを思い出してほしい。この二つの間にない値を選ぶのは理にかなっていない。もし予測値が \(10\) で観測値が \(9\) なら、推定値として \(8\) や \(11\) を選ぶのは馬鹿げている。

4.7 コードのウォークスルー

ではコードを見ていこう。

process_var = 1.
sensor_var = 2.

process_var と sensor_var はそれぞれプロセスモデルとセンサーの分散を表す。センサーの分散が何を意味するかは明らかなはずだ──それぞれの観測値が持つ変動の量を示す。プロセスの分散はプロセスモデルに含まれる誤差の量を表す。ここでは各タイムステップで犬が \(1~\text{m}\) 前に進むとしているが、この予測通りに犬が動くことはまずないだろうし、上り坂やリスの匂いによって移動量が変化する可能性もある。もし追跡しているのがデジタルなコマンドに応答するロボットなら移動量をずっと正確に予測できるので、分散も \(\sigma^2=0.05\) のように小さくできるだろう。こういった値は「マジックナンバー」ではない: 分散の平方根はメートルで表した誤差を表す。カルマンフィルタへ適当に数字を突っ込んで動かすのは簡単だが、その数字が現実世界を反映していなければフィルタの性能は落ちてしまう。

x = gaussian(0., 20.**2)

これは犬の初期位置をガウス分布として表したものである。位置は \(0~\text{m}\)、分散は \(400~\text{m²}\) (標準偏差は \(20~\text{m}\)) となっている。これは「犬は \(0~\text{m}\) 地点から前後 \(60~\text{m}\) の間にいる確率が 99.7% だと私は信じている」と言うのに等しいとみなせる: ガウス分布では全サンプルの 99.7% が平均から両方向に \(\pm3\sigma\) の区間に収まるためだ。

process_model = gaussian(velocity, process_var)

これはプロセルモデル──犬の移動を私たちがどう考えているかを記述したもの──である。速度をどうやって決めたのだろうか？魔法か？これは何らかの方法で予測できたのだと考えよう。あるいは補助の速度センサーがあるのかもしれない。もしロボットを追跡しているなら、これはロボットに入力された制御入力が表す移動の表現となる。速度センサーや制御入力が存在しない状況の扱い方は後の章で学ぶので、どうかここでは単純化を受け入れてほしい。

その後シミュレーションを初期化して、十個の観測値を作成する:

dog = DogSimulation(
    x0=x.mean,
    velocity=process_model.mean,
    measurement_var=sensor_var,
    process_var=process_model.var)
zs = [dog.move_and_sense() for _ in range(10)]

続いて predict ... update のループがある:

for z in zs:
    prior = predict(x, process_model)
    likelihood = gaussian(z, sensor_var)
    x = update(prior, likelihood)

実行したときの出力から分かるように、最初のループで prior は 𝒩(μ=1.0, 𝜎²=400.1) となる。一度目の予測で私たちは、犬は \(1~\text{m}\) 地点に移動して、その分散は \(400~\text{m²}\) から \(401~\text{m²}\) に増大したと信じることになる。分散が大きくなって信念が不正確になるが、これは予測で情報の損失が起こるために予測ステップで必ず起きる現象である。

その後 update が呼び出され、そのときは prior が現在位置を表す引数として渡される。

以上のループで pos = 𝒩(μ=1.352, 𝜎²=1.990), z = 1.354 という結果が手に入る。

何が起きているのだろうか？まず犬は実際には \(1~\text{m}\) 地点にいるものの、センサーからはノイズのために \(1.354~\text{m}\) が観測された。これは予測された値 \(1~\text{m}\) から遠く離れている。一方で事前分布の分散は \(401~\text{m²}\) と非常に大きく、この値の自信が非常に低いことを示している。このため、推定された位置は観測値にとても近い \(1.352~\text{m}\) になったということだ。

続いて事後分布の分散 \(1.99~\text{m²}\) に注目しよう。\(401~\text{m²}\) から一気に減少しているが、なぜだろうか？ RFID トラッカーの分散は \(2.0~\text{m²}\) と非常に小さいので、事前分布よりはずっと信用できる。しかしそれでも前回の信念 (事前分布) にも情報が多少は含まれているから、計算される分散は \(2.0~\text{m²}\) よりほんの少しだけ小さくなる。

以降は predict と update が交互に呼ばれてループが進んでいく。最後には位置が \(15.053~\text{m}\) で分散が \(1.0~\text{m²}\) と推定され、そのときの実際の位置は \(14.838~\text{m}\) である。

次はグラフに注目しよう。ノイズが含まれる観測値は黒い点で、フィルタの結果は青い実線でプロットされている。どちらも値がぶれているが、観測値のぶれ幅の方が大きいことが分かる。また赤い三角形でプロットした予測値 (事前分布) と観測値の間に推定値が必ず収まっているので、あなたが初めて書いたカルマンフィルタは正しく動いているようだ！

フィルタリングの実装はわずか数行のコードであり、大部分のコードは初期化・データの格納・犬の移動のシミュレート・結果の出力に費やされた。実際のフィルタリングは非常に簡潔である:

prior = predict(x, process_model)
likelihood = gaussian(z, sensor_var)
x = update(prior, likelihood)

predict と update を使わなければ、次のようなコードとなる:

for z in zs:
    # 予測
    dx = velocity*dt
    pos = pos + dx
    var = var + process_var
    # 更新
    pos  = (var*z + sensor_var*pos) / (var + sensor_var)
    var = (var * sensor_var) / (var + sensor_var)

ごく簡単な計算からなるたった五行のコードで完全な一次元カルマンフィルタが実装できる！

この例では print からの出力が多くなり過ぎないようデータ点を十個としていた。今度はデータがもっと多い場合のフィルタの性能を見てみよう。次のグラフでは破線の間の暗い黄色の領域が分散を表す。コードではプロセスモデルとセンサーの分散をグラフでの見栄えが良くなるよう調整してあるが、現実のカルマンフィルタでこの二つの値を適当に変えることは当然ない。

In [19]

process_var = 2.
sensor_var = 4.5
x = gaussian(0., 400.)
process_model = gaussian(1., process_var)
N = 25

dog = DogSimulation(x.mean, process_model.mean, sensor_var, process_var)
zs = [dog.move_and_sense() for _ in range(N)]

xs, priors = np.zeros((N, 2)), np.zeros((N, 2))
for i, z in enumerate(zs):
    prior = predict(x, process_model)
    x = update(prior, gaussian(z, sensor_var))
    priors[i] = prior

    xs[i] = x

book_plots.plot_measurements(zs)
book_plots.plot_filter(xs[:, 0], var=priors[:, 1])
book_plots.plot_predictions(priors[:, 0])
book_plots.show_legend()
kf_internal.print_variance(xs)

Out [19]

      4.4502 2.6507 2.2871 2.1955 2.1712
      2.1647 2.1629 2.1625 2.1623 2.1623
      2.1623 2.1623 2.1623 2.1623 2.1623
      2.1623 2.1623 2.1623 2.1623 2.1623
      2.1623 2.1623 2.1623 2.1623 2.1623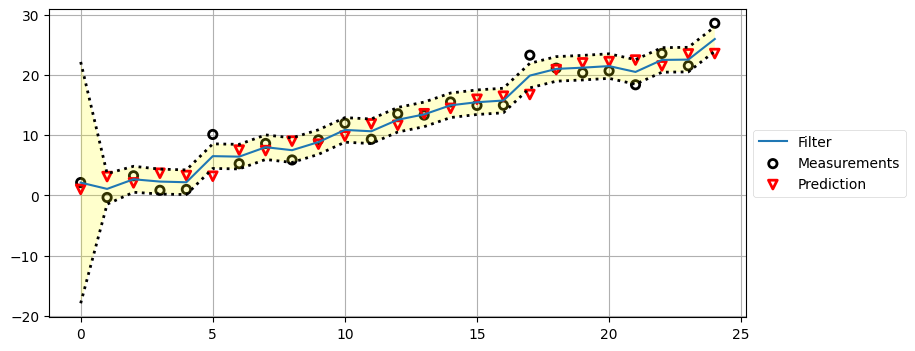

分散が九ステップで \(2.1623~\text{m²}\) に収束していることが分かる。これは位置の推定値に大きな自信が持てていることを示し、\(\sigma=1.45\) m に等しい。推定値の標準偏差をセンサーの標準偏差 \(\sigma=2.12\) m と比べてみるとよい。初期値が不正確なために最初の数ステップでは推定値が不確かであるものの、フィルタはセンサーより低い分散を持つ推定値へと素早く収束している！

このコードがカルマンフィルタを完全に実装する。カルマンフィルタの本格的な文献を読もうとしたことがあるなら驚いたかもしれない: そういった本に延々と並ぶ難しい数式とこのコードは似ても似つかない。カルマンフィルタの導出ではなく利用だけを考える限り、このトピックの理解は難しくない。加えて、各ステップで何が起きているのかを私の説明で直感的に理解できたことを願っている。信念がガウス分布で表され、観測値を受け取るごとに情報が増えて信念が確かなものになっていく。

カルマンフィルタのアニメーション

本書をブラウザで呼んでいるなら、カルマンフィルタによる犬の追跡を次のアニメーションで見ることができる:

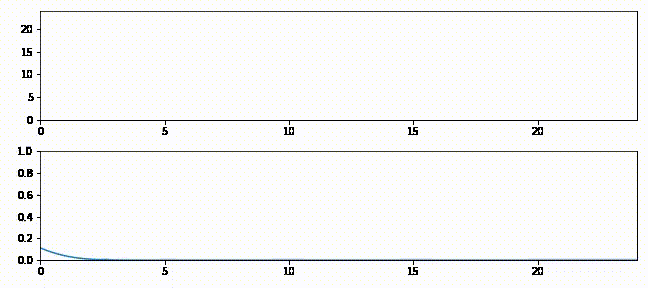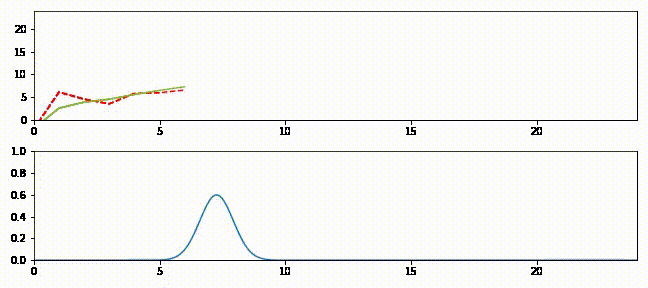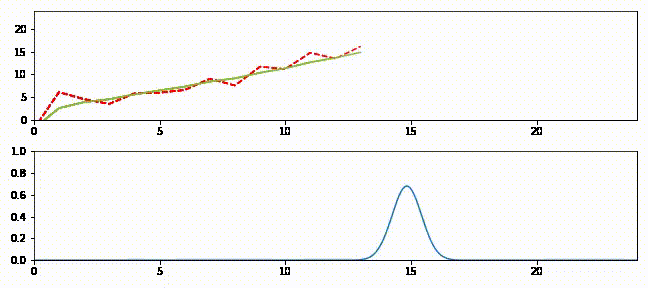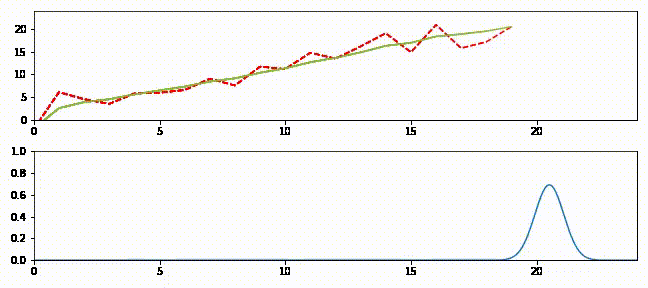
上のグラフはフィルタの出力を緑の実線、観測値を赤の破線で示している。下のグラフは各ステップにおける推定値を表すガウス分布を示す。

追跡の最初では予測値と観測値が大きく離れているのが分かる。このときガウス分布は小さく (曲線が低くて広く)、フィルタは予測値をあまり信用していない。そのためフィルタは推定値を観測値に向けて大きく修正する。またフィルタが発展するとガウス分布が高くなることも確認できる。この段階でフィルタは推定値に大きな確信を抱いており、出力は直線に非常に近い。時刻 \(15\) 以降では観測値に大きなノイズが含まれるもののフィルタはあまり影響を受けておらず、最初の観測値を受け取ったときほどには推定値を修正しない。

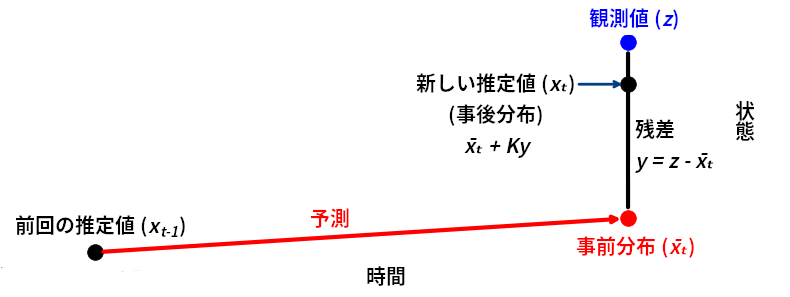
4.8 カルマンゲイン

フィルタが正しく動作することは分かったので、次は何が起きているのかを理解するために数学をもう一度考えよう。

事後分布の平均は次の式で与えられる:

\[ \mu=\frac{\bar\sigma^2\, \mu_z + \sigma_z^2 \, \bar\mu} {\bar\sigma^2 + \sigma_z^2} \]

添え字の \(z\) は観測値の平均/分散であることを示す。この等式は次のように変形できる:

\[ \mu = \left( \frac{\bar\sigma^2}{\bar\sigma^2 + \sigma_z^2}\right) \mu_z + \left(\frac{\sigma_z^2}{\bar\sigma^2 + \sigma_z^2}\right)\bar\mu \]

この形にすると、特定の重みを使って観測値と事前分布をスケーリングしていることが分かりやすくなる:

\[ \mu = W_1 \mu_z + W_2 \bar\mu \]

分母が正規化係数になっているので、重みを足すと \(1\) になる。よって \(K=W_1\) と定義すると、さらに変形できる:

\[ \begin{aligned} \mu &= K \mu_z + (1-K) \bar\mu\\ &= \bar\mu + K(\mu_z - \bar\mu) \end{aligned} \]

ここで次が成り立つ:

\[ K = \frac {\bar\sigma^2}{\bar\sigma^2 + \sigma_z^2} \]

この \(K\) をカルマンゲイン (Kalman gain) と呼ぶ。カルマンゲインはカルマンフィルタで最も重要な値である。これはスケーリングのための項であり、\(\mu_z\) と \(\bar\mu\) の間の値を選択する

いくつか例を見てみよう。観測値が事前分布より九倍正確だとする。このとき \(\bar\sigma^2 = 9\sigma_z^2\) だから

\[ \begin{aligned} \mu&=\frac{9 \sigma_z^2 \mu_z + \sigma_z^2\, \bar\mu} {9 \sigma_z^2 + \sigma_\mathtt{z}^2} \\ &= \left(\frac{9}{10}\right) \mu_z + \left(\frac{1}{10}\right) \bar\mu \end{aligned} \]

より \(K = \frac{9}{10}\) が分かる。事後分布の計算では観測値の \(\frac{9}{10}\) と事前分布の \(\frac{1}{10}\) を足すことになる。

観測値と事前分布の正確さが同じだとする。このとき \(\bar\sigma^2 = \sigma_z^2\) より

\[ \begin{gathered} \mu=\frac{\sigma_z^2\, (\bar\mu + \mu_z)}{2\sigma_\mathtt{z}^2} \\ = \left(\frac{1}{2}\right)\bar\mu + \left(\frac{1}{2}\right)\mu_z \end{gathered} \]

であり、\(\mu\) は観測値と予測値の平均となる。正確さが同じなら二つの値の平均を取るべきだというのは直感とも合致する。

カルマンゲインを使って分散を表すこともできる:

\[ \begin{aligned} \sigma^2 &= \frac{\bar\sigma^2 \sigma_z^2 } {\bar\sigma^2 + \sigma_z^2} \\ &= K\sigma_z^2 \\ &= (1-K)\bar\sigma^2 \end{aligned} \]

次の図を見ても理解できるだろう:

In [20]

import kf_book.book_plots as book_plots
book_plots.show_residual_chart()

カルマンゲイン \(K\) は残差を表す直線上の点を選択するスケーリング係数である。以上の考え方を使うと、update と predict の (上で示したのと等価な) 別実装を書くことができる:

In [21]

def update(prior, measurement):
    x, P = prior        # 事前分布の平均と分散
    z, R = measurement  # 観測値の平均と分散

    y = z - x        # 残差
    K = P / (P + R)  # カルマンゲイン

    x = x + K*y      # 事後分布の平均
    P = (1 - K) * P  # 事後分布の分散
    return gaussian(x, P)

def predict(posterior, movement):
    x, P = posterior # 事後分布の平均と分散
    dx, Q = movement # 移動量の平均と分散
    x = x + dx
    P = P + Q
    return gaussian(x, P)

この形で書いたのはなぜだろうか？おかしな変数の名前を使っているのはなぜ？理由はいくつかある。まず、専門書や論文の多くはカルマンフィルタをこの形で示す。本書で示したベイズ推定による導出は全く知られていないわけではないが、あまり使われていない。ここで示していない別の導出だとこの形の式が自然に得られる。それから、多変量のカルマンフィルタで使う式はこの形とほぼ同じなので、ここで学んで理解しておかなければならない。

z, P, Q, R といった名前はどこから来たのだろうか？フィルタリングの文献ではまず間違いなく \(R\) が観測ノイズ (行列)、\(Q\) がプロセスノイズ (行列)、\(P\) が状態の共分散行列を表す。観測値を \(z\) で表すのもよく使われるが、これは必ずそうというわけではない。あなたが読むことになる専門書や論文のほぼ全てでこうした記号が使われるので、慣れておく必要がある。

これはフィルタリングを理解する上で強力な考え方でもある。g-h フィルタでも同じ考え方を使っていた。残差 \(y = \mu_z - \bar\mu\) を計算し、事前分布と観測値の不確実性の比としてカルマンゲイン \(K = P/(P+R)\) を計算し、事前分布に \(Ky\) を加えることで事後分布を計算するという事実がこの考え方だと強調される。

この形式だと「尤度と事前分布の積として事後確率を計算する」というベイズ的な側面は分かりにくくなる。しかし、もちろん数式は同じなので、どちらのアプローチも同じことを言っている。私がベイズ的なアプローチを使ったのは、こちらの方が確率的な考え方を直感的かつ深く理解できると思ったからだ。\(K\) を使ったもう一つの定式化だと、直交射影 (orthogonal projection) と呼ばれる手法を用いるアプローチを深く理解できる。カルマン博士はカルマンフィルタを直交射影のアプローチで導出しており、ベイズ的なアプローチは使っていない。これからの数章を読めば \(K\) を使った定式化をさらに理解できるだろう。

4.9 アルゴリズムの完全な説明

g-h フィルタが行う処理を次の図に示す:

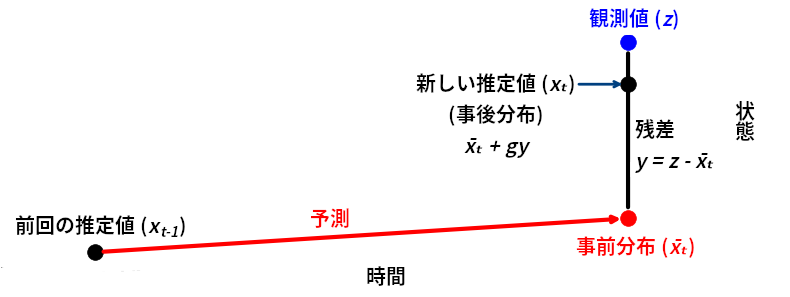
本章でも同じことを行ってきた: カルマンフィルタは予測値を計算し、観測値を取得し、その二つの間のどこかにある値を新しい推定値として採用する。

この点を理解するのは非常に重要である: 本書で登場するフィルタは全て同じアルゴリズムを実装しており、ただ数学的な詳細が異なるだけだ。後半の章では数学が難しくなるものの、そのアイデアは簡単に理解できる。

特定のフィルタで使われる数式の詳細には注目せずに、その数式が何を計算しているのか、そしてなぜ計算しているのかを理解するのが重要である。この世には数えきれないほどのフィルタが存在するものの、どれも異なる数式で同じアルゴリズムを実装している。数式を変えても結果の質や表現できる問題の種類が変化するだけで、土台にあるアイデアは変わらない。

一般的なアルゴリズムを次に示す:

初期化

フィルタの状態を初期化する。
状態に関する信念を初期化する。

予測

系の振る舞いを利用して次のタイムステップにおける状態を予測する。
予測の不確実性に応じて信念を調整する。

更新

観測値とその正確さに関する信念を取得する。
予測値と観測値の残差を計算する。
予測値の正確さと観測値の正確さからスケーリング係数を計算する。
計算されたスケーリング係数を使って予測値と観測値の間の値に状態を設定する。
予測値の正確さと観測値の正確さに基づいて状態に関する信念を更新する。

この形式で表せないベイズフィルタアルゴリズムを見つけるのは非常に難しいだろう。予測値の誤差といった一部の値を考えないフィルタもあるし、非常に複雑な計算を行うフィルタもある。しかし、そういったフィルタはどれも上述のアルゴリズムを実行する。

単変量カルマンフィルタの式を次にまとめる:

予測

\[ \def\arraystretch{1.75} \begin{array}{l|l|l} \text{式} & \text{実装} & \text{カルマンの形式} \\ \hline \bar x = x + f_x & \bar\mu\ \, = \mu + \mu_{f_x} & \bar x\ = x + dx \\ & \bar\sigma^2 = \sigma^2 + \sigma_{f_x}^2 & \bar P = P + Q \\[7pt] \end{array} \]

更新

\[ \def\arraystretch{2} \begin{array}{l|l|l} \text{式} & \text{実装} & \text{カルマンの形式} \\ \hline x = \| \mathcal L\bar x\| & y\ \, = z - \bar\mu & y\ \, = z - \bar x\\ &\displaystyle K = \frac {\bar\sigma^2} {\bar\sigma^2 + \sigma_z^2} & \displaystyle K = \frac {\bar P}{\bar P+R}\\ & \mu\ \, = \bar \mu + Ky & x\ = \bar x + Ky\\ &\displaystyle \sigma^2 = \frac {\bar\sigma^2 \sigma_z^2} {\bar\sigma^2 + \sigma_z^2} & P = (1-K)\bar P \\[7pt] \end{array} \]

4.10 g-h フィルタと離散ベイズフィルタとの比較

ここは g-h フィルタ、離散ベイズフィルタ、カルマンフィルタという三つのフィルタの差異を理解する良い機会だ。誤差のモデルに注目して差異を考えよう。g-h フィルタでは観測値を次のグラフのようにモデル化した:

In [22]

book_plots.plot_errorbars([(160, 3, 'A'), (170, 9, 'B')], xlims=(150, 180))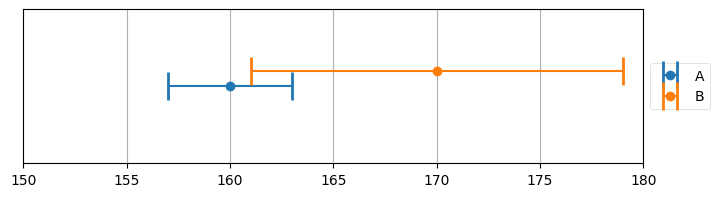

センサー A は 160 の観測値を返し、センサー B は 170 の観測値を返している。両方向に伸びているのはエラーバーであり、観測値に含まれる可能性のある誤差を表す。例えば A が観測している対象の真の値は 157 から 163 の間にある値であり、B では 161 から 179 となる。

前に説明したときは指摘しなかったが、これは一様分布 (uniform distribution) を使った誤差のモデルである。一様分布は特定の区間に含まれる全ての事象に同じ確率を割り当てる。このモデルに従えば、センサー A が 157, 160, 163 を出力する確率は等しい。そして区間の外側にある値の確率は \(0\) となる。

誤差をガウス分布でモデル化することもできる。センサー A には \(\mathcal{N}(160, 3^2)\) を、センサー B には \(\mathcal{N}(170, 9^2)\) を使うとする。これらのガウス分布のグラフを次に示す。比較のため一様分布のエラーバーもプロットしてある:

In [23]

xs = np.arange(145, 190, 0.1)
ys = [stats.gaussian(x, 160, 3**2) for x in xs]
plt.plot(xs, ys, label='A', color='g')

ys = [stats.gaussian(x, 170, 9**2) for x in xs]
plt.plot(xs, ys, label='B', color='b')
plt.legend();
plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='g', capthick=2, capsize=10)
plt.errorbar(170, [0.015], xerr=[9], fmt='o', color='b', capthick=2, capsize=10);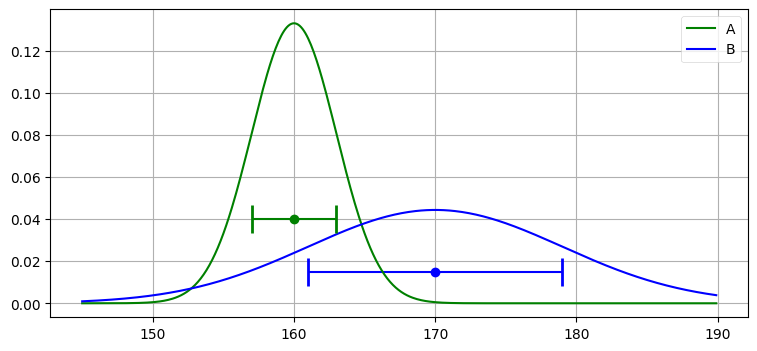

一様分布とガウス分布のどちらを選ぶかはモデルの選択と言える。どちら選んだとしても現実を正確に記述できるわけではない。ただ、たいていの場合でガウス分布の方が現実に近い。多くのセンサーは観測対象の実際の値に近い値を出力する確率が高く、その値から遠く離れた値を出力する確率が低い。ガウス分布ならこの傾向をモデル化できるのに対して、一様分布だと区間に含まれる観測値が全て同じ確率で得られることが仮定される。

次は離散ベイズフィルタで利用した離散分布 (discrete distribution) を使うモデルを見よう。このモデルは可能な値をいくつかの離散的な区間に分け、それぞれのバケット (区間) に確率を割り当てる。この割り当ては和が 1 になる限り完全に自由に行える。

一様分布、ガウス分布、離散分布によるセンサーのモデルを次のグラフに示す:

In [24]

from random import random
xs = np.arange(145, 190, 0.1)
ys = [stats.gaussian(x, 160, 3**2) for x in xs]
belief = np.array([random() for _ in range(40)])
belief = belief / sum(belief)

x = np.linspace(155, 165, len(belief))
plt.gca().bar(x, belief, width=0.2)
plt.plot(xs, ys, label='A', color='g')
plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='k', capthick=2, capsize=10)
plt.xlim(150, 170);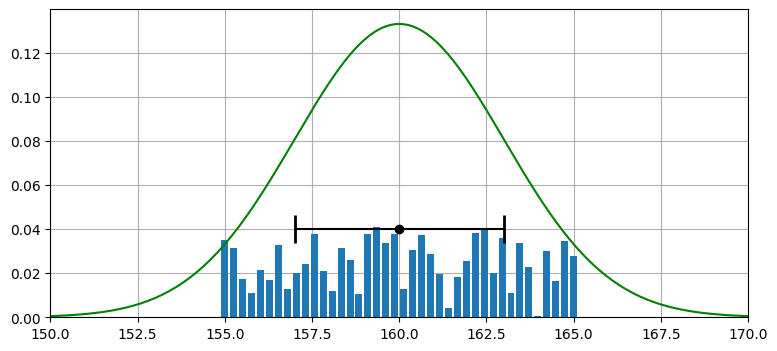

離散分布は任意の確率分布を扱えることを強調するために、離散分布では乱数で分布を構成している。これは離散分布に大きな力を与える: 離散的なバケットが十分にあれば、あらゆるセンサーの誤差特性をどんなに複雑なものであれモデル化できる。ただしこの力がある代わりに、離散分布はすぐに計算量的に手に負えなくなる。ガウス分布の和や積は二行の数式で計算でき、結果は別のガウス分布となる。この正規性のおかげで、フィルタの性能や振る舞いに関する強力な解析が可能になる。一方で離散分布の和や積を計算するにはデータ全体をループしなければならず、さらに結果を特徴付ける簡単な方法は存在しない。離散分布を用いるフィルタの性能特性を解析するのは非常に難しく、ほぼ不可能である。

ここに "正しい" 選択肢は存在しない。例えば本書の後半で解説する粒子フィルタ (particle filter) は離散分布を用いる。粒子フィルタはどんな複雑な状況にも対応できるので非常に強力な手法となっているものの、計算は遅く、解析的な議論も難しい。

今のところはこういった話題を無視することにして、今後数章はガウス分布の利用法をさらに考える。読み進めるにつれ数学モデルでガウス分布を使うことの強みと弱みが分かってくるだろう。

4.11 カルマンフィルタの設計入門

これまでに私たちは位置センサーに対するフィルタを開発した。ずっと考えてきたこの問題には慣れたかもしれないが、別の問題に対してカルマンフィルタを実装することを考えると準備不足に感じることだろう。正直に言うと、上述したカルマンフィルタには欠けている情報が多くある。以降の章でこのギャップを埋めていくが、ここではカルマンフィルタに慣れるために温度計に対するカルマンフィルタの設計・実装を考えてみよう。温度計は測定しようとしている温度に対応する電圧を出力するとして、センサーの製造元が発行する仕様書にはセンサーの出力に標準偏差 0.13 ボルトの白色ノイズが加わると記載があると仮定する。

温度計センサーからの観測値は次の関数でシミュレートできる:

In [25]

def volt(voltage, std):
    return voltage + (randn() * std)

続いてカルマンフィルタの処理を行うループを書く必要がある。一つ前に考えた問題と同じように、予測と更新のサイクルを行わなければならない。更新ステップは明らかだ──volt 関数を呼んで観測値を取得し、観測値を update 関数に渡せばいい。では予測ステップはどうだろうか？電圧の "移動量" を検出するセンサーは存在せず、短い期間で電圧は変わらないと期待される。こういった状況はどう処理すべきだろうか？

いつも通り、私たちは数学を信じることになる。電圧の移動量は事前に分からないので、移動量はゼロに設定する。しかし、これは温度が全く変化しないと予測するのに等しい。このとき、時間が経つにつれフィルタが抱く推定値への自信が極端に大きくなる。そしてフィルタが十分な個数の観測値を処理すると温度予測への自信が過剰に大きくなり、実際の温度変化による観測値の変化をノイズだとして無視するようになる。このようなフィルタは独善的 (smug) なフィルタと呼ばれ、避けなければならない。そのため予測に誤差を少し入れることで時間の経過で起こる電圧変化を無視しないようにする必要がある。以下のコードでは process_var = .05**2 としている。process_var は各タイムステップにおける電圧変化に期待される分散であり、.05**2 という値は更新ステップと予測ステップを通して分散の変化が見えるようするためだけに選んでいる。実際のセンサーからの出力をフィルタリングするときは実際に期待される変化量に合わせて設定しなければならない。例えば室温を測る温度計では非常に小さくできるし、化学反応チャンバーに設置する熱電対では大きくする必要がある。実際の数値を選択する方法については以降の章でも触れる。

何が起こるかを見てみよう:

In [26]

temp_change = 0
voltage_std = .13
process_var = .05**2
actual_voltage = 16.3

x = gaussian(25., 1000.) # 初期状態
process_model = gaussian(0., process_var)

N = 50
zs = [volt(actual_voltage, voltage_std) for i in range(N)]
ps = []
estimates = []

for z in zs:
    prior = predict(x, process_model)
    x = update(prior, gaussian(z, voltage_std**2))

    # グラフにするために記録する
    estimates.append(x.mean)
    ps.append(x.var)

# フィルタの出力と分散をプロットする
book_plots.plot_measurements(zs)
book_plots.plot_filter(estimates, var=np.array(ps))
book_plots.show_legend()
plt.ylim(16, 17)
book_plots.set_labels(x='step', y='volts')
plt.show()

plt.plot(ps)
plt.title('Variance')
print('Variance converges to {:.3f}'.format(ps[-1]))

Out [26]

Variance converges to 0.005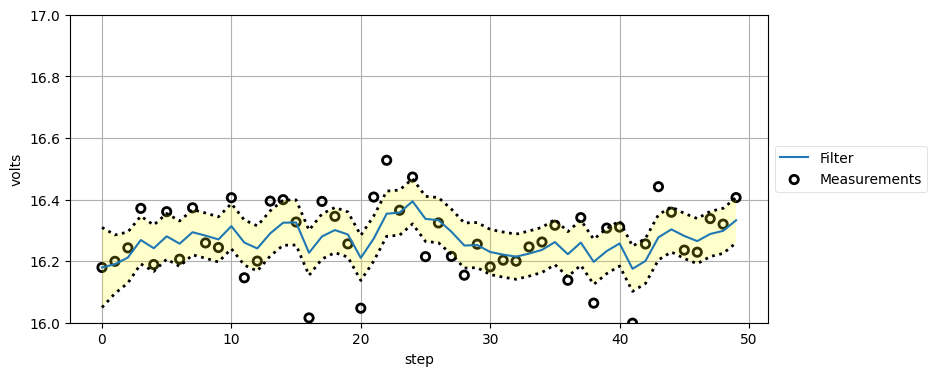

一つ目のグラフはセンサーの観測値とフィルタの出力を示している。センサーにはノイズが多く含まれるものの、フィルタは電圧の近似値を素早く見つけている。執筆時に実行した結果ではフィルタからの最終的な出力は 16.213 であり、volt 関数で使われている 16.4 にかなり近い。この値は実行するたびに多少変化する。

スペックシート (spec sheet) とは文字通りスペックが書かれた紙のことを言う (「仕様書」「スペック」「データシート」などと呼ぶこともある)。通常センサーは製造で生じるばらつきにより一つずつ異なる性能を示す。スペックシートには誤差の最大値が記載されることが多い──最低でもそれだけの性能が保証されていることを意味する。高価な機器を購入すると、あなたが手にしたその機器に対するテスト結果が載ったスペックシートが付いてくることが多く、通常その値は非常に信頼性が高い。一方で安価なセンサーだと販売前のテストはほとんど (または全く) 行われない可能性が高い。通常は製造元が少数の製品を試し、期待される性能レンジに収まることを検証する。クリティカルなアプリケーションに取り組むときは、スペックシートを注意深く読んで、そこに載っている区間が何を意味するかを正確に読み取らなければならない。その数値は最大値なのか、それとも (例えば) \(3\sigma\) 誤差レートなのか？全ての機器がテストされているのか？分散は正規分布か、それとも他の分布か？最後に、製造は完璧でないことも忘れてはいけない。どこかに欠陥があって、スペックシート通りの性能が出ない可能性もゼロではない。

例えば空調センサーのデータシートを見ていて、再現性 (repeatability) という欄に ±0.50% と記載があったとする。これはガウス分布なのか、それともバイアスなのか？例えば低い温度では再現性がほぼ 0.0% で、高い温度では再現性が常に +0.50% なのかもしれない。電子機器のデータシートは一般的性能特性 (typical performance characteristics) という節を持つことが多い。これは表では簡単に伝えられない情報を示すために使われる。例えば LM555 タイマーの出力電圧 vs 電流グラフを見ると、異なる温度における性能を示した三つの曲線が載っている。理想的な応答は線形だが、三つの直線はどれも曲がっている。ここから出力電圧に含まれる誤差がおそらくガウス分布に従わないことが明らかになる──このチップの場合には、温度が高いと出力電圧が下がり、電流が非常に高いと出力電圧は線形の関係から大きく離れる。

気が付いたかもしれないが、センサーの性能をモデル化するのは高性能なカルマンフィルタを作る上で手間のかかる作業の一つである。

アニメーション

本書をブラウザで読んでいる人に向けて、フィルタの動作が分かるアニメーションを示す。ブラウザで読んでいる場合は https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/animations/05_volt_animate.gif から確認できる。

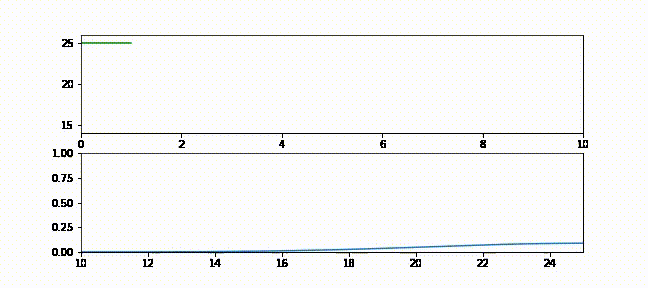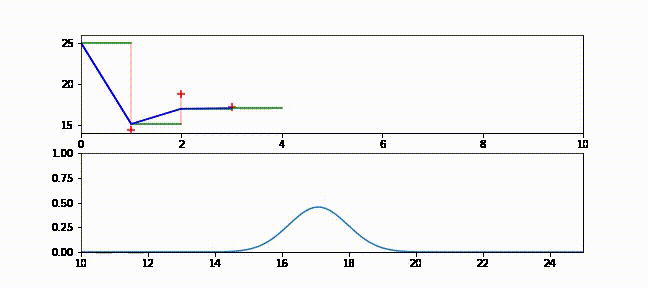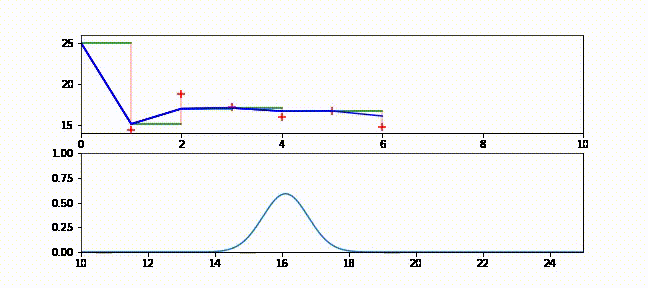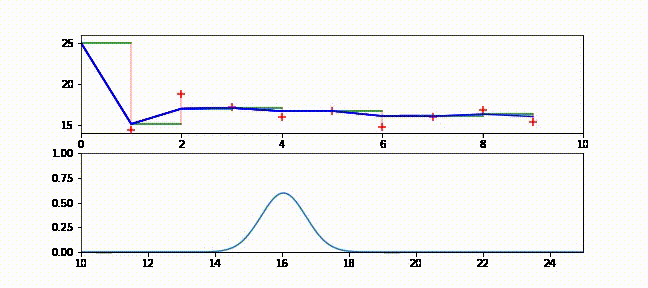
上のグラフでは緑の実線が次の時刻における電圧の予測値、赤い + が実際の観測値、赤い実線が残差、青い実線がフィルタの出力を表す。フィルタリングを開始した直後は修正が非常に大きいものの、数回の更新の後には観測値が予測値から大きく離れたときでも少ししか修正されないことが確認できる。

下のグラフはガウス分布として表された信念がフィルタの発展と共にどう変化するかを示す。フィルタリングが開始された直後ガウス曲線の中心は \(25\) (電圧の初期推測値) であり、初期の不確実性を反映して曲線は背が低く裾が広い。しかしフィルタが発展すると電圧の推定値に自信が高まり、それを受けてガウス分布は素早く \(16\) の近くに移動して背が高くなる。またガウス分布の背が高くなったり低くなったりするのも確認できるだろう。注意深く観察すると、ガウス分布は予測ステップで背が低く裾が広くなり、更新ステップで観測値を取り入れると背が高く裾が狭くなっているのが分かる。

g-h フィルタの用語を使ってこのアニメーションを考えてみよう。g-h フィルタは各ステップで予測を行い、観測値を取得し、残差 (予測値と観測値の差) を計算し、スケーリング係数 \(g\) を使って残差直線上の点を選ぶ。カルマンフィルタも基本的には同じだが、スケーリング係数 \(g\) がステップごとに異なっている。フィルタが状態に関して自信を高めると、スケーリング係数は観測値ではなくフィルタの予測を重視するようになる。

4.12 例: 極端に大きい観測ノイズ

先ほど考えた犬のフィルタの問題では信号にノイズはそれほど大きくなく、さらに観測を始めるとき犬は位置 0 にいると "推測" していた。もっと現実的な条件ではフィルタはどのように振る舞うだろうか？ RFID トラッカーにさらにノイズを加えて、プロセスモデルの分散を \(2~\text{m²}\) のままにしてみよう。まずは極端に大きいノイズを加える──見た目からは実際の観測値は分からないように思えるほどだ。センサーに加わるノイズの標準偏差を \(300~\text{m}\) としてフィルタを動作させるとして、直感的に性能はどうなると思うだろうか？別の言い方をすれば、実際の位置が \(1.0~\text{m}\) のとき、観測値は \(287.9~\text{m}\) や \(-589.6~\text{m}\)、あるいはそういった範囲に含まれる任意の値になるということである。考えてからスクロールしてほしい。

In [27]

sensor_var = 300.**2
process_var = 2.
process_model = gaussian(1., process_var)
pos = gaussian(0., 500.)
N = 1000
dog = DogSimulation(pos.mean, 1., sensor_var, process_var)
zs = [dog.move_and_sense() for _ in range(N)]
ps = []

for i in range(N):
    prior = predict(pos, process_model)
    pos = update(prior, gaussian(zs[i], sensor_var))
    ps.append(pos.mean)

book_plots.plot_measurements(zs, lw=1)
book_plots.plot_filter(ps)
plt.legend(loc=4);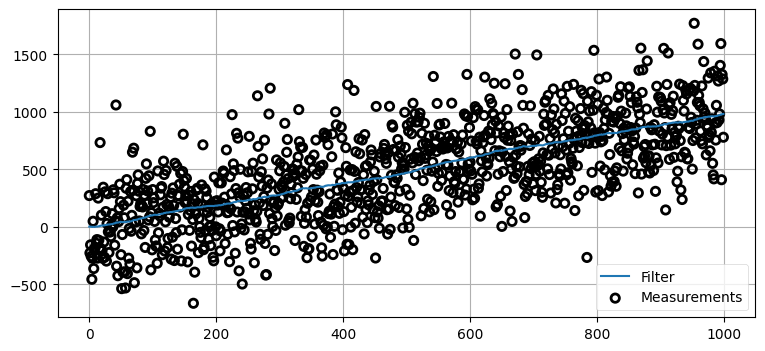

この例ではノイズが非常に大きいにもかかわらずフィルタの出力はほぼ直線を描いている！素晴らしい結果だ！こうなった理由が分かるだろうか？

出力がほぼ直線となるのは、プロセス誤差を小さく見積もっているためである。小さいプロセス誤差が「予測値は非常に信用できる」とフィルタに伝えるので、そして予測は直線なので、フィルタの出力は直線にとても近くなる。

4.13 例: 極端に小さいプロセス分散

前節のフィルタは素晴らしい！ではプロセス分散 (予測の不確実性) を非常に小さく設定して、結果が滑らかな直線になることを保証したらどうだろうか？

プロセス分散は時間の経過によって系がどれくらい変化するかをフィルタに伝える。フィルタに嘘をついてこの値を無理やり小さく設定すると、フィルタは変化が起きたときに反応できなくなる。犬がタイムステップごとに少しずつ速度を増すようにして、そのときプロセス分散を \(0.001~\text{m²}\) としたフィルタがどう振る舞うかを見てみよう:

In [28]

sensor_var = 20.
process_var = .001
process_model = gaussian(1., process_var)
pos = gaussian(0., 500.)
N = 100
dog = DogSimulation(pos.mean, 1, sensor_var, process_var*10000)
zs, ps = [], []
for _ in range(N):
    dog.velocity += 0.04
    zs.append(dog.move_and_sense())

for z in zs:
    prior = predict(pos, process_model)
    pos = update(prior, gaussian(z, sensor_var))
    ps.append(pos.mean)

book_plots.plot_measurements(zs, lw=1)
book_plots.plot_filter(ps)
plt.legend(loc=4);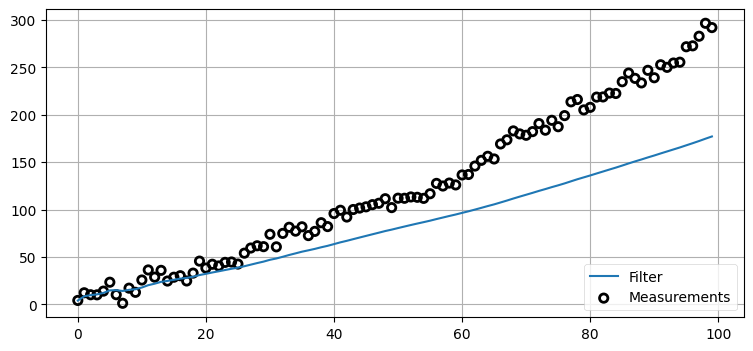

フィルタが観測値に反応できていないことは簡単に見て取れる。観測値は明らかに速度を変えているものの、フィルタは「予測値は完璧に近い」と言われているために観測値をほぼ無視してしまう。犬の移動量とプロセス分散を変化させて結果を確認してみてほしい。この話題は以降の章で深く掘り下げる。理解してほしい重要なポイントは、フィルタに設定されるプロセスノイズの値が系を正しく記述することが数式から要請されることだ。フィルタは自身が観測値から離れていてもそれに "気付く" ことはできず、自身を修正することもできない。フィルタは事前分布の分散と観測値の分散からカルマンゲインを計算し、どちらが正確かに応じて推定値を計算しているだけだ。

4.14 例: 大きく間違った初期推測値

位置の初期推測値を大きく間違った値にした場合の結果を見てみよう。結果を分かりやすくするためにセンサー分散を \(25~\text{m²}\) に減らし、位置の初期値を \(1000~\text{m}\) にする。フィルタは \(1000~\text{m}\) 分の間違いを修正できるだろうか？

In [29]

sensor_var = 5.**2
process_var = 2.
pos = gaussian(1000., 500.)
process_model = gaussian(1., process_var)
N = 100
dog = DogSimulation(0, 1, sensor_var, process_var)
zs = [dog.move_and_sense() for _ in range(N)]
ps = []

for z in zs:
    prior = predict(pos, process_model)
    pos = update(prior, gaussian(z, sensor_var))
    ps.append(pos.mean)

book_plots.plot_measurements(zs, lw=1)
book_plots.plot_filter(ps)
plt.legend(loc=4);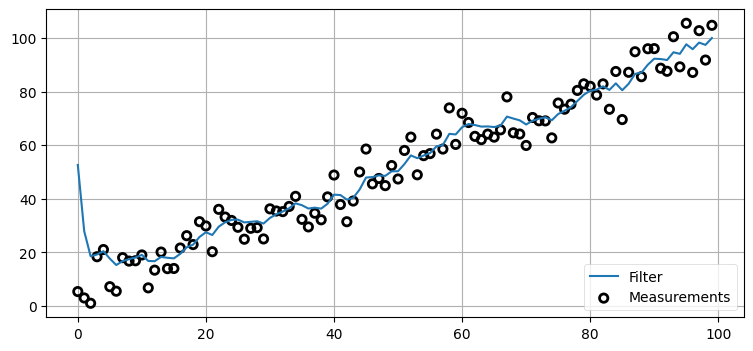

ここでも答えは「できる」だ！センサーに関する信念が比較的強い (\(\sigma^2=5^2\)) ので、最初のステップで位置の推定値が \(1000~\text{m}\) から約 \(50~\text{m}\) まで一気に変化し、それから十個程度の観測値を取り入れるとフィルタの出力は正しい値に収束する。初期推測値に関する「鶏と卵のどちらが先か問題」はこの事実を使って回避される。実際にフィルタを使うときはセンサーからの最初の観測値を最初の値とする場合が多いが、初期条件が大きく間違っていても影響はあまりないことがここから分かる──カルマンフィルタは二つの分散がそれぞれ実際のプロセスおよび観測値の分散と一致する限り正しく動作する。

4.15 例: 大きいノイズと大きく間違った初期推測値

二つの悪いところを取り入れたら、つまり大きなノイズと大きく間違った初期推測値を設定したらどうなるだろうか？

In [30]

sensor_var = 30000.
process_var = 2.
pos = gaussian(1000., 500.)
process_model = gaussian(1., process_var)

N = 1000
dog = DogSimulation(0, 1, sensor_var, process_var)
zs = [dog.move_and_sense() for _ in range(N)]
ps = []

for z in zs:
    prior = predict(pos, process_model)
    pos = update(prior, gaussian(z, sensor_var))
    ps.append(pos.mean)

book_plots.plot_measurements(zs, lw=1)
book_plots.plot_filter(ps)
plt.legend(loc=4);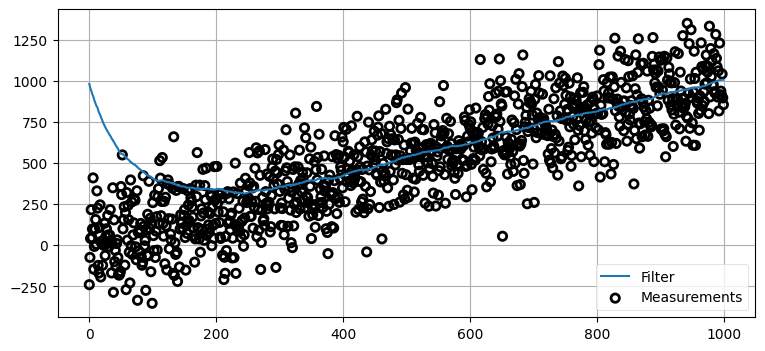

今回はフィルタも苦労している。一つ前の例では更新 100 回分をプロットしたのに対して、ここでは 1,000 回分をプロットしていることに注意してほしい。グラフを見ると、それなりの正確さとなるのに 200 回程度の反復を要しており、およそ 400 回を超えると正しい結果となっている。カルマンフィルタは優秀だが、奇跡を起こせると期待してはいけない。データに大きなノイズが含まれて初期条件が非常に悪ければ、最大でもこの程度の結果しか得られない。

最後に、最初の観測値を初期推測値にするというアイデアを実装してみよう:

In [31]

sensor_var = 30000.
process_var = 2.
process_model = gaussian(1., process_var)
N = 1000
dog = DogSimulation(0, 1, sensor_var, process_var)
zs = [dog.move_and_sense() for _ in range(N)]

pos = gaussian(zs[0], 500.)
ps = []
for z in zs:
    prior = predict(pos, process_model)
    pos = update(prior, gaussian(z, sensor_var))
    ps.append(pos.mean)

book_plots.plot_measurements(zs, lw=1)
book_plots.plot_filter(ps)
plt.legend(loc='best');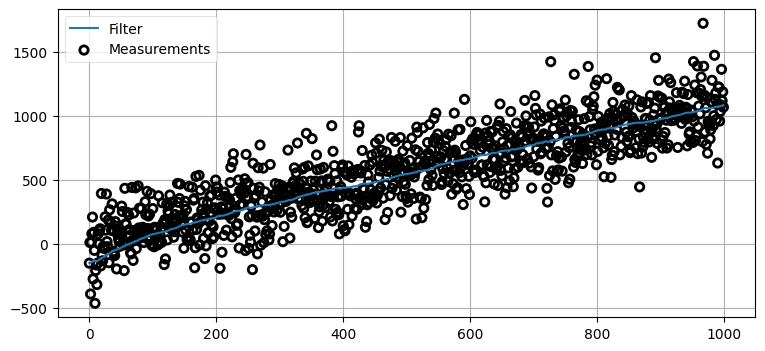

この小さな変更により、結果は大きく改善された。正確な解に落ち着くまでに乱数の調子によっては 200 回程度かかる場合もあるが、それより早く収束することもある。収束するまでの反復回数は最初の観測値によって決まる。ノイズが大きいので、初期推測値が犬の実際の位置から大きく離れることもある。

200 回の反復は長く思えるかもしれないが、ここで加えているノイズは非常に大きい。現実世界で用いられるセンサーは温度計、レーザー距離計、GPS 衛星、コンピュータービジョンといったものであり、こういったセンサーにこの例ほど巨大な誤差が含まれることはない。安価な温度計であれば分散は 0.2°C² 程度であり、今のコードでは 30,000°C² を設定している。

4.16 練習問題: 対話的なプロット

Jupyter Notebook のアニメーション機能を使って、スライダーで様々な定数を改変できるようにした形でカルマンフィルタを実装せよ。第 3 章の対話的なガウス分布の節を参考にするとよい。interact 関数にデータを計算してプロットする関数を渡すとグラフが対話的になり、interact への追加のパラメータそれぞれに対してスライダーが作成される。ボイラープレートは用意されているので、必要なコードを加えること:

In [32]

from ipywidgets import interact
from kf_book.book_plots import FloatSlider

def plot_kalman_filter(start_pos,
                       sensor_noise,
                       velocity,
                       process_noise):
    plt.figure();
    # ここに解答を書く
    plt.show()

interact(plot_kalman_filter,
         start_pos=(-10, 10),
         sensor_noise=FloatSlider(value=5, min=0, max=100),
         velocity=FloatSlider(value=1, min=-2., max=2.),
         process_noise=FloatSlider(value=5, min=0, max=100.));

解答

考えられる解答の一つを次に示す。スライダーは初期推測値、センサーに加わるノイズの量、ステップごとの移動量、移動量に加わるノイズ (プロセスノイズ) の量に対して作成される。おそらくもっとも分かりにくいのはプロセスノイズの量だろう──この値は各タイムステップで犬がどれくらい進路を外れるかをモデル化する。以下のコードでは最初に乱数のシードを設定してグラフの再描画で同じ乱数が使われるようにしているので、スライダーを動かした場合でもグラフを比較できる:

In [33]

from numpy.random import seed
from ipywidgets import interact

def plot_kalman_filter(start_pos,
                       sensor_noise,
                       velocity,
                       process_noise):
    N = 20
    zs, ps = [], []
    seed(303)
    dog = DogSimulation(start_pos, velocity, sensor_noise, process_noise)
    zs = [dog.move_and_sense() for _ in range(N)]
    pos = gaussian(0., 1000.) # 平均と分散
    process_model = gaussian(velocity, process_noise)

    for z in zs:
        pos = predict(pos, process_model)
        pos = update(pos, gaussian(z, sensor_noise))
        ps.append(pos.mean)

    plt.figure()
    plt.plot(zs, c='k', marker='o', linestyle='', label='measurement')
    plt.plot(ps, c='#004080', alpha=0.7, label='filter')
    plt.legend(loc=4)
    plt.show()

interact(plot_kalman_filter,
         start_pos=(-10, 10),
         sensor_noise=FloatSlider(value=5, min=0., max=100),
         velocity=FloatSlider(value=1, min=-2., max=2.),
         process_noise=FloatSlider(value=.1, min=0, max=40));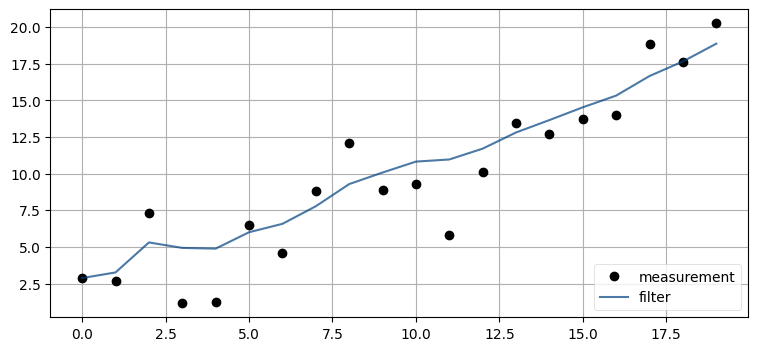

Out [33]対話的なカルマンフィルタの実行 (Jupyter Notebook でのみ実行可能)

4.17 練習問題: 非線形な系

今考えているカルマンフィルタの式は線形である:

\[ \begin{aligned} \mathcal{N}(\bar\mu,\, \bar\sigma^2) &= \mathcal{N}(\mu,\, \sigma^2) + \mathcal{N}(\mu_\mathtt{move},\, \sigma^2_\mathtt{move})\\ \mathcal{N}(\mu,\, \sigma^2) &= \mathcal{N}(\bar\mu,\, \bar\sigma^2) \times \mathcal{N}(\mu_\mathtt{z},\, \sigma^2_\mathtt{z}) \end{aligned} \]

線形でない系に対するこのフィルタの振る舞いはどうなるだろうか？

次のコードで生成される観測値に対するカルマンフィルタを実装せよ:

for i in range(100):
    z = math.sin(i/3.) * 2

分散と初期値を変化させ、その影響を調べよ。例えば初期推測値が大きく間違っていると何が起こるか？

In [34]

# ここに解答を書く

解答

In [35]

import math

sensor_var = 30.
process_var = 2.
pos = gaussian(100., 500.)
process_model = gaussian(1., process_var)

zs, ps = [], []

for i in range(100):
    pos = predict(pos, process_model)

    z = math.sin(i/3.)*2 + randn()*1.2
    zs.append(z)

    pos = update(pos, gaussian(z, sensor_var))
    ps.append(pos.mean)

plt.plot(zs, c='r', linestyle='dashed', label='measurement')
plt.plot(ps, c='#004080', label='filter')
plt.legend(loc='best');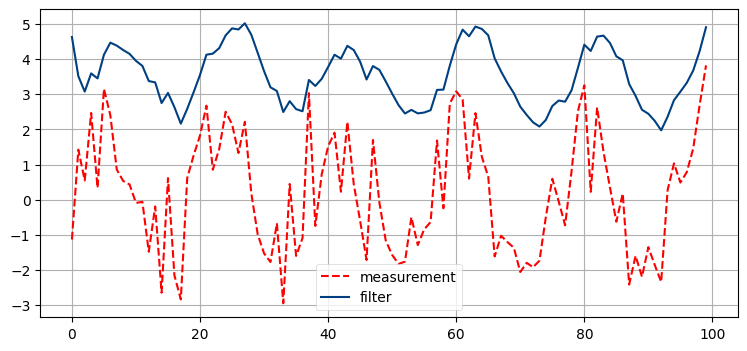

考察

これはめちゃくちゃだ！出力は全くサイン曲線には見えず、非常に巨視的な目線で見れば何となく似ている程度である。線形な系に対しては極端に大きなノイズを加えても非常に正確な結果が得られたのに対して、ここではノイズを少し加えただけで非常に質の低い結果となってしまう。

g-h フィルタの章を思い出せば、ここで何が起こっているかを理解できる。g-h フィルタでは構造的に予測値と観測値の間の値としてフィルタの出力を選ばなければならなかった。ここで示したような変動する信号は常に加速しているのに対して、使っているプロセスモデルは速度が一定なことを仮定している。そのためフィルタが入力信号に送れることが数学的に保証される。

カルマンフィルタを使い始めた専門家たちは非線形な系に対する振る舞いが優れないことにすぐに気が付き、対処方法を考案し始めた。後半の章ではこの問題を扱う。

4.18 固定ゲインフィルタ

組み込みコンピューターは通常とても性能の低いプロセッサしか持たず、浮動小数点数用の回路を持たないコンピューターも多くある。そういったチップでは上述の単純な式さえ大きな負担となる可能性がある。技術の進歩によって状況は改善しているものの、数百万個単位で購入するプロセッサの値段を一ドル下げる価値を過小評価してはいけない。

これまでに述べた例ではフィルタの分散が固定された値に収束していた。この現象は観測値の分散とプロセスの分散が固定である限り必ず起こる。分散が収束する値をシミュレーションで決定すれば、この事実を活用できる。判明したカルマンゲインの値をフィルタにハードコードすれば、初期推測値を実際の値に近い値に初期化する限りフィルタは非常に良く動作する (最初の観測値を初期推測値とすることが推奨される)。例えば、犬の追跡問題を解くコードはここまで簡単になる:

def update(x, z):
    K = .13232  # 実験で求まったカルマンゲイン
    y = z - x   # 残差
    x = x + K*y # 事後分布
    return x

def predict(x):
    return x + vel*dt

カルマンゲインを使った形式で update 関数を書いたのは、分散を考えなくて済むことを強調するためだ。分散が単一の値に収束するなら、カルマンゲインも単一の値に収束する。

4.19 FilterPy の実装

FilterPy は predict 関数と update 関数を実装する。これらの関数は本章で考えた単変量の問題だけではなく、以降の章で学ぶ多変量の問題に対しても動作する。そのためインターフェースが少し異なり、ガウス分布はタプルではなく二つの名前付き変数として渡される。

predict 関数はいくつかの引数を受け取るが、本書で使うのは次の四つだけだ:

predict(x, P, u, Q)

x は系の状態、P は系の分散、u はプロセスによる移動量、Q はプロセスのノイズを表す。predict の引数はほとんどが省略可能なので、呼び出すときは名前付き引数を使う必要がある。例えば predict の第三引数は u ではない。

なんて分かりにくい名前なんだと驚くかもしれない。全くその通りだ！前に触れたようにこういった変数の名前の裏には制御理論の長い歴史があり、あなたが読むことになる論文や書籍はこういった名前を使う。そのため私たちも慣れるほかない。変数名を覚えないと、いつまでたっても専門的な文献が読めるようにならないだろう。

状態 \(\mathcal N(10, 3)\) と移動量 \(\mathcal N(1, 4)\) を使って試してみよう。次の位置は \(10+1=11\) で、分散は \(3+4=7\) であるはずだ:

In [36]

import filterpy.kalman as kf
kf.predict(x=10., P=3., u=1., Q=4.)

Out [36]

(11.0, 7.0)

同様に update 関数もいくつか引数を取るが、次の四つをよく使うことになるだろう:

update(x, P, z, R)

前と同じく x と P は系の状態と分散であり、z は観測値、R は観測値の分散を表す。predict で事前分布を計算し、update で事後分布を計算してみよう:

In [37]

x, P = kf.predict(x=10., P=3., u=1., Q=2.**2)
print('%.3f' % x)

x, P = kf.update(x=x, P=P, z=12., R=3.5**2)
print('%.3f' % x, '%.3f' % P)

Out [37]

11.000
11.364 4.455

ノイズが入った分散の大きい観測値を与えているので、推定値は事前分布の平均 \(11\) に近い。

最後に一つ。このコードでは予測ステップの出力に prior (事前分布) と名前を付けていない。これ以降も本書では prior を使わず x で統一する。カルマンフィルタの式が \(\mathbf x\) を使っているためだ。事前分布と事後分布はどちらも推定された系の状態であり、前者は観測値を取り入れる前に、後者は観測値を取り入れた後に計算している点が違うだけである。

4.20 まとめ

本章で説明したカルマンフィルタは次に学ぶもっと一般的なフィルタの制限された特殊ケースである。ほとんどの教科書はこの一次元の形式を説明しないのだが、私はこれを非常に重要な足掛かりだと考えている。本書は g-h フィルタに始まり、次に離散ベイズフィルタ、そして本章で一次元カルマンフィルタを実装した。その中で私はこういったフィルタがどれも同じアルゴリズムと考え方を使っていることを示そうと努力した。次に学ぶカルマンフィルタで使われる数学はかなり洗練されており、フィルタの土台にある単純さを理解するのは難しい可能性がある。その洗練された数学には大きな恩恵がある: 一般化されたフィルタは本章で説明したフィルタより格段に優れた性能を持つ。

本章を理解するのには時間がかかるだろう。本当に理解するには何度も読み直す必要があるかもしれない。コードに含まれる様々な定数を変化させて結果を観察することを勧める。廊下にいる犬の位置、空を飛んでいる航空機の位置、化学反応チャンバーの温度といった値に関する単峰性の信念を表現するのにガウス分布が優れているという事実をよく納得しておくべきだ。それから事前分布と新しい観測値があればガウス分布の積を計算することで新しい信念が得られること、そして運動を観測しているときはガウス分布に従う二つの独立な確率変数を足すことで新しい信念が得られることも理解しておかなければならない。

何よりも、アルゴリズムの完全な説明の節に時間を十分に費やしてアルゴリズムを理解し、g-h フィルタや離散ベイズフィルタとの結び付きを把握しておく必要がある。"トリック"は一つだけしか存在しない──予測値と観測値の間にある値を選ぶ部分だ。異なるアルゴリズムは異なる数式を使ってこのトリックを行うが、大筋の考え方は変わらない。

第 4 章 一次元カルマンフィルタ