第 3 章確率・ガウス分布・ベイズの定理

前章の最後で離散ベイズフィルタの欠点にいくつか触れた。追跡とフィルタリングの問題の多くで、私たちが望むのは単峰性で連続なフィルタである。つまり、考えている系は浮動小数点数で (連続に) モデル化され、信念から得られる結論は一つだけ (単峰性) であるのが望ましい。例えばフィルタには「航空機は緯度・経度・高度が \((12.34,\ -95.54,\ 2389.5)\) の位置にいます」と言ってほしいのであって、「\((1.65,\ -78.01,\ 2100.45)\) かもしれないし、\((34.36,\ -98.23,\ 2543.79)\) かもしれない」とは言ってほしくない。物体が同じ瞬間に複数の位置に存在するというのは現実世界に対して私たちが抱く直感と合致しない。さらに前にも触れた通り、多峰性のフィルタは計算量がとてつもなく大きくなる可能性がある。加えて当然、推定された位置が複数あるとナビゲーションが不可能になる。

私たちは、現実世界における振る舞いをモデル化できる単峰性で連続なフィルタであって計算が効率的に行えるものを探している。ガウス分布を使うとこれらの特徴が全て手に入る。

3.1 平均・分散・標準偏差

読者の多くは統計学を学んだことがあると思うが、ここでも触れることを許してほしい。統計学はもう知っているという人にもこの部分を読むようにお願いする。これには二つの理由がある。一つは読者と私が記号を同じ意味で使うことを確認したいから。もう一つは以降の章で役立つ統計学の直感的な理解をここで得られるように説明が書かれているからだ。統計学の講義を受けて公式と計算手法だけを覚えるのは簡単だが、そうするとおそらくは学習内容が意味することはあやふやなままだろう。

確率変数

サイコロを振ると \(1\) から \(6\) の整数が得られる。これを「サイコロを振るという試行 (trial または experiment) によって \(1\) から \(6\) の整数という結果 (outcome) が得られる」と表現する。公平なサイコロを百万回振ると、サイコロの六分の一は目が一になることを私たちは期待する。これを「サイコロを振るという試行で結果が \(1\) となる確率 (probability) は \(1/6\) である」と表現する。同様に、これから振るサイコロの目が \(1\) になる確率をあなたに尋ねれば \(1/6\) と答えるはずだ。

何らかの確率に従って値を取る変数を確率変数 (random variable) と呼ぶ。前章のコードで言えば、位置を表す値とその位置の確率の組を全て集めたものが一つの確率変数と表すとみなせる。名前の random は手続きが非決定的だと言っているのではなく、結果に関する情報が欠けていることを意味する。サイコロを振った結果は決定的だが、その結果を計算するだけの情報を私たちは持っていないということだ。どの値を取るかが確率的にしか分からないことを確率変数は表す。

用語の定義を進めると、結果として得られる値の範囲を標本空間 (sample space) と呼ぶ。例えばサイコロを振る試行では \(\{1, 2, 3, 4, 5, 6\}\) が標本区間で、コイン投げの試行では \(\{H, T\}\) が標本空間となる。空間 (space) は数学用語であり、何らかの構造持った集合を表す。サイコロの標本空間は \(1\) から \(6\) までの整数で、これは自然数全体の集合の部分集合である。

確率変数の例をもう一つ示しておくと、ある大学に所属している学生の身長も確率変数として表せる。このとき標本空間は何らかの実数の範囲であり、その上限と下限は生物学的な限界によって定義される。

コイン投げのような試行を表す確率変数を離散確率変数 (discrete random variables) と呼ぶ。これは標本空間が有限集合もしくは加算無限集合 (自然数の集合など) であることを意味する。人間の身長のような値を表す確率変数は特定の区間に含まれる任意の実数値を取れるので、連続確率変数 (continuous random variable) と呼ばれる。

確率変数の観測値 (measurement) と実際の値を混同しないように注意する必要がある。もし身長を \(0.1~\text{m}\) きざみでしか測定できないなら、記録される値は \(0.1\), \(0.2\), \(\ldots\), \(2.7\) のような離散的な値だけになる。もちろんこうしたとしても、人間の身長は同じ区間に含まれる任意の値を取れるので、連続確率変数とみなされる。

統計学では大文字で確率変数を表す。通常はアルファベットの後半の文字を利用し、例えば「\(X\) をサイコロの出目を表す確率変数とする」あるいは「新入生向けの詩の講義を取った学生の身長を \(Y\) とする」などと言う。後半の章でフィルタリングを解くのに線形代数を使うときはベクトルを小文字で、行列を大文字で表す慣習に従う。残念ながら二つの慣習は衝突するので、どちらを意味しているかは文脈から読み取る必要がある。

確率分布

確率分布 (probability distribution) は標本空間に属する任意の値に対して確率変数がその値を取る確率を与える。例えば公平な六面サイコロの出目を表す確率変数の確率分布は次のようになる:

結果	確率
1	1/6
2	1/6
3	1/6
4	1/6
5	1/6
6	1/6

こういった分布は小文字を使って \(p(x)\) などと表す。一般的な関数の表記を使って次のようにも書く:

\[ P(X{=}4) = p(4) = \frac{1}{6} \]

これはサイコロを振る試行の結果 (出目) が \(4\) になる確率が \(\frac{1}{6}\) であることを意味する。\(P(X{=}a)\) は「\(X\) が \(a\) になる確率」を表す。記号の細かな違いに注意してほしい: 大文字の \(P\) は単一の事象の確率を表すのに対して、小文字の \(p\) は確率分布を表す。気を付けないと、文章が読み取れなくなる。この点を区別しやすくするために \(P\) の代わりに \(Pr\) を使う文献もある。

もう一つ公平なコイン投げの試行に関する例を示す。この試行の標本空間は \(\{H, T\}\) である。コインは公平だから、表 (\(H\)) と裏 (\(T\)) はどちらも 50% の確率で得られる。この事実は次のように表せる:

\[ \begin{aligned} P(X{=}H) &= 0.5 \\ P(X{=}T) &= 0.5 \end{aligned} \]

標本空間は一意でない。サイコロの例で言えば、\(\{1, 2, 3, 4, 5, 6\}\) は正当な標本区間だが、\(\{\text{偶数}, \text{奇数}\}\) も正当であり、さらに \(\{\text{四隅に点がある}, \text{四隅に点がない}\}\) も正当である。可能性のある全ての結果がいずれかの要素によって記述され、かつそれぞれの結果が一度だけ記述されるときに限って標本空間は正当になる。例えば \(\{\text{偶数}, 1, 3, 4, 5\}\) では出目の \(4\) が "偶数" と "\(4\)" の両方にマッチするので、この集合は正当な標本空間ではない。

離散的な乱数に対して確率を与える確率分布を離散確率分布 (discrete probability distribution) と呼び、連続的な乱数に対して確率を与える確率分布を連続確率分布 (continuous probability distribution) と呼ぶ。

確率分布となるためには、各値に対する確率 \(x_i\) が \(x_i \ge 0\) を満たす必要がある。負の確率は存在しないためだ。加えて全ての値に対する確率の和は \(1\) である必要もある。コイン投げを考えれば自然に理解できるだろう: もし表になる確率が 70% なら、裏になる確率は 30% となる。離散確率分布に対するこの要件は次の等式で表せる:

\[ \sum\limits_u P(X{=}u)= 1 \]

連続確率分布では次の等式となる:

\[ \int\limits_u P(X{=}u) \,du= 1 \]

前章では確率分布を使って廊下における犬の位置を推定した。例えば:

In [3]

import numpy as np
import kf_book.book_plots as book_plots

belief = np.array([1, 4, 2, 0, 8, 2, 2, 35, 4, 3, 2])
belief = belief / np.sum(belief)
with book_plots.figsize(y=2):
    book_plots.bar_plot(belief)
print('確率の和 = ', np.sum(belief))

Out [3]

確率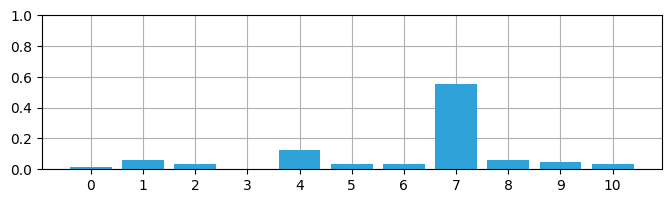の和 =  1.0

それぞれの位置は \(0\) から \(1\) の確率を持っており、確率の和は \(1\) となる。よって belief は確率分布と言える。標本空間は離散的だから、正確に言えば belief は離散確率分布となる。これからは区別する理由が特別にない限り「確率分布」の前に付く「離散」と「連続」は省略する。

確率変数の平均・中央値・最頻値

データの集合が与えられたとき、その集合を代表する値 (例えば平均) を知りたいことがある。この値の選び方は一通りではなく、データの集合を代表する値は統計用語で中心傾向 (central tendency) と呼ばれる。例えばクラスにいる学生の身長では平均 (average または mean) を計算するだろう。平均は誰でも計算できるが、より正式な記号と用語を導入するために、ここで平均について少し話をする。平均は全ての値の和を値の個数で割ると得られる。例えば学生の身長がメートルで

\[ X = \{1.8, 2.0, 1.7, 1.9, 1.6\} \]

と表されているなら、平均は次のように計算できる:

\[ \mu = \frac{1.8 + 2.0 + 1.7 + 1.9 + 1.6}{5} = 1.8 \]

平均は \(\mu\)ミューと表記する伝統がある。

この計算は次の等式で表せる:

\[ \mu = \frac{1}{n}\sum^n_{i=1} x_i \]

NumPy で平均を計算するには numpy.mean 関数を使う:

In [4]

x = [1.8, 2.0, 1.7, 1.9, 1.6]
np.mean(x)

Out [4]

1.8

利便性のため、NumPy 配列に対する mean メソッドも提供される:

In [5]

x = np.array([1.8, 2.0, 1.7, 1.9, 1.6])
x.mean()

Out [5]

1.8

数値の集合の最頻値 (mode) とは最も多く出現する値を言う。最も多く出現する値が一つしかない集合を単峰性 (unimodal) と呼び、最も多く出現する値が複数存在する集合を多峰性 (multimodal) と呼ぶ。例えば \(\{1, 2, 2, 2, 3, 4, 4, 4\}\) は最頻値 \(2\) と \(4\) を持つ多峰性の集合であり、また \(\{5, 7, 7, 13\}\) は最頻値 \(7\) を持つ単峰性の集合である。本書で最頻値を明示的に求めることはないものの、単峰性と多峰性という概念をより一般的な意味で用いる。離散ベイズフィルタの章では異なる位置に異なる確率を割り当てたので、サイモンの位置は多峰性の確率分布に従うとして話をしていたことになる。

最後に、数値の集合の中央値 (median) とは半分の要素がそれより大きく半分の要素がそれより小さくなるような値を言う。ここで「より大きい」と「より小さい」は通常の数値としての比較を意味する。集合に偶数個の値が含まれるときは、中央の二つの値の平均が中央値となる。

NumPy は中央値を計算する numpy.median 関数を提供する。以下のように \(\{1.8, 2.0, 1.7, 1.9, 1.6\}\) の中央値が \(1.8\) となるのは、この集合をソートした後に三番目に来るのが \(1.8\) であるためだ。この集合では中央値と平均が等しいが、一般に等しいわけではない:

In [6]

np.median(x)

Out [6]

1.8

3.2 確率変数の期待値

確率変数の期待値 (expected value) とは、その確率変数から無限に取得したサンプルの平均を言う。標本空間が \([1,3,5]\) でそれぞれの確率が等しい確率変数を \(X\) とする。このとき平均的な \(X\) の値はどれくらいになると私たちは期待するだろうか？

もちろん期待される値は \(1\), \(3\), \(5\) の平均 \(3\) となる。これは直感的にも理解できるはずだ: \(X\) の値を無限に取得すると \(1\), \(3\), \(5\) が同じ頻度で得られるから、その平均は \((1+3+5)/3=3\) となる。言い方を変えれば、この集合に対する期待値は標本空間の平均に等しい。

今度はそれぞれの値が異なる確率で取得されるとしてみよう。\(1\) は 80%、\(3\) は 15%、\(5\) は 5% の確率で得られると仮定する。このとき期待値は \(X\) が取りうる値とその確率の積を計算し、その結果を足し合わせることで計算できる:

\[ \mathbb E[X] = 1 \times 0.8 + 3 \times 0.15 + 5 \times 0.05 = 1.5 \]

ここで使った \(\mathbb{E}[X]\) は \(X\) の期待値を表す記法である (期待値に \(E(X)\) を使う文献もある)。\(X\) の期待値が \(1.5\) というのは直感とも矛盾しない: \(X\) は \(3\) より \(1\) になる確率がずっと高く、さらに \(5\) より \(3\) になる確率がずっと高いので、\(X\) から取得した値は \(1\) に近い。

\(X\) の \(i\) 番目の要素を \(x_i\) として、\(x_i\) が取得される確率を \(p_i\) とする。このとき次の等式が成り立つ:

\[ \mathbb E[X] = \sum_{i=1}^n p_ix_i \]

簡単な代数計算を使えば、全ての要素の確率が等しいとき期待値と平均が等しいことが示せる:

\[ \mathbb E[X] = \sum_{i=1}^n p_ix_i = \frac{1}{n}\sum_{i=1}^n x_i = \mu_x \]

\(X\) が連続確率変数のときは、期待値の定義の総和が積分に入れ替わって次のようになる:

\[ \mathbb E[X] = \int_{a}^b\, xf(x) \,dx \]

ここで \(f(x)\) は \(X\) の確率密度関数 (後述) である。この等式は本章ではまだ使わないが、次章で使うことになる。

Python を使って期待値を遠回りに計算してみよう。次のコードでは前述の確率分布から 1,000,000 個のサンプルを取得して期待値を計算している:

In [7]

total = 0
N = 1000000
for r in np.random.rand(N):
    if r <= .80: total += 1
    elif r < .95: total += 3
    else: total += 5

total / N

Out [7]

1.49846

計算された値が解析的に求めた値 \(1.5\) に近いことが分かる。ちょうど \(1.5\) になるには無限のサンプルサイズが必要なので、計算される値は \(1.5\) と正確に等しくはない。

練習問題

サイコロを振ったとき、出目の期待値はいくつか？

解答

どの面も出る確率は同じだから、\(1/6\) の確率で出る。よって

\[ \begin{aligned} \mathbb E[X] &= 1/6\times1 + 1/6\times 2 + 1/6\times 3 + 1/6\times 4 + 1/6\times 5 + 1/6\times6 \\ &= 1/6(1+2+3+4+5+6)\\&= 3.5 \end{aligned} \]

練習問題

一様連続分布

\[ f(x) = \frac{1}{b - a} \]

を考える。\(a=0\), \(b=20\) のときの期待値を求めよ。

解答

\[ \begin{aligned} \mathbb E[X] &= \int_0^{20}\, x\frac{1}{20} \,dx \\ &= \bigg[\frac{x^2}{40}\bigg]_0^{20} \\ &= 10 - 0 \\ &= 10 \end{aligned} \]

3.3 確率変数の分散

上述の計算により学生の身長の平均は分かるが、私たちが知りたいのはそれだけではない。例えば \(X\), \(Y\), \(Z\) の三つのクラスで身長を計測したところ、次の結果になったとする:

In [8]

X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]

NumPy を使うとクラスごとの平均身長が同じことが分かる:

In [9]

print(np.mean(X), np.mean(Y), np.mean(Z))

Out [9]

1.8 1.8 1.8

どのクラスも平均身長は \(1.8~\text{m}\) である。しかし \(Y\) の生徒の身長は \(X\) と \(Z\) の生徒の身長より大きく変動しており、\(Z\) の生徒は身長が全く変動していない。

平均を見ればデータを少しは理解できるが、全体が分かるわけではない。学生の身長がどれくらい変動しているかを表す何らかの指標が望まれる。変動の情報が必要になる理由はいくつも考えられるだろう。例えば学区で 5,000 個の机を購入することになって、選んだ机のサイズが学生の身長の範囲に対応していることを確認したいのかもしれない。

統計学ではデータの変動を計測するための概念として標準偏差 (standard deviation) と分散 (variance) が定式化されている。確率変数 \(X\) の分散 \(\mathit{VAR}(X)\) を計算する式を示す:

\[ \mathit{VAR}(X) = \mathbb E[(X - \mu)^2] \]

今は二乗を気にしないことにすると、分散は \(X\) と \(\mu\) の距離 \(X-\mu\) の期待値となっている。分散の定義に含まれる二乗に関しては後で説明する。期待値の公式は \(\mathbb E[X] = \sum\limits_{i=1}^n p_ix_i\) だから、これを上の定義に代入すれば次を得る:

\[ \mathit{VAR}(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2 \]

この概念に慣れるために、\(X\) に対して分散を計算してみよう:

\(X\) の平均は \(1.8\) (\(\mu = 1.8\)) より

\[ \small\begin{aligned} \mathit{VAR}(X) &=\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5} \\ &= \frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5} \\ \mathit{VAR}(X) &= 0.02 \, \mathrm{m^2} \end{aligned} \]

となる。NumPy は分散を計算する numpy.var 関数を提供する:

In [10]

print(f"{np.var(X):.2f} メートル二乗")

Out [10]

0.02 メートル二乗

この結果は少し理解しにくいかもしれない。身長の単位はメートルにもかかわらず分散の単位はメートル二乗となっているからだ。そのため、分散ではなく標準偏差 (standard deviation) が使われることが多い。標準偏差は分散の平方根として定義される:

\[ \sigma = \sqrt{\mathit{VAR}(X)}=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2} \]

通常は標準偏差を \(\sigma\) で、分散を \(\sigma^2\) で表す。本書ではこれから分散を表すのに \(\sigma^2\) を使い、\(\mathit{VAR}(X)\) は使わないことにする。この二つの記号は同じ値を表す。

\(X\) に対する標準偏差 \(\sigma_x\) は次のようになる:

\[ \small\begin{aligned} \sigma_x &=\sqrt{\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5}} \\ &= \sqrt{\frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5}} \\ \sigma_x &= 0.1414\,\mathrm{m} \end{aligned} \]

この計算の正しさは NumPy の numpy.std 関数で確認できる。std は標準偏差 (standard deviation) の省略形であり、よく使われる。

In [11]

print(f"標準偏差 {np.std(X):.4f}")
print(f"分散     {np.std(X)**2:.4f}")

Out [11]

標準偏差 0.1414
分散     0.0200

また当然 \(0.1414^2 = 0.02\) であり、前に計算とした分散と矛盾しない。

標準偏差はクラスの身長の散らばり具合いを示す。ただ「散らばり具合い」というのは数学的な言葉ではない。次節でガウス分布を学ぶと、標準偏差をより正確な言葉で定義できるようになる。現時点では「たいていの場合、平均から両方向に標準偏差一つ分だけ離れた区間に全データの 68% が収まる」とだけ言うに留める。具体的に言うと、ランダムなクラスの学生の身長は \(1.8-0.1414 = 1.66~\text{m}\) と \(1.8+0.1414= 1.94~\text{m}\) の間に 68% が収まるだろうと結論できる。

これはグラフからも分かる:

In [12]

from kf_book.gaussian_internal import plot_height_std
import matplotlib.pyplot as plt

plot_height_std(X)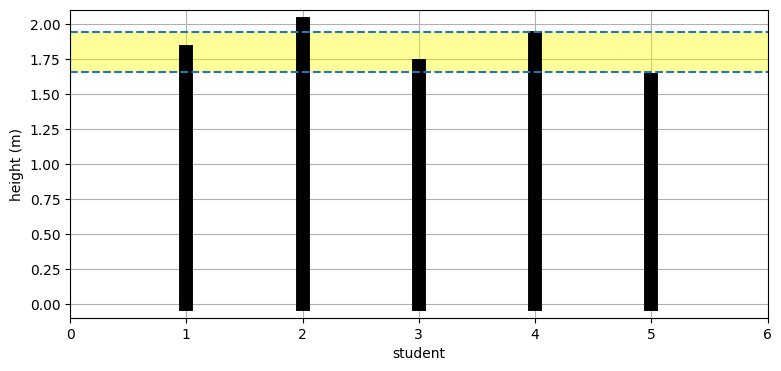

クラスに五人しかいないので正確に 68% が標準偏差一つ分の中に入るわけではない。ただ五人のうち三人 (60%) は平均から \(\pm 1\sigma\) の間にあることが分かる。

用語について: 標準偏差一つ分を \(1\sigma\) と書き、「いちシグマ」と読む。同様に \(2\sigma\) と \(3\sigma\) はそれぞれ標準偏差二つ分と三つ分のことであり、「にシグマ」「さんシグマ」と読む。

続いて 100 人のクラスに対する結果を見てみよう:

In [13]

from numpy.random import randn
data = 1.8 + randn(100)*.1414
mean, std = data.mean(), data.std()

plot_height_std(data, lw=2)
print(f'平均      = {mean:.3f}')
print(f'標準偏差  = {std:.3f}')

Out [13]

平均      = 1.813
標準偏差  = 0.147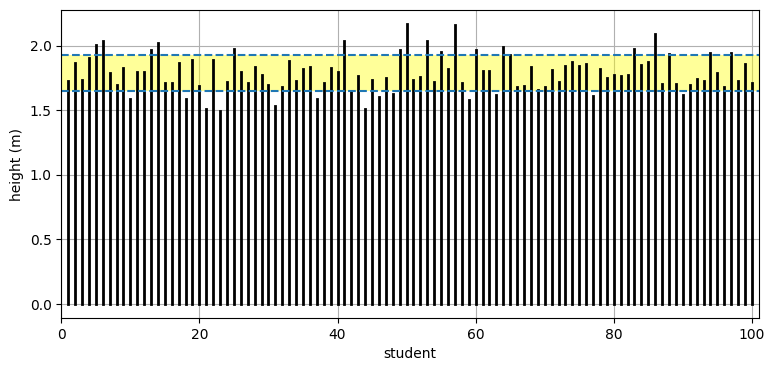

だいたい 68% が平均 \(1.8\) から \(\pm 1 \sigma\) だけ離れた区間に収まっているように見える。この事実はコードで確認できる:

In [14]

np.sum((data > mean-std) & (data < mean+std)) / len(data) * 100.

Out [14]

65.0

標準偏差については後で非常に詳しく議論する。ここでは

\[ Y = [2.2, 1.5, 2.3, 1.7, 1.3] \]

の標準偏差を計算してみよう。\(Y\) の平均は \(\mu=1.8\) だから、

\[ \small\begin{aligned} \sigma_y &=\sqrt{\frac{(2.2-1.8)^2 + (1.5-1.8)^2 + (2.3-1.8)^2 + (1.7-1.8)^2 + (1.3-1.8)^2} {5}} \\ &= \sqrt{0.152} = 0.39~\text{m} \end{aligned} \]

となる。NumPy でも確認できる:

In [15]

print(f'Y の std は {np.std(Y):.2f} m')

Out [15]

Y の std は 0.39 m

期待通りの値が返る。\(Y\) の方が値の変動が高かったから、標準偏差も大きくなっている。

最後に \(Z\) の標準偏差を計算しよう。\(Z\) の値は全く変動しないから、標準偏差は \(0\) になると期待できる:

\[ \small\begin{aligned} \sigma_z &=\sqrt{\frac{(1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2} {5}} \\ &= \sqrt{\frac{0+0+0+0+0}{5}} \\ \sigma_z&= 0.0 \ \text{m} \end{aligned} \]

In [16]

print(np.std(Z))

Out [16]

0.0

次の話題に映る前に、男性は女性より身長が高いという事実を私が無視していることを指摘しておく必要がある。一般に男性もしくは女性だけからなるクラスでは、どちらの性別も含まれるクラスより身長の変動が小さくなる。同じことは他の要因についても言える。栄養状態の良い子供は栄養状態の悪い子供より背が高いだろうし、スカンジナビア人はイタリア人より背が高い。実験を設計する統計学者は様々な要因を考えに入れなくてはならない。

学区単位で机を購入するために身長の解析を行っているとしてみよう。このとき、各年齢グループで二つのこぶが存在する可能性が高い──男子の平均身長の周りにあるこぶと、女子の平均身長の周りにあるこぶである。クラス全体の平均身長は二つのこぶの中間にあるだろう。全ての生徒の平均に合った机を購入すると、男子にも女子にも合わない机になる可能性がある！

本書ではこういった問題を考えない。こういった問題に対処する手法を学びたいなら、標準的な確率論の教科書を参考にしてほしい。

分散で差の二乗を考える理由

分散で差の二乗を考えているのはなぜだろうか？数式をたっぷり使った説明もできるが、ここでは簡単な説明を示そう。\(X=[3,-3,3,-3]\) というデータを平均と共にプロットしたグラフを示す:

In [17]

X = [3, -3, 3, -3]
mean = np.average(X)
for i in range(len(X)):
    plt.plot([i ,i], [mean, X[i]], color='k')
plt.axhline(mean)
plt.xlim(-1, len(X))
plt.tick_params(axis='x', labelbottom=False)

もし分散の計算で差の二乗を取らないと、打ち消されて \(0\) になってしまう:

\[ \frac{(3-0) + (-3-0) + (3-0) + (-3-0)}{4} = 0 \]

\(X\) にはゼロでない変動があるので、これは明らかに間違いである。

絶対値ならどうだろうか？実際に計算すると \(X\) の "分散" が \(12/4=3\) になることが分かる。これならよさそうだ──どの値も平均から \(3\) だけ離れていることが示されている。では \(Y=[6, -2, -3, 1]\) に対してはどうなるだろうか？実はこの \(Y\) でも "分散" が \(12/4=3\) になる。しかし明らかに、\(Y\) は \(X\) より大きく変動する。二乗を使う通常の分散では \(Y\) の分散が (\(3\) ではなく) \(3.5\) となって変動が大きいことが反映される。

これで分散の定義が正しいことを証明できたわけではない。実は分散という技法を発見したカール・フリードリヒ・ガウスも分散の定義がいくらか恣意的であることを認めていた。二乗を使った分散の定義が持つ欠点の一つが、外れ値に対して不釣り合いなほど大きな重みを割り当てることである。例えば次のコードを見てほしい:

In [18]

X = [1, -1, 1, -2, -1, 2, 1, 2, -1, 1, -1, 2, 1, -2, 100]
print(f'外れ値を入れた X の分散 = {np.var(X):6.2f}')
print(f'外れ値を除いた X の分散 = {np.var(X[:-1]):6.2f}')

Out [18]

外れ値を入れた X の分散 = 621.45
外れ値を除いた X の分散 =   2.03

これは変動の指標として "正しい" のだろうか？それは分からない。外れ値 \(100\) を除いたときの分散 \(\sigma^2=2.03\) は \(X\) に含まれる外れ値以外のデータの変動を正しく表している。しかし外れ値が一つあると、分散はあまり意味のない値になってしまう。意味のない値を結果として外れ値の存在が分かるようにすべきだろうか、それとも外れ値を除いたデータの変動を推定するような値を結果とするべきだろうか？繰り返すが、分かりっこない。どちらが優れるかが問題によって異なるのは明らかだ。

この道には深入りしない: もし興味があるなら、Bayesian robustness と呼ばれる分野における James Berger の研究を見てみるといいかもしれない。あるいはロバスト統計学 (robust statistics) に関する Peter J. Huber の優れた書籍 Robust Statistical Procedures¹もある。本書では必ずガウスが定義した分散と標準偏差を使う。

以上の議論の要点は、平均・分散・標準偏差といった要約統計量 (summary statistics) はどんなときでもデータに関する不完全な形の情報しか伝えないということだ。ここで示した例で言えば、ガウスが定義した分散は単一の大きな外れ値があることを伝えられない。しかし、大きなデータセットを少数の数値で分かりやすく記述できる点で要約統計量は強力なツールである。一億個のデータ点があるときに数値が並んだ表やグラフを見ても何も分からないだろう。要約統計量はそういったデータの形状を便利な形で記述する手段を提供する。

3.4 ガウス分布

以上でガウス分布を学ぶ準備が整った。本章のモチベーションをもう一度書いておく:

私たちは、現実世界における振る舞いをモデル化する単峰性で連続なフィルタであって計算が効率的に行えるものを探している。

まずはガウス分布のグラフを見て感覚を掴もう:

In [19]

from filterpy.stats import plot_gaussian_pdf
plot_gaussian_pdf(mean=1.8, variance=0.1414**2,
                  xlabel='Student Height', ylabel='pdf');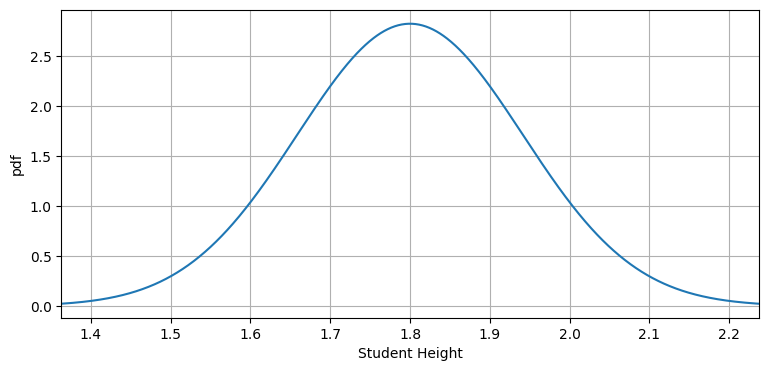

この曲線はガウス分布の確率密度関数 (probability density function, PDF) である。PDF は確率変数が特定の値となる相対的尤度を示す。例えばこのグラフからは、学生の身長が \(1.8~\text{m}\) の確率は \(1.7~\text{m}\) の確率より少し高いこと、そして \(1.9~\text{m}\) の確率が \(1.4~\text{m}\) の確率よりずっと高いことが分かる。別の言い方をすれば、\(1.8~\text{m}\) の周りには多くの学生が集まり、\(1.4~\text{m}\) や \(2.2~\text{m}\) の周りには学生がほとんどいない。最後に、曲線の中心が平均 \(1.8~\text{m}\) であることにも注目してほしい。

この曲線を「釣鐘曲線」という名前で知っているかもしれない。現実世界の条件では多くの観測値がガウス分布に従うので、この曲線はいたるところで登場する。ただ PDF が釣鐘の形になる確率分布は多くあるので、本書ではガウス分布のグラフを「釣鐘曲線」とは呼ばない。数学的でない文章では言葉を本書ほど正確に使っていない可能性があるので、「釣鐘曲線」という言葉が定義されずに出てきたときは何を意味するかをよく考えて読む必要がある。

この曲線が現れるのは身長だけではない──非常に多くの自然現象がこの種の分布を示し、フィルタリングの問題で使われるセンサーから得られる値も例外ではない。これから見るように、ガウス分布は私たちが探していた特徴を全て持つ──単峰性の信念あるいは値を確率として表現し、連続であり、効率的に計算できる。私たちがまだ望んでいると気付いていないその他の特徴も持っていることもすぐに分かる。

さらなる動機付けとして、離散ベイズフィルタの章で見た確率分布の形状を思い出そう:

In [20]

import kf_book.book_plots as book_plots
belief = [0., 0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]
book_plots.bar_plot(belief)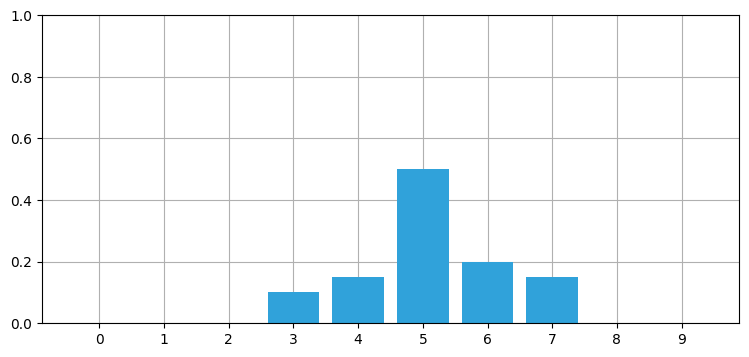

これは完璧なガウス曲線ではないが、似た形をしている。本章ではガウス分布を使って前章で使った離散確率を置き換える！

3.5 用語について

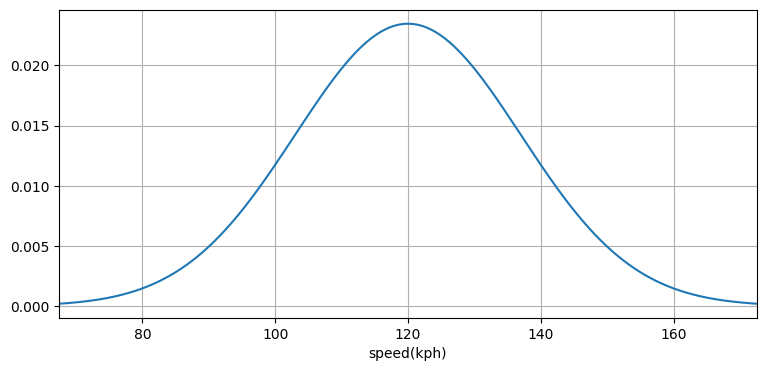
話を進める前に用語について少し説明を加える──ガウス分布のグラフは確率変数の確率密度が \((-\infty, \infty)\) に属する任意の値に対して定義されることを示している。これは何を意味するのだろうか？高速道路の特定の区間を通る車の速度を無限の精度で無限回測定したところを想像してほしい。そして任意の速度を観測した相対的な回数をグラフにプロットとしたとする。測定した車の平均速度が \(120~\text{km/h}\) なら、そのグラフは次のガウス分布のようになるかもしれない:

In [21]

plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)');

このとき曲線上の点の \(y\) 座標が確率密度を表す──その点の \(x\) 座標に対応する速度の車が観測された相対的な回数である。詳しくは次節で説明する。

ガウス分布を使ったモデルは完璧でない。この図には入っていないが、この分布の裾は両方向に無限に広がっている。人間の身長や車の速度は当然ゼロより小さくならないし、\(-\infty\) や \(\infty\) にもならない。「地図は現地ではない」という有名な言葉は、ベイズフィルタとベイズ統計でも成り立つ。上に示したガウス分布は観測された車の速度の分布をモデル化するものの、モデルになった時点で正確でなくなることは避けられない。モデルと現実の違いはフィルタリングでたびたび問題になる。ガウス分布は数学の様々な分野で使われているが、それはガウス分布が現実を完璧にモデル化するためではなく、他の比較的正確な選択肢と比べて簡単に扱えるためである。しかし本書で考えるような問題でさえ、ガウス分布では現実の挙動を正確にモデル化できず、より計算コストのかかる他の選択肢を使わざるを得ない場合がある。

こういった分布がガウス分布 (Gaussian distribution) あるいは正規分布 (normal distribution) と呼ばれているのを聞いたことがあるかもしれない。この文脈で「ガウス」と「正規」は同じ意味であり、どちらの名前で呼んでも構わない。本書では両方の呼称を使う: 資料によってどちらも使われるので、慣れておいてほしいためだ。英語では Gaussian distribution (ガウス分布) を省略して Gaussian あるいは normal と呼ぶこともある。

3.6 ガウス分布の特徴

ガウス分布の振る舞いを調べよう。ガウス分布は連続確率分布であり、平均 \(\mu\) と分散 \(\sigma^2\) という二つのパラメータで完全に記述される。ガウス分布の確率密度関数は

\[ f(x, \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp \left[ {-\frac{(x-\mu)^2}{2\sigma^2} } \right] \]

と定義される。ここで \(\exp[x]\) は \(e^x\) の別表記である。

この定義を見たことがなくても諦めないでほしい。ガウス分布の定義を記憶する必要はないし、こういった数式を操作できる必要もない。この関数の計算は FilterPy の filterpy.stats.gaussian(x, mean, var, normed=True) で行える。

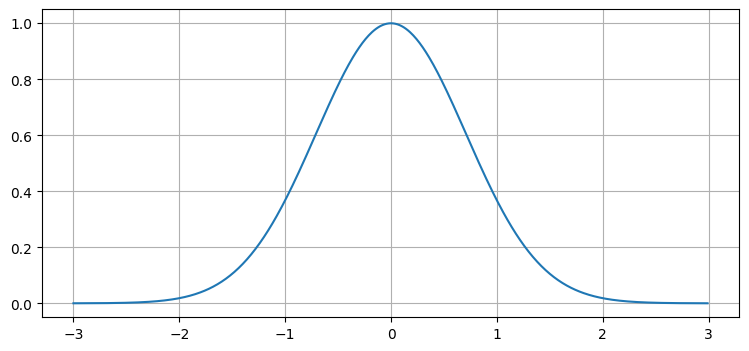
定数部分を消すと、\(f\) は単純な指数関数になる:

\[ f(x)\propto e^{-x^2} \]

これは見覚えのある釣鐘の形をしている:

In [22]

x = np.arange(-3, 3, .01)
plt.plot(x, np.exp(-x**2));

Jupyter Notebook 上で関数の定義を確認する方法を再掲しておく。セルで関数の名前の後ろに ? を二つ付けてから Ctrl+Enter を押すと、ソースコードを表示するウィンドウが開かれる。次のセルのコメントを外すと試せる:

In [23]

from filterpy.stats import gaussian
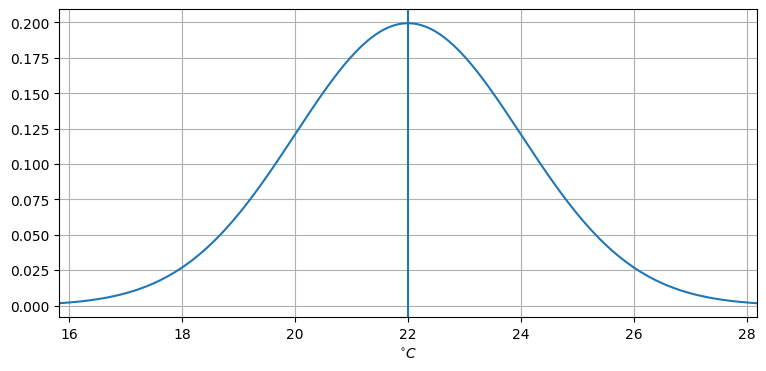
# gaussian??

平均が \(22\) (\(\mu=22\)) で分散が \(4\) (\(\sigma^2=4\)) のガウス分布をプロットしてみよう:

In [24]

plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$');

この曲線は何を意味するのだろうか？ある温度計が 22°C を指したとしよう。どんな温度計も完全ではないから、実際の温度は目盛りが指す値とは少し異なるだろうと私たちは期待する。しかし中心極限定理 (central limit theorem) と呼ばれる定理によると、測定を何度も行うと観測値の平均は正規分布に近づいていく。つまり上のグラフが表すのは、実際の温度が 22°C のときに温度計による測定を何度も行ったときの観測値の平均が特定の温度となる相対的な確率である。

ガウス分布は連続だったことを思い出そう。無限に長い数直線を考えるとき、そこからランダムに選んだ点がちょうど \(2\) になる確率はいくつだろうか？選択肢が無限にあるので、その確率は明らかに \(0\) である。正規分布でも同じ問題が起こる: 上のグラフによると、目盛りがちょうど 22°C を指す確率は \(0\) である。温度計の目盛りが指せる値は無限に存在するためだ。

この曲線は確率密度関数を表す。つまり \(x\) 軸上に適当な二点を取り、それらの点を通る垂直な直線と確率密度関数の曲線と \(x\) 軸が囲む領域の面積を計算すると、その面積は \(x\) 軸上の二点の間にある値が得られる確率に等しくなる。例えば上の曲線で \(x=20\) と \(x=22\) の間の領域の面積を計算すれば、温度計が 20°C と 22°C の間を指す確率が得られる。

こう考えても理解できる。岩、あるいはスポンジの密度とは何だろうか？密度とは、一定の空間に収まる重さを測った値である。岩の密度は高いが、スポンジの密度は低い。岩の重さが直接は分からないときでも、密度と体積を乗じることで重さを計算できる。実際には物体の内部で密度は変化するから、岩の体積全体に関して密度と体積の積を積分することになる:

\[ M = \iiint_R p(x,y,z)\, dV \]

確率密度でも同様となる。温度計が 20°C と 21°C の間の値を指す確率を知りたいなら、\(x=20\) から \(x=21\) にかけて図中の曲線を積分すればよい。知っての通り、曲線を積分すると曲線と \(x\) 軸の囲む領域の面積が得られる。図中の曲線は確率密度を表す曲線だから、積分すると確率になる。

この温度計が指す温度が 22°C になる確率は？直感的に考えると \(0\) である: 温度計が指す温度は実数だから、22°C になる確率と (例えば) 22.00000000000017°C になる確率はどちらも無限に小さい。数学的に考えると、この確率は確率密度関数を \(22\) から \(22\) まで積分した値、つまり \(0\) と分かる。

岩の例に戻ろう。岩内部の特定の一点の質量は？無限に小さい点は重さを持たないから、単一の点の重さを尋ねるのは質問としておかしい。同様に連続分布で単一の値の確率を尋ねるのも質問としておかしい。両方の質問の答えは明らかに \(0\) である。

実際のセンサーは無限の精度を持たないので、22°C を指す目盛りは 22±0.05°C のような何らかの区間を意味する。そのため (この例では) \(21.95\) から \(22.05\) まで確率密度関数を積分すれば、目盛りが 22°C を指す確率を計算できる。

ベイズ統計と頻度主義的統計の用語を使って考えることもできる。ベイズ主義者は、実際の (系の) 温度がちょうど 22°C のとき温度計が指す温度に関する信念が上述のガウス曲線によって表されると考える──例えば 22°C を指す確率は非常に高く、18°C を指す確率は非常に低い。これに対して頻度主義者は、ちょうど 22°C の系を温度計で無限回測定すると、観測値のヒストグラムが上述のガウス曲線になると考える。

値が特定の区間 \([x_0, x_1]\) に収まる確率、つまりこの二点を通る垂直な直線と確率密度関数を表す曲線と \(x\) 軸で囲まれる領域の面積はどうすれば計算できるだろうか？積分を使えば計算できる:

\[ \int^{x_1}_{x_0} \frac{1}{\sigma\sqrt{2\pi}} \exp \left[ {-\frac{1}{2}{(x-\mu)^2}/\sigma^2 } \right] dx \]

この積分を計算する filterpy.stats.norm_cdf 関数が用意されている。例えば次のように使う:

In [25]

from filterpy.stats import norm_cdf
print('21.5 から 22.5 の区間に対する累積確率: {:.2f}%'.format(
      norm_cdf((21.5, 22.5), 22,4)*100))
print('23.5 から 24.5 の区間に対する累積確率: {:.2f}%'.format(
      norm_cdf((23.5, 24.5), 22,4)*100))

Out [25]

21.5 から 22.5 の区間に対する累積確率: 19.74%
23.5 から 24.5 の区間に対する累積確率: 12.10%

平均 \(\mu\) は文字通り全ての確率の平均を表す。曲線は対称だから、平均は曲線の中で最も高い場所でもある。温度計が 22°C を指すとき、平均も 22°C になる。

確率変数 \(X\) の従う確率分布が正規分布であることを \(X \sim\ \mathcal{N}(\mu,\sigma^2)\) と表す。ここで \(\sim\) は「...に従って分布する」を意味する。これまでの例に適用すれば、温度計の目盛りが指す値 \(\text{temp}\) は次の式で表せる:

\[ \text{temp} \sim \mathcal{N}(22,4) \]

これは非常に重要な結果である。ガウス分布を使うと、無限にある可能な数値をたった二つの数値で表せる！ \(\mu=22\) と \(\sigma^2=4\) という値があるだけで、任意の区間に観測値が収まる確率を計算できる。

\(\mathcal N (\mu, \sigma^2)\) ではなく \(\mathcal N (\mu, \sigma)\) を使う文献もある。どちらでもよく、両方とも使われている。そのため \(\mathcal{N}(22,4)\) のような表記を見たときは、どちらを意味しているのかを確認しなければならない。私は必ず \(\mathcal N (\mu, \sigma^2)\) の形を使うから、\(\mathcal{N}(22,4)\) は \(\sigma=2\) と \(\sigma^2=4\) を意味する。

3.7 分散と信念

\(\mathcal N (\mu, \sigma^2)\) は確率密度関数だから、曲線と \(x\) 軸が囲む領域の面積は \(1\) である必要がある。これは直感的に明らかなはずだ──この領域は全ての結果を表すから、試行によって何かが起きたなら、何かが起こった確率は \(1\) である: つまり確率の和は \(1\) でなければならない。これは簡単なコードで確認できる (もし数学に自信があるなら、ガウス分布の確率密度関数を \(-\infty\) から \(\infty\) まで積分してみるとよい):

In [26]

print(norm_cdf((-1e8, 1e8), mu=0, var=4))

Out [26]

1.0

ここから非常に重要な洞察が得られる。分散はサンプルが平均からどれくらい散らばるかを示す指標なので、分散が小さいとき曲線の幅が狭くなる。一方で曲線が囲む領域の面積は \(1\) で一定なので、分散が小さいとき曲線は高くなる。逆に分散が大きいと曲線の幅は大きくなり、面積を一定にするために曲線は低くなる。

これをグラフで確認してみよう。前述の filterpy.stats.gaussian 関数は配列を受け取ることもできる:

In [27]

from filterpy.stats import gaussian

print(gaussian(x=3.0, mean=2.0, var=1))
print(gaussian(x=[3.0, 2.0], mean=2.0, var=1))

Out [27]

0.24197072451914337
[0.378 0.622]

デフォルトだと gaussian 関数は出力を正規化する。これは出力を確率分布にするための処理である。キーワード引数で normed=False とすればこの処理を無効化できる:

In [28]

print(gaussian(x=[3.0, 2.0], mean=2.0, var=1, normed=False))

Out [28]

[0.242 0.399]

なおガウス分布の確率密度関数が正規化されていないとき、それをガウス関数 (Gaussian function) と呼ぶ。異なるガウス分布をプロットしてみよう:

In [29]

xs = np.arange(15, 30, 0.05)
plt.plot(xs, gaussian(xs, 23, 0.2**2), label='$\sigma^2=0.2^2$')
plt.plot(xs, gaussian(xs, 23, .5**2), label='$\sigma^2=0.5^2$', ls=':')
plt.plot(xs, gaussian(xs, 23, 1**2), label='$\sigma^2=1^2$', ls='--')
plt.legend();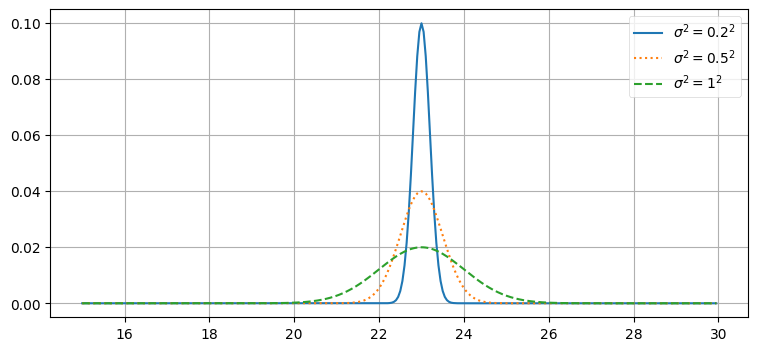

ここから何が分かるだろうか？ \(\sigma^2=0.2^2\) のガウス分布は非常に幅が狭い。私たちが \(x=23\) だと信じていて、信じる度合いが非常に強いことをこの分布は示している: 標準偏差は \(\pm 0.2\) である。これに対して、\(\sigma^2=1^2\) のガウス分布の場合は \(x=23\) と信じているものの、その度合いはずっと弱い。\(x=23\) の信念は低いので、\(x\) として可能性のある値に関する信念は広がる──例えば \(x=22\) や \(x=24\) も十分あり得ると考えている。\(\sigma^2=0.2^2\) のガウス分布では \(x=22\) と \(x=24\) の確率はほとんど存在しない。

温度計の例に戻れば、これらの曲線は異なる温度計からの出力を表していると考えることができる。\(\sigma^2=0.2^2\) の曲線はとても正確な温度計を表し、\(\sigma^2=1^2\) の曲線はあまり正確でない温度計を表す。ガウス分布で可能になった非常に強力な手法に注目してほしい──温度計が指す値とその誤差を平均と分散という二つの値で完全に表現できている。

ガウス分布を \(\mathcal{N}(\mu,1/\tau)\) と定式化することもできる。ここで \(\mu\) は平均、\(\tau\) は精度 (precision) を表す。\(1/\tau = \sigma^2\) であり、精度は分散の逆数である。本書ではこの定式化を使わないものの、精度という言葉を使うと分散がデータの正確さを表していることが強調される。分散が小さいとき精度は大きくなる──測定が非常に正確なことを示す。逆に分散が大きいと精度は小さくなる──このとき信念は大きく広がる。精度を使ったこの等価な形式のガウス分布の考え方にも慣れておくべきだろう。ベイズ統計の言葉を使えば、ガウス分布は観測値に関する信念を表す: 観測の精度、そして観測値の持つ分散がガウス分布によって表される。これらは同じ事実の異なる言い方である。

少し話の先取りをしておくと、次章では追跡している物体の推定された位置や観測を行うセンサーの正確さをガウス分布で表現する。

3.8 68-95-99.7 則

標準偏差について少し解説をしておいた方がよいだろう。標準偏差は何の意味もない値ではなく、データの変動の度合いを表す指標である。ガウス分布では、全体のデータの 68% が平均から標準偏差一つ分 (\(\pm1\sigma\)) の区間に収まることが示せる。同様に 95% は標準偏差二つ分 (\(\pm2\sigma\))、99.7% は標準偏差三つ分 (\(\pm3\sigma\)) だけ平均から離れた区間に収まる。この事実を 68-95-99.7 則と呼ぶことがある。もしテストの平均点が 71 点で標準偏差が 9.4 点だと伝えられたとしたら、(点数の分布が正規分布という仮定の下で) \(71-2\cdot9.4=52.2\) 点から \(71+2\cdot9.4=89.8\) 点の間に 95% の生徒が収まると結論できる。

あるいは何らかの長さが平均 \(\mu=22\) のガウス分布に従うとき、標準偏差もメートルの単位を持つ。そして \(\sigma=0.2\) は観測値の 68% が \(21.8~\text{m}\) から \(22.2~\text{m}\) に収まることを意味する。分散は標準偏差の二乗だから、\(\sigma^2=0.04\) の単位はメートル二乗となる。前節で使った \(\sigma^2=0.2^2\) という表記だと、データと同じ単位を持つ \(0.2\) が強調されるのでガウス分布の特徴が分かりやすくなる。

標準偏差と正規分布の関係を次の図に示す:

In [30]

from kf_book.gaussian_internal import display_stddev_plot
display_stddev_plot()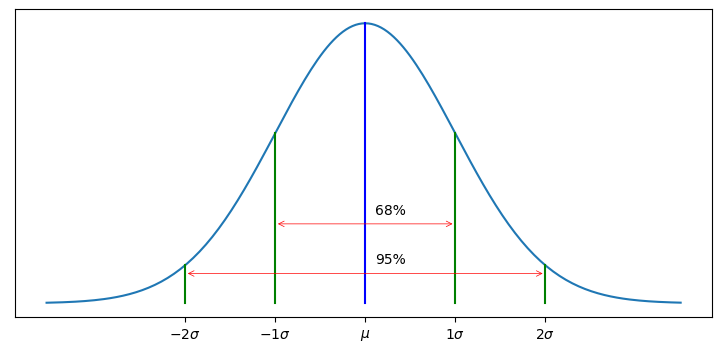

3.9 対話的なガウス分布

本書を Jupyter Notebook で読んでいる読者に向けて、対話的なバージョンのガウス分布のプロットを示す。スライダーを使うと \(\mu\) と \(\sigma^2\) を変更できる。\(\mu\) を動かすと平均が変わるのでグラフが左右に動き、\(\sigma^2\) を動かすと釣鐘曲線が狭くなったり広がったりする。

In [31]

import math
from ipywidgets import interact
from kf_book.book_plots import FloatSlider

def plt_g(mu,variance):
    plt.figure()
    xs = np.arange(2, 8, 0.01)
    ys = gaussian(xs, mu, variance)
    plt.plot(xs, ys)
    plt.ylim(0, 0.04)
    plt.show()

interact(plt_g, mu=FloatSlider(value=5, min=3, max=7),
         variance=FloatSlider(value = .03, min=.01, max=1.));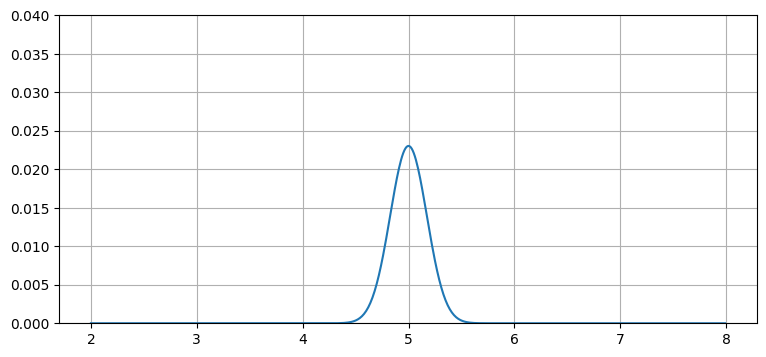

Out [31]対話的なガウス分布のプロット (Jupyter Notebook でのみ実行可能)

本書をオンラインで読んでいる人に向けて、ガウス分布のアニメーションを示す。最初に平均を大きくして、それから平均を \(\mu=5\) に固定して分散を変化させている:

3.10 ガウス分布の計算量的特徴

離散ベイズフィルタは任意の確率分布の和や積を計算することで動作した。カルマンフィルタは任意の確率分布ではなくガウス分布を使うものの、それ以外のアルゴリズムは変わらない。これは、ガウス分布の和と積を計算できる必要があることを意味する²。

ガウス分布は次の驚くべき特徴を持つ: 二つ確率変数が独立にガウス分布に従うとき、それらの和も正規分布に従う！ガウス分布に従う二つの独立な確率変数の積はガウス分布に従わないものの、二つのガウス分布の確率密度関数の積はガウス分布の確率密度関数に比例する。つまり二つのガウス分布を乗じるとガウス関数となる (この文脈で「ガウス関数」の「関数」は全区間の積分が 1 になる特徴が保証されていないことを意味する)。

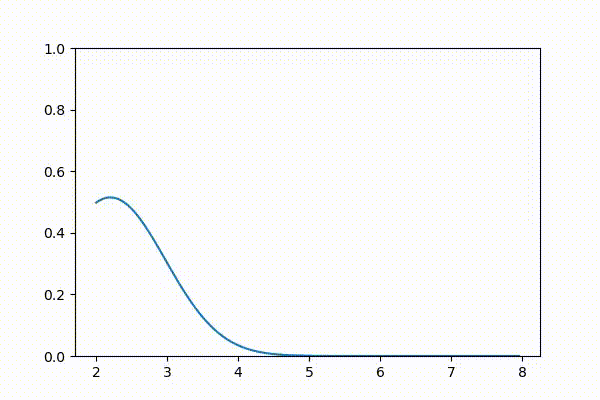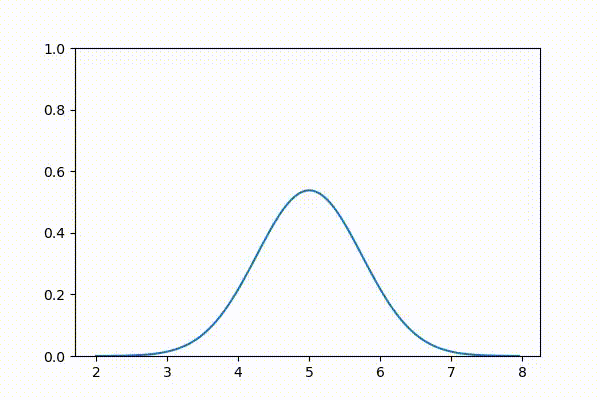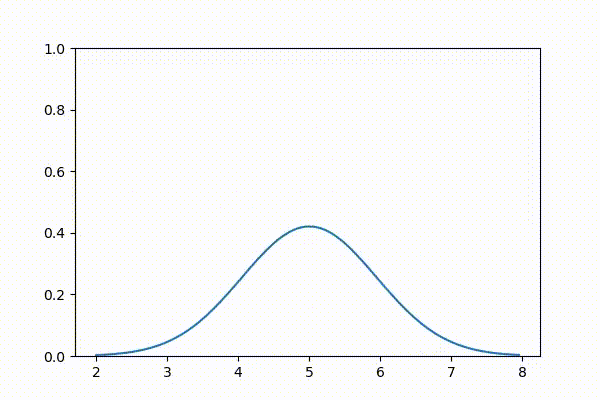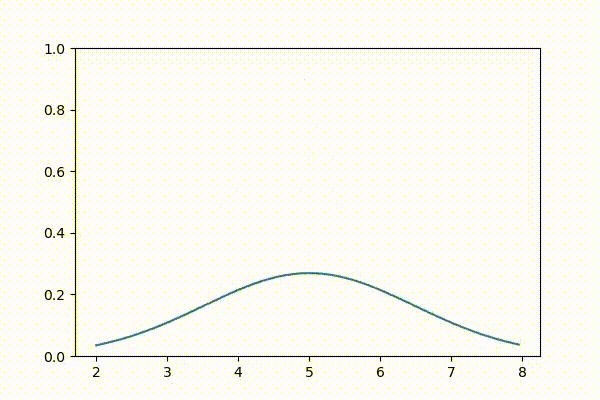
数式を示す前に、視覚的にテストしてみよう:

In [32]

x = np.arange(-1, 3, 0.01)
g1 = gaussian(x, mean=0.8, var=.1)
g2 = gaussian(x, mean=1.3, var=.2)
plt.plot(x, g1, x, g2)

g = g1 * g2     # 要素ごとの積
g = g / sum(g)  # 正規化
plt.plot(x, g, ls='-.');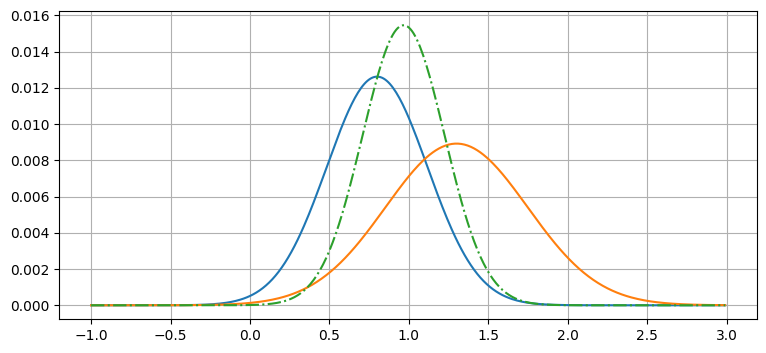

ここでは \(g1=\mathcal N(0.8, 0.1)\) と \(g2=\mathcal N(1.3, 0.2)\) という二つのガウス分布を作成してプロットし、加えてそれらの積を正規化したものをプロットしている。グラフの結果はガウス分布に見える。

ガウス分布の確率密度関数は非線形である。一般に、非線形の関数を乗じると異なる種類の関数が得られる。例えば、二つのサイン関数の積は sin(x) と大きく異なる:

In [33]

x = np.arange(0, 4*np.pi, 0.01)
plt.plot(np.sin(1.2*x))
plt.plot(np.sin(1.2*x) * np.sin(2*x));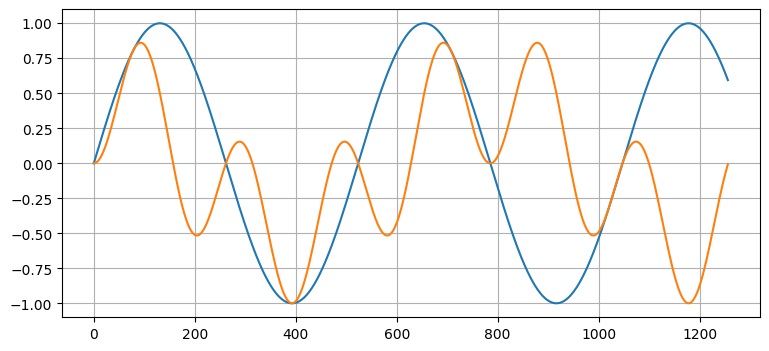

しかしガウス分布の確率密度関数を二つ乗じるとガウス関数になる。この事実はカルマンフィルタが計算量的に実現可能になる上で非常に重要である。別の言い方をすれば、カルマンフィルタは計算量的に有利だからガウス分布を使っている。

数式を使ってまとめておこう。二つのガウス分布 \(\mathcal N(\mu_1, \sigma_1^2),\ \mathcal N(\mu_2, \sigma_2^2)\) の確率密度関数の積はガウス関数であり、その平均 \(\mu\) と分散 \(\sigma^2\) は次の関係を満たす:

\[ \begin{aligned}\mu &=\frac{\sigma_1^2\mu_2 + \sigma_2^2\mu_1}{\sigma_1^2+\sigma_2^2}\\ \sigma^2 &=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{aligned} \]

二つの確率変数がそれぞれガウス分布 \(\mathcal N(\mu_1, \sigma_1^2),\ \mathcal N(\mu_2, \sigma_2^2)\) に独立に従うとき、その和もガウス分布 \(\mathcal N(\mu, \sigma^2)\) に従う。このとき \(\mu\) と \(\sigma\) は次の関係を満たす:

\[ \begin{gathered}\mu = \mu_1 + \mu_2 \\ \sigma^2 = \sigma^2_1 + \sigma^2_2 \end{gathered} \]

章末にこれらの関係の導出を示すが、導出を理解するのはあまり重要でない。

3.11 全てをまとめる

ガウス分布がフィルタリングでどう使われるかを説明する準備がこれで整った。ガウス分布を使ったフィルタの実装は次章にまわして、ここではガウス分布をどう使えるのかを説明する。

前章の離散ベイズフィルタでは確率分布を配列で表した。離散ベイズフィルタの更新ステップでは、事前分布を表す配列と各点における観測値の尤度を表す配列の要素ごとの積が計算される。次のような処理である:

In [34]

def normalize(p):
    return p / sum(p)

def update(likelihood, prior):
    return normalize(likelihood * prior)

prior      = normalize(np.array([4, 2, 0, 7, 2, 12, 35, 20, 3, 2]))
likelihood = normalize(np.array([3, 4, 1, 4, 2, 38, 20, 18, 1, 16]))
posterior  = update(likelihood, prior)
book_plots.bar_plot(posterior)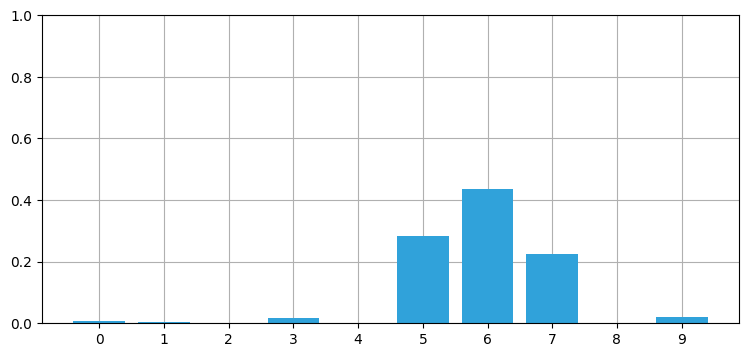

言い換えると、更新ステップの計算には 10 回の乗算が必要になる。現実の問題で使われるフィルタでは大規模な多次元配列が使われるので、数十億回の乗算と数ギガバイトのメモリを費やしても計算は終わらないかもしれない。

ただ、この分布は見た目がガウス分布に似ている。配列ではなくガウス分布を使ったらどうなるだろうか？事後分布の平均と分散を計算して、ガウス分布と棒グラフを同時にプロットしてみよう:

In [35]

xs = np.arange(0, 10, .01)

def mean_var(p):
    x = np.arange(len(p))
    mean = np.sum(p * x,dtype=float)
    var = np.sum((x - mean)**2 * p)
    return mean, var

mean, var = mean_var(posterior)
book_plots.bar_plot(posterior)
plt.plot(xs, gaussian(xs, mean, var, normed=False), c='r');
print('平均: %.2f' % mean, '分散: %.2f' % var)

Out [35]

平均: 5.88 分散: 1.24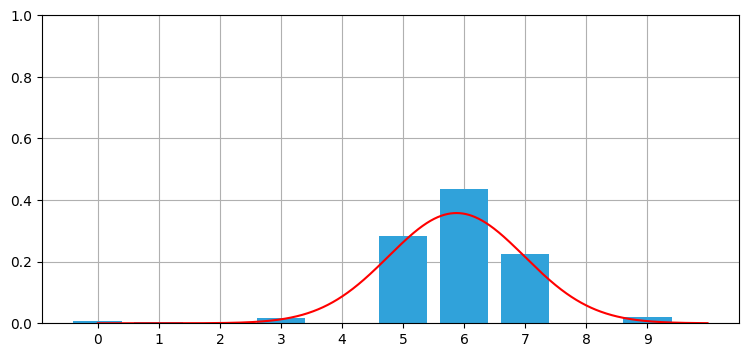

これは素晴らしい。たくさんの数値からなる分布全体をたった二つの数値で記述できている。この例では分布に含まれる数値が 10 個だけだから説得力があまりないかもしれないが、現実の問題では数百万の数値を扱わなければならない。そのような場合でも、ガウス分布を使えば二つの数値で分布を記述できる。

続いて、離散ベイズフィルタの更新関数の定義を思い出そう:

def update(likelihood, prior):
    return normalize(likelihood * prior)

配列が百万個の要素を持つなら、この計算で百万回の乗算が行われる。しかし配列をガウス分布で置き換えれば、その計算が次の計算で済む:

\[ \begin{aligned}\mu &=\frac{\sigma_1^2\mu_2 + \sigma_2^2\mu_1}{\sigma_1^2+\sigma_2^2}\\ \sigma^2 &=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{aligned} \]

これは三度の乗算と二度の除算である。

3.12 ベイズの定理

前章では各時点で持っている情報について考えることでアルゴリズムを開発し、そのとき情報を離散確率分布として表現した。その中で私たちはベイズの定理を発見した。ベイズの定理を使うと、何らかの事象の確率を与えられた事前情報から計算する方法が分かる。

update 関数は次の確率計算を使って実装した:

\[ \text{事後分布} = \frac{\text{尤度}\times \text{事前分布}}{\text{正規化係数}} \]

これこそがベイズの定理である。数式を使った表現はすぐに示すが、様々な意味で、その表現だとこの式で表される簡単なアイデアが分かりにくい。この式は次のように読める:

\[ \text{更新された知識} = \big\|\text{新しい知識の尤度} \times \text{事前の知識} \big\| \]

ここで \(\| \cdot\|\) は正規化を表す。

この単純な考え方には廊下を歩く犬を考えることで到達していた。しかしこれから見るように、同じ等式はフィルタリングの問題の全てに適用できる。この等式は以降の全ての章で登場する。

復習しておくと、事前分布とは観測値の確率 (尤度) を取り入れる前の段階における何かが起こる確率であり、事後分布は観測値から情報を取り入れた後に計算する確率である。

ベイズの定理を示す:

\[ P(A \mid B) = \frac{P(B \mid A)\, P(A)}{P(B)} \]

ここで \(P(A \mid B)\) は条件付き確率と呼ばれるもので、\(B\) が起こったという条件の下で \(A\) が起こる確率を示す。例えば降水確率を考えると、前線は数日にわたって停滞することが多いので、昨日雨が降っていたなら今日も雨が降る確率が (普通の日と比べて) 高い。この「昨日雨が降ったという条件の下で今日雨が降る確率」を記号で書けば \(P(\text{今日雨が降る} \mid \text{昨日雨が降った})\) となる。このとき

\[P(\text{今日雨が降る} \mid \text{昨日雨が降った}) > P(\text{今日雨が降る})\]

が成り立つことだろう。

重要なポイントを軽く触れてしまっている。上で示したコードは単一の確率を計算しているのではなく、確率の配列によって表される確率分布を計算している。ベイズの定理と言って示したのは確率に関する等式であり、確率分布に関する等式ではない。しかし、この等式は確率分布に対しても同様に成り立つ。確率分布は小文字の \(p\) で表すから、次のようになる:

\[ p(A \mid B) = \frac{p(B \mid A)\, p(A)}{p(B)} \]

ここで \(B\) は証拠 (evidence)、\(p(A)\) は事前分布 (prior distribution)、\(p(B \mid A)\) は尤度 (likelihood)、\(p(A \mid B)\) は事後分布 (posterior distribution) を表す。数学的な記号を対応する言葉に置き換えると、私たちが離散ベイズフィルタの更新ステップで使った等式とベイズの定理の等式が一致することが分かるだろう。

ベイズの定理を前章で考えた問題に合うように書き換えてみよう。\(i\) 番目の位置を \(x_i\) で表すことにする。このとき求めたいのは観測値 \(z\) が与えられたときにサイモンが位置 \(x_i\) にいる確率 \(P(x_i \mid z)\) である。上述の等式に代入して解けば、次を得る:

\[ p(x_i \mid z) = \frac{p(z \mid x_i) p(x_i)}{p(z)} \]

おっかない見た目をしているが、実は非常に簡単なことを主張している。右辺にある項を一つずつ確認していこう。最初の \(p(z \mid x_i)\) は尤度であり、サイモンが位置 \(x_i\) にいる状態で観測値 \(z\) が出力される確率を表す。\(p(x_i)\) は事前分布であり、観測値を取り入れる前に私たちが抱いている信念を表す。実際のコードでは、この二つを乗じてから正規化を行っている:

def update(likelihood, prior):
    posterior = likelihood * prior # p(z|x) * p(x)
    return normalize(posterior)

最後に分母の \(p(z)\) があるが、これは位置を考えに入れない状態における観測値 \(z\) が出力される確率であり、証拠 (evidence) と呼ばれることが多い。私たちは分子の和を取ることで \(p(z)\) を計算しており、この計算はコードの sum(belief) に対応する。これは正規化の計算方法そのものだ！というわけで、update 関数はまさにベイズの定理の等式を計算している。

ベイズの定理を紹介する文献では積分を使った次の形が与えられることも多い。ごく簡単に言えば積分は連続関数に対する総和だとみなせるから、ベイズの定理は次のようにも書ける:

\[ p(A \mid B) = \frac{p(B \mid A)\, p(A)}{\displaystyle \int p(B \mid A_j) p(A_j) \,\, dA_j} \]

この式の分母は解析的に解けない場合が多く、解ける場合でもひどく手間がかかる。王立統計学会に最近掲載された意見記事はこの分母を「犬の朝飯³」と表現している。ベイズ確率を使ったアプローチを取るフィルタリングの教科書では解析的な解を持たない積分まみれの等式がいたるところで登場するものの、そういった等式を恐れることはない: 積分を計算せずとも分子を正規化するだけで事後分布は得られる。積分を処理する手法は粒子フィルタの章で触れる。それまでの間は、実際の計算においてこの積分は和を使って計算できる正規化のための項だと理解しておけば十分だ。要するに積分の計算で埋まったページに直面したら、それはただの和だと考えた上で本章の説明と見比べれば、難しい部分は消えるだろう。「この値の和を求めているのはなぜ？」あるいは「この項で割るのはなぜ？」などと自問すれば、驚くほど頻繁に答えはすぐに明らかになる。驚くほど頻繁に専門的な文献の著者はこの解釈に触れるのを忘れてしまう。

ベイズの定理の強みがまだ完全にはつかめていないかもしれない。計算したいのは \(p(x_i \mid Z)\)、つまりステップ \(i\) において観測値が与えられたときの状態の確率的表現である。例えば癌検診の結果から癌を患っている可能性を計算したい場合もあるし、様々なセンサーの出力から降水確率を計算したい場合もある。このように表現されると問題が一般的すぎて解けないように思える。しかしベイズの定理は一般的な定理である。

ベイズの定理があると、逆の \(p(Z \mid x_i)\) を使って \(p(x_i \mid Z)\) の計算ができるようになる。つまり次の関係が使える:

\[ p(x_i \mid Z) \propto p(Z\mid x_i)\, p(x_i) \]

言い換えると、センサーの出力が与えられたときの降水確率を計算するときに、雨が降っているときのセンサーの出力の尤度を計算するだけで済む。これは難易度がはるかに低い問題である！もちろん気象予報は難しい問題だが、ベイズの定理によって少なくとも手の届く問題になる。

同様に離散ベイズフィルタの章では、サイモンが特定の位置にいるときセンサーがどのような確率で観測値を出力するかを考えることで、サイモンがそれぞれの位置にいる尤度を計算した。これによって難しい問題は簡単になる。

3.13 全確率の定理

これで update 関数の背後にある数学を理解できた。では predict 関数についてはどうだろうか？この関数は全確率の定理 (total probability theorem) を実装する。predict が何をするかを思い出そう: サイモンの移動量の確率を受け取って、サイモンが移動した後の位置を確率的に計算していた。これを等式として表してみる。サイモンが時刻 \(t\) に位置 \(i\) にいる確率を \(P(X_i^t)\) とする。すると時刻 \(t-1\) における確率 \(P(X_j^{t-1})\) と位置 \(x_j\) から位置 \(x_i\) に移動する確率を乗じたものを足し上げれば \(P(X_j^t)\) となる。つまり次の等式が成り立つ:

\[ P(X_i^t) = \sum_j P(X_j^{t-1}) P(x_i | x_j) \]

この等式は全確率の定理と呼ばれる。Wikipedia から引用すれば、全確率は「いくつかの異なる事象を通して実現される結果の確率」を表す。最初からこの等式を示して predict を実装することもできたかもしれないが、そうしても等式が正しい理由を理解できる確率は低いだろう。前章で使った確率の計算を再掲しておく:

for i in range(N):
    for k in range (kN):
        index = (i + (k-width) - offset) % N
        result[i] += pdf[index] * kernel[k]

3.14 `scipy.stats` を使った確率の計算

この章ではガウス分布をプロットするのに FilterPy のコードを使ってきた。こうしたのは読者に関数の実装を確認する機会を与えるためである。しかし Python はよく言われるように「バッテリー内蔵」なので、scipy.stats モジュールに様々な統計関数が用意されている。scipy.stats を使って統計や確率を計算する方法を軽く見てみよう。

scipy.stats モジュールには様々な確率分布に関連する値を計算するためのオブジェクトが数多く含まれている。完全なドキュメントは http://docs.scipy.org/doc/scipy/reference/stats.html にある。ここでは正規分布を実装するオブジェクトを作成する norm 関数を使って機能を紹介する。まずは scipy.stats.norm を使ってガウス分布を計算し、その返り値を FilterPy の gaussian と比べてみよう:

In [36]

from scipy.stats import norm
import filterpy.stats
print(norm(2, 3).pdf(1.5))
print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))

Out [36]

0.13114657203397997
0.13114657203397995

norm(2, 3) という呼び出しによって、scipy が「固まった分布 (frozen distribution)」と呼ぶオブジェクト──ここでは平均が \(2\) で標準偏差が \(3\) の正規分布を表すオブジェクト──が計算される。後はこのオブジェクトだけで複数の値における確率密度を計算できる:

In [37]

n23 = norm(2, 3)
print('1.5 における PDF は %.4f' % n23.pdf(1.5))
print('2.5 における PDF も %.4f' % n23.pdf(2.5))
print('2   における PDF は %.4f' % n23.pdf(2))

Out [37]

1.5 における PDF は 0.1311
2.5 における PDF も 0.1311
2   における PDF は 0.1330

この他にも多くの関数やメソッドが用意されており、scipy.stats.norm のドキュメントから確認できる。例えば確率分布から \(n\) 個のサンプルを生成するには rvs メソッドを使う:

In [38]

np.set_printoptions(precision=3, linewidth=50)
print(n23.rvs(size=15))

Out [38]

[ 3.432 -3.14  -0.06   3.784 -1.313  7.706 -2.831
  3.926  2.522  5.042  0.603 -3.388 -5.413  4.421
  3.746]

累積確率分布関数 (cumulative distribution function, CDF) の計算も行える。この関数の返り値は確率分布からランダムに生成した値が \(x\) 以下である確率を示す:

In [39]

# n23 からランダムに取り出した値が平均 2 以下である確率
print(n23.cdf(2))

Out [39]

0.5

確率分布の特徴量も取得できる:

In [40]

print('分散:     ', n23.var())
print('標準偏差: ', n23.std())
print('平均:     ', n23.mean())

Out [40]

分散:     9.0
標準偏差: 3.0
平均:     2.0

3.15 ガウス分布を使ったモデルの欠点

前に中心極限定理について触れた。この定理は「任意の確率分布に従う独立な確率変数をいくつか平均して新しい確率変数を作ったとする。このときある条件の下で、確率分布がどんなものであったとしても、平均する確率変数の個数を増やしていくと平均の従う分布が正規分布に近づく」ことを示す。自然現象では正規分布でない分布が多く現れるものの、たくさんのサンプルを考えれば平均が正規分布となることが中心極限定理から分かるので、この定理は非常に重要である。

しかし、その証明では「ある条件の下で」が重要な役割を果たす。この条件は現実世界で成り立たないことが多い。例えばキッチンスケールの出力が \(0\) より小さくなることはない。しかしガウス曲線の左側は負の無限大まで伸びるので、計測誤差をガウス分布と仮定すると負の計測値が出力される確率が (非常に小さく) 存在することになる。

これは広いトピックであり、ここで完全な形で扱うことはできない。

簡単な例として、テストの点数が正規分布するという仮定を考える。相対評価 (grade on a curve) を使う講義を受けたことがあるなら、その講義ではあなたにこの仮定が適用されたということだ。しかし当然、点数が正規分布に従うことはあり得ない: ガウス分布はどれだけ平均から離れていようと任意の値にゼロでない確率を割り当てるためだ。例えば点数の平均が 90 点で標準偏差が 13 点だとしよう。このとき点数が正規分布に従うという仮定により生徒は 90 点を取る確率が高く、40 点を取る確率が低いことが分かる。しかし正規分布は -10 点や 150 点の生徒が存在する確率がゼロでないことも意味する。ガウス分布の裾は無限に長く伸びるので、\(-10^{300}\) や \(10^{32986}\) といった極端な値にさえゼロでない確率が割り当てられる。

しかしテストの点数としてこれらの点数があり得ないことを私たちは知っている。追加で加えられる点数を除けば、0 点より小さい値と 100 点より大きい値は実現不可能である。可能な範囲だけで正規分布をプロットすると、現実の点数の分布を正規分布で表せていないことが分かる:

In [41]

xs = np.arange(10, 100, 0.05)
ys = [gaussian(x, 90, 30) for x in xs]
plt.plot(xs, ys, label='var=0.2')
plt.xlim(0, 120)
plt.ylim(-0.02, 0.09);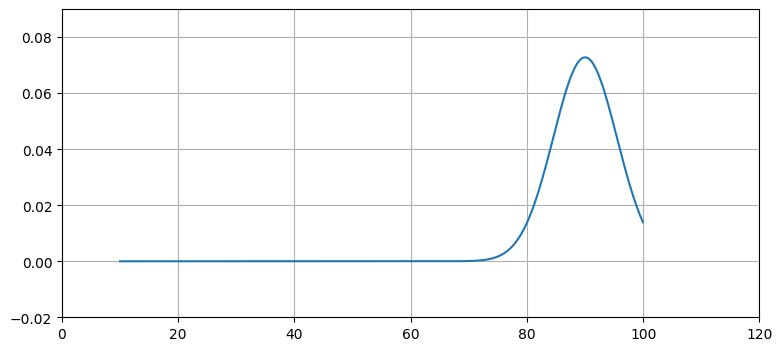

曲線と \(x\) 軸が囲む領域の面積は 1 に等しくないから、これは確率分布ではない。実際には (例えば) 両端に近い点数の生徒がこれより多くいて、裾が "太って" いるのだろう。あるいはテストが生徒のスキルを細かく区別できていなくて、平均の左側に何人かの集まりがいくつか生まれるかもしれない。

センサーが世界を観測するとき、センサーの観測値に含まれる誤差がガウス分布であることはまずない。この事実がカルマンフィルタの設計をどう難しくするかを話すのはまだ早すぎるが、カルマンフィルタで使われる数学が理想化された世界のモデルを土台にしていることは頭の片隅に入れておくべきだろう。ここでは誤差として使える正規分布でない分布としてスチューデントの \(t\)-分布 (Student's \(t\)-distribution) を紹介する。

出力に白色ノイズが加わるセンサーをモデル化したいとする。簡単のため信号は定数 \(10\) として、ノイズの標準偏差は \(2\) とする。numpy.random.randn 関数を使うと平均 \(0\) で標準偏差 \(1\) の正規分布に従う乱数を得られるので、このセンサーは次のようにシミュレートできる:

In [42]

from numpy.random import randn
def sense():
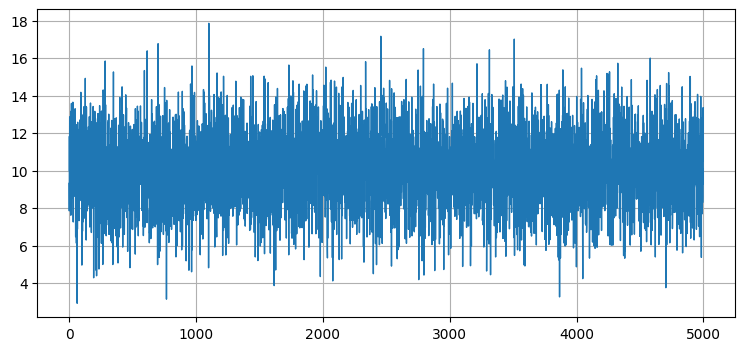
    return 10 + randn()*2

出力される信号をプロットして見た目を確認しよう:

In [43]

zs = [sense() for i in range(5000)]
plt.plot(zs, lw=1);

これは予想通りと言える。まず出力信号は \(10\) が中心となっている。また標準偏差が \(2\) だから観測値の 68% が \(10 \pm 2\) に含まれ、99% は \(10 \pm 6\) に含まれるはずだが、確かにそうなっているように見える。

続いてスチューデントの \(t\)-分布で生成した信号を見てみよう。数式の説明は飛ばして、ソースコードとプロットだけを見せることにする:

In [44]

import random
import math

def rand_student_t(df, mu=0, std=1):
    """
    自由度 df・平均 mu・標準偏差 std を持つスチューデントの t-分布
    によって生成される乱数を返す。
    """
    x = random.gauss(0, std)
    y = 2.0*random.gammavariate(0.5*df, 2.0)
    return x / (math.sqrt(y / df)) + mu

In [45]

def sense_t():
    return 10 + rand_student_t(7)*2

zs = [sense_t() for i in range(5000)]
plt.plot(zs, lw=1);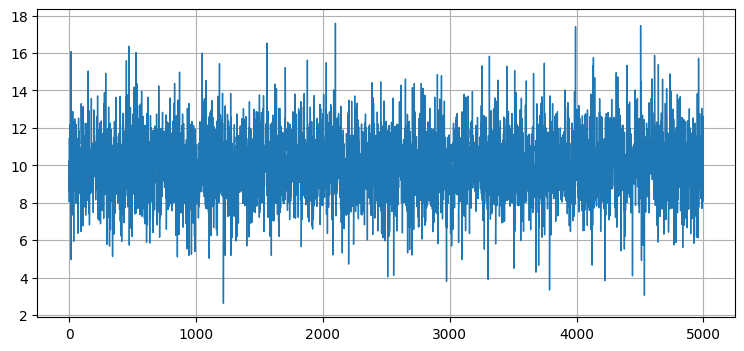

グラフは正規分布を誤差に使ったときと大きくは変わらないが、よく見ると平均から標準偏差三つ分以上離れた (\(7\) 以下および \(13\) 以上の)外れ値がいくつか存在することが分かる。

考えているセンサー (例えば GPS やドップラーレーダー) に含まれる誤差をスチューデントの \(t\)-分布で正確なモデル化できる可能性は低い。本書は物理系のモデル化に関する本ではないので、この点については詳しく説明しない。ただ、現実的なノイズがあるときのフィルタの性能をテストするためのデータを生成するときはこの分布が使える。本書では以降シミュレーションとテストでこういった分布を使っていく。

スチューデントの \(t\)-分布を考えたのは無駄ではない。カルマンフィルタの数式はノイズが正規分布に従うことを仮定しており、そうでないと性能が落ちる。航空機などに搭載されるミッションクリティカルなフィルタを設計するには、理論だけではなくフィルタが搭載される装置に関する実践的知識も数多く習得しなければならない。例えば私が見たことのある NASA のプレゼンテーションでは、理論的には正当な観測値とノイズを区別するのに標準偏差三つ分の差を使うべきとされるが、実際には標準偏差五つ分あるいは六つ分を使わなければならなかったと報告されていた。この値は実験によって決定されたそうだ。

rand_student_t のコードは filterpy.stats にモジュール存在するので、次のようにすると使える:

from filterpy.stats import rand_student_t

ここでは詳しく説明しないが、統計学では確率分布の形が左右対称からどれくらい離れているかを表す指標が定義されている。正規分布は平均をまたいで対称に──釣鐘曲線という言葉がぴったりな形に──なっているが、この対称性を持たない確率分布も存在する。この指標は歪度 (skewness) と呼ばれる。また正規分布と比べたときに裾が短かったり、長かったり、厚かったり、薄かったりすることを表す指標として尖度 (kurtosis) も定義される。scipy.stats モジュールの describe 関数を使うとこういった特徴量を確認できる:

In [46]

import scipy
scipy.stats.describe(zs)

Out [46]

DescribeResult(nobs=5000, minmax=(-5.979216191283138, 19.545171178231744), mean=9.978744378222718, variance=2.8876006850158005, skewness=-0.18733104074238008, kurtosis=3.0543020487114356)

試しに正規分布から二種類の標本を抽出して確認してみよう。一つの標本は小さく、もう一つの標本は大きい:

In [47]

print(scipy.stats.describe(np.random.randn(10)))
print()
print(scipy.stats.describe(np.random.randn(300000)))

Out [47]

DescribeResult(nobs=10, minmax=(-1.8569512704660722, 1.2963954433744118), mean=-0.08256205820824643, variance=1.2072793639581079, skewness=-0.6506481625753222, kurtosis=-0.971071297157593)

DescribeResult(nobs=300000, minmax=(-4.557204727077382, 4.388618039310767), mean=-0.0009518659843635722, variance=0.9992485564953709, skewness=0.004976558364738024, kurtosis=-0.022141584107537415)

小さいサンプルでは歪度と尖度がゼロから離れた値になっているが、これはサンプルが少ないために分布が正規分布本来の形になっていないためである。この事実は平均と分散が理論的な値 (\(0\) と \(1\)) になっていないことからも分かる。これに対して大きなサンプルでは平均と分散が理論的な値に近く、歪度と尖度もゼロに近い。

3.16 ガウス分布の確率密度関数の積 (スキップ可)

この節は重要でないので飛ばしてよい。これからガウス分布の確率密度関数の積を計算する公式の導出を示す。

二つの確率密度関数を乗じて項を整理すれば結果は得られるが、式変形はそれなりに手間がかかる。ここでは以降の解説の都合上ベイズの定理を使った導出を示す。これから「事前分布 \(p(x) = N(\bar\mu, \bar\sigma^2)\) と観測値の尤度 \(p(z \mid x) = N(z, \sigma_z^2)\) が与えられたとき、\(z\) を取り入れた事後分布を求めよ」という問題を考える。

事後分布を \(p(x \mid z)\) と書く。このときベイズの定理から

\[ p(x \mid z) = \frac{p(z \mid x)p(x)}{p(z)} \]

が分かる。ここで \(p(z)\) は正規化のための定数だから、比例の形で次のように書ける:

\[ p(x \mid z) \propto p(z \mid x)p(x) \]

続いてガウス分布の式をここに代入する。代入する式は次の通りである:

\[ \begin{aligned} p(z \mid x) &= \frac{1}{\sqrt{2\pi\sigma_z^2}}\exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big] \\ p(x) &= \frac{1}{\sqrt{2\pi\bar\sigma^2}}\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big] \end{aligned} \]

最初に付いている項は定数なので無視できることに注意すると、次のように式変形できる:

\[ \begin{aligned} p(x \mid z) &\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big]\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big]\\ &\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big] \\ &\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z-x)^2+\sigma_z^2(x-\bar\mu)^2]\Big] \end{aligned} \]

二乗を展開し、\(x\) のべきでまとめる:

\[ \small\begin{aligned} p(x \mid z) &\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z^2 -2xz + x^2) + \sigma_z^2(x^2 - 2x\bar\mu+\bar\mu^2)]\Big ] \\ &\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z) + (\bar\sigma^2z^2+\sigma_z^2\bar\mu^2)]\Big ] \end{aligned} \]

指数関数の引数の最後の項 \(\bar\sigma^2z^2+\sigma_z^2\bar\mu^2\) は \(x\) が関係しないから、比例定数として無視できる:

\[ p(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z)}{\sigma_z^2\bar\sigma^2}\Big ] \]

分母と分子を \(\bar\sigma^2+\sigma_z^2\) で割ると次を得る:

\[ p(x \mid z) \propto \exp \left[-\frac{1}{2}\frac{x^2-2x\left(\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2}\right)}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\right] \]

これは比例の関係だから、指数関数の引数に対して定数を自由に足したり引いたりできる。よって

\[ p(x \mid z) \propto \exp \left[-\frac{1}{2}\frac{\left(x-\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2}\right)^2}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\right] \]

が分かる。ガウス分布の確率密度関数は

\[ N(\mu,\, \sigma^2) \propto \exp\Big [-\frac{1}{2}\frac{(x - \mu)^2}{\sigma^2}\Big ] \]

だったから、二つの式を見比べると \(p(x \mid z)\) は平均

\[ \mu_\mathtt{posterior} = \frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2} \]

および分散

\[ \sigma_\mathtt{posterior} = \frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2} \]

のガウス関数と分かる。

式変形で定数を落としているために、積 \(p(z \mid x)p(x)\) は正規分布の確率密度関数ではなく、それに比例するガウス関数となる。ベイズの定理は分母の \(p(z)\) で正規化を行うので、事後分布は正規分布となる。実際のコードではフィルタの更新ステップで正規化を行うことで推定値がガウス分布であることを保証する。

3.17 ガウス分布に従う確率変数の和 (スキップ可)

この節も同様にあまり重要でない。ガウス分布に従う二つの独立な確率変数の和が従う分布がガウス分布であることを導出する。

二つの確率変数がそれぞれガウス分布 \(\mathcal N(\mu_1, \sigma_1^2),\ \mathcal N(\mu_2, \sigma_2^2)\) に独立に従うとき、その和もガウス分布 \(\mathcal N(\mu, \sigma^2)\) に従う。このとき \(\mu\) と \(\sigma^2\) は次の関係を満たす:

\[ \begin{gathered}\mu = \mu_1 + \mu_2 \\ \sigma^2 = \sigma^2_1 + \sigma^2_2 \end{gathered} \]

この証明は何種類か知られている。前章で確率のヒストグラムに対する畳み込みを考えたので、ここでは畳み込みを使った証明を示す。

和の確率密度関数を求めるには、それぞれの確率密度関数を "加える" 操作をすればよい。ガウス分布の確率密度関数は非線形の連続関数だから、"加える" には積分を利用する。二つの確率変数を \(X\) と \(Y\) (例えば事前分布と観測値) として、この二つが独立だと仮定する。\(X\), \(Y\) の確率密度関数を \(p_X\), \(p_Y\) とすれば、和 \(Z = X + Y\) の確率密度関数 \(p_{X+Y}\) は

\[ p_{X+Y}(z) = \int_{-\infty}^\infty p_X(z-t)p_Y(t)\, dt \]

と計算できる。これは畳み込みの計算である。後は数学の問題となる:

\[ \footnotesize\begin{aligned} p_{X+Y}(z) &= \int_{-\infty}^\infty p_X(z-t)p_Y(t)\, dt \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}\sigma_1}\exp\left[-\frac{(z - t - \mu_1)^2}{2\sigma^2_1}\right] \frac{1}{\sqrt{2\pi}\sigma_2}\exp\left[-\frac{(t - \mu_2)^2}{2\sigma^2_2}\right] \, dt \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}\sqrt{\sigma_1^2 + \sigma_2^2}} \exp\left[ -\frac{(z - (\mu_1 + \mu_2))^2}{2(\sigma_1^2+\sigma_2^2)}\right] \\ & \qquad\qquad\qquad \frac{1}{\sqrt{2\pi}\frac{\sigma_1\sigma_2}{\sqrt{\sigma_1^2 + \sigma_2^2}}} \exp\left[ -\frac{\left(t - \frac{\sigma_1^2(t-\mu_1) + \sigma_2^2\mu_2}{\sigma_1^2+\sigma_2^2}\right)^2}{2\left(\frac{\sigma_1\sigma_2}{\sqrt{\sigma_1^2+\sigma_2^2}}\right)^2}\right] \, dt \\[10pt] &= \frac{1}{\sqrt{2\pi}\sqrt{\sigma_1^2 + \sigma_2^2}} \exp\left[ -\frac{(z - (\mu_1 + \mu_2))^2}{2(\sigma_1^2+\sigma_2^2)}\right] \\ &\qquad\qquad\qquad\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}\frac{\sigma_1\sigma_2}{\sqrt{\sigma_1^2 + \sigma_2^2}}} \exp\left[ -\frac{\left(t - \frac{\sigma_1^2(t-\mu_1) + \sigma_2^2\mu_2}{\sigma_1^2+\sigma_2^2})\right)^2}{2\left(\frac{\sigma_1\sigma_2}{\sqrt{\sigma_1^2+\sigma_2^2}}\right)^2}\right] \, dt \end{aligned} \]

被積分関数は正規分布の確率密度関数だから、積分は \(1\) となる。よって

\[ p_{X+Y}(z) = \frac{1}{\sqrt{2\pi}\sqrt{\sigma_1^2 + \sigma_2^2}} \exp\left[ -\frac{(z - (\mu_1 + \mu_2))^2}{2(\sigma_1^2+\sigma_2^2)}\right] \]

が分かる。これは正規分布の確率密度関数であり、次を満たす:

\[ \begin{aligned} \mu_z &= \mu_1 + \mu_2 \\ \sigma_z^2 &= \sigma_1^2+\sigma_2^2 \quad \square \end{aligned} \]

3.18 まとめとポイント

本章は統計学の入門としてはお粗末である。これから本書でガウス分布を使う上で必要になる概念には触れたが、それ以上は触れなかった。カルマンフィルタに関する文献を読みたいと思っているなら、ここで説明したことだけでは足りないだろう。本格的に学んだことがない場合は統計学の教科書を一冊読むことを勧める。統計学の独習なら私は Schaum シリーズが気に入っている。また Alan B. Downey 著 Think Stats も良書であり、これはオンラインから無料で閲覧できる。

話を進める前に、次の点必ず理解しなければならない:

正規分布は連続確率分布である。
正規分布は平均 \(\mu\) と分散 \(\sigma^2\) という二つのパラメータで完全に記述される。
平均 \(\mu\) は無限個の観測値の平均を表す。
分散 \(\sigma^2\) は観測値が平均からどれくらい散らばるかを表す。
標準偏差 \(\sigma\) は分散の平方根である。
現実世界の様々な現象は正規分布で近似できるが、完璧に記述できるわけではない。
フィルタリングの問題で \(p(x \mid z)\) を直接計算するのは不可能に近い。しかし \(p(z \mid x)\) なら簡単に計算できる。ベイズの定理を使うと \(p(z \mid x)\) から \(p(x \mid z)\) を計算できる。

これからの数章ではガウス分布とベイズの定理を使ってフィルタリングを行う。先述したように、ガウス分布だけでは現実世界の振る舞いを上手く記述できないもある。本書の後半ではノイズや系の振る舞いがガウス分布から大きく離れるときでも正しく動作するフィルタが解説される。

Peter J. Huber, Robust Statistical Procedures, Society for Industrial and Applied Mathematics, 1987.^[return]
訳注: この一文では「ガウス分布に独立に従う二つの確率変数の和/積 (が従う分布)」と「ガウス分布の確率密度関数の和/積 (が関係する分布)」が混同されている。英語版ではこれ以降も二つがあまり区別されていなかったが、翻訳ではこれ以降できる限り区別するようにしている。^[return]
訳注: 「犬の朝飯 (dog's breakfast)」は見た目がひどく散らかっているもの、あるいはひどく失敗したものを表すイディオム。^[return]

第 3 章 確率・ガウス分布・ベイズの定理

3.1 平均・分散・標準偏差

確率変数

確率分布

確率変数の平均・中央値・最頻値

3.2 確率変数の期待値

練習問題

解答

練習問題

解答

3.3 確率変数の分散

分散で差の二乗を考える理由

3.4 ガウス分布

3.5 用語について

3.6 ガウス分布の特徴

3.7 分散と信念

3.8 68-95-99.7 則

3.9 対話的なガウス分布

3.10 ガウス分布の計算量的特徴

3.11 全てをまとめる

3.12 ベイズの定理

3.13 全確率の定理

3.14 scipy.stats を使った確率の計算

3.15 ガウス分布を使ったモデルの欠点

3.16 ガウス分布の確率密度関数の積 (スキップ可)

3.17 ガウス分布に従う確率変数の和 (スキップ可)

3.18 まとめとポイント

第 3 章確率・ガウス分布・ベイズの定理

3.14 `scipy.stats` を使った確率の計算