第 12 章粒子フィルタ

12.1 動機

こんな問題を考えよう。移動している複数の物体があって、それらを追跡したいとする。追跡する物体は複数のジェット戦闘機や複数のミサイルかもしれないし、球場でクリケットをしている人々かもしれない。なんでもいい。これまでに学んだフィルタにこの問題を扱えるものはあるだろうか？残念ながら、どのフィルタも理想的ではない。この問題の特徴を考えよう:

多峰性 (マルチモーダル): ゼロ個、一つ、あるいは複数の物体を同時に追跡したい。
遮蔽 (オクルージョン): 物体が他の物体を隠し、複数のオブジェクトから観測値が一つしか得られない場合がある。
非線形な観測値: レーダーは物体への距離を観測するので、\((x,y,z)\) の座標に変換するとき非線形な平方根が必要になる。
ガウス分布に従わないノイズ: 背景が大きく変化すると、コンピュータービジョンのアルゴリズムが背景を物体と誤認する場合がある。
連続: 物体の位置と速度 (つまり状態) は時間の経過とともに滑らかに変化する。
多変量: 位置、速度、旋回速度といった複数の属性を追跡したい。
未知のプロセスモデル: 系のプロセスモデルを私たちは知らない。

これまでに学んだフィルタはどれも、こういった制約があるとき上手く動作しない:

離散ベイズフィルタ: 離散ベイズフィルタは最も多くの制約に対応できる。多峰性であり、非線形な観測値を処理でき、非線形な振る舞いに対応できるよう拡張することもできる。しかし、このフィルタは離散的かつ単変量である。
カルマンフィルタ: カルマンフィルタはガウス分布に従うノイズを持った単峰性の線形系に対して最適な推定値を生成する。この問題ではどの仮定も成り立たない。
無香料カルマンフィルタ: UKF は非線形、連続、多変量の問題に対応できる。しかし多峰性ではなく、遮蔽を処理することもできない。また UKF はガウス分布と少しだけ異なる分布に従うノイズなら処理できるが、ノイズがガウス分布から大きく離れている場合や問題が非常に非線形な場合は上手く処理できない。
拡張カルマンフィルタ: EKF は基本的に UKF と同じ強みと弱みを持つ。ただし EKF はガウス分布に従わないノイズと非線形性からの影響をさらに受けやすい。

12.2 モンテカルロサンプリング

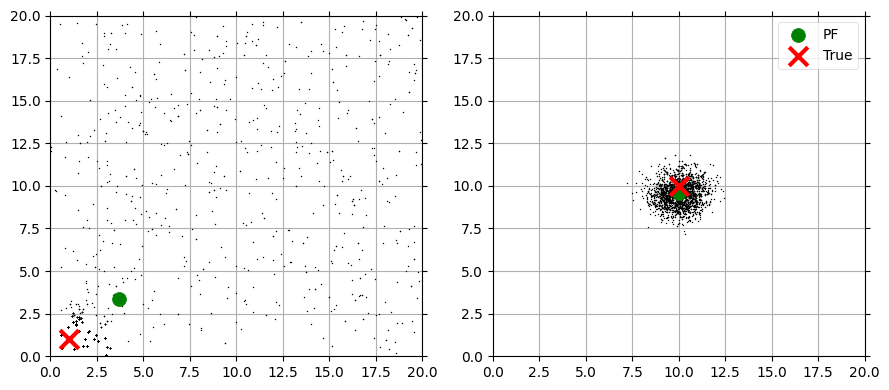
無香料カルマンフィルタの章で、ガウス分布を非線形な系で変換したときの効果を説明するために次のような図を示した:

In [3]

import kf_book.pf_internal as pf_internal
pf_internal.plot_monte_carlo_ukf()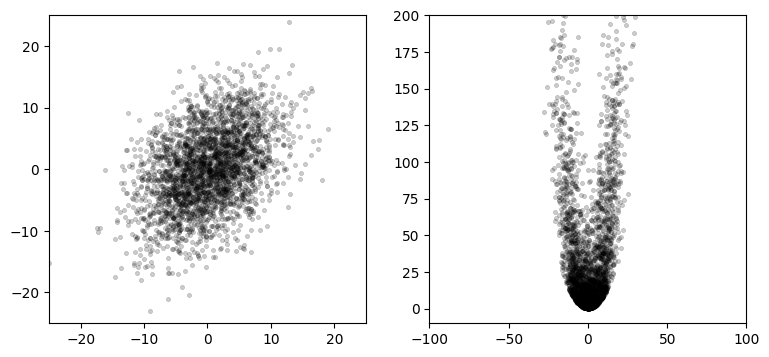

左のグラフは次のガウス分布に独立に従う 3,000 個の点を示す:

\[ \mu = \begin{bmatrix}0\\0\end{bmatrix},\, \, \, \Sigma = \begin{bmatrix}32&15\\15&40\end{bmatrix} \]

右のグラフはそれらの点を次の関数に通したときに得られる点を示す:

\[ \begin{aligned}x&=x+y\\ y &= 0.1x^2 + y^2\end{aligned} \]

ランダムに生成された有限個の点 (サンプル) を使って結果を計算する手法をモンテカルロ法 (Monte Carlo method, MC) と呼ぶ。アイデアは簡単だ: 状態を表現するサンプル (点) を十分多く生成し、モデル化している系にそれらの点を通し、変換された点から結果を計算する。

簡単に言えばこれが粒子フィルタの処理である。本書を通して使ってきたベイズフィルタのアルゴリズムが数千個の粒子に適用される。一つ一つの粒子は系の状態の可能性を表す。数千個の粒子から状態の推定値を取り出すときは重み付き統計量が使われる。

12.3 一般的な粒子フィルタアルゴリズム

粒子フィルタのアルゴリズムを一般的に説明すると次のようになる:

粒子の生成

大量の粒子をランダムに生成する。粒子には位置や向きといった推定したい状態変数を好きなだけ持たせて構わない。それぞれの粒子は重みを持ち、系の実際の状態と粒子の状態が合致する可能性が重みによって (確率的に) 表される。最初の重みは全て同じとする。
予測

粒子の次の状態を予測する。あなたが予測した実際の系の振る舞いに基づいて、全ての粒子を移動させる。
更新

観測値に基づいて粒子の重みを更新する。観測値に近い粒子には観測値から遠い粒子よりも大きい重みが割り当てられる。
再サンプリング

確率が非常に低い粒子を破棄して、確率の高い粒子のコピーで置き換える。
推定値の計算

もし必要なら、粒子の重み付き平均と重み付き共分散行列を計算して状態の推定値を得る。

このナイーブなアルゴリズムには克服しなければならない実際的な困難があるものの、一般的なアイデアはこの通りである。一つ例を示そう。UKF と UKF の章で考えたロボットの自己位置推定問題を解く粒子フィルタの実行結果を次に示す。ロボットに対する旋回角と速度の制御入力は一定に設定して、ロボットから見えるランドマークへの距離を観測値とした。またセンサーと制御機構の両方にノイズがあり、ロボットの位置を追跡すると仮定してある。

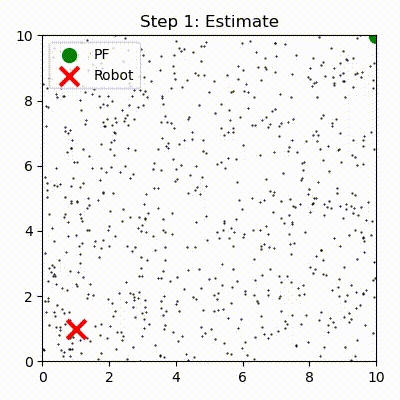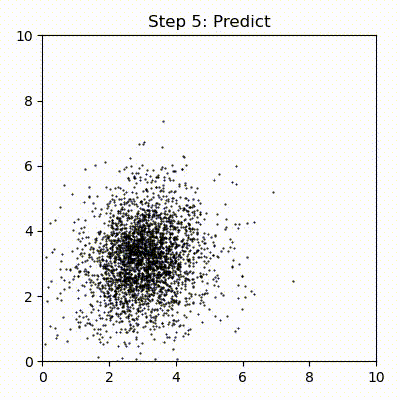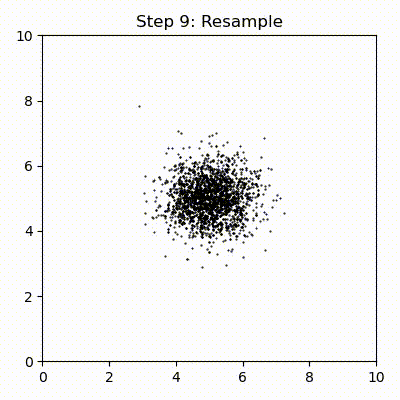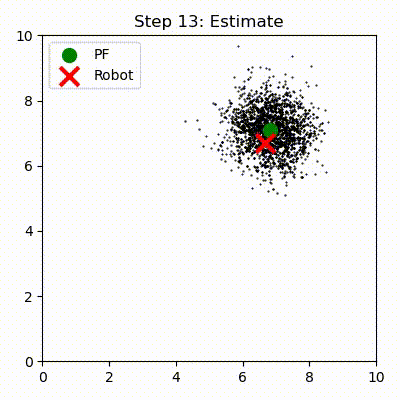
粒子フィルタを繰り返し実行したときの粒子の位置を次のグラフにプロットした。左のグラフは一反復後の位置を示し、右のグラフは十反復後の位置を示す。赤い X がロボットの実際の位置を、緑色の大きな円が重み付き平均として計算されたロボットの位置の推定値を表す:

In [4]

pf_internal.show_two_pf_plots()

本書をブラウザで読んでいる読者に向けて、粒子フィルタの実行を示すアニメーションを次に示す:

最初の反復が終わった段階では粒子はまだ全体にわたってほぼランダムに散らばっている。ただロボットの位置の近くに集まっている粒子があるのも分かる。これは観測値にどれだけ近いかに応じて全ての粒子が重み付けされるためである。ロボットは \((1,1)\) の近くにいるので、\((1,1)\) の近くにある粒子には観測値に近いということで大きな重みが割り当てられ、生き残る可能性が高くなる。ロボットから遠い粒子は観測値から遠いので、そういった粒子の重みは低くなる。位置の推定値は粒子の位置の重み付き平均として計算される。その計算ではロボットに近い粒子からの寄与が大きいので、推定値は最初の反復でも正確になる。

何度か反復すると全ての粒子がロボットの周りに集まるのが分かる。これは再サンプリングステップが存在するためである。再サンプリングでは確率が低い (重みが小さい) 粒子を破棄して、確率の高い粒子に置き換える。

粒子フィルタが動作する理由はまだ説明していないし、粒子の重み付けや再サンプリングのアルゴリズムもまだ説明していない。ただ直感的には理解できたと思う。大量の粒子をランダムに作成し、全ての粒子を「ロボットっぽく」動かし、観測値との近さに応じて重みを付け、確率が高いものを優先して残すということだ。正しく動きそうに思えるし、実際正しく動く。

12.4 モンテカルロ法を使った確率分布の計算

曲線 \(y= e^{\sin x}\) の \([0, \pi]\) の部分が \(x\) 軸と囲む領域の面積を求めたいとしよう。この面積は定積分 \(\displaystyle \int_0^\pi e^{\sin x}\, dx\) として計算できる。練習問題として、この不定積分を自分の手で計算してみてほしい。あなたが解けるまで待っていよう。

この挑戦を引き受けなかったなら賢い: \(e^{\sin x}\) は解析的に積分できない。世界は積分できない式に満ちている。例えば物体の明るさを計算したいとしよう。物体は自身に向かう光の一部を反射する。反射した光の一部は別の物体に反射して元の物体に戻り、それによって物体の明るさが増す。このため明るさの計算には再帰的な積分が必要になる。これを解析的に解くなら、幸運を祈る。

しかし、モンテカルロ法を使うと積分が非常に簡単に計算できる。ある曲線と \(x\) 軸が囲む領域の面積が求めたいなら、その領域を囲む長方形を考え、その長方形の中にランダムな点を大量に生成し、曲線の下に入った点の個数と生成した点の個数を計算すればよい。例えば面積を求めたい領域を囲む長方形の面積が \(1\) で、曲線の下に入った点が全体の約 40% なら、領域の面積は \(0.4\) だと分かる。点の個数を無限大に近づけていくと、面積を好きなだけ正確に計算できる。実際に使うときは数千個の点があれば正確な結果が求まる。

この手法を使うとどれだけ難しい関数でも数値積分でき、積分不可能な関数や不連続な関数も積分できる。モンテカルロ法による積分計算はロスアラモス国立研究所の Stanley Ulam によって、紙上では行えない核反応の計算を行うために考案された。

円の面積を求めることで \(\pi\) を計算してみよう。半径 \(r=1\) の円とそれを囲む正方形を考える。この正方形の一辺の長さは \(2\) だから、面積は \(4\) となる。正方形の中に一様ランダムに点を生成し、その中で円の中に収まる点の個数を数える。円の中に入った点の個数を生成した点の個数で割り、それに正方形の面積を乗じると円の面積 \(A\) が求まる。また \(A = \pi r^2\) も知っているから、\(\pi = A/r^2\) と計算できる。

まず点の生成から始める:

N = 20000
pts = uniform(-1, 1, (N, 2))

点が円の中に入るのは、その点から円の中心までの距離が半径以下のときである。距離の計算にはベクトルの長さを求める numpy.linalg.norm を利用する。今考えている円の中心は \((0,0)\) だから、この関数で円の中心からの距離が計算できる:

dist = np.linalg.norm(pts, axis=1)

次に、こうして計算された距離の中で条件を満たすものだけを取り出す。次のコードを実行すると in_circle は dist と同じ長さの真偽値配列になる。添え字 i が条件 dist[i] <= 1 を満たすとき in_circle[i] = True になり、そうでないとき in_circle[i] = False となる:

in_circle = dist <= 1

後は円の中に入った点の個数を求め、\(\pi\) を計算し、結果をプロットする。異なる N を使って試せるよう全てのコードを一つのセルにまとめておいた:

In [5]

import matplotlib.pyplot as plt
import numpy as np
from numpy.random import uniform

N = 20000  # 点の個数
radius = 1.
area = (2*radius)**2

pts = uniform(-1, 1, (N, 2))

# 円の中心 (0,0) からの距離
dist = np.linalg.norm(pts, axis=1)
in_circle = dist <= 1

pts_in_circle = np.count_nonzero(in_circle)
pi = 4 * (pts_in_circle / N)

# 結果のプロット
plt.scatter(pts[in_circle,0], pts[in_circle,1],
            marker=',', edgecolor='k', s=1)
plt.scatter(pts[~in_circle,0], pts[~in_circle,1],
            marker=',', edgecolor='r', s=1)
plt.axis('equal')

print(f'平均 pi(N={N})= {pi:.4f}')
print(f'誤差 pi(N={N})= {np.pi-pi:.4f}')

Out [5]

平均 pi(N=20000)= 3.1684
誤差 pi(N=20000)= -0.0268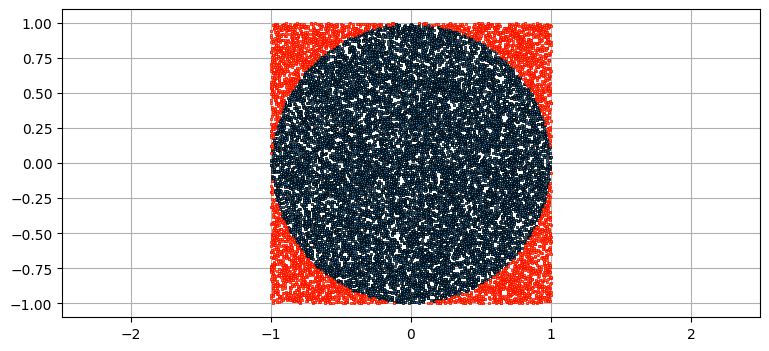

この考え方を使うと、モンテカルロ法で任意の確率分布の確率密度を計算できることが分かる。例として次のガウス分布を考える:

In [6]

from filterpy.stats import plot_gaussian_pdf
plot_gaussian_pdf(mean=2, variance=3);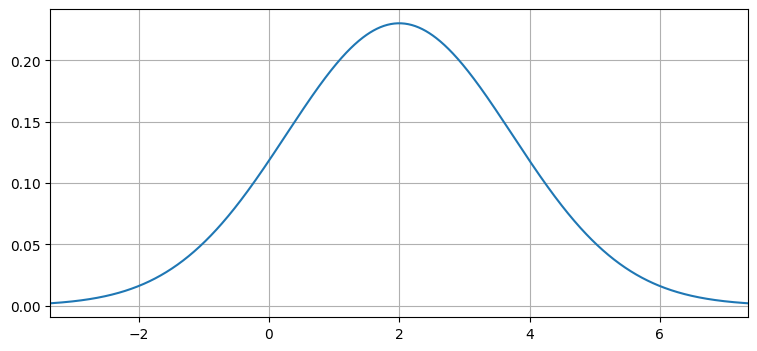

確率分布の確率密度関数 (PDF) があると、その確率分布に従うランダムな値が特定の二つの値の間に収まる確率を積分で計算できる。例えば上のガウス分布に従うランダムな値 \(x\) が \(0\) から \(2\) の間の値となる確率を知りたいとしよう。上に示したのは連続確率分布の確率密度関数だから、考えている範囲の曲線と \(x\) 軸が囲む部分の領域の面積がその確率に等しい。一般的に言えば次の通りである:

\[ P[a \le X \le b] = \int_a^b f_X(x) \, dx \]

この積分はガウス分布に対してなら簡単に計算できる。しかし現実世界はそれほど簡単ではない。例えば確率分布は次に示すような確率密度関数を持っているかもしれない。任意の曲線を考える場合、積分の計算はおろか、解析的に表す方法が存在しない可能性もある:

In [7]

pf_internal.plot_random_pd()

モンテカルロ法を使うと任意の積分を計算でき、確率は PDF を積分することで計算できる。よって確率はモンテカルロ法で計算できる。確率だけではなく統計量 (平均や標準偏差) の計算も同様にモンテカルロ法で行える。

12.5 粒子フィルタ

こういった考え方を全てまとめると粒子フィルタとなる。都市環境を移動するロボットあるいは車を追跡する問題を考えよう。ここでは UKF と UKF の章と合わせるためロボットの自己位置推定問題とする。この問題ではロボットが周りにある既知のランドマークへの距離と方位を観測する。

粒子フィルタはアルゴリズムの族である。これから直感的に理解しやすく本書で考えた問題に適用しやすい形式の粒子フィルタを示す。この節ではアルゴリズムを完全には説明しないので、いくつか「魔法の」ステップを残すことになる。そういったステップは本章の最後で説明する。

前節の議論で得られた洞察を取り入れ、数千個の粒子 (particle) を生成する処理から始める。それぞれの粒子はシーン内のロボットの位置 (そしておそらくは向きと速度) として可能な値に関する信念を表す。私たちはロボットの位置に関しては知識を全く持たないと仮定する。このときシーン全体に粒子を一様に分散させることになる。粒子全体が一つの確率分布を表すと考えれば、粒子の多い場所の信念が高く、粒子の少ない場所の信念は低い。また粒子が特定の位置に密集していたら、ロボットがそこにいるのだろうという確信の度合いが高まる。

各粒子は重みを必要とする──理想的には、その粒子がロボットの真の位置を表す確率が重みとなる。この確率はまず計算できないので、重みはその確率に比例することだけを要求する。確率に比例する値なら計算できる。初期化で特定の粒子を優先する理由はないので、全ての粒子の重みは最初 \(1/N\) とする (\(N\) は粒子の個数)。重みが \(1/N\) だと和が \(1\) になるので、この値は確率と解釈できる。

粒子と重みの組を全て集めると、考えている問題に対する解答が確率分布として構成される。離散ベイズフィルタの章を思い出そう。あのときは廊下の位置を等間隔に並んだ点で離散的にモデル化した。ここで行っているのも同様の処理と言える。ただし粒子フィルタの粒子は離散的な位置に制限されず、連続な多次元空間に自由に分布する。

ロボットの追跡では \(x\) 座標・\(y\) 座標・向きの三つを状態として管理する必要がある。N 個の粒子を (N, 3) という形状の配列に格納することにしよう。三つの列には \(x\) 座標・\(y\) 座標・向きをこの順番で格納する。

受動的に (制御入力を与えずに) 追跡を行っているなら、予測を行うために速度を状態に含める必要があるだろう。次元を増やすと同じ程度の正確さを持つ推定値を得るのに必要な粒子の個数が指数的に増えるので、状態に入れる確率変数の個数は必ず最小限にしなければならない。

一様分布およびガウス分布に従う粒子を特定の領域に生成するコードを示す:

In [8]

from numpy.random import uniform

def create_uniform_particles(x_range, y_range, hdg_range, N):
    particles = np.empty((N, 3))
    particles[:, 0] = uniform(x_range[0], x_range[1], size=N)
    particles[:, 1] = uniform(y_range[0], y_range[1], size=N)
    particles[:, 2] = uniform(hdg_range[0], hdg_range[1], size=N)
    particles[:, 2] %= 2 * np.pi
    return particles

def create_gaussian_particles(mean, std, N):
    particles = np.empty((N, 3))
    particles[:, 0] = mean[0] + (randn(N) * std[0])
    particles[:, 1] = mean[1] + (randn(N) * std[1])
    particles[:, 2] = mean[2] + (randn(N) * std[2])
    particles[:, 2] %= 2 * np.pi
    return particles

使用例を示す:

In [9]

create_uniform_particles((0,1), (0,1), (0, np.pi*2), 4)

Out [9]

array([[0.772, 0.336, 4.171],
       [0.333, 0.34 , 4.319],
       [0.6  , 0.274, 5.02 ],
       [0.054, 0.022, 5.034]])

予測ステップ

ベイズアルゴリズムの予測ステップはプロセスモデルを使って系の状態に関する信念を更新する。粒子を使うときはどうすれば更新を行えるだろうか？ロボットへのコマンドとして \(0.1~\text{m}\) の前進と \(0.007~\text{rad}\) の旋回を指示したとしよう。このとき全ての粒子をこれだけ移動させることもできる。しかしそうすると、すぐに問題が発生する: ロボットの制御は完璧ではないので、ロボットはコマンドの通りには動かない。よって実際の動きを捉える可能性を残すために、粒子の動きにノイズを加えなくてはならない。系が持つ不確実性を考慮しないと、ロボットの位置に関する私たちの信念を表す確率分布を粒子フィルタは正しくモデル化できない。

In [10]

def predict(particles, u, std, dt=1.):
    """
    制御入力 u [向きの変化, 速度] を使って粒子を移動させる。
    Q はノイズ [向きの変化の標準偏差, 速度の標準偏差] を表す。
    """

    N = len(particles)
    # 向きの更新
    particles[:, 2] += u[0] + (randn(N) * std[0])
    particles[:, 2] %= 2 * np.pi

    # 位置の更新
    dist = (u[1] * dt) + (randn(N) * std[1])
    particles[:, 0] += np.cos(particles[:, 2]) * dist
    particles[:, 1] += np.sin(particles[:, 2]) * dist

更新ステップ

続いて観測値が現在見えているランドマーク一つにつき一つ手に入る。これらの観測値を使って粒子がモデル化する確率分布を更新するにはどうするべきだろうか？

もう一度離散ベイズフィルタの章を思い出そう。あのときは廊下の位置を等間隔に並んだ点で離散的にモデル化した。観測値を取り入れる前の段階で事前確率という確率が各位置に対して計算されており、観測値を手に入れるとそれぞれの位置に対して事前分布における確率とその位置から観測された観測値が得られる尤度を乗じることで更新を行っていた:

def update(likelihood, prior):
    posterior = likelihood * prior
    return normalize(posterior)

このコードは次の式を実装する:

\[ x = \| \mathcal L \bar x \| \]

そしてこの式はベイズの定理の式に具体的な値を代入したものである:

\[ \begin{aligned}P(x \mid z) &= \frac{P(z \mid x)\, P(x)}{P(z)} \\ &= \frac{\text{尤度}\times \text{事前分布}}{\text{正規化係数}}\end{aligned} \]

粒子フィルタでは同じことを粒子に対して行う。各粒子は位置と重みを持ち、位置が観測値とどれくらいマッチするかが重みによって表される。また粒子全体が確率分布を表すよう、最後に重みを正規化する。ロボットの近くにある粒子には遠くにある粒子よりも大きな重みが割り振られる:

In [11]

def update(particles, weights, z, R, landmarks):
    for i, landmark in enumerate(landmarks):
        distance = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
        weights *= scipy.stats.norm(distance, R).pdf(z[i])

    weights += 1.e-300      # 打ち切り誤差で生じる 0 を防ぐ。
    weights /= sum(weights) # 正規化する。

専門的な文献では、粒子フィルタのアルゴリズムのこの部分を逐次重点サンプリング (sequential importance sampling, SIS) と呼ぶ。この考え方の理論的な基礎付けは次節で行う。今の段階では、上の説明で正しさを直感的に理解できればいい。観測値との近さに応じて粒子を重み付けすれば、観測値を取り入れた事後分布としておそらく正しいだろう。理論的に考察するとその正しさが証明される。この重みはベイズの定理における尤度である。問題によってはこのステップで少しだけ異なる手法が使われることもあるものの、このコードにあるのが一般的な考え方となる。

状態推定値の計算

多くの応用では更新のたびに推定値を知りたいはずだが、フィルタの出力は粒子の集まりでしかない。追跡する物体が一つ (フィルタは単峰性) と仮定すると、粒子の集まりが表す推定値は位置の重み付き平均として計算できる:

\[ \displaystyle \mu = \sum_{i=1}^N w^ix^i \]

ここで \(x^i\) と \(w^i\) はそれぞれ \(i\) 番目の粒子の位置と重みを表す。上付き添え字を使っているのは、時刻を表すのに下付き添え字を使わなければならないことが多いためだ。例えば時刻 \(k+1\) における \(i\) 番目の粒子の位置は \(x^i_{k+1}\) となる。

共分散行列も同様に計算できる。次の関数は粒子の平均と分散を計算する:

In [12]

def estimate(particles, weights):
    """ 重みの付いた粒子の平均と共分散行列を返す。 """
    w = weights.reshape(len(particles), 1)
    pos = particles[:, 0:2]
    mean = np.sum(pos * w, axis=0)
    var  = np.sum((pos - mean)**2 * w, axis=0)
    return mean, var

一辺の長さが \(1\) の正方形の中に等しい重みを持った点を一様ランダムに生成すると、その平均は正方形の中心に近く、分散は小さいはずである。このことを確認してみよう:

In [13]

N = 1000
particles = create_uniform_particles((0,1), (0,1), (0, 5), N)
weights = np.array([1.0/N]*N)
estimate(particles, weights)

Out [13]

(array([0.494, 0.514]), array([0.083, 0.085]))

粒子の再サンプリング

SIS アルゴリズムでは縮退 (degeneracy) が問題になる。粒子フィルタのアルゴリズムは最初に等しく重み付けされた粒子を一様ランダムに生成するので、ロボットの周りには少ししか粒子が存在しない。そしてアルゴリズムの実行が進むと観測値から離れた粒子には非常に小さい重みが割り当てられる。このため 5,000 個の粒子を用意しても、状態の推定値に少しでも寄与している粒子が 3 個しか存在しない、といった状況になる可能性がある！このように少数の粒子に重みが集中してしまう状況を指して、「フィルタが縮退している」と言う。通常この問題は粒子の再サンプリング (resampling) を行うことで解決される。

非常に小さい重みをもつ粒子はロボットの状態を表す確率分布を記述する上でほとんど役に立っていない。再サンプリングのアルゴリズムは確率の非常に低い粒子を破棄して、新しく作った確率の高い粒子で置き換える。実際には確率の高い粒子を複製することで置き換えが行われる。複製された新しい粒子は予測ステップで加わるノイズによって少しずつ散らばっていくので、再サンプリングがあれば大部分の粒子を使って確率分布を正確に表現するようにできる。

再サンプリングのアルゴリズムは多く存在する。ここでは最も簡単なアルゴリズムの一つを見よう。これは単純ランダム再サンプリング (simple random resampling) あるいは多項再サンプリング (multinomial resampling) と呼ばれる。このアルゴリズムでは現在の粒子の集合から一つの粒子を選択する処理を \(N\) 回行うことで新しい粒子の集合を計算し、毎回の選択で任意の粒子が選ばれる確率をその重みに比例させる。

実装では配列の累積和を計算する NumPy の関数 cumsum を利用する。累積和は配列であり、第一要素は元の配列の第一要素、第二要素は元の配列の第一要素と第二要素の和、第三要素は元の配列の第一要素と第二要素と第三要素の和に等しく、以下同様に並ぶ。その後 0.0 から 1.0 の一様乱数を N 個生成し、二分探索を使って乱数に対応する添え字を計算する:

In [14]

def simple_resample(particles, weights):
    N = len(particles)
    cumulative_sum = np.cumsum(weights)
    cumulative_sum[-1] = 1. # 浮動小数点数誤差を避ける。
    indexes = np.searchsorted(cumulative_sum, random(N))

    # indexes を使って再サンプリングを行う。
    particles[:] = particles[indexes]
    weights.fill(1.0 / N)

再サンプリングは毎エポック行うわけではない。例えば観測値を受け取っていないなら、再サンプリングで取り出せる情報は存在しない。再サンプリングを行うタイミングは実効サンプルサイズ (effective sample size) と呼ばれる値を使って決定する。これは確率分布に少しでも寄与している粒子の個数の近似値であり、次の式で計算できる:

\[ \hat{N}_\text{eff} = \frac{1}{\sum w^2} \]

Python では次のように実装できる:

In [15]

def neff(weights):
    return 1. / np.sum(np.square(weights))

もし \(\hat{N}_\text{eff}\) が何らかの基準より小さくなったら、再サンプリングの時間だと分かる。なお、\(\hat{N}_\text{eff} = N\) となる可能性もある。これは全ての点が全く同じ重みを持つ (おそらく全く同じ位置にある) ことを意味する。私は \(\hat{N}_\text{eff} = N\) になったとき分布を再生成するようにしている。理論的にはおかしいかもしれないが、粒子の多様性を増加させるためだ。もしこれが頻繁に起こるなら、粒子の個数を増やすかフィルタを調整した方がいいかもしれない。この話題は後でさらに議論する。

12.6 SIR フィルタ──完全な例

学ぶべきことはまだあるものの、完全な粒子フィルタを実装するだけの知識はこれで揃った。これからサンプリング-重み付け-再サンプリングフィルタ (sampling importance resampling filter, SIR フィルタ) を実装する。

SIR フィルタでは上述した再サンプリングのアルゴリズムより洗練されたアルゴリズムが必要になる。FilterPy は様々な手法を実装しているので、その一つを利用する。アルゴリズムの詳細は後述する。FilterPy の再サンプリング関数は重みの配列を受け取り、選択された粒子の添え字を返す。そのため利用する側は返り値の添え字を使って再サンプリングを行う関数を書くだけで済む:

In [16]

def resample_from_index(particles, weights, indexes):
    particles[:] = particles[indexes]
    weights.resize(len(particles))
    weights.fill(1.0 / len(weights))

SIR フィルタを実装するには、粒子とランドマークを作成する必要がある。それからループに入り、各反復で予測 (predict)・更新 (update)・再サンプリング・状態推定値の計算 (estimate) を実行する:

In [17]

from filterpy.monte_carlo import systematic_resample
from numpy.linalg import norm
from numpy.random import randn
import scipy.stats

def run_pf1(N, iters=18, sensor_std_err=.1,
            do_plot=True, plot_particles=False,
            xlim=(0, 20), ylim=(0, 20),
            initial_x=None):
    landmarks = np.array([[-1, 2], [5, 10], [12,14], [18,21]])
    NL = len(landmarks)

    plt.figure()

    # 粒子の位置と重みを作成する。
    if initial_x is not None:
        particles = create_gaussian_particles(
            mean=initial_x, std=(5, 5, np.pi/4), N=N)
    else:
        particles = create_uniform_particles((0,20), (0,20), (0, 6.28), N)
    weights = np.ones(N) / N

    if plot_particles:
        alpha = .20
        if N > 5000:
            alpha *= np.sqrt(5000)/np.sqrt(N)
        plt.scatter(particles[:, 0], particles[:, 1],
                    alpha=alpha, color='g')

    xs = []
    robot_pos = np.array([0., 0.])
    for x in range(iters):
        robot_pos += (1, 1)

        # ロボットから各ランドマークへの距離を計算する。
        zs = (norm(landmarks - robot_pos, axis=1) +
              (randn(NL) * sensor_std_err))

        # だいたい (x+1, y+1) に向かって前進する。
        predict(particles, u=(0.00, 1.414), std=(.2, .05))

        # 観測値を取り入れる。
        update(particles, weights, z=zs, R=sensor_std_err, landmarks=landmarks)

        # 実行サンプルサイズが小さいなら、再サンプリングを行う。
        if neff(weights) < N/2:
            indexes = systematic_resample(weights)
            resample_from_index(particles, weights, indexes)
            assert np.allclose(weights, 1/N)
        mu, var = estimate(particles, weights)
        xs.append(mu)

        if plot_particles:
            plt.scatter(particles[:, 0], particles[:, 1],
                        color='k', marker=',', s=1)
        p1 = plt.scatter(robot_pos[0], robot_pos[1], marker='+',
                         color='k', s=180, lw=3)
        p2 = plt.scatter(mu[0], mu[1], marker='s', color='r')

    xs = np.array(xs)
    # plt.plot(xs[:, 0], xs[:, 1])
    plt.legend([p1, p2], ['Actual', 'PF'], loc=4, numpoints=1)
    plt.xlim(*xlim)
    plt.ylim(*ylim)
    print('最後の位置の誤差と共分散行列:\n\t', mu - np.array([iters, iters]), var)
    plt.show()

from numpy.random import seed
seed(2)
run_pf1(N=5000, plot_particles=False)

Out [17]

最後の位置の誤差と共分散行列:
       [-0.106  0.106] [0.009 0.008]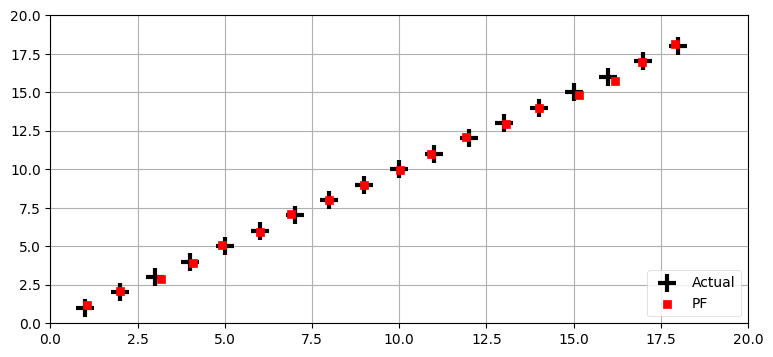

このコードは大部分が初期化とプロットであり、粒子フィルタの処理は次の部分が全てである:

# だいたい (x+1, y+1) に向かって前進する。
predict(particles, u=(0.00, 1.414), std=(.2, .05))
# 観測値を取り入れる。
update(particles, weights, z=zs, R=sensor_std_err, landmarks=landmarks)

# 実効サンプルサイズが小さいなら、再サンプリングを行う。
if neff(weights) < N/2:
    indexes = systematic_resample(weights)
    resample_from_index(particles, weights, indexes)
mu, var = estimate(particles, weights)

最初の行は粒子を移動させており、ここにはロボットが向きを変えずに (u[0] == 0) \(1.414\) だけ前方に移動する (u[1]==1.414) という仮定がある。旋回角の標準偏差は \(0.2\) であり、距離の標準偏差は \(0.05\) である。この predict の呼び出しによって全ての粒子が移動し、まだ更新していない重みは正しくない値となる。

次の行ではフィルタが観測値を取り入れる。ここでは粒子の位置は変化せず、重みだけが変化する。思い出せば、粒子の重みはセンサーの誤差モデルと観測値が定めるガウス分布と粒子の位置が合致する確率に比例する値として計算される。粒子とランドマークの距離が観測された距離から離れればそれだけ、その粒子が状態の優れた表現である確率は低く、割り当てられる重みも小さい。

次の行では実行サンプルサイズ \(\hat{N}_\text{eff}\) の計算が行われる。これが \(N/2\) より小さければ、粒子の集合を実際の確率分布の優れた表現とするために粒子の再サンプリングが行われる。

全ての粒子をプロットしてみよう。対話的に行うとより教育的なのだが、画像を見るだけでも有用な情報が分かる。次のプロットでは最初の一様ランダムに分布する粒子は薄い緑色の大きな円で示し、以降の反復における粒子を表す黒い点と区別しやすいようにしている。粒子の数が多くて見にくいので、反復は八回に制限してプロットを拡大している:

In [18]

seed(2)
run_pf1(N=5000, iters=8, plot_particles=True,
        xlim=(0,8), ylim=(0,8))

Out [18]

最後の位置の誤差と共分散行列:
       [-0.019 -0.005] [0.005 0.006]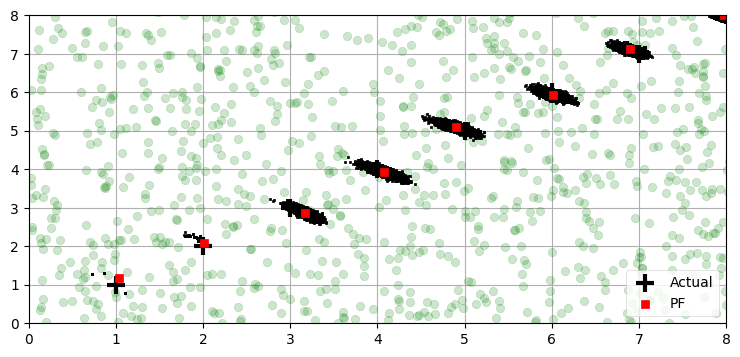

プロットを見ると、ロボットが最初の二つの位置にあるとき、粒子はいくつかしか存在しないように見える。しかし、本当にそうであるわけではない: 粒子は 5,000 個存在しているものの、再サンプリングにより多くが同じ点に存在しているだけである。再サンプリングでほとんどの点が重なるのは、センサーのノイズを持った観測値を表すガウス分布が非常に狭いためだ。これはサンプルの窮乏 (impoverishment) と呼ばれる問題であり、フィルタの発散につながる可能性がある。詳しくは以降で解説する。今の段階では、ロボットが x=2 にいる二回目の反復で粒子が前回より分散していることを確認してほしい。この分散は運動モデルのノイズによって発生する。全ての粒子は同じ制御入力 u によって次の時間の状態に射影されるものの、各粒子に加わるノイズはそれぞれ異なる。三度目の反復では粒子が十分広がり、ロボットの周りにそれらしい粒子の雲が生成される。

粒子が形作る雲は楕円の形をしている。これは偶然ではない。ロボットの制御機構とセンサーはどちらもガウス分布でモデル化しているので、系を表す確率分布もガウス分布となる。粒子フィルタの粒子は理想的には系を表す確率分布からサンプルしたものと見分けが付かなくなるから、粒子が形作る雲も楕円になるはずである。

事実な重要として、粒子フィルタではセンサーあるいは系のモデルがガウス分布かつ線形でなくても構わない。確率分布は粒子の雲として表されるので、どんな確率分布がどれだけ強い非線形性に晒されようと粒子フィルタは問題なく処理できる。確率モデルに不連続性があったり、取れる値に厳密な制限があったりしても問題は起こらない。

粒子フィルタにおけるセンサー誤差の影響

今の例では最初の数反復で大量の粒子が重なっている。こうなるのは、センサーのモデルがガウス分布であり、センサーの誤差として \(\sigma = 0.1\) という非常に小さい標準偏差を設定しているためだ。一見すると直感に反するかもしれないが、ノイズが小さいと性能が向上するカルマンフィルタと異なり、粒子フィルタではノイズを小さくすると性能が悪くなる場合がある。

こうなる理由は次のように考えることができる。\(\sigma=0.1\) だと、ロボットが \((1,1)\) にいるとき \((2,2)\) にある粒子は \(14\sigma\) ほど離れており、ほぼ \(0\) の重みが割り当てられる。その粒子は平均の推定値にほとんど寄与せず、再サンプリングで生き残る可能性はまずない。一方で、もし \(\sigma=1.4\) なら \((2,2)\) にある粒子は \(1\sigma\) しか離れていないから、平均の推定値にいくらか寄与する。そのため再サンプリングでは何度かコピーされるだろう。

この点を理解するのは非常に重要である──非常に正確なセンサーを仮定すると、系の状態を推定する確率分布が少数の粒子によって記述されることになり、粒子フィルタの性能が悪化する可能性がある。この問題にはいくつか解決法がある。まず、センサーノイズの標準偏差を人工的に大きくして、粒子フィルタが多くの粒子を受け入れるようにする方法がある。これは本当は観測値と合っていない粒子を受け入れることになるので最適な解決法とは言えない。本当の問題は粒子の個数が少なくて初期状態においてロボットの周りに十分な粒子が存在しないことであり、この問題は N を大きくすれば通常は解決される。もちろん粒子の個数を増やすと計算時間が大きく伸びるので、この解決法はいつでも採用できるわけでない。粒子を 100,000 個に増やしたときの結果を次に示す:

In [19]

seed(2)
run_pf1(N=100000, iters=8, plot_particles=True,
        xlim=(0,8), ylim=(0,8))

Out [19]

最後の位置の誤差と共分散行列:
       [-0.17   0.084] [0.005 0.005]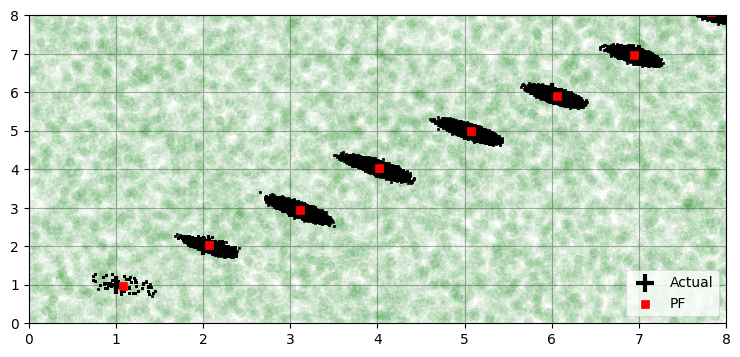

x=1 の時点で推定値の周りにある粒子が増えており、x=2 の時点で楕円がはっきりと確認できる。明らかにフィルタの性能は向上している。ただし、その代わりメモリ使用量は増え実行時間は長くなる。

別のアプローチとして、最初の粒子の雲を生成するときに賢くなる方法がある。ロボットが最初 \((0,0)\) の近くにいると予想したとしよう。ロボットの実際の位置は \((1,1)\) なのでこれは正確ではないものの、実際の位置の近くではある。\((0,0)\) を中心とした正規分布を使って点を生成すれば、ロボットの位置の周りに存在する粒子の個数がずっと増える。

run_pf1 関数は省略可能引数 initial_x を受け取る。この引数を使うとロボットの位置に対する初期推測値を指定できる。initial_x が指定されると、run_pf1 は create_gaussian_particles(mean, std, N) で初期推測値を中心とした正規分布に従う粒子を生成する。この機能は次節で利用する。

不適切なサンプルによるフィルタの縮退

ここまでに実装した粒子フィルタが完璧だとはとても言えない。異なる乱数シードを使ったときの振る舞いを次に示す:

In [20]

seed(6)
run_pf1(N=5000, plot_particles=True, ylim=(-20, 20))

Out [20]

最後の位置の誤差と共分散行列:
       [ -2.688 -31.47 ] [47.065 47.03 ]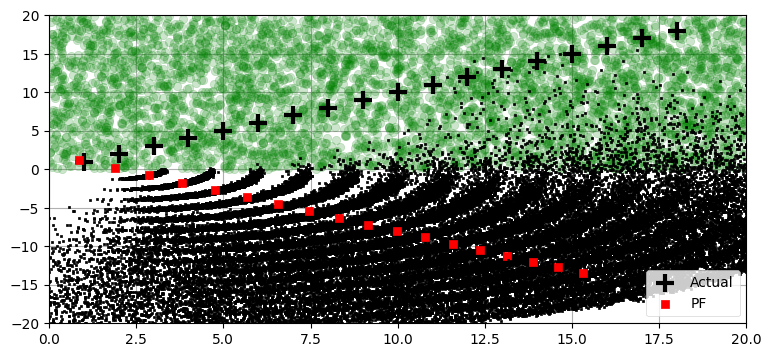

ここでは最初のサンプルでロボットの近くに粒子が一つも生成されていない。粒子フィルタは再サンプリングで新しい粒子を作成しないので、実際の確率分布を表さない点が複製されてしまっている。前述したように、この現象をサンプルの窮乏 (impoverishment) と呼ぶ。フィルタは数反復で手に負えない状況になる。ランドマークの観測値に合致する粒子が存在しないために、粒子は非常に非線形な、曲がった分布に分散し、粒子フィルタは現実から発散してしまう。ロボットの近くに粒子が存在しないので、このフィルタが収束することはあり得ない。

create_gaussian_particles 関数を利用してロボットに近い点を多く生成するようにしてみよう。これは省略可能引数 initial_x を通じて粒子を作成する位置を指定すると行える:

In [21]

seed(6)
run_pf1(N=5000, plot_particles=True, initial_x=(1,1, np.pi/4))

Out [21]

最後の位置の誤差と共分散行列:
       [ 0.035 -0.077] [0.007 0.009]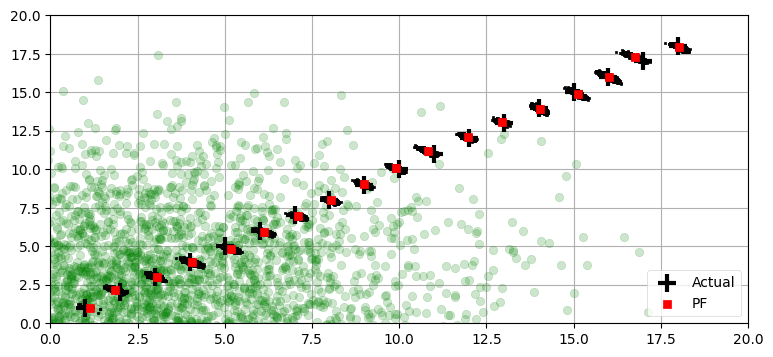

素晴らしい結果が得られた。何らかの方法で初期位置が推定できるなら、必ずその近くに粒子を生成するべきである。ただ注意深くなりすぎてもいけない──全ての粒子を特定の点のすぐ近くに生成すると、粒子が密集しすぎて系の非線形性を捉えられなくなる恐れがある。この例では系が非常に線形なので、小さな分散を持った分布でも正確な予測ができる。しかし一般には問題によって状況が異なる。粒子の個数を増加させれば必ず優れたサンプルとなるものの、処理コストは受け入れられないほど大きくなる可能性がある。

12.7 重点サンプリング

ここまでの説明では難しい話題を一つ飛ばしていた。そろそろこれに向き合わなければならない。ロボットの位置と移動を記述する確率分布がある。この確率分布から粒子のサンプルを取得して、モンテカルロ法を使った積分の計算 (例えば平均や分散の計算) を行いたい。

私たちが直面している困難は、多くの問題で確率分布が分からないことである。例えば追跡している物体の移動は状態モデルの予測と大きく異なるかもしれない。分からない確率分布からサンプルを得るにはどうすればいいだろうか？

重点サンプリング (importance sampling) と呼ばれる統計学的なテクニックがある。驚くべきことに、重点サンプリングを使うと既知の確率分布から得たサンプルを使って未知の確率分布の特徴量を計算できる。これは心を喜びで満たす素晴らしいテクニックである。

重点サンプリングのアイデアは簡単で、これまでも使ってきた: 既知の確率分布からサンプルを取得し、そのサンプルに対して考えている未知の確率分布に合うよう重みを付けるのである。そうしておけば、平均や分散といった特徴量をサンプルの重み付き平均/分散として計算できる。

ロボットの自己位置推定問題では、サンプルの取得は予測ステップで状態モデルを用いて計算された確率分布から行われる。言い換えれば、私たちは「一つ前の時刻にロボットはここにいた。ロボットはこの方向にこの速度で動いていると思われるから、現在の位置はこのあたりだろう」と考える。しかしロボットは全く異なる動きをする可能性もある: 崖から転落したり、迫撃砲で吹き飛ばされたりするかもしれない。そこまではいかなくても、予測ステップで計算される確率分布は正確でない。これは困ったと思うかもしれないが、重点サンプリングが使えるので恐れることはない。サンプルの取得はどうやら正確でない確率分布で行われたようであるものの、粒子が観測値とどれだけマッチするかに応じて粒子に重みを付ければ問題は起こらない。その重みは真の確率分布を使って計算されるから、理論的に、重みを使って計算される平均や分散は正しくなる！

これはなぜ正しいのだろうか？これから数学を示す。学びたいのがロボットの自己位置推定問題だけなら飛ばしても問題はない。ただし、他の粒子フィルタの問題では異なるアプローチの重点サンプリングが必要になり、数学を多少でも知っておくと役立つ。それから、一部の書籍と大部分のウェブコンテンツでは「... を想像すると ...」というこれまでの説明と同様の厳密でない説明が使われることが多い。もし専門的な書籍を理解したいなら、次に示す数式も知っておかなければならない。

何らかの確率分布 \(\pi(x)\) があり、その \(\pi(x)\) からサンプルを取得したいとする。しかし私たちは \(\pi(x)\) を知らず、代わりの確率分布 \(q(x)\) しか知らない。ロボットの自己位置推定問題の文脈で言えば \(\pi(x)\) は全ての観測値を取り入れた現在のロボットの状態を表す確率分布であり、私たちはこれを知らない。また \(q(x)\) は一つ前の時刻における粒子を使って予測した現在のロボットの状態を表す確率分布であり、これなら知っている。

確率変数 \(x\) が確率分布 \(\pi(x)\) に従うとき、関数 \(f(x)\) の期待値は次のように表せる:

\[ \mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\, dx \]

私たちは \(\pi(x)\) を知らないから、この積分は計算できない。しかし \(\pi(x)\) とは異なるもう一つの確率分布 \(q(x)\) なら知っている。次のようにすれば値を変えずに積分の式へ \(q(x)\) を加えることができる:

\[ \mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\frac{q(x)}{q(x)}\, dx \]

並べ替えて項をまとめると、次を得る:

\[ \mathbb{E}\big[f(x)\big] = \int f(x) \frac{\pi(x)}{q(x)} \, \cdot \, q(x) dx \]

ここで比 \(\pi(x)/q(x)\) を重み \(w(x)\) と定義する。するとこの式は

\[ \mathbb{E}\big[f(x)\big] = \int f(x) w(x) \, \cdot \, q(x) dx \]

となり、モンテカルロ法を使って計算できる積分となる。具体的に言えば、\(x^1,\ x^2,\ \ldots,\ x^N\) を確率密度関数が \(q(x)\) である分布から独立にサンプルした点とするとき、次が成り立つ:

\[ \mathbb{E}\big[f(x)\big] \approx \frac{1}{N} \sum\limits_{i=1}^N f(x^i)w(x^i) \]

ただし、本章で説明した粒子フィルタで使った重み \(w^i\) は \(\pi(x)/q(x)\) に等しくはなく、\(\pi(x)/q(x)\) に比例するだけだった。このような場合には自己正規化重点サンプリング (self-normalized importance sampling) と呼ばれる手法が使える。この手法によると、\(w^i = A w(x^i)\) (\(A > 0\)) のとき次が成り立つことが分かる:

\[ \mathbb{E}\big[f(x)\big] \approx \frac{\sum\limits_{i=1}^N f(x^i)w^i}{\sum\limits_{i=1}^N w^i} \]

粒子フィルタで使った重み \(w^i\) は \(\sum\limits_{i=1}^N w^i = 1\) となるよう正規化していたから、

\[ \mathbb{E}\big[f(x)\big] \approx \sum\limits_{i=1}^N f(x^i)w^i \]

となる。例えば粒子の位置の平均は \(\sum x^i w^i\) と推定でき、本章の前半で示した数式と一致する。

粒子フィルタのアルゴリズムを自分で定式化するときは、考えている状況の特徴に応じて重みの計算ステップの実装を変える必要がある。ロボットの自己位置推定問題で \(q(x)\) に最も適した分布はフィルタの予測ステップで計算した粒子の分布となる。コードをもう一度見てみよう:

def update(particles, weights, z, R, landmarks):
    for i, landmark in enumerate(landmarks):
        dist = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
        weights *= scipy.stats.norm(dist, R).pdf(z[i])
    weights += 1.e-300      # 浮動小数点数誤差を避ける。
    weights /= sum(weights) # 正規化する。

ここではベイズの定理を使って \(\| \text{尤度} \times \text{事前分布}\|\) として重みを計算している。

もちろん、事前確率分布から事後確率分布を計算できるなら計算すべきである。もしできないなら、重点サンプリングがその問題を解く方法を提供する。現実の問題で事後分布は非常に複雑になる。カルマンフィルタが大きな成功を収めたのは、ガウス分布の特徴を利用すると解析解が求まるためだ。カルマンフィルタの仮定 (マルコフ性、観測値およびプロセスのガウス性と線形性) が緩和された場合は、重点サンプリングとモンテカルロ法があると問題が手に負えるようになる。

12.8 再サンプリングの手法

再サンプリングのアルゴリズムはフィルタの性能に影響する。例えば粒子をランダムに選んだとしよう。すると重みが小さい粒子も多く選ぶことになるので、出力される粒子の集合が表す確率分布は問題の解答として全く適切でなくなる。

このトピックの研究は続いているものの、多くの現実的な状況で優れた振る舞いを見せるアルゴリズムがいくつか知られている。再サンプリングのアルゴリズムはいくつかの特徴を持つのが望ましい。まず、高い確率を持った粒子を優先して選ぶこと。次に、サンプルの窮乏を避けるために高い確率を持つ粒子をまんべんなく選ぶこと。さらに、大きな非線形性を持つ振る舞いを検出できるように低い確率の粒子も十分に選択することが望まれる。

FilterPy は有名なアルゴリズムをいくつか実装する。FilterPy はあなたが粒子フィルタをどう実装するかを知らないので、新しいサンプルを生成することはできない。そこで実装では選択された粒子の添え字からなる NumPy 配列を作成して返すようにしてある。そのため再サンプリングステップは FilterPy を使う側が書く必要がある。例えばロボットの自己位置推定問題では次のコードを使った:

In [22]

def resample_from_index(particles, weights, indexes):
    particles[:] = particles[indexes]
    weights.resize(len(particles))
    weights.fill(1.0 / len(weights))

多項再サンプリング

多項再サンプリング (multinomial resampling) はロボットの自己位置推定の例で再サンプリングを説明するときに使ったアルゴリズムである。アイデアは簡単だ: まず正規化された重みの累積和を計算する。すると \(0\) から \(1\) まで単調に増加する要素からなる配列が手に入る。次の図に重みと累積和の関係を示す。色は区別しやすいように付けているだけで、特に意味は無い:

In [23]

from kf_book.pf_internal import plot_cumsum
print('累積和: ', np.cumsum([.1, .2, .1, .6]))
plot_cumsum([.1, .2, .1, .6])

Out [23]

累積和: [0.1 0.3 0.4 1. ]

続いて重みを選ぶために、\(0\) から \(1\) の一様乱数を生成し、その値が先ほどの累積和の配列でどの重みを指すかを二分探索で求める。大きい重みは小さい重みより大きな空間を占めるから、それだけ選択されやすくなる。

以上の処理は NumPy の universal function (ufunc) という機能を利用すると非常に簡単に実装できる。ufunc に対応した関数に配列を渡すと、配列の要素ごとに関数が適用され、結果からなる配列が返る。二分探索を行う NumPy の関数 numpy.searchsorted は ufunc に対応しており、探索を行う値を表す引数に配列を渡すと配列の各要素に対する探索結果からなる配列が計算される:

In [24]

def multinomal_resample(weights):
    cumulative_sum = np.cumsum(weights)
    cumulative_sum[-1] = 1.  # 浮動小数点数誤差を避ける。
    return np.searchsorted(cumulative_sum, random(len(weights)))

実行例を示す:

In [25]

from kf_book.pf_internal import plot_multinomial_resample
plot_multinomial_resample([.1, .2, .3, .4, .2, .3, .1])

多項再サンプリングは \(O(n \log n)\) のアルゴリズムである。この性能が悪いわけではないものの、サンプルの一様性に関してこれより優れた特徴を持つ \(O(n)\) のアルゴリズムも存在する。多項再サンプリングのアルゴリズムを示したのは、他のアルゴリズムがこのアルゴリズムの変種として理解できるためだ。確率分布の CDF の逆関数を利用する高速な多項再サンプリングの実装も存在する。もし興味があるならインターネットで検索してほしい。

多項再サンプリングを実装する FilterPy の関数 multinomal_resample は次のようにインポートする:

from filterpy.monte_carlo import multinomal_resample

残差再サンプリング

残差再サンプリング (residual sampling) は多項再サンプリングより高速であり、さらに粒子が全体からまんべんなくサンプルが取得されることが保証される。このアルゴリズムは非常に独創的である: まず正規化された重みに \(N\) を乗じて、その結果 (を整数に丸めた値) を各粒子が選択される回数として解釈する。例えばある粒子の重みが \(0.0012\) で \(N=3000\) だとしよう。このとき重みと粒子数の積は \(0.0012 * 3000 = 3.6\) だから、その粒子は \(3\) 回選択される。こうすると一定以上 (具体的には \(1/N\) 以上) の重みを持つ粒子が全て一回以上選択されることが保証される。このアルゴリズムの実行時間は \(O(N)\) であり、多項再サンプリングより高速である。

しかし、以上の処理はちょうど \(N\) 個のサンプルを選択するわけではない。サンプルを \(N\) 個にするために、スケールした重みの小数部分 (残差) に注目する。多項再サンプリングといったより単純なアルゴリズムを使って残差を重みとして残りの粒子を生成すれば、元の重みに従った全部で \(N\) 個の粒子が生成できる。一つ前の段落で示した例ではスケールした重みが \(3.6\) だったから、残差は \(3.6 - \lfloor 3.6 \rfloor = 0.6\) となる。この残差はそれなりに大きいから、この粒子はもう一度選択される可能性が高い。残差が大きい粒子は整数を使った一度目のサンプリングで本来より少ない回数しか選択されないので、これは理にかなっている。

残差再サンプリングの実装を示す:

In [26]

def residual_resample(weights):
    N = len(weights)
    indexes = np.zeros(N, 'i')

    # 粒子 i を int(N*w)[i] 個だけ選択する。
    Nw = N*weights
    num_copies = Nw.astype(int)
    k = 0
    for i in range(N):
        for _ in range(num_copies[i]): # num_copies[i] 個だけ i を選択する。
            indexes[k] = i
            k += 1

    # 残差を重みとした多項再サンプリングで残りの部分を埋める。
    residual = Nw - num_copies # 小数部分を求める。
    residual /= sum(residual)  # 正規化する。
    cumulative_sum = np.cumsum(residual)
    cumulative_sum[-1] = 1.    # 和が 1 であることを保証する。
    indexes[k:N] = np.searchsorted(cumulative_sum, random(N-k))

    return indexes

内側のループを indexes[k:k+num_copies[i]] = i としたくなるかもしれないが、非常に小さなスライスは比較的遅く、for ループを使った方が普通は高速になる。

実効例を示す:

In [27]

from kf_book.pf_internal import plot_residual_resample
plot_residual_resample([.1, .2, .3, .4, .2, .3, .1])

残差再サンプリングを実装する FilterPy の関数 residual_resample は次のようにインポートする:

from filterpy.monte_carlo import residual_resample

層化再サンプリング

層化再サンプリング (stratified resampling) は粒子を全体から比較的一様に選択することを目標とする。これは \([0,1]\) を \(N\) 個の等しい区間に分け、それぞれの区間から一つずつランダムに取った点に対応する粒子を累積和から選択するというアルゴリズムである。こうすると隣り合うサンプル間の距離が \(\frac{2}{N}\) 以下であることが保証される。

層化再サンプリングの例を次の図に示す。色付きのバーが重みの累積和を表し、灰色の縦線が \(N\) 個の小区間を区切る。黒い点で示される粒子は各小区間に一つずつランダムに配置されている:

In [28]

from kf_book.pf_internal import plot_stratified_resample
plot_stratified_resample([.1, .2, .3, .4, .2, .3, .1])

このアルゴリズムを実装するコードは非常に簡単である:

In [29]

def stratified_resample(weights):
    N = len(weights)
    # N 個の小区間を作り、それぞれの内部にランダムな点を生成する。
    positions = (random(N) + range(N)) / N

    indexes = np.zeros(N, 'i')
    cumulative_sum = np.cumsum(weights)
    i, j = 0, 0
    while i < N:
        if positions[i] < cumulative_sum[j]:
            indexes[i] = j
            i += 1
        else:
            j += 1
    return indexes

層化再サンプリングを実装する FilterPy の関数 stratified_resample は次のコードでインポートする:

from filterpy.monte_carlo import stratified_resample

等間隔再サンプリング

最後に等間隔再サンプリング (systematic resampling) を紹介する。このアルゴリズムは \([0,1]\) を \(N\) 等分する点は層化再サンプリングと同様だが、それから全ての小区間で利用するランダムなオフセットを一度だけ計算する。このため全ての点はちょうど \(\frac{1}{N}\) だけ離れる。等間隔再サンプリングの例を次の図に示す:

In [30]

from kf_book.pf_internal import plot_systematic_resample
plot_systematic_resample([.1, .2, .3, .4, .2, .3, .1])

実装は層化再サンプリングのコードをほんの少し変えるだけで済む:

In [31]

def systematic_resample(weights):
    N = len(weights)

    # N 個の小区間を作り、共通のランダムなオフセットを足す。
    positions = (np.arange(N) + random()) / N

    indexes = np.zeros(N, 'i')
    cumulative_sum = np.cumsum(weights)
    i, j = 0, 0
    while i < N:
        if positions[i] < cumulative_sum[j]:
            indexes[i] = j
            i += 1
        else:
            j += 1
    return indexes

等間隔再サンプリングを実装する FilterPy の関数 systematic_resample は次のようにインポートする:

from filterpy.monte_carlo import systematic_resample

再サンプリングアルゴリズムの選択

比較しやすいように、四つのアルゴリズムをまとめて示そう:

In [32]

a = [.1, .2, .3, .4, .2, .3, .1]
np.random.seed(4)
plot_multinomial_resample(a)
plot_residual_resample(a)
plot_systematic_resample(a)
plot_stratified_resample(a)

多項再サンプリングの性能は非常に悪い。大きい重みを持つにもかかわらず一度もサンプルされていない粒子が存在する。さらに、最も大きい重みの粒子は一度しかサンプルされていないのにもかかわらず、ずっと小さい重みが二度もサンプルされている。インターネット上にあるチュートリアルで私が読んだものの多くは多項再サンプリングを使っていたのだが、私にはその理由が分からない。専門的な文献や現実の問題で多項再サンプリングが使われることはほとんどない。特別な理由がない限り使わないことを推奨する。

残差再サンプリングでは狙い通りのことが起きている: 大きな重みを持つ粒子が複数回サンプルされる。ただ粒子が公平にサンプルされたわけではない──それなりに大きな多数の粒子が一つもサンプルされていない。

等間隔再サンプリングと層化再サンプリングはどちらも非常に良く動作している。前者では \([0,1]\) に点が均等に配置され、大きな重みを持つ粒子が多くサンプルされることが保証される。後者は前者ほど点が一様ではないものの、大きな重みを持つ粒子が多くサンプルという点では少し優れている。

こういったアルゴリズムの理論的な性能については多くの文献がある。もし気になるなら読んでみることだ。ただ実際に粒子フィルタを適用するのは解析的な手段が通用しない問題だから、そういった問題に特定の理論的解析が通用するのだろうかと私は少し疑問を持っている。現実の問題に対しては、層化再サンプリングまたは等間隔再サンプリングを使っておけばの多くの場合で非常に優れた性能が得られる。どちらかを試して、上手く行ったらそれを採用することを勧める。フィルタの性能が非常に重要な場合は両方を試すべきだ。さらに、あなたが取り組んでいる特定の問題を扱った文献で参考にできるものが公開されていないかどうかを確認するべきだろう。

12.9 まとめ

本章は広大なトピックの表面をなでただけに過ぎない。私の目標はあなたを粒子フィルタの専門家にすることではなく、フィルタリングにおけるモンテカルロ法というベイズ的な実践的テクニックを紹介することにある。

粒子フィルタはアンサンブル (ensemble) なフィルタリングの一種である。カルマンフィルタは状態をガウス分布で表現する。観測値はベイズの定理を使ってそのガウス分布に組み込まれ、予測は状態空間法で行われる。こういった処理はガウス分布に──確率分布に──適用される。

これに対して、粒子フィルタをはじめとするアンサンブルな手法は確率分布を点の集合とそれぞれの点に対する確率で表現する。観測値はガウス分布ではなく点に組み込まれ、同様にプロセスモデルもガウス分布ではなく点に組み込まれる。そうして得られる点の集合と確率から統計的性質が計算される。

二つの選択肢には多くのトレードオフがある。カルマンフィルタは非常に効率的であり、線形性とガウス性の仮定が正しいとき最適な推定値を出力する。もし問題が非線形なときは線形化が必要になる。また問題が多峰性 (追跡する物体が複数ある) なら、カルマンフィルタは求めたい確率分布を表現できない。またカルマンフィルタでは状態モデルを知っていることも必要とされ、システムの振る舞いが分からなければ優れた性能は得られない。

これに対して、粒子フィルタは解析的でない任意の確率分布が絡む問題で利用できる。十分多くの粒子があれば粒子の全体アンサンブルが考えている確率分布の正確な近似を構成するためだ。極端な線形性が存在する場合でも優れた性能を発揮する。また重点サンプリングにより本当の確率分布を知らなくても統計量を計算できる。加えて他の種類のフィルタで必要になる解析的な積分はモンテカルロ法に置き換わる。

この力にはコストがかかる。最も明らかなコストは高い計算量とメモリ使用量だ。それほど明らかでないコストはアンサンブルなフィルタが気まぐれなことである。粒子の縮退や発散に注意しなければならない。また多峰性の確率分布を扱うときは、さらに粒子をクラスタリングして複数の物体の軌跡を決定しなければならない。これは物体が互いに近づくとき非常に難しくなる。

粒子フィルタには多くの異なるクラスが存在する: 本章では最初にナイーブな SIS アルゴリズムを説明し、その後 SIR アルゴリズムを説明して上手く動作することを見た。他にもたくさんのフィルタのクラスがあり、それぞれのクラスに様々なフィルタがある。全てを説明するには小さな本が一冊必要になるだろう。

粒子フィルタに関する専門的な文献を読むと積分がそこら中にあることに気が付くはずだ。確率分布に対する計算は積分で行われるので、積分は強力かつ簡潔な記法を可能にする。そういった数式をコードに落とすときは、確率分布は粒子で表現され、積分は粒子に関する和に置き換わることを意識する必要がある。本章で学んだ核となる考え方を理解していれば、積分を使って書かれた専門的な文章も怖くはないはずだ。

第 12 章 粒子フィルタ