第 10 章 無香料カルマンフィルタ
前章では非線形な系がもたらす難しさを議論した。この非線形性は二つの場所で現れる。一つは観測値である。例えばレーダーが直距離 (slant, 自身と目標を直線で結んだ距離) を観測するとき、\(x\) 座標を計算するには平方根を取らなければならない:
非線形性がプロセスモデルで発生することもある──大気中を運動するボールを追跡するとき、空気抗力により非線形な振る舞いが引き起こされる。通常のカルマンフィルタはこういった問題に対して性能が悪かったり、全く見当違いな値を返したりする。
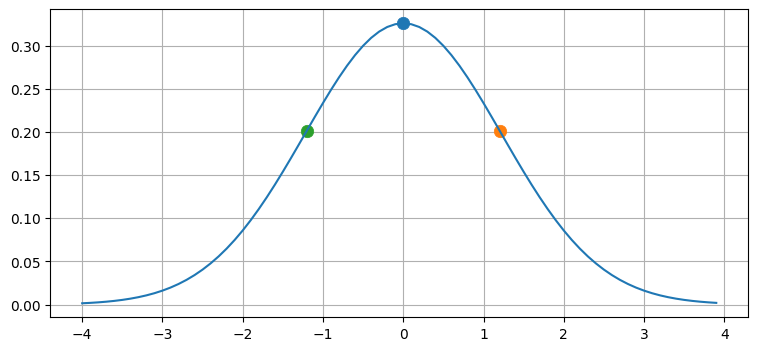
前章でいくつか示したプロットをもう一度示す。ここでは非線形性の効果が強調されるような関数を使っている:
from kf_book.book_plots import set_figsize, figsize
import matplotlib.pyplot as plt
from kf_book.nonlinear_plots import plot_nonlinear_func
from numpy.random import normal
import numpy as np
# 平均 0, 標準偏差 1 の正規分布から 500,000 個のサンプルを生成する。
gaussian = (0., 1.)
data = normal(loc=gaussian[0], scale=gaussian[1], size=500000)
def f(x):
return (np.cos(4*(x/2 + 0.7))) - 1.3*x
plot_nonlinear_func(data, f)
ここでは 500,000 個のサンプルを入力の分布から生成し、非線形な変換を適用し、その結果からヒストグラムを構築している。このとき使う点をシグマ点 (sigma point) と呼ぶ。出力のヒストグラムからは平均と標準偏差を計算でき、そこからは更新後の (出力の分布を近似する) ガウス分布が得られる。
f(x) に通す前後のデータを散布図にプロットすると次のようになる:
N = 30000
plt.subplot(121)
plt.scatter(data[:N], range(N), alpha=.2, s=1)
plt.title('Input')
plt.subplot(122)
plt.title('Output')
plt.scatter(f(data[:N]), range(N), alpha=.2, s=1);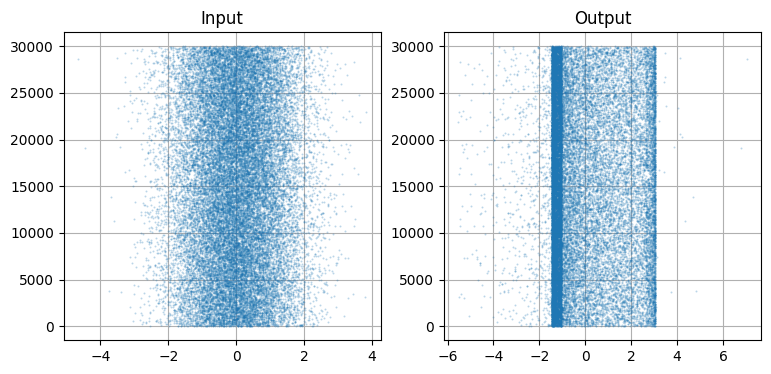
ガウス分布なので当然だが、左の散布図はガウス分布らしく見える。「ガウス分布らしい」とは平均 \(0\) を中心とした白色ノイズに見えるという意味である。これに対して f(data) の散布図には目に見える構造がある。垂直の帯が二つあり、その間に大量の点が存在する。帯の外側には点がほとんど存在せず、どちらかと言えば負の部分に点が多い。
このサンプリング処理が今考えている問題の解法になるのではないかと思ったかもしれない。更新ごとに (例えば) 500,000 個の点を生成し、関数を適用し、その結果の平均と分散を計算すればいい。これはモンテカルロ法と呼ばれる手法であり、アンサンブルカルマンフィルタや粒子フィルタといった一部のカルマンフィルタの設計で使われる。モンテカルロ法ではサンプリングに特殊な知識が必要とされず、閉じた形の解も必要ない。関数がどれだけ非線形であっても、どれだけ振る舞いが厄介でも、十分多いシグマ点でサンプルすれば必ず正確な出力の分布が得られる。
ただ「十分多くの」が問題になる。上のグラフは 500,000 個のシグマ点を使って作成しているにもかかわらず、出力のグラフは滑らかでない。さらに悪いことに、これはたった一次元しか計算していない。次元数が増えれば必要になるシグマ点の個数は指数的に増えていく。例えば一次元に必要なのが 500 点だったとしても、二次元では 250,000 点、三次元では 125,000,000 点を用意しなければならない。つまり、この手法は正しく動作するものの、計算量的にコストが非常に高い。アンサンブルカルマンフィルタと粒子フィルタはこの次元数を大きく削減する賢いテクニックだが、それでも計算量は非常に大きい。無香料カルマンフィルタもシグマ点を利用するが、シグマ点を決定的に選択することで計算量を大幅に削減する。
10.1 シグマ点──分布からのサンプリング
非線形関数による確率分布の変換を二次元の共分散楕円を使って考えてみよう。二次元を使うのはプロットしやすいからであり、これからの議論は高次元にも拡張できる。任意の非線形関数を仮定する。変換したい分布の共分散楕円からランダムに点を取り、点を非線形関数に通し、計算される新しい位置をプロットする。変換された点の平均と共分散行列を計算すれば、それを変換後の確率分布の推定された平均と共分散行列として利用できる。これを次の図に示す:
import kf_book.ukf_internal as ukf_internal
ukf_internal.show_2d_transform()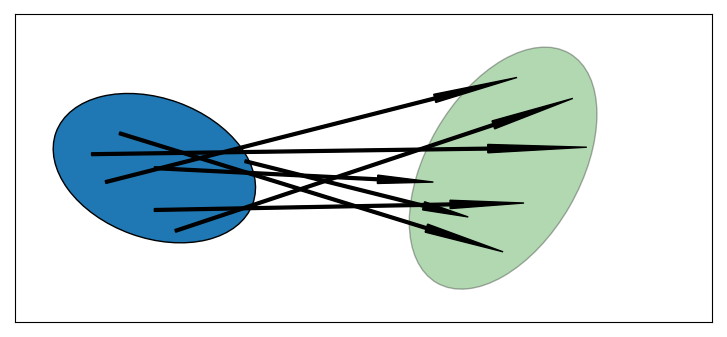
左の青い楕円は変換前の二次元確率分布の \(1\sigma\) を示し、矢印はランダムにサンプルされた点が非線形関数によって新しい分布における点に移ることを表す。右の新しい共分散楕円は計算された点の集合の平均と共分散行列による推定値なので、薄い色になっている。
10,000 個の点をガウス分布
からランダムに取り、関数
に通したときに得られる分布をプロットするコードを書こう:
import numpy as np
from numpy.random import multivariate_normal
from kf_book.nonlinear_plots import plot_monte_carlo_mean
def f_nonlinear_xy(x, y):
return np.array([x + y, .1*x**2 + y*y])
mean = (0., 0.)
p = np.array([[32., 15.], [15., 40.]])
# 線形化を通して平均を計算する。
mean_fx = f_nonlinear_xy(*mean)
# ランダムな点を生成する。
xs, ys = multivariate_normal(mean=mean, cov=p, size=10000).T
plot_monte_carlo_mean(xs, ys, f_nonlinear_xy, mean_fx, 'Linearized Mean');Difference in mean x=0.027, y=42.956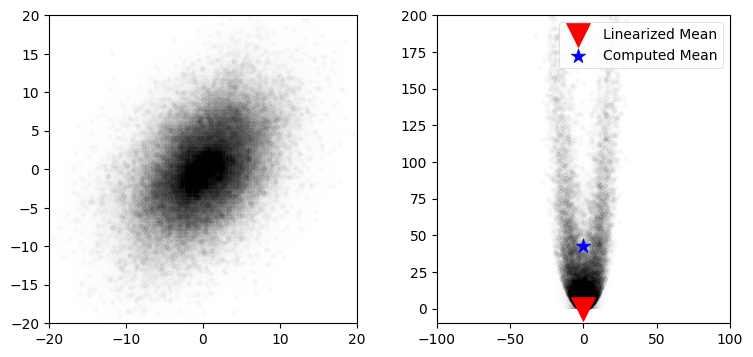
このプロットからは関数 f_nonlinear_xy が持つ強い非線形性が分かる。また拡張カルマンフィルタ (次章で学ぶ) と同じ方法で線形化したときに計算される平均 (赤い下三角) の誤差が大きいのも確認できる。
10.2 簡単な例
これから無香料カルマンフィルタ (unscented Kalman filter, UKF) がシグマ点を選ぶときに使う数式を学ぶ。ただその前に、まずは例を使って "目的地" を確認しよう。
UKF で使えるシグマ点生成アルゴリズムは一つではないことを後で見る。FilterPy もいくつか提供している。シグマ点アルゴリズムの一つを示す:
from filterpy.kalman import JulierSigmaPoints
sigmas = JulierSigmaPoints(n=2, kappa=1)具体的な処理は後で明らかになる。オブジェクト sigmas は平均と共分散行列を受け取って重み付きシグマ点を生成する。試しに使って見よう。次のプロットでは点の大きさが重みを表す:
from kf_book.ukf_internal import plot_sigmas
plot_sigmas(sigmas, x=[3, 17], cov=[[1, .5], [.5, 3]])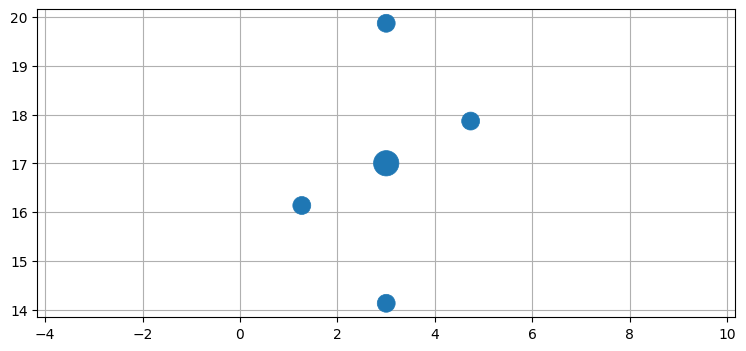
\((3,17)\) を中心とする奇妙なパターンをした五つの点が得られた。この五つの点を使うとランダムに生成された 500,000 個の点を使ったときの同程度の (ときには上回る) 性能が得られるというのは馬鹿げた話に思えるかもしれないが、本当の話である!
ではフィルタを実装してみよう。非線形フィルタに挑戦する準備はまだ整っていないので、これから標準的な一次元線形フィルタを実装する。フィルタの設計はこれまでと大きくは変わらないものの、一つ違う部分がある。KalmanFilter クラスは行列 \(\mathbf{F}\) を状態遷移関数として使っていた。線形代数の概念である行列は線形関数を表すには都合がいいのだが、非線形関数を表すことはできない。そこで上の実行例と同じように、行列の代わりに関数を渡すことになる。KalmanFilter クラスは観測関数を実装する行列 \(\mathbf{H}\) も持っていて、\(\mathbf{H}\) は状態を等価な観測値に変換していた。ここでも行列は線形性を意味するので、行列の代わりに関数を渡すことになる。\(\mathbf{F}\) と \(\mathbf{H}\) が「状態遷移関数」および「観測関数」と呼ばれる理由がこれで分かったはずだ: 線形カルマンフィルタでは \(\mathbf{F}\) と \(\mathbf{H}\) が行列だったが、これは関数がたまたま線形なときは行列を使った方が計算を簡単に行えるというだけである。
難しい話はこれぐらいにして、一次元の追跡問題に対する状態遷移関数と観測関数の実装を次に示す。状態は \(\mathbf x = \Big[x \, \, \dot x\Big]^ \mathsf T\) としている:
def fx(x, dt):
xout = np.empty_like(x)
xout[0] = x[1] * dt + x[0]
xout[1] = x[1]
return xout
def hx(x):
return x[:1] # 位置 [x] を返す。はっきり言っておくと、これは線形な問題である。本当は UKF を使う必要はないのだが、最も簡単な問題から説明を始めている。\(\mathbf{\bar x}\) の計算が行列乗算ではなく関数 fx における式の計算で行われることに注意してほしい。こう書いたのは任意の非線形関数を実装できることを示すためだ。この計算は線形な式に制限されない。
他の部分の設計は変わらない。\(\mathbf{P}\), \(\mathbf{Q}\), \(\mathbf{R}\) の設計方法は分かっているはずだ。フィルタの残りの部分を書いて、実行してみよう:
from numpy.random import randn
from filterpy.kalman import UnscentedKalmanFilter
from filterpy.common import Q_discrete_white_noise
ukf = UnscentedKalmanFilter(dim_x=2, dim_z=1, dt=1., hx=hx, fx=fx, points=sigmas)
ukf.P *= 10
ukf.R *= .5
ukf.Q = Q_discrete_white_noise(2, dt=1., var=0.03)
zs, xs = [], []
for i in range(50):
z = i + randn()*.5
ukf.predict()
ukf.update(z)
xs.append(ukf.x[0])
zs.append(z)
plt.plot(xs);
plt.plot(zs, marker='x', ls='');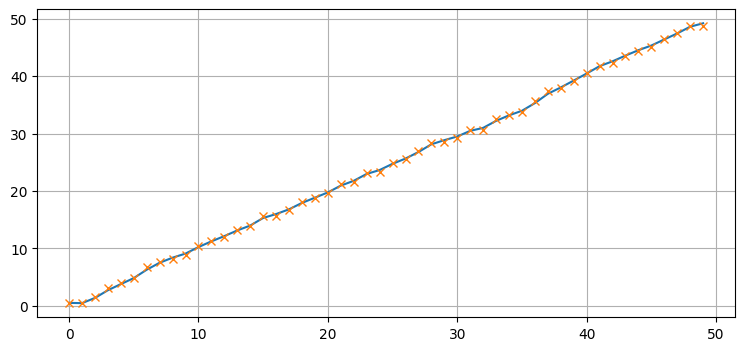
ここに本質的に新しい事項はない。シグマ点を自分で計算し、\(\mathbf{F}\) と \(\mathbf{H}\) による乗算を行列ではなく関数として実装しただけだ。これで UKF の理解に必要な少しばかりの数学とアルゴリズムを苦労して理解するのに十分な自信が付いたことを願う。
10.3 シグマ点の選択
本章の最初で、ランダムに生成された 500,000 個のシグマ点を使ってガウス分布を非線形関数に通したときの確率分布を計算した。計算された平均は非常に正確ではあったものの、更新のたびに 500,000 個の点を計算しているとフィルタは非常に遅くなってしまう。では、シグマ点はいくつまで減らせるだろうか? 問題の定式化はシグマ点にどのような制約を課すだろうか? 任意の関数に対して動作する一般的な関数を見つけようとしているので、非線形関数に関する特殊な知識は存在しないと仮定する。
最も単純なケースを考えて、何か分からないかを見てみよう。最も単純な系は恒等関数 (identity function) \(f(x) = x\) で記述される。私たちのアルゴリズムが恒等関数に対して正しく動作しないなら、フィルタが収束することはあり得ない。言い換えれば、恒等関数で記述される (一次元の) 系に \(1\) が入力されるときは、計算される出力も \(1\) でなければならない。もし出力が \(1\) でない値、例えば \(1.1\) だったとすると、次のタイムステップでは \(1.1\) がさらに別の値 (おそらくは \(1.23\)) になるので、フィルタは発散してしまう。
選択できる最も少ないシグマ点の個数は次元ごとに一つである。線形カルマンフィルタは次元ごとに一つの点を使う: 状態がガウス分布 \(\mathcal{N}(\mu,\sigma^2)\) で表されるとき、線形カルマンフィルタへの入力は \(\mu\) そのものとなる。よって次元ごとに点が一つあれば線形の問題に対しては正しく動作する。しかし非線形の問題に対しては優れた結果が得られない。
次元ごとに取る一つの点を変化させれば結果が改善されるのではないかと思うかもしれない。しかしシグマ点を \(\mu + \Delta\ (\Delta \neq 0)\) と表される点にすると、恒等関数 \(f(x)=x\) で記述される系に対してフィルタが収束しなくなるので上手く行かない。\(\mu\) を変えなければ普通のカルマンフィルタになるので、次元ごとに一つのサンプルでは非線形の問題に対する状況を改善できないという結論になる。
次に少ない点の個数はいくつだろうか? 二つだ。しかしガウス分布は対称であり、恒等関数に対して正しく動作するにはおそらくシグマ点の一つが入力分布の平均でなければならない。二つの点のうち一つを平均に配置すると、もう一つの点をどこに配置しても望ましくないであろう非対称性が生まれてしまう。シグマ点を二つ使うフィルタリングを恒等関数 \(f(x)=x\) に対して正しく動作させるには大きな手間がかかると思われる。
次に少ない点の個数は三つだ。点が三つなら、平均から逆方向に同じ距離だけ離れた二点と平均を選択できる。これを次の図に示す:
この三つの点を非線形関数 \(f(x)\) に通して、その結果の平均と共分散行列を計算すればよさそうだ。平均の計算では三つの点における値を足して \(3\) で割ってもいいのだが、それはあまり一般的ではない。例えば非常に非線形性の大きい問題に対しては中心の点に大きな重みを与えたい場合もあるかもしれないし、外側の点の重みを大きくしたい場合もあるだろう。
より一般的な手法は重み付き平均 \(\mu = \sum_i w_i\, f(\mathcal{X}_i)\) を使うというものだ。ここで飾りの付いた \(\mathcal{X}=\{\mathcal{X}_1,\ \mathcal{X}_2,\ \ldots,\ \mathcal{X}_n\}\) がシグマ点の集合を表す。重みの和は \(1\) である必要がある。この制約の下で、変換されたシグマ点から計算された平均と共分散行列が正確な推定値となるようにシグマ点とその重みを求めることが私たちの仕事となる。
平均の計算で重み付け平均を使うなら、共分散行列の計算でも重みを使ってもよさそうだ。また平均に対する重み \(w^m\) と共分散行列に対する重み \(w^c\) を別にすることもできる。以降の数式では下付き添え字を見やすくするために上付き添え字で平均と共分散行列のどちらの重みかを表すことにする。このときシグマ点に関する制約は次のように書ける:
最初の二つの数式は「重みの和は \(1\) でなければならない」という制約を表す。三つ目の数式は重み付き平均の計算方法を表す。四つ目の数式は馴染みがないかもしれないが、二つの確率変数の間の共分散行列を計算する式を思い出してほしい:
これらの制約は一意の解を構成しない。例えば \(w^m_0\) を適当に小さくしても、\(w^m_1\) と \(w^m_2\) を大きくして埋め合わせれば問題ない。平均と共分散行列で異なる重みを使うこともできるし、同じ重みを使うこともできる。実を言えば、上述の制約はシグマ点のいずれかが入力の平均でなければならないとは言っていない。ただ、そうしたほうが「良い」ようには思われる。
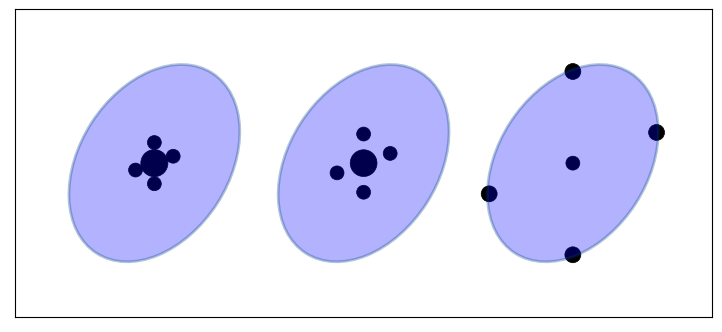
これらの制約を満たすアルゴリズムを私たちは探しており、次元ごとにシグマ点を三つだけ使うのが望ましい。話を次に進める前に、今考えていることの理解を確認しておこう。同じ共分散楕円に対するシグマ点の三つの異なる配置を次に示す。シグマ点の大きさは重みを表す:
シグマ点は共分散楕円の長軸と短軸に沿って並んでいない: それは制約によって強制されない。またシグマ点は等間隔で並んでいるものの、これは制約から強制されたわけではない。
シグマ点の配置と重み付けは分布のサンプル方法に影響を及ぼす。密集したシグマ点は局所的な変化をサンプルするので、非常に非線形な問題では性能が向上するだろう。またシグマ点が散らばっていたり共分散楕円の軸から大きく離れていたりすれば、局所的でない変化やガウス分布的でない振る舞いがサンプルされるだろう。ただし、各点に対する重みを調整すればこの傾向を和らげることができる。例えば平均から離れた点を使っても、重みを非常に小さくしておけば、問題の非線形によって推定値が悪くなるのを防ぎつつも分布の知識をいくらか取り入れることができるだろう。
シグマ点の選び方は無限に存在することをどうか理解してほしい。私が選んだ制約は選択肢の一つに過ぎない。例えば、シグマ点を作成するアルゴリズムの中には重みの和が \(1\) になることを要求しないものが存在する。実を言えば、本書で私が選んだアルゴリズムはこの特徴を持たない。
10.4 無香料変換
しばらくの間、シグマ点と重みを選択するアルゴリズムが存在すると仮定する。フィルタの実装でシグマ点はどのように使われるだろうか?
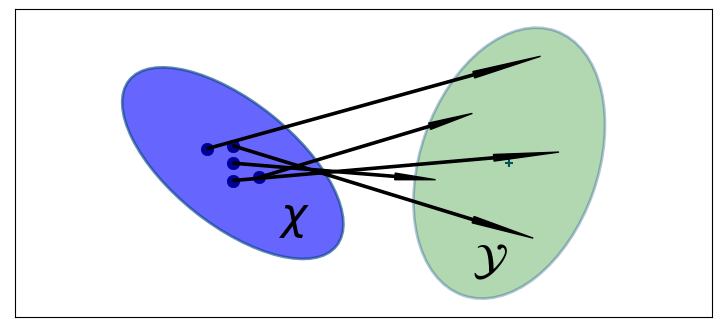
無香料変換 (unscented transform, UT) は UKF のアルゴリズムで核となる概念であり、その割には驚くほど簡単である。これまでに説明してきた処理をまとめると、まずシグマ点の集合 \(\mathcal{X}\) に非線形関数 \(f\) を適用し、変換された点の集合 \(\mathcal{Y}\) を生成する:
そうしたら変換された点の平均と共分散行列を計算し、その値を新しい推定値とする。シグマ点を使って非線形関数を適用した後の分布を推定するこの処理を無香料変換と呼ぶ。無香料変換の概略図を次に示す。右の緑色の楕円が変換後のシグマ点から計算された平均と共分散行列を表す:
変換後のシグマ点の平均と共分散行列は次のように計算される:
この式には見覚えがあるはずだ──前に考えた制約の式と同じである。
短くまとめると、無香料変換は任意の確率分布から点をサンプルし、任意の非線形関数に通し、変換後の点の平均と共分散行列からガウス分布を推定する。これを使ってどうすれば非線形カルマンフィルタを実装できるかが想像できることを願う。ガウス分布にできれば、これまでに学んできた数学的装置が働き始める!
「無香料 (unscented)」という名前は分かりにくいかもしれない。この言葉には実のところ大した意味がない。UKF の考案者が「このアルゴリズムには "変な香りが付いていない"」と冗談めかして付けた名前であり、それが今でも使われている1。「無香料」に数学的な意味はない。
無香料変換の正確さ
本章の最初で、50,000 個の点を生成して非線形関数に通すことで分布の平均を見つける関数を書いた。同じ関数に五つのシグマ点を渡して、平均を無香料変換で計算してみよう。FilterPy の MerweScaledSigmaPoints クラスでシグマ点を作成し、unscented_transform 関数で変換を行う: この関数については後で説明する。前に示したシグマ点の例では JulierSigmaPoints クラスを使っていた。二つのクラスはどちらもシグマ点を作成するが、後で説明するようにその方法が異なる。
from filterpy.kalman import unscented_transform, MerweScaledSigmaPoints
import scipy.stats as stats
# 最初の平均と共分散行列
mean = (0., 0.)
p = np.array([[32., 15], [15., 40.]])
# シグマ点と重みを作成する。
points = MerweScaledSigmaPoints(n=2, alpha=.3, beta=2., kappa=.1)
sigmas = points.sigma_points(mean, p)
# シグマ点を非線形関数に通す。
sigmas_f = np.empty((5, 2))
for i in range(5):
sigmas_f[i] = f_nonlinear_xy(sigmas[i, 0], sigmas[i ,1])
# 無香料変換で新しい平均と共分散行列を取得する。
ukf_mean, ukf_cov = unscented_transform(sigmas_f, points.Wm, points.Wc)
# ランダムな点を生成する。
np.random.seed(100)
xs, ys = multivariate_normal(mean=mean, cov=p, size=5000).T
plot_monte_carlo_mean(xs, ys, f_nonlinear_xy, ukf_mean, 'Unscented Mean')
ax = plt.gcf().axes[0]
ax.scatter(sigmas[:,0], sigmas[:,1], c='r', s=30);Difference in mean x=-0.097, y=0.549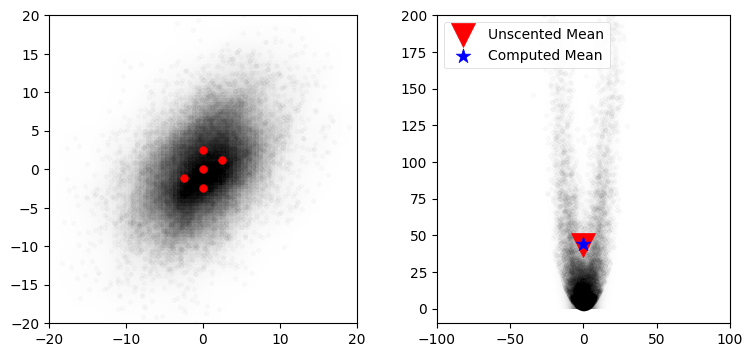
この結果は驚くべきものだと私は思う。たった五つの点しか使っていないのに、平均を素晴らしい正確さで計算できている。\(x\) 方向と \(y\) 方向の誤差はそれぞれ \(-0.097,\ 0.549\) しかない。これに対して、線形化を使う (次章で学ぶ EKF が採用する) 手法だと \(y\) 方向の誤差が \(43\) にも及ぶ。コードのシグマ点を生成する部分を見れば、シグマ点の生成処理は考えている非線形関数の知識を一切持たず、初期分布の平均と共分散行列だけを使っているのが分かる。全く異なる非線形関数を使ったとしても、同じ五つのシグマ点が生成される。
EKF と比較したときの無香料変換の性能が際立つように非線形関数を選んだことは認めよう。しかし物理世界は非線形性の大きい振る舞いに満ちており、そのような振る舞いであっても UKF なら楽々と処理できる。無香料変換が良い性能を達成できる例を見つけるのに苦労はしなかった。次章を読めば EKF という伝統的な手法だと強い非線形性があるときに性能が落ちることが分かるだろう。UKF や UKF に似た現代的な手法が使えるときはそれを使った方がいいとアドバイスした理由の土台にあるのが上のグラフである。
予測ステップ
UKF の予測ステップはプロセスモデル \(f\) を使って事前分布を計算する。\(f\) は非線形と仮定されるので、まず何らかの関数に従ってシグマ点 \(\mathcal{X}\) と対応する重み \(W^m,\ w^c\) を生成する:
続いてそれぞれのシグマ点を \(f(\mathbf x, \Delta t)\) に渡す。シグマ点はプロセスモデルによって次の時刻に射影され、新しい事前分布を構成する。\(f\) に通した後のシグマ点の集合を \(\mathcal{Y}\) とする:
そうしたら、変換されたシグマ点に対する無香料変換 (UT) で事前分布の平均と共分散行列を計算する:
無香料変換の式は次の通りである:
カルマンフィルタと無香料カルマンフィルタの式を比較した表を次に示す。可読性のため添え字 \(i\) は省略した:
更新ステップ
カルマンフィルタは更新を観測空間で行う。そのため事前分布を表すシグマ点を観測関数 \(h(x)\) で観測空間に移さなければならない。この \(h(x)\) はこちらで用意する:
ここから無香料変換を使って平均と共分散行列を計算する。添え字の \(z\) は観測空間に移したシグマ点の平均と共分散行列であることを表す:
続いて残差とカルマンゲインを計算する。観測値 \(\mathbf{z}\) の残差は自明に計算できる:
カルマンゲインの計算では状態と観測値の相互共分散が必要になる。これは次のように定義される:
このときカルマンゲインは
と定義される。逆行列は行列の逆数のようなものだと思えば、このカルマンゲインは次の単純な比と解釈できる:
最後に、状態の新しい推定値が残差とカルマンゲインを使って計算される:
新しい共分散行列は次の式で計算される:
このステップには証明を付けずに示した式がいくつかある。ただ線形カルマンフィルタの式とどのように関連付くかは理解できるはずだ。線形カルマンフィルタで使った線形代数とは少し異なっているものの、根本的なアルゴリズムは本書でずっと使ってきたベイズ的なアルゴリズムである。
線形カルマンフィルタの式と UKF の式を比較した表を示す:
10.6 Van der Merwe の拡大シグマ点アルゴリズム
シグマ点を選択するアルゴリズムは多数存在する。ただ 2005 年あたりから、研究界と産業界の研究者の多くは 2004 年に公開された Rudolph Van der Merwe の博士論文2にあるバージョンに落ち着いた。このバージョンは多くの問題で高い性能を発揮し、性能と正確さの優れたトレードオフを持つ。これは 2002 年に Simon J. Julier が発表3した拡大無香料変換 (scaled unscented transform) を少し変えた再定式化である。
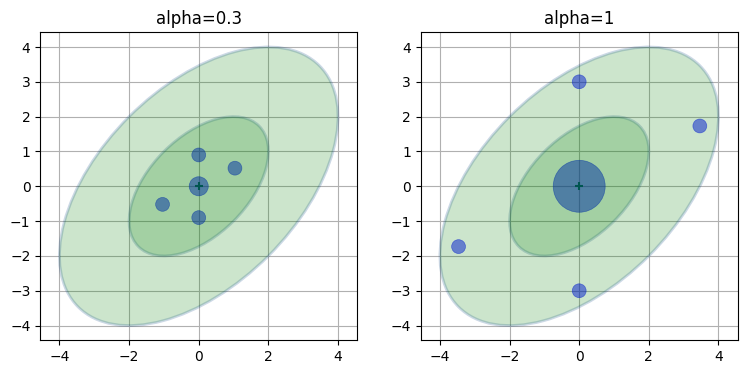
この定式化は \(\alpha\), \(\beta\), \(\kappa\) という三つのパラメータを使ってシグマ点の配置と重みを制御する。数式を見ていく前に、例を一つ示す。次の図に \(1\sigma\) と \(2\sigma\) を示す共分散楕円と二種類のシグマ点をプロットした。\(\beta\) と \(\kappa\) には共通の値を使い、\(\alpha\) はそれぞれ \(0.3\) および \(1.0\) としている。点の大きさは平均に対する重みを表す:
両方のシグマ点は \(2\sigma\) より内側に配置されており、\(\alpha\) を大きくすると散らばるのが分かる。さらに、\(\alpha\) を大きくすると平均 (中央の点) に割り当てられる重みが大きく、周りの点の重みが小さくなるのも確認できる。これは直感とも矛盾しないはずだ──点が平均から離れればそれだけ、その点の重みは小さくするべきである。シグマ点の位置と重みの計算方法はまだ分からないものの、その結果におかしな部分はない。
位置の計算
一つ目のシグマ点は入力された平均である。このシグマ点は上の図で共分散楕円の中心として表示されている。この点をこれから \(\mathcal{X}_0\) と呼ぶ:
式を簡単にするため \(\lambda = \alpha^2(n+\kappa)-n\) と定義する (\(n\) は \(\mathbf{x}\) の次元)。このとき残りのシグマ点は次のように計算される:
添え字の \(i\) は行列の \(i\) 番目の行ベクトルを表す。
言葉を使って説明すると、共分散行列を定数で拡大して平方根を取り、その行ベクトルを平均に足したベクトルと平均から引いたベクトルをシグマ点にするということだ。行ベクトル一つにつき二つのシグマ点が追加されるのは対称性を担保するためである。行列の平方根を取る方法については後で議論する。
重さの計算
この定式化では平均に対する重みと共分散行列に対する重みが異なる。まず、平均の計算における \(\mathcal{X}_0\) の重み \(W^m_0\) は
と定義され、共分散行列の計算における \(\mathcal{X}_0\) の重み \(W^c_0\) は次のように定義される:
その他のシグマ点 \({\mathcal{X}}_1,\ \ldots,\ {\mathcal{X}}_{2n}\) に対する重みは平均と共分散行列で共通であり、次のように定義される:
この配置と重み付けが「正しい」理由は明らかでないかもしれない。というより実は、これが全ての非線形問題に対して理想的であると証明することはできない。ただシグマ点は共分散行列の平方根に比例した分だけ平均から離れており、分散の平均は標準偏差である。そのため、このシグマ点は大まかに言って \(\pm 1\sigma\) を定数倍した距離だけ散らばる。またシグマ点の位置と重みをよく見ると、次元が増えると点は散らばって重みは小さくなるのが分かる。
重要: 通常こうして計算される重みは和が \(1\) にならない。この点について多くの質問を受け取った。重みの和が \(1\) より大きくなることもあるし、ときには負になることさえある。この点については後でさらに説明する。
パラメータの選び方
ガウシアンの問題に対しては \(\beta=2\) にするとよい。\(\kappa\) は \(\mathbf{x}\) の次元を \(n\) として \(\kappa=3-n\) とするのがよく、\(\alpha\) は \(0 \le \alpha \le 1\) を満たす値が適切である。\(\alpha\) を大きくすると、シグマ点は平均から遠くに離れていく。
10.7 UKF を使う
UKF が簡単に使えることを納得してもらうために、いくつか問題を解いてみよう。最初は線形のカルマンフィルタによる解き方を知っている線形の問題から始める。UKF は非線形の問題を念頭に設計されてはいるものの、線形の問題に対しては線形カルマンフィルタと同じ最適な解を見つけることができる。これから定常速度モデルを使って二次元空間を動く物体を追跡するフィルタを書く。前に扱った問題なので、UKF を使うときに何が同じで何が違うのに注目できるはずだ (ほとんど同じなのだが!)。
カルマンフィルタの設計では \(\textbf{x}\), \(\textbf{F}\), \(\textbf{H}\), \(\textbf{R}\), \(\textbf{Q}\) を指定しなければならない。これまでに何度も行ったので、説明は最小限にして行列を示すことにする。定常速度モデルを使うので、状態は
となる。状態変数をこのように並べるとき、状態遷移行列は
となる。これは次の運動方程式を実装する:
センサーは位置を報告し、速度は報告しない。よって観測関数は
である。センサーの出力の単位はメートルで、誤差は \(x\) 方向および \(y\) 方向に \(\sigma=0.3~\text{m}\) だとする。ここから観測ノイズ行列が分かる:
最後に、プロセスノイズは離散白色ノイズモデルで表されると仮定しよう──つまり、離散化された時刻の間で加速度は一定とする。このときプロセスノイズ行列は FilterPy の Q_discrete_white_noise 関数で計算できる。復習しておくと、この関数は次の行列を計算する:
このフィルタを実装するコードを示す:
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
from numpy.random import randn
std_x, std_y = .3, .3
dt = 1.0
np.random.seed(1234)
kf = KalmanFilter(4, 2)
kf.x = np.array([0., 0., 0., 0.])
kf.R = np.diag([std_x**2, std_y**2])
kf.F = np.array([[1, dt, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, dt],
[0, 0, 0, 1]])
kf.H = np.array([[1, 0, 0, 0],
[0, 0, 1, 0]])
kf.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=1, var=0.02)
kf.Q[2:4, 2:4] = Q_discrete_white_noise(2, dt=1, var=0.02)
zs = [np.array([i + randn()*std_x,
i + randn()*std_y]) for i in range(100)]
xs, _, _, _ = kf.batch_filter(zs)
plt.plot(xs[:, 0], xs[:, 2]);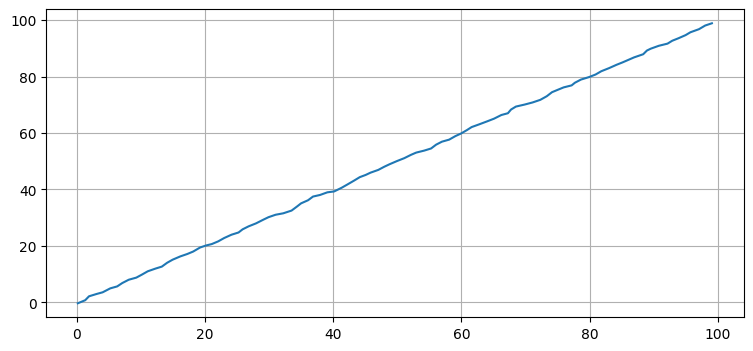
ここに驚くような部分はないはずだ。では UKF を実装しよう。繰り返すが、この実装は教育目的である。線形の問題に対して UKF を実装しても得るものはない。FilterPy は UKF を UnscentedKalmanFilter クラスで実装する。
最初に二つの関数 f(x, dt), h(x) を実装する。f(x, dt) は状態遷移関数を実装し、h(x) は観測関数を実装する。これらは線形カルマンフィルタの \(\mathbf{F}\) と \(\mathbf{H}\) に対応する。
次に二つの関数の実装 (の選択肢の一つ) を示す。それぞれ一次元の NumPy 配列と結果からなるリストを返している。f や h でない意味のある名前を与えても構わない:
def f_cv(x, dt):
""" 等速度で飛行する航空機の状態遷移関数 """
F = np.array([[1, dt, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, dt],
[0, 0, 0, 1]])
return F @ x
def h_cv(x):
return x[[0, 2]]続いてシグマ点とその重みを計算する方法を指定する。Van der Merwe のバージョンを上に示したが、選択肢は他にも多く存在する。FilterPy は SigmaPoints という基底クラスを使って実装されており、このクラスを継承するクラスは次のメソッドを実装しなければならない:
def sigma_points(self, x, P)
加えて Wm および Wc という属性も持っている必要がある。これらには平均および共分散行列を計算するときの重みが格納される。
FilterPy の MerweScaledSigmaPoints クラスは SigmaPoints クラスを継承し、sigma_points メソッドを実装する。
FilterPy の UnscentedKalmanFilter オブジェクトを作成するときは、\(f\) と \(h\) および SigmaPoints オブジェクトを渡す必要がある。この例を示す:
from filterpy.kalman import MerweScaledSigmaPoints
from filterpy.kalman import UnscentedKalmanFilter as UKF
points = MerweScaledSigmaPoints(n=4, alpha=.1, beta=2., kappa=-1)
ukf = UKF(dim_x=4, dim_z=2, fx=f_cv, hx=h_cv, dt=dt, points=points)
以降のコードは線形カルマンフィルタと変わらない。次のコードでは同じ観測値を入力し、二つの解の標準偏差を計算している:
from filterpy.kalman import UnscentedKalmanFilter as UKF
import numpy as np
sigmas = MerweScaledSigmaPoints(4, alpha=.1, beta=2., kappa=1.)
ukf = UKF(dim_x=4, dim_z=2, fx=f_cv,
hx=h_cv, dt=dt, points=sigmas)
ukf.x = np.array([0., 0., 0., 0.])
ukf.R = np.diag([0.09, 0.09])
ukf.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=1, var=0.02)
ukf.Q[2:4, 2:4] = Q_discrete_white_noise(2, dt=1, var=0.02)
uxs = []
for z in zs:
ukf.predict()
ukf.update(z)
uxs.append(ukf.x.copy())
uxs = np.array(uxs)
plt.plot(uxs[:, 0], uxs[:, 2])
print(f'標準偏差: {np.std(uxs - xs):.3f} m')標準偏差: 0.013 m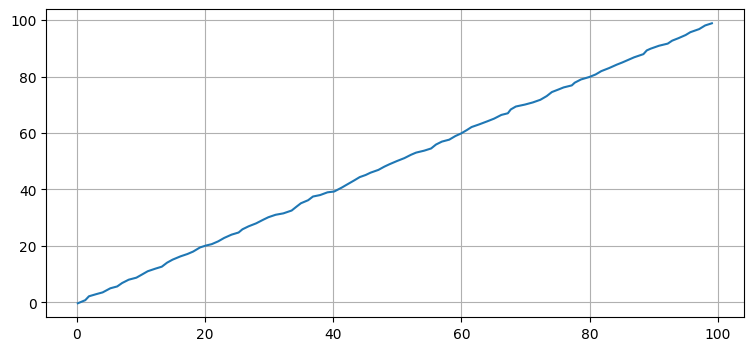
標準偏差は \(0.013~\text{m}\) であり、非常に小さい。
UKF の実装は線形カルマンフィルタの実装と大きくは変わらない。状態遷移関数と観測関数を行列 \(\mathbf{F}\), \(\mathbf{H}\) として実装する代わりに非線形関数 f と h として実装しただけで、それ以外の理論と実装は同一となる。predict 関数と update 関数を実装するコードは異なるものの、フィルタの設計者の視点だと定式化と設計の手順は非常に似ている。
10.8 航空機の追跡
では私たちにとって初めての非線形な問題に挑戦しよう。これからレーダーをセンサーとして航空機を追跡するフィルタを作成する。一つ前の問題とできる限り似せるために、追跡は二次元で行う。一つの次元は地面に沿った距離で、もう一つの次元は航空機の高度とする。各次元は独立だから、こう仮定しても一般性は失われない。
レーダーは電波 (マイクロ波) を周りに発射することで動作する。ビームの軌跡上にある任意の物体は信号の一部をレーダーに反射するので、反射信号がレーダーに戻ってくるまでの時間を計ることで目標までの直距離 (slant distance) が計算できる。直距離はレーダーと物体を直線で結んだ距離を表す。またアンテナの指向性利得(directive gain) からは方位 (仰角) が計算される。仰角 (elevation angle) とは照準線と水平線がなす角度を言う。
航空機の位置 \((x,y)\) は直距離 \(r\) と仰角 \(\varepsilon\) から計算される。この様子を次に示す:
import kf_book.ekf_internal as ekf_internal
ekf_internal.show_radar_chart()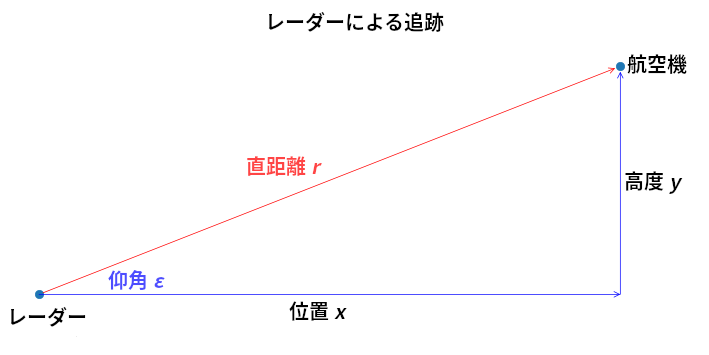
航空機は高度を変えずに (等高度で) 飛行すると仮定する。このとき状態変数は次の三要素のベクトルとなる:
状態遷移関数は線形である:
これを計算する関数を示す:
def f_radar(x, dt):
"""
等高度で飛行する航空機に対する状態遷移関数
状態ベクトルは [x, x 方向の速度, 高度]
"""
F = np.array([[1, dt, 0],
[0, 1, 0],
[0, 0, 1]], dtype=float)
return F @ x続いて観測関数を設計する。線形カルマンフィルタの場合と同じように、観測関数はフィルタの事前分布を観測値に変換する。つまり航空機の位置と速度と高度から仰角と直距離を計算する関数を設計しなければならない。
直距離はピタゴラスの定理で計算できる。以降の式で添え字の \(\text{ac}\) は aircraft (航空機) を表す:
仰角 \(\varepsilon\) はタンジェントが \(y/x\) となる値である:
これを計算する Python 関数を定義しよう。次のコードでは Python の関数が変数を持てる事実を利用し、h_radar にレーダーの位置を格納している。この問題でこうする必要はない (ハードコードしてもいいし、グローバル変数を使ってもいい) ものの、こうすると関数の柔軟性が増す:
def h_radar(x):
dx = x[0] - h_radar.radar_pos[0]
dy = x[2] - h_radar.radar_pos[1]
slant_range = math.sqrt(dx**2 + dy**2)
elevation_angle = math.atan2(dy, dx)
return [slant_range, elevation_angle]
h_radar.radar_pos = (0, 0)ここには私たちが考えてこなかった非線形性がある: 角度は一周すると元に戻る。残差は観測空間に射影した事前分布と観測値の差として計算される。そのため例えば仰角が \(359^\circ\) から \(1^\circ\) になったとき、本当の差は \(2^\circ\) であるにもかかわらず、残差は \(359^\circ - 1^\circ = 358^\circ\) と計算されてしまう。この問題は無香料変換で重み付き和を利用する UKF でさらに悪化する。ここではこういった非線形性が起こる範囲の値を避けるようにレーダーと航空機を配置することで対処する。きちんとした対処方法は後で説明する。
レーダーと航空機をシミュレートする必要もある。ここまで読んできた読者ならシミュレーションなど朝飯前だろうから、説明はせずにコードだけを示す:
from numpy.linalg import norm
from math import atan2
class RadarStation:
def __init__(self, pos, range_std, elev_angle_std):
self.pos = np.asarray(pos)
self.range_std = range_std
self.elev_angle_std = elev_angle_std
def reading_of(self, ac_pos):
""" (直距離, 仰角) を返す。仰角の単位はラジアン。 """
diff = np.subtract(ac_pos, self.pos)
rng = norm(diff)
brg = atan2(diff[1], diff[0])
return rng, brg
def noisy_reading(self, ac_pos):
""" シミュレートされたノイズを持った 直距離と仰角の観測値を返す。 """
rng, brg = self.reading_of(ac_pos)
rng += randn() * self.range_std
brg += randn() * self.elev_angle_std
return rng, brg
class ACSim:
def __init__(self, pos, vel, vel_std):
self.pos = np.asarray(pos, dtype=float)
self.vel = np.asarray(vel, dtype=float)
self.vel_std = vel_std
def update(self, dt):
""" 次の位置を計算して返す。速度をランダムに変動させる。 """
dx = self.vel*dt + (randn() * self.vel_std) * dt
self.pos += dx
return self.pos軍用レーダーは標準偏差 \(1~\text{m}\) 程度の距離精度と標準偏差 \(0.1~\text{mrad}\) 程度の仰角精度を持つ4。ここでは問題を難しくするために中ぐらいの精度を想定し、距離の標準偏差は \(5~\text{m}\)、仰角の標準偏差は \(0.5^\circ\) とする。
\(\mathbf{Q}\) の設計には多少の議論が必要になる。状態は \(\Big[x \ \ \dot x \ \ y\Big]^\mathtt{T}\) だった。最初の二要素は水平方向の距離と速度なので、\(\mathbf{Q}\) の左上部分は Q_discrete_white_noise 関数で計算できる。第三要素の高度は \(x\) と独立だと仮定しているので、\(\mathbf{Q}\) は次のようなブロック行列となる:
航空機は最初レーダーの真上を \(100~\text{m/s}\) で飛行しているとする。また典型的な航空機追跡器の更新頻度は三秒ごと程度だろうから、その値をエポックの周期に採用する:
import math
from kf_book.ukf_internal import plot_radar
dt = 3. # エポックは 3 秒ごと
range_std = 5 # 単位はメートル
elevation_angle_std = math.radians(0.5)
ac_pos = (0., 1000.)
ac_vel = (100., 0.)
radar_pos = (0., 0.)
h_radar.radar_pos = radar_pos
points = MerweScaledSigmaPoints(n=3, alpha=.1, beta=2., kappa=0.)
kf = UKF(3, 2, dt, fx=f_radar, hx=h_radar, points=points)
kf.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
kf.Q[2,2] = 0.1
kf.R = np.diag([range_std**2, elevation_angle_std**2])
kf.x = np.array([0., 90., 1100.])
kf.P = np.diag([300**2, 30**2, 150**2])
np.random.seed(200)
pos = (0, 0)
radar = RadarStation(pos, range_std, elevation_angle_std)
ac = ACSim(ac_pos, (100, 0), 0.02)
time = np.arange(0, 360 + dt, dt)
xs = []
for _ in time:
ac.update(dt)
r = radar.noisy_reading(ac.pos)
kf.predict()
kf.update([r[0], r[1]])
xs.append(kf.x)
plot_radar(xs, time)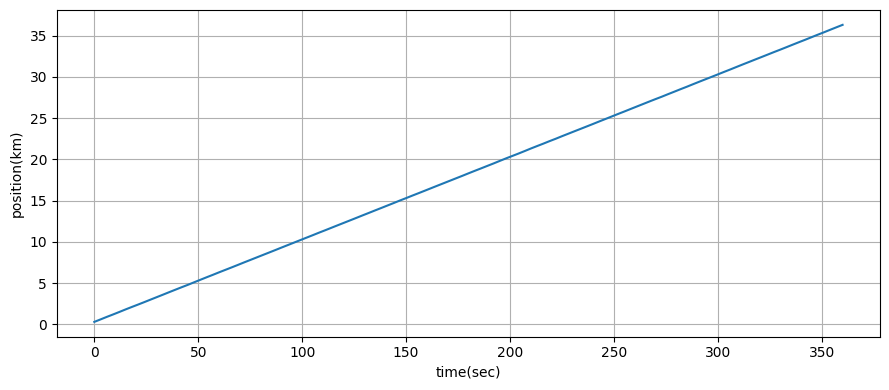
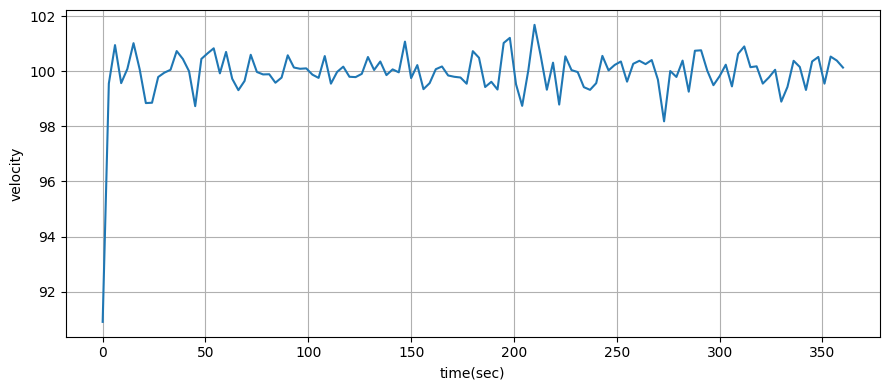
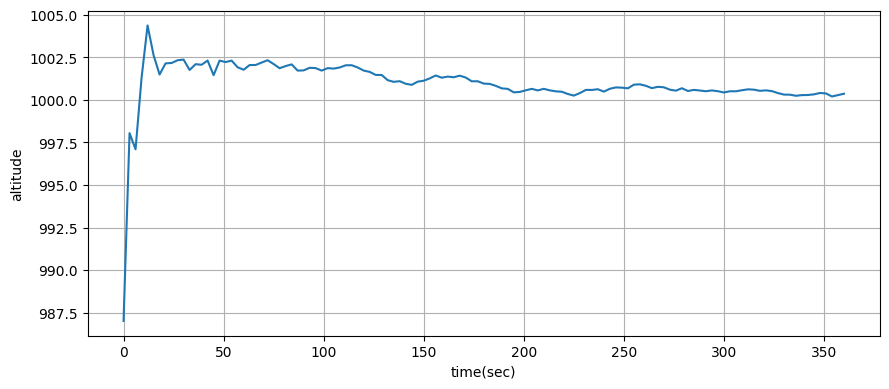
あなたがどう思うかは分からないが、私はこの結果に感動した! 拡張カルマンフィルタの章でも同じ問題に取り組むが、そこでは大量の数式が必要になる。
from kf_book.ukf_internal import plot_altitude
# 航空機の位置をリセットする。
kf.x = np.array([0., 90., 1100.])
kf.P = np.diag([300**2, 30**2, 150**2])
ac = ACSim(ac_pos, (100, 0), 0.02)
np.random.seed(200)
time = np.arange(0, 360 + dt, dt)
xs, ys = [], []
for t in time:
if t >= 60:
ac.vel[1] = 300/60 # 300 メートル/分 の上昇
ac.update(dt)
r = radar.noisy_reading(ac.pos)
ys.append(ac.pos[1])
kf.predict()
kf.update([r[0], r[1]])
xs.append(kf.x)
plot_altitude(xs, time, ys)
print(f'実際の高度 : {ac.pos[1]:.1f}')
print(f'UKF が推定した高度: {xs[-1][2]:.1f}')実際の高度 : 2515.6
UKF が推定した高度: 1042.1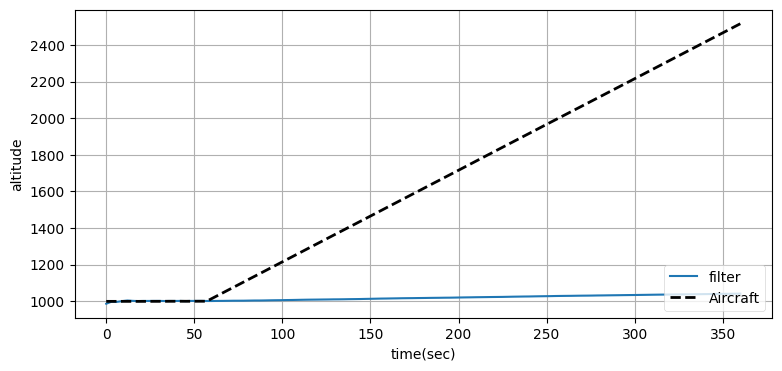
フィルタは高度の変化を追跡できていない。どう設計を変更すべきだろうか?
「高度の上昇率を状態に加える」と答えてくれたことを願う。つまりこういうことだ:
こうするとき状態遷移関数にも変更が必要になる。ただ線形であることに変わりはない:
観測関数は同じで、\(\mathbf{Q}\) には \(\mathbf{x}\) の次元の変化を反映させる:
def f_cv_radar(x, dt):
""" 等速度で飛行する航空機に対する状態遷移関数 """
F = np.array([[1, dt, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, dt],
[0, 0, 0, 1]], dtype=float)
return F @ x
def cv_UKF(fx, hx, R_std):
points = MerweScaledSigmaPoints(n=4, alpha=.1, beta=2., kappa=-1.)
kf = UKF(4, len(R_std), dt, fx=fx, hx=hx, points=points)
kf.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
kf.Q[2:4, 2:4] = Q_discrete_white_noise(2, dt=dt, var=0.1)
kf.R = np.diag(R_std)
kf.R = kf.R @ kf.R # 二乗して分散にする。
kf.x = np.array([0., 90., 1100., 0.])
kf.P = np.diag([300**2, 3**2, 150**2, 3**2])
return kfnp.random.seed(200)
ac = ACSim(ac_pos, (100, 0), 0.02)
kf_cv = cv_UKF(f_cv_radar, h_radar, R_std=[range_std, elevation_angle_std])
time = np.arange(0, 360 + dt, dt)
xs, ys = [], []
for t in time:
if t >= 60:
ac.vel[1] = 300/60 # 300 メートル/分 の上昇
ac.update(dt)
r = radar.noisy_reading(ac.pos)
ys.append(ac.pos[1])
kf_cv.predict()
kf_cv.update([r[0], r[1]])
xs.append(kf_cv.x)
plot_altitude(xs, time, ys)
print(f'実際の高度 : {ac.pos[1]:.1f}')
print(f'UKF が推定した高度: {xs[-1][2]:.1f}')実際の高度 : 2515.6
UKF が推定した高度: 2500.1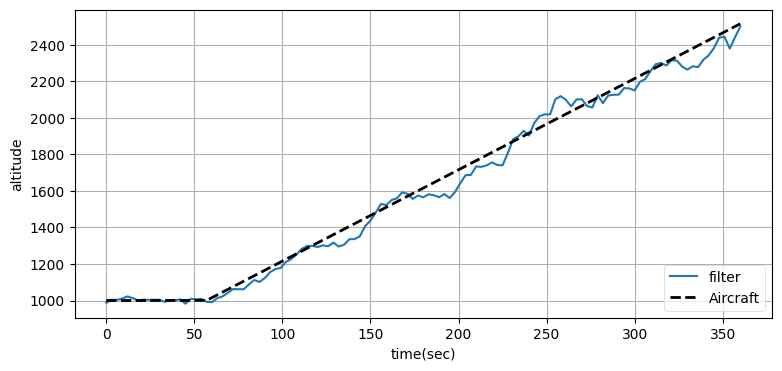
高度の推定値には大きなノイズが加わっているものの、高度の追跡は行えている。
センサー統合
次はセンサー統合の例を考えよう。標準偏差 \(2~\text{m/s}\) の精度で速度を観測するドップラーシステムの一種が利用できるとする。ドップラーシステムの「一種」としたのは、レーダーと同様に本当のドップラーシステムに対する正確なフィルタの設計方法を教えるつもりはないからだ。完全な実装は S/N 比や大気による影響、システムの幾何学的構成などを考慮しなければならない。
前節の例で使ったレーダーの精度だと速度の推定値は実際の値から約 \(1~\text{m/s}\) 離れていた。センサー統合の効果を分かりやすくするため、この例では精度を落とすことにする。観測される距離に含まれる誤差の標準偏差を \(500~\text{m}\) として、推定された速度の標準偏差を計算しよう。そのとき最初フィルタが収束するまでのいくつかの観測値は無視する。
ドップラーシステムを使わないときの標準偏差はこうなる:
range_std = 500.
elevation_angle_std = math.degrees(0.5)
np.random.seed(200)
pos = (0, 0)
radar = RadarStation(pos, range_std, elevation_angle_std)
ac = ACSim(ac_pos, (100, 0), 0.02)
kf_sf = cv_UKF(f_cv_radar, h_radar, R_std=[range_std, elevation_angle_std])
time = np.arange(0, 360 + dt, dt)
xs = []
for _ in time:
ac.update(dt)
r = radar.noisy_reading(ac.pos)
kf_sf.predict()
kf_sf.update([r[0], r[1]])
xs.append(kf_sf.x)
xs = np.asarray(xs)
plot_radar(xs, time, plot_x=False, plot_vel=True, plot_alt=False)
print(f'速度の標準偏差: {np.std(xs[10:, 1]):.1f} m/s')速度の標準偏差: 3.4 m/s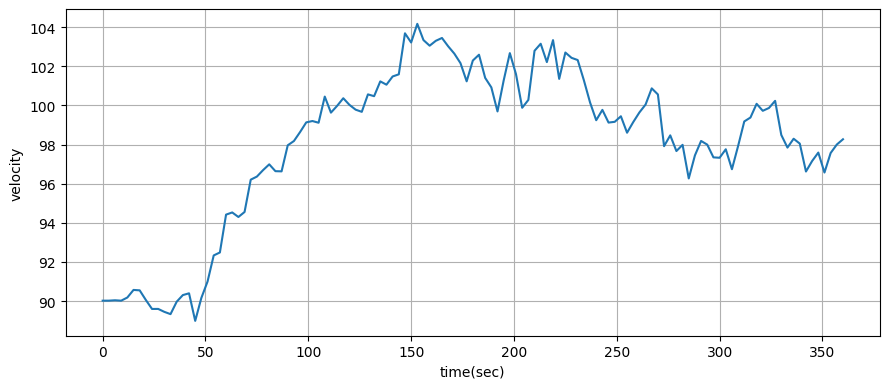
ドップラーシステムからの情報を取り入れるには \(x\) 方向の速度と \(y\) 方向の速度を観測値として含める必要がある。ACSim クラスは速度を vel 属性に格納する。カルマンフィルタの更新を行うには update 関数に直距離、仰角、\(x\) 方向の速度、\(y\) 方向の速度からなるリストを渡すだけで済む:
観測値が四要素になったので、観測関数も四つの値を返すよう変更しなければならない。直距離と仰角は前と同じように計算され、\(x\) 方向と \(y\) 方向の速度は状態の推定値から直接取得できるので計算する必要はない:
def h_vel(x):
dx = x[0] - h_vel.radar_pos[0]
dz = x[2] - h_vel.radar_pos[1]
slant_range = math.sqrt(dx**2 + dz**2)
elevation_angle = math.atan2(dz, dx)
return slant_range, elevation_angle, x[1], x[3]以上でフィルタを実装できる:
h_radar.radar_pos = (0, 0)
h_vel.radar_pos = (0, 0)
range_std = 500.
elevation_angle_std = math.degrees(0.5)
vel_std = 2.
np.random.seed(200)
ac = ACSim(ac_pos, (100, 0), 0.02)
radar = RadarStation((0, 0), range_std, elevation_angle_std)
kf_sf2 = cv_UKF(f_cv_radar, h_vel,
R_std=[range_std, elevation_angle_std, vel_std, vel_std])
time = np.arange(0, 360 + dt, dt)
xs = []
for t in time:
ac.update(dt)
r = radar.noisy_reading(ac.pos)
# ドップラーレーダーによる速度の観測をシミュレートする。
vx = ac.vel[0] + randn()*vel_std
vz = ac.vel[1] + randn()*vel_std
kf_sf2.predict()
kf_sf2.update([r[0], r[1], vx, vz])
xs.append(kf_sf2.x)
xs = np.asarray(xs)
plot_radar(xs, time, plot_x=False, plot_vel=True, plot_alt=False)
print(f'速度の標準偏差: {np.std(xs[10:,1]):.1f} m/s')速度の標準偏差: 0.9 m/s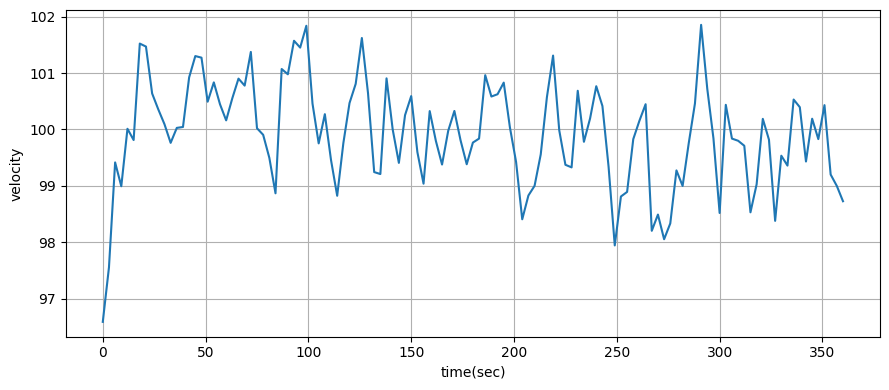
速度を観測するドップラーシステムによって速度の推定値の標準偏差が \(3.4~\text{m/s}\) から \(0.9~\text{m/s}\) に減少したのが分かる。また速度のグラフからは収束が速いのも分かる。
センサー統合は大きなトピックであり、ここで示したのはかなり単純な実装である。典型的なナビゲーションの問題ではセンサーが補完的な情報を提供する。例えば GPS では正確な位置情報が一秒に一度更新されるものの速度は不正確に推定され、慣性装置では非常に正確な速度が \(50~\text{Hz}\) で観測されるものの位置は非常に不正確に推定されるかもしれない。この二つのセンサーは強みと弱みを互いに補完し合う。高い頻度で更新される慣性装置からの速度の観測値と正確で更新が遅い GPS からの位置の推定値を合成する補完フィルタ (complementary filter) という考え方がここから生まれる。高頻度の速度の推定値を GPS の更新と組み合わせると、高頻度かつ正確な位置の推定値が得られる。
複数の位置センサー
前節で示したセンサー統合の問題はおもちゃのような例だった。もう少しおもちゃでない問題に挑戦してみよう。GPS が開発される前、船や航空機は VOR, LORAN, TACAN, DME といった距離・方位の観測システムを使ってナビゲーションを行っていた。こういったシステムでは地上に設置されたビーコンが電波を発射し、船舶や航空機に搭載されたセンサー (受信機) が受信した電波から距離や方位の情報を取り出す。例えば航空機は二つの VOR 受信機を持つかもしれない。このときパイロットが二つの受信機をそれぞれ異なる VOR 基地に選局すると、それぞれの受信機はラジアル (radial)──地上にある VOR 基地から見た自身の方位──を表示する。その後パイロットが地図を使って二つのラジアルの交点を求めることで航空機の位置が判明する。
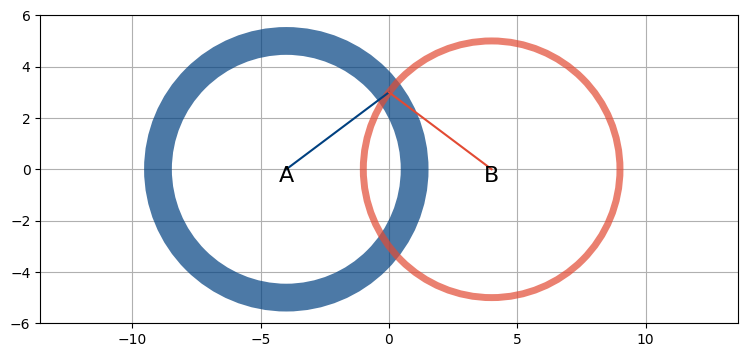
これは手動のアプローチであり、精度も低い。カルマンフィルタを使うと格段に正確な位置の推定値を得られるだろう。二つのセンサーがあり、次の図に示すようにそれぞれのセンサーは航空機の方位だけを報告すると仮定する (図中の輪の幅はセンサーノイズを表す)。このとき航空機は高い確率で二つの輪の重なる部分を飛行している。
センサーから見た航空機の方位 (bearing) は次のように計算できる:
def bearing(sensor, target_pos):
return math.atan2(target_pos[1] - sensor[1],
target_pos[0] - sensor[0])フィルタは二つのセンサーからの観測値をベクトルで受け取る。これは次のようにシミュレートできる。measurement 関数は任意の反復可能コンテナを受け取ることになるので、効率のため Python リストを返している:
def measurement(A_pos, B_pos, pos):
angle_a = bearing(A_pos, pos)
angle_b = bearing(B_pos, pos)
return [angle_a, angle_b]航空機の運動には定常速度モデルを仮定する。次のコードでは趣向を変えて、新しい位置を求めるときに行列とベクトルの積ではなく明示的な計算を行っている:
def fx_VOR(x, dt):
x[0] += x[1] * dt
x[2] += x[3] * dt
return x続いて観測関数を実装する。事前分布を両方のレーダーの観測値からなる配列に変換するのが観測関数である。グローバル変数は好きでないのだが、\(h\) の実装でデータを共有する手法を示すために、レーダーの位置は sa_pos と sb_pos というグローバル変数に格納する:
sa_pos = [-400, 0]
sb_pos = [400, 0]
def hx_VOR(x):
pos = (x[0], x[2])
return measurement(sa_pos, sb_pos, pos)フィルタの構築、フィルタリングの実行、結果のプロットを行うボイラープレートを次に示す:
def moving_target_filter(pos, std_noise, Q, dt=0.1, kappa=0.0):
points = MerweScaledSigmaPoints(n=4, alpha=.1, beta=2., kappa=kappa)
f = UKF(dim_x=4, dim_z=2, dt=dt,
hx=hx_VOR, fx=fx_VOR, points=points)
f.x = np.array([pos[0], 1., pos[1], 1.])
q = Q_discrete_white_noise(2, dt, Q)
f.Q[0:2, 0:2] = q
f.Q[2:4, 2:4] = q
f.R *= std_noise**2
f.P *= 1000
return f
def plot_straight_line_target(f, std_noise):
xs, txs = [], []
for i in range(300):
target_pos[0] += 1 + randn()*0.0001
target_pos[1] += 1 + randn()*0.0001
txs.append((target_pos[0], target_pos[1]))
z = measurement(sa_pos, sb_pos, target_pos)
z[0] += randn() * std_noise
z[1] += randn() * std_noise
f.predict()
f.update(z)
xs.append(f.x)
xs = np.asarray(xs)
txs = np.asarray(txs)
plt.plot(xs[:, 0], xs[:, 2])
plt.plot(txs[:, 0], txs[:, 1], ls='--', lw=2, c='k')
plt.show()
np.random.seed(123)
target_pos = [100, 200]
std_noise = math.radians(0.5)
f = moving_target_filter(target_pos, std_noise, Q=1.0)
plot_straight_line_target(f, std_noise)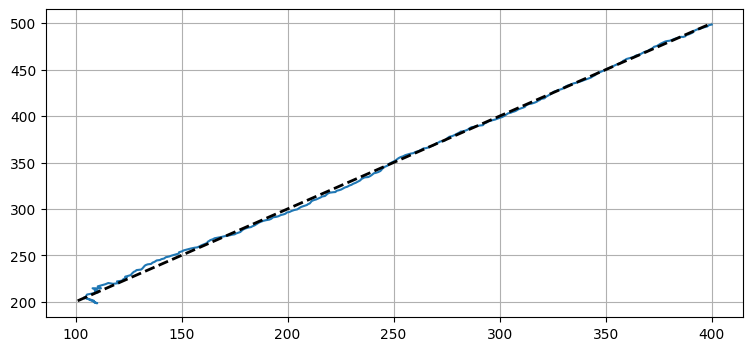
とても良いように思える。最初は大きな誤差があるものの、フィルタはすぐに落ち着いて優れた推定値を出力している。
角度の非線形性の問題をもう一度考えよう。航空機を二つのセンサーの中央 \((0,0)\) に配置する。このとき左のセンサーから見た航空機の方位が \(0\) に近くなるので5、残差の計算で非線形性が発生する。角度が \(0\) より小さくなると観測関数は \(2\pi\) に近い大きな値を返すので、予測と観測値の残差が \(0\) ではなく \(2\pi\) に近い非常に大きな値となる。このため次の図が示すように、フィルタは正確に振る舞えなくなる:
target_pos = [0, 0]
f = moving_target_filter(target_pos, std_noise, Q=1.0)
plot_straight_line_target(f, std_noise)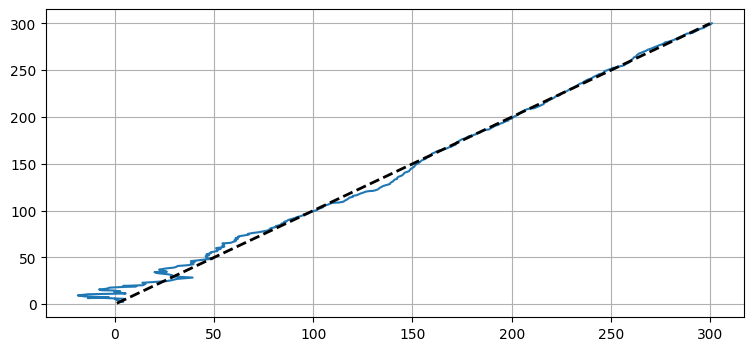
この性能は受け入れられない。こういった非線形な振る舞いに対処するために、FilterPy の UKF コードには残差を計算する関数を指定できる機能がある。この章の最後の例で使い方を示す。
10.9 センサーの誤差と幾何学的関係の影響
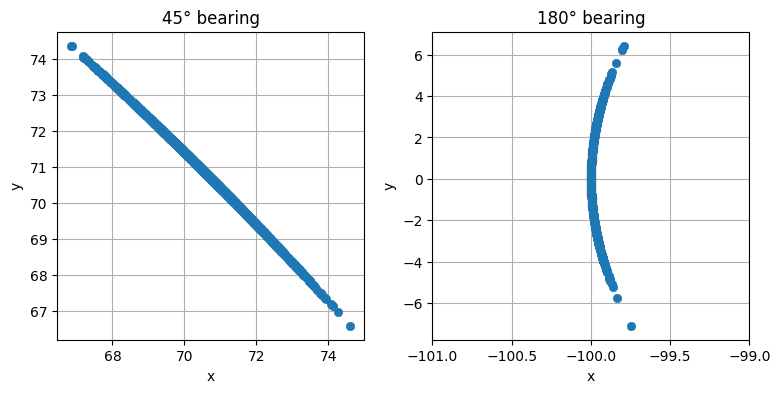
センサーと追跡している物体の幾何学的関係によっては物理的に厄介な状況になり、フィルタでの扱いが非常に困難になる場合がある。例えば二つの VOR 基地からのラジアルがほぼ平行になると、小さな角度の誤差が大きな距離の誤差につながる。さらに悪いことに、この誤差の振る舞いは非線形である──\(x\) 方向の誤差と \(y\) 方向の誤差は実際の方位によって変化する。次のグラフは二つの異なる方位において誤差の標準偏差が \(1^\circ\) のときどのような点が得られるかを示している:
10.10 練習問題: フィルタの性能の説明
方位に小さな誤差があるだけでも位置の誤差が非常に大きくなることを見た。では、本章の物体追跡問題で UKF が比較的良い性能を収めたのはなぜかを説明せよ。センサーが一つの場合とセンサーが二つの場合の両方について答えよ。
解答
これを理解するのは非常に重要である。よく考えてから以降の解答を読んでほしい。答えられない場合は多変量カルマンフィルタの章を読み直すといいかもしれない。
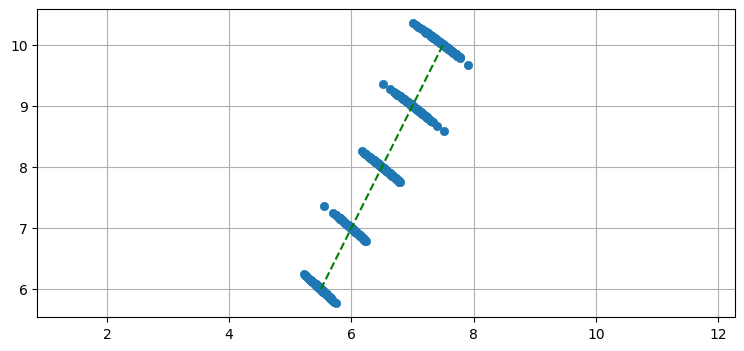
本章で示した例の成功に寄与した要因はいくつかある。まずセンサーが一つだけの場合を考えよう。単一の観測値が表す位置の可能性は非常に大きい。ただ追跡している物体は移動しており、UKF はその運動を考慮する。移動する追跡対象から取得されたいくつかの観測値を並べてプロットしてみよう:
個々の観測値に含まれる位置の誤差はとても大きい。しかし、連続した観測値からは明確な傾向が読み取れる──追跡対象は明らかに右上に向かって移動している。カルマンフィルタがカルマンゲインを計算するときは、観測関数を通じて誤差の分布が取り込まれる。この例では観測値の誤差を示す線はほぼ斜め右下 \(45^\circ\) の直線であり、それと直交する方向には誤差がほとんど存在しないことがカルマンフィルタに伝わる。
このグラフでは位置の更新ごとに 100 個の観測値をプロットしているので誤差の様子が分かりやすく、航空機の移動は明らかである。しかしカルマンフィルタは更新ごとに観測値を一つしか受け取らないので、フィルタは緑の破線ほどには優れた結果を生成することはできない。
次は距離の情報が存在せず方位だけがセンサーから報告される事実を考えよう。初期推定値がセンサーから \(1000~\text{km}\) 離れた場所 (実際の距離は \(7.07~\text{km}\)) で、\(\mathbf{P}\) の初期値は非常に小さいと仮定する。これだけ距離があると、\(1^\circ\) の方位の誤差は \(17.5~\text{km}\) の位置の誤差に変換される。KF は位置の推定値を誤って正しいと強く信じており、さらに距離の情報は観測値から得られないので、実際の追跡対象の位置を見つけることはできないだろう。
続いて二つ目のセンサーを追加したときに何が変わるかを考える。次の二つのプロットを見ると、センサーの配置を変えたときの影響が分かる。二つのセンサーは青い正方形と黒い三角形で表され、センサーによる誤差の分布を同じ色の点で表している。ノイズが混じった二つの方位観測値から計算される \((x,y)\) 座標が赤いドットとしてプロットされている (見やすいよう \(x\) 軸方向に一定量だけずらしてある)。
最初のプロットでは二つのセンサーが対象をほぼ直交して捉えており、二つの観測値の誤差の分布は素敵な X の形を描いている。また追跡対象の物体が移動すると計算される位置の \(x\) 方向と \(y\) 方向の誤差も変化することが赤いドットから分かる──物体が右上に移動すると相対的に右側のセンサーに近づくので、赤いドットの集まりは楕円になる。
二つ目のプロットでは航空機が下のセンサーに近いところからスタートし、二つ目のセンサーの前を横切る。二つの観測値の誤差の分布は全く直交しておらず、そのため計算される位置の誤差を示す分布は大きく広がる。
10.11 UKF の実装
FilterPy は UKF を実装する。しかし数式をコードに変換する方法を学んでおくのが教育上は望ましいだろう。UKF は非常に簡単に実装できる。
最初にシグマ点を使って平均と共分散行列を計算するコードを書こう。シグマ点と重みは次のように行列とベクトルを使って格納する:
簡単なものを表すために添え字がやたらと使われている。二次元 (\(n=2\)) の問題に対するシグマ点と重みの例を示す:
points = MerweScaledSigmaPoints(n=2, alpha=.1, beta=2., kappa=1.)
points.sigma_points(x=[0.,0], P=[[1.,.1],[.1, 1]])array([[ 0. , 0. ],
[ 0.173, 0.017],
[ 0. , 0.172],
[-0.173, -0.017],
[ 0. , -0.172]])第一行が入力の分布の平均に対応するシグマ点を表す。この例で第一行は \((0,0)\) であり、平均 \((0,0)\) に等しい。二番目のシグマ点は \((0.173,0.017)\) の位置にあり、以下同様となる。\(2n+1=5\) 個の行があり、各行が一つのシグマ点を表す。\(n=3\) のときは三列七行の行列が返る。
シグマ点の格納の仕方 (行ベクトルと列ベクトルのどちらをシグマ点にするか) は恣意的に決められる。行ベクトルをシグマ点にする方式を私が選択したのは、i 番目のシグマ点を sigmas[:, i] ではなく sigmas[i] と参照できるのでコードが簡単になるためだ。
重み
重みは NumPy で簡単に計算できる。Van der Merwe の拡大シグマ点アルゴリズムは次のように重みを計算したことを思い出そう:
これは次のコードで実装できる:
lambda_ = alpha**2 * (n + kappa) - n
Wc = np.full(2*n + 1, 1. / (2*(n + lambda_))
Wm = np.full(2*n + 1, 1. / (2*(n + lambda_))
Wc[0] = lambda_ / (n + lambda_) + (1. - alpha**2 + beta)
Wm[0] = lambda_ / (n + lambda_)
lambda ではなく lambda_ としたのは、lambda が Python で予約されているためだ。最後にアンダースコアを付けるのが Python らしい回避策とされる。
シグマ点
シグマ点を求める式を示す:
\(\left[\sqrt{(n+\lambda)\Sigma} \right]_i\) の意味が理解できれば Python コードにするのは難しくない。
\(\Sigma\) が行列なので \(\sqrt{(n+\lambda)\Sigma}\) も行列である。\(\left[\sqrt{(n+\lambda)\Sigma}\right]_i\) の添え字 \(i\) は行列の \(i\) 番目の行ベクトルを選択する。では行列の平方根とは何だろうか? 一意な定義が存在するわけではない。行列 \(\Sigma\) の平方根の定義の一つは、自身を乗じたときに \(\Sigma\) となる行列 \(S\) を平方根とするものだ。つまり \(\Sigma = \mathbf{S}\mathbf{S}\) なら \(\mathbf{S} = \sqrt{\Sigma}\) となる。
計算が簡単になる数値的性質を持った別の定義をここでは採用する: 行列 \(\Sigma\) の平方根は、自身の転置と乗じたときに \(\Sigma\) となる行列 \(\mathbf{S}\) と定義される:
この定義を選択するのは、\(\mathbf{S}\) をコレスキー分解 (Cholesky decomposition) で計算できるためだ。コレスキー分解は正定値エルミート行列を三角行列とその共役転置の積に分解する。ここで分解後の行列は上三角または下三角にできる:
アスタリスクは共役転置を表す。今は実数の行列しか考えていないから、次を得る:
今考えている共分散行列 \(\mathbf{P}\) は正定値エルミートという性質を持つので、\(\mathbf{P}\) の平方根は \(\mathbf S = \text{cholesky}(\mathbf P)\) で計算できる。
SciPy は scipy.linalg モジュールに cholesky 関数を提供する。あなたが選んだ言語が Fortarn, C, C++ なら、LAPACK といったライブラリがコレスキー分解のルーチンを提供する。MATLAB では chol 関数がある。
デフォルトで scipy.linalg.cholesky は上三角行列を返すので、FilterPy のコードは上三角行列を使うように書いてある。このため結果には行でアクセスし、ゼロ要素が含まれない完全な行が最初のシグマ点 (平均) に対応する。この事実は平方根の実装を独自に提供するとき注意が必要になる。文献によってはシグマ点が列ベクトルとして格納されることを仮定して UKF アルゴリズムが記述される場合もある。コレスキー分解が下三角行列を返すとき、あるいは列と行が問題にならない対称行列を平方根として計算する異なるアルゴリズムを使うときはそれでも問題はない。
import scipy
a = np.array([[2., .1], [.1, 3]])
s = scipy.linalg.cholesky(a)
print("コレスキー分解:")
print(s)
print("\nコレスキー分解の二乗:")
print(s @ s.T)コレスキー分解:
[[1.414 0.071]
[0. 1.731]]
コレスキー分解の二乗:
[[2.005 0.122]
[0.122 2.995]]というわけで、シグマ点の計算は次のコードで実装できる:
sigmas = np.zeros((2*n+1, n))
U = scipy.linalg.cholesky((n+lambda_)*P) # 平方根
sigmas[0] = X
for k in range (n):
sigmas[k+1] = X + U[k]
sigmas[n+k+1] = X - U[k]
無香料変換
次は無香料変換を実装しよう。無香料変換の式を思い出せば
だった。平均は次のように計算できる:
x = np.dot(Wm, sigmas)
NumPy のヘビーユーザーでなければ何をしているのか分からないかもしれない。NumPy はただ線形代数演算を可能にするだけのライブラリではない: Python では不可能な速度を達成するために NumPy の内部は C と Fortran で書かれており、そのコードを使うと典型的には二十倍から百倍の速度向上が得られる。この速度向上を得るには for ループを避け NumPy の関数を使って計算を行わなければならない。そのため上のコードでは積の和の計算で for ループではなく numpy.dot(x, y) を使っている。二つのベクトルのドット積は要素ごとの積の和であり、一次元配列と二次元配列を渡すと内積の和が計算される:
a = np.array([10, 100])
b = np.array([[1, 2, 3],
[4, 5, 6]])
np.dot(a, b)array([410, 520, 630])後は \(\mathbf P = \sum_i w_i{(\mathcal{X}_i-\mu)(\mathcal{X}_i-\mu)^\mathsf{T}} + \mathbf Q\) が残るだけとなった:
kmax, n = sigmas.shape
P = zeros((n, n))
for k in range(kmax):
y = sigmas[k] - x
P += Wc[k] * np.outer(y, y)
P += Q
ここでも新しい NumPy の機能を使っている。状態変数 x と k 番目のシグマ点 sigmas[k] はどちらも一次元配列なので、その差 sigmas[k]-x も一次元配列である。ただ NumPy は一次元配列の転置を計算せず、[1,2,3] の転置を取ると [1,2,3] のままとなる。そのため、一次元配列 \(\mathbf{y}\) に対して \(\mathbf{yy}^\mathsf T\) を計算するには np.outer(y,y) を使わなければならない。なお次のように実装することもできる:
y = (sigmas[k] - x).reshape(kmax, 1) # 二次元配列に変換する。
P += Wc[K] * np.dot(y, y.T)
ただ、このコードは遅い上に NumPy らしくないので使わない。
予測ステップ
予測ステップではまず、これまでに実装したコードを使ってシグマ点と重みを生成し、それぞれのシグマ点を関数 \(f\) に渡す。つまり次の数式を計算する:
そうしたら無香料変換で平均と共分散行列を計算する。次のコードではフィルタを表すオブジェクト self のメソッド self.fx が予測ステップであり、フィルタが必要とする様々な行列やベクトルは self の属性として格納されると仮定している:
def predict(self, sigma_points_fn):
"""
UKF の予測ステップを実行する。
この関数が返ると、self.xp と self.Pp にそれぞれ予測された
状態と共分散行列が格納される。p は prediction (予測) を意味する。
"""
# 与えられた平均と共分散行列からシグマ点を計算する。
sigmas = sigma_points_fn(self.x, self.Pp)
for i in range(self._num_sigmas):
self.sigmas_f[i] = self.fx(sigmas[i], self._dt)
self.xp, self.Pp = unscented_transform(self.sigmas_f, self.Wm, self.Wc, self.Q)
更新ステップ
更新ステップでは、まず関数 h(x) でシグマ点が観測空間に移される:
その後 \(\mathcal{Z}\) の平均と共分散行列が無香料変換で計算される。続いて残差とカルマンゲインの計算が行われる。\(\mathcal{Y}\) と \(\mathcal{Z}\) の相互共分散行列は次の式で定義される:
最後に、新しい状態の推定値が残差とカルマンゲインから計算される:
新しい共分散行列は次のように求められる:
以上の処理の実装を示す。予測ステップはフィルタを表すオブジェクト self のメソッドであり、必要な行列は self の属性に格納されると仮定している:
def update(self, z):
# 可読性のため名前を付け替える。
sigmas_f = self.sigmas_f
sigmas_h = self.sigmas_h
# シグマ点を観測空間に移す。
for i in range(self._num_sigmas):
sigmas_h[i] = self.hx(sigmas_f[i])
# 平均と共分散行列を無香料変換で計算する。
zp, Pz = unscented_transform(sigmas_h, self.Wm, self.Wc, self.R)
# 状態と観測値の相互共分散行列を計算する。
Pxz = np.zeros((self._dim_x, self._dim_z))
for i in range(self._num_sigmas):
Pxz += self.Wc[i] * np.outer(sigmas_f[i] - self.xp,
sigmas_h[i] - zp)
K = np.dot(Pxz, inv(Pz)) # カルマンゲイン
self.x = self.xp + np.dot(K, z - zp)
self.P = self.Pp - np.dot(K, Pz).dot(K.T)
FilterPy の実装
FilterPy はコードをいくらか一般化している。シグマ点を計算するアルゴリズムを指定でき、状態変数の残差を計算する方法を指定でき (例えば角度を単純に引くことはできない)、行列平方根の関数を指定することもできる。他にも機能があるので、ヘルプ (https://filterpy.readthedocs.org/#unscented-kalman-filter) から確認してほしい。
10.12 バッチ処理
カルマンフィルタは再帰的であり、推定値は現在の観測値と事前推定値から計算される。しかし事前に収集されたひとまとまりのデータに対してフィルタリングを行いたいという場合もよくある。その場合はフィルタをバッチモードで実行できる。バッチモードでは全ての観測値が一度にまとめて処理される。
バッチモードの処理を行うには、まず観測値を配列またはリストに収集する:
zs = read_altitude_from_csv()
それから batch_filter メソッドを呼ぶ:
Xs, Ps = ukf.batch_filter(zs)
この関数は観測値からなるリストまたは配列を受け取り、フィルタリングを行い、完全なデータセットに対する状態の推定値 Xs と対応する共分散行列 Px を返す。
前に考えたレーダー追跡の問題に対してバッチ処理を行った例を示す:
dt = 12. # エポックは 12 秒ごと
range_std = 5 # メートル
bearing_std = math.radians(0.5)
ac_pos = (0., 1000.)
ac_vel = (100., 0.)
radar_pos = (0., 0.)
h_radar.radar_pos = radar_pos
points = MerweScaledSigmaPoints(n=3, alpha=.1, beta=2., kappa=0.)
kf = UKF(3, 2, dt, fx=f_radar, hx=h_radar, points=points)
kf.Q[0:2 ,0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
kf.Q[2, 2] = 0.1
kf.R = np.diag([range_std**2, bearing_std**2])
kf.x = np.array([0., 90., 1100.])
kf.P = np.diag([300**2, 30**2, 150**2])
radar = RadarStation((0, 0), range_std, bearing_std)
ac = ACSim(ac_pos, (100, 0), 0.02)
np.random.seed(200)
t = np.arange(0, 360 + dt, dt)
n = len(t)
zs = []
for i in range(len(t)):
ac.update(dt)
r = radar.noisy_reading(ac.pos)
zs.append([r[0], r[1]])
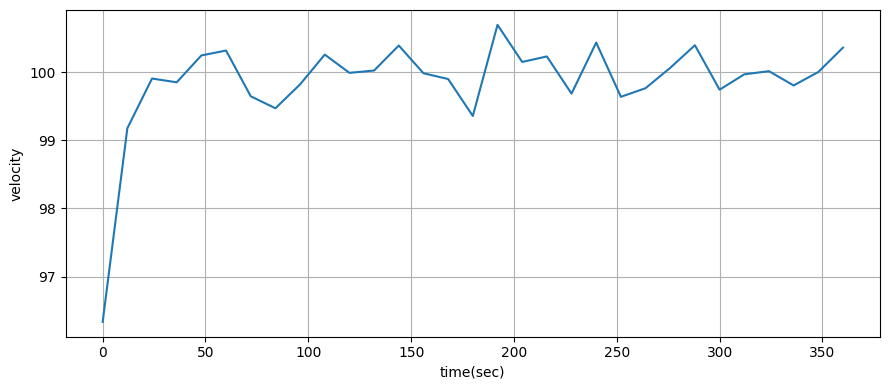
xs, covs = kf.batch_filter(zs)
ukf_internal.plot_radar(xs, t)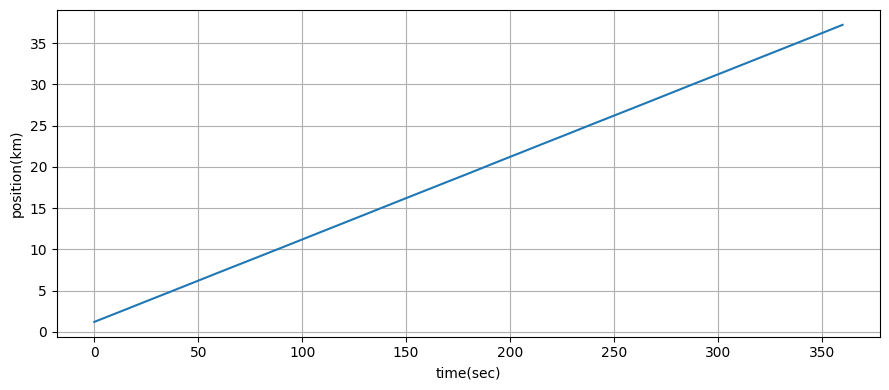
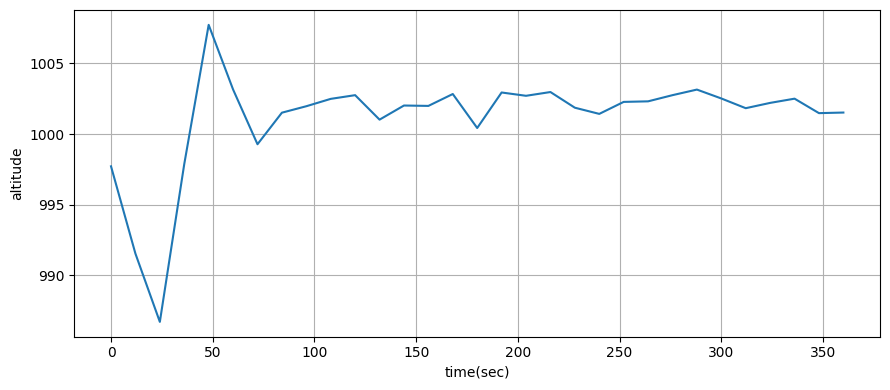
10.13 結果の平滑化
車を追跡しているとしよう。ノイズの含まれる観測値は車が左に旋回し始めたことを示しており、それに対して状態関数は車が真っ直ぐに移動すると予測したとする。カルマンフィルタは観測値のノイズがたまたま大きくなったのか車が本当に旋回したのかが分からないので、状態の推定値を多少ノイズの含まれる観測値に向けなければならない。
もし収集したデータに対する後処理としてフィルタを実行しているなら、問題のある観測値より後ろの観測値を見ることで旋回が本当に起こったかどうかを判定できる。例えば後ろの観測値が全て左へ旋回しているなら、ノイズではなく実際の旋回によって観測値が旋回しているように見えたのだろうと確信できる。
ここで数式やアルゴリズムを考えることはせず、FilterPy にあるアルゴリズムを呼び出す方法を示すだけとする。FilterPy が実装するアルゴリズムは RTS スムーザー (RTS smoother) と呼ばれる。この名前は考案者 Rauch, Tung, Striebel の頭文字を取ったものだ。
RTS スムーザーは UnscentedKalmanFilter クラスの rts_smoother メソッドで呼び出せる。使い方は非常に簡単で、batch_filter メソッドが返す平均と共分散行列の配列を渡せば、平滑になった平均と共分散行列、そしてカルマンゲインからなる配列が得られる:
Ms, P, K = kf.rts_smoother(xs, covs)
ukf_internal.plot_rts_output(xs, Ms, t)位置の差 (単位はメートル):
[-1.4166 -0.2815 1.2679 -1.2405 -2.1863]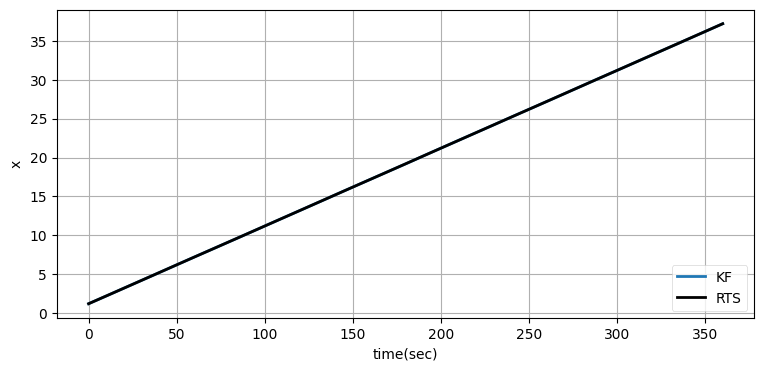
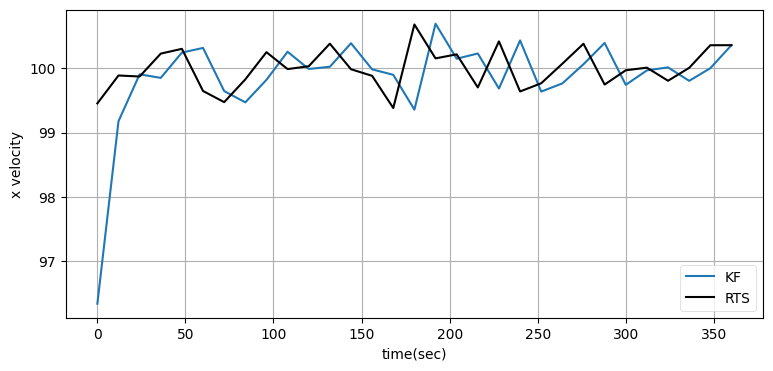
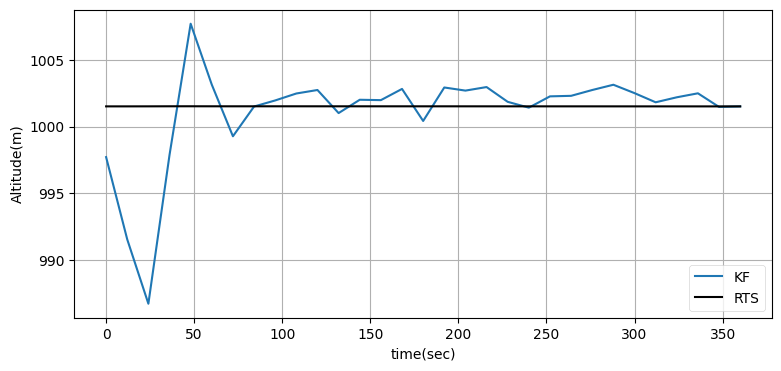
グラフを見ると位置の改善は小さいものの、速度はそれなりに改善され、高度は大きく改善されている。位置の差は分かりにくいので、最後の五つの点に対して UKF の出力と RTS スムーザーの出力の差を出力している。データを全て受け取ってから処理を始められる場合は必ず RTS スムーザーを使うことが推奨される。
10.14 シグマ点に対するパラメータの選択
\(\alpha\), \(\beta\), \(\kappa\) の選択方法に関する文献はあまり存在しないように思える。一番詳しいのは Van der Merwe の博士論文だが、それも詳細に説明されているとは言えない。これらのパラメータがどのような意味を持つかを考えよう。
Van der Merwe はガウシアンの問題に対して \(\beta=2\) と \(\kappa=3-n\) を推奨している。そこで \(\beta\) と \(\kappa\) に対してはこの値を採用し、\(\alpha\) の値を変化させることを最初に考える。配列のサイズを小さくして、行列の平方根を考えずに済むよう \(n=1\) とする。
from kf_book.ukf_internal import print_sigmas
print_sigmas(mean=0, cov=3, alpha=1)シグマ点: [ 0. 3. -3.]
平均に対する重み: [0.6667 0.1667 0.1667]
共分散行列に対する重み: [2.6667 0.1667 0.1667]
ラムダ: 2
共分散行列に対する重みの和: 2.9999999999999996何が起きているのだろうか? 平均 \(0\) の分布に対して Van der Merwe のアルゴリズムが \(0\), \(3\), \(-3\) を選んだのが分かるが、なぜ? シグマ点を計算する式を思い出そう:
\(n=1\) のときシグマ点は全てスカラーとなり、行列平方根の計算は必要なくなる。よって今の例でこの式は
となる。この式からは \(\alpha\) を大きくするとシグマ点が散らばることも分かる。非常に大きな値にしてみよう:
print_sigmas(mean=0, cov=3, alpha=200)シグマ点: [ 0. 600. -600.]
平均に対する重み: [1. 0. 0.]
共分散行列に対する重み: [-39996. 0. 0.]
ラムダ: 119999
共分散行列に対する重みの和: -39996.00000000001シグマ点が \(100\sigma\) より遠くに散らばるのが確認できる。このとき平均からかけ離れた点がシグマ点になるので、データがガウス分布に従うなら非線形な問題で優れた結果が得られる可能性は低い。しかしデータがガウス分布に従っておらず、非常に厚い裾を持っていたら? そのときは裾の部分からもサンプルが必要になり、\(\alpha\) を大きくする必要が生じる場合もある (ただし \(\alpha=200\) にすべきではない: この値は馬鹿げており、そのようなシグマ点を配置する意味はない)。
同様の議論により、分布が裾をほとんど持たないとき──ひっくり返した放物線のような形をした確率分布のとき──は、シグマ点を平均の周りに寄せるべきだと言える。実際のデータが存在しない領域からサンプルを行う意味はない。
続いて平均に対する重みの変化を見よう。\(\alpha=1\) のとき重みは最初のシグマ点に対して \(0.667\) で、外側にある二つのシグマ点に対して \(0.1667\) だった。一方で \(\alpha=200\) のとき最初のシグマ点に対する重みは \(0.99999\) に跳ね上がり、外側の二つのシグマ点の重みは \(0.000004\) になる。重みの式を思い出そう:
\(\lambda\) が大きくなると \(W_0\) (平均 \(\mu\) の重み) は \(1\) に近づき、他のシグマ点に対する重みは \(0\) に近づくことがこの式から分かる。これはこちらが与えた共分散行列によらない事実である。つまり平均から離れたシグマ点には小さな重みが割り振られ、平均に近いシグマ点には平均と同じような重みが割り振られる。
しかし、Julier は \(\alpha\) を \(0 \lt \alpha \le 1\) の範囲に制限すべきだとアドバイスした上で \(\alpha = 10^{-3}\) を提案している。これも試しておこう:
print_sigmas(mean=0, cov=13, alpha=.001, kappa=0)シグマ点: [ 0. 0.0036 -0.0036]
平均に対する重み: [-999999. 500000. 500000.]
共分散行列に対する重み: [-999996. 500000. 500000.]
ラムダ: -0.999999
共分散行列に対する重みの和: 3.999998999992385510.15 ロボットの自己位置推定──完全な例
非常に重要な問題に取り掛かるときがやってきた。多くの書籍は簡単で教科書的な問題を選んで簡単な答えを示すだけで済ませているものの、そうすると読者は学んだ知識を使って現実の問題をどのように解決すればいいのだろうかと疑問に思ったまま本を読み終えることになる。これから示す例は任意の問題を解決する方法を示すわけではない。しかし、実際の問題でフィルタを設計・実装するときに考えなければならないことが説明される。
この節ではロボットの自己位置推定 (localization) の問題を考える。このシナリオでは、周りにあるランドマークを検出するセンサーを利用して環境内を移動するロボットが登場する。このロボットはコンピュータービジョンを使って木や歩行者などを特定する自動運転車かもしれないし、家の中を掃除する小さなロボットかもしれないし、倉庫で使われるロボットかもしれない。
ロボットには四つの車輪があり、その構成は自動車と同じとする。ロボットは二つの前輪を回すことで機動するので、旋回はロボットが前に進みながら後輪を軸に起こる。これは非線形な振る舞いであり、私たちはこれをモデル化しなければならない。
ロボットにはセンサーが付いていて、周りにある既知の対象への距離と方位の近似値を報告すると仮定する。距離と方位から位置を計算するには平方根と三角関数が必要なので、ここにも非線形性がある。
この問題ではプロセスモデルと観測モデルが両方とも非線形である。UKF は両方に対応できるから、UKF ならこの問題に対応できそうだと暫定的に結論できる。
ロボットの運動モデル
簡単な近似として、自動車は前に進みながら前輪を回すことで旋回を行うとする考え方がある。つまり自動車は後輪を軸として旋回し、そのとき車の前方部分が前輪の向く方向に移動するということだ。この単純な説明が考慮していない要素は多くある: 摩擦によるスリップ、異なる速度におけるゴムタイヤの振る舞いの変化、あるいは外側のタイヤが内側のタイヤより長い距離を動かなければならない事実は無視されており、これらを取り入れたモデルはさらに複雑になる。自動車の旋回を正確にモデル化するには複雑な微分方程式の集合が必要である。
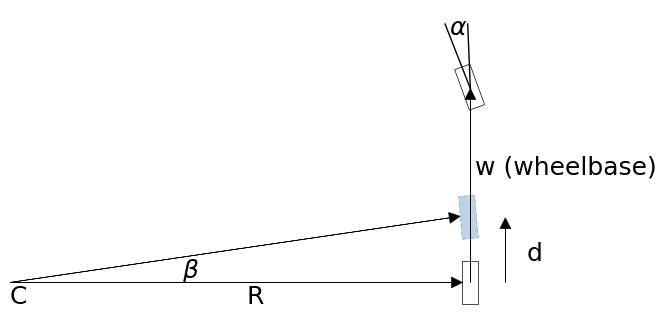
カルマンフィルタでフィルタリングを行うとき、特に低速度のロボットに対して行うときは、これより単純な自転車モデル (bicycle model) で優れた結果が得られることが分かっている。このモデルを表す図を示す:
最初は前輪だけがホイールベース (wheelbase) に対して \(\alpha\) だけ傾いている。短い時間が経過すると車体が前進し、そのとき後輪は少しだけ内側に進んで図中の暗い水色の地点まで移動する。この短い時間の間における運動は回転半径 \(R\) の回転運動として近似でき、図中の角度 \(\beta\) は次のように計算できる:
また回転半径 \(R\) は
と計算できる。ここで \(d\) は前輪が進んだ距離であり、速度を \(v\) とすれば \(d=v\Delta t\) と求められる。
旋回が始まる前のロボットの向きを \(\theta\)、 位置を \((x,y)\) とすれば、図中の点 \(C\) の座標は
と表せる。その後 \(\Delta t\) の間だけロボットが回転運動したとき、ロボットの新しい向きと位置は
と計算できる。\(C\) の座標を代入すれば次を得る:
車両の旋回モデルに興味がないなら導出を理解する必要はない。ここで重要なのは、私たちの考えている運動モデルが非線形であり、それをカルマンフィルタで扱う必要があると理解することだ。
状態変数の設計
このロボットに対しては位置と向きを状態として管理する:
このモデルに速度を加えることもできるものの、以降で見るようにこれだけでも数式は非常に難しくなる。
制御入力 \(\mathbf{u}\) は命令した速度と旋回角とする:
プロセスモデルの設計
今考えている系を (非線形な) 運動モデルと白色ノイズの和としてモデル化する:
先述の運動モデルは次のように実装できる:
from math import tan, sin, cos, sqrt
def move(x, dt, u, wheelbase):
hdg = x[2]
vel = u[0]
steering_angle = u[1]
dist = vel * dt
if abs(steering_angle) > 0.001: # ロボットは旋回しているか?
beta = (dist / wheelbase) * tan(steering_angle)
r = wheelbase / tan(steering_angle) # 回転半径
sinh, sinhb = sin(hdg), sin(hdg + beta)
cosh, coshb = cos(hdg), cos(hdg + beta)
return x + np.array([-r*sinh + r*sinhb,
r*cosh - r*coshb, beta])
else: # 直線に沿って移動している。
return x + np.array([dist*cos(hdg), dist*sin(hdg), 0])この関数は状態遷移関数 f(x) を実装するときに利用する。
この UKF の設計では \(\Delta t\) を小さく取る。加えてロボットの移動がゆっくりなら、上に示した move の実装でそれなりに正確な予測が計算できるはずである。もし \(\Delta t\) が大きかったり系のダイナミクスが大きな非線形性を持っていたりすると、この方法では上手く行かない可能性が生じる。そういった場合には、ルンゲ=クッタ法といったさらに洗練された数値積分手法を使ってモデルを実装する必要があるだろう。数値積分についてはカルマンフィルタの数学の章で軽く触れた。
観測モデルの設計
センサーは周りにある既知の地点 (ランドマーク) との距離と方位を観測し、その観測値にはノイズが含まれる。観測モデルは状態 \(\Big[ x \ \ y \ \ \theta \Big]^\mathsf{T}\) をランドマークとの距離と方位に変換する。ランドマークの座標を \(p = (p_x, p_y)\) とすると、距離 \(r\) は次のように表せる:
センサーが観測する方位はロボットの向きとの相対的な方位であると仮定する。そのためセンサーが観測する方位の計算では本来の方位からロボットの向きを引かなければならない:
ここから観測関数が得られる:
まだ実装はしない。実装の項で説明するように、この関数の実装では注意が必要な点がある。
観測ノイズ行列の設計
距離と方位のノイズは独立だと仮定するのが理にかなっている。よって観測ノイズ行列 \(\mathbf{R}\) は次のようになる:
実装
コーディングを始める前に、解決すべき問題が一つある。残差は \(y = z - h(x)\) である。\(z\) の方位が \(1^\circ\) で \(h(x)\) の方位が \(359^\circ\) だったとしよう。このとき二つの角度を引くと \(-358^\circ\) となるが、本当の角度の差は \(2^\circ\) なのでこのままだとカルマンゲインの計算で困ったことになる。そのため方位の残差を正しく計算する処理を特別に用意する必要がある。この処理で使う関数と実行例を示す:
def normalize_angle(x):
x = x % (2 * np.pi) # x を [0, 2 pi) の範囲に変換する。
if x > np.pi: # x を [-pi, pi) に移す。
x -= 2 * np.pi
return xprint(np.degrees(normalize_angle(np.radians(1-359))))1.9999999999999774状態ベクトルは位置 2 に方位を持つのに対して、観測ベクトルは位置 1 に方位を持つ。そのため両方を処理する関数が必要になる。これとは別の問題として、ロボットが機動すると見えていたランドマークが隠れたり隠れていたランドマークが見えるようになったりするので、この問題では可変個の観測値を処理しなければならない。そのため観測値の残差を計算する関数には見えているランドマークごとに一つの観測値からなる配列が渡される:
def residual_h(a, b):
# a, b は [dist_1, bearing_1, dist_2, bearing_2, ...] という形をしている。
y = a - b
for i in range(0, len(y), 2):
y[i + 1] = normalize_angle(y[i + 1])
return y
def residual_x(a, b):
y = a - b
y[2] = normalize_angle(y[2])
return y以上で観測モデルを実装する準備が整った。ランドマークごとに計算すべき数式を次に示す。ランドマークの座標を \(\mathbf{p} = (p_x, p_y)\) としている:
式 \(\tan^{-1}\left(\frac{p_y - y}{p_x - x}\right) - \theta\) は \([-\pi, \pi)\) の外側にある値を生成する可能性があるので、この区間内に収まるよう正規化する必要がある。
観測関数 Hx が受け取るのは状態 x とランドマークの位置を表す配列 landmarks で、Hx は返り値として [dist_to_1, bearing_to_1, dist_to_2, bearing_to_2, ...] という配列を返す:
def Hx(x, landmarks):
""" 状態を受け取り、それに対応する観測値を返す。 """
hx = []
for lmark in landmarks:
px, py = lmark
dist = sqrt((px - x[0])**2 + (py - x[1])**2)
angle = atan2(py - x[1], px - x[0])
hx.extend([dist, normalize_angle(angle - x[2])])
return np.array(hx)考えるべきことはまだある。無香料変換では状態ベクトルまたは観測ベクトルの平均が計算される。しかし、両方のベクトルには方位が含まれ、角度の集合の平均は一意に計算できない。例えば \(359^\circ\) と \(3^\circ\) の平均はいくつだろうか? 直感的には \(1^\circ\) だと思うかもしれないが、ナイーブに \(\frac{1}{n}\sum \theta_i\) を計算すると \(181^\circ\) になる。
この問題に対してよく取られる解決策は、サインの和とコサインの和を計算してアークタンジェントを取るというものだ:
UnscentedKalmanFilter.__init__ 関数の引数には、状態の平均を計算する関数を指定する x_mean_fn と観測値の平均を計算する関数を指定する z_mean_fn が存在する。この引数に渡す関数は次のように書ける:
def state_mean(sigmas, Wm):
x = np.zeros(3)
sum_sin = np.sum(np.dot(np.sin(sigmas[:, 2]), Wm))
sum_cos = np.sum(np.dot(np.cos(sigmas[:, 2]), Wm))
x[0] = np.sum(np.dot(sigmas[:, 0], Wm))
x[1] = np.sum(np.dot(sigmas[:, 1], Wm))
x[2] = atan2(sum_sin, sum_cos)
return x
def z_mean(sigmas, Wm):
z_count = sigmas.shape[1]
x = np.zeros(z_count)
for z in range(0, z_count, 2):
sum_sin = np.sum(np.dot(np.sin(sigmas[:, z+1]), Wm))
sum_cos = np.sum(np.dot(np.cos(sigmas[:, z+1]), Wm))
x[z] = np.sum(np.dot(sigmas[:,z], Wm))
x[z+1] = atan2(sum_sin, sum_cos)
return xこの二つの関数では配列に対する三角関数や dot による要素ごとの乗算といった NumPy の機能を利用している。NumPy は C や Fortran で実装されるので、sum(dot(sin(x), w)) はループを使った等価な Python コードより格段に速く実行される。
これでやっと、UKF を実装する準備が整った。なお私がこのフィルタを設計したときに、ここまでの関数を全てゼロから一気に設計したわけではないことは指摘しておきたい。私はまずハードコードされたランドマークを使って普通の UKF を実装し、正しく動作することを確認し、それから少しずつピースを埋めていった。「今までに見えていなかったランドマークが見えるようになったら?」と考えて観測関数がランドマークの配列を受け取れるように変更し、「角度の残差が正しく計算できていないのはどうすれば?」と考えて角度の正規化コードを書き、「角度の集合の平均とは何だ?」と考えてウェブを検索し、Wikipedia の記事を見つけ、そこにあったアルゴリズムを実装した。怖じ気付くことはない。自分が設計できることを設計し、疑問に思ったことを一つずつ解決していけばいい。
UKF の実装はこれまでにも見たので、詳しくは説明しない。次のコードには新しい要素が二つある。シグマ点とフィルタを構築するときに、先ほど書いた残差と平均を計算する関数を渡している:
points = SigmaPoints(n=3, alpha=.00001, beta=2, kappa=0,
subtract=residual_x)
ukf = UKF(dim_x=3, dim_z=2, fx=fx, hx=Hx, dt=dt, points=points,
x_mean_fn=state_mean, z_mean_fn=z_mean,
residual_x=residual_x, residual_z=residual_h)
続いて f(x, dt) と h(x) に追加データを渡す必要がある。f(x, dt) では move(x, dt, u, wheelbase) を、h(x) では Hx(x, landmarks) を実行しなければならない。これを行うには、次のように predict と update にキーワード引数を渡す:
ukf.predict(u=u, wheelbase=wheelbase)
ukf.update(z, landmarks=landmarks)
残りの部分はシミュレーションを実行して結果をプロットするコードである。landmark という変数を作成し、ここにランドマークの座標を格納している。またシミュレーションではロボットの位置を一秒に十回更新するのに対して、UKF は一秒に一度しか実行されない。これは運動を表す微分方程式の積分でルンゲ=クッタ法を使っていないためで、タイムステップを小さくしてシミュレーションを正確にしている:
from filterpy.stats import plot_covariance_ellipse
dt = 1.0
wheelbase = 0.5
def run_localization(
cmds, landmarks, sigma_vel, sigma_steer, sigma_range,
sigma_bearing, ellipse_step=1, step=10):
plt.figure()
points = MerweScaledSigmaPoints(n=3, alpha=.00001, beta=2, kappa=0,
subtract=residual_x)
ukf = UKF(dim_x=3, dim_z=2*len(landmarks), fx=move, hx=Hx,
dt=dt, points=points, x_mean_fn=state_mean,
z_mean_fn=z_mean, residual_x=residual_x,
residual_z=residual_h)
ukf.x = np.array([2, 6, .3])
ukf.P = np.diag([.1, .1, .05])
ukf.R = np.diag([sigma_range**2,
sigma_bearing**2]*len(landmarks))
ukf.Q = np.eye(3)*0.0001
sim_pos = ukf.x.copy()
# ランドマークをプロットする。
if len(landmarks) > 0:
plt.scatter(landmarks[:, 0], landmarks[:, 1],
marker='s', s=60)
track = []
for i, u in enumerate(cmds):
sim_pos = move(sim_pos, dt/step, u, wheelbase)
track.append(sim_pos)
if i % step == 0:
ukf.predict(u=u, wheelbase=wheelbase)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ukf.x[0], ukf.x[1]), ukf.P[0:2, 0:2], std=6,
facecolor='k', alpha=0.3)
x, y = sim_pos[0], sim_pos[1]
z = []
for lmark in landmarks:
dx, dy = lmark[0] - x, lmark[1] - y
d = sqrt(dx**2 + dy**2) + randn()*sigma_range
bearing = atan2(lmark[1] - y, lmark[0] - x)
a = (normalize_angle(bearing - sim_pos[2] +
randn()*sigma_bearing))
z.extend([d, a])
ukf.update(z, landmarks=landmarks)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ukf.x[0], ukf.x[1]), ukf.P[0:2, 0:2], std=6,
facecolor='g', alpha=0.8)
track = np.array(track)
plt.plot(track[:, 0], track[:,1], color='k', lw=2)
plt.axis('equal')
plt.title("UKF Robot localization")
plt.show()
return ukflandmarks = np.array([[5, 10], [10, 5], [15, 15]])
cmds = [np.array([1.1, .01])] * 200
ukf = run_localization(
cmds, landmarks, sigma_vel=0.1, sigma_steer=np.radians(1),
sigma_range=0.3, sigma_bearing=0.1)
print('最後の P:', ukf.P.diagonal())最後の P: [0.0092 0.0187 0.0007]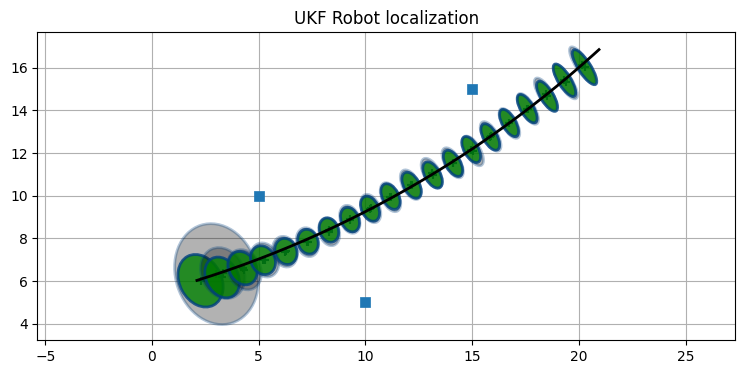
フィルタはロボットを正しく追跡できている。
ロボットの旋回
上のコードで実行したロボットのシミュレーションは現実的でない。速度と旋回角が全く変化しておらず、これではカルマンフィルタに有利すぎる。複雑な PID 制御を持つロボットシミュレーションを書いてもいいのだが、ここでは NumPy の linspace 関数を使って様々な旋回コマンドを生成することにしよう。このシミュレーションでロボットはずっと遠くまで移動するので、ランドマークを追加している:
landmarks = np.array([[5, 10], [10, 5], [15, 15], [20, 5],
[0, 30], [50, 30], [40, 10]])
dt = 0.1
wheelbase = 0.5
sigma_range=0.3
sigma_bearing=0.1
def turn(v, t0, t1, steps):
return [[v, a] for a in np.linspace(
np.radians(t0), np.radians(t1), steps)]
# 静止状態からの加速
cmds = [[v, .0] for v in np.linspace(0.001, 1.1, 30)]
cmds.extend([cmds[-1]]*50)
# 左への旋回
v = cmds[-1][0]
cmds.extend(turn(v, 0, 2, 15))
cmds.extend([cmds[-1]]*100)
# 右への旋回
cmds.extend(turn(v, 2, -2, 15))
cmds.extend([cmds[-1]]*200)
cmds.extend(turn(v, -2, 0, 15))
cmds.extend([cmds[-1]]*150)
cmds.extend(turn(v, 0, 1, 25))
cmds.extend([cmds[-1]]*100)ukf = run_localization(
cmds, landmarks, sigma_vel=0.1, sigma_steer=np.radians(1),
sigma_range=0.3, sigma_bearing=0.1, step=1,
ellipse_step=20)
print('最後の共分散行列:', ukf.P.diagonal())最後の共分散行列: [0.0013 0.0043 0.0004]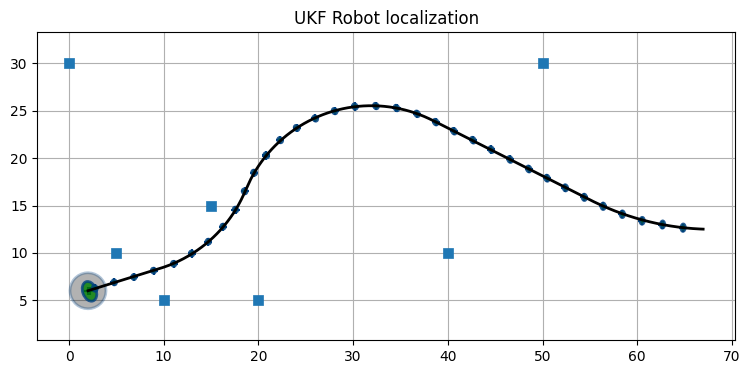
不確実性はすぐにとても小さくなる。共分散楕円は \(6\sigma\) を示しているにもかかわらず、楕円は小さくてほとんど見えないほどだ。出力に含まれる誤差を大きくするために、スタート地点の近くにある最初の二つのランドマークだけを使うようにしてみよう。このときフィルタを実行すると、ロボットがランドマークから離れたとき誤差が大きくなる:
ukf = run_localization(
cmds, landmarks[0:2], sigma_vel=0.1, sigma_steer=np.radians(1),
sigma_range=0.3, sigma_bearing=0.1, step=1,
ellipse_step=20)
print('final covariance', ukf.P.diagonal())final covariance [0.0026 0.0657 0.0008]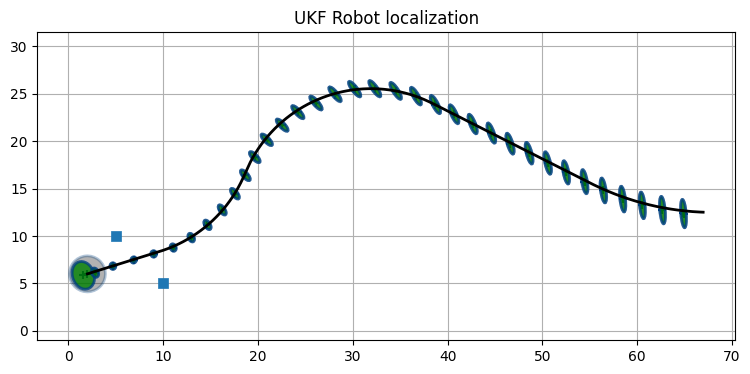
10.16 考察
この章を読んで抱く印象は、今までにどれだけ非線形カルマンフィルタを実装したことがあるかによって変わるだろう。これが初めて見る非線形カルマンフィルタなら、\(2n+1\) 個のシグマ点を計算して \(f(x)\) と \(h(x)\) を定義しなければならないのを細かくて面倒だと思うかもしれない。確かに、角度の正規化があったせいで全てが正しく動作すると私が納得できるまでには予想よりも時間がかかった。一方で、もし拡張カルマンフィルタ (EKF) を実装したことがあるなら、UKF はなんて簡単なんだと笑みがこぼれたかもしれない。UKF で必要になる関数を書くのは多少面倒ではあるものの、必要になる概念は非常に簡単である。同じ問題に対する EKF は非常に難しい数学を必要とする。多くの問題で EKF の式に対する閉形式の解を見つけることはできず、何らかの反復解法に頼るしかない。
UKF が EKF に対して優れている点は相対的な実装の優しさだけではない。EKF を学んでいないので話すのは少し早いが、EKF は問題を一点で線形化し、その点を線形カルマンフィルタに入力する。これに対して UKF は \(2n+1\) 個の点をサンプルする。そのため特に問題が非常に非線形である場合には、UKF は EKF より正確になることが多い。UKF が EKF より優れた性能を持つことが証明されているわけではないものの、UKF を実際に使うと少なくとも EKF と同程度の、多くの場合で EKF を上回る性能が得られることが分かっている。
そのため、どんなときでも UKF を最初に実装することを私は推奨する。ただし、あなたの設計するフィルタが発散した場合の現実世界への影響が重大である (人が死ぬ、大金を失う、発電所が爆発する) ときは、当然だが高度な解析と実験を通して最良のフィルタを選ばなければならない。これは本書の範囲を超える。そういった理論を学ぶには大学院に入らなければならないだろう。
最後に、本章ではシグマ点を使うフィルタが UKF だけであるかのように話をしたが、これは正しくない。私が選んだのは Van der Merwe が 2004 年の博士論文で示したバージョンであり、これは Julier が示した拡大無香料フィルタのパラメータを変更したものである。Julier, Van der Merwe, Uhlmann, Wan といった名前を調べれば、彼らによって考案されたシグマ点を使う同じようなフィルタの族を確認できる。ただし話はそこで終わりではない。例えば特異値分解 (singular value decomposition, SVD 分解) を使って確率分布の平均と共分散行列を近似する SVD カルマンフィルタというフィルタも存在する。本章はシグマ点を使うフィルタの入門だと考えてほしい。そういったフィルタの決定的な論説ではない。
-
訳注: このエピソードは UKF の考案者 Jeffrey Uhlmann への インタビューで語られている。[return]
-
Rudolph Van der Merwe, Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models, Ph.D. Dissertation, 2004.[return]
-
Simon J. Julier, "The Scaled Unscented Transformation," Proceedings of the 2002 American Control Conference, 6, IEEE, 2002.[return]
-
例えば https://www.baesystems.com/en-us/product/precision-tracking-radar などを参照。[return]
-
訳注:
atan2は \(-\pi \le \theta \le \pi\) を満たす角度 \(\theta\) を返すので、残差の計算で不都合が起きるのは左のセンサーではなく右のセンサーである (観測値が \(\pi\) から \(-\pi\) に飛ぶ)。以降の説明はatan2が \(0 < \theta \le 2\pi\) を返すと思って読むと正しい。[return]