第 7 章カルマンフィルタの数学

本書をここまで読んできた読者が「カルマンフィルタは恐ろしく難しい」という評判はいくらか不相応なようだと思えていることを願っている。もちろん数式の細かい部分はごまかしたが、実装はすぐに理解できたはずだ。基礎にある考え方は非常に簡単である──二つの観測値、あるいは観測値と予測値が入力され、その二つの間にある値が出力される。観測値が正確だと信じているなら推定値は観測値に近づき、予測値が正確だと信じているなら推定値は予測値に近づく。これはロケットサイエンス¹ではない (軽いジョークだ: アポロ 11 号が月と地球を往復するときにはまさにこの数式が使われた！)。

正直に言うと、これまでは問題を注意深く選んでいた。適当に問題を選ぶとカルマンフィルタで使う行列の設計が非常に困難になってしまう。ただ、全く意味のないことを説明したわけではない。ニュートンの運動方程式のような式はカルマンフィルタで簡単に利用でき、私たちが取り組む問題の大部分で姿を見せる。

ここまで私はカルマンフィルタの考え方をコードと論理で説明し、数学はあまり使わなかった。しかし、ここまでに使った以上の数学が必要となるトピックも存在するので、本章ではこれから本書で必要になる数学を説明する。

7.1 動的系のモデル化

動的系 (dynamic system) とは状態 (位置や温度など) が時間の経過とともに発展する物理系のことを言う。微積分とは値の変化に関する数学だから、動的系のモデル化には微分方程式が使われる。微分方程式でモデル化できない系も存在するが、そういった系は本書に登場しない。

動的系のモデル化は本来なら大学でいくつもの講義を通して扱われるべき話題である。数セメスターをかけて常微分方程式と偏微分方程式を学び、それから大学院で制御理論を学ぶのに代わる勉強方法は存在しないと言ってもいい。ただ、もしあなたがホビイストなら、あるいは仕事で特定のフィルタリングの問題に取り組むエンジニアなら、そういったことを勉強する年単位の時間を持ってはいないだろうし、持っていたとしても気が乗らないだろう。

幸いにも、カルマンフィルタで利用される様々な種類のシステム方程式の作成が可能になる十分な理論を私は示すことができる。私の目標は、あなたが出版された論文を読んだときに、そこで説明されるアルゴリズムを自分で実装できる程度に論文を理解できるようにすることだ。背景にある数学は深いものの、実際に使われるときはいくつかの簡単な手法が最終的に使われる。

本書の中で最も純粋数学が多いのがこの節である。拡張カルマンフィルタ (EKF) という最もよく使われる非線形フィルタを理解するにはここにある内容を全てマスターしておかなければならない。この節の内容がほとんど必要にならない現代的なフィルタにも触れるので、今は飛ばしておいて後で EKF を学びたくなったときに読んでも構わない。

まずカルマンフィルタの基礎にある数式と仮定を理解する必要がある。現実世界の現象をモデル化するとき、何を考える必要があるだろうか？

どんな物理系もプロセスを持つ。例えば何らかの速度で進む車は固定された時間ごとに速度に応じた距離だけ移動し、速度は加速度の関数として変化する。このプロセスは高校で学ぶ有名なニュートンの運動方程式で記述される:

\[ \begin{aligned} v &=at \\ x &= \frac{1}{2}at^2 + v_0t + x_0 \end{aligned} \]

微積分を学ぶと、この方程式は次の形で書かれる:

\[ \begin{aligned} \mathbf v &= \frac{d \mathbf x}{d t} \\ \mathbf a &= \frac{d \mathbf v}{d t} = \frac{d^2 \mathbf x}{d t^2} \end{aligned} \]

典型的な車両追跡の問題では速度あるいは加速度が固定されたときに車が進む距離を求めさせられる。これは前章でも同様だった。しかし当然、それが全てではない。完璧な道路を進む車など存在せず、道路のくぼみ、風、坂道、下り坂によって車の速度は変化する。また車に搭載されるサスペンションは機械的なシステムであり、摩擦と完璧でないばねを持つ。

最も簡単な問題を除けば系を完璧にモデル化するのは不可能であり、私たちは単純化を強いられる。このため任意の時刻 \(t\) における真の状態 (例えば車の位置) は不完全なモデルから予測された値と未知のプロセスノイズ (process noise) の和であるとされる:

\[ x(t) = x_{pred}(t) + noise(t) \]

こう書いたからといって、\(noise(t)\) が解析的に導ける関数であると言っているのではない。この式は事実の表明である──どんなときでも予測された値とプロセスノイズを足すと真の値が得られるという事実を表明している。ここでの「ノイズ」は確率的な事象を意味しない。大気中に投げられたボールを追跡していて、ボールが真空中にあるというモデルを使っているなら、空気抵抗の影響がこの文脈におけるプロセスノイズとなる。

次節で高階微分方程式を一階微分方程式に変換する手法を学ぶ。この変換を行うと、ノイズのない系のモデルは次のように書ける:

\[ \dot{\mathbf x} = \mathbf{Ax} \]

\(\mathbf{A}\) は系のダイナミクスを記述するので、系ダイナミクス行列 (systems dynamics matrix) と呼ばれる。続いてプロセスノイズをモデル化する必要がある。プロセスノイズは \(\mathbf w\) と呼ばれ、この等式に付け足される:

\[ \dot{\mathbf x} = \mathbf{Ax} + \mathbf w \]

ノイズに \(\mathbf{w}\) とはひどい命名だと思うかもしれないが、カルマンフィルタが白色ノイズ (white noise) を仮定していることを後で見る。

最後に、系への入力 (制御入力) を考える必要がある。制御入力はベクトル \(\mathbf{u}\) であり、制御入力による系の変化を記述する線形モデルが存在すると仮定する。例えばアクセルを踏むと車は加速し、重力があるとボールは下に落ちる。これらはどちらも制御入力による系の変化である。制御入力 \(\mathbf{u}\) を系の変化に変換する線形モデルは行列 \(\mathbf{B}\) で表すことにして、これも等式に加える:

\[ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w} \]

これで方程式が完成した。これはカルマン博士が取り組んだ方程式の一つであり、彼は \(\mathbf{w}\) に特定の特徴を仮定した場合の最適推定量を発見した。

7.2 動的系の状態空間表現

私たちは次の方程式を導いた:

\[ \dot{\mathbf x} = \mathbf{Ax}+ \mathbf{Bu} + \mathbf{w} \]

しかし、私たちは \(\mathbf{x}\) の微分ではなく \(\mathbf{x}\) そのものに興味がある。しばらくノイズを無視して考えると、私たちが探しているのは時刻 \(t_{k-1}\) における \(\mathbf{x}\) の値から時刻 \(t_k\) における \(\mathbf{x}\) の値を再帰的に計算する方程式である:

\[ \mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) + \mathbf B(t_k)\mathbf u (t_k) \]

\(k\) 番目の時刻 \(t_k\) における何らかの変数 \(\mathbf{y}\) の値 \(\mathbf{y}(t_k)\) を \(\mathbf{y}_k\) と書く慣習がある。この慣習を使うとこう書ける:

\[ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k \]

ここで \(\mathbf{F}\) はこれまでも使ってきた状態遷移行列 (state transition matrix) を表す。離散的なタイムステップだけ状態の値を遷移させるのでこの名前が付いている。状態遷移行列 \(\mathbf{F}\) は系ダイナミクス行列 \(\mathbf{A}\) と非常に似ている。違いは \(\mathbf{A}\) がいくつかの線形微分方程式をモデル化する連続なものであるのに対して、\(\mathbf{F}\) は \(\mathbf{x}_{k-1}\) を離散的なタイムステップ \(\Delta t\) だけ進めて \(\mathbf{x}_k\) とするための線形方程式 (微分方程式ではない) を表す離散的なものである点にある。

状態遷移行列 \(\mathbf{F}\) を求めるのは非常に難しいことが多い。ただ \(\dot x = v\) のような最も簡単な部類の微分方程式に対してなら簡単に求められる。まず、この微分方程式は自明に積分できる:

\[ \int_{x_{k-1}}^{x_k} dx = \int_{0}^{\Delta t} v\, \mathrm{d}t \]

\[ x_k-x_{k-1} = v \Delta t \]

\[ \therefore \ \ x_k = v \Delta t + x_{k-1} \]

この方程式は再帰的である: 時刻 \(t\) における \(x\) の値が \(t-1\) における \(x\) 値から計算できる。この再帰的な関係があると、系 (プロセスモデル) をカルマンフィルタが要求する形で書くことができる:

\[ \begin{aligned} \mathbf x_k &= \mathbf{Fx}_{k-1} \\ &= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix} \begin{bmatrix}x_{k-1} \\ \dot x_{k-1}\end{bmatrix} \end{aligned} \]

これができたのは \(\dot x = v\) が可能な中で最も単純な微分方程式であるためだ。これ以外のほぼ全て物理系ではもっと複雑な微分方程式が現れるので、このアプローチは使えない。

状態空間法 (state-space method) はアポロ計画のころ、主にカルマン博士の研究によって有名になった。そのアイデアは簡単だ。まず \(n\) 階の線形微分方程式で系をモデル化し、それらを等価な一階の部分方程式に変換して前節で説明した \(\dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu}\) というベクトルと行列の形式にする。この形式にできたら、後は線形微分方程式を再帰方程式に変換する手法のいずれかを使うと次の形の式が得られる:

\[ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k \]

状態遷移行列 \(\mathbf{F}\) を基礎行列 (fundamental matrix) と呼ぶ文献もある。また \(\mathbf{F}\) ではなく \(\Phi\) が使われることも多い。制御理論に近い文献ほど「基礎行列」という言葉と \(\Phi\) の記号を使う傾向にある。

この方法が状態空間法と呼ばれるのは、微分方程式の解を系の状態で表しているためである。

高階線形微分方程式から一階線形微分方程式への変換

物理系のモデルは制御入力 \(u\) を持った二階以上の線形微分方程式になることが多い。つまり次の形の微分方程式である:

\[ a_n \frac{d^ny}{dt^n} + a_{n-1} \frac{d^{n-1}y}{dt^{n-1}} + \dots + a_2 \frac{d^2y}{dt^2} + a_1 \frac{dy}{dt} + a_0 = u \]

状態空間法は一階線形微分方程式を必要とする。微分係数を表す新しい変数を定義した上で解くことで、任意の高階線形微分方程式系を一階に落とすことができる。

一つ例を考えてみよう。\(\ddot{x} - 6\dot x + 9x = u\) という系があるとき、これと等価な一階線形微分方程式系を見つけたいとする。表記を簡単にするため、時間に関する微分をドットで表す。

最初のステップとして、最高次の項を等式の片側に分離する:

\[ \ddot{x} = 6\dot x - 9x + u \]

次に二つの新しい変数を定義する:

\[ \begin{aligned} x_1(u) &= x \\ x_2(u) &= \dot x \end{aligned} \]

これを元の方程式に代入して解くと、これらの新しい変数に関する一階線形微分方程式系が解として得られる。表記を簡単にするため \((u)\) を省略するのが慣習となっているので、これからは省略する。

\(\dot x_1 = x_2\) および \(\dot x_2 = \ddot{x}\) だから

\[ \begin{aligned} \dot x_2 &= \ddot{x} \\ &= 6\dot x - 9x + u \\ &= 6x_2-9x_1 + u \end{aligned} \]

となる。この問題における一階線形微分方程式系がこれで求まった:

\[ \begin{aligned}\dot x_1 &= x_2 \\ \dot x_2 &= 6x_2-9x_1 + u\end{aligned} \]

以上の処理は少し練習すれば習得できるだろう。高次の項を分離し、新しい変数とその微分係数を定義し、置換して解くだけである。

一階線形微分方程式の状態空間形式

一階微分方程式への変換で新しく定義された変数

\[ \frac{dx_1}{dt} = x_2,\quad \frac{dx_2}{dt} = x_3, \,\quad \ldots, \quad \frac{dx_{n-1}}{dt} = x_n \]

を元の微分方程式に代入すると次を得る:

\[ \frac{dx_n}{dt} = \frac{1}{a_n}\sum\limits_{i=0}^{n-1}a_ix_{i+1} + \frac{1}{a_n}u \]

この等式および \(x_i\) の定義をベクトルと行列を使った記法を使って書くと

\[ \begin{bmatrix} \frac{dx_1}{dt} \\[5pt] \frac{dx_2}{dt} \\[5pt] \vdots \\[5pt] \frac{dx_n}{dt} \end{bmatrix} = \begin{bmatrix} \dot x_1 \\[5pt] \dot x_2 \\[5pt] \vdots \\[5pt] \dot x_n \end{bmatrix}= \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\[5pt] 0 & 0 & 1 & \cdots & 0 \\[5pt] \vdots & \vdots & \vdots & \ddots & \vdots \\[5pt] -\frac{a_0}{a_n} & -\frac{a_1}{a_n} & -\frac{a_2}{a_n} & \cdots & -\frac{a_{n-1}}{a_n} \end{bmatrix} \begin{bmatrix} x_1 \\[5pt] x_2 \\[5pt] \vdots \\[5pt] x_n \end{bmatrix} + \begin{bmatrix} 0 \\[5pt] 0 \\[5pt] \vdots \\[5pt] \frac{1}{a_n} \end{bmatrix}u \]

となる。これは \(\dot{\mathbf x} = \mathbf{Ax} + \mathbf{B}u\) と書ける。

時不変系の基礎行列の計算

ここまでの変形で系の方程式は状態空間形式で表された (これから制御入力は無視する):

\[ \dot{\mathbf x} = \mathbf{Ax} \]

ここで \(\mathbf{A}\) は系ダイナミクス行列である。続いて基礎行列 \(\mathbf{F}\) を求めたい。基礎行列は次の式で状態 \(\mathbf{x}\) を間隔 \(\Delta t\) だけ伝播させる:

\[ \begin{aligned} \mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) \end{aligned} \]

言い換えると、\(\mathbf{A}\) は連続な微分方程式の集合を表しており、次は \(\mathbf{A}\) が表す微分方程式系の離散的なタイムステップにおける変化を計算する離散的な線形方程式として \(\mathbf{F}\) を求めたい。

簡単のため \((\Delta t)\) と \((t_k)\) を省略するのが慣習なので、これからは省略して次のように書く:

\[ \mathbf x_k = \mathbf {Fx}_{k-1} \]

大まかに言って、カルマンフィルタで使われる基礎行列の計算方法としてよく知られたものが三つある。最もよく使われるのは行列指数であり、線形時不変理論 (linear time invariant theory, LTI システム理論とも) が二番目の手法、最後に数値的な手法がある。他にも知っているかもしれないが、カルマンフィルタの文献や実践で最もよく目にするのはこの三つである。

行列指数

微分方程式 \(\displaystyle\frac{dx}{dt} = kx\) は次のように解ける:

\[ \begin{gathered} \frac{dx}{dt} = kx \\ \frac{dx}{x} = k\, dt \\ \int \frac{1}{x}\, dx = \int k\, dt \\ \log x = kt + c \\ x = e^{kt+c} \\ x = e^ce^{kt} \\ x = c_0e^{kt} \end{gathered} \]

同じように考えると、定数行列 \(A\) を持つ一階微分方程式

\[ \dot{\mathbf x} = \mathbf{Ax} ,\, \, \, \mathbf x(0) = \mathbf x_0 \]

の解は次のように表せる (ことが示せる。証明は省略する):

\[ \mathbf x = e^{\mathbf At}\mathbf x_0 \]

\(\mathbf{F} = e^{\mathbf{A}t}\) と書き換えれば、これは

\[ \mathbf x_k = \mathbf F\mathbf x_{k-1} \]

となって求めたかった形になる！よって基礎行列を求める問題は \(e^{\mathbf At}\) を求める問題に帰着された。

\(e^{\mathbf At}\) は行列指数と呼ばれ、次のべき級数で計算できる:

\[ e^{\mathbf At} = \mathbf{I} + \mathbf{A}t + \frac{(\mathbf{A}t)^2}{2!} + \frac{(\mathbf{A}t)^3}{3!} + \cdots \]

この級数は \(e^{\mathbf At}\) をテイラー級数展開すると得られる。詳細は省略する。

行列指数を使ってニュートンの運動方程式の例 (\(\dot{x} = v\)) における基礎行列を求めてみよう。速度は定数と仮定する。このとき微分方程式をベクトルと行列を使って書くと次のようになる:

\[ \mathbf{\dot x} = \begin{bmatrix}\dot x \\ \ddot x\end{bmatrix} =\begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ \dot{x}\end{bmatrix} \]

これは一階微分方程式だから、\(\mathbf{A}=\Big[\begin{smallmatrix}0&1\\0&0\end{smallmatrix}\Big]\) とすれば次のべき級数で \(\mathbf{F}\) が求まる。基礎行列が離散的であることを強調するために間隔 \(t\) を \(\Delta t\) で置き換えている:

\[ \mathbf F = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A\Delta t)^3}{3!} + \cdots \]

乗算を実際に計算すると \(\mathbf{A}^2=\Big[\begin{smallmatrix}0&0\\0&0\end{smallmatrix}\Big]\) が分かる。これは \(\mathbf{A}\) の 2 以上のべきは全て \(\mathbf{0}\) になることを意味する。よって無限個の項を足すことなく答えが求まる:

\[ \begin{aligned} \mathbf F &=\mathbf{I} + \mathbf A \Delta t + \mathbf{0} \\ &= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\ &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix} \end{aligned} \]

これを \(\mathbf x_k= \mathbf{Fx}_{k-1}\) に代入すれば次を得る:

\[ \begin{aligned} \mathbf{x}_k &=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}\mathbf{x}_{k-1} \end{aligned} \]

これは多変量カルマンフィルタの章でカルマンフィルタを設計するときに解析的に求めた行列と一致することが分かるだろう。

SciPy の linalg モジュールには行列指数を計算する expm 関数が含まれる。この関数はテイラー級数ではなくパデ近似 (Padé approximant) を利用して計算を行う。行列指数の計算方法は多く (最低でも 19 個) 存在し、そのどれもが数値的な問題を抱えている²。特に \(\mathbf{A}\) が大きいときはこの問題に注意する必要がある。"pade approximation matrix exponential" などと検索すればこの問題を論じた文献が多く見つかるだろう。

カルマンフィルタで必要な基礎行列を行列指数で計算するときは普通テイラー級数の先頭の数項を取って計算してしまうので、細かい計算方法は問題にならないことも多い。しかし、私の取り扱いが絶対に正しいと決め込んで数値的性能解析を行わずにこの手法を他の問題に適用してはいけない。興味深いことに、よく使われる \(e^{\mathbf At}\) の計算方法の一つは一般的な ode ソルバを使う方法である。これは私たちがしていることと正反対と言える──\(\mathbf{A}\) を微分方程式の集合に変換し、それを数値的手法で解くことで行列指数が計算される！

expm 関数を使って \(e^{\mathbf At}\) を計算する方法を示す:

In [3]

import numpy as np
from scipy.linalg import expm

dt = 0.1
A = np.array([[0, 1],
              [0, 0]])
expm(A*dt)

Out [3]

array([[1. , 0.1],
       [0. , 1. ]])

時不変性

系の振る舞いが時間に依存するとき、その系は次の一階微分方程式で記述できる:

\[ g(t) = \dot x \]

しかし、もし系が時不変 (time invariant) なら、次の形の方程式となる:

\[ f(x) = \dot x \]

系が時不変とは出力が時刻に依存しないことを言う。例えば家庭用のステレオシステムを考えよう。制御入力 \(x\) を時刻 \(t\) に入力すると、ステレオシステムは何らかの出力 \(f(x)\) を出力する。もし時刻 \(t + \Delta t\) に同じ制御入力 \(x\) を入力したとしても、出力は時間がずれるだけで \(f(x)\) のままである。よってこの系は時不変と言える。

一方 \(f(t) = t\, x(t) = t \sin(t)\) で記述される系は時不変でない。先頭に \(t\) があるために、制御入力が同じでも時刻によって出力が異なるためだ。また航空機も時不変でない。航空機は飛行中に燃料を燃やして重量が減るので、同じ制御入力でも時刻によって振る舞いが異なる。

時不変な系は両辺を積分すれば解ける。前節では \(v = \dot x\) という時不変な系の積分を示した。しかし一般的な式 \(\dot x = f(x)\) を積分するのはそれほど簡単ではない。変数分離 (separation of variables) と呼ばれる手法を念頭に置いて両辺を \(f(x)\) で割ってから \(dt\) を右辺に移項すると積分できる:

\[ \begin{gathered} \frac{dx}{dt} = f(x) \\ \int^x_{x_0} \frac{1}{f(x)} dx = \int^t_{t_0} dt \end{gathered} \]

\(F(x) = \displaystyle\int \frac{1}{f(x)}\) とすると

\[ F(x) - F(x_0) = t-t_0 \]

を得る。これを \(x\) について解けば

\[ \begin{gathered} F(x) = t - t_0 + F(x_0) \\ x = F^{-1}[t-t_0 + F(x_0)] \end{gathered} \]

が分かる。言い換えれば時不変の系を解くには \(F\) の逆関数が必要になる。様々なトリックを使ってこの問題の解析解を求める方法は STEM 教育の大きな部分を占める。

しかしそういった解法は手が込んでおり、単純な \(f(x)\) でも閉形式の解が存在しなかったり非常に難しかったりする。そのため実際の問題に取り込むエンジニアは状態空間法を利用して近似解を求めることが多い。

行列指数を使う方法の利点は、時不変な任意の微分方程式系に対して使えることである。しかし、この手法は時不変でない系に対してもよく使われる。航空機が燃料を燃やすと重量が減る。しかし一秒間の重量の減少は無視できる程度なので、そのタイムステップでなら系が時不変とみなせる。タイムステップが十分短い限りこうしてもそれなりに正確な解が得られる。

例: 質量-ばね-ダンパーモデル

車のサスペンションのように、ダンパー (制動器) に接続されたばねに付いている重りを追跡したいとする。\(m\) を重りの質量、\(k\) をばね定数、\(c\) をダンパーからの力、\(u\) を何らかの外力とすると、運動方程式は次のようになる:

\[ m\frac{d^2x}{dt^2} + c\frac{dx}{dt} +kx = u \]

表記を簡単にするため、以後は省略して次のように書く:

\[ m\ddot x + c\dot x + kx = u \]

この系を一階微分方程式系に変換するために、\(x_1(t) = x(t)\) とおいて次の関係を代入・整理する:

\[ \begin{aligned} x_1 &= x \\ x_2 &= \dot x_1 \\ \dot x_2 &= \ddot x_1 = \ddot x \end{aligned} \]

よくあるように、表記を簡単にするため \((t)\) を省略している。ここから次の等式を得る:

\[ m\dot x_2 + c x_2 +kx_1 = u \]

\(\dot x_2\) について解くと一階微分方程式となる:

\[ \dot x_2 = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u \]

\(x_1\) および \(x_2\) とそれらの微分の関係を行列形式に表す:

\[ \begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix} = \begin{bmatrix}0 & 1 \\ -k/m & -c/m \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1/m \end{bmatrix}u \]

続いて行列指数で状態遷移行列を計算する:

\[ \Phi(t) = e^{\mathbf At} = \mathbf{I} + \mathbf At + \frac{(\mathbf At)^2}{2!} + \frac{(\mathbf At)^3}{3!} + \cdots \]

最初の二項を計算すれば

\[ \mathbf F = \begin{bmatrix}1 & t \\ -(k/m) t & 1-(c/m) t \end{bmatrix} \]

となる。これが十分な精度を与えるかどうかは分からない。\(\frac{(\mathbf At)^2}{2!}\) に定数を代入して計算すれば結果への影響がどの程度かが分かる。

線形時不変理論

線形時不変理論 (LTI システム理論とも呼ばれる) は逆ラプラス変換を使って \(\Phi\) を計算する方法を与える。これを聞いた読者はうなずいているか何のことだかさっぱり分からないかのどちらかだろう。本書ではラプラス変換を扱わない。LTI システム理論によると、次の関係が成り立つことが分かる:

\[ \Phi(t) = \mathcal{L}^{-1}[(s\mathbf{I} - \mathbf{A})^{-1}] \]

これ以上ラプラス変換については触れないが、ラプラス変換 \(\mathcal{L}\) は信号を時間の含まれない空間における \(s\) の関数に変換すること、そして上に示した等式の解を求めるのは非自明な問題であることは言及しておく。もし興味があるなら、Wikipedia の LTI システム理論のページが入門となっている。難しい問題でカルマンフィルタの行列を求めるときに LTI システム理論を使う文献があるので、ここで触れておいた。

数値解

最後に、\(\mathbf{F}\) を求める数値的手法がある。フィルタが大規模になると解析解を求めるのが非常に面倒になる (SymPy などのパッケージを使えば多少は楽になる)。C. F. van Loan³ は \(\Phi\) と \(\mathbf{Q}\) を数値的に求める手法を考案した。単位白色ノイズ \(\mathbf{w}\) を含む連続モデル

\[ \dot x = \mathbf{Ax} + \mathbf{Gw} \]

が与えられたとき、van Loan の方法は \(\mathbf{F}_k\) と \(\mathbf{Q}_k\) の両方を計算する。

van Loan の方法は FilterPy に van_loan_discretization 関数として実装してある。次のように使う:

from filterpy.common import van_loan_discretization
A = np.array([[0., 1.], [-1., 0.]])
G = np.array([[0.], [2.]]) # 白色ノイズのスケーリング係数
F, Q = van_loan_discretization(A, G, dt=0.1)

微分方程式の数値積分の節ではカルマンフィルタでよく使われる別の方法を紹介する。

7.3 プロセスノイズ行列の設計

一般にプロセスノイズ行列 \(\mathbf{Q}\) の設計はカルマンフィルタの設計の中で最も難しい部分である。これにはいくつか理由がある。第一に、\(\mathbf{Q}\) の設計に関する数学が信号理論の基礎知識を広く必要とする。第二に、ほとんど情報がない現象からのノイズをモデル化しなければならない。例えば投げられた野球ボールに対するプロセスノイズをモデル化したいとしよう。ボールは大気中を移動する球としてモデル化できるものの、それ以外にも要素は多く存在する──ボールの回転、回転の減衰、傷のついたボールの抗力係数、風や空気密度の係数などがある。考えているプロセスモデルに対する数学的厳密解は求められても、プロセスモデルが不完全なために \(\mathbf{Q}\) も不完全になる。この事実はカルマンフィルタの振る舞いに予期しない結果をもたらす。\(\mathbf{Q}\) が小さすぎるとフィルタは予測モデルに自信を持ちすぎて、実際の解から離れていってしまう。逆に \(\mathbf{Q}\) が大きすぎるとフィルタが観測値に加わるノイズから過度に影響を受け、振る舞いが最適でなくなる。実際にカルマンフィルタを使うときはシミュレーションの実行と収集された現実のデータを使った評価に長い時間を費やして適切な \(\mathbf{Q}\) を選択することになる。ここではまずプロセスノイズ行列に関する数学を説明する。

運動学的な系──ニュートンの運動方程式でモデル化できる系──を考える。このプロセスのノイズに関して異なる仮定がいくつか考えられる。

これまでは白色ノイズ \(\mathbf{w}\) を使った

\[ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w} \]

というプロセスモデルを使ってきた。運動学的な系は連続であり、入力と出力は任意の時刻で変更できる。しかし私たちが考えているカルマンフィルタは離散的であり、一定の間隔で系をサンプルする (連続なカルマンフィルタも存在するが、本書では扱わない)。よって上の等式に対応するノイズの離散的な表現 (モデル) を見つけなければならない。ノイズの振る舞いに関する仮定によってモデルも異なる。これから二つの異なるノイズのモデルを紹介する。

連続白色ノイズモデル

運動学的な系をニュートンの運動方程式でモデル化するとき、私たちは位置と速度もしくは位置と速度と加速度をモデルに含めた。しかしそこで止まる理由はない──躍度、加加加速度、加加加加速度をモデルに含めることもできる。普通これを行わないのは、実際の系のダイナミクスを超えて項を追加すると推定値が劣化するためだ。

位置と速度と加速度をモデルに含めるとしよう。このとき離散的なタイムステップで加速度は定数だと仮定される。もちろん系にはプロセスノイズが存在するから、本当に定数なわけではない。追跡中の物体は外部からのモデルにない力によって加速度を変える。一つ目のノイズモデルでは、加速度が平均ゼロの白色ノイズ \(w(t)\) の値だけ連続的に変化すると仮定する。言い換えれば、速度に加わる小さな変動は時間に関する平均がゼロだと仮定する。

このノイズを仮定したときのプロセスノイズ行列 \(\mathbf{Q}\) を求めよう。ノイズは連続的に変化するので、離散化されたタイムステップの式で使うための離散的な値を得るには積分が必要になる。証明はしないが、白色ノイズの離散化は次の式で行える:

\[ \mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t) dt \]

ここで \(\mathbf{Q}_c\) は連続ノイズの共分散行列を表す。この等式の大まかな意味は明らかなはずだ。\(\mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t)\) は時刻 \(t\) における連続ノイズを考えているプロセスモデル \(\mathbf{F}(t)\) で射影した値を表す。求めたいのは離散化に用いる間隔 \(\Delta t\) を通して系に加わるノイズだから、\(\mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t)\) を \([0, \Delta t]\) で積分している。

ニュートン系に対する基礎行列は

\[ \mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix} \]

だった。今考えているノイズモデルでは、連続ノイズの共分散行列 \(\mathbf{Q}_c\) は

\[ \mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s \]

と定義される。ここで \(\Phi_s\) は白色ノイズのスペクトル密度 (spectral density) と呼ばれる値を表す。スペクトル密度の定義と \(\mathbf Q_c\) のスペクトル密度が \(\Phi_s\) になることの証明は本書の範囲を超えるので省略する。詳細は確率過程の標準的な教科書を参考にしてほしい。実際の問題ではノイズのスペクトル密度は分からない場合が多いので、これは「エンジニアリング」の対象になる──フィルタの性能が期待通りになるまで実験を通して調整する値である。\(\Phi_s\) に乗じられる行列に注目すると、スペクトル密度が加速度の項に割り当てられるのが分かる。これはおかしなことではない: 系の加速度は基本的に一定でノイズによってだけ変化すると仮定していたので、ノイズは加速度の分散だけを変化させるのが正しい。

\(\mathbf{Q}\) の計算を手で行うこともできるが、私なら次のように SymPy を使って解くだろう:

In [4]

import sympy
from sympy import (init_printing, Matrix, MatMul,
                   integrate, symbols)

init_printing(use_latex='mathjax')
dt, phi = symbols('\Delta{t} \Phi_s')
F_k = Matrix([[1, dt, dt**2/2],
              [0,  1,      dt],
              [0,  0,       1]])
Q_c = Matrix([[0, 0, 0],
              [0, 0, 0],
              [0, 0, 1]])*phi

Q = integrate(F_k * Q_c * F_k.T, (dt, 0, dt))

# 読みやすくするために一度 phi で割る
Q = Q / phi
MatMul(Q, phi)

Out [4]

\(\displaystyle \left[\begin{matrix}\frac{\Delta{t}^{5}}{20} & \frac{\Delta{t}^{4}}{8} & \frac{\Delta{t}^{3}}{6}\\\frac{\Delta{t}^{4}}{8} & \frac{\Delta{t}^{3}}{3} & \frac{\Delta{t}^{2}}{2}\\\frac{\Delta{t}^{3}}{6} & \frac{\Delta{t}^{2}}{2} & \Delta{t}\end{matrix}\right] \Phi_{s}\)

参考として、零次 (位置のみ) および一次 (位置と速度) のモデルに対する同じ式を計算しておく:

In [5]

F_k = Matrix([[1]])
Q_c = Matrix([[phi]])

print('零次の離散プロセスノイズの共分散行列')
integrate(F_k*Q_c*F_k.T,(dt, 0, dt))

Out [5]

零次の離散プロセスノイズの共分散行列

Out [5]

\(\displaystyle \left[\begin{matrix}\Delta{t} \Phi_{s}\end{matrix}\right]\)

In [6]

F_k = Matrix([[1, dt],
              [0, 1]])
Q_c = Matrix([[0, 0],
              [0, 1]]) * phi

Q = integrate(F_k * Q_c * F_k.T, (dt, 0, dt))

print('一次の離散プロセスノイズの共分散行列')
# 読みやすくするために一度 phi で割る
Q = Q / phi
MatMul(Q, phi)

Out [6]

一次の離散プロセスノイズの共分散行列

Out [6]

\(\displaystyle \left[\begin{matrix}\frac{\Delta{t}^{3}}{3} & \frac{\Delta{t}^{2}}{2}\\\frac{\Delta{t}^{2}}{2} & \Delta{t}\end{matrix}\right] \Phi_{s}\)

区分白色ノイズモデル

もう一つのノイズモデルは、最も高次の項 (例えば加速度) が離散化された時刻の間でそれぞれ異なる定数になるとして、その値同士は相関を持たないとするモデルである。言い換えれば、タイムステップごとに加速度が不連続にジャンプする。これは一つ前のモデルと少し異なる。一つ前のモデルでは連続的に変化するノイズ信号が加速度を常に変化させると仮定していた。

このノイズは次のようにモデル化される:

\[ f(\mathbf{x})=\mathbf{Fx}+ \Gamma \mathbf{w} \]

ここで \(\Gamma\) は系のノイズゲイン (noise gain) を表し、\(w\) はタイムステップの間で一定の区分加速度 (piecewise acceleration) (あるいは区分速度、区分躍度など) を表す。

最初は一次の系を考えよう。このとき状態遷移関数は

\[ \mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0& 1\end{bmatrix} \]

である。離散化された時刻の間で速度は \(w(t)\Delta t\) だけ変化し、位置は \(w(t)\Delta t^2/2\) だけ変化する。よって次を得る:

\[ \Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\end{bmatrix} \]

プロセスノイズ行列 \(\mathbf{Q}\) は次の等式で計算できる:

\[ \mathbf{Q} = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T} \]

これは SymPy で次のように求められる:

In [7]

var = symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt]])

Q = v * var * v.T

# 読みやすくするために一度 var で割る
Q = Q / var
MatMul(Q, var)

Out [7]

\(\displaystyle \left[\begin{matrix}\frac{\Delta{t}^{4}}{4} & \frac{\Delta{t}^{3}}{2}\\\frac{\Delta{t}^{3}}{2} & \Delta{t}^{2}\end{matrix}\right] \sigma^{2}_{v}\)

二次の系でも同様に求められる。まず状態遷移行列は次の通りとなる:

\[ \mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix} \]

ここで区分白色ノイズモデルを仮定すると、次が分かる:

\[ \Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\\ 1\end{bmatrix} \]

このモデルに "正しさ" があるわけではない。ただ便利で優れた結果を生むというだけだ。例えばノイズが躍度を変化させるとすることも (式が複雑にはなるが) できる。

このときプロセスノイズ行列は

\[ \mathbf{Q} = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T} \]

となる (\(\sigma_v^2\) はノイズの分散)。これは SymPy を使って次のようにも計算できる:

In [8]

var = symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt], [1]])

Q = v * var * v.T

# 読みやすくするために一度 var で割る
Q = Q / var
MatMul(Q, var)

Out [8]

\(\displaystyle \left[\begin{matrix}\frac{\Delta{t}^{4}}{4} & \frac{\Delta{t}^{3}}{2} & \frac{\Delta{t}^{2}}{2}\\\frac{\Delta{t}^{3}}{2} & \Delta{t}^{2} & \Delta{t}\\\frac{\Delta{t}^{2}}{2} & \Delta{t} & 1\end{matrix}\right] \sigma^{2}_{v}\)

このノイズモデルが一つ目の連続白色ノイズモデルより正しいのかどうかは分からない──どちらも実際に物体に対して起こることを近似している。あなたを適切なモデルへ導けるのは経験と実験だけだ。実際には両方のモデルからそれなりの結果が得られることが多いが、一方だけがもう一方より優れた結果を生む。

二つ目のモデルの利点としてノイズを分散 \(\sigma^2\) でモデル化できることがある。\(\sigma^2\) は運動と運動に期待される誤差を使って記述できる。一つ目のモデルはスペクトル密度というあまり直感的でない値を指定する必要があるものの、ノイズをタイムステップで積分して計算するのでタイムステップを簡単に変えられるという利点がある。ただし、どちらを使うべきかが明確に定まっているわけではない──フィルタの振る舞いや物理系の振る舞いに関する知識に基づいて、いずれかのモデル (あるいは自分で考案したモデル) を使えばよい。

\(\sigma\) は \(\frac{1}{2}\Delta a\) と \(\Delta a\) の間に設定すべきであることが経験則として知られている。ここで \(\Delta a\) は離散化された時間間隔における加速度の変化量の最大値を表す。実際にカルマンフィルタを利用するときはいくつか値を選んでシミュレーションを実行し、性能が良かった値を選択するべきである。

FilterPy を使った \(\mathbf{Q}\) の計算

FilterPy は行列 \(\mathbf{Q}\) を計算する関数をいくつか提供する。Q_continuous_white_noise 関数は与えられた \(\Delta t\) とスペクトル密度から連続白色ノイズモデルの \(\mathbf{Q}\) を計算する:

In [9]

from filterpy.common import Q_continuous_white_noise

Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
print(Q)

Out [9]

[[0.333 0.5  ]
 [0.5   1.   ]]

In [10]

Q = Q_continuous_white_noise(dim=3, dt=1, spectral_density=1)
print(Q)

Out [10]

[[0.05  0.125 0.167]
 [0.125 0.333 0.5  ]
 [0.167 0.5   1.   ]]

Q_discrete_white_noise 関数は区分白色ノイズモデルの \(\mathbf{Q}\) を計算する:

In [11]

from filterpy.common import Q_discrete_white_noise

Q = Q_discrete_white_noise(2, var=1.)
print(Q)

Out [11]

[[0.25 0.5 ]
 [0.5  1.  ]]

In [12]

Q = Q_discrete_white_noise(3, var=1.)
print(Q)

Out [12]

[[0.25 0.5  0.5 ]
 [0.5  1.   1.  ]
 [0.5  1.   1.  ]]

\(\mathbf{Q}\) の単純化

実際の処理では \(\mathbf{Q}\) を大きく単純化して、各ブロックで最も右下にある要素だけを残してそれ以外を全てゼロにすることが多い。これは正当化されるのだろうか？ \(\Delta t\) が小さいときの \(\mathbf{Q}\) を考えてみよう:

In [13]

import numpy as np

np.set_printoptions(precision=8)
Q = Q_continuous_white_noise(
    dim=3, dt=0.05, spectral_density=1)
print(Q)
np.set_printoptions(precision=3)

Out [13]

[[0.00000002 0.00000078 0.00002083]
 [0.00000078 0.00004167 0.00125   ]
 [0.00002083 0.00125    0.05      ]]

ほとんどの項は非常に小さくなる。この行列を使うカルマンフィルタの式は次の一つだけだったことを思い出そう:

\[ \bar{\mathbf{P}}=\mathbf{FPF}^\mathsf{T} + \mathbf Q \]

\(\mathbf{Q}\) が \(\mathbf{P}\) と比較して小さいなら、計算される \(\bar{\mathbf{P}}\) に \(\mathbf{P}\) はほとんど寄与しない。よって \(\mathbf{Q}\) の右下以外をゼロにした

\[ \mathbf Q=\begin{bmatrix}0&0&0\\0&0&0\\0&0&\sigma^2\end{bmatrix} \]

は、正しくはないものの、便利な近似になることが多い。ただもちろん、この近似を重要なアプリケーションで使うときは様々な状況におけるフィルタの正しい動作を保証するために徹底的な調査を行う必要がある。

この近似を使うときは、「各ブロックの最も右下の項」が各変数に対する最も早く変化する項を意味することを頭に入れておくとよい。例えば状態が \(x=\Big[x \ \ \dot x \ \ \ddot{x} \ \ y \ \ \dot{y} \ \ \ddot{y}\Big]^\mathsf{T}\) なら \(\mathbf{Q}\) は \(6{\times}6\) になり、\(\mathbf{Q}\) は \(\ddot{x}\) と \(\ddot{y}\) に対応する要素だけが非ゼロ要素となる。

7.4 事後共分散行列の安定な計算

前に事後共分散行列の計算式として次の式を示した:

\[ \mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P} \]

これでも間違ってはいないものの、FilterPy では異なる式が使われている。私は次の Joseph の式を使った:

\[ \mathbf P = (\mathbf I-\mathbf {KH})\mathbf{\bar P}(\mathbf I-\mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T \]

この実装がバグではないかと指摘するメールや GitHub issue をよくもらう。これはバグではなく、いくつかの理由があって使っている。第一に、\(\mathbf I - \mathbf{KH}\) の減算結果が浮動小数点数の誤差によって非対称な行列になることがある。共分散行列は対称でなくてはならず、非対称な行列を共分散行列として使うとカルマンフィルタが発散したり NumPy で行われるチェックで例外が発生したりする可能性がある。

対称性を保存する伝統的な方法は次の式を使うものである:

\[ \mathbf P = (\mathbf P + \mathbf P^\mathsf T) / 2 \]

これが安全なのは、こうして計算される \(\mathbf{P}\) の任意の要素で \(\mathbf{P}_{ij} = \mathbf{P}_{ji}\) が成り立つためだ。つまりこの操作は浮動小数点数による誤差で異なる値となった本来同じになるべき二つの値を平均することで対称性を保証している。

Joseph の式を見ると、両方の項が見覚えのある \(\mathbf{ABA}^\mathsf T\) の形をしているのが分かる。この形の式は対称性を保存することが知られている。しかし、この式はどこから来たのだろうか？次の二つの式ではいけないのはなぜだろうか？

\[ \begin{aligned} \mathbf P &= (\mathbf I - \mathbf{KH})\mathbf{\bar P} \\ \mathbf P &= (\mathbf P + \mathbf P^\mathsf T) / 2 \end{aligned} \]

Joseph の式を第一原理から導出してみよう。難しすぎるほどではないし、式の役割を理解するには導出を理解する必要がある。さらに需要なこととして、導出を知っておかないと数値的安定性の問題が原因でフィルタが発散したとき問題を診断できなくなる。この導出は Brown ら著 Introduction to Random Signals and Applied Kalman Filtering⁴ から取った。

まず記号を定義する。\(\mathbf{x}\) は考えている系の真の状態、\(\mathbf{\hat x}\) は推定された系の状態 (事後分布)、\(\mathbf{\bar x}\) は予測された系の状態 (事前分布) とする。

このとき、考えているモデルは次のように定義できる:

\[ \begin{aligned} \mathbf x_{k+1} &= \mathbf F_k \mathbf x_k + \mathbf w_k \\ \mathbf z_k &= \mathbf H_k \mathbf x_k + \mathbf v_k \end{aligned} \]

言葉で言えば、次の時刻における系の状態 \(\mathbf{x}_{k+1}\) は現在 (時刻 \(k\)) の状態 \(\mathbf{x}_k\) を状態遷移関数 \(\mathbf{F}_k\) で遷移させ、それにノイズ \(\mathbf{w}_k\) を加えると得られる。また時刻 \(k\) の観測値 \(\mathbf{z}_k\) は時刻 \(k\) の状態 \(\mathbf{x}_k\) に観測関数を作用させ、それにノイズ \(\mathbf{v}_k\) を加えると得られる。

この二つの式が定義であることに注意してほしい。数学的モデルに完璧に従う系が存在しない事実はノイズを表す項 \(\mathbf{w}_k\) でモデル化され、センサーに誤差があるために完璧な観測も存在しない事実は \(\mathbf{v}_k\) でモデル化される。

以降の導出では時刻 \(k\) における値だけを考えるので、添え字の \(k\) を省略する。

推定誤差 \(\mathbf{e}\) を真の状態と推定された状態の差として定義する:

\[ \mathbf e = \mathbf x - \mathbf{\hat x} \]

ここでも、これは定義である。\(\mathbf{e}\) の計算方法を私たちは知らない。\(\mathbf{e}\) は真の状態と推定された状態の差として定義されるというだけだ。

\(\mathbf{e}\) が定義されると、推定値の共分散行列を \(\mathbf{ee}^\mathsf T\) と定義できるようになる:

\[ \begin{aligned} \mathbf{P} &= \mathbb E[\mathbf{ee}^\mathsf T] \\ &= \mathbb E[(\mathbf x - \mathbf{\hat x})(\mathbf x - \mathbf{\hat x})^\mathsf T] \end{aligned} \]

続いて事後推定値を

\[ \mathbf {\hat x} = \mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x}) \]

と定義する。これはカルマンフィルタの式と似ているが、それには理由がある。しかし、これまでの式と同様これは定義である。特に \(\mathbf{K}\) は定義されないので、これをカルマンゲインと思ってはいけない。今は線形カルマンフィルタとは限らない任意の問題を考えている。\(\mathbf{K}\) は \(0\) と \(1\) の間の値を取る未指定の定数である。

これで定義が揃ったので、代入と代数計算を行おう。

\((\mathbf x - \mathbf{\hat x})\) の \(\mathbf{\hat x}\) を上述の定義と置き換えることで、次を得る:

\[ (\mathbf x - \mathbf{\hat x}) = \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x})) \]

さらに \(\mathbf{z} = \mathbf H \mathbf x + \mathbf v\) を代入すれば次のように変形できる:

\[ \begin{aligned} (\mathbf x - \mathbf{\hat x}) &= \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x})) \\ &= \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf H \mathbf x + \mathbf v - \mathbf{H \bar x})) \\ &= (\mathbf x - \mathbf{\bar x}) - \mathbf K(\mathbf H \mathbf x + \mathbf v - \mathbf{H \bar x}) \\ &= (\mathbf x - \mathbf{\bar x}) - \mathbf{KH}(\mathbf x - \mathbf{ \bar x}) - \mathbf{Kv} \\ &= (\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv} \end{aligned} \]

\((\mathbf x - \mathbf{\bar x})(\mathbf x - \mathbf{\bar x})^\mathsf T\) の期待値が事前共分散行列 \(\mathbf{\bar P}\) であり、\(\mathbf{v}\mathbf{v}^\mathsf T\) の期待値が \(\mathbf R\) であることに注意すると、\(\mathbf{P}\) の定義を変形できる:

\[ \begin{aligned} \mathbf P &= \mathbb{E}\big[[(\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv})] [(\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv}]^\mathsf T\big ] \\ &= (\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T \end{aligned} \]

これが証明したかった等式である。

この等式は任意の \(\mathbf{K}\) に対して正しいことに注意してほしい。カルマンフィルタで使われる最適な \(\mathbf{K}\) でだけ正しいのではない。なお実際のデータに対してカルマンフィルタが計算するカルマンゲインは最適ではない。現実世界は線形でもなければガウス分布にも従わず、さらに計算による浮動小数点誤差数の誤差も存在するためだ。現実世界の条件において、この式がカルマンフィルタを収束させる可能性はずっと低い。

\(\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P}\) はどこから来たのだろうか？難しくないので導出してしまおう。カルマンフィルタの (最適) ゲインは次の式で与えられた:

\[ \mathbf K = \mathbf{\bar P H^\mathsf T}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)^{-1} \]

ちょうど今導いた等式にこれを代入すれば、次を得る:

\[ \begin{aligned} \mathbf{P} &= (\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T\\ &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf K(\mathbf{H \bar P H}^\mathsf T + \mathbf R)\mathbf K^\mathsf T \\ &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf{\bar P H^\mathsf T}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)^{-1}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)\mathbf K^\mathsf T\\ &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf{\bar P H^\mathsf T}\mathbf K^\mathsf T\\ &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P}\\ &= (\mathbf I - \mathbf{KH})\mathbf{\bar P} \end{aligned} \]

よって \(\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P}\) はゲインが最適なとき正しい。ただし

\[\mathbf{P} = (\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T\]

も正しい。前述したように後者の等式はゲインが最適でないときも成り立つので、数値的な安定性が高い。私が FilterPy でこちらの等式を使ったのはこれが理由である。

この式を使ってもフィルタが発散する可能性は残る。特にフィルタを数百あるいは数千エポックにわたって実行すると発散しやすい。そのときはここで示した式を詳しく調べる必要が生じるだろう。カルマンフィルタの文献を見ればこれとはさらに別の形の式が載っているので、それをあなたの問題に適用できるかもしれない。繰り返しになるが、もし失敗が機器や人命の損失を意味する真剣なエンジニアリングの問題に取り組んでいるなら、本書だけではなく専門的なエンジニアリングの文献にも当たらなくてはならない。一方で取り組んでいるのが失敗しても平気な "おもちゃの" 問題なら、フィルタが発散したら \(\mathbf{P}\) を "よさげな" 値にリセットしてフィルタリングをやり直す手法で構わない。例えば非対角要素をゼロにして、それによる情報の損失を反映させるために \(1\) より大きい適当な定数を全体に乗じるといった方法が考えられる。想像力を働かせて、思いついた方法をテストすればよい。

7.5 カルマンゲインの導出

もし一つ前の節を読んだなら、この節も読んだ方がいいかもしれない。この節を読むとカルマンフィルタの式を全て導出したことになる。

この導出はベイズの定理の式を使っていないことに注意してほしい。私は少なくとも四種類の異なるカルマンフィルタの式の導出を見たことがある。この導出はカルマンフィルタに関する文献でよく見られるもので、ソースはここでも Brown ら著 Introduction to Random Signals and Applied Kalman Filtering⁵である。

前節では未指定のスケーリング係数 \(\mathbf{K}\) を使って Joseph が示した形式の共分散行列の式を導出した。最適なフィルタを得るには、微積分を使って誤差を最小にする必要がある。この考え方は目新しいものではないはずだ。関数 \(f(x)\) の極大値や極小値を求めるために \(f\) を微分して \(0\) と等号で結んだ方程式 \(\displaystyle \frac{x}{dx}f(x) = 0\) を解いたことがあるだろう。

今考えている問題では誤差が共分散行列 \(\mathbf{P}\) として表される。特に、\(\mathbf{P}\) の対角要素は状態ベクトルの各要素の誤差 (分散) を表す。よって最適なゲインを得るには \(\mathbf{P}\) の対角要素の和 (トレース) の微分を取ればよい。

Brown らはまずトレースの微分に関する二つの等式を示している:

\[ \begin{gathered} \frac{d \operatorname{tr}(\mathbf{AB})}{d\mathbf A} = \mathbf B^\mathsf T \\ \frac{d \operatorname{tr}(\mathbf{ACA}^\mathsf T)}{d\mathbf A} = 2\mathbf{AC} \end{gathered} \]

ここで \(\mathbf{AB}\) は正方行列、\(\mathbf{C}\) は対称行列である。

Joseph の式を展開すると次が得られる:

\[ \mathbf P = \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar P}\mathbf H^\mathsf T \mathbf K^\mathsf T + \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)\mathbf K^\mathsf T \]

ここから \(\mathbf{P}\) のトレースの \(\mathbf K\) に関する微分 \(\displaystyle \frac{d \operatorname{tr}(\mathbf P)}{d\mathbf K}\) を計算できる。

第一項 \(\mathbf{\bar P}\) は \(\mathbf{K}\) を持たないので、トレースの \(\mathbf{K}\) に関する微分は \(0\) となる。

第二項 \(\mathbf{KH \bar{P}}\) のトレースの微分は \((\mathbf H\mathbf{\bar P})^\mathsf T\) である。

第三項 \(\mathbf{\bar P}\mathbf H^\mathsf T \mathbf K^\mathsf T\) が第二項 \(\mathbf{KH}\mathbf{\bar P}\) の転置であることに気が付けば、第三項の微分は簡単に計算できる。転置のトレースは元の行列のトレースと等しいから、微分も同じになる。

最後に、第四項 \(\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)\mathbf K^\mathsf T\) の微分は \(2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)\) である。

以上より最終的な値が求まる:

\[ \frac{d \operatorname{tr}(\mathbf P)}{d\mathbf K} = -2(\mathbf H\mathbf{\bar P})^\mathsf T + 2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) \]

これを \(0\) と等号で結び、その方程式を \(\mathbf{K}\) について解けば誤差を最小にする \(\mathbf{K}\) が得られる:

\[ \begin{aligned} -2(\mathbf H\mathbf{\bar P})^\mathsf T + 2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) &= 0 \\ \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) &= (\mathbf H\mathbf{\bar P})^\mathsf T \\ \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) &= \mathbf{\bar P}\mathbf H^\mathsf T \\ \therefore \ \ \mathbf K &= \mathbf{\bar P}\mathbf H^\mathsf T (\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)^{-1} \end{aligned} \]

トレースを最小化すると全体の誤差が最小になる理由を議論していないので以上の導出は厳密ではないのだが、本書ではこれで十分だと判断した。もし厳密な証明が必要なら、どんな標準的な教科書にもこれよりずっと詳細な証明が載っている。

7.6 微分方程式の数値積分

ここまでに線形微分方程式を解くときに利用できるテクニックにいくつか触れた。例えば状態空間法、ラプラス変換、van Loan の方法がある。

こういった手法は線形の常微分方程式 (ordinary differential equations, ODE) に対しては上手く動作するものの、非線形な微分方程式では使えない。例えば急に旋回している車の位置予測を考えよう。車は前輪を傾けることで旋回を行うので、前方に進みながら旋回すると後輪を軸に回転が起こる。そのため車の軌跡は連続的に変化し、線形の予測による出力は不正確な値にしかならない。系の変化が \(\Delta t\) と比較して十分小さいなら線形の予測でも適切な結果が得られるものの、本書の後半で学ぶ非線形カルマンフィルタが扱うような系では変化が十分小さくなることはまずない。

こういった理由により、ODE を数値的に積分する手法を知っておく必要がある。これは数冊の本が必要となる広大な分野だが、ここではあなたが遭遇するほとんどの問題に適用できる簡単な方法をいくつか示す。

オイラー法

次の ODE と初期条件が与えられたとする:

\[ \left\{ \begin{aligned} y' &= y \\ y(0) &= 1 \end{aligned} \right. \]

この特定の ODE に対する厳密解 \(y=e^t\) は先ほど解いたのでたまたま分かっているものの、一般の ODE では厳密解は分からないだろう。一般に分かっているのは各点における関数の微分 (グラフの傾き) の求め方と、\(t=0\) では \(y=1\) といった初期値だけである。ただこの二つの情報があると、\(y(0)\) の値と \(t=0\) におけるグラフの傾きから \(y(1)\) の値を予測できる。この予測を次のグラフに示す:

In [14]

import matplotlib.pyplot as plt

t = np.linspace(-1, 1, 10)
plt.plot(t, np.exp(t))
t = np.linspace(-1, 1, 2)
plt.plot(t,t+1, ls='--', c='k');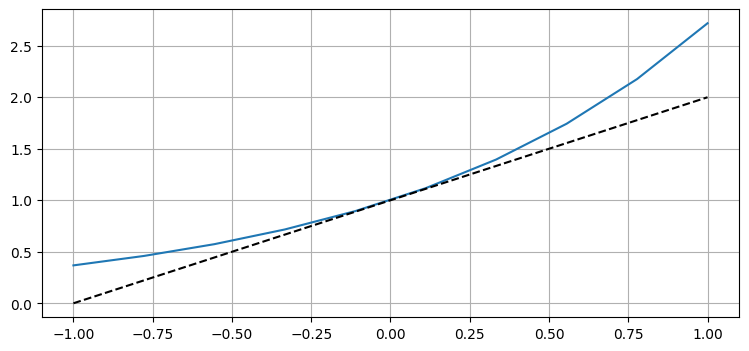

Out [14]\(t=0\) における値と傾きを使った \(y(1)\) の予測

\(t=0\) におけるグラフの傾き \(y' (0) = y(0) = 1\) は \(t=0.1\) では曲線と非常に近いものの、\(t=1\) では大きく離れているのがグラフから分かる。続いて \(t=2\) における \(y\) の値を \(t=1\) における曲線の傾きを計算して予測値に足すことで計算してみよう。\(t=1\) で予測された \(y\) の値は \(2\) だから、\(t=1\) におけるグラフの傾きは \(y' (2) = y(2)\) より \(2\) となる:

In [15]

import kf_book.book_plots as book_plots

t = np.linspace(-1, 2, 20)
plt.plot(t, np.exp(t))
t = np.linspace(0, 1, 2)
plt.plot([1, 2, 4], ls='--', c='k')
book_plots.set_labels(x='x', y='y');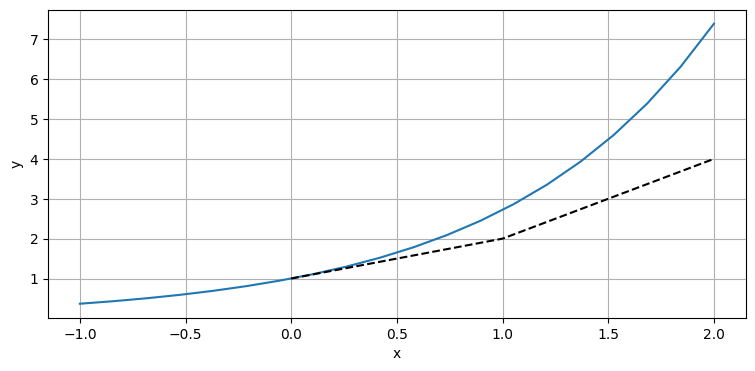

次の予測値は \(4\) となった。誤差は大きくなっており、上手く行っていないと思うかもしれない。しかし \(1\) というのはステップサイズとして非常に大きい。このアルゴリズムをコードにして、ステップサイズを小さくしたときの動作を確認しよう:

In [16]

def euler(t, tmax, y, dx, step=1.):
    ys = []
    while t < tmax:
        y = y + step*dx(t, y)
        ys.append(y)
        t +=step
    return ys

In [17]

def dx(t, y): return y

print(euler(0, 1, 1, dx, step=1.)[-1])
print(euler(0, 2, 1, dx, step=1.)[-1])

Out [17]

2.0
4.0

コードは正しいようだ。続いてステップサイズを小さくしたときの結果をプロットしてみる:

In [18]

ys = euler(0, 4, 1, dx, step=0.00001)
plt.subplot(1,2,1)
plt.title('Computed')
plt.plot(np.linspace(0, 4, len(ys)),ys)
plt.subplot(1,2,2)
t = np.linspace(0, 4, 20)
plt.title('Exact')
plt.plot(t, np.exp(t));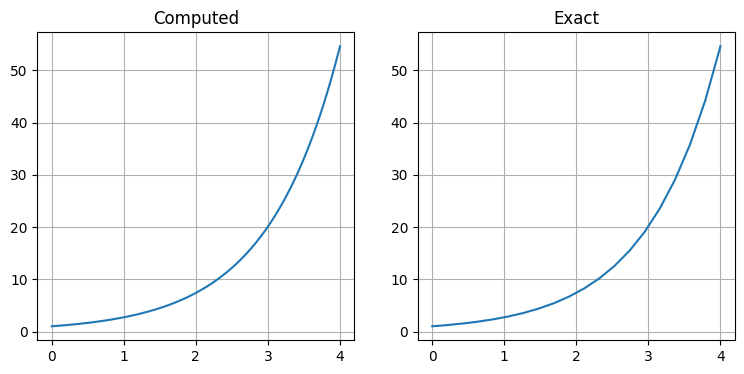

In [19]

print('厳密解         =', np.exp(4))
print('オイラー法の解 =', ys[-1])
print('誤差           =', np.exp(4) - ys[-1])
print('反復回数       =', len(ys))

Out [19]

厳密解         = 54.598150033144236
オイラー法の解 = 54.59705808834125
誤差            = 0.0010919448029866885
反復回数       = 400000

誤差は小さいものの、三桁の精度を得るのにかかった反復の回数が非常に多いことが分かる。このオイラー法は実際の問題の大部分に対して遅すぎるので、より洗練された手法が使われる。

次の話題に進む前に、オイラー法のきちんとした導出を示しておく。これは次節で説明するルンゲ=クッタ法というオイラー法より高度な手法の基礎となる考え方である。実はオイラー法はルンゲ=クッタ法の最も簡単な形と言える。

\(y\) のテイラー展開から最初の三項を取った式を次に示す。級数を無限に展開しないと厳密な答えは得られないので、級数を有限で打ち切ったことによる誤差を \(O(h^4)\) と表している:

\[ y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2!}h^2 y''(t_0) + \frac{1}{3!}h^3 y'''(t_0) + O(h^4) \]

ここからオイラー法はテイラー展開の最初の二項を使っているのだと分かる。後ろにある項はそれまでの項より小さいので、予測値が真の値から大きく離れることはないことが確信できる。

ルンゲ=クッタ法

ルンゲ=クッタ法は数値積分の馬車馬である。数値積分の文献には大量の手法が載っているものの、実際には今から説明するルンゲ=クッタ法を使えばあなたが直面する問題のほとんどが解けてしまうはずだ。速度・精度・安定性のバランスが非常に優れており、別の方法を使う特別な理由がない限り「これを使っておけば大丈夫」とされる数値積分手法である。

では説明しよう。次の微分方程式を考える:

\[ \dot y = f(y,t) \]

このとき RK4 と呼ばれるルンゲ=クッタ法は次の式で定義される。この式の導出は本書の範囲を超える:

\[ \begin{aligned} y(t+\Delta t) &= y(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) + O(\Delta t^4) \\ k_1 &= f(y,t)\Delta t \\ k_2 &= f(y+\frac{1}{2}k_1, t+\frac{1}{2}\Delta t)\Delta t \\ k_3 &= f(y+\frac{1}{2}k_2, t+\frac{1}{2}\Delta t)\Delta t \\ k_4 &= f(y+k_3, t+\Delta t)\Delta t \end{aligned} \]

これを実装したコードを示す:

In [20]

def runge_kutta4(y, x, dx, f):
    """
    dy/dx に対する四次のルンゲ=クッタ法を計算する。
    x は x の初期値。
    y は y の初期値。
    dx は次の x との差 (タイムステップ)。
    f は dy/dx を計算する関数。f(y, x) と呼び出される。
    """
    k1 = dx * f(y, x)
    k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
    k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
    k4 = dx * f(y + k3, x + dx)
    return y + (k1 + 2*k2 + 2*k3 + k4) / 6.

簡単な例で RK4 を使ってみよう。微分方程式を

\[ \dot{y} = t\sqrt{y(t)} \]

として、初期値を次のようにする:

\[ \begin{aligned} t_0 &= 0 \\ y_0 &= y(t_0) = 1 \end{aligned} \]

実装を示す:

In [21]

import math
import numpy as np

t = 0.
y = 1.
dt = .1
ys, ts = [], []

def func(y,t):
    return t*math.sqrt(y)

while t <= 10:
    y = runge_kutta4(y, t, dt, func)
    t += dt
    ys.append(y)
    ts.append(t)

exact = [(t**2 + 4)**2 / 16. for t in ts]
plt.plot(ts, ys)
plt.plot(ts, exact)
error = np.array(exact) - np.array(ys)
print(f"最大の誤差: {max(error):.5f}")

Out [21]

最大の誤差: 0.00005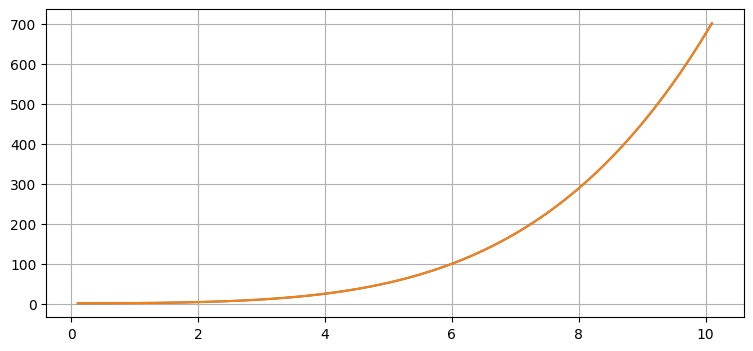

実際の値と計算された値が非常に近いのが分かる。

7.7 ベイズフィルタの考え方

本書では離散ベイズフィルタの章からベイズ的なフィルタの定式化を使ってきた。特定の時刻における状態を位置や速度などとして定義し、「時刻 \(t\) における状態が \(\mathbf x_t = \Big[x_t \ \ \dot x_t \Big]^\mathsf T\) である」などと議論した。

物体を観測すると、状態 (もしくは状態の一部) の観測値が手に入る。センサーにはノイズが含まれるので、観測値にもノイズが混じっている。しかし明らかに、観測値は状態によって決定される。つまり状態が変われば (一般に) 観測値も変わるのに対して、観測値が変わったからといって状態が変化したとは必ずしも言えない。

フィルタリングにおける私たちの目標は時刻 \(0\) から時刻 \(t\) までの状態の集合 \(\mathbf{x}_{0:t}\) の最適な推定値を計算することである。もし \(\mathbf{x}_{0:t}\) が分かっていれば、それらの状態に対応する観測値の集合 \(\mathbf{z}_{0:t}\) は自明に計算できる。しかし私たちが受け取るのは観測値の集合 \(\mathbf{z}_{0:t}\) であり、ここから対応する状態の集合 \(\mathbf{x}_{0:t}\) を求めなければならない。このように出力から入力を計算しようとする問題を統計的反転 (statistical inversion) と呼ぶ。

統計的反転は一意な解を持たないのが普通なので、難しい問題となる。与えられた状態の集合から得られる観測値としてあり得るのは (ノイズを除けば) 一つの集合だけなのに対して、与えられた観測値の集合を生み出せる状態の集合は無数に考えられる。

ベイズの定理を思い出そう:

\[ P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)} \]

ここで \(P(z \mid x)\) は観測値 \(z\) の尤度、\(P(x)\) はプロセスモデルに基づいた事前分布、\(P(z)\) は正規化係数を表す。\(P(x \mid z)\) は事後分布、つまり観測値 \(z\) を取り入れた後の分布を表す。観測値 \(z\) は証拠とも呼ばれる。

この式は \(P(z \mid x)\) から \(P(x \mid z)\) を導いているので、統計的反転を計算している。私たちが考えているフィルタリング問題への解は次のように表せる:

\[ P(\mathbf x_{0:t} \mid \mathbf z_{0:t}) = \frac{P(\mathbf z_{0:t} \mid \mathbf x_{0:t})P(\mathbf x_{0:t})}{P(\mathbf z_{0:t})} \]

この式に問題は何もないのだが、次の観測値 \(\mathbf{z}_{t+1}\) がやってくると問題が発生する。このとき区間 \(0:t+1\) に対する式をまるごと再計算しなくてはならない。

事後分布を \(P(\mathbf x_{0:t} \mid \mathbf z_{0:t})\) と全ての時刻に対して考えているために、実際のデータにこの式を適用すると手に負えなくなる。しかし十個目の観測値を受け取ったときに (例えば) 時刻 \(3\) の確率分布を気にする必要などあるのだろうか？普通はない。よって現在の時刻における分布だけを計算することにして、さらにいくつか条件を緩和することになる。

一つ目の単純化として、私たちは考えているプロセスをマルコフ連鎖 (Markov chain) として記述する。つまり、現在の状態は一つ前の状態 \(\mathbf{x}_{k-1}\) と遷移確率 \(P(\mathbf x_k \mid \mathbf x_{k-1})\) だけに依存すると仮定する。遷移確率は一つ前の状態から現在の状態へ移る確率というだけだ。この仮定は次のように書ける:

\[ \mathbf x_k \sim P(\mathbf x_k \mid \mathbf x_{k-1}) \]

現実世界の様々な現象はマルコフ性 (Markov property) を持つので、この仮定は実際の問題でも非常に理にかなっている。例えばあなたが駐車場で車を運転しているとき、一秒後の車の位置はその日に高速で車を止めたことや一分前に悪路を通ったことに影響を受けるだろうか？そんなことはない。一秒後の車の位置は現在の位置、速度、制御入力だけに依存し、一分前に起こったことからは影響を受けない。よって車の位置はマルコフ性を持ち、マルコフ連鎖を仮定する単純化を行っても精度や一般性を失うことはない。

二つ目の単純化として、私たちは観測モデルを、現在状態が与えられたときの観測値の条件付き確率 \(P(\mathbf z_k \mid \mathbf x_k)\) と現在状態 \(\mathbf{x}_k\) だけに観測値 \(\mathbf{z}_k\) が依存するものとして定義する。これは次のように書ける:

\[ \mathbf z_k \sim P(\mathbf z_k \mid \mathbf x_k) \]

これで再帰的な関係が手に入ったので、後は無限ループを止めるための初期条件が必要になる。そこで初期分布は状態 \(\mathbf{x}_0\) の確率であることを利用する:

\[ \mathbf x_0 \sim P(\mathbf x_0) \]

これらの関係を使ってベイズの定理の式が計算される。初期状態 \(\mathbf{x}_0\) と初期観測値 \(\mathbf{z}_0\) があれば \(P(\mathbf{x}_0 \mid \mathbf{z}_0)\) を計算でき、プロセスモデルを使えばそこから事前分布 \(P(\mathbf{x}_1 \mid \mathbf{x}_0)\) を計算できる。さらにこれをベイズの定理の式に代入すれば \(P(\mathbf{x}_1 \mid \mathbf{z}_1)\) が得られる。この予測子修正子アルゴリズムを続けることで、状態と分布を再帰的に計算できる。そのとき時刻 \(t\) の状態と分布は時刻 \(t-1\) の状態と分布だけに依存する。

この計算の数学的な詳細は問題によって異なる。離散ベイズフィルタと単変量カルマンフィルタの章では二つの異なる定期化を示した。あなたも理解できたことだろう。単変量カルマンフィルタはスカラーの状態と観測値および線形なノイズとプロセスを仮定し、モデルは平均ゼロの独立なガウスノイズに影響されるとした。

多変量カルマンフィルタはスカラーではなくベクトルの状態と観測値に対して同じ仮定をおいた。カルマン博士はこういった仮定が成り立つときカルマンフィルタが最小二乗の意味で最適であることの証明に成功している。くだけて言えば、これは (カルマンフィルタが仮定する種類の) ノイズが含まれる観測値からこれ以上の情報を取り出す方法が存在しないことを意味する。本書ではこれから線形性とガウスノイズという制約を緩めたフィルタを見ていく。

次の話題に進む前に、統計的反転について少し説明しておく。Calvetti と Somersalo が Introduction to Bayesian Scientific Computing⁶ に記したように、「私たちはベイズ的な視点を採用する: ランダム性は情報の欠如を意味しているだけだ」。私たちが考える状態は物理的現象 (例えば速度や空気抵抗など) をパラメータ化する。原理上は状態の値を観測あるいは計算できるものの、そのために必要となる十分な情報を私たちは持っていないので、確率変数を使って状態を表現することになる。速度や空気抵抗といった値は正確に言えば確率的ではないから、これは主観的な立場である。

Calvetti と Somersalo はこの話題に丸々一章を使っているが、私は一段落だけしか割けない。ベイズフィルタは可能なのは、未知のパラメータが統計的性質を持つとみなしているためだ。カルマンフィルタの場合は最適な推定値を求める閉形式の解が存在するものの、離散ベイズフィルタや後述する粒子フィルタといった他のフィルタでは確率をよりアドホックで最適でない形でモデル化する。ベイズフィルタという手法の力は情報の欠如を確率変数として扱い、確率変数を確率分布として記述し、ベイズの定理を使って統計的推論の問題を解くところから生じている。

7.8 カルマンフィルタから g-h フィルタへの変換

カルマンフィルタは g-h フィルタの形を変えたものだと前に言及した。この証明には代数計算が少し必要になるだけだ。一次元の場合の方が簡単なので、ここでは一次元のカルマンフィルタと g-h フィルタを考える。次の等式を思い出そう:

\[ \mu_{x}=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2} \]

これは次のように記すと目に優しくなる:

\[ \mu_{x}=\frac{ya + xb} {a+b} \]

これは簡単に g-h フィルタの形式へ変換できる:

\[ \begin{aligned} \mu_{x} &= (x-x) + \frac{ya + xb} {a+b} \\ &= x-\frac{a+b}{a+b}x + \frac{ya + xb} {a+b} \\ &= x +\frac{-x(a+b) + xb+ya}{a+b} \\ &= x+ \frac{-xa+ya}{a+b} \\ &= x+ \frac{a}{a+b}(y-x) \\ \end{aligned} \]

これでほとんど導出は完了した。推定値の分散が次のように与えられたことを思い出そう:

\[ \begin{aligned} \sigma_{x}^2 &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \\ &= \frac{1}{\frac{1}{a} + \frac{1}{b}} \end{aligned} \]

これを使って \(\mu_x\) の式にある \(\displaystyle \frac{a}{a+b}\) を変形すると

\[ \begin{aligned} \frac{a}{a+b} &= \frac{a/a}{(a+b)/a} = \frac{1}{(a+b)/a} \\ &= \frac{1}{1 + \frac{b}{a}} = \frac{1}{\frac{b}{b} + \frac{b}{a}} \\ &= \frac{1}{b}\frac{1}{\frac{1}{b} + \frac{1}{a}} \\ &= \frac{\sigma^2_{x}}{b} \end{aligned} \]

となる。全てまとめれば

\[ \begin{aligned} \mu_{x} &= x+ \frac{a}{a+b}(y-x) \\ &= x + \frac{\sigma^2_{x}}{b}(y-x) \\ &= x + g_n(y-x) \end{aligned} \]

を得る。ここで

\[ g_n = \frac{\sigma^2_{x}}{\sigma^2_{y}} \]

である。最終的な結果は残差と定数の積に前回の値を足した値であり、g-h フィルタの \(g\) の式と一致する。\(g\) は新しい推定値の分散を観測値の分散で割った値となっている。もちろんカルマンフィルタでは \(g\) の値が各ステップで分散が変化するごとに変化する。\(h\) に対しても同様の式を導けるものの、特に面白いわけではないのでここではスキップする。結果は次のようになる:

\[ h_n = \frac{COV (x,\dot x)}{\sigma^2_{y}} \]

注目してほしいのは \(g\) と \(h\) が時刻 \(n\) における観測値と予測値の分散および共分散で完全に指定されるという事実である。言い換えれば、二つの入力の質によって決まるスケーリング係数を使って観測値と予測値の間の値が選択される。

訳注: 「ロケットサイエンス (rocket science)」は「とても難しいこと」を表すイディオム。^[return]
Cleve Moler and Charles Van Loan, "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later," SIAM Review, 45, 2003, 3-49.^[return]
Charles Van Loan, "Computing Integrals Involving the Matrix Exponential," IEEE Transactions Automatic Control, 23, 3, 1978, 395-404.^[return]
Robert Grover Brown and Patrick Y. C. Hwang, Introduction to Random Signals and Applied Kalman Filtering, Wiley and Sons, 2012, 143-147.^[return]
Robert Grover Brown and Patrick Y. C. Hwang, Introduction to Random Signals and Applied Kalman Filtering, Wiley and Sons, 2012, 143-147.^[return]
Daniela Calvetti and Erkki Somersalo, Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing, Springer, 2007.^[return]

第 7 章 カルマンフィルタの数学