補遺 D 反復最小二乗法によるセンサー統合
カルマンフィルタはセンサー統合 (sensor fusion) の分野で広く利用される。例えば位置センサーと速度センサーを手にしていて、両方のセンサーからのデータを組み合わせて最適な状態推定値を求めるような状況である。この章では異なるケース、具体的には複数のセンサーから同じ種類の観測値が手に入るケースを考える。
グローバル・ポジショニング・システム (Global Positioning System, GPS) は地球上の任意の場所が最低でも六つの衛星から観測できるように設計されている。GPS 受信機は地球から見た衛星の相対位置を知っており、各エポック (時刻) でそれぞれの衛星から信号を受信して衛星への疑似距離 (pseudorange) を計算する。詳しく言うと、GPS 受信機が受け取る衛星からの信号には発信された瞬間のタイムスタンプが含まれる。GPS 衛星に搭載されるのは原子時計なので、このタイムスタンプは精度が非常に高い。理論上は信号の速度は光速であり、光速は真空中で一定なので、GPS 受信機は自身に届くまでにかかった時間を測定することで非常に正確な距離を生成できる。
以上は理論上の話であり、実際にはいくつか問題がある。第一に、信号は真空ではなく大気中を進む。大気があると信号が曲がって軌跡が直線でなくなり、理論が示すより長い時間をかけて信号が受信機に到達することになる。第二に、GPS 受信機に搭載される時計は精度がそれほど高くない。そのため経過時刻を厳密に求めるのは自明な問題ではない。第三に、多くの環境で建物や木といった物体が信号を反射するので、軌跡が長くなったりマルチパスになったりする。マルチパスとは直接届いた信号とどこかに反射した信号の両方を受信する現象を言う。
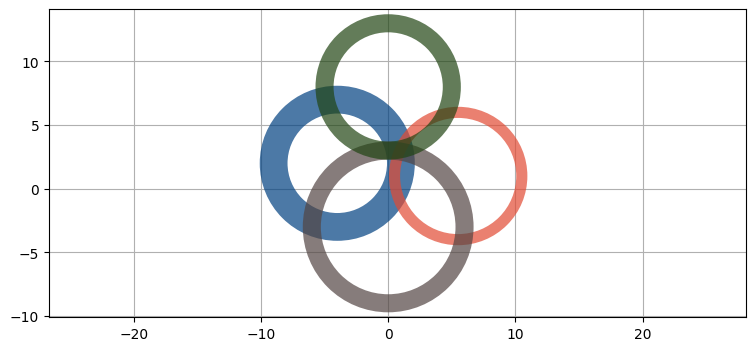
この問題を図にして考えよう。グラフの作成と解釈が簡単になるように二次元の図を使うが、もちろん今からの説明は三次元に一般化できる。私たちはそれぞれの衛星の位置とそこまでの距離 (疑似距離) を知っている。距離は正確に測定できないので、距離の観測値にはノイズが存在する。このノイズは図中の輪の厚みとして表される。次の図に四つの衛星から観測された四つの疑似距離の例を示す。交点を見やすくするために、現実の衛星の位置としてはあり得ないような位置に和の中心を配置している。また誤差と距離の比もおかしいが、これも見やすさのためだ:
二次元空間を考えるときは観測値が二つあれば位置が一意に決定する。距離が示す円が二つあると交点が二つ生じるものの、どちらかは物理的に不可能である (宇宙空間あるいは地下にある) ことが多いためだ。ただ GPS では時間についても解く必要があることを考えると、二次元の位置を手に入れるには三つ目の観測値も必要になる。
GPS は三次元のシステムなので、空間の三次元と時間の一次元を考える必要がある。つまり未知数は四つであり、理論上は四つの衛星があれば必要な情報が全て手に入る。しかし GPS では最低でも六つの衛星が観測でき、それより多い場合もよくある。これは系が優決定 (overdetermined) であることを意味する。最後に、観測値にはノイズが含まれるので、どの疑似距離も正確に交わりはしない。
線形代数に明るいなら、これが科学計算で非常に頻繁に登場する問題であり、優決定系を解く様々な手法が存在することを知っているだろう。GPS 受信機が位置を求めるときに使われる最も一般的なアプローチはおそらく反復最小二乗 (iterative least squares, ILS) アルゴリズムである。知っての通り、誤差がガウス分布に従うなら最小二乗のアルゴリズムは最適な解を計算する。別の言葉を使えば、私たちは優決定系の残差の二乗を最小化するアルゴリズムを考えている。
あなたが知っているはずの定義から始めよう。まず、イノベーションを次のように定義する:
ここで \(\mathbf{z}\) は観測値、\(h(\bullet)\) は観測関数、\(\delta \mathbf{z}^-\) はイノベーションを表す。\(\delta \mathbf{z}^-\) は FilterPy で y と表記される。言い換えると、イノベーションは線形カルマンフィルタの更新ステップで \(\mathbf{y} = \mathbf z - \mathbf{H\bar{x}}\) と表される値である。
続いて観測残差 (mearurement residual) を次のように定義する:
添え字のプラスは読みにくくなると思って本書ではこれまで使ってこなかった。\(\mathbf{x}^+\) は事後状態推定値を表す。つまり予測された (未知の将来の) 状態を表す。別の言い方をすれば、線形カルマンフィルタの予測ステップが計算するのが \(\mathbf{x}^+\) である。ここでは ILS が反復のたびに計算する値が \(\mathbf{x}^+\) で表される。
式の最小値を求めるには微分してゼロと等号で結べばいいのだった。今は最小化したいのは残差の二乗だから、次の方程式を解くことになる:
ここで
である。上式で観測関数 \(h(x)\) は線形化して行列 \(\mathbf{H}\) に置き換えている。ILS を行うには線形代数が必要になるので、各反復で \(h(\mathbf{x^-})\) に対応する \(\mathbf{H}\) を計算しなければならない。今考えているような問題では通常 \(h(\bullet)\) が非線形なので、線形化が必要になる (後述)。
様々な理由により、特定の観測値に他の観測値より大きな重みを割り当てたいことがある。例えば問題の幾何学的構成の関係で直交する観測値を重視したい場合や、ノイズの多い観測値がある場合である。このときは重み \(\mathbf{W}\) が加えた次の方程式を解くことになる:
一つ目の方程式を \(\delta \mathbf{x}\) について解くと次を得る (導出は次節):
二つ目の方程式からは次を得る:
方程式が優決定なので厳密な解を求めることはできず、反復的なアプローチを使うことになる。最初に位置の初期推定値を決め、そこから上述の式で \(\delta \mathbf{x}\) を計算する。計算された \(\delta \mathbf{x}\) を初期推測値に足して新しい推定値を作成し、その値を同じ式にもう一度入力されてさらに \(\delta \mathbf{x}\) を計算する。以上の処理を観測残差が十分小さくなるまで繰り返すのが ILS のアルゴリズムである。
ILS の導出
後で ILS をコードで実装するが、まずは \(\delta \mathbf{x}\) を計算する式を導出してみよう。興味が無いなら飛ばしても構わない。ただ、この導出はいくらか教育的であり、線形代数と偏微分方程式の基礎的な知識があれば難しすぎることはないはずだ。
偏微分方程式 \(\displaystyle \frac{\partial}{\partial \mathbf x}({\delta \mathbf z^+}^\mathsf{T}\delta \mathbf z^+) = 0\) に \(\delta \mathbf z^+=\delta \mathbf z^- - \mathbf H\delta \mathbf x\) を代入すると次を得る:
これを展開すれば次の式を得る:
ここで次の等式が成り立つ:
よって第三項は次のように計算できる:
同様に第二項も計算できる:
また次の等式も成り立つ:
これを使うと第一項を変形できる:
最後に、第四項は
となる。展開した偏微分方程式の項を以上の結果で置き換えれば
を得る。両辺に \((\mathbf H^\mathsf{T}\mathbf H)^{-1}\) を右から乗じれば
が分かる。両辺の転置を取れば
を得る。観測値に重みがある場合は偏微分方程式が
となり、同様の計算で次の解が求まる:
ILS の実装
私たちの目標は次の式を計算する反復解法を実装することである:
まず \(\mathbf H = \partial\mathbf z/\partial \mathbf x\) を計算しなければならない。例を小さく分かりやすくするために、問題は二次元とする。よって \(n\) 個の衛星があるとき \(\mathbf{H}\) は
\(x\) による偏微分は次のように計算できる:
\(y\) による偏微分はこの式の \(x\) を \(y\) に変えれば得られる。
ILS のアルゴリズムの疑似コードを示す:
def ILS:
位置を推測する。
while 収束していない:
現在の推定位置と各衛星との距離を計算する。
推定位置で線形化された H を計算する。
新しい推定位置とのデルタ (H^T H)'H^T dz を計算する。
新しい推定値 = 現在の推定値 + デルタ
収束を判定する。
これを Python で実装すると次のようになる:
import numpy as np
from numpy.linalg import norm, inv
from numpy.random import randn
from numpy import dot
np.random.seed(1234)
user_pos = np.array([800, 200])
sat_pos = np.asarray(
[[0, 1000],
[0, -1000],
[500, 500]], dtype=float)
def satellite_range(pos, sat_pos):
""" sat_pos に含まれる各位置と pos の距離を計算する。 """
diff = np.asarray(pos) - sat_pos
return norm(diff, axis=1)
def hx_ils(pos, sat_pos, range_est):
""" 観測関数を計算する。
pos : array_like
現在の推定位置。例えば (23, 45) など。
sat_pos : 二次元位置の array_like
各衛星の位置。例えば [(0,100), (100,0)] など。
range_est : floats の array_like
各衛星への距離。
"""
N = len(sat_pos)
H = np.zeros((N, 2))
for j in range(N):
H[j, 0] = (pos[0] - sat_pos[j, 0]) / range_est[j]
H[j, 1] = (pos[1] - sat_pos[j, 1]) / range_est[j]
return H
def lop_ils(zs, sat_pos, pos_est, hx, eps=1.e-6):
""" 既知の送信機の位置を利用して、
観測値の集合に対する解を反復的に求める。 """
pos = np.array(pos_est)
with book_format.numpy_precision(precision=4):
converged = False
for i in range(20):
r_est = satellite_range(pos, sat_pos)
print('反復:', i+1)
H = hx(pos, sat_pos, r_est)
Hinv = inv(dot(H.T, H)).dot(H.T)
# update position estimate
y = zs - r_est
print('イノベーション', y)
Hy = np.dot(Hinv, y)
pos = pos + Hy
print('位置 {}\n\n'.format(pos))
if max(abs(Hy)) < eps:
converged = True
break
return pos, converged
# 各センサーへの距離を計算する。
rz = satellite_range(user_pos, sat_pos)
pos, converted = lop_ils(rz, sat_pos, (900, 90), hx=hx_ils)
print('反復二乗法の解: ', pos)反復: 1
イノベーション [-148.512 28.6789 -148.5361]
位置 [805.4175 205.2868]
反復: 2
イノベーション [-0.1177 -7.4049 -0.1599]
位置 [800.04 199.9746]
反復: 3
イノベーション [-0.0463 -0.001 -0.0463]
位置 [800. 200.]
反復: 4
イノベーション [-0. -0. -0.]
位置 [800. 200.]
反復二乗法の解: [800. 200.]この結果について考えよう。最初の反復の計算は本質的に線形カルマンフィルタの更新ステップで行われる計算と等しい:
ここで ILS ではカルマンゲインは \(1\) である。初期推測値 \((900, 90)\) は非常に不正確であるのに対して、\(\mathbf{x}\) の推定値 \((805.4, 205.3)\) は実際の値 \((800, 200)\) に非常に近いことが分かる。最初の反復では推定値は完璧ではないものの、ILS は三回の反復で正確な解を求められている。センサー統合にカルマンフィルタではなく ILS を使う理由がこれで明らかになったことを願う──ILS を使った方が正確な結果が得られる。この実行例では初期推測値は非常に悪かった。もっとましな値に設定するとどうなるだろうか?
pos, converted = lop_ils(rz, sat_pos, (801, 201), hx=hx_ils)
print('反復二乗法の解: ', pos)反復: 1
イノベーション [-0.0009 -1.3868 -0.0024]
位置 [800.0014 199.9991]
反復: 2
イノベーション [-0.0016 -0. -0.0016]
位置 [800. 200.]
反復: 3
イノベーション [-0. -0. -0.]
位置 [800. 200.]
反復二乗法の解: [800. 200.]最初の反復で初期推測値より優れた推定値が生成され、その後の反復でさらに改善されているのが分かる。
上記の例ではフィルタの理論的性能を検証するために観測値にノイズを加えなかった。今度はノイズを加えたときにどうなるかを確認しよう:
# ノイズを加える。
nrz = []
for z in rz:
nrz.append(z + randn())
pos, converted = lop_ils(nrz, sat_pos, (601,198.3), hx=hx_ils)
print('反復二乗法の解: ', pos)反復: 1
イノベーション [129.8823 100.461 107.5398]
位置 [831.4474 186.1222]
反復: 2
イノベーション [-31.6446 -7.4837 -30.7861]
位置 [800.3284 198.8076]
反復: 3
イノベーション [-0.6041 -0.3813 0.3569]
位置 [799.948 198.6026]
反復: 4
イノベーション [-0.4803 0.0004 0.4802]
位置 [799.9476 198.6025]
反復: 5
イノベーション [-0.4802 0.0007 0.4803]
位置 [799.9476 198.6025]
反復二乗法の解: [799.948 198.602]ノイズがあると正確な解を求めることはできないものの、ILS の計算する推定値は反復ごとに素早く改善されている。