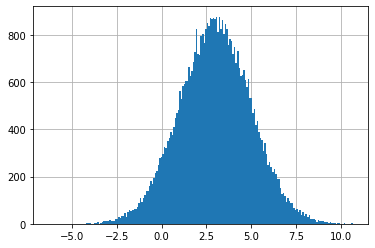
補遺 C 離散データの PDF の計算とプロット

確率分布の計算とプロットについて詳しく調べよう。

まず正規分布に従うデータをいくつか生成する。この処理には numpy.random.normal 関数を使う。この関数のパラメータの名前は少しわかりにくく、loc が分布の平均、scale が標準偏差を表す。呼び出すと、指定した平均と標準偏差を持つ正規分布に従う任意の個数のデータ点が生成される:

In [2]

import numpy as np
import numpy.random as random

mean = 3
std = 2

data = random.normal(loc=mean, scale=std, size=50000)
print(len(data))
print(data.mean())
print(data.std())

Out [2]

50000
2.9947741815932556
2.0063665533914694

出力から分かるように、生成された 5,000 個の点の平均は非常に \(3\) に近く、標準偏差もほぼ \(2\) に等しい。

ガウス分布をプロットしたいなら、scipy.stats.norm 関数を使って「固まった」正規分布を表すオブジェクトを作成し、ガウス分布の PDF (probability distribution function, 確率密度関数) を計算することで行える:

In [3]

%matplotlib inline
import matplotlib.pyplot as plt
import scipy.stats as stats

def plot_normal(xs, mean, std, **kwargs):
    norm = stats.norm(mean, std)
    plt.plot(xs, norm.pdf(xs), **kwargs)

xs = np.linspace(-5, 15, num=200)
plot_normal(xs, mean, std, color='k')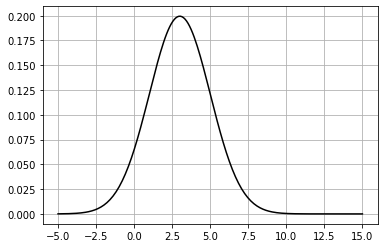

ただ私たちは数式として表された理想的な分布だけではなく、離散データとして与えられた分布に対してもプロットを行いたい。

ヒストグラムのプロット

これを行う方法はいくつかある。一つ目の方法は、データの集合のヒストグラムをプロットする Matplotlib の関数 matplotlib.hist を使うものだ。デフォルトだと hist はビン (小区間) に収まる点の個数を計算し、個数に応じてビンの高さを設定する:

In [4]

plt.hist(data, bins=200)
plt.show()

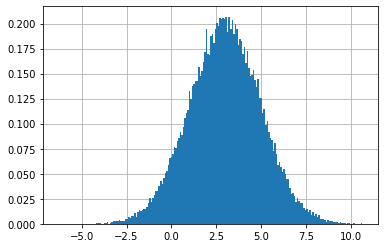
しかし、これはあまり有用でない──私たちがプロットしたいのは PDF であって、ビンに含まれるデータの個数ではない。幸いにも、hist のキーワード引数 density を True に設定すると PDF を描画させることができる:

In [5]

plt.hist(data, bins=200, density=True)
plt.show()

縦棒が気に入らなければ、histtype を 'step' にすることで曲線にできる:

In [6]

plt.hist(data, bins=200, density=True, histtype='step', lw=2)
plt.show()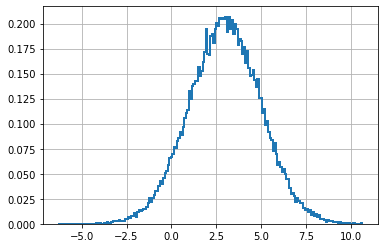

動作が正しいことを確認するために、理想的なガウス分布を黒でプロットしてみよう:

In [7]

plt.hist(data, bins=70, density=True, histtype='step', lw=2)
norm = stats.norm(mean, std)
plt.plot(xs, norm.pdf(xs), color='k', lw=2)
plt.show()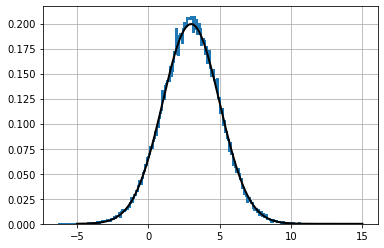

カーネル密度推定 (KDE)

データの集合を近似する分布を得る手法はもう一つある。カーネル密度推定 (kernel density estimate, KDE) と呼ばれるテクニックは特定のカーネルを利用してデータの集合を近似する確率分布を推定する。SciPy は KDE を scipy.stats.gaussian_kde 関数で実装する。この名前を誤解しないようにしてほしい──この gaussian は計算で使われるカーネルの種類を表しているだけで、この関数はガウス分布に従っていないデータに対しても行える。この節で使うデータはガウス分布に従っているものの、次節でそうでないデータを近似するときも同じ関数を利用できる。

In [8]

kde = stats.gaussian_kde(data)

xs = np.linspace(-5, 15, num=200)
plt.plot(xs, kde(xs))
plt.show()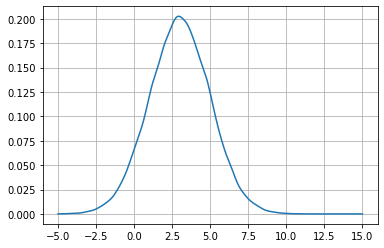

モンテカルロシミュレーション

こういったことを私たち (というより私) が行いたいのは、モンテカルロシミュレーションを使って分布を計算したいからである。ガウス分布に線形関数を適用するときは結果のガウス分布を簡単に計算できるのに対して、非線形関数を適用するときは解析的な計算が困難あるいは不可能になる。粒子フィルタのような手法は点を大量にサンプルして非線形関数に通し、変形された点を使って統計量を計算する。

コードが正しいことを納得しながら話を進めるために、最初は線形関数 \(f(x) = 2x + 12\) を考える。また出力を分かりやすくするために、実験で使うデータの平均と標準偏差を変更する。例えば \(x\) の係数が \(2\) で分布の平均と標準偏差も \(2\) だと、間違った結果が得られたときにどこが間違っているのかが分かりにくくなる。

In [9]

def f(x):
    return 2*x + 12

mean = 1.
std = 1.4
data = random.normal(loc=mean, scale=std, size=50000)

d_t = f(data) # f(x) でデータを変形する。

plt.hist(data, bins=200, density=True, histtype='step', lw=2)
plt.hist(d_t, bins=200, density=True, histtype='step', lw=2)

plt.ylim(0, .35)
plt.show()
print('平均      = {:.2f}'.format(d_t.mean()))
print('標準偏差  = {:.2f}'.format(d_t.std()))

Out [9]

平均      = 14.00
標準偏差  = 2.80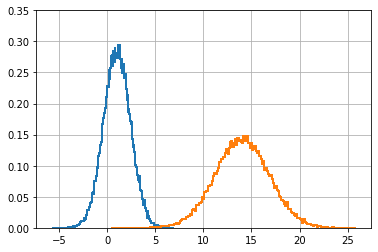

結果は期待通りである。入力のガウス分布 \(\mathcal{N}(\mu=1, \sigma=1.4)\) に対して関数 \(f(x) = 2x+12\) による変形が行われるから、平均は \(f(\mu) = 2*1 + 12 = 14\) にシフトされると期待できる。プロットと出力はそのようになっているのが確認できる。

次に進む前に、標準偏差で何が起きているかを説明できるだろうか？ \(f(x)\) に通した後の新しい標準偏差は \(2 \times 1.4 + 12 = 14.81\) になると思ったかもしれない。しかし、これは正しくない──標準偏差は乗算の係数にだけ影響を受け、足される値には影響を受けない。少し考えれば納得できるはずだ。分布に \(2\) を乗じると二倍だけ広がるようになるのに対して、\(12\) だけスライドさせても (いくらスライドさせても) 広がり具合いは変わらない──よって \(f(x)\) に通したデータは標準偏差が二倍になる。

非線形関数

これでコードの正しさに自信が持てたので、次は非線形関数を試そう。

In [10]

def f2(x):
    return (np.cos((1.5*x + 2.1))) * np.sin(0.3*x) - 1.6*x

d_t = f2(data)
plt.subplot(121)
plt.hist(d_t, bins=200, density=True, histtype='step', lw=2)

plt.subplot(122)
kde = stats.gaussian_kde(d_t)
xs = np.linspace(-10, 10, 200)
plt.plot(xs, kde(xs), 'k')
plot_normal(xs, d_t.mean(), d_t.std(), color='g', lw=3)
plt.show()
print('平均      = {:.2f}'.format(d_t.mean()))
print('標準偏差  = {:.2f}'.format(d_t.std()))

Out [10]

平均      = -1.59
標準偏差  = 2.09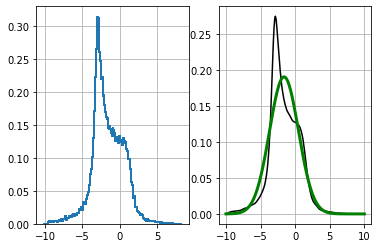

ここではデータを非線形関数 \(f(x) = \cos(1.5x+2.1)\sin\left(\frac{x}{3}\right) - 1.6x\) に通している。この関数は線形に非常に近いものの、プロットからはサンプルされたデータの PDF が大きくゆがんでいるのが分かる。

50,000 個の点を変形して変形後の点の PDF を計算する処理の裏では大量の計算が行われる。拡張カルマンフィルタ (EKF) は関数を平均で線形化してガウス分布を線形関数に通すことでこの計算を行わないで変換を済ませる。ガウス分布を線形関数に通す例は上で見たから、試してみよう。

非線形関数の線形化は \(x\) で微分することで行う。微分は SymPy を使うと計算できる:

In [11]

import sympy
x = sympy.symbols('x')
f = sympy.cos(1.5*x+2.1) * sympy.sin(x/3) - 1.6*x
dfx = sympy.diff(f, x)
dfx

Out [11]

\(\small -1.5*\sin(x/3)*\sin(1.5*x + 2.1) + \cos(x/3)*\cos(1.5*x + 2.1)/3 - 1.6\)

微分を平均値で評価すれば関数の傾きを計算できる:

In [25]

m = dfx.subs(x, mean)
m

Out [25]

-1.66528051815545

直線の方程式は \(y=mx + b\) だから、新しい標準偏差は元の値の約 \(1.67\) 倍になると分かる。また新しい平均は元の平均を元の関数 \(f(x)\) に通せば求められる。線形化された関数は点 \((x, f(x))\) を通る \(f(x)\) の接線であり、平均で評価すれば当然 \(f(x)\) と同じ値が得られる。この結果をプロットして、モンテカルロシミュレーションの結果と比較してみよう:

In [26]

plt.hist(d_t, bins=200, density=True, histtype='step', lw=2)
plot_normal(xs, f2(mean), abs(float(m)*std), color='k', lw=3, label='EKF')
plot_normal(xs, d_t.mean(), d_t.std(), color='r', lw=3, label='MC')
plt.legend()
plt.show()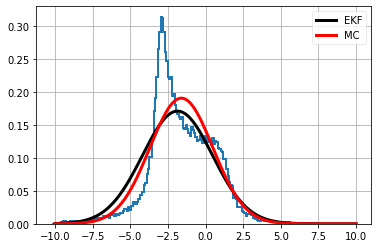

EKF で使われる近似は厳密ではないものの、大外れでもないことが分かる。