第 11 章 拡張カルマンフィルタ

目次

本書では前半の章で線形カルマンフィルタの理論を構築し、最後の二つの章では非線形な問題に対するカルマンフィルタの利用という話題に踏み込んだ。本章では拡張カルマンフィルタ (extended Kalman filter, EKF) を学ぶ。EKF は現在の推定値で系を線形化することで非線形性に対処し、線形化した系に対するフィルタリングに線形カルマンフィルタを利用する。EKF は非線形な問題に対する手法として最初に考案されたものの一つであり、現在最もよく使われる手法でもある。

EKF はフィルタの設計者に難しい数学の問題を提示する。そのため本章は本書の中で最も難しい章である。非線形なフィルタリングの問題に取り組むとき、私は EKF の利用を避けるためならどんなことでもするつもりで他の手法を優先する。ただ、この話題は避けられない: 古典的な論文は全て EKF を使っており、今の論文で使われることも多い。たとえ自分の仕事で EKF を使わないとしても、カルマンフィルタに関する文献を読めるようになるには EKF について知っておかなければならない。

11.1 問題の線形化

カルマンフィルタは線形な式を使っているので、非線形な問題には適用できない。問題が非線形になる原因は二つある。第一に、プロセスモデルが非線形になる可能性がある。例えば大気中を落下する物体は空気抗力を受けて加速度を失う。空気抗力の大きさは物体の速度に依存しているために、最終的な振る舞いは非線形になる──物体の動きを線形方程式でモデル化することはできない。第二に、観測モデルが非線形になる可能性がある。例えばレーダーは対象との直距離と方位を与える。そのため物体の位置を計算するには、非線形な三角関数を使わなければならない。

線形なフィルタではプロセスモデルと観測モデルを表す次の式が存在した:

\[ \begin{aligned}\dot{\mathbf x} &= \mathbf{Ax} + \mathbf{Bu} + w_x\\ \mathbf z &= \mathbf{Hx} + w_z \end{aligned} \]

ここで \(\mathbf{A}\) は系ダイナミクス行列を表す。カルマンフィルタの数学の章で説明した状態空間法を使うと、これらの式を次の形に変形できる:

\[ \begin{aligned} \bar{\mathbf x} &= \mathbf{Fx} + \mathbf{Bu} \\ \mathbf z &= \mathbf{Hx} \end{aligned} \]

ここで \(\mathbf{F}\) は基礎行列を表し、\(\mathbf{B}\) は一つ前の式に含まれる \(\mathbf{B}\) と異なる行列を表す。ノイズ \(w_x\) と \(w_z\) は行列 \(\mathbf{Q}\) と \(\mathbf{R}\) に組み込まれる。この形の式があると、ステップ \(k\) における状態をステップ \(k\) の観測値とステップ \(k-1\) の状態推定値から計算できる。これまでの章では直感的な理解を優先し、ニュートンの運動方程式で解ける問題だけを考えることで数式を最小限にしてきた。そういった問題では高校の物理学を使えば \(\mathbf{F}\) を設計できる。

非線形なモデルでは線形の式 \(\mathbf{Fx} + \mathbf{Bu}\) が非線形関数 \(f(\mathbf{x}, \mathbf{u})\) に置き換わり、線形の式 \(\mathbf{Hx}\) は非線形関数 \(h(\mathbf{x})\) に置き換わる:

\[ \begin{aligned}\bar{\mathbf x} &= f(\mathbf x, \mathbf u) \\ \mathbf z &= h(\mathbf x) \end{aligned} \]

この方程式を最適に解く新しいカルマンフィルタの式を求めればいいのではないかと思うかもしれない。しかし非線形フィルタの章で示したグラフを思い出せば、ガウス分布に非線形関数を適用して得られる確率分布はもはやガウス分布でない。よってカルマンフィルタの式を作成するアプローチは上手く行かない。

EKF はカルマンフィルタの線形な式を置き換えることはしない。そうではなく、EKF は非線形な式を現在の推定値で線形化し、線形化の結果を線形カルマンフィルタで使う。

線形化 (linearization) とは名前の通りのことを意味する。特定の点において曲線に最もよくマッチする直線を求め、それを曲線の代わりに使うということだ。次のグラフは放物線 \(f(x)=x^2-2x\) の \(x=1.5\) における線形化を示している:

In [3] 
import kf_book.ekf_internal as ekf_internal
ekf_internal.show_linearization()
線形化の例
Out [3]線形化の例

この曲線がプロセスモデルだとすれば、推定値 \(x=1.5\) で曲線を線形化した結果が破線の直線である。

系の線形化は微分を取ることで行われる。微分によって曲線の傾きが分かる:

\[ \begin{aligned} f(x) &= x^2 -2x \\ \frac{df}{dx} &= 2x - 2 \end{aligned} \]

これを \(x\) の実際の値で評価すれば、その点における曲線の傾きが分かる:

\[ \begin{aligned}m &= \frac{\partial f}{\partial x} \biggr|_{x=1.5} \\&= 2 \times 1.5 - 2 \\&= 1\end{aligned} \]

微分方程式で表される系の線形化も同様に行える。偏微分を取ることで \(f(\mathbf x, \mathbf u)\) と \(h(\mathbf x)\) を線形化し、それを \(\mathbf{x_t}\) と \(\mathbf{u_t}\) で評価すれば離散的な状態遷移行列 \(\mathbf{F}\) と観測行列 \(\mathbf{H}\) が得られる:

\[ \begin{aligned} \mathbf F &= {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}} \\ \mathbf H &= \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t} \end{aligned} \]

ここから次に示す EKF の式が得られる。線形カルマンフィルタと異なる部分を枠で囲った:

\[ \def\arraystretch{1.5} \begin{array}{l|l} \text{線形カルマンフィルタ} & \text{EKF} \\ \hline & \vphantom{\frac{\Huge M}{}} \boxed{\mathbf F = {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}}} \\ \mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} & \boxed{\mathbf{\bar x} = f(\mathbf x, \mathbf u)} \\ \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q & \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q \\ \hline & \vphantom{\frac{\Huge M}{}} \boxed{\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}} \\ \textbf{y} = \mathbf z - \mathbf{H \bar{x}} & \textbf{y} = \mathbf z - \boxed{h(\bar{x})}\\ \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} & \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} \\ \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} & \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} \\ \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} & \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} \end{array} \]

普通 EKF では状態を遷移させるのに \(\mathbf{Fx}\) を使わない: 線形化で正確さが失われるためだ。典型的に \(\bar{\mathbf{x}}\) の計算ではオイラー法やルンゲ=クッタ法といった適切な数値積分が使われるので、状態の遷移は \(\mathbf{Fx} + \mathbf{Bu}\) ではなく \(f(\mathbf x, \mathbf u)\) となる。同様の理由により残差の計算で \(\mathbf{H\bar{x}}\) は使われず、より正確な \(h(\bar{\mathbf x})\) が使われる。

EKF は例を最初に見るのが最も分かりやすいと思う。次の例を一度読んでからもう一度この節を読んでもいいかもしれない。

11.2 例: 航空機の追跡

この例では地上にあるレーダーを使って航空機を追跡する。前章ではこの問題に対する UKF を実装した。本章では同じ問題に対する EKF を実装し、フィルタの性能と実装の手間を比較してみよう。

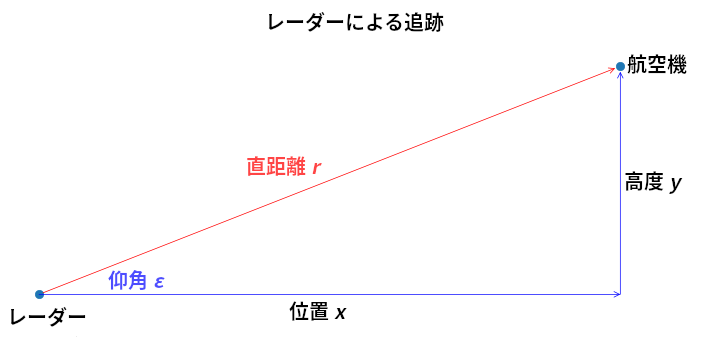
レーダーは電波 (マイクロ波) を周りに発射することで動作する。ビームの軌跡上にある任意の物体は信号の一部をレーダーに反射するので、反射信号がレーダーに戻ってくるまでの時間を計ることで目標までの直距離 (slant distance) が計算できる。直距離はレーダーと物体を直線で結んだ距離を表す。またアンテナの指向性利得(directive gain) からは方位 (仰角) が計算される。

\(x\) 方向を水平方向、\(y\) 方向を高度としたときに、レーダーが観測する直距離 \(r\) と仰角 \(\varepsilon\) の関係を次の図に示す:

In [4] 
ekf_internal.show_radar_chart()
レーダーの観測する直距離と仰角
Out [4]レーダーの観測する直距離と仰角

ここから次の関係が分かる:

\[ \begin{aligned} \varepsilon &= \tan^{-1} \frac y x \\[5pt] r^2 &= x^2 + y^2 \end{aligned} \]

状態変数の設計

航空機の速度と高度は一定で、観測値は航空機への直距離と仮定する。このとき位置を追跡したいとすると、三つの状態変数が必要になる──水平方向の距離、水平方向の速度、そして高度である:

\[ \mathbf x = \begin{bmatrix}\text{水平方向の距離} \\\text{水平方向の速度}\\ \text{高度}\end{bmatrix}= \begin{bmatrix}x \\ \dot x\\ y\end{bmatrix} \]

プロセスモデルの設計

航空機に対してはニュートンの運動方程式に支配される力学系を仮定する。このモデルはこれまでの章で使ってきたから、少し考えれば状態遷移行列が

\[ \mathbf F = \left[\begin{array}{cc|c} 1 & \Delta t & 0\\ 0 & 1 & 0 \\ \hline 0 & 0 & 1\end{array}\right] \]

であることが分かるだろう。行列がブロックに分かれているのは、左上のブロックが \(x\) に対する定常速度モデルに対応し、右下のブロックが \(y\) に対する定常位置モデルに対応することを目立たせるためだ。

ただここでは、こういった行列を求める練習をしてみよう。まず系を微分方程式の集合としてモデル化する。必要なのは次の形をした方程式である:

\[ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{w} \]

ここで \(\mathbf{w}\) はプロセスノイズを表す。

\(x\) と \(y\) は独立だから、個別に計算できる。一次元の運動を表す微分方程式は次の通りである:

\[ \begin{aligned}v &= \dot x \\ a &= \ddot{x} = 0\end{aligned} \]

この微分方程式を状態空間形式に書き換えよう。もし微分方程式が二階以上なら、最初にそれを等価な一階微分方程式の集合に変換する必要がある。今の微分方程式は一階だから、状態空間法が必要とする行列形式にそのまま書き換えられる:

\[ \begin{aligned}\begin{bmatrix}\dot x \\ \ddot{x}\end{bmatrix} &= \begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ \dot x\end{bmatrix} \\ \dot{\mathbf x} &= \mathbf{Ax}\end{aligned} \]

よって \(\mathbf A=\Big[\begin{smallmatrix}0&1\\0&0\end{smallmatrix}\Big]\) である。

\(\mathbf{A}\) が系ダイナミクス行列と呼ばれていたことを思い出してほしい。系ダイナミクス行列は微分方程式の集合を表し、これがあれば状態遷移行列 \(\mathbf{F}\) を計算できる。\(\mathbf{F}\) は離散タイムステップ \(\Delta t\) が経過した後の \(\mathbf{x}\) を計算する離散化された方程式の集合を表す。

\(\mathbf{F}\) の計算では行列指数のべき級数展開が使われることが多い:

\[ \mathbf F(\Delta t) = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A \Delta t)^3}{3!} + \cdots \]

\(\mathbf A^2 = \Big[\begin{smallmatrix}0&0\\0&0\end{smallmatrix}\Big]\) だから、\(\mathbf{A}\) の \(2\) 以上のべきは全て \(\mathbf{0}\) になる。よってこの級数が求まる:

\[ \begin{aligned} \mathbf F &=\mathbf{I} + \mathbf At + \mathbf{0} \\[5pt] &= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t \\[10pt] \mathbf F &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix} \end{aligned} \]

これは運動方程式を使ったときの結果と一致する！ 以上の導出には、線形微分方程式から状態遷移行列を求める方法を説明する以上の意味はない。この手法が必要になる例を本章の最後で見る。

観測モデルの設計

観測関数 \(h\) は状態の推定値 (事前分布) \(\bar{\mathbf{x}}\) を受け取り、それを観測値 (直距離) に変換する。この変換はピタゴラスの定理を使って行える:

\[ h({\mathbf x}) = \sqrt{x^2 + y^2} \]

平方根があるために、直距離と状態の関係は非線形である。\(\mathbf{x}_t\) における \(h({\mathbf{x}})\) の微分係数を計算することで \(h(\bar{\mathbf{x}})\) を線形化できる:

\[ \mathbf H = \frac{\partial{h(\bar{\mathbf x})}}{\partial{{\mathbf x}}}\biggr|_{{\mathbf x}_t} \]

行列の偏微分はヤコビ行列 (Jacobian) と呼ばれ、次のように定義される:

\[ \frac{\partial h({\mathbf x})}{\partial {\mathbf x}} = \begin{bmatrix} \displaystyle \frac{\partial h_1}{\partial x_1} & \displaystyle \frac{\partial h_1}{\partial x_2} &\dots \\[10pt] \displaystyle \frac{\partial h_2}{\partial x_1} & \displaystyle \frac{\partial h_2}{\partial x_2} &\dots \\[10pt] \vdots & \vdots & \ddots \end{bmatrix} \]

言い換えれば、 \(\mathbf{x}\) のいずれかの要素に関する関数 \(h\) の微分がヤコビ行列の要素となる。今考えている問題では

\[ \mathbf H = \begin{bmatrix} \displaystyle \frac{\partial h}{\partial x} & \displaystyle \frac{\partial h}{\partial \dot{x}} & \displaystyle \frac{\partial h}{\partial y} \end{bmatrix} \]

となる。それぞれ計算すると:

\[ \begin{aligned} \frac{\partial h}{\partial x} &= \frac{\partial}{\partial x} \sqrt{x^2 + y^2} \\ &= \frac{x}{\sqrt{x^2 + y^2}} \end{aligned} \]
\[ \begin{aligned} \frac{\partial h}{\partial \dot{x}} &= \frac{\partial}{\partial \dot{x}} \sqrt{x^2 + y^2} \\ &= 0 \end{aligned} \]
\[ \begin{aligned} \frac{\partial h}{\partial y} &= \frac{\partial}{\partial y} \sqrt{x^2 + y^2} \\ &= \frac{y}{\sqrt{x^2 + y^2}} \end{aligned} \]

以上より、\(\mathbf{H}\) が求まる:

\[ \mathbf H = \begin{bmatrix} \displaystyle \frac{x}{\sqrt{x^2 + y^2}} & 0 & & \displaystyle \frac{y}{\sqrt{x^2 + y^2}} \end{bmatrix} \]

この式が複雑に思えるかもしれない。一歩後ろに下がって、この数式が非常に単純なことを表しているのだと納得しておこう。私たちは航空機への直距離を表す式を手にしていて、それは非線形だった。カルマンフィルタは線形な式だけを扱えるので、\(\mathbf{H}\) を近似する線形方程式を見つける必要がある。先述の通り、考えている点における非線形な式の微分係数は良い線形近似になる。カルマンフィルタにおける「考えている点」とは状態変数 \(\mathbf{x}\) だから、直距離の \(\mathbf{x}\) における微分係数を計算する必要がある。線形カルマンフィルタの \(\mathbf{H}\) はフィルタの実行前に計算される定数だったのに対して、EKF の \(\mathbf{H}\) は \(\bar{\mathbf{x}}\) がエポックごとに変化するためにエポックごとに再計算される。

さらに理解を深めるために、この問題の \(h(\mathbf{x})\) に対するヤコビ行列を計算する Python 関数を書いてみよう:

In [5] 
from math import sqrt
def HJacobian_at(x):
    """ x におけるヤコビ行列 H を計算する。 """
    horiz_dist = x[0]
    altitude   = x[2]
    denom = sqrt(horiz_dist**2 + altitude**2)
    return array ([[horiz_dist/denom, 0., altitude/denom]])

最後に \(h(\mathbf x)\) を計算するコードを書く:

In [6] 
def hx(x):
    """ 状態 x に対応する直距離の観測値を計算する。"""
    return (x[0]**2 + x[2]**2) ** 0.5

続いてレーダーのシミュレーターを書こう:

In [7] 
from numpy.random import randn
import math

class RadarSim:
    """
    一定の速度と高度で飛行する航空機をシミュレートし、
    航空機からの信号を返す。
    """
    def __init__(self, dt, pos, vel, alt):
        self.pos = pos
        self.vel = vel
        self.alt = alt
        self.dt = dt

    def get_range(self):
        """
        航空機への直距離を返す。
        最後に呼び出してから dt 秒が経過して新しい観測値が
        必要になったときに一度だけ呼ばれるべきである。
        """
        # プロセスノイズを加える。
        self.vel = self.vel  + .1*randn()
        self.alt = self.alt + .1*randn()
        self.pos = self.pos + self.vel*self.dt

        # 観測ノイズを加える。
        err = self.pos * 0.05*randn()
        slant_dist = math.sqrt(self.pos**2 + self.alt**2)

        return slant_dist + err

プロセスノイズ行列と観測ノイズ行列の設計

レーダーは目標への直距離を返す。この距離に加わるノイズは \(\sigma_{range}= 5\) とする。ここから次を得る:

\[ \mathbf R = \begin{bmatrix}\sigma_{range}^2\end{bmatrix} = \begin{bmatrix}25\end{bmatrix} \]

\(\mathbf{Q}\) の設計には多少の議論が必要になる。状態 \(\mathbf x= \Big[x \ \ \dot x \ \ y\Big]^\mathtt{T}\) の最初の二つの要素は位置 (水平方向の距離) と速度だから、\(\mathbf{Q}\) の左上部分は Q_discrete_white_noise 関数で計算できる。\(\mathbf{x}\) の三つ目の要素は高度であり、これは水平方向の距離と独立だと仮定していた。以上より \(\mathbf{Q}\) の構成が分かる:

\[ \mathbf Q = \begin{bmatrix}\mathbf Q_\mathbf{x} & 0 \\ 0 & Q_{y}\end{bmatrix} \]

実装

FilterPy は ExtendedKalmanFilter クラスを提供する。このクラスの動作はこれまでに使ってきた KalmanFilter クラスと基本的に同様だが、\(h(\mathbf{x})\) を計算する関数と \(h(x)\) のヤコビ行列を計算する関数を提供できるようになっている。

コードはフィルタクラスをインポートして作成するところから始まる。x の次元は 3 であり、z の次元は 1 である:

from filterpy.kalman import ExtendedKalmanFilter
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)

続いてレーダーのシミュレーターを作成する:

radar = RadarSim(dt, pos=0., vel=100., alt=1000.)

フィルタは航空機の実際の位置に近い地点で初期化する:

rk.x = array([radar.pos, radar.vel-10, radar.alt+100])

先述したテイラー級数展開の最初の項を使って状態遷移行列を計算する:

dt = 0.05
rk.F = eye(3) + array([[0, 1, 0], [0, 0, 0], [0, 0, 0]]) * dt

\(\mathbf{R}\), \(\mathbf{Q}\), \(\mathbf{P}\) に適当な値を設定したら、フィルタは簡単なループで実行できる。update メソッドには観測関数 \(h(\mathbf{x})\) を計算する関数と \(h(\mathbf{x})\) のヤコビ行列を計算する関数を渡している:

for i in range(int(20/dt)):
    z = radar.get_range()
    rk.predict()
    rk.update(array([z]), HJacobian_at, hx)

結果を保存してプロットするボイラープレートコードをいくらか加えれば次のコードとなる:

In [8] 
from filterpy.common import Q_discrete_white_noise
from filterpy.kalman import ExtendedKalmanFilter
from numpy import eye, array, asarray
import numpy as np

dt = 0.05
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)
radar = RadarSim(dt, pos=0., vel=100., alt=1000.)

# 初期推測値を実際の値とずらす。
rk.x = array([radar.pos-100, radar.vel+100, radar.alt+1000])
rk.F = eye(3) + array([[0, 1, 0], [0, 0, 0], [0, 0, 0]]) * dt
range_std = 5. # メートル
rk.R = np.diag([range_std**2])
rk.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
rk.Q[2,2] = 0.1
rk.P *= 50

xs, track = [], []
for i in range(int(20/dt)):
    z = radar.get_range()
    track.append((radar.pos, radar.vel, radar.alt))

    rk.predict()
    rk.update(array([z]), HJacobian_at, hx)
    xs.append(rk.x)

xs = asarray(xs)
track = asarray(track)
time = np.arange(0, len(xs)*dt, dt)
ekf_internal.plot_radar(xs, track, time)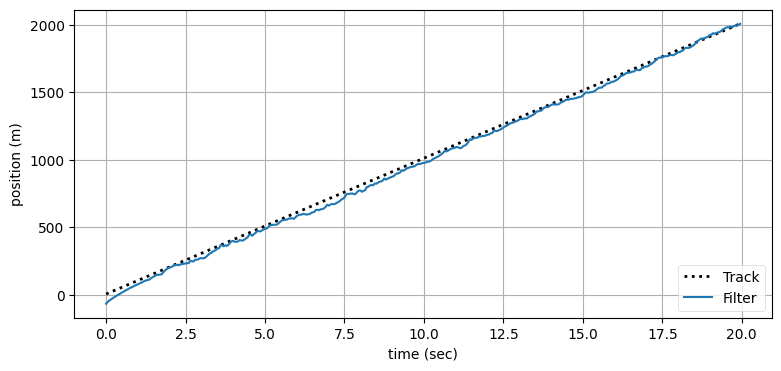
EKF の実行結果 (位置)
Out [8]EKF の実行結果 (位置)
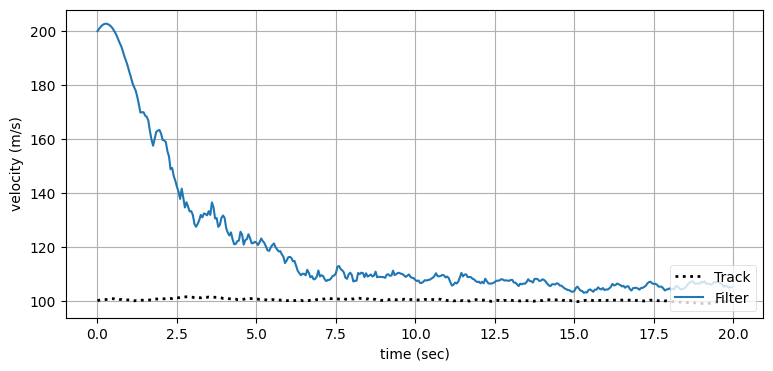
EKF の実行結果 (速度)
Out [8]EKF の実行結果 (速度)
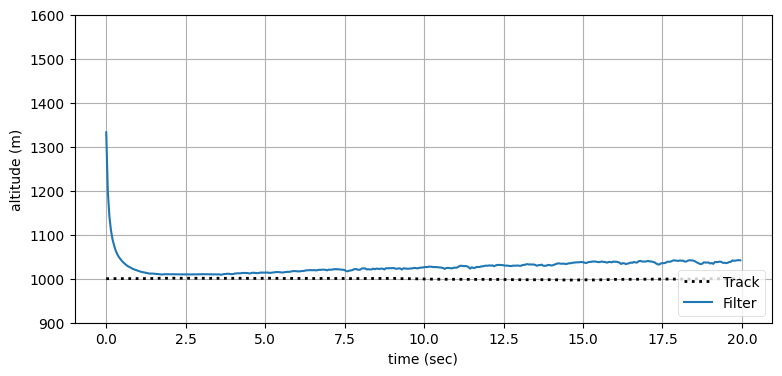
EKF の実行結果 (高度)
Out [8]EKF の実行結果 (高度)

フィルタは航空機を正しく追跡できている。

11.3 SymPy を使ったヤコビ行列の計算

微分の計算に慣れていない読者は上のヤコビ行列の計算を難しく感じたかもしれない。また、たとえこの程度の微分が簡単に行えたとしても、問題が少しでも難しくなれば微分の計算は非常に難しくなる。

補遺 A で説明されるように、SymPy パッケージを使うとヤコビ行列を Python に計算させることができる:

In [9] 
import sympy
from IPython.display import display
sympy.init_printing(use_latex='mathjax')

x, x_vel, y = sympy.symbols('x, x_vel y')

H = sympy.Matrix([sympy.sqrt(x**2 + y**2)])

state = sympy.Matrix([x, x_vel, y])
J = H.jacobian(state)

display(state)
display(J)
Out [9]
\(\displaystyle \left[\begin{matrix}x\\x_{vel}\\y\end{matrix}\right]\)
Out [9]
\(\displaystyle \left[\begin{matrix}\displaystyle \frac{x}{\sqrt{x^{2} + y^{2}}} & 0 &\displaystyle \frac{y}{\sqrt{x^{2} + y^{2}}}\end{matrix}\right]\)

結果は以前の計算と同じであり、ヤコビ行列をずっと簡単に計算できた！

11.4 ロボットの自己位置推定

次は現実的な問題を考えよう。この節は難しいと最初に警告しておく。ただ多くの書籍は簡単で教科書的な問題を選んで簡単な答えを示すだけで済ませており、そうすると読者は学んだ知識を使って現実の問題をどのように解決すればいいのだろうかと疑問に思ったまま本を読み終えることになる。

これからロボットの自己位置推定の問題を考える。この問題に対する UKF は無香料カルマンフィルタで実装したので、もし読んでなければ読んでおくことを推奨する。このシナリオでは、周りにあるランドマークを検出するセンサーを利用して環境内を移動するロボットが登場する。このロボットはコンピュータービジョンを使って木や歩行者などを特定する自動運転車かもしれないし、家の中を掃除する小さなロボットかもしれないし、倉庫で使われるロボットかもしれない。

ロボットには四つの車輪があり、その構成は自動車と同じとする。ロボットは二つの前輪を回すことで機動するので、旋回はロボットが前に進みながら後車軸を中心に起こる。これは非線形な振る舞いであり、私たちはこれをモデル化しなければならない。

ロボットにはセンサーが付いていて、周りにある既知の対象への距離と方位の近似値を報告すると仮定する。距離と方位から位置を計算するには平方根と三角関数が必要なので、ここにも非線形性がある。

この問題ではプロセスモデルと観測モデルが両方とも非線形である。EKF は両方に対応できるから、EKF ならこの問題に対応できそうだと暫定的に結論できる。

ロボットの運動モデル

簡単な近似として、自動車は前に進みながら前輪を回すことで旋回を行うとする考え方がある。つまり自動車は後輪を軸に旋回し、そのとき車の前方部分が前輪の向く方向に移動するということだ。この単純な説明が考慮していない要素は多くある: 摩擦によるスリップ、異なる速度におけるゴムタイヤの振る舞いの変化、あるいは外側のタイヤが内側のタイヤより長い距離を動かなければならない事実は無視されており、これらを取り入れたモデルはさらに複雑になる。自動車の旋回を正確にモデル化するには複雑な微分方程式の集合が必要である。

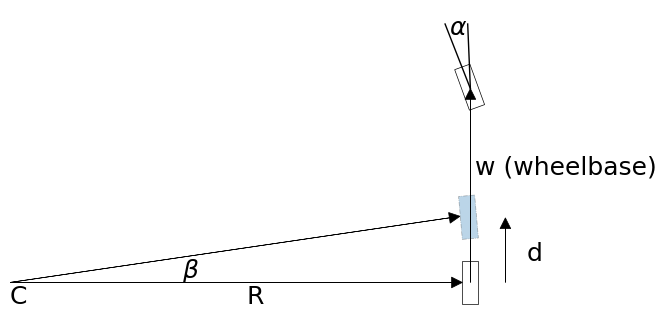
カルマンフィルタでフィルタリングを行うとき、特に低速度のロボットに対して行うときは、これより単純な自転車モデル (bicycle model) で優れた結果が得られることが分かっている。このモデルを表す図を示す:

In [10] 
ekf_internal.plot_bicycle()
自転車モデル
Out [10]自転車モデル

無香料カルマンフィルタの章で次の等式を導いた:

\[ \begin{aligned} d &= v \Delta t \\ R &= \frac{d}{\beta} \\ \beta &= \frac d w \tan(\alpha) \\ \bar x &= x - R\sin(\theta) + R\sin(\theta + \beta) \\ \bar y &= y + R\cos(\theta) - R\cos(\theta + \beta) \\ \bar \theta &= \theta + \beta \end{aligned} \]

ここで \(x\), \(y\) はロボットの位置、\(\theta\) はロボットの向きを表す。

車両の旋回モデルに興味がないなら導出を理解する必要はない。ここで重要なのは、私たちの考えている運動モデルが非線形であり、それをカルマンフィルタで扱う必要があると理解することだ。

状態変数の設計

この問題に対するフィルタではロボットの位置 \(x\), \(y\) と向き \(\theta\) を状態とする:

\[ \mathbf x = \begin{bmatrix}x \\ y \\ \theta\end{bmatrix} \]

制御入力 \(\mathbf{u}\) は速度 \(v\) と旋回角 \(\alpha\) から構成されるとする:

\[ \mathbf u = \begin{bmatrix}v \\ \alpha\end{bmatrix} \]

プロセスモデルの設計

非線形な運動モデルにノイズを加えたものを系のモデルとする:

\[ \bar x = f(\mathbf{x}, \mathbf{u}) + \mathcal{N}(\mathbf{0}, \mathbf{Q}) \]

先述したロボットの運動モデルを代入すると次を得る:

\[ \begin{bmatrix} \bar{x} \\[3pt] \bar{y} \\[5pt] \bar{\theta} \end{bmatrix} = \begin{bmatrix}x \\[3pt] y \\[5pt] \theta \end{bmatrix} + \begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\[3pt] R\cos(\theta) - R\cos(\theta + \beta) \\[3pt] \beta\end{bmatrix} \]

\(\mathbf{F}\) は \(f(\mathbf{x},\mathbf{u})\) のヤコビ行列として計算される。定義は次の通りである:

\[ \mathbf F = \frac{\partial f(\mathbf{x}, \mathbf{u})}{\partial \mathbf{x}} = \begin{bmatrix} \displaystyle \frac{\partial f_1}{\partial x} & \displaystyle \frac{\partial f_1}{\partial y} & \displaystyle \frac{\partial f_1}{\partial \theta}\\[10pt] \displaystyle \frac{\partial f_2}{\partial x} & \displaystyle \frac{\partial f_2}{\partial y} & \displaystyle \frac{\partial f_2}{\partial \theta} \\[10pt] \displaystyle \frac{\partial f_3}{\partial x} & \displaystyle \frac{\partial f_3}{\partial y} & \displaystyle \frac{\partial f_3}{\partial \theta} \end{bmatrix} \]

これを実際に計算すれば、次を得る:

\[ \mathbf F = \begin{bmatrix} 1 & 0 & -R\cos(\theta) + R\cos(\theta+\beta) \\ 0 & 1 & -R\sin(\theta) + R\sin(\theta+\beta) \\ 0 & 0 & 1 \end{bmatrix} \]

SymPy を使って検算しておこう:

In [11] 
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
from sympy import symbols, Matrix
sympy.init_printing(use_latex="mathjax", fontsize='16pt')
time = symbols('t')
d = v*time
beta = (d/w)*sympy.tan(alpha)
r = w/sympy.tan(alpha)

fxu = Matrix([[x-r*sympy.sin(theta) + r*sympy.sin(theta+beta)],
              [y+r*sympy.cos(theta)- r*sympy.cos(theta+beta)],
              [theta+beta]])
F = fxu.jacobian(Matrix([x, y, theta]))
F
Out [11]
\(\displaystyle \left[\begin{matrix}1 & 0 & \displaystyle - \frac{w \cos{\left(\theta \right)}}{\tan{\left(\alpha \right)}} + \frac{w \cos{\left(\frac{t v \tan{\left(\alpha \right)}}{w} + \theta \right)}}{\tan{\left(\alpha \right)}}\\[10pt] 0 & 1 & \displaystyle - \frac{w \sin{\left(\theta \right)}}{\tan{\left(\alpha \right)}} + \frac{w \sin{\left(\frac{t v \tan{\left(\alpha \right)}}{w} + \theta \right)}}{\tan{\left(\alpha \right)}}\\[15pt] 0 & 0 & 1\end{matrix}\right]\)

かなり複雑に見える。こういった場合は項を置換する SymPy の機能が使える:

In [12] 
# 共通する式を置き換える。
B, R = symbols('beta, R')
F = F.subs((d/w)*sympy.tan(alpha), B)
F.subs(w/sympy.tan(alpha), R)
Out [12]
\(\displaystyle \left[\begin{matrix}1 & 0 & - R \cos{\left(\theta \right)} + R \cos{\left(\beta + \theta \right)}\\0 & 1 & - R \sin{\left(\theta \right)} + R \sin{\left(\beta + \theta \right)}\\0 & 0 & 1\end{matrix}\right]\)

ヤコビ行列の計算が正しいことが確認できた。

続いてノイズに注意を向けよう。この例ではノイズが制御入力に加わるとする: つまりノイズは制御空間で発生する。言い換えれば、速度と旋回角を指定するコマンドにノイズが加わる。このため \(x\), \(y\), \(\theta\) に生じるノイズは制御入力へのノイズを変換することで求める必要がある。さらに現実の系では制御入力に加わるノイズが速度によって変わる可能性もあり、もし変わるなら予測のたびにノイズを再計算する必要がある。この例ではこれをノイズモデルとして選択する。現実のロボットを考えるときは、系の誤差を正確に描写するモデルを選択しなければならない。このノイズは \(\mathbf{M}\) で表す:

\[ \mathbf{M} = \begin{bmatrix}\sigma_{vel}^2 & 0 \\ 0 & \sigma_\alpha^2\end{bmatrix} \]

これが線形の問題なら、制御空間から状態空間の変換はお馴染みの \(\mathbf{FMF}^\mathsf T\) で行える。しかし今考えている運動モデルは非線形なので、変換後のノイズ共分散行列を計算する閉じた形式の式を求めることはせずに、ヤコビ行列を使って線形化を行う。ヤコビ行列には \(\mathbf{V}\) と名前を付けておく:

\[ \mathbf{V} = \frac{\partial f(\mathbf{x}, \mathbf{u})}{\partial \mathbf{u}} = \begin{bmatrix} \displaystyle \frac{\partial f_1}{\partial v} & \displaystyle \frac{\partial f_1}{\partial \alpha} \\[10pt] \displaystyle \frac{\partial f_2}{\partial v} & \displaystyle \frac{\partial f_2}{\partial \alpha} \\[10pt] \displaystyle \frac{\partial f_3}{\partial v} & \displaystyle \frac{\partial f_3}{\partial \alpha} \end{bmatrix} \]

このとき変換後のノイズ共分散行列は \(\mathbf{VMV}^\mathsf{T}\) となる。\(\mathbf{V}\) に含まれる偏微分は非常に難しいので、SymPy を使って計算しよう:

In [13] 
V = fxu.jacobian(Matrix([v, alpha]))
V = V.subs(sympy.tan(alpha)/w, 1/R)
V = V.subs(time*v/R, B)
V = V.subs(time*v, 'd')
V
Out [13]
\(\displaystyle \left[\begin{matrix}t \cos{\left(\beta + \theta \right)} & \frac{d \left(\tan^{2}{\left(\alpha \right)} + 1\right) \cos{\left(\beta + \theta \right)}}{\tan{\left(\alpha \right)}} - \frac{w \left(- \tan^{2}{\left(\alpha \right)} - 1\right) \sin{\left(\theta \right)}}{\tan^{2}{\left(\alpha \right)}} + \frac{w \left(- \tan^{2}{\left(\alpha \right)} - 1\right) \sin{\left(\beta + \theta \right)}}{\tan^{2}{\left(\alpha \right)}}\\t \sin{\left(\beta + \theta \right)} & \frac{d \left(\tan^{2}{\left(\alpha \right)} + 1\right) \sin{\left(\beta + \theta \right)}}{\tan{\left(\alpha \right)}} + \frac{w \left(- \tan^{2}{\left(\alpha \right)} - 1\right) \cos{\left(\theta \right)}}{\tan^{2}{\left(\alpha \right)}} - \frac{w \left(- \tan^{2}{\left(\alpha \right)} - 1\right) \cos{\left(\beta + \theta \right)}}{\tan^{2}{\left(\alpha \right)}}\\\frac{t}{R} & \frac{d \left(\tan^{2}{\left(\alpha \right)} + 1\right)}{w}\end{matrix}\right]\)

EKF では数式がすぐに手に負えなくなることが実感できるはずだ。

以上で予測ステップの式が完成する:

\[ \begin{aligned} \mathbf{\bar x} &= \mathbf x + \begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\ R\cos(\theta) - R\cos(\theta + \beta) \\ \beta\end{bmatrix}\\[10pt] \mathbf{\bar P} &=\mathbf{FPF}^{\mathsf T} + \mathbf{VMV}^{\mathsf T} \end{aligned} \]

これが \(\mathbf{x}\) を予測する唯一の方法というわけではない。例えばルンゲ=クッタ法といった数値積分の手法でロボットの運動を計算することもできる。タイムステップが大きいときは高度な数値積分手法が必要になるだろう。EKF はカルマンフィルタほど型が決まっていないので、現実の問題に対して EKF を使うときは系を注意深くモデル化し、系を最も正確に解く方法を見つけなければならない。正しいアプローチを定める要素には、要求する正確さ、方程式の非線形性の程度、処理能力の予算、そして数値的安定性の問題などがある。

観測モデルの設計

ロボットのセンサーは既知のランドマークに対する距離と方位を観測し、観測値にはノイズが含まれる。観測モデルは状態 \(\Big[x \ \ y \ \ \theta\Big]^\mathsf T\) をランドマークに対する距離と方位に変換しなければならない。ランドマークの位置を \(\mathbf{p} = (p_x,\ p_y)\) とすれば、ロボットとの距離 \(r\) は

\[ r = \sqrt{(p_x - x)^2 + (p_y - y)^2} \]

と計算できる。センサーが観測する方位はロボットの向きとの相対的な方位であると仮定する。そのためセンサーが観測する方位の計算では本来の方位からロボットの向きを引かなければならない:

\[ \phi = \arctan\left(\frac{p_y - y}{p_x - x}\right) - \theta \]

よって今の問題に対する観測モデル \(h\) は次のようになる:

\[ \begin{aligned} \mathbf z& = h(\bar{\mathbf x}, \mathbf p) &+\ \ \mathcal{N}(0, R)\\[5pt] &= \begin{bmatrix} \sqrt{(p_x - x)^2 + (p_y - y)^2}\ \ \\[5pt] \displaystyle \arctan \left(\frac{p_y - y}{p_x - x}\right) - \theta \end{bmatrix} &+\ \ \mathcal{N}(0, R) \end{aligned} \]

これは明らかに線形でない。よってヤコビ行列の計算を通じて \(h\) を \(\mathbf{x}\) に関して線形化する必要がある。SymPy を使ったヤコビ行列の計算を示す:

In [14] 
px, py = symbols('p_x, p_y')
z = Matrix([[sympy.sqrt((px-x)**2 + (py-y)**2)],
            [sympy.atan2(py-y, px-x) - theta]])
z.jacobian(Matrix([x, y, theta]))
Out [14]
\(\displaystyle \left[\begin{matrix}\frac{- p_{x} + x}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & \frac{- p_{y} + y}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & 0\\- \frac{- p_{y} + y}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & - \frac{p_{x} - x}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & -1\end{matrix}\right]\)

次はこれを Python の関数にしよう。例えば次のように書ける:

In [15] 
from math import sqrt

def H_of(x, landmark_pos):
    """
    h(x) のヤコビ行列 H を計算する。
    h(x) は状態 x からランドマークの位置と方位を計算する。
    """
    px = landmark_pos[0]
    py = landmark_pos[1]
    hyp = (px - x[0, 0])**2 + (py - x[1, 0])**2
    dist = sqrt(hyp)

    H = array(
        [[-(px - x[0, 0]) / dist, -(py - x[1, 0]) / dist, 0],
         [ (py - x[1, 0]) / hyp,  -(px - x[0, 0]) / hyp, -1]])
    return H

系の状態を観測値に変換する関数も定義する必要がある:

In [16] 
from math import atan2

def Hx(x, landmark_pos):
    """ 状態を受け取り、その状態が生成する観測値を返す。 """
    px = landmark_pos[0]
    py = landmark_pos[1]
    dist = sqrt((px - x[0, 0])**2 + (py - x[1, 0])**2)

    Hx = array([[dist],
                [atan2(py - x[1, 0], px - x[0, 0]) - x[2, 0]]])
    return Hx

観測ノイズの設計

距離と方位の観測値に含まれるノイズは独立だと仮定するのが理にかなっている。よって

\[ \mathbf R=\begin{bmatrix}\sigma_{range}^2 & 0 \\ 0 & \sigma_{bearing}^2\end{bmatrix} \]

となる。

実装

EKF の実装では FilterPy の ExtendedKalmanFilter クラスを使う。このクラスの predict メソッドはプロセスモデルを表す通常の線形方程式を使って予測を行う。今の問題では予測ステップが非線形だから、ExtendedKalmanFilter クラスを継承した新しいクラスを作って predict を独自の実装でオーバーライドする必要がある。このクラスにはロボットのシミュレートも行わせたいので、ロボットの位置を計算する move メソッドを作成し、それを predict とシミュレーションの両方から使うようにする。

予測ステップで使う行列 \(\mathbf{V}\) は非常に大きい。私がこのコードを書いたとき、正しく動くようになるまでに何度か実装を間違った。この間違いが判明したのは、SymPy の数式オブジェクトに値を代入して値を評価する evalf 関数のおかげだった。この手法を示しておくべきだと思ったので、次のカルマンフィルタのコードでは evalf を直接使っている。evalf に関していくつか理解しておくべき事項がある。

まず、evalf は辞書を使って値を指定する。例えば行列 M に x と y が含まれるなら、evalf は次のように使う:

M.evalf(subs={x:3, y:17})

このコードは M の x に 3 を、y に 17 を代入した行列を計算する。

次に、evalf の返り値は sympy.Matrix オブジェクトであり、numpy.array(M).astype(float) とすると NumPy 配列に変換できる。numpy.array(M) だと要素型が object の配列になるので、計算に使うことができない。

EKF のコードを示す:

In [17] 
from filterpy.kalman import ExtendedKalmanFilter as EKF
from numpy import array, sqrt
class RobotEKF(EKF):
    def __init__(self, dt, wheelbase, std_vel, std_steer):
        EKF.__init__(self, 3, 2, 2)
        self.dt = dt
        self.wheelbase = wheelbase
        self.std_vel = std_vel
        self.std_steer = std_steer

        a, x, y, v, w, theta, time = symbols(
            'a, x, y, v, w, theta, t')
        d = v*time
        beta = (d/w)*sympy.tan(a)
        r = w/sympy.tan(a)

        self.fxu = Matrix(
            [[x-r*sympy.sin(theta)+r*sympy.sin(theta+beta)],
             [y+r*sympy.cos(theta)-r*sympy.cos(theta+beta)],
             [theta+beta]])

        self.F_j = self.fxu.jacobian(Matrix([x, y, theta]))
        self.V_j = self.fxu.jacobian(Matrix([v, a]))

        # 変数を後で使うために辞書へ保存する。
        self.subs = {x: 0, y: 0, v:0, a:0,
                     time:dt, w:wheelbase, theta:0}
        self.x_x, self.x_y, = x, y
        self.v, self.a, self.theta = v, a, theta

    def predict(self, u):
        self.x = self.move(self.x, u, self.dt)

        self.subs[self.x_x] = self.x[0, 0]
        self.subs[self.x_y] = self.x[1, 0]
        self.subs[self.theta] = self.x[2, 0]
        self.subs[self.v] = u[0]
        self.subs[self.a] = u[1]

        F = array(self.F_j.evalf(subs=self.subs)).astype(float)
        V = array(self.V_j.evalf(subs=self.subs)).astype(float)

        # 制御空間における運動ノイズの共分散行列
        M = array([[self.std_vel*u[0]**2, 0],
                   [0, self.std_steer**2]])

        self.P = F @ self.P @ F.T + V @ M @ V.T

    def move(self, x, u, dt):
        hdg = x[2, 0]
        vel = u[0]
        steering_angle = u[1]
        dist = vel * dt

        if abs(steering_angle) > 0.001: # ロボットは旋回しているか？
            beta = (dist / self.wheelbase) * tan(steering_angle)
            r = self.wheelbase / tan(steering_angle) # 半径

            dx = np.array([[-r*sin(hdg) + r*sin(hdg + beta)],
                           [r*cos(hdg) - r*cos(hdg + beta)],
                           [beta]])
        else: # 直線に沿って移動している。
            dx = np.array([[dist*cos(hdg)],
                           [dist*sin(hdg)],
                           [0]])
        return x + dx

解決しなければならない問題がもう一つある。残差は数式的には \(y = z - h(x)\) と計算されるものの、今考えている観測値には角度が含まれる。観測値 \(\mathbf{z}\) が \(1^\circ\) の方位を持っていて、\(h(\bar{\mathbf{x}})\) の方位は \(359^\circ\) だとしよう。ナイーブに二つの値を引くと角度の差は \(-358^\circ\) となるが、正しい値は \(2^\circ\) である。このため方位の残差を正しく計算するコードが必要になる:

In [18] 
def residual(a, b):
    """
    [直距離, 方位] という形をした観測値の残差 (a-b) を計算する。
    方位の差は [-pi,pi) に正規化される。
    """
    y = a - b
    y[1] = y[1] % (2 * np.pi)    # y[1] を [0, 2 pi) の範囲に変換する。
    if y[1] > np.pi:             # y[1] を [-pi, pi) に移す。
        y[1] -= 2 * np.pi
    return y

残りのコードはシミュレーションと結果のプロットであり、コメントはあまり必要ないだろう。ランドマークの座標は landmarks という変数に格納している。またシミュレーションではロボットの位置を一秒に十回更新するのに対して、UKF は一秒に一度しか実行されない。これには二つ理由がある。一つ目の理由は運動を表す微分方程式の積分でルンゲ=クッタ法を使っていないためで、タイムステップを小さくしてシミュレーションを正確にしている。二つ目の理由は組み込みシステムでは処理速度が限られていることが非常に多く、その場合はカルマンフィルタを絶対に必要なときにだけ実行しなければならないためだ。

In [19] 
from filterpy.stats import plot_covariance_ellipse
from math import sqrt, tan, cos, sin, atan2
import matplotlib.pyplot as plt

dt = 1.0

def z_landmark(lmark, sim_pos, std_rng, std_brg):
    x, y = sim_pos[0, 0], sim_pos[1, 0]
    d = np.sqrt((lmark[0] - x)**2 + (lmark[1] - y)**2)
    a = atan2(lmark[1] - y, lmark[0] - x) - sim_pos[2, 0]
    z = np.array([[d + randn()*std_rng],
                  [a + randn()*std_brg]])
    return z

def ekf_update(ekf, z, landmark):
    ekf.update(z, HJacobian=H_of, Hx=Hx, residual=residual,
               args=(landmark), hx_args=(landmark))


def run_localization(landmarks, std_vel, std_steer,
                     std_range, std_bearing,
                     step=10, ellipse_step=20, ylim=None):
    ekf = RobotEKF(dt, wheelbase=0.5, std_vel=std_vel,
                   std_steer=std_steer)
    ekf.x = array([[2, 6, .3]]).T # x, y, 旋回角
    ekf.P = np.diag([.1, .1, .1])
    ekf.R = np.diag([std_range**2, std_bearing**2])

    sim_pos = ekf.x.copy() # シミュレートされた位置
    u = array([1.1, .01])  # 操縦コマンド (速度と旋回角)
    plt.figure()
    plt.scatter(landmarks[:, 0], landmarks[:, 1], marker='s', s=60)

    track = []
    for i in range(200):
        sim_pos = ekf.move(sim_pos, u, dt/10.) # ロボットのシミュレート
        track.append(sim_pos)

        if i % step == 0:
            ekf.predict(u=u)

            if i % ellipse_step == 0:
                plot_covariance_ellipse(
                    (ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
                     std=6, facecolor='k', alpha=0.3)

            x, y = sim_pos[0, 0], sim_pos[1, 0]
            for lmark in landmarks:
                z = z_landmark(lmark, sim_pos, std_range, std_bearing)
                ekf_update(ekf, z, lmark)

            if i % ellipse_step == 0:
                plot_covariance_ellipse(
                    (ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
                    std=6, facecolor='g', alpha=0.8)
    track = np.array(track)
    plt.plot(track[:, 0], track[:,1], color='k', lw=2)
    plt.axis('equal')
    plt.title("EKF Robot localization")
    if ylim is not None: plt.ylim(*ylim)
    plt.show()
    return ekf
In [20] 
landmarks = array([[5, 10], [10, 5], [15, 15]])

ekf = run_localization(
    landmarks, std_vel=0.1, std_steer=np.radians(1),
    std_range=0.3, std_bearing=0.1)
print('最後の P:', ekf.P.diagonal())
Out [20] 
最後の P: [0.024 0.041 0.002]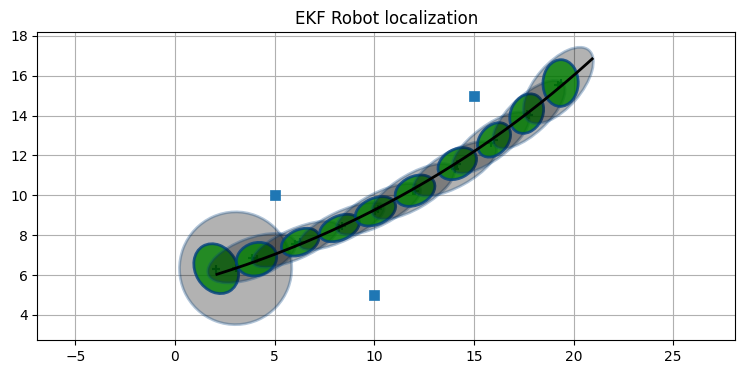
EKF による自己位置推定
Out [20]EKF による自己位置推定

ランドマークは青い四角で、ロボットの実際の軌跡は黒い実線で、予測ステップで計算される事前分布の共分散楕円は薄い灰色で、更新ステップで計算される事後分布の共分散楕円は緑色で示されている。共分散楕円をグラフで見える程度に大きくするために \(6\sigma\) をプロットした。

グラフからは、運動モデルによって追加された不確実性が非常に大きいことが分かる。また緑色の共分散楕円に注目すると、位置の不確実性がロボットの向いている方向に大きいことも確認できる。最初の数反復でフィルタは観測値として渡されるランドマークとの距離を取り込み、不確実性は小さくなっている。

ここでは無香料カルマンフィルタの章と同じランドマークの位置と初期条件を使った。共分散楕円の大きさで言えば、UKF の方がずっと正確である1。ただ \(\mathbf{x}\) の推定値について言えば同程度に正確な値が出力されている。

ランドマークを追加してみよう:

In [21] 
landmarks = array([[5, 10], [10, 5], [15, 15], [20, 5]])

ekf = run_localization(
    landmarks, std_vel=0.1, std_steer=np.radians(1),
    std_range=0.3, std_bearing=0.1)
plt.show()
print('最後の P:', ekf.P.diagonal())
Out [21] 
最後の P: [0.02  0.021 0.002]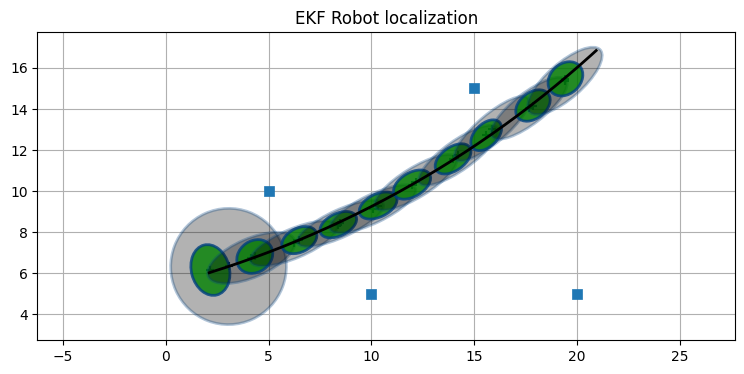
四つのランドマークを使った自己位置推定
Out [21]四つのランドマークを使った自己位置推定

最後の方の推定値が持つ不確実性が小さくなったのが分かる。二つのランドマークだけを使うようにすれば、複数のランドマークを利用する効果を確認できる:

In [22] 
ekf = run_localization(
    landmarks[0:2], std_vel=0.1, std_steer=np.radians(1),
    std_range=0.3, std_bearing=0.1)
print('最後の P:', ekf.P.diagonal())
Out [22] 
最後の P: [0.019 0.047 0.   ]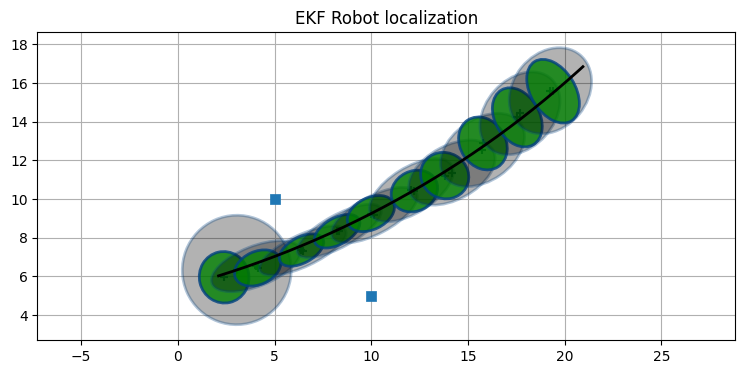
二つのランドマークを使った自己位置推定
Out [22]二つのランドマークを使った自己位置推定

推定値は正しい軌跡上にあるものの、共分散楕円は素早く大きくなる。次にフィルタが発散する例を示す。利用するランドマークを一つだけとして、ノイズも調整している:

In [23] 
ekf = run_localization(
    landmarks[0:1], std_vel=1.e-10, std_steer=1.e-10,
    std_range=1.4, std_bearing=.05)
print('最後の P:', ekf.P.diagonal())
Out [23] 
最後の P: [0.288 0.774 0.004]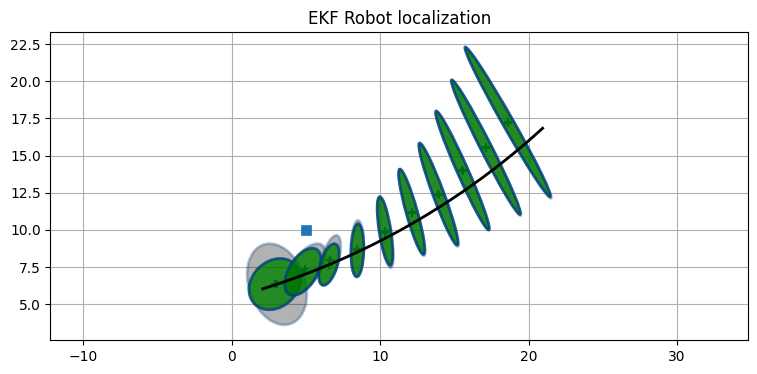
発散するフィルタ
Out [23]発散するフィルタ

逆にランドマークを増やせば非常に正確な推定値が得られる:

In [24] 
landmarks = array([[5, 10], [10,  5], [15, 15], [20,  5], [15, 10],
                   [10,14], [23, 14], [25, 20], [10, 20]])

ekf = run_localization(
    landmarks, std_vel=0.1, std_steer=np.radians(1),
    std_range=0.3, std_bearing=0.1, ylim=(0, 21))
print('最後の P:', ekf.P.diagonal())
Out [24] 
最後の P: [0.009 0.008 0.001]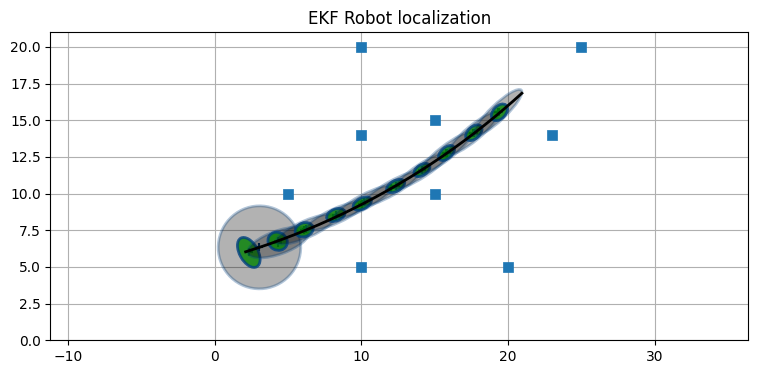
多数のランドマークを使ったロボットの自己位置推定
Out [24]多数のランドマークを使ったロボットの自己位置推定

考察

この問題は現実的だと前に言った。いくつかの点でこれは正しい。例えばヤコビ行列がもっと簡単になるロボットの運動モデルを使った説明も見たことがある。ただ一方で、この問題で使った運動モデルはいくつかの点で単純である。第一に、自転車モデルを使っている。現実の車に付いているタイヤは二つ一組であり、旋回するとき二つのタイヤは異なる距離を移動する。またロボットは制御入力へ瞬時に反応するとも仮定している。Sebastian Thrun は Probabilistic Robotics2 で、この単純化が正当化されるのは実際に実装したフィルタで現実の車両を上手く追跡できるからだ、と述べている。ここでの教訓は、フィルタはそれなりに正確な非線形モデルを使わなければならないものの、完璧でなくても十分な性能が得られるということだ。あなたはフィルタの設計者として、モデルの忠実度を優先するか、それとも必要になる数学の単純さと実行にかかる CPU 時間を優先するかを選択する必要があるだろう。

この例が問題を単純にしていると言えるもう一つの理由が、ランドマークと観測値の対応関係が分かると仮定している点である。レーダーを使っていると仮定しよう──特定の反射信号が周辺環境に存在する特定の建物に対応することは、どうすれば分かるだろうか？ この疑問は SLAM (simultaneous localization and mapping) アルゴリズムの導入と言える。本書は SLAM の本ではないので、これ以上は SLAM を説明しない。

11.5 UKF vs EKF

前章では UKF を使って同じ問題に取り組んだ。二つの実装の差異は明らかなはずである。プロセスモデルと観測モデルに対してヤコビ行列を計算するのは、初歩的な運動モデルであるにもかかわらず簡単ではなかった。難しい問題ではヤコビ行列の計算が困難あるいは解析的に不可能になることもある。これに対して UKF では、プロセスモデルと観測モデルを実装する関数を一つずつ与えるだけで済む。

ヤコビ行列を解析的に計算できない場合は多くある。詳細は本書の範囲を超えるものの、そのような場合は数値的手法を使ってヤコビ行列を計算しなければならない。この手法は簡単ではなく、STEM 関連の修士課程の少なくない部分がこういった状況を上手く扱うためのテクニックを学ぶのに費やされる。さらに、そういったカリキュラムを終えても専門領域に関連する問題しか解決できない可能性が高い──航空力学のエンジニアはナビエ=ストークス方程式に関して多くのことを学ぶものの、化学反応の速度をモデル化する方法はほとんど学ばない。

つまり UKF の方が簡単である。では正確さはどうだろうか？ 実際に UKF を使うと EKF より優れた性能となることが多い。UKF が EKF を上回ったことを報告する研究論文は様々な問題ドメインで大量に存在している。なぜこうなるかを理解するのは難しくない: EKF はプロセスモデルと観測モデルを一点で線形化するのに対して、UKF では \(2n+1\) 個の点が使われる。

具体的な例を見よう。\(f(x) = x^3\) として、ガウス分布を \(f\) に通したときに何が起こるかを見る。まず比較用にモンテカルロシミュレーションを使って正確な解答を作成する。ガウス分布に従う \(50,000\) 個の点をランダムに生成し、それぞれを \(f\) に適用し、結果の平均と分散を計算する。

EKF は考えている点における関数の微分を計算することで関数を線形化する。この微分 (傾き) が線形関数を定め、この線形関数を使ってガウス分布全体が変換される。次の図にこれを示す:

In [25] 
import kf_book.nonlinear_plots as nonlinear_plots
nonlinear_plots.plot_ekf_vs_mc()
Out [25] 
実際の値 mean=1.30, std=1.13
EKF      mean=1.00, std=0.95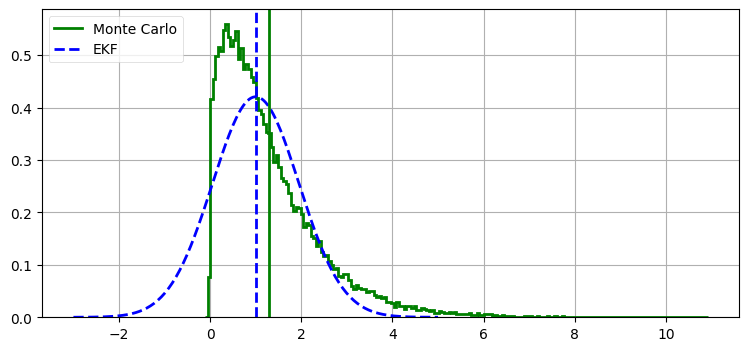
EKF が行うガウス分布の変換
Out [25]EKF が行うガウス分布の変換

EKF による計算はかなり不正確である。これに対して、UKF の性能を次に示す:

In [26] 
nonlinear_plots.plot_ukf_vs_mc(alpha=0.001, beta=3., kappa=1.)
Out [26] 
実際の値 mean=1.30, std=1.13
UKF      mean=1.30, std=1.08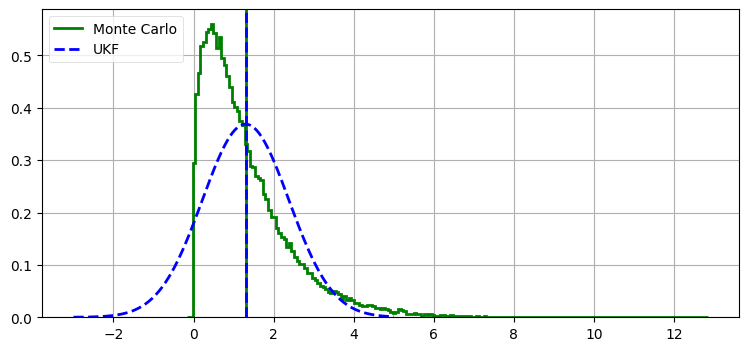
UKF が行うガウス分布の変換
Out [26]UKF が行うガウス分布の変換

UKF が計算する平均が小数点以下第二位まで正確なことが分かる。標準偏差は正確な値から少し離れているものの、UKF の計算はシグマ点の生成に使うパラメータ \(\alpha\), \(\beta\), \(\gamma\) を通じて微調整できる。ここでは \(\alpha=0.001\), \(\beta=3\), \(\gamma=3\) を使った。パラメータを自由に変えて結果を確認してみてほしい。ここに示した例より優れた結果が得られるはずだ。ただし、UKF を特定のテストに対して調整しすぎないように注意しなければならない。そのテストに対しては優れた結果が得られても、一般のデータに対しては性能が劣化する可能性がある。

  1. 訳注: ここで示した EKF の例と前章で示した UKF の例は同じランドマークの位置と同じ初期条件を使ってはいるものの、プロセスノイズのモデルが異なる。そのため必ずしもフェアな比較ではない。[return]

  2. Sebastian Thrun, Wolfram Burgard, and Dieter Fox, Probabilistic Robotics, The MIT Press, 2005.[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。