はじめに

カルマンフィルタとベイズフィルタ

センサーにはノイズがつきものだ。世界にあふれるデータやイベントを私たちは計測・追跡したいのだが、センサーから完璧な情報が取得できるとは期待できない。例えば私の車に搭載されている GPS は高度を報告するが、同じ道路の同じ場所を通ったとしても報告される高度は少し異なる。また私が持っているキッチンスケールの上に同じものを二度載せると、目盛りは異なる値を指す。

すぐに解決できる簡単なケースもある。もしキッチンスケールが多少異なる値を指すなら、追加で何度か測定して平均を取ればいい。あるいはもっと正確なキッチンスケールと取り換えることもできる。しかしセンサーに含まれるノイズが非常に大きかったり、データの収集が困難な環境だったりしたら？例えば低高度を飛行する航空機の動きを追跡したいとき、ドローンを自動操縦したいとき、あるいは農業用トラクターが畑全体に種をまくことを保証したいときは、どうすればよいだろうか？私が取り組んだことのあるコンピュータービジョン関係の課題で画像に含まれる動くオブジェクトを追跡する必要があったとき、コンピュータービジョンのアルゴリズムが出力する結果はノイズが非常に大きく、信頼性も低かった。

本書はこういった種類のフィルタリングの問題を解決する方法を読者に示す。私は普段たくさんの異なるアルゴリズムを使っているが、どのアルゴリズムもベイズ確率の考え方に基づいている。簡単に言うと、ベイズ確率は過去の情報を使って真になる可能性の高い値を決定する。

「今この瞬間の私の車の向きは？」とあなたに尋ねたとしても、あなたは見当もつかないだろう。1° から 360° までの角度を適当に選ぶしかないから、正しい角度を選べる確率は 360 分の 1 しかない。では「二秒前、私の車の向きは 243° だった」と伝えたらどうだろうか？二秒の間に車が大きく向きを変えることはないから、より正確な予測ができるはずだ。このとき、あなたは過去の情報を使って現在あるいは未来の情報をより正確に推定している。

世界にはノイズも含まれる。過去の情報を使って予測を行えば使わないときより優れた推定値を得られるものの、その推定値もノイズの影響を受ける。私がちょうどいま犬を見つけてブレーキをかけたかもしれないし、道路のくぼみを避けるためにハンドルを切ったかもしれない。また強い風や路面の氷も車の進行に影響する。意外かもしれないが、制御工学ではこういった要素を全てノイズ (noise) と呼ぶ。

これだけがベイズ確率というわけではないが、これであなたは中心的なアイデアを理解できた。知識が不正確なので、手にしている証拠の強さに基づいて確証の度合いを調整するということだ。カルマンフィルタとベイズフィルタを使うと、系の振る舞いに関する知識にノイズが含まれ正確さに欠ける場合でも、その知識をノイズが含まれ正確さに欠けるセンサーからの値と混ぜ合わせ、系の状態の可能な中で最も可能性の高い推定値を計算できる。そのときは「絶対に情報を捨てない」が原則となる。

物体を追跡していて、センサーが急な方向の変化を報告したとしよう。物体は本当に曲がったのだろうか、それともデータのノイズでそう見えただけだろうか？これは場合による。ジェット戦闘機を追跡しているなら、おそらく急な旋回を行ったのだろうと私たちは自然に考える。しかしまっすぐな線路を走る貨物列車を追跡しているなら、本当に曲がったとはあまり考えない。さらに私たちはセンサーの精度によっても確証の度合いを変えるだろう。私たちの抱く確証の度合いは過去のデータと追跡している系の知識、そしてセンサーの特性に依存する。

カルマンフィルタはこの種の問題を数学的に最適な形で解く方法としてルドルフ・カルマン (Rudolf Emil Kálmán) によって発明された。初めて使われたのはアポロ計画であり、それから非常に広範な分野で使われてきた。航空機、潜水艦、巡航ミサイルにもカルマンフィルタは存在する。ウォールストリートはマーケットの追跡に使っており、他にもロボット、IoT (Internet of Things)、実験器具でもカルマンフィルタ使われている。化学工場はカルマンフィルタを使って反応を制御・監視するし、医療用画像処理や心臓信号のノイズ除去にも利用される。問題にセンサーや時系列データが絡むときは、カルマンフィルタあるいはカルマンフィルタの親戚も姿を現す。

この本を書いた理由

私はソフトウェアエンジニアとして航空宇宙産業で約二十年を過ごしてきた。そのためカルマンフィルタとはずっと「肘タッチ」をしてきたものの、実装したことはなかった。その間に絶え間なく聞いてきたのが「カルマンフィルタは恐ろしく難しい」という噂である: 「理論は美しいが、様々な分野を知っていないと学ぶのが難しい」と。なんでも、信号処理、制御理論、確率と統計、誘導制御理論を知らなければ理解できないらしい。私がコンピュータービジョンを使った追跡問題に取り組むようになると、カルマンフィルタをどうしても実装しなければならなくなった。

この分野には素晴らしい教科書 (例えば Mohinder S. Grewal と Angus P. Andrews による Kalman Filtering: Theory and Practice with MATLAB¹ など) があるものの、腰を下ろしてそういった本を読むのは必要とされる前提知識を持っていない限り憂鬱で苦しい体験になる。典型的な教科書は最初の数章で学部生が数年かけて学ぶ数学を駆け足で復習し、軽率に伊藤微積分学の教科書を紹介して、半期の講義に相当する統計学の知識を数段落でサッと終わらせてしまう。有名なカルマンフィルタの教科書は学部の上級生や大学院生用の講義で使うために書かれており、研究者や専門家にとってはこの上なく価値のある参考文献であるものの、そういった人々ほど本腰を据えていない読者にとっては理解するのが本当に難しい。記号は説明なしに導入され、同じ概念を指す名前や変数名は書籍ごとに異なり、具体例や最初から最後まで解かれた練習問題はほとんど存在しない。文章をパースして定義から数式を追うことはできても、文章や数式が現実世界のどんな現象を記述しようとしているのかがさっぱり分からない、という状況に私はよく直面した。「で、それは何を意味するのか？」と心の中で何度もつぶやいたものだ。私を混乱させたのは次のような数式である:

\[ \begin{aligned} \hat{x}_{k} &= \Phi_{k}\hat{x}_{k-1} + G_k u_{k-1} + K_k [z_k - H \Phi_{k} \hat{x}_{k-1} - H G_k u_{k-1}] \\ \mathbf{P}_{k\mid k} &= (I - \mathbf{K}_k \mathbf{H}_{k})\textrm{cov}(\mathbf{x}_k - \hat{\mathbf{x}}_{k\mid k-1})(I - \mathbf{K}_k \mathbf{H}_{k})^{\text{T}} + \mathbf{K}_k\textrm{cov}(\mathbf{v}_k )\mathbf{K}_k^{\text{T}} \end{aligned} \]

しかし、やっとカルマンフィルタが分かってくると、根元にある考え方は非常に簡単なものであることに私は気が付いた。いくつかのとても簡単な確率の規則が分かっていて、不正確な知識を合成する方法を直感的に理解していれば、カルマンフィルタの概念は手の届く場所にある。カルマンフィルタは難しいことで有名だ。しかし正式な用語を抜いて考えれば、この分野とそこで使われる数学の美しさが明らかになり、私はカルマンフィルタを気に入るようになった。

カルマンフィルタの数学と理論を理解し始めると、さらなる困難が現れた。書籍や論文が何らかの事実を表明するとき、証拠としてグラフを示すのである。残念ながらその命題の正しさは私にとって明らかでないし、グラフを再現することもできない。あるいは「\(R=0\) だとどうなるんだ？」などと考えたりもするし、著者の示す疑似コードが高水準で実装に手間取ることもある。MATLAB のコードを示す書籍もあるが、その高価なパッケージのライセンスを私は持っていない。それから、理解に役立つ練習問題が章の終わりにたくさん載っている書籍は多くある。自分でカルマンフィルタを実装するときに理解しておくべき練習問題なのだが、そういった問題にはまず答えが付いていない。講義の一環として書籍を使っているならそれで問題ないかもしれないが、書籍しか持っていない読者にとっては非常に都合が悪い。おそらくは講義を受ける学生の「カンニング」を避けるために著者が情報を出し惜しみするのが私は嫌で嫌でたまらなかった。

こういった事実はどれも学習を妨げる。私は画面上の物体を追跡したり、Arduino プロジェクトでちょっとしたコードを書いたりしたい。書籍に載っているグラフを作る方法を知りたいし、著者が選んだパラメータの値を動かしてみたい。シミュレーションも走らせたいし、信号に対するノイズを増やしたときのフィルタの動作も確認したい。日常のコードでカルマンフィルタを使う機会は何千とあるのに、たいして難しくもないこのトピックは天才と大学人のものとなっている。

そういった問題を全て解決するために私は本書を書いた。もし軍事用レーダーを設計しているなら、この本の他にも様々な文献を読まなければならないだろう。どうせ必要になるのだから、立派な大学で STEM を学んで修士号か博士号を取るべきだ。本書の対象読者はホビイスト、カルマンフィルタに興味のある人、そしてデータのフィルタリングや平滑化が必要な課題に取り組んでいるエンジニアである。あなたがホビイストなら、必要なことは全て本書で提供されるはずだ。一方であなたがカルマンフィルタについて真剣に知りたいと思っているなら、他の文献を当たる必要がある。教科書や論文が読めるだけの考え方や数式を説明することを本書は意図している。

本書は対話的である。静的な内容をオンラインで読むこともできるものの、私が書いた通り対話的に読むことを強く勧める。Jupyter Notebook を使って書かれているので、テキスト・数式・Python コード・Python コードの出力を一つのノートブックにまとめられる。本書に含まれるグラフとデータは全て Python で生成されており、そのコードはノートブックに含まれる。パラメータの値を二倍にしたい？コード中のパラメータの値を変えて、CTRL+Enter を押すだけだ。新しいグラフまたは出力がコードの下に現れる。

本書には練習問題が含まれるが、その答えも含まれる。あなたのことは信じている。もし答えが読みたいなら、さっさと読んでしまって構わない。もし知識を深く理解したいなら、答えを読む前に練習問題を実装してみるべきだ。本書は対話的なので、本の中に練習問題の解答を書き込んでその場で実行できる。他の環境に移動したり、始める前に何かをインポートしたりする必要はない。

本書²は無料である。私はカルマンフィルタに関する本に数千ドルは費やした。そういった本が経済不況の国に住む人々や経済的に恵まれない学生の手が届く金額であるとは思えない。Python のような無料のソフトウェアや Allen B. Downey の Green Tea Press が公開している書籍をはじめとした無料の書籍からはたくさんのものを受け取った。今度は私が恩返しをする番だ。というわけで本書は無料であり、GitHub の無料サーバーでホストされており、IPython や MathJax といった無料でオープンなソフトウェアだけを使っている。

本書は対話的に読まれるものとして書かれているので、対話的に読むことを推奨する。準備は少し手間だが、その価値はあるはずだ。IPython といくつかの補助ライブラリを自分のコンピューターにインストールしてから本書を開けば、本書に含まれる全てのコードを自分の環境で実行できる。実験を行ったり、異なるデータに対するフィルタの振る舞いを確認したり、同じデータに対する異なるフィルタの振る舞いを確認したりできる。「ここを変えたらどうなる？」と不思議がる必要はない。試してみればいい！

必要なパッケージのインストール方法の説明は補遺 A にある。

必要なソフトウェアがインストールできたら、本書のソースコードのあるディレクトリでコマンドラインから次のコマンドを実行すると Jupyter Notebook を起動できる:

jupyter notebook

するとブラウザが開き、現在のディレクトリに含まれるファイルとフォルダを示したウィンドウが表示される。本書は章ごとに構成され、XX-NAME.ipynb という名前のファイルに各章が含まれる (XX は章を表す数字、NAME は章の名前)。.ipynb は Jupyter Notebook が使う拡張子である。例えば第 2 章を読みたいなら、先ほど開いたブラウザで 02-Discrete-Bayes.ipynb を開けばよい。補助的な機能 (グラフの体裁の調整やアニメーションの生成など) を収めた Python コードも Jupyter Notebook とは別に存在するが、これは読者が読むことを意図していない。ただもちろん、例えばアニメーションがどのように生成されるかを知りたくなったら読んでもらって構わない。

以上が本を読むのに面倒な手順であることは否定しない。Jupyter Notebook をまるごと本にするプロジェクトがいくつかあり、私はその手法を真似した。最初は少し手間がかかるのだが、得られるものは非常に大きい──コードベースをダウンロードして本を読みながら IDE を個別に実行する必要はなく、コードと文章を同時に読むことができる。コードを変更したくなったらすぐに変更して何が起こるかを確認できるし、バグを見つけたら私のレポジトリに修正を送ることで世界中の人々が恩恵を受けられる。それからもちろん、私が昔ながらの本で絶え間なく遭遇した「本文とコードが矛盾していて、どちらを信じればよいのか分からない」という問題も起こらない。

Jupyter Notebook について

本題に入る前に、本書を Jupter Notebook として読む人に向けて少し説明をしておく。本書は対話的である。コード例を実行するとき、特にグラフのアニメーションを見たいときは、コードセルを実行する必要がある。Jupyter Notebook について全てをここで教えることはできないが、重要な点をいくつか示しておく。さらに詳しくは http://jupyter.org/ を見てほしい。

第一に、各章の最初の方にある "# 体裁を整える" で始まるコードセルは必ず実行しなければならない。このページの上部にもある。このコードセルは本の体裁の調整 (あまり気にしないかもしれない処理) だけではなく、必要なモジュールの読み込みやプロットとデータ出力に関連するグローバル変数の設定も行うので、コードセルを一つでも実行する場合は忘れずに実行しなければならない。

それから、次のコード:

%matplotlib inline

を実行すると、Matplotlib が出力するグラフが Jupyter Notebook の中に表示されるようになる。Matplotlib については以下で説明する。理由はよく分からないのだが、デフォルトだと Jupyter Notebook は別のウィンドウにグラフを表示する。

%matplotlib の最初に付いているパーセント記号 % は、この文が Python のコードではなく IPython のマジック (カーネルへ向けたコマンド) であることを示す。便利なマジックは他にもある。一覧は http://ipython.readthedocs.io/en/stable/interactive/magics.html から確認できる。

セルに含まれるコードは簡単に実行できる。セルをクリックしてフォーカスを移し (このときセルの周りに四角が表示される)、それから CTRL+Enter を押すだけだ。

第二に、セルは順番通りに実行する必要がある。一つの問題をいくつかのセルを使って解決することがあるので、いきなり十番目のセルを実行しても当然正しく動作しない。何も実行していないなら、実行したいセルを選択してから Menu の Run All Above をクリックするだけで済む。そのセルを実行するのに必要なコードが全て実行されることを保証するにはこれが一番簡単だ。

一度セルを順番通りに実行すれば、それからは好きなセルを編集してそれだけを再実行してもたいていは問題ない。ただし必ずではない。私は問題が起こらないようにコードを構成しているものの、トレードオフは存在する。例えばセル 10 で定義される変数をセル 11 とセル 12 で変更したとする。その後セル 11 に戻ると変数の値はセル 12 で設定した値のまま実行されるが、セル 11 のコードはセル 10 で設定される変数の値を期待しているかもしれない。このような理由により、順番を無視してセルを実行すると奇妙な結果が得られることがある。そうなったときは、正しい状態を復元するために全てのセルを最初からもう一度実行した方がよい。変な結果が得られるのはじれったいが、Jupter Notebook の対話的なコード実行にはそれを埋め合わせるだけの価値がある。あるいは GitHub に issue を立ててもらえれば、私が直せるかもしれない！

最後に、特定のブラウザではアニメーション付きのグラフが正しく動作しないことが一部の読者から報告されている。私はこれを再現できていないが、%matplotlib notebook という対話的なグラフを使うためのマジックが原因であるようだ。もしグラフのアニメーションが正しく動作しないなら、この部分を %matplotlib inline に変更してほしい。アニメーションは失われるが、こちらなら全てのプラットフォームとブラウザで動作する。

SciPy, NumPy, Matplotlib について

SciPy はオープンソース数学ソフトウェアの集合体である。NumPy は SciPy に含まれるモジュールで、配列オブジェクト・線形代数・乱数といった機能を提供する。Matplotlib は NumPy 配列をプロットする機能を提供する。SciPy の機能は一部が NumPy とかぶっているが、加えて最適化や画像処理といった機能を持っている。

この本が長くなり過ぎないように、読者は Python でプログラムを書く方法を知っていて、この三つのパッケージの使い方も分かっているものとする。ただ、ここで各パッケージの機能を簡単に紹介する。現実的には、使い方を学ぶために外部の資料を見つける必要があるだろう。最初に目を通すものとしては SciPy のホームページが一番だ。その後は関連するチュートリアルや動画を探すとよい。

NumPy, SciPy, Matplotlib はデフォルトの Python ディストリビューションに付属しない。まだインストールしていないなら、補遺 A にインストールの手順をまとめてある。

本書では全体を通して NumPy の配列データ構造を使っていくので、ここで少し学んでおこう。初歩的なことだけを説明するので、詳しくは NumPy のドキュメントを見てほしい。

numpy.array 関数が一次元および多次元の配列を実装する。返り値の型は numpy.ndarray であり、これからはこの型の値を NumPy 配列と呼ぶ。NumPy 配列はリストに似た任意のオブジェクトから構築できる。次のコードはリストから一次元の NumPy 配列を構築する:

In [3]

import numpy as np
x = np.array([1, 2, 3])
print(type(x))
x

Out [3]

<class 'numpy.ndarray'>

Out [3]

array([1, 2, 3])

NumPy の numpy モジュールを import numpy as np として使うのは業界標準となっている。

numpy.array にはタプルも渡せる:

In [4]

x = np.array((4,5,6))
x

Out [4]

array([4, 5, 6])

括弧を入れ子にすると多次元の NumPy 配列が構築できる:

In [5]

x = np.array([[1, 2, 3],
              [4, 5, 6]])
print(x)

Out [5]

[[1 2 3]
 [4 5 6]]

三つ以上の次元を持つ NumPy 配列も作成できるものの、本書では必要にならないので説明しない。

NumPy 配列はデフォルトではリストに含まれる値と同じデータ型を持つ。リストに複数の型の値が含まれるなら、全ての値を最も正確に表せる型が選択される。例えばリストに int 型の値と float 型の値が両方含まれるなら、構築される配列のデータ型は float となる。この振る舞いはキーワード引数 dtype で上書きできる:

In [6]

x = np.array([1, 2, 3], dtype=float)
print(x)

Out [6]

[1. 2. 3.]

NumPy 配列の要素には添え字を位置として使ってアクセスする:

In [7]

x = np.array([[1, 2, 3],
              [4, 5, 6]])

print(x[1,2])

Out [7]

列または行にアクセスするにはスライスを使う。対応する列または行の全ての要素を選択する特殊な記号としてコロン : が用意されており、例えば x[:,0] は第一列 (0 が指定する列) に含まれる全てのデータを返す:

In [8]

x[:, 0]

Out [8]

array([1, 4])

第二行は次のように取得できる:

In [9]

x[1, :]

Out [9]

array([4, 5, 6])

第二行の最後の二つの要素は次のように取得できる:

In [10]

x[1, 1:]

Out [10]

array([5, 6])

Python の list と同様に、負のインデックスを使って配列の後ろから数えた位置を指定することもできる。-1 が最後の位置を指すので、例えば第二行の最後の二つの要素を取得するコードは次のようにも書ける:

In [11]

x[-1, -2:]

Out [11]

array([5, 6])

行列加算は + 演算子で行う。一方、行列乗算はメソッド dot または関数 numpy.dot として使う必要がある。* 演算子が表すのは要素ごとの乗算であり、線形代数で使われる乗算ではない:

In [12]

x = np.array([[1., 2.],
              [3., 4.]])
print('加算:\n', x + x)
print('\n要素ごとの乗算:\n', x * x)
print('\n乗算:\n', np.dot(x, x))
print('\ndot は np.array のメンバーでもある:\n', x.dot(x))

Out [12]

加算:
 [[2. 4.]
 [6. 8.]]

要素ごとの乗算:
 [[ 1.  4.]
 [ 9. 16.]]

乗算:
 [[ 7. 10.]
 [15. 22.]]

dot は np.array のメンバーでもある:
 [[ 7. 10.]
 [15. 22.]]

行列乗算を行う @ 演算子が Python 3.5 で追加された:

In [13]

x @ x

Out [13]

array([[ 7., 10.],
       [15., 22.]])

このコードは Python 3.5 以降でのみ動作する。なお、本書は Python 3.6 以降を要求するので、使えるときは @ を使っていく。この演算子は両辺が配列でなければならないことに注意してほしい。そのため x @ 3 は ValueError を送出する。一方 np.dot(X, 3.) なら正しく動作する。

転置は属性として .T で、逆行列は numpy.linalg.inv 関数で計算できる。SciPy も scipy.linalg.inv という似た名前で逆行列関数を提供している:

In [14]

import scipy.linalg as linalg
print('転置:\n', x.T)
print('\nNumPy の 逆行列:\n', np.linalg.inv(x))
print('\nSciPy の 逆行列:\n', linalg.inv(x))

Out [14]

転置:
 [[1. 3.]
 [2. 4.]]

NumPy の逆行列:
 [[-2.   1. ]
 [ 1.5 -0.5]]

SciPy の逆行列:
 [[-2.   1. ]
 [ 1.5 -0.5]]

ヘルパー関数もいくつかある。例えば全ての要素が 0 の行列を作る numpy.zeros、全て 1 の行列を作る numpy.ones、恒等行列を作る numpy.eye が利用できる:

In [15]

print('zeros\n', np.zeros(7))
print('\nzeros(3x2)\n', np.zeros((3, 2)))
print('\neye\n', np.eye(3))

Out [15]

zeros
 [0. 0. 0. 0. 0. 0. 0.]

zeros(3x2)
 [[0. 0.]
 [0. 0.]
 [0. 0.]]

eye
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

等間隔で並ぶデータを生成するための関数もある。numpy.arange 関数の動作は基本的に Python の range 関数と同様だが、NumPy 配列が返る点が異なる。numpy.linspace の動作は少し異なり、作成したい配列の要素数を num として linspace(start, stop, num) と呼び出す:

In [16]

np.arange(0, 2, 0.1)

Out [16]

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. , 1.1,
       1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9])

In [17]

np.linspace(0, 2, 20)

Out [17]

array([0.   , 0.105, 0.211, 0.316, 0.421, 0.526, 0.632, 0.737, 0.842,
       0.947, 1.053, 1.158, 1.263, 1.368, 1.474, 1.579, 1.684, 1.789,
       1.895, 2.   ])

続いてデータをプロットしてみよう。たいていの処理はとても簡単に行える。Matplotlib はプロットを担当するモジュール pyplot を持ち、これを plt という名前でインポートするのが業界標準となっている。インポートした後は plt.plot 関数で数値のリストもしくは数値の配列をプロットできる:

In [18]

import matplotlib.pyplot as plt
a = np.array([6, 3, 5, 2, 4, 1])
plt.plot([1, 4, 2, 5, 3, 6])
plt.plot(a)

Out [18]

[<matplotlib.lines.Line2D at 0x16f3ec12250>]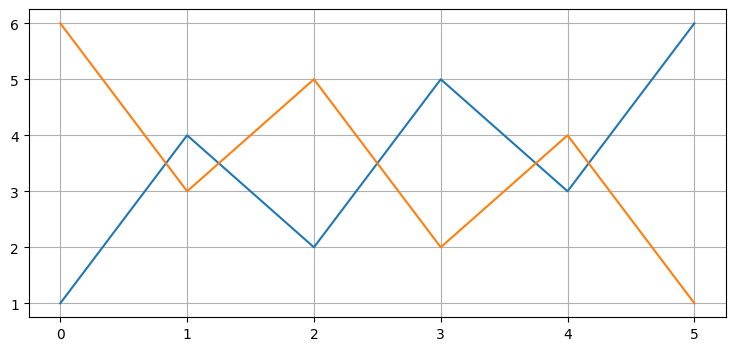

出力に [<matplotlib.lines.Line2D at 0x16f3ec12250>] が表示されるのは、plt.plot が作成したグラフオブジェクトを返すためだ。普通はこの情報を出力しても意味がないので、以降では plt.plot の呼び出しの後に ; を付けて出力しないようにする。

デフォルトだと plt.plot は \(x\) 系列の値が 1 ずつ増加するものとしてグラフを作成する。引数に \(x\) 系列を明示的に渡すこともできる:

In [19]

plt.plot(np.arange(0,1, 0.1), [1,4,3,2,6,4,7,3,4,5]);

この本ではこれらのパッケージに含まれる機能をこの他にもたくさん使っていく。初めて使うときでも特に説明はしないので、文脈から読み取るかウェブで検索するかしてほしい。いつも通り、よく分からなかったら新しいセルを作るか Python コンソールを起動して実験すればいい！

練習問題: 配列の作成

各要素が 1/10 で長さが 10 の NumPy 配列を作成せよ。これを行う方法はいくつもあるので、できるだけ多くの方法で実装せよ。

In [20]

# 解答をここに書く

解答

三つの方法を示す。特に一つ目の方法を知っておいてほしい。一つ目の方法では / 演算子を使って十要素の配列の各要素を 10 で割っている。この方法はすぐ後にメートルをキロメートルに変換するのに利用する:

In [21]

print(np.ones(10) / 10.)
print(np.array([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]))
print(np.array([.1] * 10))

Out [21]

[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]
[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]
[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]

次の解答では初出の関数を使っている。numpy.asarray 関数は引数が NumPy 配列でなければ NumPy 配列にして返し、引数が NumPy 配列なら何もしないで返す。これは Python リストと NumPy 配列の両方を受け取る関数を書くときに便利であり、引数が NumPy 配列のときは何も新しく作成されないので効率にも非常に優れている:

In [22]

def one_tenth(x):
    x = np.asarray(x)
    return x / 10.

print(one_tenth([1, 2, 3]))            # 正しく動く
print(one_tenth(np.array([4, 5, 6])))  # これでも正しく動く！

Out [22]

[0.1 0.2 0.3]
[0.4 0.5 0.6]

付属ソフトウェアについて

FilterPy は私が開発したオープンソースの Python 用ベイズフィルタライブラリであり、本書で利用される。インストールの方法は補遺 A で説明した。FilterPy は GitHub (https://github.com/rlabbe/filterpy) でホストされているが、pip でインストールされるバージョンで十分なはずである。

本書に特有なコード (例えば本の体裁を整えるコード) はサブディレクトリ kf_book にある。このディレクトリには XXX_internal.py という名前のファイルもある。これらは特定の章にだけ関係するコードを書くのに使われるファイルであり、あまり面白くない Python コードを隠すのに使われる。グラフを作成するときはデータを生成するコードにだけ集中するべきであり、Python でグラフをどう作るかは重要でない。もちろん気になるならソースを読んでも構わない。

一部の章では以降の章で利用する関数を定義する。こういった関数は最初 Jupyter Notebook の中で定義されるが、同じコードは kf_book ディレクトリの Python ファイルにも含まれており、後の章で必要になったときはそこからインポートされる。以前の章で定義した関数を使うときはそのことをドキュメントするようにしているが、この作業は進行中である。また私はコピペによる関数の使い回しを避けるようにしている: Python ファイルにあるコードが本文中のコードと違ってしまう状況を避けるためだ。しかし私の知る限り Jupyter Notebook には他のノートブックからコードをインポートする機能がないので、コードをノートブック間で共有するにはコピペを使うしかない。

ドキュメントされていない experiments というディレクトリもある³。これは本文に入れる前に私がコードを書いたりテストしたりするための場所である。興味深いコードもあると思うから、好きに見てほしい。本を書き進めながら例やプロジェクトを追加する予定なので、このディレクトリにあるコードもいずれ本文中に移されるだろう。小さい実験はそのまま削除されるかもしれない。本書を読むことだけに興味があるなら、このディレクトリは無視しても構わない。

kf_book ディレクトリには本の体裁を整えるための CSS ファイルが含まれる⁴。デフォルトだと Jupyter Notebook の見た目は少し味気ない。この CSS ファイルは Probabilistic Programming and Bayesian Methods for Hackers といった本を真似て作られている。それから Lorena Barba 博士による素晴らしい講義ノート CFDPython にも大きな影響を受けた。本書の体裁を整えられたのはこういったプロジェクトのおかげである。

Python と数式のコーディングについて

カルマンフィルタの教科書、およびその他の工学の教科書は大部分が数学者あるいは大学人によって書かれている。ソフトウェアが (奇跡的に) 付属したとしても、それがプロダクションクオリティであることはない。Paul Zarchan と Howard Musoff による Fundamentals of Kalman Filtering: A Practical Approach⁵ を例として見てみよう。これは大学の図書館に必ず置かれている素晴らしい本であり、全ての例とグラフに対する完全なソースコードが提供される数少ない本の一つである。しかしコードは Fortran で書かれており、MATMUL のような関数を除くとサブルーチンが一切使われておらず、カルマンフィルタは本の中で何度も再実装される。さらに同じ枠の中にシミュレーションとフィルタリングのコードが混ぜて書いてあり、区別が難しい。また同じフィルタの実装が章によって微妙に異なっていて、変更された数行が太字で書かれている。ルンゲ=クッタ法が必要なときはコード中に埋め込まれ、コメントも付いていない。

これより優れた方法がある。私なら、ルンゲ=クッタ法を行うときは ode45 関数を呼ぶだけにして、その実装は本文中に示さない。ルンゲ=クッタ法を何度も実装して何度もデバッグするのは嫌だし、バグを見つけて修正するときは本に含まれるプロジェクトの全てで動作が修正されるのが望ましい。さらに、こうした方が読みやすい: ルンゲ=クッタ法の実装を私 (あるいは読者) が気にかけることはほとんどない。

「そうは言ってもこの本はカルマンフィルタの教科書なのだから、カルマンフィルタの実装は重要なのでは」と思う人もいるかもしれない。たしかにそうだが、実際にフィルタリングを行うコードは 10 行ほどしかない。数式を実装するコードは非常に簡単で、カルマンフィルタを使うとき一番大変なのは数式へ代入する行列を組み立てる部分である。

このアプローチが持つ可能性のある欠点の一つが、フィルタリングを行う数式が関数の中に隠れてしまうことだ。これは教育的な文書としてはよろしくないと言われるかもしれない。しかし私は逆のことを指摘したい。読者が学ぶべきは現実世界の本当のプロジェクトで様々なカルマンフィルタを使い分ける方法、そして既存のアルゴリズムをあらゆる場所にコピペして使うべきではないという事実である。

それから、私は Python のクラスを使う。クラスはフィルタに必要なデータをまとめるのに使うのがほとんどで、継承といったオブジェクト指向 (OO) が持つ機能を実装するために使うのではない。例えば KalmanFilter クラスには x, P, R, Q, S, y, K といった行列やベクトルが格納される。私が見かけたことのある手続き的なカルマンフィルタライブラリでは、こういった行列やベクトルをプログラマーが全て管理する必要があった。おもちゃのプログラムならこれでもそれほど悪くないが、カルマンフィルタをいくつも利用するプログラムで全ての行列と関連するデータを管理するのはあまり楽しくないだろう。私は自分の仕事ではこういったクラスを派生させることもあり、そうすると便利に使えるのだが、OO が好きでない人が大勢いることも知っているので OO を読者に強制することはしない。

Mohinder S. Grewal and Angus P. Andrews, Kalman Filtering: Theory and Practice with MATLAB, Wiley-IEEE Press, 2008.^[return]
訳注: 英語版のこと。^[return]
訳注: 翻訳では experiments ディレクトリを省略した。このディレクトリの英語版は https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/tree/master/experiments から確認できる。^[return]
訳注: 現在のバージョンで custom.css は使われていない。^[return]
Paul Zarchan and Howard Musoff, Fundamentals of Kalman Filtering: A Practical Approach, American Institute of Aeronautics and Astronautics, 2000.^[return]