第 13 章平滑化

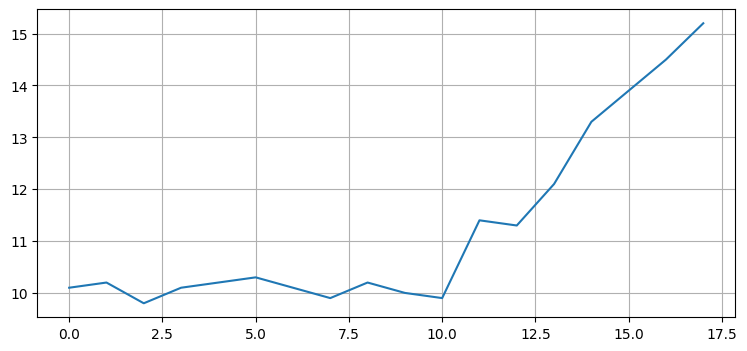
カルマンフィルタの性能は未来のデータを考えに入れるとき最適ではない。例えば航空機を追跡していて、最後の観測値が次のように現在の軌跡から大きく離れたとしよう (簡単のため、これからは一次元の問題だけを考える):

In [3]

import matplotlib.pyplot as plt

data = [10.1, 10.2, 9.8, 10.1, 10.2, 10.3,
        10.1, 9.9, 10.2, 10.0, 9.9, 11.4]
plt.plot(data)
plt.xlabel('time')
plt.ylabel('position');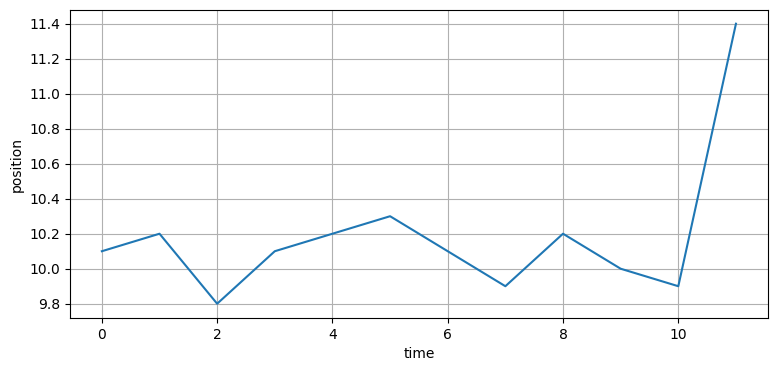

航空機はしばらくじっとしていて、最後に突然大きく位置を変えている。この位置の変化は航空機のフライトエンベロープ (安全に飛行できる速度) の限界を超えていると仮定しよう。そうだとしてもカルマンフィルタは最後の観測値を取り入れ、状態を更新する。これほど急激に旋回する可能性は低いものの、次の可能性はある:

航空機はしばらく前から旋回しており、ノイズのせいでここまでの観測値に旋回が確認できなかった。
航空機は旋回しており、この観測値のノイズが大きい。
航空機は旋回しておらず、この観測値のノイズが非常に大きい。
航空機は逆方向に旋回しており、この観測値のノイズが極端に大きい。

では、これ以降の観測値なら次のようになっていたらどうだろうか？この航空機は旋回しているだろうか？

In [4]

data2 = [11.3, 12.1, 13.3, 13.9, 14.5, 15.2]
plt.plot(data + data2);

この将来の観測値が与えられれば、答えは「旋回している」となる。data の最後の観測値は比較的小さなノイズで上に振れたようだ。

では次の観測値が次の通りだったらどうだろうか？

In [5]

data3 = [9.8, 10.2, 9.9, 10.1, 10.0, 10.3, 9.9, 10.1]
plt.plot(data + data3);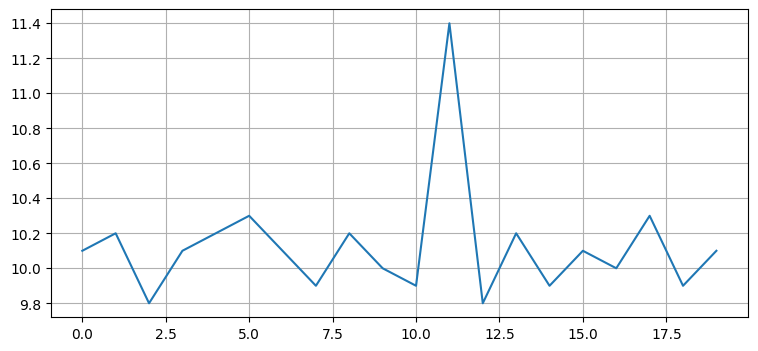

この場合は「旋回していない」が答えになる。data の最後の観測値にはたまたま非常に大きなノイズが乗っただけだ。

13.1 平滑化の概要

カルマンフィルタは再帰的なフィルタであり、マルコフ性を持つ──時刻 \(k\) の推定値は時刻 \(k-1\) の推定値と時刻 \(k\) の観測値だけに依存する。ただこれは、時刻 \(k-1\) の推定値は時刻 \(k-2\) の推定値に依存し、以下同様に最初のエポックまで遡れることを意味する。つまり時刻 \(k\) の推定値は (程度の違いはあれど) 以前の時刻における観測値全てに影響を受ける。時刻 \(k-1\) の観測値が最も大きく影響し、その次に影響するのが時刻 \(k-2\) の観測値、といったことが言える。

平滑化フィルタは時刻 \(k\) の推定値の計算で将来の観測値も考えに入れる。時刻 \(k+1\) の観測値が最も大きく影響し、その次に大きく影響するのが時刻 \(k+2\) の観測値、その次が時刻 \(k+3\) の観測値、と続く。

このトピックは平滑化 (smoothing) と呼ばれるのだが、この名前はミスリーディングだと私は思う。というのも、データを滑らかにするだけならローパスフィルタに通すだけ済むからだ。しかしローパスフィルタはノイズだけではなく実際の変動も取り除いてしまうので、その結果は滑らかなだけで正確とは限らない。これに対して、カルマンフィルタと同じ考え方を使った平滑化アルゴリズム (カルマンスムーザー) は最適である──利用可能な全ての情報を取り入れ、数学的に保証された最良の推定値を計算する。

13.2 スムーザーの種類

カルマンスムーザーには次の三つの種類がある。どれも未来の観測値が利用可能な状況でカルマンフィルタより優れた推定値を生成する:

固定区間スムーザー (fixed-interval smoother)

固定区間スムーザーはバッチ処理ベースのフィルタである。この種類のスムーザーは全てのデータが収集されるまで待機し、それまで一つも推定値を生成しない。例えば、あなたが実験のデータを収集している科学者で、実験が全て終わるまで結果を知らなくても構わないとしよう。このような場合には固定区間スムーザーを利用できる。固定区間スムーザーは全てのデータを収集し、全ての時刻における推定値を利用可能な現在・過去・未来の観測値を全て使って計算する。もしカルマンフィルタをバッチ処理として実行できるなら、何らかの固定区間スムーザーを使うことが常に推奨される。これまでに本書で示した再帰的なフィルタよりずっと優れた結果が出力されるだろう。
固定遅延スムーザー (fixed-lag smoother)

固定遅延スムーザーは出力を遅らせて出力する。例えば遅延が四ステップの固定遅延スムーザーは最初の三つの観測値を受け取った段階では出力を何も生成しない。それから四つ目の観測値を受け取ると、フィルタは一つ目の観測値に対応する推定値を四つの観測値を使って計算して出力する。同様に五つ目の観測値を受け取ると、二つ目の観測値から五つ目の観測値を使って計算した二つ目の観測値に対応する推定値が出力される。この種のフィルタは最近のデータが必要であるものの多少の遅延は許容できる場合に有用である。例えば何らかの製品の製造プロセスでマシンビジョンを使っているとしよう。このときフィルタが入力を受け取って推定値を出力するまでに数秒の間が空いても構わないなら、固定遅延スムーザーを利用して非常に正確で滑らかな推定値を生成できる。
固定点スムーザー (fixed-point smoother)

固定点スムーザーは基本的に通常のカルマンフィルタと同様に動作するが、通常のフィルタの出力に加えて固定された時刻 \(j\) に対する推定値を常に出力する。時刻 \(j\) に達するまでは通常のフィルタと動作は同じで、それ以降の時刻 \(k > j\) でフィルタは \(x_k\) の推定値の生成だけではなく時刻 \(j,\ \ldots,\ k\) の観測値を使った \(x_j\) の推定値の更新も行う。これは系の初期パラメータを推定するときや何らかの事象が発生する特定の時刻における最良推定値を生成するときに有用である。例えば時刻 \(j\) で写真を撮るロボットがあるとしよう。このとき固定点スムーザーを使えば、移動を続けるロボットの観測値から時刻 \(j\) のカメラの姿勢に関する可能な限りの情報を取り出すことができる。

13.3 スムーザーの選択

選択すべきスムーザーはあなたが行いたいことや用意できるメモリ量・処理時間によって変わる。固定点スムーザーは全ての観測値を保存する必要があり、さらに毎時刻で全ての観測値を使った計算を行うので計算コストも大きい。一方で現在の観測値に対する出力は遅延なく得られるので、リアルタイムの応用に適している。

固定遅延スムーザーは一定のウィンドウ分だけのデータしか格納せず、また観測値ごとにウィンドウに収まるデータだけが処理されるので計算コストはあまり大きくない。欠点はフィルタの出力が入力と比べて常に遅れること、そして平滑化の結果が固定区間スムーザーほどには滑らかにならないことである。

固定区間スムーザーは必ずバッチ処理しなければならないことと引き換えに最も滑らかな出力を生成する。多くの固定区間スムーザーは forward-backward アルゴリズムの一種を使っており、再帰的カルマンフィルタの二倍程度しか遅くならない。

13.4 固定区間平滑化

専門的な文献を見れば多くの固定区間スムーザーが見つけられる。私はここで Rauch, Tung, Striebel の三人によって考案されたスムーザーを実装することにした。その理由は実装が簡単で効率的に計算できるためだ。またこれは、私が現実世界の応用で使われているのを最も頻繁に目にするスムーザーでもある。これから説明するスムーザーは通常 RTS スムーザー¹と呼ばれる。

RTS スムーザーの導出には数式がぎっしり詰まったページがいくつも必要になる。それをあなたに押し付けることはしない。その代わりアルゴリズムと数式を簡単に説明し、すぐに RTS スムーザーの実装と実行例を示す。

RTS スムーザーは最初にカルマンフィルタをバッチモードで実行し、各ステップにおける推定値を計算する。それぞれの観測値に対応するカルマンフィルタの推定値とそれぞれの推定値に対応する共分散行列を求め終わると、RTS スムーザーは観測値を逆方向に見ていって、未来の知識を過去の推定値に組み込んでいく。そうして最初の推定値に達すると RTS スムーザーの実行が終了し、全ての情報を最適な形で取り入れた値が最終的なフィルタの出力となる。

RTS スムーザーの式は非常に簡単で、実装もすぐにできる。次に示すのは線形カルマンフィルタに対する式であり、EKF と UKF に対しても同様の式が存在する。この二つのステップはバッチ処理の出力に対して実行され、最後の時刻から最初の時刻に向かって逆方向に進んでいく。各反復で未来の知識が状態推定値に組み込まれる。カルマンフィルタのバッチ処理で得られる状態推定値には過去の観測値が全て組み込まれているから、こうして得られる RTS スムーザーの出力には過去と未来の観測値が全て組み込まれる。RTS スムーザーでは過去・現在・未来の区別が非常に重要なので、添え字を使って時刻を示すようにした。

予測ステップ

\[ \begin{aligned} \mathbf{P} &= \mathbf{FP}_k\mathbf{F}^\mathsf{T} + \mathbf{Q } \end{aligned} \]

更新ステップ

\[ \begin{aligned} \mathbf{K}_k &= \mathbf{P}_k\mathbf{F}^\mathsf{T}\mathbf{P}^{-1} \\ \mathbf{x}_k &= \mathbf{x}_k + \mathbf{K}_k(\mathbf{x}_{k+1} - \mathbf{Fx}_k) \\ \mathbf{P}_k &= \mathbf{P}_k + \mathbf{K}_k(\mathbf{P}_{k+1} - \mathbf{P})\mathbf{K}_k^\mathsf{T} \end{aligned} \]

いつものように、実装で最も難しいのは添え字を正しくする部分である。コメントやエラーチェックを省いた基本的な実装を示す:

def rts_smoother(Xs, Ps, F, Q):
    n, dim_x, _ = Xs.shape
    K = zeros((n,dim_x, dim_x)) # スムーザーゲイン
    x, P, Pp = Xs.copy(), Ps.copy(), Ps.copy
    for k in range(n-2,-1,-1):
        Pp[k] = F @ P[k] @ F.T + Q # 予測された共分散行列
        K[k]  = P[k] @ F.T @inv(Pp[k])
        x[k] += K[k] @ (x[k+1] - (F @ x[k]))
        P[k] += K[k] @ (P[k+1] - Pp[k]) @ K[k].T
    return (x, P, K, Pp)

この実装は FilterPy の実装と同様である。カルマンフィルタがこの関数とは別にバッチモードで実行され、カルマンフィルタが返す推定値と共分散行列が Xs と Ps に渡されると仮定している。

使用例を示す:

In [6]

import numpy as np
from numpy import random
from numpy.random import randn
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import kf_book.book_plots as bp

def plot_rts(noise, Q=0.001, show_velocity=False):
    random.seed(123)
    fk = KalmanFilter(dim_x=2, dim_z=1)

    fk.x = np.array([0., 1.])      # 状態 (x と dx)

    fk.F = np.array([[1., 1.],
                     [0., 1.]])    # 状態遷移行列

    fk.H = np.array([[1., 0.]])    # 観測関数
    fk.P*= 10.                     # 共分散行列
    fk.R = noise                   # 観測ノイズ行列
    fk.Q = Q_discrete_white_noise(dim=2, dt=1., var=Q)  # プロセスノイズ行列

    # ノイズの入ったデータを作る。
    zs = np.asarray([t + randn()*noise for t in range (40)])

    # データをカルマンフィルタに通し、さらにスムーザーを実行する。
    mu, cov, _, _ = fk.batch_filter(zs)
    M, P, C, _ = fk.rts_smoother(mu, cov)

    # データをプロットする。
    if show_velocity:
        index = 1
    else:
        index = 0
    if not show_velocity:
        bp.plot_measurements(zs, lw=1)
    plt.plot(M[:, index], c='b', label='RTS')
    plt.plot(mu[:, index], c='g', ls='--', label='KF output')
    if not show_velocity:
        N = len(zs)
        plt.plot([0, N], [0, N], 'k', lw=2, label='track')
    plt.legend(loc=4)
    plt.show()

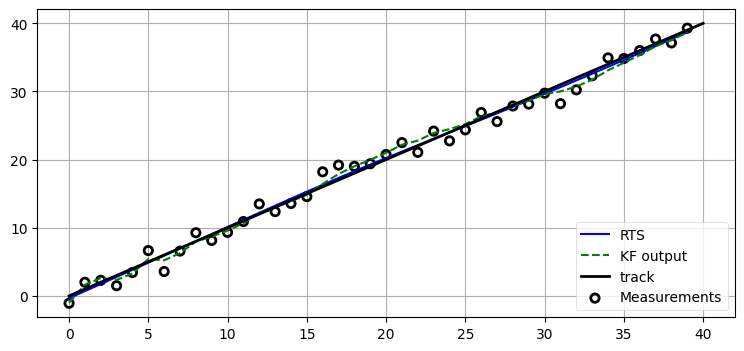
plot_rts(7.)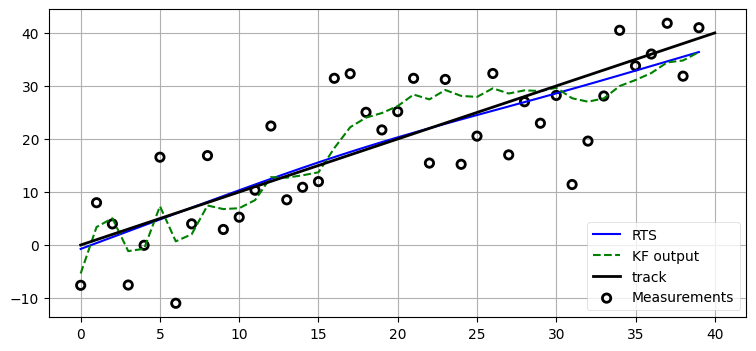

RTS スムーザーの出力と理想的な出力の見分けが付くように大きなノイズを加えている。このグラフを見ると、緑色の破線が示すカルマンフィルタの出力は入力と比べれば滑らかであるものの、いくつかの観測値が連続して実際の値の上または下に偏ると理想的な直線から離れることが分かる。これに対して RTS スムーザーの出力は非常に滑らかであり、さらに理想的な出力に非常に近い。

ノイズをもっと現実的な値にすれば、RTS スムーザーの出力は理想的な直線とほぼ一致するだろう。そのときでもカルマンフィルタの出力は (ノイズが小さくなるので正確にはなるものの) 理想的な直線からは離れるはずだ:

In [7]

plot_rts(noise=1.)

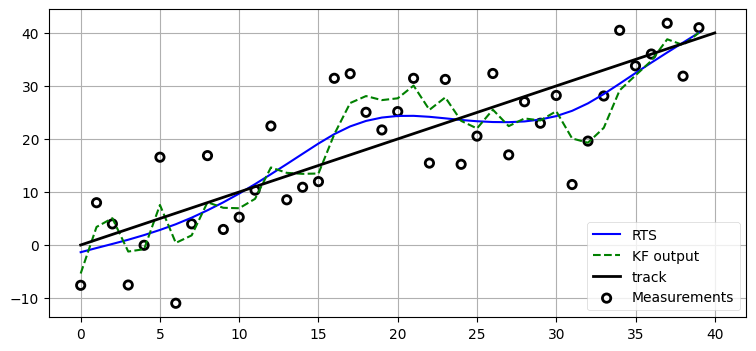
ただし、この平滑化がシステムモデルを使って行われたことは理解しておかなくてはならない。フィルタには追跡対象が定常速度モデルに従い、プロセスノイズが小さいことを伝えている。そのためフィルタは将来の観測値を見て物体の振る舞いが定常速度モデルに近いことを確認でき、入力に含まれるノイズの大半を除去できる。では、系のプロセスノイズが大きい場合はどうなるだろうか？例えば激しい風の吹く中を飛行する軽い飛行機は速度が頻繁に変化するので、フィルタは風によって起こるモデルに入っていない変化とノイズを区別しにくくなる。この設定における結果を次のグラフに示す:

In [8]

plot_rts(noise=7., Q=.1)

このグラフから、RTS スムーザーが行う「平滑化」は普通の意味での平滑化ではないことが分かる。RTS スムーザーはこちらが伝えた系の振る舞いおよび系と観測値のノイズ、そして過去と未来の観測値を使って最適な推定値を計算する。

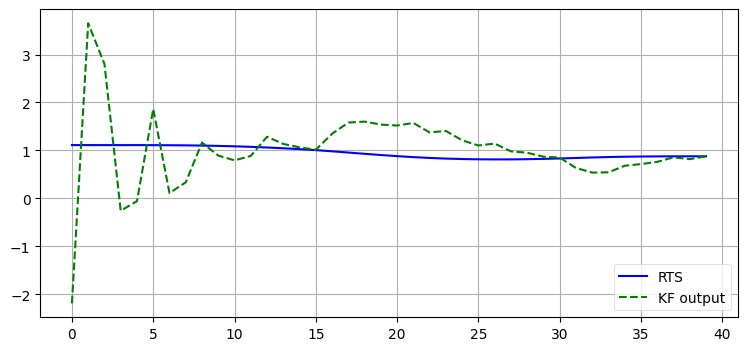
最後にカルマンフィルタと RTS スムーザーにおける速度の推定値を確認しよう:

In [9]

plot_rts(7.,show_velocity=True);

隠れ変数である速度はさらに著しく改善しているのが分かる。

13.5 固定遅延平滑化

前節で示した RTS スムーザーは利用可能な全てのデータを考慮して各推定値を計算するので、バッチモードでデータを処理できるなら必ず使うべきアルゴリズムである。ただバッチモードは全ての問題で使えるわけではない。バッチモードでなくても平滑化された過去の推定値を計算したい場合はもちろんある。この状況を次の図に示す:

In [10]

from kf_book.smoothing_internal import show_fixed_lag_numberline

show_fixed_lag_numberline()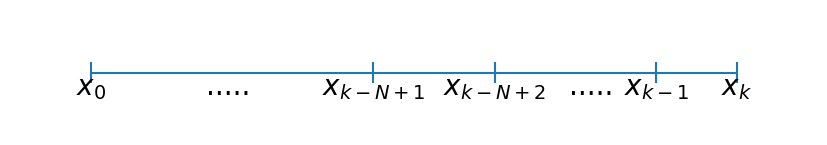

普通のカルマンフィルタを使うと時刻 \(k\) で \(x_k\) の推定値を計算できる。しかし時刻 \(k\) で受け取った観測値を使えば、\(x_{k-1}\) の推定値を改善できる。同様に時刻 \(k-1\) と \(k\) の観測値を使えば \(x_{k-2}\) の観測値を改善でき、この考え方は \(N\) 個前の時刻まで繰り返すことができる。

固定遅延平滑化の数式の導出は本書の範囲を超える。もし興味があるなら、Dan Simon 著 Optimal State Estimation² に素晴らしい解説がある。核となるアイデアは、状態ベクトル \(\mathbf{x}\) を考える代わりに、次の拡張された状態を考えるというものだ:

\[ \mathbf{x} = \begin{bmatrix}\mathbf{x}_k \\ \mathbf{x}_{k-1} \\ \vdots\\ \mathbf{x}_{k-N+1}\end{bmatrix} \]

この状態を採用すると、異なるステップにおける状態の間の関係を示す非常に大きな共分散行列が定義される。FilterPy の FixedLagSmoother クラスが拡張された行列の定義を含めた全ての計算を受け持つ。KalmanFilter クラスを使うときと同様に FixedLagSmoother クラスのオブジェクトを構築すれば、後はアルゴリズムの予測ステップと更新ステップを実装する smooth メソッドを呼び出すだけで済む。

FixedLagSmoother クラスの smooth メソッドに新しい観測値を渡すと、その観測値に対応する時刻における状態が推定される。それだけではなく、FixedLagSmoother は過去の N-1 個の推定値の調整も行う。平滑化された推定値は FixedLagSmoother.xSmooth というリストに格納される。FixedLagSmoother.x には最新の推定値が格納される。これは平滑化されていないので、通常のカルマンフィルタの出力と同じである。

In [11]

from filterpy.kalman import FixedLagSmoother, KalmanFilter
import numpy.random as random

fls = FixedLagSmoother(dim_x=2, dim_z=1, N=8)

fls.x = np.array([0., .5])
fls.F = np.array([[1.,1.],
                  [0.,1.]])

fls.H = np.array([[1.,0.]])
fls.P *= 200
fls.R *= 5.
fls.Q *= 0.001

kf = KalmanFilter(dim_x=2, dim_z=1)
kf.x = np.array([0., .5])
kf.F = np.array([[1.,1.],
                 [0.,1.]])
kf.H = np.array([[1.,0.]])
kf.P *= 200
kf.R *= 5.
kf.Q = Q_discrete_white_noise(dim=2, dt=1., var=0.001)

N = 4 # 遅延のサイズ

nom =  np.array([t/2. for t in range (0, 40)])
zs = np.array([t + random.randn()*5.1 for t in nom])

for z in zs:
    fls.smooth(z)

kf_x, _, _, _ = kf.batch_filter(zs)
x_smooth = np.array(fls.xSmooth)[:, 0]


fls_res = abs(x_smooth - nom)
kf_res = abs(kf_x[:, 0] - nom)

plt.plot(zs, alpha=0.5, marker='o', label='zs')
plt.plot(x_smooth, label='FLS')
plt.plot(kf_x[:, 0], label='KF', ls='--')
plt.legend(loc=4)

print(f'固定遅延スムーザーからの出力の標準偏差: {np.mean(fls_res):.3f}')
print(f'カルマンフィルタからの出力の標準偏差: {np.mean(kf_res):.3f}')

Out [11]

固定遅延スムーザーからの出力の標準偏差: 2.616
カルマンフィルタからの出力の標準偏差: 3.564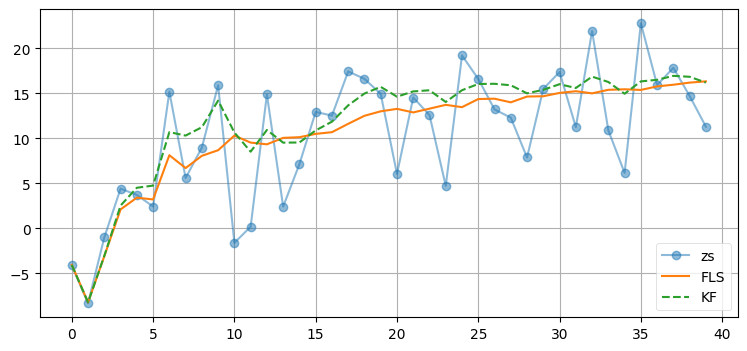

ここでは N=4 としているので、それぞれの推定値は四つの観測値を使って計算される。このためフィルタは収束さえすれば非常に滑らかな推定値を生成するものの、引き換えに計算コストは通常のカルマンフィルタと比べて約四倍となる。N の値を大きくしたり小さくしたりしてみてほしい。4 は適当に選んだ値であり、この値に理論的な裏付けがあるわけではない。

H. Rauch, F. Tung, and C. Striebel, "Maximum likelihood estimates of linear dynamic systems," AIAA Journal, vol. 3, no. 8, pp. 1445-1450, 1965.^[return]
Dan Simon, Optimal State Estimation, John Wiley & Sons, 2006.^[return]

第 13 章 平滑化