第 6 章多変量カルマンフィルタ

これで多変量形式の完全なカルマンフィルタを解説・実装する準備が整った。前章では多変量ガウス分布が複数の確率変数 (例えば航空機の位置と速度) の間に存在する相関関係を表現することを学び、変数の間に相関関係があると事後分布が格段に改善されることを見た。たとえ位置と速度が大まかにしか分からなくても、その間に相関があることを知っていれば、非常に正確な推定値が得られる。

完全な解説付きの例をいくつか使ってフィルタの動作を直感的に理解していくのが望ましいと思っているので、これからたくさんの例を示す。ただし、本章で示す例では多くの問題がごまかされている。特殊ケースでしか動かなかったり、"魔法" が含まれていたり──特定の結果を導いた理由が明らかでなかったり──する。しかし一般化された厳密な等式から始めたとしたら、たくさんある記号が何を表して、実際の問題にどうすれば適用できるのだろうかと途方に暮れてしまうだろう。厳密な数学的基礎は次章に回し、本章で触れられない正しい近似の仕方や追加情報はそこで提供する。

このため、ここではニュートンの運動方程式で表せる問題だけを考えることにする。こういったフィルタは離散化連続時間キネマティックフィルタ (discretized continuous-time kinematic filters) などと呼ばれる。ニュートンの運動方程式で表せないこれ以外の系に対する数式は次章カルマンフィルタの数学で考える。

6.1 ニュートンの運動方程式

ニュートンの運動方程式によると、位置 \(x_0\) から速度 \(v\) で等速運動を開始した物体の時刻 \(t\) における位置 \(x\) は次の等式で与えられる:

\[ x = vt + x_0 \]

例えば \(13~\text{m}\) 地点から速度が \(10~\text{m/s}\) で運動を開始したなら、12 秒後の位置は \(10×12 + 13 = 133~\text{m}\) と計算できる。

一定の加速度を仮定した等式もある:

\[ x = \frac{1}{2}at^2 + v_0t + x_0 \]

一定の躍度 (jerk, 加速度の変化率) があるとすれば次の等式となる:

\[ x = \frac{1}{6}jt^3 + \frac{1}{2}a_0 t^2 + v_0 t + x_0 \]

こういった等式は微分方程式を積分することで得られる。例えば速度が \(v\) で一定のとき時刻 \(t\) における位置を表す等式は

\[ x = vt + x_0 \]

であり、これは次のように導出できる:

\[ \begin{aligned} v &= \frac{dx}{dt}\\ dx &= v\, dt \\ \int_{x_0}^x\, dx &= \int_0^t v\, dt\\ x - x_0 &= vt - 0\\ x &= vt + x_0 \end{aligned} \]

カルマンフィルタの設計は系のダイナミクスを記述する微分方程式系から始まる。大部分の微分方程式系はこの例のように簡単に積分できない。ただ積分で閉形式の解が手に入るとカルマンフィルタの設計が簡単になるので、ここではニュートンの運動方程式を最初に考える。またもう一つの利点として、カルマンフィルタの主な応用例である物体の追跡で使われるのもニュートンの運動方程式である。

6.2 カルマンフィルタのアルゴリズム

次に示すカルマンフィルタのアルゴリズムはここまでに何度も使ってきたベイズフィルタのアルゴリズムと同じである。更新ステップが少し複雑になるのだが、これについてはそこまで行ったときに説明する。

初期化

フィルタの状態を初期化する。
状態に関する信念を初期化する。

予測

プロセスモデルを使って次のタイムステップにおける状態を予測する。
予測の不確実性に応じて信念を調整する。

更新

観測値とその正確さに関する信念を取得する。
予測値と観測値の残差を計算する。
予測値の正確さと観測値の正確さからスケーリング係数を計算する。
計算されたスケーリング係数を使って予測値と観測値の間の値に状態を設定する。
予測値の正確さと観測値の正確さに基づいて状態に関する信念を更新する。

このアルゴリズムを思い出してもらうために、図を使った説明を再掲しておく:

In [3]

import kf_book.book_plots as book_plots
book_plots.show_residual_chart()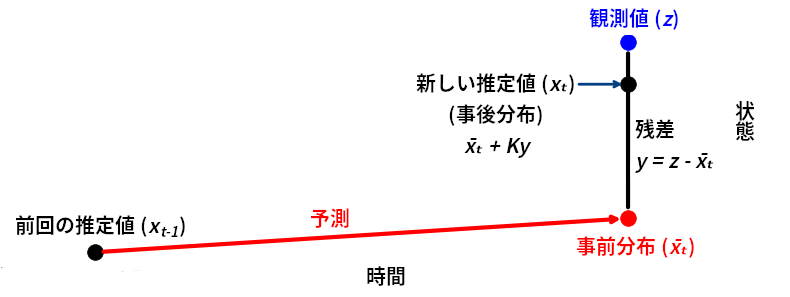

単変量カルマンフィルタでは単変量ガウス分布で状態を表したので、多変量カルマンフィルタでは多変量ガウス分布で状態を表すのが自然である。前章では多変量ガウス分布の平均にはベクトル、(共) 分散には行列を使うと学んだ。これはカルマンフィルタで推定を行うときに線形代数が必要なことを意味する。

覚えてほしいわけではないが、単変量および多変量の等式を次に示す。二つが非常に似ていることに注目してほしい:

予測

\[ \def\arraystretch{1.5} \begin{array}{l|l|l} \text{単変量} & \text{単変量} & \text{多変量} \\[-5px] & \text{(カルマンの形式)} & \\ \hline \bar \mu = \mu + \mu_{f_x} & \bar x = x + dx & \bar{\mathbf x} = \mathbf{Fx} + \mathbf{Bu}\\ \bar\sigma^2 = \sigma_x^2 + \sigma_{f_x}^2 & \bar P = P + Q & \bar{\mathbf P} = \mathbf{FPF}^\mathsf T + \mathbf Q \\[3pt] \end{array} \]

線形代数について詳しく知らなくても、次の説明は理解できるはずだ:

\(\mathbf x,\, \mathbf P\) は状態を表す多変量ガウス分布の平均と共分散行列であり、それぞれ \(x\) と \(\sigma^2\) に対応する。
\(\mathbf F\) は状態遷移関数 (state transition function) である。\(\mathbf x\) に \(\mathbf{F}\) を乗じると事前分布が計算される。
\(\mathbf Q\) はプロセスモデルに加わるノイズの共分散行列 (プロセスノイズ行列 process noise matrix) を表す。\(\sigma^2_{f_x}\) に対応する。
\(\mathbf B\) と \(\mathbf u\) は多変量カルマンフィルタで新しく登場する概念であり、系に対する制御入力をモデル化する。

更新

\[ \def\arraystretch{1.5} \begin{array}{l|l|l} \text{単変量} & \text{単変量} & \text{多変量} \\[-5pt] & \text{(カルマンの形式)} & \\ \hline & y = z - \bar x & \mathbf y = \mathbf z - \mathbf{H\bar x} \\[8pt] & \displaystyle K = \frac{\bar P}{\bar P+R}& \mathbf K = \mathbf{\bar{P}H}^\mathsf T (\mathbf{H\bar{P}H}^\mathsf T + \mathbf R)^{-1} \\[8pt] \displaystyle \mu=\frac{\bar\sigma^2\, \mu_z + \sigma_z^2 \, \bar\mu} {\bar\sigma^2 + \sigma_z^2} & x = \bar x + Ky & \mathbf x = \bar{\mathbf x} + \mathbf{Ky} \\[8pt] \displaystyle \sigma^2 = \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} & P = (1-K)\bar P & \mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar{P}} \\[8pt] \end{array} \]

記号の説明を示す:

\(\mathbf H\) は観測関数 (measurement function) である。本書で初めて登場する概念であり、後で説明される。\(\mathbf H\) を無視して等式を読むと、ここでも単変量と多変量のカルマンフィルタがよく似ていることが分かるはずだ。
\(\mathbf z\) は観測された状態、\(\mathbf R\) は観測された状態に含まれる誤差の共分散行列 (観測ノイズ行列 measurement noise matrix) である。\(z\) と \(\sigma_z^2\) に対応する (単変量の「カルマンの形式」で \(\mu\) を \(x\) としたのは、記法を可能な限り似せるためだ)。
\(\mathbf y\) と \(\mathbf K\) はそれぞれ残差とカルマンゲインである。

ベクトルと行列が使われるので細かい部分は単変量のカルマンフィルタと異なるものの、基本的な考え方は全く変わらない:

ガウス分布で状態の推定値とその不確実性を表す。
ガウス分布で観測値とその誤差を表す。
入力がガウス分布のとき出力もガウス分布になるように、プロセスモデルを線形に表現する。
線形のプロセスモデルを使って次の状態 (事前分布) を予測する。
観測値と事前分布の間にある値を推定値として採用する。

カルマンフィルタの設計者としてあなたがすべきことは、状態 \(\left(\mathbf x,\ \mathbf P\right)\)、プロセスモデル \(\left(\mathbf F,\ \mathbf Q\right)\)、観測値 \(\left(\mathbf z,\ \mathbf R\right)\)、そして観測関数 \(\mathbf H\) の設計である。制御入力を持つ (ロボットなどの) 系では \(\mathbf B\) と \(\mathbf u\) の設計も必要になる。

カルマンフィルタの式は FilterPy で predict 関数および update 関数として実装してある。次のようにするとインポートできる:

from filterpy.kalman import predict, update

6.3 犬の追跡

これまでに何度も考えてきた犬の追跡問題をもう一度考えよう。今回は前章で得られた非常に重要な考察を取り入れ、隠れ変数を使うことで推定値を改善させる。最初に数式を見せてもいいのだが、ここではさっさとフィルタの実装に取り掛かって、その途中で数式を学ぶことにする。表面的には数式が前章と違っていておそらくは複雑になっているものの、基本的なアイデアは同じだ──ガウス分布を足したり乗じたりしているだけである。

犬のシミュレーションを書くところから始める。シミュレーションは count ステップ実行され、各ステップで犬は約 \(1~\text{m}\) だけ前に進む。各ステップで速度が変動し、その変動の分散は process_var だとする。位置を更新した後に観測値が計算され、そのときセンサーに加わるノイズの分散は z_var だと仮定する。次の関数は位置と観測値を NumPy 配列として返す:

In [4]

import math
import numpy as np
from numpy.random import randn

def compute_dog_data(z_var, process_var, count=1, dt=1.):
    """ 犬が通った点と観測値からなる一次元 ndarray を返す。 """
    x, vel = 0., 1.
    z_std = math.sqrt(z_var)
    p_std = math.sqrt(process_var)
    xs, zs = [], []
    for _ in range(count):
        v = vel + (randn() * p_std)
        x += v*dt
        xs.append(x)
        zs.append(x + randn() * z_std)
    return np.array(xs), np.array(zs)

6.4 予測ステップ

予測では状態変数、状態共分散行列、プロセスモデル、プロセスノイズを設計する必要があり、場合によっては制御入力も設計しなければならない。順に見ていく。

状態変数の設計

前に一次元空間を動く犬を追跡したときはガウス分布を利用した。平均 \(\mu\) が最も可能性の高い位置を表し、分散 \(\sigma^2\) が位置の確率分布の形を表す。このとき犬の位置が系の状態であり、\(\mu\) を状態変数 (state variable) と呼ぶ。

今考えている問題では犬の位置と速度の両方を考慮するので、多変量のガウス分布を使わなければならない。つまり状態変数として状態ベクトル \(\mathbf x\) を考え、対応する共分散行列 \(\mathbf P\) を考える必要がある。

状態変数には二つの種類がある。センサーによって直接観測される観測変数 (observed variable) と、観測変数から導かれる隠れ変数 (observed variable) である。今考えている犬の追跡問題ではセンサーが位置だけを出力できるので、位置が観測変数、速度が隠れ変数となる。隠れ変数を追跡する方法はすぐに説明する。

理解しておくべき重要なこととして、位置と速度を追跡すると決めたのは設計判断であるという事実がある (この判断が意味すること、あるいは仮定していることはまだ議論できない)。例えば位置と速度に加えて加速度や躍度を追跡することもできた。今の段階では、速度を共分散行列に含めると位置の分散がずっと小さくなった前章の議論を思い出してほしい。カルマンフィルタがどのように隠れ変数の推定値を計算するかは本章の後半で説明する。

単変量のカルマンフィルタを考えたときは犬の位置をスカラー (例えば \(\mu=3.27\)) で表し、前章では多変量ガウス分布を使うと複数の変数を表せることを学んだ。例えば位置 \(10.0~\text{m}\) と速度 \(4.5~\text{m/s}\) を指定したいなら、次のように書ける:

\[ \mu = \begin{bmatrix}10.0\\4.5\end{bmatrix} \]

多変量カルマンフィルタは線形代数を利用して実装され、\(n\) 個の状態変数は \(n{\times}1\) 行列 (ベクトル) で表される。カルマンフィルタの式では状態を \(\mathbf x\) で表すので、\(\mathbf x\) は次のように定義する:

\[ \mathbf x =\begin{bmatrix}x \\ \dot x\end{bmatrix} \]

ここで \(x\) は犬の位置、\(\dot x\) は \(x\) の一次微分係数を表す。これは微分をドットで表すニュートンの記法であり、\(\dot x\) は \(x\) の \(t\) に関する一次微分係数を表す: つまり \(\dot x = \frac{dx}{dt}\) である。\(\mu\) ではなく \(\mathbf x\) となっているが、これは多変量ガウス分布の平均を表すことを理解してほしい。

この等式を \(\mathbf x =\Big[x \ \ \dot x\Big]^\mathsf T\) と書くこともできる。行ベクトルを転置すると列ベクトルになるので同じことだ。この記法だと垂直方向のスペースが節約できるので、テキストでは重宝する。

状態ベクトル \(\mathbf x\) と位置 \(x\) が同じ名前を持つのは偶然である。例えば \(y\) 軸に沿って犬を追跡するとしたら状態ベクトルは \(\mathbf x =\Big[y \ \ \dot y\Big]^\mathsf T\) であり、\(\mathbf y = \Big[y \ \ \dot y\Big]^\mathsf T\) ではない。カルマンフィルタの文献で \(\mathbf x\) は状態変数を表す標準的な名前なので、分かりやすさを優先して他の名前を付けることはしなかった。変数の命名を一致させておけば、他の人々とのコミュニケーションが簡単になる。

これをコードにしよう。x の初期化は簡単だ:

In [5]

x = np.array([[10.0],
              [4.5]])
x

Out [5]

array([[10. ],
       [ 4.5]])

私は列ベクトルを作るときに行ベクトルを作ってから転置することが多い。こうした方が読みやすいだろう:

In [6]

x = np.array([[10., 4.5]]).T
x

Out [6]

array([[10. ],
       [ 4.5]])

ただ NumPy は一次元配列をベクトルとして認識するので、次のようにも書ける:

In [7]

x = np.array([10.0, 4.5])
x

Out [7]

array([10. ,  4.5])

NumPy 配列では全ての要素が同じ型を持つ。たいていは int か float である。numpy.array に渡すリストの要素が全て int ならデータ型は int になり、そうでなければデータ型は float になる。この仕様を利用すると、引数のリストの要素を一つだけ浮動小数点数にして float の NumPy 配列を作成できる:

In [8]

np.array([1., 0, 0, 0, 0, 0])

Out [8]

array([1., 0., 0., 0., 0., 0.])

さらに例を示す:

In [9]

A = np.array([[1, 2], [3, 4]])
x = np.array([[10.0], [4.5]])

# 行列乗算
print(np.dot(A, x))

Out [9]

[[19.]
 [48.]]

Python 3.5 以降では行列乗算演算子 @ が利用でき、np.dot(A, B) = A @ B が成り立つ。ただ A と B が両方とも配列でなくてはならないので、そこまで便利ではない。特に本書では考えている等式にはスカラーを代入できるので、@ が使えない場合が多い。@ 演算子の使用例を示す:

In [10]

# @ を使った行列乗算
print(A @ x)
print()

x = np.array([[10.0, 4.5]]).T
print(A @ x)
print()

x = np.array([10.0, 4.5])
print(A @ x)

Out [10]

[[19.]
 [48.]]

[[19.]
 [48.]]

[19. 48.]

最後の A @ x は一次元配列を返しているが、私が書いたカルマンフィルタクラスはこういった一次元配列を処理できるようにしてある。今考えるとこの仕様が混乱を招いたかもしれないが、動作は正しい。

状態共分散行列の設計

状態を表すガウス分布のもう半分は共分散行列 \(\mathbf P\) である。単変量カルマンフィルタでは \(\sigma^2\) の初期値を指定し、後はフィルタが観測値を受け取るたびに \(\sigma^2\) を自分で更新した。同じことが多変量カルマンフィルタでも起こる: \(\mathbf P\) の初期値を設定すれば、その後はフィルタがエポックごとに \(\mathbf P\) を更新する。

共分散行列中の分散は適当な値に設定する必要がある。例えば初期位置がほとんど分からないなら \(\sigma_\mathtt{pos}^2=500\, \text{m}^2\) と選択できる。また犬の最高速度は \(21~\text{m/s}\) 程度だから、速度に関して事前情報が何もないなら \(3\sigma_\mathtt{vel}=21\) つまり \(\sigma_\mathtt{vel}^2=7^2=49\) と設定できる。

前章では位置と速度に相関があると示した。では犬の場合に相関はどれくらいだろうか？私には分からない。これから見るように相関はフィルタが自分で計算してくれるので、共分散はゼロに初期化する。もちろん共分散を知っているならその値を使うべきだ。

共分散行列の対角線に各変数の分散が並び、非対角要素が共分散となることを思い出そう。そのため状態共分散行列 \(\mathbf{P}\) は次のようになる:

\[ \mathbf P = \begin{bmatrix}500 & 0 \\ 0&49\end{bmatrix} \]

これをコードにするときは、対角要素の値を受け取って対角行列を作成する numpy.diag 関数が利用できる。線形代数で対角行列 (diagonal matrix) とは非対角要素が全てゼロである行列のことを言う:

In [11]

P = np.diag([500., 49.])
P

Out [11]

array([[500.,   0.],
       [  0.,  49.]])

こうも書ける:

In [12]

P = np.array([[500., 0.],
              [0., 49.]])
P

Out [12]

array([[500.,   0.],
       [  0.,  49.]])

これで状態については終わりだ。フィルタの状態を多変量ガウス分布で表し、それをコードに実装できた。

プロセスモデルの設計

次のステップはプロセスモデルの設計である。プロセスモデルは系の振る舞いを記述する数学的モデルのことであり、カルマンフィルタは離散的なタイムステップが経過した後の状態を予測するときにこれを利用する。プロセスモデルは系のダイナミクスを記述する方程式の集合として定義される。

単変量カルマンフィルタの章では犬の動きを次の方程式でモデル化した:

\[ x = v \Delta t + x_0 \]

このモデルは次のように実装された:

def predict(pos, movement):
    return gaussian(pos.mean + movement.mean,
                    pos.var + movement.var)

本章では単変量ガウス分布を多変量ガウス分布に変えて同じことを行う。こう聞いて次のような実装を思い浮かべるかもしれない:

\[ \mathbf x = \begin{bmatrix}5.4\\4.2\end{bmatrix}, \, \, \dot{\mathbf x} = \begin{bmatrix}1.1\\0.0\end{bmatrix} \\ \mathbf x = \dot{\mathbf x}t + \mathbf x \]

しかし私たちはこれを一般化しなければならない。カルマンフィルタの式はニュートンの運動方程式で記述される系だけではなく任意の線形系に対して適用される。例えばフィルタを適用しようとしている系は化学工場の配管システムで、それぞれのパイプに対する流量は様々な値の線形結合として定まるかもしれない:

\[ \begin{aligned} \mathtt{pipe_1} &= 0.134(\mathtt{valve}_1) + 0.41(\mathtt{valve}_2 - \mathtt{valve}_3) + 1.34 \\ \mathtt{pipe_2} &= 0.210(\mathtt{valve}_2) - 0.62(\mathtt{valve}_1 - \mathtt{valve}_5) + 1.86 \end{aligned} \]

線形代数を使うと複数の線形方程式からなる系を簡単に表せる。例えば系

\[ \begin{cases} 2x + 3y = 8 \\ 4x - \hphantom{3} y = 2 \end{cases} \]

は、次のように行列を使って書くことができる:

\[ \begin{bmatrix}2& 3 \\ 4&-1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}8\\2\end{bmatrix} \]

この等式にある行列乗算を行うと、元の二つの方程式が得られる。線形代数ではこの等式を \(\mathbf{Ax}=\mathbf{B}\) と書く。ここで記号は次のように定義される:

\[ \mathbf{A} = \begin{bmatrix}2& 3 \\ 4&-1\end{bmatrix},\quad \mathbf x = \begin{bmatrix}x\\y\end{bmatrix},\quad \mathbf B=\begin{bmatrix}8\\2\end{bmatrix} \]

線形方程式 \(\mathbf{Ax}=\mathbf{B}\) は SciPy の linalg パッケージを使うと解ける:

In [13]

from scipy.linalg import solve
A = np.array([[2, 3],[4, -1]])
b = np.array([[8], [2]])
x = solve(A, b)
x

Out [13]

array([[1.],
       [2.]])

プロセスモデルの方程式があれば現在の状態から次の状態を計算できるので、私たちはフィルタを発展させるためにこの式を使う。カルマンフィルタは上述の線形方程式を利用してプロセスモデルを記述する:

\[ \mathbf{\bar x} = \mathbf{Fx} \]

ここで \(\mathbf{\bar x}\) は事前分布、つまり予測された状態を表す。今の問題に合うよう具体的に書くとこうなる:

\[ \begin{bmatrix} \bar x \\ \bar{\dot x}\end{bmatrix} = \begin{bmatrix}? & ? \\? & ?\end{bmatrix}\begin{bmatrix}x\\\dot x\end{bmatrix} \]

カルマンフィルタの設計者としての私たちの仕事は、\(\bar{\mathbf x} = \mathbf{Fx}\) が考えている系の発展 (予測) となるように \(\mathbf F\) を選ぶことである。このために各状態変数につき一つの方程式が必要になる。今考えている問題では \(\mathbf x = \Big[x \ \ \dot x\Big]^\mathtt{T}\) だから、位置 \(x\) を計算する式と速度 \(\dot x\) を計算する式が必要になる。位置の発展を記述する式なら既に知っている:

\[ \bar x = x + \dot x \Delta t \]

速度に対する式はどうなるだろうか？追跡する犬の速度の時間変化に対する予測モデルを私たちは持っていない。この場合は発展において速度は一定だと仮定することになる。もちろん正確に言えばこれは正しくないが、こうしても発展で速度が大きく変化しない限りフィルタは非常に良く動作する。よって速度に対しては次の式を使う:

\[ \bar{\dot x} = \dot x \]

犬の追跡問題における系のプロセスモデルがこれで求まった:

\[ \begin{cases} \begin{aligned} \bar x &= x + \dot x \Delta t \\ \bar{\dot x} &= \dot x \end{aligned} \end{cases} \]

確かに状態に含まれる各変数につき一つの式が (発展後の変数が左辺にだけ存在する状態で) 与えられている。さらにこの方程式の集合を \(\bar{\mathbf x} = \mathbf{Fx}\) の形に表す必要がある。項を整理すればすべきことが分かりやすくなる:

\[ \begin{cases} \begin{aligned} \bar x &= 1x + &\Delta t\, \dot x \\ \bar{\dot x} &=0x + &1\, \dot x \end{aligned} \end{cases} \]

これを行列形式に書き直すと次のようになる:

\[ \begin{aligned} \begin{bmatrix}\bar x \\ \bar{\dot x}\end{bmatrix} = \begin{bmatrix}1&\Delta t \\ 0&1\end{bmatrix} \begin{bmatrix}x \\ \dot x\end{bmatrix} \\[15px] \therefore\ \mathbf{\bar x} = \mathbf{Fx},\quad \mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0&1\end{bmatrix} \end{aligned} \]

\(\mathbf F\) は状態遷移関数 (state transition function) あるいは状態遷移行列 (state transition matrix) と呼ばれる。本書後半では \(\mathbf F\) が行列ではなく一般の関数になるので、「関数」と呼んだ方が一般性が増す。

In [14]

dt = 0.1
F = np.array([[1, dt],
              [0, 1]])
F

Out [14]

array([[1. , 0.1],
       [0. , 1. ]])

これを試してみよう！ FilterPy には \(\mathbf{\bar x} = \mathbf{Fx}\) を計算することで予測を行う predict 関数がある。これを呼び出して何が起こるかを見る。初期位置は \(10.0~\text{m}\)、初期速度は \(4.5~\text{m/s}\)、タイムステップは 0.1 秒 (dt = 0.1) と定義する。このとき発展後の新しい位置は \(10.45~\text{m}\) となり、速度は変わらないはずである:

In [15]

from filterpy.kalman import predict

x = np.array([10.0, 4.5])
P = np.diag([500, 49])
F = np.array([[1, dt], [0, 1]])

# Q はプロセスノイズ行列
x, P = predict(x=x, P=P, F=F, Q=0)
print('x =', x)

Out [15]

x = [10.45  4.5 ]

正しく動いているようだ。predict を何回か連続で呼び出せば、そのたびに状態が更新される:

In [16]

for _ in range(4):
    x, P = predict(x=x, P=P, F=F, Q=0)
    print('x =', x)

Out [16]

x = [10.9  4.5]
x = [11.35  4.5 ]
x = [11.8  4.5]
x = [12.25  4.5 ]

predict は発展後の平均と共分散行列を計算する。現在の P は発展 (予測) を五回行った後の共分散行列であり、カルマンフィルタの式の \(\mathbf P\) に対応する。この値を確認してみよう:

In [17]

print(P)

Out [17]

[[512.25  24.5 ]
 [ 24.5   49.  ]]

対角要素に注目すると、位置の分散が大きくなったことが分かる。更新を行わずに五回の予測ステップを実行したので、位置はより不確実になる。また非対角要素は非ゼロとなっている──カルマンフィルタが位置と速度の間の相関を検出したということだ！最後に、速度の分散は変化していない。

予測前後における共分散行列のプロットを次に示す。初期値は赤の実線で、事前分布 (予測値) は黒の破線で描かれている。変化が分かりやすくなるよう分散とタイムステップを調整してある:

In [18]

from filterpy.stats import plot_covariance_ellipse

dt = 0.3
F = np.array([[1, dt], [0, 1]])
x = np.array([10.0, 4.5])
P = np.diag([500, 500])
plot_covariance_ellipse(x, P, edgecolor='r')
x, P = predict(x, P, F, Q=0)
plot_covariance_ellipse(x, P, edgecolor='k', ls='dashed')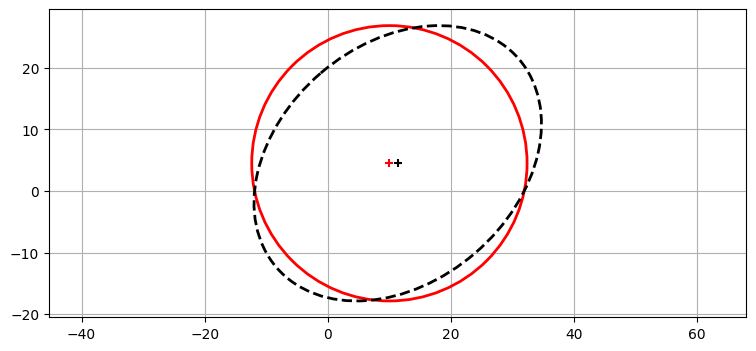

まず楕円の中心が少しだけ (10 から 11.35 に) 移動したのが分かる。これは移動によって位置が変化したためだ。また楕円が斜め方向に細長く、位置と速度に相関があることを示している。さらに、これまでに見てきたフィルタと同様に、予測ステップで情報の散逸が起こっている。フィルタは新しい \(\mathbf{\bar P}\) の値をどのように計算し、そのときどの情報を使ったのだろうか？プロセスノイズ行列 \(\mathbf{Q}\) は \(\mathbf{0}\) に設定してあるから、ノイズが影響したのではない。この点を議論するのはまだ早い。詳しくは基礎的な事項の後に説明する。

プロセスノイズの設計

プロセスノイズについて簡単に復習しよう。クルーズコントロールを有効にした状態で走行する車を考える。この車は一定の速度で走行するはずだから、その位置は \(\bar x_k=\dot x_k\Delta t + x_{k-1}\) とモデル化できる。しかし車は様々な未知の要因からの影響を受ける。クルーズコントロールは速度を完璧に一定に保てるわけではないし、坂道や道路のくぼみ、あるいは風も車に影響する。誰かが車の窓を開けて空気抵抗が変わるかもしれない。

この系は次の微分方程式でモデル化できる:

\[ \dot{\mathbf x} = f(\mathbf x) + \mathbf{w} \]

ここで \(f(\mathbf x)\) は状態の遷移をモデル化し、\(\mathbf{w}\) はプロセスに加わるノイズをモデル化する。カルマンフィルタでは白色ノイズ (white noise) と呼ばれるノイズが仮定される。

微分方程式の集合からカルマンフィルタ用の行列を導く方法はカルマンフィルタの数学の章で学ぶ。本章ではニュートンが私たちのために導いてくれた運動方程式を使わせてもらうことにする。今は計算された共分散行列 \(\mathbf P\) にプロセスノイズ行列 \(\mathbf Q\) を加えれば系のノイズを考慮できることを知っておくだけで構わない。今考えているノイズは白色ノイズであり平均が \(\mathbf{0}\) なので、ノイズによって \(\mathbf{\bar x}\) は変動しない。

単変量カルマンフィルタは予測ステップにおける分散を variance = variance + process_noise で計算した。多変量カルマンフィルタも同様であり、P = P + Q と本質的に同じ計算が行われる。「本質的に」と言ったのは共分散行列を求める等式にノイズと関係のない項が含まれるためだ (この項は後で説明される)。

プロセスノイズ行列の導出は非常に手間がかかるので、カルマンフィルタの数学の章に回す。ここでは \(\mathbf Q\) は白色ノイズ \(\mathbf{w}\) の期待値に等しく、\(\mathbf Q = \mathbb E[\mathbf{ww}^\mathsf T]\) と計算されることを知っておけばよい。本章ではこの行列を変えるとフィルタの振る舞いがどう変わるかについて直感的な理解を得ることに集中する。

FilterPy は本章の運動問題に対する \(\mathbf Q\) を求める関数 Q_discrete_white_noise を提供する。この関数は三つのパラメータを受け取る。dim は行列の次元、dt はタイムステップ (単位は秒)、var はノイズの分散を表す。この関数は後述する仮定の下で指定された期間におけるノイズを離散化する。例えば次のコードは分散が \(2.35\) でタイムステップが 1 秒の白色ノイズに対する \(\mathbf Q\) を計算する:

In [19]

from filterpy.common import Q_discrete_white_noise
Q = Q_discrete_white_noise(dim=2, dt=1., var=2.35)
print(Q)

Out [19]

[[0.588 1.175]
 [1.175 2.35 ]]

制御関数の設計

カルマンフィルタはデータをフィルタリングするだけではなく、ロボットや航空機といった系に送られる制御入力を取り入れることもできる。例えばロボットを制御しているとしよう。このとき各タイムステップで現在位置と目標位置に基づいた旋回信号と加速信号がロボットに送信される。カルマンフィルタではこういった知識をフィルタに取り入れることができ、現在の速度と制御入力の両方を取り入れた予測位置の計算が行える。思い出そう: 私たちは絶対に情報を捨てない。

線形系では制御入力の効果を線形方程式の集合で表せる。線形方程式の集合を線形代数の記法を使って表せば

\[ \Delta\mathbf x = \mathbf{Bu} \]

となる。ここで \(\mathbf u\) は制御入力 (control input)、\(\mathbf B\) は制御入力モデル (control input model) あるいは制御関数 (control function) と呼ばれる。例えば \(\mathbf u\) は車輪のモーターが回る速度を制御する電圧で、\(\mathbf B\) を乗じると \(\Delta[\begin{smallmatrix}x\\\dot x\end{smallmatrix}]\) が得られるのかもしれない。言い換えれば、\(\mathbf B\) は制御入力によって \(\mathbf x\) がどれくらい変動するかを計算する必要がある。

こんなわけで、カルマンフィルタにおいて事前分布の平均を求める完全な等式は

\[ \mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} \]

となる。KalmanFilter.predict を呼んだときに計算されるのもこの値である。

犬は訓練すれば声による指示に反応できるから、\(\mathbf{u}\) を犬に与えた指示だと考えよう。しかし追跡している私の犬はどう見ても指示に反応する様子はないので、\(\mathbf B\) はゼロに設定する。Python で予測を行うコードを示す:

In [20]

B = 0.  # 私の犬は言うことを聞きやしない！
u = 0
x, P = predict(x, P, F, Q, B, u)
print('x =', x)
print('P =', P)

Out [20]

x = [12.7  4.5]
P = [[680.587 301.175]
 [301.175 502.35 ]]

predict で \(\mathbf B\) のデフォルト値は \(0\) なので、\(\mathbf B\) と \(\mathbf u\) は渡さなくても構わない:

In [21]

predict(x, P, F, Q)[0] == predict(x, P, F, Q, B, u)[0]

Out [21]

array([ True,  True])

In [22]

predict(x, P, F, Q)[1] == predict(x, P, F, Q, B, u)[1]

Out [22]

array([[ True,  True],
       [ True,  True]])

予測ステップのまとめ

カルマンフィルタの設計者としてのあなたの仕事は、次の行列およびベクトルを指定することである:

\(\mathbf x,\ \mathbf P\): 状態と共分散行列
\(\mathbf F,\ \mathbf Q\): 状態遷移行列とプロセスノイズ行列
\(\mathbf u,\ \mathbf B\): 制御入力と制御関数 (省略可能)

6.5 更新ステップ

続いてフィルタの更新ステップを実装しよう。ここで指定が必要な行列は二つだけであり、どちらも理解は難しくない。

観測関数の設計

カルマンフィルタは更新ステップを観測空間 (measurement space) と呼ばれる空間で計算する。単変量カルマンフィルタの章では話が複雑になりすぎると思ってこの話題には触れなかった。そこで私たちはセンサーで犬を追跡し、センサーは犬の位置を報告した。このとき残差の計算は簡単に行える──フィルタが予測した位置を観測値から引けばいい:

\[ \text{残差} = \text{観測された位置} - \text{予測された位置} \]

残差を計算する必要があったのは、新しい推定値の計算で残差にカルマンゲインを乗じた値が必要なためだ。

もし温度計で温度を追跡していて、温度計の出力が温度に対応する電圧だったらどうなるだろうか？このとき残差を求める等式が意味をなさなくなる。温度から電圧を引くことはできない:

\[ \text{残差} = \text{電圧} - \text{温度}\;\;\;(\text{無意味！}) \]

というわけで温度を電圧に変換して引き算が行えるようにする必要がある。温度計の例であれば次のようなコードとなる:

CELSIUS_TO_VOLTS = 0.21475
residual = voltage - (CELSIUS_TO_VOLTS * predicted_temperature)

カルマンフィルタではこの問題が一般化されており、状態を観測値に変換する観測関数 (measurement function) をこちらから与えることになっている。状態と同じ変数を持つ値は状態空間 (state space) にあると言い、観測値と同じ変数を持つ値は観測空間 (measurement space) にあると言う。この言葉を使えば、状態空間にある値を観測空間にある値に変換するのが観測関数であり、カルマンフィルタの設計では観測関数を与えなければならない。

なぜ観測空間で考えるのだろうか？状態空間で計算するようにして、先ほどの例で言えば電圧を温度に変換することで残差を温度の差として求めるのではなぜいけないのだろうか？

それができない理由は、多くの観測値が非可逆であるためだ。例えば追跡問題の状態には隠れ変数 \(\dot x\) が含まれるが、観測値 (位置) から速度を含んだ状態を完全に復元する方法は存在しない。逆に位置と速度からなる状態を位置だけからなる "観測値" に変換する処理は自明に行える (速度を捨てるだけだ)。つまり更新ステップを観測空間で考えるのは、残差の計算を可能にするためである。

観測値 \(\mathbf z\) と状態 \(\mathbf x\) は両方ともベクトルだから、変換を行うには行列が必要になる。以前に示したカルマンフィルタの式の中でこの変換と残差の計算を行うのは次の式である:

\[ \mathbf y = \mathbf z - \mathbf{H \bar x} \]

\(\mathbf y\) が残差、\(\mathbf{\bar x}\) が事前分布、\(\mathbf z\) が観測値、\(\mathbf H\) が観測関数を表す。ここでは事前分布を受け取り、それに \(\mathbf H\) を乗じることで観測空間の値に変換し、変換結果を観測値から引いている。こうすると観測空間における予測値と観測値の差が計算される！

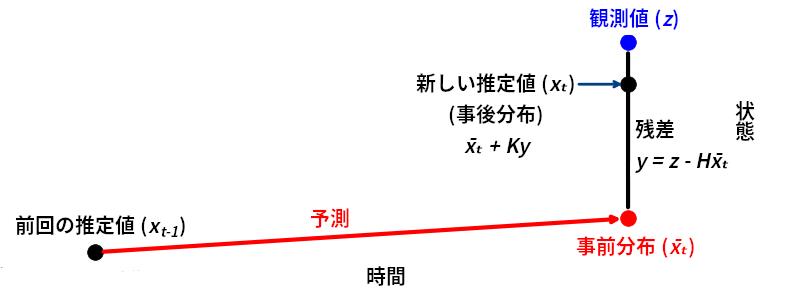
私たちは \(\mathbf{H \bar x}\) が観測値となるよう \(\mathbf H\) を設計しなければならない。今考えている問題でセンサーは位置を観測するから、\(\mathbf z\) は一次元のベクトルである:

\[ \mathbf z = \begin{bmatrix}z\end{bmatrix} \]

残差を求める式は次の形をしている:

\[ \begin{aligned} \textbf{y} &= \mathbf z - \mathbf{H\bar x} \\ \begin{bmatrix}y \end{bmatrix} &= \begin{bmatrix}z\end{bmatrix} - \begin{bmatrix}?&?\end{bmatrix} \begin{bmatrix}x \\ \dot x\end{bmatrix} \end{aligned} \]

\(\mathbf{Hx}\) が \(1{\times}1\) なので、\(\mathbf H\) は \(1{\times}2\) でなければならない。\(m{\times}n\) の行列と \(n{\times}p\) の行列を乗じると \(m{\times}p\) の行列となることを思い出そう。

位置 \(x\) には \(1\) を乗じて対応する観測値を取り出したい。また速度は位置の観測値に影響を及ぼさないので、\(\dot x\) には \(0\) を乗じたい。このとき次のように残差が計算される:

\[ \begin{aligned} \textbf{y} &= \mathbf z - \begin{bmatrix}1&0\end{bmatrix} \begin{bmatrix}x \\ \dot x\end{bmatrix} \\ &= [z] - [x] \end{aligned} \]

以上より、私たちが設計しているカルマンフィルタでは次のように設定すればよいと分かる:

\[ \mathbf H=\begin{bmatrix}1&0\end{bmatrix} \]

In [23]

H = np.array([[1., 0.]])

これでカルマンフィルタのほとんどの部分が設計できた。残るはセンサーのノイズをモデル化するだけである。

観測値の設計

観測値は平均 \(\mathbf z\) と共分散行列 \(\mathbf R\) で実装される。

平均 \(\mathbf z\) は簡単で、観測値をまとめたベクトルというだけだ。犬の追跡問題では観測値は一つだけだから、次のようになる:

\[ \mathbf z = \begin{bmatrix}z\end{bmatrix} \]

センサーあるいは観測値が二つあるときはこうなる:

\[ \mathbf z = \begin{bmatrix}z_1 \\ z_2\end{bmatrix} \]

観測ノイズ行列 (measurement noise matrix) はセンサーに含まれるノイズを共分散行列としてモデル化する。実際にカルマンフィルタを使うときはこのモデル化が難しい場合もある。大量のセンサーが存在する複雑な系では観測値の相関関係が明らかでない可能性があるし、ノイズが純粋なガウス分布にならないことも多い。例えば温度が高いときに高い温度へバイアスがかかる温度計があったとしたら、その温度計に対するノイズは平均の両側に等しく分布しない。こういった問題は後で考える。

カルマンフィルタの式で観測ノイズ行列は \(\mathbf R\) と表される。この行列は \(m{\times}m\) であり、ここで \(m\) はセンサーの個数を表す。また \(\mathbf{R}\) は共分散行列なので、センサー間の相関関係を表現できる。今考えている問題ではセンサーが一つだけだから、\(\mathbf R\) は次のように定義できる:

\[ \mathbf R = \begin{bmatrix}\sigma^2_z\end{bmatrix} \]

\(\sigma^2_z\) が \(5~\text{m²}\) なら \(\mathbf R = \begin{bmatrix}5\end{bmatrix}\) となる。

位置センサーを二つ持っていて、一つ目のセンサーは \(5~\text{m²}\) の分散、二つ目のセンサーは \(3~\text{m²}\) の分散を持つとする。このときは \(\mathbf R\) はこうなる:

\[ \mathbf R = \begin{bmatrix}5&0\\0&3\end{bmatrix} \]

分散を対角線上に配置したのは、これが共分散行列であるためだ。対角要素には分散が並び、非対角要素には共分散が (もしあれば) 配置される。ここでは二つのセンサーのノイズに相関はないと仮定しており、共分散は \(0\) になっている。

犬の追跡問題ではセンサーが一つだけなので、次のように実装できる:

In [24]

R = np.array([[5.]])

更新ステップは update 関数を呼び出すことで行う:

In [25]

from filterpy.kalman import update
z = 1.
x, P = update(x, P, z, R, H)
print('x =', x)

Out [25]

x = [ 1.085 -0.64 ]

カルマンフィルタの変数を全て管理するのは大変なので、FilterPy には KalmanFilter クラスを使ったフィルタも実装してある。本書ではこれからこのクラスを使っていく。ここまで手続き的なフィルタ関数を使ったのは、オブジェクト指向プログラミングが好きでない読者もいることを私が知っているからだ。

6.6 カルマンフィルタの実装

カルマンフィルタに必要なコードはこれまでに全て示したので、次は一つにまとめてみよう。まず KalmanFilter オブジェクトを構築する。そのとき状態に含まれる変数の個数を dim_x パラメータで、そして観測値の個数を dim_z で指定する必要がある。今考えている犬の追跡問題では二つの変数と一つの観測値が存在するから、次のように書ける:

from filterpy.kalman import KalmanFilter
dog_filter = KalmanFilter(dim_x=2, dim_z=1)

こうするとカルマンフィルタの行列とベクトルが全てデフォルトの値に初期化されたオブジェクトが作成される:

In [26]

from filterpy.kalman import KalmanFilter
dog_filter = KalmanFilter(dim_x=2, dim_z=1)
print('x = ', dog_filter.x.T)
print('R = ', dog_filter.R)
print('Q = \n', dog_filter.Q)
# など...

Out [26]

x =  [[0. 0.]]
R =  [[1.]]
Q =
 [[1. 0.]
 [0. 1.]]

続いてカルマンフィルタの行列とベクトルを考えている問題に合った値に初期化する。R, P, Q に異なる値を指定して実験できるようにするために、この処理はヘルパー関数として独立させておく。これから何種類ものカルマンフィルタを作成・実行することになるから、こうしておくと手間が大きく省ける:

In [27]

from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise

def pos_vel_filter(x, P, R, Q=0., dt=1.0):
    """ 状態 [x dx].T に対する定常速度モデルを実装する KalmanFilter を返す。 """

    kf = KalmanFilter(dim_x=2, dim_z=1)
    kf.x = np.array([x[0], x[1]]) # 位置と速度
    kf.F = np.array([[1., dt],
                     [0.,  1.]])  # 状態遷移行列
    kf.H = np.array([[1., 0]])    # 観測関数
    kf.R *= R                     # 観測の不確実性
    if np.isscalar(P):
        kf.P *= P                 # 共分散行列
    else:
        kf.P[:] = P               # [:] を使ってディープコピーを行う。
    if np.isscalar(Q):
        kf.Q = Q_discrete_white_noise(dim=2, dt=dt, var=Q)
    else:
        kf.Q[:] = Q
    return kf

KalmanFilter は R , P, Q を単位行列に初期化するので、kf.P *= P などとすれば対角要素がスカラー P の対角行列を簡単に作成できる。ではカルマンフィルタを作成しよう:

In [28]

dt = .1
x = np.array([0., 0.])
kf = pos_vel_filter(x, P=500, R=5, Q=0.1, dt=dt)

コマンドラインに KalmanFilter オブジェクトの変数名を入力すると、そのオブジェクトが持つ全ての属性の現在値を確認できる:

In [29]

kf

Out [29]

KalmanFilter object
dim_x = 2
dim_z = 1
dim_u = 0
x = [0. 0.]
P = [[500.   0.]
     [  0. 500.]]
x_prior = [[0. 0.]].T
P_prior = [[1. 0.]
           [0. 1.]]
x_post = [[0. 0.]].T
P_post = [[1. 0.]
          [0. 1.]]
F = [[1.  0.1]
     [0.  1. ]]
Q = [[0.    0.   ]
     [0.    0.001]]
R = [[5.]]
H = [[1. 0.]]
K = [[0. 0.]].T
y = [[0.]]
S = [[0.]]
SI = [[0.]]
M = [[0.]]
B = None
z = [[None]]
log-likelihood = -708.3964185322641
likelihood = 2.2250738585072014e-308
mahalanobis = 0.0
alpha = 1.0
inv = <function inv at 0x000001BDFBB21E50>

後はカルマンフィルタを実行するコードを書くだけだ:

In [30]

from kf_book.mkf_internal import plot_track

def run(x0=(0.,0.), P=500, R=0, Q=0, dt=1.0,
        track=None, zs=None,
        count=0, do_plot=True, **kwargs):
    """ track は犬の実際の位置、zs は対応する観測値を表す。 """

    # データが与えられないなら犬のシミュレーションを実行する。
    if zs is None:
        track, zs = compute_dog_data(R, Q, count)

    # カルマンフィルタを作成する。
    kf = pos_vel_filter(x0, R=R, P=P, Q=Q, dt=dt)

    # カルマンフィルタを実行し、結果を保存する。
    xs, cov = [], []
    for z in zs:
        kf.predict()
        kf.update(z)
        xs.append(kf.x)
        cov.append(kf.P)

    xs, cov = np.array(xs), np.array(cov)
    if do_plot:
        plot_track(xs[:, 0], track, zs, cov, **kwargs)
    return xs, cov

これがフィルタリングを行うコードの全てであり、そのほとんどはボイラープレートである。本章で設定を変えて何度か実験を行うので、多少冗長になっている。一行ごとに見ていこう。

最初の if 文は実際のデータと観測値データが track および zs として渡されたかどうかを確認している。もし渡されていなかったら、前に作成した compute_dog_data 関数を使ってデータを生成する。

次の行は先ほど実装したカルマンフィルタを作成するヘルパー関数を使っている:

# カルマンフィルタを作成する。
kf = pos_vel_filter(x0, R=R, P=P, Q=Q, dt=dt)

後は観測値のそれぞれに対してカルマンフィルタの予測ステップと更新ステップを行うだけだ。KalmanFilter クラスは二つのステップを実行する update メソッドと predict メソッドを提供する。update はカルマンフィルタの観測更新ステップを実行するので、センサーの観測値を引数に受け取る。

結果を記録する処理を除けば、メインのループは次の形をしている:

for z in zs:
    kf.predict()
    kf.update(z)

predict または update を呼ぶたびに状態変数 x と P が変更される。そのため predict を呼んだ直後は kf.x に事前分布が含まれ、update を読んだ直後は kf.x に事後分布が含まれる。

このコードのなんと簡単なことか！実はこれからもっと複雑な問題に取り組むときでも、この部分はほぼそのままとなる。ほとんどの労力は KalmanFilter の行列を設定することに注がれ、フィルタの実行は非常に簡単である。

残りのコードは結果をプロットする省略可能な処理であり、最後に記録された状態と共分散行列を返す。

このコードを実行してみよう。ノイズ分散 (観測値の不確実性) を \(10~\text{m²}\)、プロセス分散を \(0.01~\text{m²}\) とした 50 個の観測値を使う:

In [31]

P = np.diag([500., 49.])
Ms, Ps = run(count=50, R=10, Q=0.01, P=P)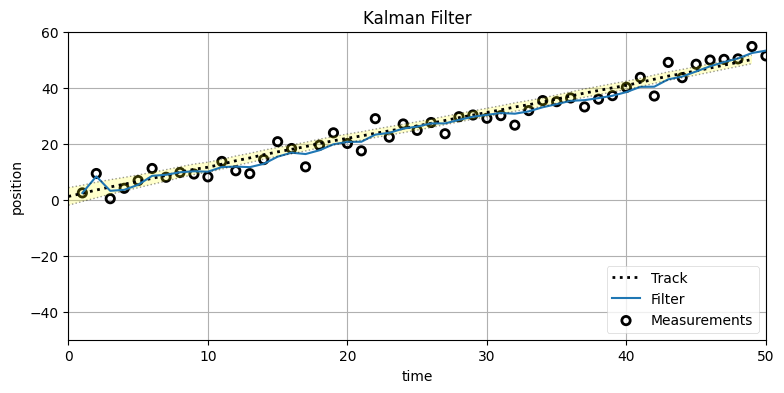

まだ学ぶことは多くあるものの、私たちはルドルフ・カルマンが発表したのと同じ理論と等式を使ってカルマンフィルタを実装できた！ GPS、飛行機、ロボットといった機械の中では、ここで書いたコードとよく似たコードが実行されている。

一つ目のグラフはカルマンフィルタの出力 (filter) と観測値 (measurements) および犬の実際の位置 (track) を示す。フィルタの出力は開始してしばらくした後に落ち着き、その後は犬の位置を非常に正確に追跡できているはずだ。黒い破線に囲まれた黄色の領域は状態変数の標準偏差一つ分だけ実際の値から離れた領域を示す。状態変数の標準偏差は次の段落で説明する分散から計算されている。

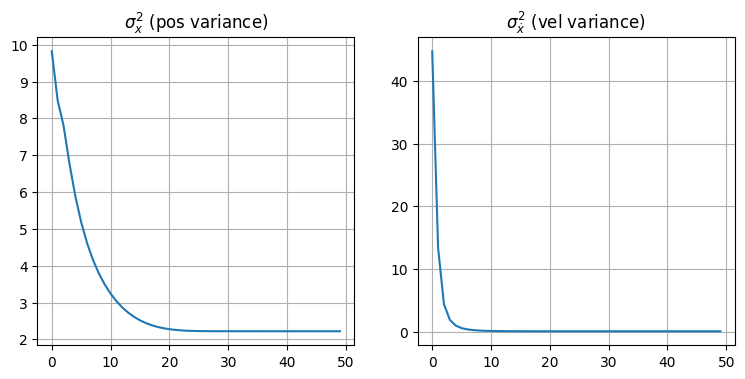
次の二つのグラフは \(x\) と \(\dot x\) の分散を示す。具体的には \(\mathbf P\) の対角要素をプロットしている: 共分散行列の対角要素は各状態変数の分散だったことを思い出そう。例えば \(\mathbf P[0,0]\) は \(x\) の分散、\(\mathbf P[1,1]\) は \(\dot x\) の分散となる。グラフからは両方の分散が素早く収束しているのが分かる。

共分散行列 \(\mathbf P\) はフィルタに伝えたことが全て正しいと仮定したときの理論的な性能を示す。標準偏差は分散の平方根であり、ガウス分布ではサンプルの 68% が平均から標準偏差一つ分の領域に収まることを思い出してほしい。つまりその領域にフィルタの出力の 68% が最低でも収まっていれば、フィルタはうまく動作しているようだと考えられる。上のグラフでは標準偏差一つ分の領域を黄色で示しているが、私の目には黄色い領域を外れているフィルタの出力が 100-68=32% より多いように見える。つまりこのフィルタにチューニングが必要な可能性が高いということだ。

単変量カルマンフィルタの章で大きなノイズの加わった信号に対するフィルタリングを行ったときは、コードが本章のものよりずっと簡単だった。しかし、今考えている例──一次元の空間を動く物体の一つのセンサーを使った追跡──は多変量カルマンフィルタの応用例としては非常に単純なものであることに注意してほしい。単変量カルマンフィルタのコードではこの例が計算できる限界に近いが、多変量カルマンフィルタではフィルタの変数に割り当てる値を変更するだけでこの例より格段に複雑な多次元フィルタを実装できる。100 次元を追跡する経済モデルだって作れるだろう。あるいは GPS・INS・TACAN・電波高度計・気圧高度計・対気速度計が付いた航空機があって、これらのセンサーを全て組み合わせて三次元の位置・速度・加速度を予測するモデルを作りたいのかもしれない。本章のコード使えばこういった処理も行える。

ガウス分布が時間の経過とともにどう変化するかをよく感じ取ってほしいので、次に 7 エポック (タイムステップ) ごとにガウス分布を三次元プロットしたグラフを示す。7 エポック離せば分布は重ならず、独立して観察できる。一番左にあるのが \(t=0\) における最初のガウス分布である:

In [32]

from kf_book.book_plots import set_figsize, figsize
from kf_book.nonlinear_plots import plot_gaussians

P = np.diag([3., 1.])
np.random.seed(3)
Ms, Ps = run(count=25, R=10, Q=0.01, P=P, do_plot=False)
with figsize(x=9, y=5):
    plot_gaussians(Ms[::7], Ps[::7], (-5,25), (-5, 5), 75)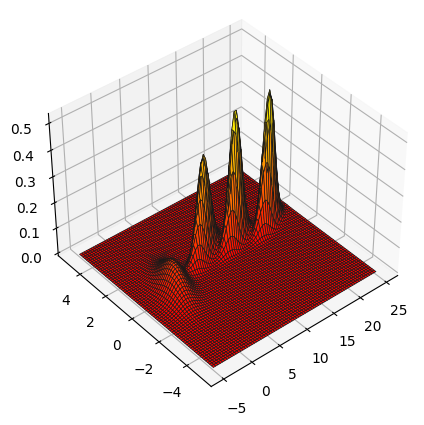

6.7 `Saver` クラス

run 関数にはフィルタの結果を記録するボイラープレートコードがある:

    xs, cov = [], []
    ...
    for z in zs:
        kf.predict()
        kf.update(z)
        xs.append(kf.x)
        cov.append(kf.P)
    ...
    xs, cov = np.array(xs), np.array(cov)

これを避ける簡単な方法がある。filterpy.common モジュールが提供する Saver クラスは、save メソッドが呼ばれるたびに自身に関連付いた KalmanFilter クラスに含まれる属性の値を全て記録する。まずコードを示してから説明しよう:

In [33]

from filterpy.common import Saver
kf = pos_vel_filter([0, .1], R=R, P=P, Q=Q, dt=1.)
s = Saver(kf)
for i in range(1, 6):
    kf.predict()
    kf.update([i])
    s.save()  # 現在状態を記録する

こうすると KalmanFilter オブジェクトに含まれる全ての属性の履歴が Saver オブジェクトに記録される。例えば s.x にはループ内部で計算された状態の推定値が全て記録される:

In [34]

s.x

Out [34]

[array([0.531, 0.304]),
 array([1.555, 0.763]),
 array([2.784, 1.036]),
 array([3.944, 1.105]),
 array([5.015, 1.086])]

記録された属性は Saver オブジェクトの keys 属性から確認できる:

In [35]

s.keys

Out [35]

['alpha',
 'likelihood',
 'log_likelihood',
 'mahalanobis',
 'dim_x',
 'dim_z',
 'dim_u',
 'x',
 'P',
 'Q',
 'B',
 'F',
 'H',
 'R',
 '_alpha_sq',
 'M',
 'z',
 'K',
 'y',
 'S',
 'SI',
 '_I',
 'x_prior',
 'P_prior',
 'x_post',
 'P_post',
 '_log_likelihood',
 '_likelihood',
 '_mahalanobis',
 'inv']

まだ説明していない属性も多くあるが、見覚えのある属性も多いはずだ。

Saver があれば好きな変数をプロットするコードが書けるようになる。ただ変数をプロットするときは通常のリストではなく NumPy 配列を使う方が便利なことが多い。そんなときは to_array メソッドを呼ぶと Saver が持つリストを NumPy 配列に変換できる。ただし一つ注意点がある: いずれかの属性の形状が実行中に変化すると to_array は例外を送出する。NumPy 配列は全ての要素が同じ型とサイズであることを要求するためだ。

もう一度 keys の返り値を見ると、z があるのが分かる。これは頼もしい: 観測値 z は記録されているようだ。観測値と推定値をプロットしてみよう:

In [36]

import matplotlib.pyplot as plt

s.to_array()
book_plots.plot_measurements(s.z);
plt.plot(s.x[:, 0]);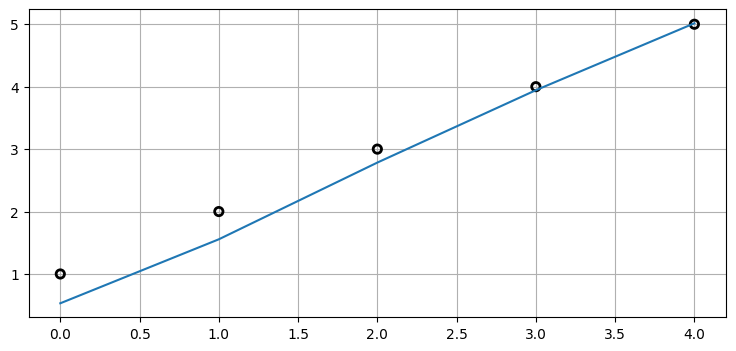

ここまで KalmanFilter クラスを例として Saver クラスの使い方を説明したが、Saver は FilterPy が実装する全てのフィルタクラスで使うことができる。さらに、Saver はコンストラクタに渡されたオブジェクトを調べることで属性の名前を取得するので、あなたが書いたクラスに対してもおそらく動作する。本書ではコードを短く読みやすくするために Saver を使っていく。Saver は裏で大量の処理を行うので実行は遅くなるのだが、学習や実験では利便性が何よりも優先される。

6.8 カルマンフィルタの式

以上で predict と update で行われる計算を見ていく準備が整った。

まず記法について少し。私はプログラマーなので、次のようなコードを見るのに慣れている:

x = x + 1

右辺と左辺は等しくないので、これは等式ではない。これは代入である。同じことを数学的な記法を使って書くときは、次のように書かなければならない:

\[ x_k = x_{k-1} + 1 \]

通常カルマンフィルタの式には上付きおよび下付きの添え字が大量に出てくる。式を数学的に正しくするためにそれらは存在するのだが、このために式は非常に読みにくくなっていると私は感じる。そこで本書では添え字を使わないで代入を表すことにした。本書でカルマンフィルタなどの式を読むときは、アルゴリズムを実装する代入がステップ・バイ・ステップに実行するものとして並んでいるのだとプログラマーらしく考えてほしい。具体例が出てきたらまたそのとき説明する。

予測ステップの式

カルマンフィルタは事前分布──次のタイムステップにおける予測された系の状態──を計算するために次の式を使う。この式は事前分布の平均 \(\mathbf{\bar x}\) と共分散行列 \(\mathbf{\bar P}\) を計算する:

\[ \begin{aligned} \mathbf{\bar x} &= \mathbf{Fx} + \mathbf{Bu}\\ \mathbf{\bar P} &= \mathbf{FPF}^\mathsf T + \mathbf Q \end{aligned} \]

平均: \(\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu}\)

思い出しておくと、線形方程式 \(\mathbf{Ax} = \mathbf b\) は方程式の集合を表す。\(\mathbf A\) には方程式の係数が含まれ、\(\mathbf x\) は変数のベクトルである。\(\mathbf{Ax}\) の乗算を行うと、方程式の右辺にある \(\mathbf b\) が計算される。

\(\mathbf F\) が考えているタイムステップにおける状態の遷移を表すから、状態 \(\mathbf x\) との積 \(\mathbf{Fx}\) は遷移後の状態を計算する。簡単だ！同様に \(\mathbf B\) は制御関数で \(\mathbf u\) が制御入力だから、\(\mathbf{Bu}\) は遷移後の状態に対する制御の寄与を計算する。よって、事前分布 \(\mathbf{\bar x}\) は \(\mathbf{Fx}\) と \(\mathbf{Bu}\) の和として計算される。

単変量カルマンフィルタでは次の式がこの式に対応する:

\[ \bar\mu = \mu + \mu_{move} \]

\(\mathbf{Fx}\) の行列積を実際に計算すれば、\(x\) に対する遷移を計算するこの式が得られる。

この式を具体的に計算してみよう。前に \(\mathbf F\) は

\[ \mathbf F = \begin{bmatrix}1&\Delta t \\ 0&1\end{bmatrix} \]

だと説明した。よって \(\mathbf{\bar x} = \mathbf{Fx}\) は次の二つの線形方程式に対応する:

\[ \begin{cases} \begin{aligned} \bar x &= 1x + &\Delta t\, \dot x \\ \bar{\dot x} &=0x + &1\, \dot x \end{aligned} \end{cases} \]

分散: \(\mathbf{\bar P} = \mathbf{FPF}^\mathsf T + \mathbf Q\)

この等式は手強いので、少し時間をかけて説明する。

単変量カルマンフィルタでは次の式を使った:

\[ \bar\sigma^2 = \sigma^2 + \sigma^2_{move} \]

移動の分散を推定値の分散に加えることで予測による知識の散逸を表している。ここでも同じことを行うのだが、多変量ガウス分布では少し難しくなる。

単純に \(\mathbf{\bar P} = \mathbf P + \mathbf Q\) と書くことはできない。なぜなら、多変量カルマンフィルタでは状態変数に相関があるからだ。これは何を意味するだろうか？例えば私たちが持つ速度に関する知識は不完全だが、予測値は速度を位置に加えることで計算される:

\[ \bar x = \dot x\Delta t + x \]

速度 \(\dot x\) の値について完璧な知識を持っていないので、和 \(\bar x = \dot x \Delta t + x\) の計算だけでも不確実性は大きくなる。つまり位置と速度に相関があるために、共分散行列を足すだけでは正しい共分散行列は得られない。例えば \(\mathbf P\) と \(\mathbf Q\) が両方とも対角行列のとき和も対角行列となるが、位置と速度は相関するのだから、次のタイムステップにおける共分散行列は非ゼロの非対角要素を持たなければならない。

正しい式を示す:

\[ \mathbf{\bar P} = \mathbf{FPF}^\mathsf T + \mathbf Q \]

\(\mathbf{ABA}^\mathsf T\) という形をした式は線形代数でよく登場する。これは内側の項を外側の項で射影していると考えることができる。この形の式は本書でもこれから何度も登場するものの、最初はこれが "魔法の" 式に思えても不思議でない。詳しく説明しよう。

\(\mathbf P\) は次の値で初期化した:

\[ \mathbf P = \begin{bmatrix}\sigma^2_x & 0 \\ 0 & \sigma^2_v\end{bmatrix} \]

このとき \(\mathbf{FPF}^\mathsf T\) を計算するとこうなる:

\[ \begin{aligned} \mathbf{FPF}^\mathsf T &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix} \begin{bmatrix}\sigma^2_x & 0 \\ 0 & \sigma^2_{v}\end{bmatrix} \begin{bmatrix}1&0\\\Delta t&1\end{bmatrix} \\ &= \begin{bmatrix}\sigma^2_x&\sigma_v^2\Delta t\\ 0 & \sigma^2_{v}\end{bmatrix} \begin{bmatrix}1&0\\\Delta t&1\end{bmatrix} \\ &= \begin{bmatrix}\sigma^2_x + \sigma_v^2\Delta t^2 & \sigma_v^2\Delta t \\ \sigma_v^2\Delta t & \sigma^2_{v}\end{bmatrix} \end{aligned} \]

\(\mathbf P\) の初期値では位置と速度の共分散が \(0\) だった。しかし新しい位置は \(\dot x\Delta t + x\) と計算されるので、新しい位置と速度には相関がある。そして \(\mathbf{FPF}^\mathsf{T}\) という乗算が \(\sigma_v^2 \Delta t\) という位置と速度の共分散を計算する。この正確な値は重要でない: \(\mathbf{FPF}^\mathsf T\) がプロセスモデルを使って自動的に位置と速度の共分散を計算することを理解するだけで十分だ！

乗算 \(\mathbf{Fx}\) について考察しても説明ができる。この乗算によって \(\mathbf{F}\) で射影された \(\mathbf{x}\) は次の時刻の値となる。\(\mathbf{FP}\) が同じ操作だと思うかもしれないが、\(\mathbf x\) はベクトルなのに対して \(\mathbf P\) は行列である。\(\mathbf P\) を \(\mathbf F\) の列と行の両方で乗じるには最後の \(\mathbf F^\mathsf T\) が必要になる。実際 \(\mathbf{FPF}^\mathsf T\) の計算の二行目に注目すると、\(\mathbf{FP}\) が上三角行列であり \(\mathbf{F}\) が完全には積に取り込まれてはいないことが分かる。

線形代数と統計学の経験があるなら、次の説明も理解に役立つだろう。予測された状態の共分散行列は予測ステップにおける誤差の期待値とモデル化できる。この値は次の等式で計算できる:

\[ \begin{aligned} \bar{\mathbf P} &= \mathbb E[(\mathbf{Fx} - \bar{\mu})(\mathbf{Fx} - \bar{\mu})^\mathsf T]\\ &= \mathbf F\, \mathbb E[(\mathbf{x}- {\mu})(\mathbf{x} - {\mu})^\mathsf T]\, \mathbf F^\mathsf T \end{aligned} \]

もちろん \(\mathbb E[(\mathbf{x} - {\mu})(\mathbf{x}- {\mu})^\mathsf T]\) は \(\mathbf{P}\) に等しいから、次を得る:

\[ \bar{\mathbf P} = \mathbf{FPF}^\mathsf T \]

この乗算の持つ効果を見てみよう。今まで使ってきた \(\mathbf{F}\) を使って状態を 0.6 秒ずつ進めた様子を次に示す。\(\mathbf{\bar P}\) の変化が見やすいように乗算を五回行っている:

In [37]

dt = 0.6
x = np.array([0., 5.])
F = np.array([[1., dt], [0, 1.]])
P = np.array([[1.5, 0], [0, 3.]])
plot_covariance_ellipse(x, P, edgecolor='r')

for _ in range(5):
    x = F @ x
    P = F @ P @ F.T
    plot_covariance_ellipse(x, P, edgecolor='k', ls='dashed')
book_plots.set_labels(x='position', y='velocity')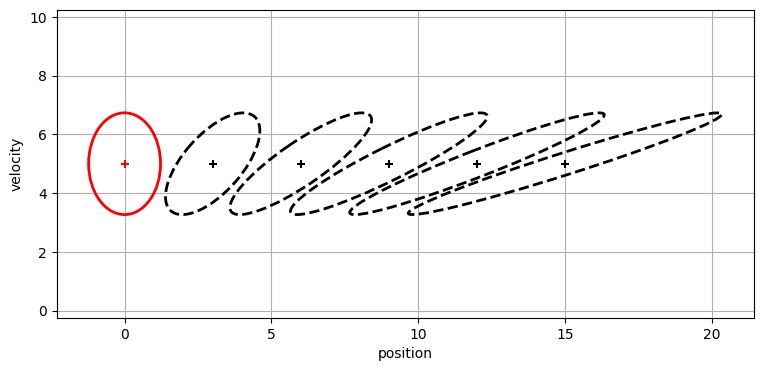

楕円の中心は 0.6 秒ごとに 3 単位だけ右に動いているが、速度が 5 だからこれは正しい。各ステップで楕円の横幅は大きくなっており、これは \(\dot x\Delta t\) を \(x\) に足すごとに位置に関する情報が失われることを示している。楕円の高さは変わっていない──今考えているモデルでは速度は変化しないとしているので、速度に関する信念も変わりようがない。時間が経過すると楕円が傾いていくことも分かる。この楕円の傾きは相関であることを思い出そう。\(\mathbf F\) が \(\bar x = \dot x \Delta t + x\) という式で \(x\) と \(\dot x\) を相関させ、\(\mathbf{FPF}^\mathsf T\) の計算がこの相関を共分散行列に正しく取り入れているということだ。

この式の対話的な実装を次に示す。\(\mathbf F\) の設計を変更したとき \(\mathbf P\) の形がどう影響を受けるかを確認できる。Fxy のスライダーは F[x,y] を変更し、covar は位置と速度の共分散 \(\sigma_{x\dot x}\) の初期値を表す。最低でも次の質問の答えを確認するとよい:

\(x\) と \(\dot x\) が相関していないとどうなるか？ (F01 を 0 にして、他はデフォルトとする)
\(x = 2\dot x \Delta t + x_0\) だとどうなるか？ (F01 を 2 にして、他はデフォルトとする)
\(x = \dot x \Delta t + 2x_0\) だとどうなるか？ (F00 を 2 にして、他はデフォルトとする)
\(x = \dot x\Delta t\) だとどうなるか？ (F00 を 0 にして、他はデフォルトとする)

In [38]

from ipywidgets import interact
from kf_book.book_plots import IntSlider, FloatSlider

def plot_FPFT(F00, F01, F10, F11, covar):
    plt.figure()
    dt = 1.
    x = np.array((0, 0.))
    P = np.array(((1, covar), (covar, 2)))
    F = np.array(((F00, F01), (F10, F11)))
    plot_covariance_ellipse(x, P)
    plot_covariance_ellipse(x, F @ P @ F.T, ec='r')
    plt.gca().set_aspect('equal')
    plt.xlim(-4, 4)
    plt.ylim(-4, 4)
    plt.xlabel('position')
    plt.ylabel('velocity')
    plt.show()

interact(plot_FPFT,
         F00=IntSlider(value=1, min=0, max=2),
         F01=FloatSlider(value=1, min=0, max=2, description='F01(dt)'),
         F10=FloatSlider(value=0, min=0, max=2),
         F11=FloatSlider(value=1, min=0, max=2),
         covar=FloatSlider(value=0, min=0, max=1));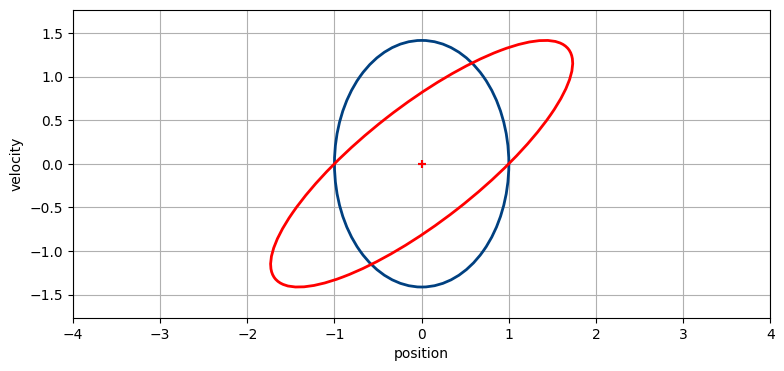

Out [38]\(\mathbf{F}\) と \(\mathbf{P}\) の関係 (Jupyter Notebook でのみ実行可能)

本書を静的なフォーマットで読んでいるなら、binder (http://mybinder.org/repo/rlabbe/Kalman-and-Bayesian-Filters-in-Python) からアニメーションを確認できる。

更新ステップの式

更新ステップの式は予測ステップの式よりずっと複雑に見えるものの、複雑に見える理由の大部分はカルマンフィルタが更新を観測空間で計算するためである。観測空間で計算しなければならないのは、観測値が不可逆なためだ。例えば対象との距離を報告するセンサーがあったとしたら、観測された距離を位置に変換することはできない──特定の円上の任意の点が同じ距離を報告する。一方で、位置 (状態) があれば距離 (観測値) を必ず計算できる。

話を進める前に、ここで行おうとしているのは非常に単純な処理だったことを思い出そう: 観測値と予測値の間にある何らかの値を推定値として選択する処理である。これを次の図に示す:

状態が多次元なので式は複雑になるが、何をしているかといえばこの図が全てである。複雑な式を見てこのアイデアの単純さを忘れてはいけない。

系不確実性: \(\textbf{S} = \mathbf{H\bar PH}^\mathsf T + \mathbf R\)

観測空間で計算を行うために、カルマンフィルタは共分散行列を観測空間に射影する必要がある。このための式が \(\mathbf{H\bar PH}^\mathsf T\) である。ここで \(\mathbf{\bar P}\) は事前分布の共分散行列、\(\mathbf H\) は観測関数を表す。

この式が \(\mathbf{ABA}^\mathsf T\) の形をしているのが分かるはずだ──予測ステップには状態遷移関数 \(\mathbf{F}\) を使った \(\mathbf{FPF}^\mathsf T\) があった。ここでは観測関数 \(\mathbf{H}\) を使った同じ形の式で更新を行っている。線形代数によって座標系が変換される。

共分散行列を観測空間に移すのに加えて、センサーノイズも考えに入れる必要がある。これは非常に簡単で、センサーに加わるノイズの共分散行列 \(\mathbf{R}\) を足すだけだ。こうして計算される \(\mathbf{S}\) は系不確実性 (system uncertainty) あるいは発展共分散行列 (innovation covariance matrix) と呼ばれる。

\(\mathbf{S}\) を計算する式の \(\mathbf H\) を無視すると、単変量カルマンフィルタにおけるカルマンゲインの式の分母と同じような式になる:

\[ K = \frac {\bar\sigma^2} {\bar\sigma^2 + \sigma_z^2} \]

系不確実性の式と事前分布の共分散行列の式を比較してみよう:

\[ \begin{aligned} \mathbf{S} &= \mathbf{H\bar PH}^\mathsf T + \mathbf R\\ \mathbf{\bar P} &= \mathbf{FPF}^\mathsf T + \mathbf Q \end{aligned} \]

両方の式で状態の共分散行列 (\(\mathbf{P}\) または \(\bar{\mathbf{P}}\)) が \(\mathbf H\) または \(\mathbf F\) によって異なる空間に移され、その空間に関連付いたノイズ行列が足されている。

カルマンゲイン: \(\mathbf K = \mathbf{\bar PH}^\mathsf T \mathbf{S}^{-1}\)

残差と推定値を示した図をもう一度見てほしい。予測値と観測値が求まったら、後はその二つの間の値を選択する必要がある。観測値の確実性が高いなら観測値に近い値を選択し、逆に予測値の確実性が高いなら予測値に近い値を選択するべきである。

単変量カルマンフィルタでは次の式を使ってスケーリングを行った:

\[ \mu =\frac{\bar\sigma^2 \mu_z + \sigma_\mathtt{z}^2 \bar{\mu}} {\bar\sigma^2 + \sigma_\mathtt{z}^2} \]

私たちはこの式を次の形に単純化した:

\[ \mu = (1-K)\bar{\mu} + K\mu_\mathtt{z} \]

ここで

\[ K = \frac {\bar\sigma^2} {\bar\sigma^2 + \sigma_z^2} \]

と定義され、\(K\) はカルマンゲインと呼ばれる \(0\) から \(1\) の実数である。カルマンゲインが予測値と観測値の間にある重み付き平均を選択しているという事実の理解を確認してほしい。カルマンゲインはパーセンテージ (比) である──もし \(K\) が \(0.9\) なら、観測値の 90% と予測値の 10% を取って \(\mu\) が計算される。

多変量カルマンフィルタでは \(\mathbf K\) はスカラーではなくベクトルとなる。式をもう一度示そう: \(\mathbf K = \mathbf{\bar PH}^\mathsf T \mathbf{S}^{-1}\) である。これは比なのか？逆行列は線形代数における逆数と考えることができる──行列による除算は定義されないが、この考え方は式の意味を理解する上で都合がいい。こう考えると、\(\textbf{K}\) の式は次のように読める:

\[ \begin{aligned} \mathbf K &\approx \frac{\mathbf{\bar P}\mathbf H^\mathsf T}{\mathbf{S}} \\ \mathbf K &\approx \frac{\text{不確実性}_\text{予測値}}{\text{不確実性}_\text{予測値} + \text{不確実性}_\text{観測値}}\mathbf H^\mathsf T \end{aligned} \]

カルマンゲインの式は予測値と観測値をどれだけ信用するかに応じて比を計算する。同じことはこれまでの全ての章で行ってきた。行列を使って多次元の状態を考えているので式は複雑だが、考え方は難しくない。\(\mathbf H^\mathsf T\) の部分は理解しにくいので、後でまた説明する。この部分を無視すれば、カルマンゲインの式は単変量の場合と同じである: 事前分布の不確実性を事前分布の不確実性と観測値の不確実性の和で割っているだけだ。

残差: \(\mathbf y = \mathbf z - \mathbf{H\bar{x}}\)

この式は観測関数 \(\mathbf H\) を設計するときに触れたので、簡単に説明できる。観測関数は状態を観測値に変換することを思い出そう。そのため \(\mathbf{Hx}\) は \(\mathbf{x}\) を等価な観測値に変換する。こうして計算した値を観測値 \(\mathbf{z}\) から引けば、残差──観測値と予測値の差──が得られる。

単変量の場合の式は

\[ y = z - \bar x \]

であり、明らかに同じ計算を (一次元で) 行っている。

状態の更新: \(\mathbf x = \mathbf{\bar x} + \mathbf{Ky}\)

残差をカルマンゲインでスケールすることで、残差の直線上にある推定値 (新しい状態) が計算される。残差をスケールしているのは \(\mathbf{Ky}\) であり、これは残差のスケールと状態空間への変換を同時に行う。\(\mathbf{K}\) に含まれる \(\mathbf{H}^\mathsf T\) は状態空間への変換のために存在する。後は残差を事前分布に足せば \(\mathbf x =\mathbf{\bar x} + \mathbf{Ky}\) が得られる。\(\mathbf{K}\) を展開して全体の計算を確認してみよう:

\[ \begin{aligned} \mathbf x &= \mathbf{\bar x} + \mathbf{Ky} \\ &= \mathbf{\bar x} + \mathbf{\bar PH}^\mathsf T \mathbf{S}^{-1}\mathbf y \\ &\approx \mathbf{\bar x} + \frac{\text{不確実性}_\text{予測値}}{\text{不確実性}_{\text{予測値}} + \text{不確実性}_\text{観測値}}\mathbf H^\mathsf T\mathbf y \end{aligned} \]

この推定値の式を次のように書き直すと、カルマンゲインが比であるという事実が分かりやすくなるだろう:

\[ \begin{aligned} \mathbf x &= \mathbf{\bar x} + \mathbf{Ky} \\ &= \mathbf{\bar x} +\mathbf K(\mathbf z - \mathbf{H\bar x}) \\ &= (\mathbf I - \mathbf{KH})\mathbf{\bar x} + \mathbf{Kz} \end{aligned} \]

単変量の場合の式との類似性は明らかなはずだ:

\[ \mu = (1-K)\bar{\mu} + K\mu_\mathtt{z} \]

共分散行列の更新: \(\mathbf P = (\mathbf{I}-\mathbf{KH})\mathbf{\bar P}\)

\(\mathbf{I}\) は単位行列であり、多次元における \(1\) を表す。\(\mathbf{H}\) は観測関数を表す定数である。この式は \(\mathbf P = (1-c\mathbf K)\mathbf P\) と考えることができる。\(\mathbf{K}\) は予測値と観測値をどれくらいずつ使うかを表す比であり、もし \(\mathbf{K}\) が大きいなら \(1 - \mathbf{cK}\) は小さくなり、新しい \(\mathbf{P}\) はこれまでより小さくなる。もし \(\mathbf{K}\) が小さいなら \(1-\mathbf{cK}\) は大きくなり、\(\mathbf P\) は比較的大きくなる。これは不確実性の大きさをカルマンゲインの定数倍で調整していることを意味する。

この式は数値的に不安定なので、FilterPy では使っていない。減算によって対称性が崩れる可能性がある上に、何度も繰り返すと浮動小数点数の誤差が溜まってしまう。より複雑で数値的に安定な形式を後で示す。

FilterPy を使わない例

FilterPy は実装の詳細を私たちに見せないようにしている。通常これは嬉しいことだが、ここでは FilterPy を使わずにカルマンフィルタを実装してみよう。このためには行列を変数として定義して、カルマンフィルタの式を明示的に実装する必要がある。

カルマンフィルタで使う行列の初期化処理を示す:

In [39]

dt = 1.
R_var = 10
Q_var = 0.01
x = np.array([[10.0, 4.5]]).T
P = np.diag([500, 49])
F = np.array([[1, dt],
              [0,  1]])
H = np.array([[1., 0.]])
R = np.array([[R_var]])
Q = Q_discrete_white_noise(dim=2, dt=dt, var=Q_var)

続いて実装を示す:

In [40]

from scipy.linalg import inv

count = 50
track, zs = compute_dog_data(R_var, Q_var, count)
xs, cov = [], []
for z in zs:
    # 予測
    x = F @ x
    P = F @ P @ F.T + Q

    # 更新
    S = H @ P @ H.T + R
    K = P @ H.T @ inv(S)
    y = z - H @ x
    x += K @ y
    P = P - K @ H @ P

    xs.append(x)
    cov.append(P)

xs, cov = np.array(xs), np.array(cov)
plot_track(xs[:, 0], track, zs, cov, plot_P=False)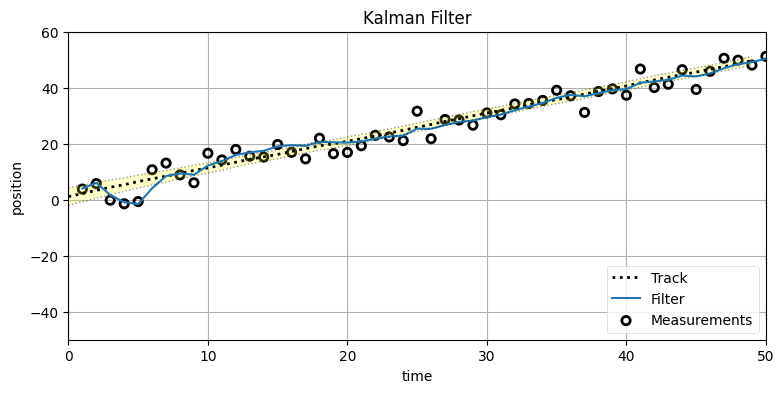

結果は FilterPy のバージョンと一致する。あなたがどちらを使うかは自分で決めてほしい。私は FilterPy の方式を選ぶ。x, P といった変数で名前空間を汚したくないし、dog_filter.x の方が私には読みやすい。

さらに重要なこととして、自分で書くようにするとカルマンフィルタの式を記憶してプログラムにしなければならない。遅かれ早かれミスをするのは避けられないだろう。FilterPy のバージョンを使っておけばコードが正しいことは保証される。一方で、変数の定義でミスをする (例えば \(\mathbf{H}\) を行列ではなくベクトルにしてしまう) と、FilterPy からのエラーメッセージは明示的なコードよりデバッグしにくくなる。

FilterPy の KalmanFilter クラスは追加の機能として平滑化・バッチ処理・減衰記憶フィルタリング・最大尤度関数の計算といった処理を持つ。FilterPy を使っておけばこういった機能もプログラムせずに得られる。

まとめ

これでカルマンフィルタの式が一通り説明できた。おさらいとして次にまとめておく。まだ学ぶべきことは多くあるが、式を一つずつ説明する中で単変量のカルマンフィルタとの類似性を理解できたことを願っている。次のカルマンフィルタの数学の章では \(\mathbf{x}\) の次元を \(1\) に設定すると、この式が単変量のカルマンフィルタの式になることを見る。この式は単変量のカルマンフィルタの式に似ているのではなく、多変量に対応させた実装そのものである。

\[ \begin{aligned} &\text{予測ステップ}\\ \mathbf{\bar x} &= \mathbf{F x} + \mathbf{B u} \\ \mathbf{\bar P} &= \mathbf{FP{F}}^\mathsf T + \mathbf Q \\ \\ &\text{更新ステップ}\\ \textbf{S} &= \mathbf{H\bar PH}^\mathsf T + \mathbf R \\ \mathbf K &= \mathbf{\bar PH}^\mathsf T \mathbf{S}^{-1} \\ \textbf{y} &= \mathbf z - \mathbf{H \bar x} \\ \mathbf x &=\mathbf{\bar x} +\mathbf{K\textbf{y}} \\ \mathbf P &= (\mathbf{I}-\mathbf{KH})\mathbf{\bar P} \end{aligned} \]

フィルタリングの文献で見ることになる形の式も次に示しておく。様々な記法が存在するものの、この形を見ればどんなものかが分かるだろう:

\[ \begin{aligned} \hat{\mathbf x}_{k\mid k-1} &= \mathbf F_k\hat{\mathbf x}_{k-1\mid k-1} + \mathbf B_k \mathbf u_k \\ \mathbf P_{k\mid k-1} &= \mathbf F_k \mathbf P_{k-1\mid k-1} \mathbf F_k^\mathsf T + \mathbf Q_k \\ \tilde{\mathbf y}_k &= \mathbf z_k - \mathbf H_k\hat{\mathbf x}_{k\mid k-1}\\ \mathbf{S}_k &= \mathbf H_k \mathbf P_{k\mid k-1} \mathbf H_k^\mathsf T + \mathbf R_k \\ \mathbf K_k &= \mathbf P_{k\mid k-1}\mathbf H_k^\mathsf T \mathbf{S}_k^{-1}\\ \hat{\mathbf x}_{k\mid k} &= \hat{\mathbf x}_{k\mid k-1} + \mathbf K_k\tilde{\mathbf y}_k\\ \mathbf P_{k|k} &= (I - \mathbf K_k \mathbf H_k) \mathbf P_{k|k-1} \\\end{aligned} \]

この式ではベイズ的な \(a \mid b\) の記法が使われている。これは「時刻 \(b\) における証拠が与えられたときの、時刻 \(a\) の...」を意味する。ハットは推定値を表すので、例えば \(\hat{\mathbf{x}}_{k \mid k}\) は「時刻 \(k\) における証拠が与えられたときの、時刻 \(k\) の \(\mathbf{x}\) の推定値」を表す。言い換えれば事後分布である。また \(\hat{\mathbf x}_{k \mid k-1}\) は「時刻 \(k-1\) における証拠が与えられたときの、時刻 \(k\) の \(\mathbf{x}\) の推定値」を表す。言い換えれば事前分布である。

Wikipedia でも使われるこの記法があると、数学者は自身の考えを正確に表現できる。新しい結果を公表する正式な出版物ではこの正確さが必要となる。しかしプログラマーとして私はこの記法がとても読みにくいと感じる。私は変数をプログラムの実行中に状態を変えるものとして捉えるのに慣れており、プログラムで計算のたびに異なる変数名を使うことはない。フィルタリングの文献で使うべきに記法ついて合意は存在せず、著者は好きな記法を勝手に選んでいる。異なる本や論文を読むたびに頭を素早く切り替えるのは難しいと感じていたので、私は (正確さに劣るのは否定できないものの) 添え字を使わないこの記法を採用した。数学者からは厳しい批判のメールが届くかもしれないが、プログラマーや学生は私が採用した単純化された記法を喜んでくれるだろうと願っている。

補遺 B に様々な文献で使われる記法がまとめてある。これを見ると、文献の読解を難しくするもう一つの問題が分かる: どの著者も異なる変数名を使うのである。\(\mathbf x\) はほぼ全ての文献で同じ意味だが、それを除けば共通している変数名はない。例えば私が \(\mathbf{F}\) と呼んでいる行列は \(\mathbf{A}\) と呼ばれることも多い。著者が変数を定義していることを願いながら (定義されていないことはよくあるのだが)、注意深く読まなければならない。

もしあなたが論文に書かれている式を理解しようとしているプログラマーなら、まず添え字とアクセント記号を取り去って、全て単一の文字に置き換えて読んでみることを勧める。複雑な式に毎日触れる人に対しては余計なアドバイスかもしれないが、私がそういった式を読むときは計算の流れを理解しようとすることが多い。「このステップの \(P\) は一つ前のステップで計算された \(P\) の新しい値を表して...」と記憶する方が、「\(P_{k-1}(+)\) は何を表して、\(P_k(-)\) とどんな関係があって、五分前に読んだ論文で使われていた全く異なる記法だと何に対応して...」と記憶するよりずっと簡単だと私には思える。

6.9 練習問題: 隠れ変数の効果

ここまでに実装したフィルタでは速度が隠れ変数だった。速度を状態に含めなかったらフィルタはどのように振る舞うだろうか？

状態に \(\mathbf x= \Big[x\Big]\) を使うカルマンフィルタを書き、状態に \(\mathbf x= \Big[x \ \ \dot x\Big]^\mathsf T\) を使うカルマンフィルタと比較せよ。

In [41]

# ここに解答を書く

解答

位置と速度を使うカルマンフィルタは既に実装したので、次のコードにコメントはあまり付いていない。プロットの処理も含まれている:

In [42]

from math import sqrt
from numpy.random import randn

def univariate_filter(x0, P, R, Q):
    f = KalmanFilter(dim_x=1, dim_z=1, dim_u=1)
    f.x = np.array([[x0]])
    f.P *= P
    f.H = np.array([[1.]])
    f.F = np.array([[1.]])
    f.B = np.array([[1.]])
    f.Q *= Q
    f.R *= R
    return f

def plot_1d_2d(xs, xs1d, xs2d):
    plt.plot(xs1d, label='1D Filter')
    plt.scatter(range(len(xs2d)), xs2d, c='r', alpha=0.7, label='2D Filter')
    plt.plot(xs, ls='--', color='k', lw=1, label='track')
    plt.title('State')
    plt.legend(loc=4)
    plt.show()

def compare_1D_2D(x0, P, R, Q, vel, u=None):
    # フィルタの出力の格納場所
    xs, xs1, xs2 = [], [], []

    # 一次元カルマンフィルタ
    f1D = univariate_filter(x0, P, R, Q)

    # 二次元カルマンフィルタ
    f2D = pos_vel_filter(x=(x0, vel), P=P, R=R, Q=0)
    if np.isscalar(u):
        u = [u]
    pos = 0 # 真の位置
    for i in range(100):
        pos += vel
        xs.append(pos)

        # 制御入力 u - 後述
        f1D.predict(u=u)
        f2D.predict()

        z = pos + randn()*sqrt(R) # 観測値
        f1D.update(z)
        f2D.update(z)

        xs1.append(f1D.x[0])
        xs2.append(f2D.x[0])
    plt.figure()
    plot_1d_2d(xs, xs1, xs2)

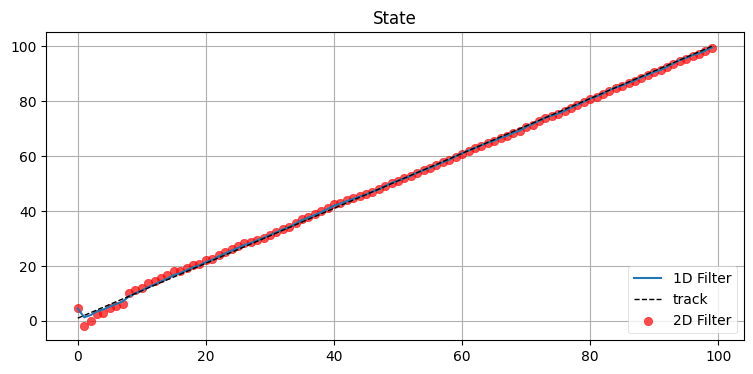
compare_1D_2D(x0=0, P=50., R=5., Q=.02, vel=1.)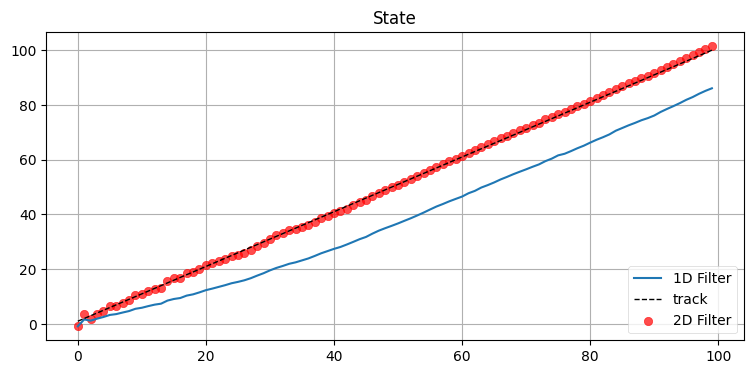

考察

状態に速度を取り入れたフィルタからは位置だけを追跡するフィルタよりずっと正確な推定値が得られる。単変量のフィルタは速度 (位置の変化) を推定する方法を持たないので、追跡するオブジェクトに遅れてしまう。

単変量カルマンフィルタの章で示した予測ステップの式には制御入力 u が含まれていた:

    def predict(self, u=0.0):
        self.x += u
        self.P += self.Q

制御入力を指定してみよう:

In [43]

compare_1D_2D(x0=0, P=50., R=5., Q=.02, vel=1., u=1.)

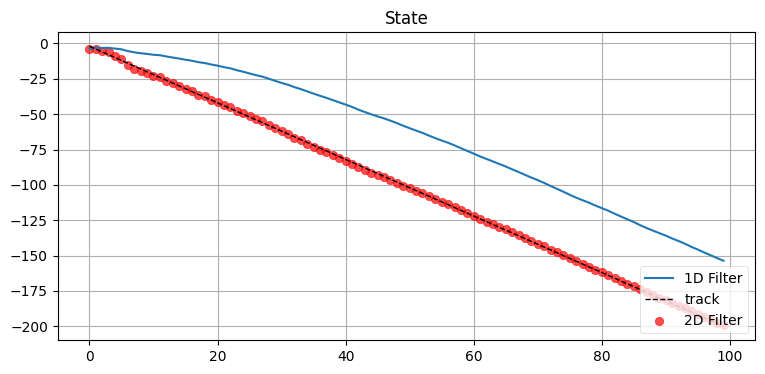
こうすると二つのフィルタは似た性能となる。単変量のフィルタの方が高性能であるとさえ言えるかもしれない。では実際の速度 vel が制御入力 \(u\) と異なっていると何が起きるだろうか？

In [44]

compare_1D_2D(x0=0, P=50., R=5., Q=.02, vel=-2., u=1.)

性能が大きく悪化しているのが分かる。もし私たちが制御しているロボットを追跡しているなら、制御入力を使って正確な予測が行えるので単変量のフィルタでも素晴らしい仕事ができるだろう。しかし物体を受動的に追跡している場合は制御信号がまず役に立たない。フィルタを実行する前に速度を正確に推測できるなら別だが、それが可能なことはほとんどない。

6.10 速度はどう計算されるか

フィルタが速度のような隠れ変数をどう計算するかはまだ詳しく説明していなかった。フィルタの行列それぞれに対して実際の値を代入して計算して何が起こるかを見てみよう。

まず系不確実性を計算する必要がある:

\[ \begin{aligned} \textbf{S} &= \mathbf{H\bar PH}^\mathsf T + \mathbf R \\ &= \begin{bmatrix} 1 & 0\end{bmatrix} \begin{bmatrix}\sigma^2_x & \sigma_{xv} \\ \sigma_{xv} & \sigma^2_v\end{bmatrix} \begin{bmatrix} 1 \\ 0\end{bmatrix} + \begin{bmatrix}\sigma_z^2\end{bmatrix}\\ &= \begin{bmatrix}\sigma_x^2 & \sigma_{xv}\end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}+ \begin{bmatrix}\sigma_z^2\end{bmatrix} \\ &= \begin{bmatrix}\sigma_x^2 +\sigma_z^2\end{bmatrix} \end{aligned} \]

\(\mathbf{S}\) があればカルマンゲインを計算できる:

\[ \begin{aligned} \mathbf K &= \mathbf{\bar PH}^\mathsf T \mathbf{S}^{-1} \\ &= \begin{bmatrix}\sigma^2_x & \sigma_{xv} \\ \sigma_{xv} & \sigma^2_v\end{bmatrix} \begin{bmatrix} 1 \\ 0\end{bmatrix} \begin{bmatrix}\frac{1}{\sigma_x^2 +\sigma_z^2}\end{bmatrix} \\ &= \begin{bmatrix}\sigma^2_x \\ \sigma_{xv}\end{bmatrix} \begin{bmatrix}\frac{1}{\sigma_x^2 +\sigma_z^2}\end{bmatrix} \\ &= \begin{bmatrix}\sigma^2_x/(\sigma_x^2 +\sigma_z^2) \\ \sigma_{xv}/(\sigma_x^2 +\sigma_z^2)\end{bmatrix} \end{aligned} \]

言い換えれば、\(x\) に対するカルマンゲインは

\[ K_x = \frac{VAR(x)}{VAR(x)+VAR(z)} \]

である。これは単変量のカルマンフィルタで見覚えのある式であるはずだ。

速度 \(\dot x\) に対するカルマンゲインは

\[ K_{\dot x} = \frac{COV(x, \dot x)}{VAR(x)+VAR(z)} \]

である。これはどんな効果を持つだろうか？状態は次のように計算されたことを思い出そう:

\[ \begin{aligned}\mathbf x &=\mathbf{\bar x}+\mathbf K(z-\mathbf{Hx)} \\ &= \mathbf{\bar x}+\mathbf K \mathbf{y}\end{aligned} \]

ここで残差 \(y\) はスカラーだから、\(\mathbf K\) の各要素に乗じられる。よって

\[ \begin{bmatrix}x \\ \dot x\end{bmatrix}=\begin{bmatrix}\bar x \\ \bar{\dot x}\end{bmatrix} + \begin{bmatrix}K_x \\ K_{\dot x}\end{bmatrix}y \]

であり、ここから次の方程式系が得られる:

\[ \begin{aligned}x& = \bar x + yK_x\\ \dot x &= \bar{\dot x} + yK_{\dot x}\end{aligned} \]

予測値 \(\bar x\) は \(x + \bar x \Delta t\) と計算されていた。予測が完璧かつ観測値にノイズがないなら残差 \(y\) は \(0\) になり、速度の推定値は変化しない。一方で、速度の推定値が非常に悪いときは予測値も悪くなるので、残差も大きくなる: \(y \gg 0\) である。この場合フィルタは速度の推定値を \(yK_{\dot x}\) だけ修正する。\(K_{\dot x}\) は \(COV(x,\dot x)\) に比例するから、位置と速度の共分散に比例する値に残差を乗じた値で速度は修正される。位置と速度の相関が高いと、それだけ修正も大きくなる。

話を一周させると、\(COV(x, \dot x)\) は \(\mathbf{P}\) の非対角要素であり、その値は \(\mathbf{FPF}^\mathsf T\) で計算される。つまり位置と速度の共分散は予測ステップで計算される。速度のカルマンゲインはこの共分散に比例し、速度の推定値にはこの共分散と残差の積に比例する修正が加えられる。

まとめると、こういった線形代数の式は見慣れないかもしれないが、計算は実際には非常に簡単である。本質的には g-h フィルタで行った計算と変わらない。本章で実装したフィルタではプロセスモデルとセンサーのノイズを考えに入れているので細かい値は異なるものの、数学的な考え方はこの節で示した通りとなる。

6.11 フィルタの調整

カルマンフィルタのパラメータを変更したときに生じる影響を調べよう。パラメータの調整はカルマンフィルタを使うとき普通に行うことである。センサーを正確にモデル化するのは難しく、不可能な場合もある。モデルが不完全だとフィルタの出力も不完全になる。エンジニアは現実世界のセンサーで上手く動くようカルマンフィルタを調整するのに長い時間を費やす。ここでは少し時間を取って、それぞれのパラメータを変更したときにどのような影響があるのかを学ぶ。変更したときの影響を知っておけば、カルマンフィルタの設計手法を直感的に理解できるだろう。カルマンフィルタの設計は科学であるのと同程度に職人技でもある。私たちは数学を使って物理系のモデルを作っており、そのモデルが完璧なことはない。

観測ノイズ行列 \(\mathbf{R}\) とプロセスノイズ行列 \(\mathbf{Q}\) の影響を調べよう。\(\mathbf{R}\) と \(\mathbf{Q}\) に異なる設定を設定したときに何が起こるかを見たいので、まずは観測値の分散を \(225~\text{m²}\) とする。これは非常に大きな値だが、様々な設計の選択肢が持つ特徴がグラフで強調されるので、何が起きているかを理解しやすくなる。最初の実験では \(\mathbf{R}\) を固定して \(\mathbf{Q}\) を変化させる:

In [45]

from numpy.random import seed
seed(2)
trk, zs = compute_dog_data(z_var=225, process_var=.02, count=50)

run(track=trk, zs=zs, R=225, Q=200, P=P, plot_P=False,
    title='R = 225 m²,  Q = 200 m²')
run(track=trk, zs=zs, R=225, Q=.02, P=P, plot_P=False,
    title='R = 225 m²,  Q = 0.02 m²');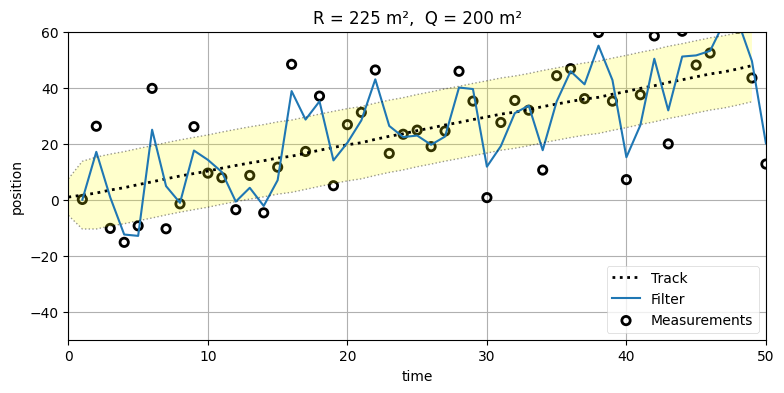

Out [45]\(R = 225\,\text{m}^2,\ Q = 200\, \text{m}^2\) とした場合のフィルタリング結果

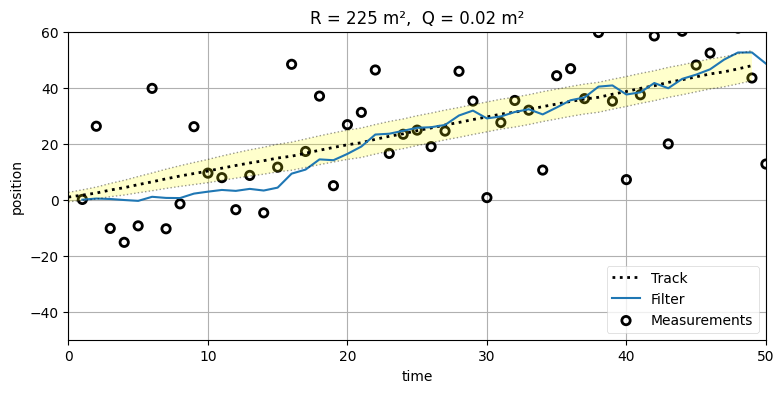
Out [45]\(R = 225\,\text{m}^2,\ Q = 0.02\, \text{m}^2\) とした場合のフィルタリング結果

一つ目のグラフではフィルタがノイズの多い観測値に近い値を取っており、二つ目のグラフではフィルタが観測値から離れた値を取って一つ目のグラフより直線に近い形をしている。なぜ \(\mathbf{Q}\) はそのような影響を及ぼすのだろうか？

系不確実性という用語の意味を思い出そう。ボールを追跡する問題を考える。真空中を進むボールの位置は数学で正確にモデル化できるものの、風・空気密度の変動・温度・ボールの回転・理想的でないボールの表面といった要素が存在するときそのモデルは現実と一致しない。

最初のグラフでは Q = 20 というかなり大きな値を設定している。ボールの問題で言えば、これは「運動の予測は信用に値しない」とフィルタに伝えるのに等しい。予測で使う速度の分散が \(20~\text{m²}\) だと言っているからだ。正確に言えば、\(\mathbf{F}\) でモデル化できていない外部ノイズが多く存在し、その結果として予測ステップが信用に値しないものになっていることがフィルタに伝わる。フィルタは \(\mathbf{F}\) を使って速度 \(\dot x\) を計算するものの、その計算は疑わしいと教えられているのでほとんど取り入れずに無視する。そのためフィルタは信用すべき値を持たず、観測値に近い値を採用し続ける。

二つ目のグラフでは Q=0.02 というかなり小さい値を設定している。ボールの問題で言えば、これは「運動の予測は非常に正確だから、信用して！」とフィルタに伝えるのに等しい。正確に言えば、プロセスノイズが非常に小さく (分散が \(0.02~\text{m²}\) で) プロセスモデルが非常に正確であることがフィルタに伝わる。そのためフィルタは観測値をあまり重視しない。正確な速度の予測と比べて観測値の変動が大きいと考えるからだ。

次は Q=0.2 にしたまま R=10000 まで大きくしてみよう。このとき観測ノイズが非常に大きいことがフィルタに伝わる。また本当は \(225~\text{m²}\) の観測ノイズの分散を \(10000~\text{m²}\) に設定するので、フィルタは最適でなくなる:

In [46]

run(track=trk, zs=zs, R=10000, Q=.2, P=P, plot_P=False,
    title='R=10,000 m²,  Q=0.2 m²');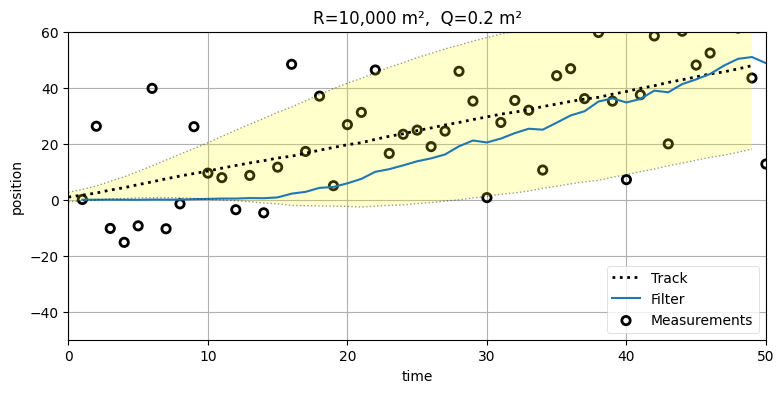

Out [46]\(R = 10{,}000\,\text{m}^2,\ Q = 0.02\, \text{m}^2\) の実験結果

観測ノイズの分散がプロセスノイズの分散より格段に大きいので、観測値ではなく予測値を重視することをフィルタは強制される。このため出力される値を結んだ曲線は非常に滑らかで上手く行っているように見える可能性があり、上のグラフでも出力が急に上下するようなことはない。しかし、このグラフではフィルタの初期推測値が実際の値とほぼ一致しているのが気になるところだ。初期推測値を悪くしたらどうなるかを確認しよう:

In [47]

run(track=trk, zs=zs, R=10000, Q=.2, P=P, plot_P=False,
    x0=np.array([50., 1.]),
    title='R=10,000 m²,  Q=0.2 m²');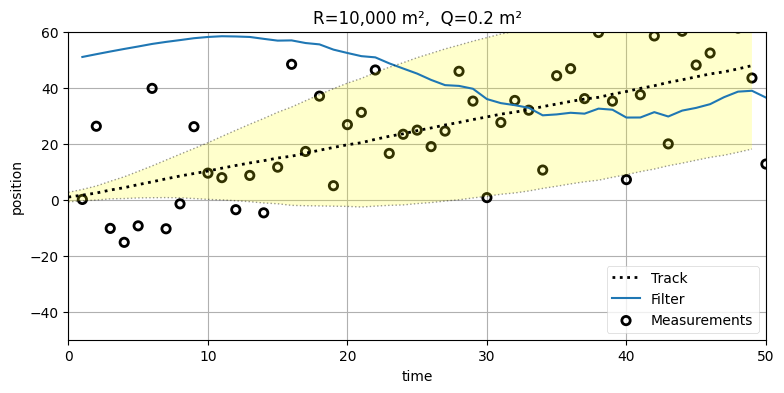

Out [47]\(R = 10,000\,\text{m}^2,\ Q = 0.02\, \text{m}^2\) で初期値を悪くしたときの実験結果

フィルタが正しい軌道に乗れていないのが分かる。こうなるのは、フィルタはそれなりに正確な観測値を受け取っているものの、観測値は正確でないと考えているために不正確な位置を使った予測を重視してしまうためだ。初期推測値が悪いなら観測ノイズが小さくても結果は同じだろうともし思うなら、観測ノイズを正しい値 \(225~\text{m²}\) に戻したときの結果を見てみよう:

In [48]

run(track=trk, zs=zs, R=225, Q=.2, P=P, plot_P=False,
    x0=np.array([20., 1.]),
    title='R=225 m²,  Q=0.2 m²');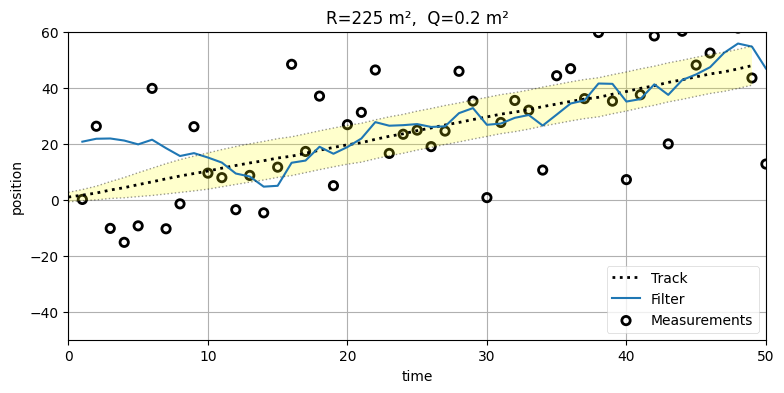

フィルタは最初正しい軌道に乗るまで数反復を要しているものの、その後は犬を追跡できている。実は、これは最適に近い──\(\mathbf{Q}\) は最適に設計できていないものの、\(\mathbf{R}\) の値は最適である。\(\mathbf{Q}\) は \(\frac{1}{2}\Delta a\) と \(\Delta a\) の間にある値にすべきであることが経験則として知られている。ここで \(\Delta a\) は考えている時刻の間隔における加速度の変化量の最大値を表す。これは本章で考えた仮定 (隣り合うサンプルの間で加速が一定かつ無相関という仮定) があるときにだけ成り立つ。カルマンフィルタの数学の章では \(\mathbf{Q}\) の設計方法をいくつか議論する。

\(\mathbf{R}\) と \(\mathbf{Q}\) のいずれかを変化させても、ある程度までは似たような出力が得られる。しかしだからといって、望む結果が得られるまで適当に値を変化させることは絶対にやってはいけない。設定する値が実際の問題で何を意味するかを必ず考え、フィルタリング対象の系に関する知識に基づいて \(\mathbf{R}\) や \(\mathbf{Q}\) を変化させるべきである。さらに徹底的なシミュレーションや実データによる試験でその値が適切なことを確認しなければならない。

6.12 共分散行列の詳しい調査

まずはフィルタの出力をプロットしよう。ランダムなデータだとこれから話したい現象が起こらない可能性があるので、zs_var_275 関数にハードコードしたデータを使うことにする。最初に P=500 とした場合を示す:

In [49]

import kf_book.mkf_internal as mkf_internal

var = 27.5
data = mkf_internal.zs_var_275()
run(track=trk, zs=zs, R=var, Q=.02, P=500., plot_P=True, title='P=500 m²');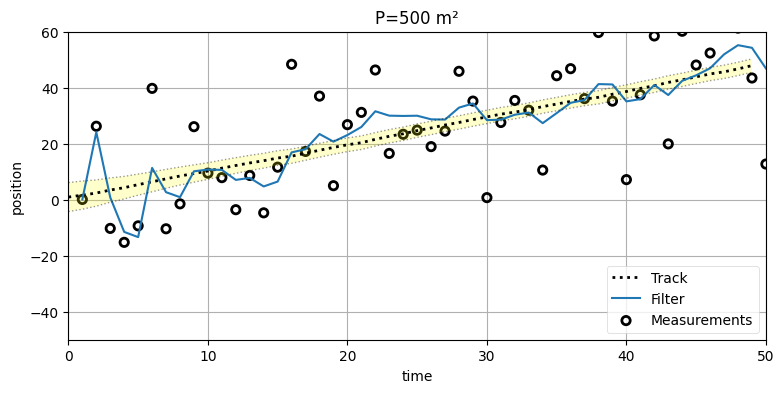

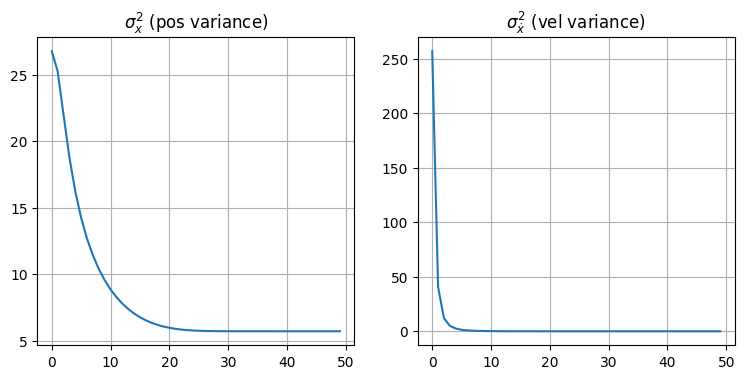
出力を見ると、初めの方に非常に大きなスパイク (値の変動) があるのが確認できる。このプロットでは \(\mathbf{P}\) の初期値を \(500\, \mathbf{I}_2\) (対角要素が \(500\) の \(2\times2\) 対角行列) としている。共分散行列の左上の \(500\) は \(\sigma^2_x\) に対応するから、最初 \(x\) の標準偏差は \(\sqrt{500} \approx 22.36\,\text{m}\) である。サンプルの 99% は \(3\sigma\) に収まるので、\(\sigma^2_x=500\) は予測 (事前分布) が実際の値から最大で \(67~\text{m}\) 離れるとカルマンフィルタに伝えるのに実質等しい。予測の不確実性が大きいので、最初の数エポックで観測値が大きく上下するとフィルタも推定値を大きく上下させる。しばらくするとフィルタは発展し、すぐに \(\mathbf{P}\) はより現実的な値に収束する。

裏にある数式を見よう。カルマンゲインは次の式で計算される:

\[ \mathbf K = \mathbf{\bar P} \mathbf H^\mathsf T\mathbf{S}^{-1} \approx \frac{\mathbf{\bar P}\mathbf H^\mathsf T}{\mathbf{S}} \approx \frac{\text{不確実性}_\text{予測値}}{\text{不確実性}_{\text{予測値}} + \text{不確実性}_\text{観測値}}\mathbf H^\mathsf T \]

これは予測値と観測値の不確実性の比を表す。今の設定では最初予測値の不確実性が大きいので、\(\mathbf{K}\) も大きく (スカラーなら \(1\) に近く) なる。\(\mathbf{K}\) は観測値から予測値を引いた残差 \(\textbf{y} = \mathbf z - \mathbf{H \bar x}\) と乗じられるので、\(\mathbf{K}\) が大きいと観測値が重視される。よって予測値の不確実性 \(\mathbf{P}\) がセンサーの不確実性 \(\mathbf{R}\) と比較して大きいと、フィルタは観測値に大部分を頼って推定値を計算する。

\(\mathbf{P}\) の初期値を \(1.0\, \mathbf{I}_2\) と小さくしたときに何が起こるかを見よう:

In [50]

run(track=trk, zs=zs, R=var, Q=.02, P=1., plot_P=True, title='P=1 m²');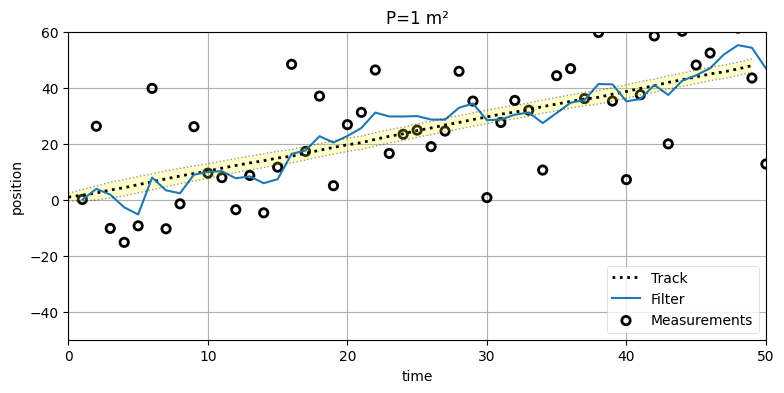

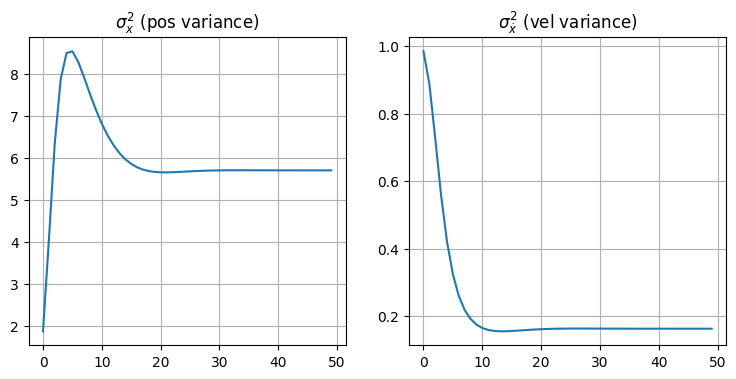
一見すると良さそうに見える。このプロットには前のようなスパイクが存在しないし、フィルタが観測値を追跡し始めるとすぐに正しい軌道に落ち着いている。しかし \(\mathbf{P}\) のプロットに注目すると、位置の分散が最初のスパイクの後戻ってこないのが分かる。このように、\(\mathbf{P}\) の設計を誤ると収束までの時間が長くなって結果も最適でなくなる。

つまりこの例ではフィルタが実際の信号を非常に正確に追跡しているものの、小さい \(\mathbf{P}\) を使うのが "魔法" だとは言い切れない。確かに、信号を正確に追跡するようにまでの時間は長くならないかもしれない。しかし最初の観測値の見当が付いていない状態だと、\(\mathbf{P}\) が小さいフィルタは非常に悪い振る舞いとなる。例えば生き物を追跡するときは、追跡を始める前に生き物の位置はほとんど分からないはずである。一方で温度計の出力をフィルタリングするときは、最初の観測値は 1000 番目の観測値と同程度に確かだと考えるだろう。カルマンフィルタを自分で使うときに振る舞いを向上させるには、データに関する自分の知識を完全に反映した値に \(\mathbf{P}\) を設定しなければならない。

非常に小さい \(\mathbf{P}\) を設定したカルマンフィルタに悪い初期推測値を入力したときの結果を確認しよう。初期推測値は \(x=100\, \text{m}\) で、\(\mathbf{P}\) は \(1.0\,\mathbf{I}_2\) とする。初期推測値と実際の初期位置 (\(0~\text{m}\)) の差は \(100~\text{m}\) であるにもかかわらずフィルタには \(3\sigma\) が \(3~\text{m}\) だと伝えているので、\(\mathbf{P}\) の選択としては明らかに正しくない:

In [51]

x = np.array([100., 0.])
run(track=trk, zs=zs, R=var, Q=.02, P=1., x0=x,
    plot_P=False, title='P=1 m²');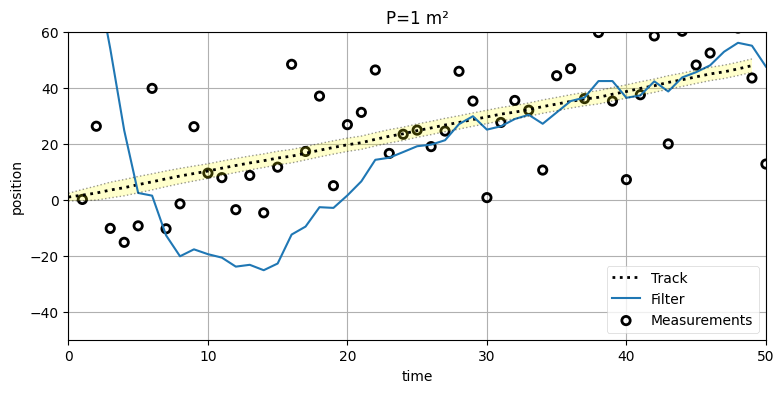

Out [51]小さい \(P\) と悪い初期推測値を設定したときのフィルタリング

初期推定値がひどいためにフィルタが信号に収束するまでに長い時間がかかっているのが分かる。これはフィルタが間違った初期推測値 \(100~\text{m}\) を強く信じているためである。

次は P に適切な値を設定したときの変化を観察しよう:

In [52]

x = np.array([100., 0.])
run(track=trk, zs=zs, R=var, Q=.02, P=500., x0=x,
   plot_P=False, title='P=500 m²');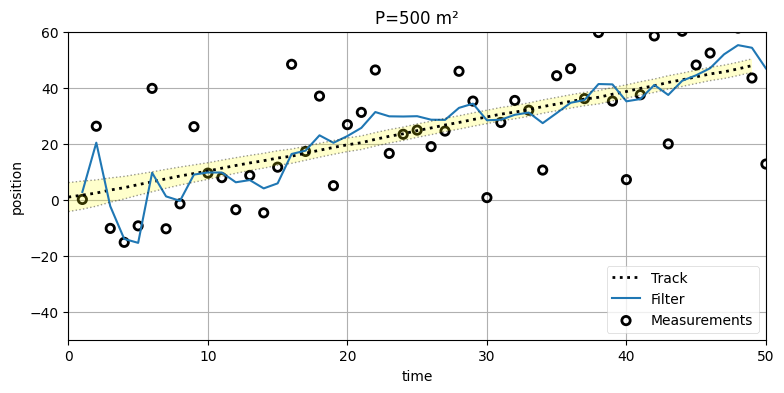

この場合カルマンフィルタは初期推測値が正確だとほとんど思っていないので、出力は信号にずっと早く収束しており、五回か六回のエポックだけで正確な出力が生成されている。ここまでに考えた理論ではこの程度が限界となる。ただし、このシナリオは人工的である: 追跡開始時の物体の位置を知らいときは、フィルタを \(0~\text{m}\) や \(100~\text{m}\) といった適当な値に初期化することはしない。この話題はフィルタの初期化の節で触れる。

犬を追跡するカルマンフィルタをもう一つ作ってみよう。今回は共分散楕円を位置と同じグラフにプロットする:

In [53]

from kf_book.mkf_internal import plot_track_ellipses

def plot_covariances(count, R, Q=0, P=20., title=''):
    track, zs = compute_dog_data(R, Q, count)
    f = pos_vel_filter(x=(0., 0.), R=R, Q=Q, P=P)

    xs, cov = [], []
    for z in zs:
        f.predict()
        f.update(z)

        xs.append(f.x[0])
        cov.append(f.P)

    # 相関係数の計算 (「質問: 楕円の傾きが違うのはなぜ？」の節の訳注を参照)
    # cor = f.P[0,1]**2 / (f.P[0,0] * f.P[1,1])
    # print(f"相関係数: {cor:.4f}")
    plot_track_ellipses(count, zs, xs, cov, title)

plt.figure(figsize=(10,6))
plt.subplot(121)
plot_covariances(R=5, Q=.02, count=20, title='R = 5 m²')
plt.subplot(122)
plot_covariances(R=0.1, Q=.02, count=20, title='R = 0.1 m²')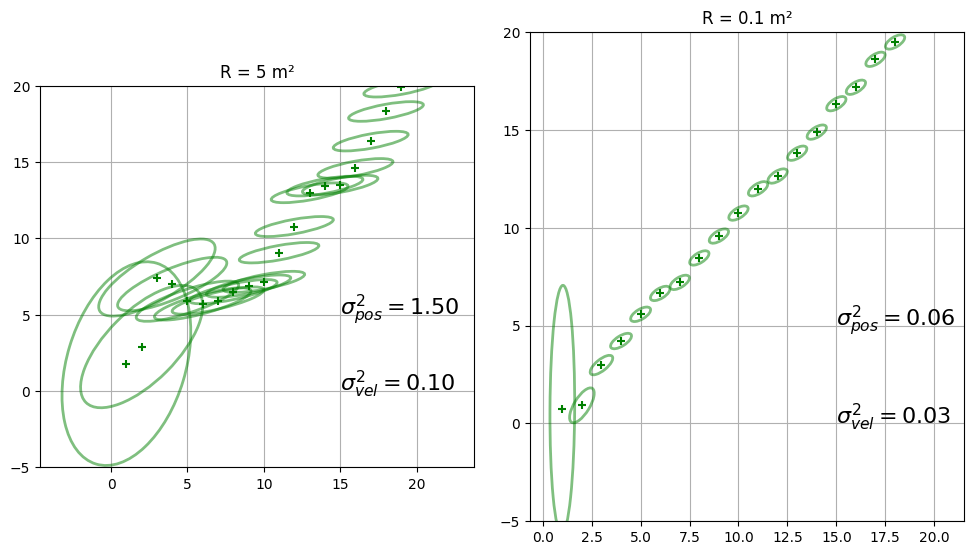

フィルタリングの進行とともに \(\mathbf{P}\) が変化するのが分かりやすいようパラメータを調整してある。本書を Jupyter Notebook またはウェブで読んでいる読者に向けて、フィルタが行うデータのフィルタリングを示すアニメーションを次に示す:

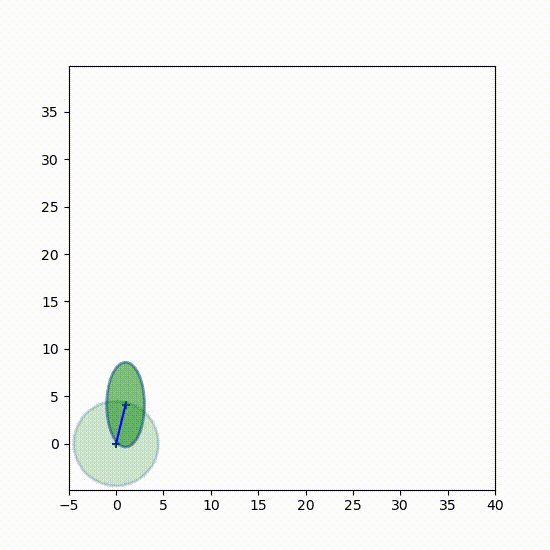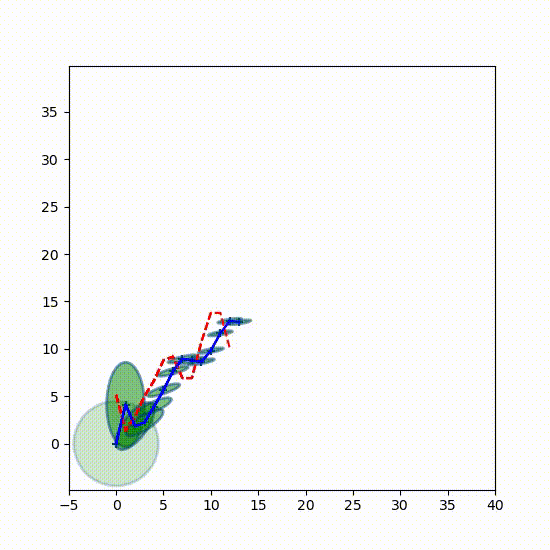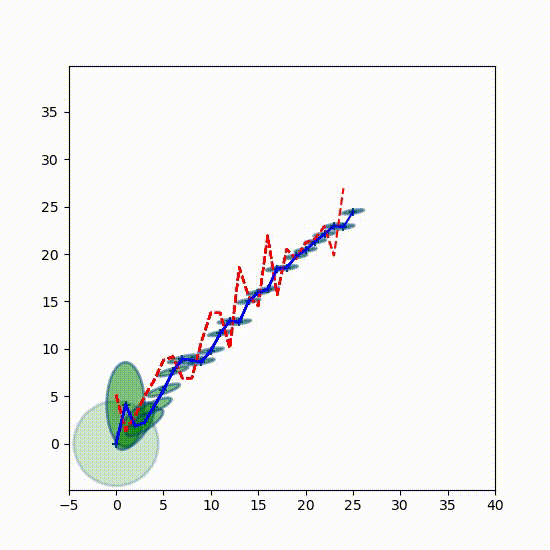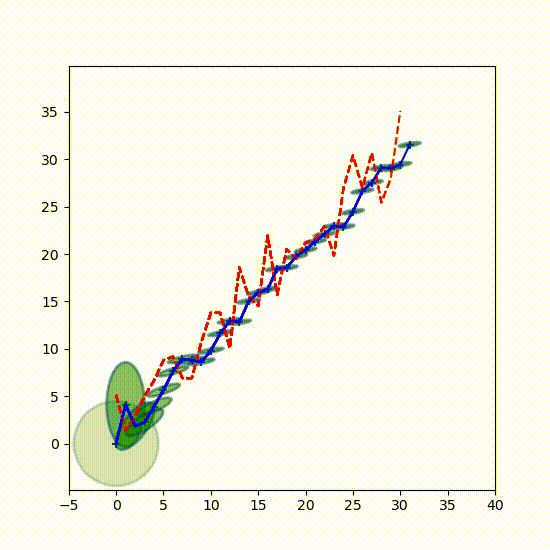
出力は多少散らかっているが、何が起きているかは理解できるはずだ。両方のプロットで各点における共分散行列が描画される。最初の共分散行列は \(\mathbf P=\Big[\begin{smallmatrix}20&0\\0&20\end{smallmatrix}\Big]\) であり、初期信念の不確実性が大きいことを示す。最初の観測値を受け取ると信念が更新され、共分散行列は小さくなる。コードで出力された二つのグラフで最初の (一番左にある) 楕円は少しだけ傾いている。フィルタが観測値の処理を進めるにつれて楕円は素早く形を変え、最終的には斜めに傾いた細長い楕円に落ち着く。

これが物理的に何を表すかを考えよう。楕円の \(x\) 軸方向の幅は位置の不確実性を表し、\(y\) 軸方向の幅は速度の不確実性を表す。そのため例えば \(x\) 軸方向より \(y\) 軸方向に長い楕円は位置より速度の方が不確実性が高いことを示す。逆に横に長い楕円は位置の不確実性が高く速度の不確実性が低いことを表す。最後に、傾きは位置と速度の相関の強さを表す。

\(R = 5\,\text{m}^2\) とした最初のグラフでは最終的な楕円が縦よりも横に長くなっている。分かりにくかったら、グラフの横に最後の楕円における位置と速度の分散を示してある。

一方で、\(R = 0.1 \, \text{m}^2\) とした二つ目のグラフでは最終的な楕円が横よりも縦に長くなっている。また二つ目のグラフの楕円は一つ目のグラフの楕円よりずっと小さい。これは \(\mathbf{R}\) が小さいために観測値のノイズが小さいのだから当然と言える。観測値のノイズが小さければ予測が正確になり、位置の信念も強くなる。

6.13 質問: 楕円の傾きが違うのはなぜ？

\(R = 5\, \text{m}^2\) における楕円が \(R = 0.1\, \text{m}^2\) における楕円より水平に近いのはなぜか？ヒント: 楕円の意味することを数学的にではなく物理的に考える。もし答えが分からないなら、\(\mathbf{R}\) を桁違いに大きい値と小さい値 (例えば \(100~\text{m²}\) と \(0.1~\text{m²}\)) としたとき何が起こるかを確認し、それが何を意味するかを考えるとよい。

解答

\(x\) 軸は位置、\(y\) 軸は速度を表す。垂直もしくは水平の楕円は位置と速度に相関がないことを示し、対角線に近い楕円は強い相関があることを示す。このように表現すると、上記の結果は辻褄が合わないように思える。二つのグラフで楕円の傾きが変化しているが、位置と速度の相関は時間が経過しても変化しないはずだからだ。しかしこれはフィルタの出力の図示であり、実際の物理世界を記述しているのではない。\(R\) が非常に大きいと観測値に大きなノイズが含まれることがフィルタに伝わる。このときカルマンゲイン \(\mathbf{K}\) は観測値より予測値を重視する値になり、その予測値は状態変数の速度から計算される。よって \(x\) と \(\dot x\) の相関は大きくなる。逆に \(R\) が小さいと、観測値が非常に信用できることがフィルタに伝わり、\(\mathbf{K}\) は予測値より観測値を重視する値となる。観測値がほぼ完璧ならどうして予測を使う必要があるだろうか？フィルタが予測値をあまり使わないなら、相関はほとんど報告されない¹。

これは理解しておくべき非常に重要なポイントである。カルマンフィルタの土台にあるのは数学的モデルであって、現実世界の系そのものではない。そのためカルマンフィルタが相関は存在しないと報告したとしても、それは物理的な系に相関が存在しないことを意味しない。数学的モデルが想定する線形の関係をフィルタが信じるに至らなかったというだけだ。相関は観測値と比べたとき予測値がどれだけフィルタに取り入れられたかを報告する。

巨大な観測誤差を設定してどうなるかを見よう。\(R=200\, \text{m}^2\) と設定するので、どうなるか考えてから結果を見てほしい:

In [54]

plot_covariances(R=200., Q=.2, count=5, title='R = 200 m²')
# run(P=20, R=200, Q=.2, count=100, plot_P=False, x0=np.array([50., 10.]));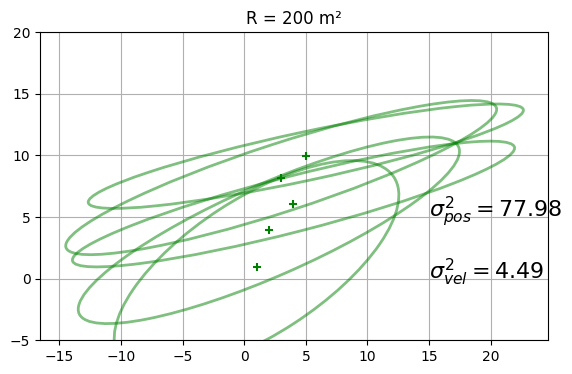

Out [54]\(R=200\, \text{m}^2\) としたときのフィルタリング

結果が期待通りであることを願う。楕円はすぐに横幅が広く、背が低くなる。これはカルマンフィルタが観測値ではなく予測値を使ってフィルタ結果を計算するためだ。また一行目をコメントアウトしてから二行目を実行すると、正しい軌道に乗るまでに時間がかかっているのも分かる。カルマンフィルタは観測値に非常に大きなノイズが存在すると思っているので、\(\dot x\) の推定値を更新するのが非常に遅い。

共分散行列 \(\mathbf{P}\) を解釈できるようになるまでグラフをよく観察しておくべきだ。\(9{\times}9\) の共分散行列などを目にしたときは圧倒されてしまうかもしれない──81 個もの数値を解釈する必要がある。そんなときでも、少しずつ考えれば難しくはない──対角要素には各状態変数の分散が含まれ、非対角要素には二つの状態変数の共分散が含まれる。\(9{\times}9\) の行列は画面にプロットできないから、この簡単な二次元の例で直感と理解を得ておく必要がある。

共分散楕円をプロットするときは、ax.set_aspect('equal') または plt.axis('equal') を使っていることを必ず確認してほしい (後者では xlim と ylim を設定できる)。これを使わないと \(x\) 軸と \(y\) 軸が異なる比率になり、楕円が歪んで描画される可能性がある。例えば本当は横に長い楕円が縦に長く描画されるといったことが起きる。

6.14 フィルタの初期化

フィルタの初期化で使えるスキームは数多く存在する。大部分の状況で上手く動作する手法をここで説明する。この手法では最初の観測値 \(z_0\) を手に入れた後にフィルタを初期化する。状態 \(\mathbf{x}\) と観測値 \(\mathbf{z}\) が同じサイズと単位を持つ (稀な) 場合には、\(\mathbf x\) の初期値を \(\mathbf{x_0} = \mathbf{z_0}\) と設定する。そうでなく \(\mathbf{z}\) が \(\mathbf{x}\) と同じサイズや単位を持たない (大部分の) 場合には、次のように観測関数を利用する:

観測関数の定義から、

\[ \mathbf z = \mathbf{Hx} \]

が分かる。ここから次を得る:

\[ \begin{aligned} \mathbf H^{-1}\mathbf{Hx} &= \mathbf H^{-1}\mathbf z \\ \mathbf x &= \mathbf H^{-1}\mathbf z \end{aligned} \]

逆行列を計算できるのは正方行列だけだが、\(\mathbf{H}\) が正方であることはまずない。その場合は SciPy の scipy.linalg.pinv 関数が計算するムーア-ペンローズの疑似逆行列を代わりに利用できる:

In [55]

from scipy.linalg import pinv

H = np.array([[1, 0.]])
z0 = 3.2
x = np.dot(pinv(H), z0)
print(x)

Out [55]

[[3.2]
 [0. ]]

いつでも使えるこの手法の他にも、問題ドメインの専門知識によって違う計算が可能になる場合もある。例えば状態に速度が含まれるなら、最初の二つの観測値から計算した速度を初期速度に設定できる。

続いて \(\mathbf{P}\) の初期値も計算しなければならない。この値の計算方法は問題によって異なるが、一般には観測変数に対応する要素には観測誤差 \(\mathbf{R}\) を割り当て、他の要素には対応する状態変数の最大値の二乗を割り当てることになる。この説明ではおそらく分からないだろう。本章では位置と速度を状態として物体を追跡し、観測値は位置だった。この場合 \(\mathbf{P}\) は次のように初期化する:

\[ \mathbf P = \begin{bmatrix}\mathbf R_0 & 0 \\0 & vel_{max}^2\end{bmatrix} \]

\(\mathbf{P}\) の対角要素は各状態変数の分散だから、適切な値を割り当てる必要がある。位置に対しては \(\mathbf{R}\) が適切な値であり、速度に対しては最大速度の二乗が適切な値となる。最大速度が二乗されるのは分散 \(\sigma^2\) に二乗が含まれるためだ。

フィルタの初期化は取り組んでいるドメインをよく理解した上で手に入る情報を全て使って行う必要がある。例えば競馬で走る馬を追跡するとしよう。このとき馬は出走ゲートからスタートすることが事前に分かるので、初期観測値でフィルタを初期化すると最適でない結果となる。このシナリオでは出走ゲートの場所を初期値とするのが理にかなっている。

6.15 バッチ処理

カルマンフィルタは再帰的なアルゴリズムとして設計されている──新しい観測値を受け取ると、すぐに新しい推定値が作成される。しかし事前に収集されたひとまとまりのデータに対してフィルタリングを行いたいという場合もよくある。カルマンフィルタは全ての観測値を一度に処理するバッチモードで実行することもでき、FilterPy では KalmanFilter.batch_filter 関数にバッチモードのカルマンフィルタが実装してある。この関数は観測値を順番にフィルタに入力して、出力される状態と共分散行列の推定値を配列に格納して返しているだけだ。batch_filter 関数があるとロジックが簡単になり、全ての出力を配列に楽に集められる。私はこの関数をよく使うのだが、読者には必ず実行される予測/更新サイクルによく慣れてほしかったので、紹介するのは章末まで待った。

batch_filter 関数の使い方を示す。最初に観測値を配列またはリストに用意する。観測値は CSV ファイルに格納されているかもしれない:

zs = read_altitude_from_csv('altitude_data.csv')

あるいはジェネレータで生成するのかもしれない:

zs = [some_func(i) for i in range(1000)]

観測値が手に入ったら batch_filter 関数を呼ぶ:

Xs, Ps, Xs_prior, Ps_prior = kfilter.batch_filter(zs)

この関数は観測値のリストを受け取り、フィルタリングを行い、四つの NumPy 配列を返す。返り値の NumPy 配列は状態推定値 (Xs) と共分散行列 (Ps) および事前分布における同じ値 (Xs_prior, Ps_prior) である。

完全な例を示す:

In [56]

count = 50
track, zs = compute_dog_data(10, .2, count)
P = np.diag([500., 49.])
f = pos_vel_filter(x=(0., 0.), R=3., Q=.02, P=P)
xs, _, _, _ = f.batch_filter(zs)

book_plots.plot_measurements(range(1, count + 1), zs)
book_plots.plot_filter(range(1, count + 1), xs[:, 0])
plt.legend(loc='best');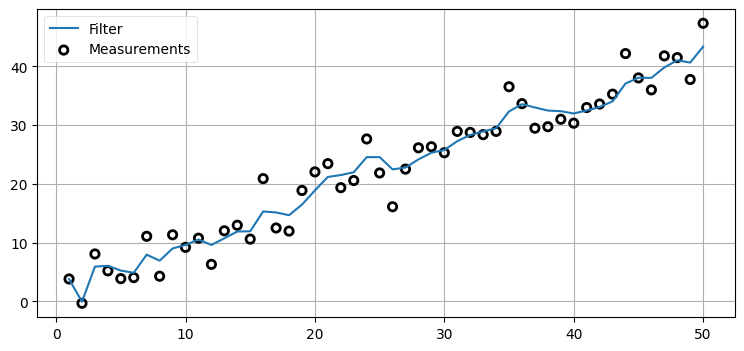

batch_filter 関数は省略可能なパラメータ引数 saver に filterpy.common.Saver オブジェクトを受け取る。これは状態と共分散行列以外の値を調べたいときに便利である。次に示すのは残差のプロットであり、ノイズが本当に \(0\) を中心としているかどうかを確認できる。これはフィルタの設計が上手く行っているかどうかを視覚的に確認するのに役立つ。もし残差が \(0\) を中心としていなかったり、そもそもノイズに見えなかったりしたら、フィルタの設計が上手くなかったり、プロセスがガウス分布で表せてない可能性がある。この話題には以降の章でも触れる。ここでは Saver クラスの利用例を示しておく:

In [57]

track, zs = compute_dog_data(10, .2, 200)
P = np.diag([500., 49.])
f = pos_vel_filter(x=(0., 0.), R=3., Q=.02, P=P)
s = Saver(f)
xs, _, _, _ = f.batch_filter(zs, saver=s)
s.to_array()
plt.plot(s.y);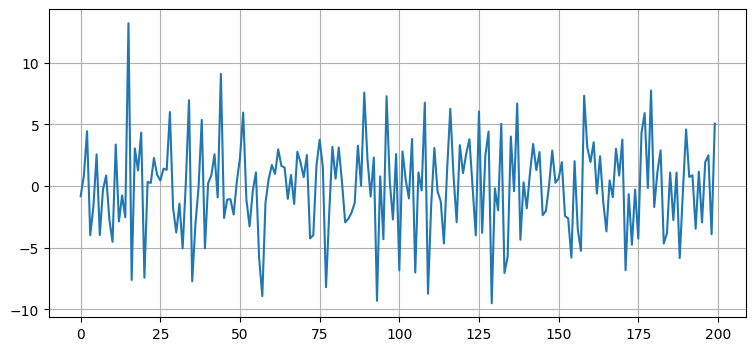

<code>Saver</code> クラスを利用した残差のプロット — Out [57]`Saver` クラスを利用した残差のプロット

6.16 出力の平滑化

本書には出力の平滑化に関する章がある。そこで書かれることをここに繰り替えすことはしない。ただ平滑化は簡単に使える上に素晴らしく結果が改善されるので、ここでいくつかの例を先取りして見せておく。平滑化の章が難しいわけではない: 今すぐに読んでも十分読めるだろう。

直線上を走る車を追跡していて、進行方向が左に変わったことを表す観測値を受け取ったとする。カルマンフィルタは状態推定値を観測値に向かって動かすものの、この観測値にたまたま大きなノイズが乗ったのか、本当に進行方向が変わったのかどうかは判断できない。

しかし、もし未来の観測値があるなら、進行方向が変わったかどうかの判定が行える。以降の観測値がずっと左に向かって進んでいたら、今考えている観測値が進行方向を変えた最初の観測値であると確信できる。逆に以降の観測値が直線的に右に進んでいたら、今考えている観測値にはノイズが多いのでほぼ無視するべきだと分かる。平滑化では一つの観測値と予測値の間から推定値を選ぶのではなく、複数の観測値それぞれを取り入れるか無視するかを判断した上で推定値が計算される。その判断には未来の観測値から得られる物体の移動に関する知識が使われる。

KalmanFilter は RTS スムーザー (RTS smoother) と呼ばれるこのアルゴリズムの一種を実装している。RTS という名前はアルゴリズムの開発者 Rauch, Tung, Striebel の頭文字である。batch_filter で計算した平均と共分散行列を rts_smoother に渡すと、平滑化された平均と共分散行列、そしてカルマンゲインが返る:

In [58]

from numpy.random import seed
count = 50
seed(8923)

P = np.diag([500., 49.])
f = pos_vel_filter(x=(0., 0.), R=3., Q=.02, P=P)
track, zs = compute_dog_data(3., .02, count)
Xs, Covs, _, _ = f.batch_filter(zs)
Ms, Ps, _, _ = f.rts_smoother(Xs, Covs)

book_plots.plot_measurements(zs)
plt.plot(Xs[:, 0], ls='--', label='Kalman Position')
plt.plot(Ms[:, 0], label='RTS Position')
plt.legend(loc=4);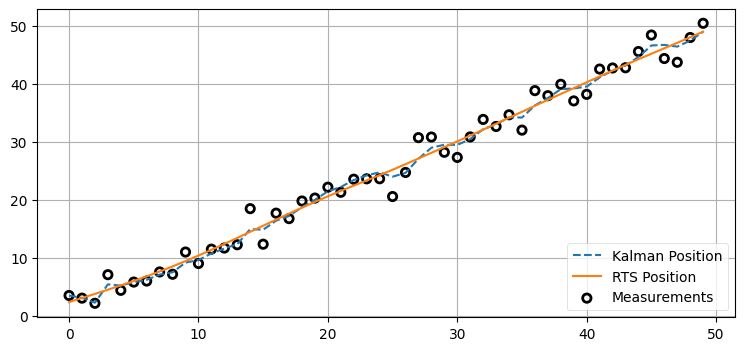

この出力は素晴らしい！このグラフからは二つのことが分かる。まず、RTS スムーザーの出力はカルマンフィルタの出力よりずっと滑らかになっている。次に、ほとんど常に RTS スムーザーの出力はカルマンフィルタの出力より正確になっている (この観察については出力の平滑化の章で扱う)。

隠れ変数である速度ではさらに顕著な改善が得られる:

In [59]

plt.plot(Xs[:, 1], ls='--', label='Kalman Velocity')
plt.plot(Ms[:, 1], label='RTS Velocity')
plt.legend(loc=4)
plt.gca().axhline(1, lw=1, c='k');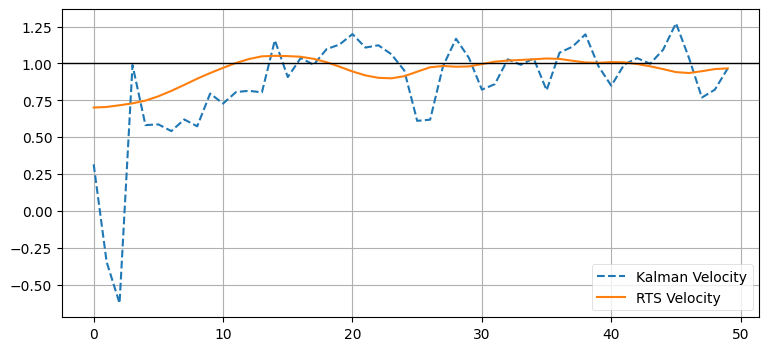

なぜこうなるのかを次の練習問題で深く掘り下げる。

6.17 練習問題: 速度の比較

ちょうど速度をプロットしているので、ここで "生の" 速度を確認してみよう。生の速度とは隣り合う観測値の差を使って計算する速度のことであり、例えば時刻 1 における生の速度は xs[1] - xs[0] を使って計算される。カルマンフィルタおよび RTS スムーザーの出力とともに生の速度をプロットし、結果について考察せよ。

In [60]

# 解答をここに書く

### 解答 {#subsection:6.17.1}

In [61]

dx = np.diff(Xs[:, 0], axis=0)
plt.scatter(range(1, len(dx) + 1), dx, facecolor='none',
            edgecolor='k', lw=2, label='Raw velocity')
plt.plot(Xs[:, 1], ls='--', label='Filter')
plt.plot(Ms[:, 1], label='RTS')
plt.legend(loc=4);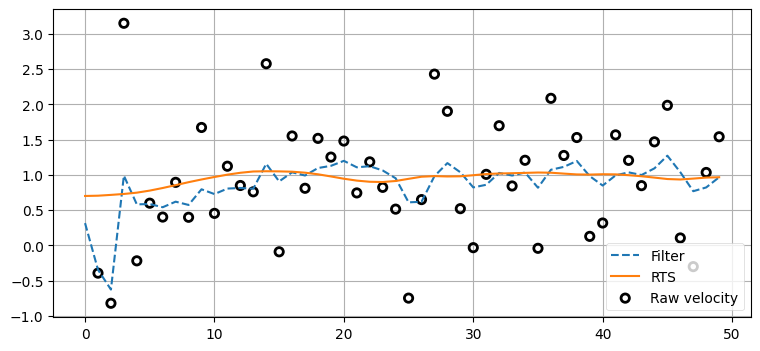

ノイズが入力信号をダメにしており、生の値には事実上価値がないことが分かる。一方で RTS スムーザーの出力は非常に正確である。フィルタは速度に対して個別の推定値を管理する。カルマンゲイン \(\mathbf K\) は多次元であり、例えば \(\mathbf K = [0.1274, 0.843]^\mathsf T\) のような値を取る。このとき一つ目の \(0.1274\) は位置の残差をスケールするのに使われ、二つ目の \(0.843\) は速度の残差をスケールするのに使われる。位置と速度の相関は共分散行列を通してフィルタに伝わり、両方の状態に最適な形でフィルタリングが行われる。

この例を示したのは、カルマンフィルタが速度や加速度、あるいはもっと高次元の値を計算することの重要性をもう一度強調するためだ。私は観測値がとても正確でフィルタリングせずに使えそうな場合であっても、速度と加速度の正確な推定値を計算するためにカルマンフィルタを使うようにしている。

6.18 まとめと考察

多変量のガウス分布を使うと複数の次元を同時に扱えるようになる。空間についての次元であってもそうでなくても (例えば速度でも) 構わない。本章で私たちは鍵となる重要な洞察を得た: 隠れ変数にはフィルタの精度を格段に向上させる効果がある。これが可能なのは、隠れ変数と観測変数に相関が存在するためだ。

本章では可観測性 (observability) の直感的な定義も与えた。可観測性はカルマン博士によって線形系に対して初めて考案され、それ以降もたくさんの理論が発展した。可観測性は系の状態が系の出力の観測によって決定できるかどうかを表す。私たちが考えた問題では可観測性があると少し考えれば分かるが、もっと複雑な系では厳密な解析が必要になる場合もある。Wikipedia の Observability のページに概観がある。可観測性について学びたいなら Mohinder S. Grewal と Angus P. Andrews による Kalman Filtering: Theory and Practice with MATLAB² が優れた資料である。

隠れ変数について一つ重要な注意点がある。隠れ変数に対する推定値を出力するフィルタは簡単に構築できる。例えば追跡している車の色を推定するフィルタも書けるだろう。しかし車の位置から車の色を計算する方法はないので、車の色の推定値は意味のない値になる。フィルタの設計者は変数が正しく推定されていることを検証する必要がある。もし速度センサーを持っていない状態で速度を推定したいなら、速度の推定値が正しいことは何らかの方法で確認しなければならない。理由もなく正しいと思ってはいけない。例えば速度が周期的な要素を持っていてサイン波のような形をしているなら、(ナイキストの定理により) その周波数の少なくとも二倍の頻度でサンプルしなければ速度を正確に推定できない。サンプル周期が速度の周波数と同じになったところを想像してほしい。このとき系のサンプルが全てサイン波の同じ場所で取得されるので、速度は定数だと報告されてしまう。

フィルタの初期化は隠れ変数に対して特に難しい問題になる。悪い初期値から開始したとしても観測変数であれば正しい値に回復できることが多いのだが、隠れ変数では回復に時間がかかったり回復できなかったりする。隠れ変数の推定は強力なツールだが、危険なツールでもある。

私はカルマンフィルタの設計を一連のステップを明確に示しながら行った。カルマンフィルタに関する文献にはこういったことが書かれないことが多い。ここには手引きとして示したので、処方箋と思わないでほしい。難しい問題に対するカルマンフィルタの設計は反復的なプロセスとなる。状態ベクトルを推測し、観測値と状態モデルを分析し、テストを実行し、必要に応じて設計を見直さなければならない。

\(\mathbf{R}\) と \(\mathbf{Q}\) の設計は非常に難しくなることが多い。本章では「センサーが \(\mathcal{N}(0, \sigma^2)\) のガウスノイズを持っているんだから \(\mathbf{R} = \sigma^2\) にすればいいんだ。簡単！」という議論を科学的に聞こえるように説明したが、これが科学的というのは真っ赤な嘘である。センサーのノイズはガウス分布ではない。本書では最初に体重計の話をした。分散 \(1~\text{kg}\) の体重計に \(0.5~\text{kg}\) の物を置いたところを想像してほしい。理論的には負の観測値が得られる可能性が生まれるが、体重計が負の値を報告することは当然ない。現実世界の典型的なセンサーは厚い裾 (fat tail, 尖度 kurtosis とも) と歪度 (skew) を持っている。体重計のように一方もしくは両方の裾が切られることもある。

\(\mathbf{Q}\) はさらに手強い。私が犬の移動予測に対して何の疑問も持たずにノイズ行列を割り当てたとき、読者が本当にそれでいいのかと疑いを持ったことを願う。犬が次に何をするかなど、誰に分かるというのか？車の GPS に搭載されるカルマンフィルタはどこに丘があるかを知らず、外の風を関知せず、私の運転スキルがひどいことも理解しない。それでもフィルタにはそういった情報を全て考慮したノイズ行列の値を設定しなければならず、その値を私が砂漠のオフロードを運転するときも、F1 王者がサーキットを走るときも使わなければならない。

こういった問題があるために、カルマンフィルタは「泥のかたまり (ball of mud)」と一部の科学者やエンジニアから軽蔑的に呼ばれることがある。言い換えれば、カルマンフィルタにはパラメータが多くて、しかも設定すべき値が必ずはっきり分かるとは限らないということだ。もう一つ知っておいた方がいい言葉がある──カルマンフィルタは独善的 (smug) になる場合がある。カルマンフィルタの推定値はこちらが伝えたノイズの形状だけに基づいて計算されるので、その値によっては推定値に自信が付きすぎる可能性がある。\(\mathbf{P}\) は小さくなっているのにフィルタが実際には不正確になっているかもしれない！最悪のケースではフィルタが発散する。非線形フィルタについて学び始めると発散の例が数多く登場する。

カルマンフィルタは現実世界の数学的なモデルである。出力はそのモデルと同程度にしか正確になれない。私たちの手に届く数学を使うためにいくつか仮定が置かれた。センサーと運動モデルがガウス分布のノイズを持つと仮定され、全ては線形であると仮定された。もしこの仮定が正しいなら、カルマンフィルタは最小二乗の意味で最適となる。これはカルマンフィルタより優れる推定値を計算する方法が存在しないことを意味する。しかし、この仮定はまず正しくない。したがってモデルが完璧であることはなく、実際にカルマンフィルタを動作させたときに最適であることはほとんどない。

後半の章では非線形性という問題に取り組む。今の段階では線形フィルタで使う行列の設計が数学というよりも実験に近い手続きであることを理解してほしい。最初に値を求めるのには数学を使うものの、その後は実験が必要になる。世界にモデルに入っていないノイズ (風など) が多くあるなら、\(\mathbf{Q}\) を大きくしなければならないだろう。しかし大きくしすぎると、今度は入力の変化に素早く反応できなくなる。適応フィルタの章では入力と性能に応じたフィルタ設計のリアルタイムな変更を可能にする手法を学ぶ。しかし今の段階では、フィルタが遭遇するどんな条件でも動作する値を見つけるしかない。アクロバット飛行機に対するノイズ行列は生徒が操縦するときとベテランが操縦するときでは異なるかもしれない。系のダイナミクスが大きく異なるためだ。

訳注: ここでは \(R\) が大きいと相関が強くなる理由が説明されているが、強い相関が存在するとき共分散行列を表す楕円が必ず水平に近づくわけではない (むしろ、楕円は対角線方向に傾くので一般には水平から遠ざかる)。\(R = 5~\text{m}^2\) の場合に楕円が水平に近くなるのは、位置の分散が速度の分散より大きいことからの影響が大きい。コード中のコメントを外して相関係数を確認すると、\(R=5~\text{m}\) のときの方が (共分散楕円は水平に近いように見えるにもかかわらず) 相関係数が大きいことが確認できる。^[return]
Mohinder S. Grewal and Angus P. Andrews, Kalman Filtering: Theory and Practice with MATLAB, Wiley-IEEE Press, 2008.^[return]

第 6 章 多変量カルマンフィルタ