週末レイトレーシング第一週 (翻訳)

はじめに

私が長年にわたって担当しているコンピューターグラフィックスの講義では、レイトレーシングを扱うことが多い。レイトレーシングでは全てのコードを自分で書く必要があるが、外部 API を使わずにクールな画像を生成できるからだ。その講義ために作ったノートをここに書籍としてまとめることにした。この本の目的はクールなプログラムをなるべく簡潔に読者へ示すことである。出来上がるのは機能全部載せのレイトレーサーとはいかないが、映画でレイトレーシングが使われる主な理由の一つである間接光がサポートされる。この本のステップ通りに実装していけば、レイトレーサーのアーキテクチャは簡単に拡張できるものになる。レイトレーシングにさらに興味が湧いた場合にも勉強に役立つだろう。

「レイトレーシング」という言葉は人によって様々な意味で使われる。この本で私が解説するのは正確には「パストレーサー」であり、それもかなり一般的なものである。「仕事はコンピューターにさせよう」ということでコードは非常に簡単だが、それでも生成される画像には十分満足してもらえると思う。

これからレイトレーサーを書く方法を私が書く順番通りに、デバッグのコツを交えながら示していく。最後まで読めば、素晴らしい画像を生成するレイトレーサーが手に入るだろう。この本は週末で読み切れると思うが、それより長くかかっても気にすることはない。言語は C++ を使う。他の言語を使っても構わないものの、私は C++ を勧める。C++ は高速かつポータブルで、プロダクションムービーやゲームのレンダラの多くが使っている言語でもあるからだ。C++ の「モダンな」機能は使わないようにしたが、レイトレーサーで特に活躍するオペレーターのオーバーロードと継承は使った。ソースコードをオンラインで入手できるようにはしていないものの、コードは本物であり、vec3 クラスの簡単なオペレーターの一部を除いて全て本文中に示される。私はコードを学ぶには自分でそのコードをタイプするべきだと強く信じているが、どこかから利用可能だとそれを使ってしまう。つまり私が自分の教えを実践できるのはコードが入手できないときだけだ。というわけで、ソースコードを公開してくれなどと言わないように！

(一つ前の段落の最後の部分は私が実際にしたことと 180° 違って面白いので、意図的に残してある。入り組んだバグに遭遇した読者には見比べるためのコードが役立つようだ。コードはぜひ自分でタイプしてほしいと思っているが、もし私のコードが見たいなら https://github.com/RayTracing/raytracing.github.io/ から入手できる)

この本はベクトルの基礎的な事項 (ベクトル同士の内積や加算など) を知っている読者を想定している。もし知らないなら、簡単に勉強しておくべきだろう。ベクトルの学習・復習には、Marchener と私が書いた Fundamentals of Computer Graphics, Foley, Van Dam, et al. によるComputer Graphics: Principles and Practice, あるいは McGuire の graphics codex を見てみるとよい¹。

何か問題が起きたり、クールな画像ができて誰かに見せたくなったときは ptrshrl@gmail.com までメールしてほしい。

この本に関連する書籍やリンクをブログ https://in1weekend.blogspot.com/ にまとめている。

このプロジェクトに手を貸してくれた全ての人に感謝する。名前は巻末の謝辞にある。

では始めよう！

画像の出力

PPM フォーマット

レンダラを書き始めると、すぐに画像を確認する手段が必要になる。一番簡単なのはファイルに書き出してしまうことだ。ただ画像フォーマットがたくさんあってどれも複雑なのが問題となる。私はいつもプレーンテキストの PPM ファイルから始めることにしている。Wikipedia にこのフォーマットの分かりやすい説明がある:

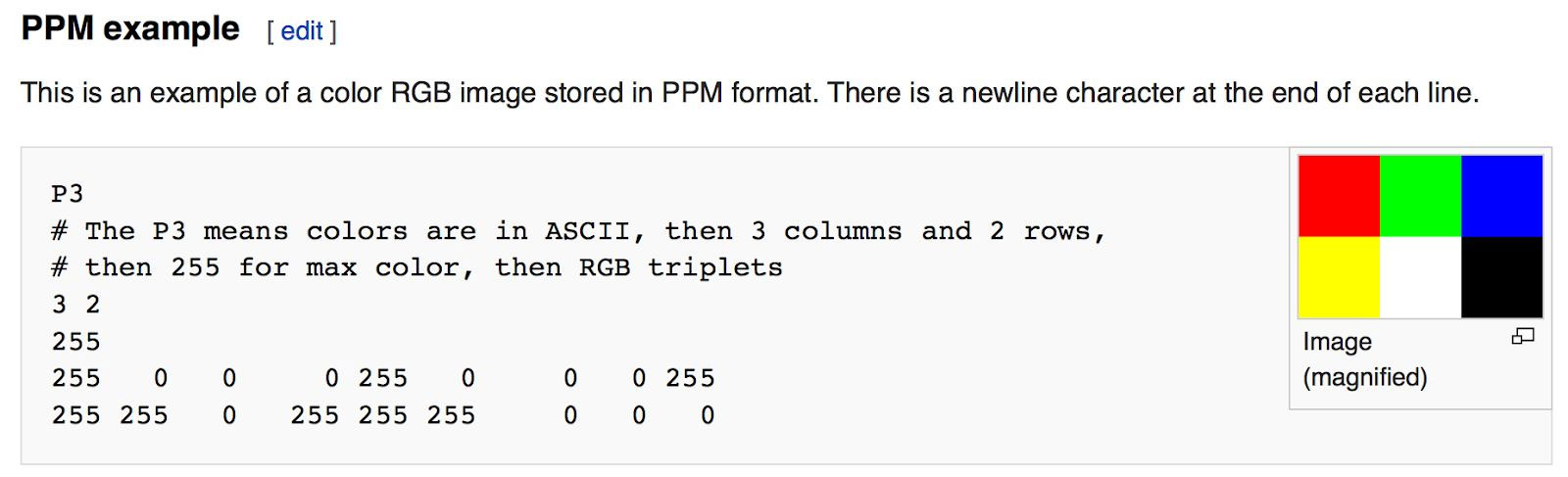
PPM フォーマットを出力する簡単な C++ コードを書こう:

#include <iostream>

int main() {
  const int image_width = 256;
  const int image_height = 256;

  std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

  for (int j = image_height-1; j >= 0; --j) {
    for (int i = 0; i < image_width; ++i) {
      auto r = double(i) / (image_width-1);
      auto g = double(j) / (image_height-1);
      auto b = 0.25;

      int ir = static_cast<int>(255.999 * r);
      int ig = static_cast<int>(255.999 * g);
      int ib = static_cast<int>(255.999 * b);

      std::cout << ir << ' ' << ig << ' ' << ib << '\n';
    }
  }
}

リスト 1.1 [main.cc] 簡単な PPM ファイルを出力するプログラム

このコードに関して注意すべき点がある:

ピクセルは行ごとに、左から右へ出力される。
列は上から下に出力される。
グラフィックスプログラミングの慣習として、赤 (red) 緑 (green) 青 (blue) の各要素は 0.0 から 1.0 の値を取る。後でハイダイナミックレンジを考えるときにはこの範囲外の値をレンダラの内部で扱うが、その場合でも出力時にはトーンマップで 0.0 から 1.0 の値に変換する。そのためこの部分のコードはこれから変化しない。

画像ファイルの作成

このプログラムは PPM ファイルの内容を標準出力に書き出すので、ファイルに保存するには標準出力をリダイレクトする必要がある。コマンドラインでリダイレクト演算子 < を使えば行える:

build\Release\inOneWeekend.exe > image.ppm

このコマンドは Winodws の例であり、Mac や Linux では次のようにする:

build/inOneWeekend > image.ppm

出力ファイルを画像ビューアで開けば内容を確認できる。私は Mac で ToyViewer を使っているが、どんなものでも構わない。ビューアによっては PPM ファイルをサポートしていない可能性もあるので、その場合には "PPM ビューア" と Google で検索してほしい。

やった！これがグラフィックスにおける "hello world" だ。もし画像がこのようになっていないなら、出力された PPM ファイルをテキストエディタで開いて内容を確認しよう。正しいファイルでは最初の部分が次のようになっている:

リスト 1.2 [image.ppm] 出力される PPM ファイルの先頭部分

画像が表示されないなら、ファイルに余分な改行や文字があるのだろう。すると画像ビューアはデータを読み取れない。

PPM 以外のフォーマットで画像を生成するときには、私はヘッダーオンリーの画像ライブラリ stb_image.h をよく使う。GitHub のページから入手できる。

進捗インジケータの追加

次に進む前に、出力に進捗インジケータを追加しておこう。これがあれば長いレンダリングがどこまで進んだかを確認できるし、無限ループなどの問題によって実行が進まなくなったのを検出することもできる。

現在のプログラムは画像を標準出力ストリーム (std::cout) に出力するので、インジケータはエラー出力ストリーム (std::cerr) に書くことにする。

  ...
  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      auto r = double(i) / (image_width-1);
      auto g = double(j) / (image_height-1);
      auto b = 0.25;

      int ir = static_cast<int>(255.999 * r);
      int ig = static_cast<int>(255.999 * g);
      int ib = static_cast<int>(255.999 * b);

      std::cout << ir << ' ' << ig << ' ' << ib << '\n';
    }
  }
  std::cerr << "\nDone.\n";
  ...

リスト 1.3 [main.cc] 進捗インジケータを付けたレンダリングのメインループ

`vec3` クラス

どんなグラフィックスプログラムにも幾何学的なベクトルと色を表すためのクラスが (ときには複数) ある。多くのシステムでは 4D のベクトル (幾何学であれば三次元座標と同次座標、色であれば RGB と透明度を表すアルファ値) が使われるが、今の私たちには三つの座標で十分だ。さらに同じ vec3 クラスを使って色・位置・方向・オフセットといった情報を表すことにする。こうすると「位置に色を足す」のような馬鹿げた操作が可能になってしまうという理由でこのやり方を好まない人もいる。この意見はもっともだが、私たちはこれから「コードが少なくなる」方の選択肢を (まるっきり間違っていない限り) 取るものとする。この上で vec3 には point3 と color という二つの型エイリアスを定義しておく。この二つの型は vec3 の別名に過ぎないので、例えば point3 を受け取る関数に color を渡しても警告は起きない。しかしそれでもコードの意図や使い方を表現するのに役立つ。

`vec3` の変数とメソッド

vec3 クラスの定義を示す:

#ifndef VEC3_H
#define VEC3_H

#include <cmath>
#include <iostream>

using std::sqrt;

class vec3 {
public:
  vec3() : e{0,0,0} {}
  vec3(double e0, double e1, double e2) : e{e0, e1, e2} {}

  double x() const { return e[0]; }
  double y() const { return e[1]; }
  double z() const { return e[2]; }

  vec3 operator-() const { return vec3(-e[0], -e[1], -e[2]); }
  double operator[](int i) const { return e[i]; }
  double& operator[](int i) { return e[i]; }

  vec3& operator+=(const vec3 &v) {
    e[0] += v.e[0];
    e[1] += v.e[1];
    e[2] += v.e[2];
    return *this;
  }

  vec3& operator*=(const double t) {
    e[0] *= t;
    e[1] *= t;
    e[2] *= t;
    return *this;
  }

  vec3& operator/=(const double t) {
    return *this *= 1/t;
  }

  double length() const {
    return sqrt(length_squared());
  }

  double length_squared() const {
    return e[0]*e[0] + e[1]*e[1] + e[2]*e[2];
  }

public:
  double e[3];
};

// vec3 の型エイリアス
using point3 = vec3; // 3D 点
using color = vec3;  // RGB 色

#endif

リスト 1.4 [vec3.h] vec3 クラス

ここでは double を使ったが、float を使うレイトレーサーもある。どちらでもよい ──好きな方を選ぼう。

`vec3` のユーティリティ関数

vec3 のヘッダーファイルにはユーティリティ関数が続く:

// vec3 ユーティリティ関数
inline std::ostream& operator<<(std::ostream &out, const vec3 &v) {
  return out << v.e[0] << ' ' << v.e[1] << ' ' << v.e[2];
}

inline vec3 operator+(const vec3 &u, const vec3 &v) {
  return vec3(u.e[0] + v.e[0], u.e[1] + v.e[1], u.e[2] + v.e[2]);
}

inline vec3 operator-(const vec3 &u, const vec3 &v) {
  return vec3(u.e[0] - v.e[0], u.e[1] - v.e[1], u.e[2] - v.e[2]);
}

inline vec3 operator*(const vec3 &u, const vec3 &v) {
  return vec3(u.e[0] * v.e[0], u.e[1] * v.e[1], u.e[2] * v.e[2]);
}

inline vec3 operator*(double t, const vec3 &v) {
  return vec3(t*v.e[0], t*v.e[1], t*v.e[2]);
}

inline vec3 operator*(const vec3 &v, double t) {
  return t * v;
}

inline vec3 operator/(vec3 v, double t) {
  return (1/t) * v;
}

inline double dot(const vec3 &u, const vec3 &v) {
  return u.e[0] * v.e[0]
     + u.e[1] * v.e[1]
     + u.e[2] * v.e[2];
}

inline vec3 cross(const vec3 &u, const vec3 &v) {
  return vec3(u.e[1] * v.e[2] - u.e[2] * v.e[1],
        u.e[2] * v.e[0] - u.e[0] * v.e[2],
        u.e[0] * v.e[1] - u.e[1] * v.e[0]);
}

inline vec3 unit_vector(vec3 v) {
  return v / v.length();
}

リスト 1.5 [vec3.h] vec3 ユーティリティ関数

色に関するユーティリティ関数

ちょうど今作った vec3 クラスを使って、ピクセルの色を標準出力ストリームに出力するユーティリティ関数を作っておく。

#ifndef COLOR_H
#define COLOR_H

#include "vec3.h"

#include <iostream>

void write_color(std::ostream &out, color pixel_color) {
  // 各成分を [0,255] に変換して出力する
  out << static_cast<int>(255.999 * pixel_color.x()) << ' '
      << static_cast<int>(255.999 * pixel_color.y()) << ' '
      << static_cast<int>(255.999 * pixel_color.z()) << '\n';
}

#endif

リスト 1.6 [color.h] 色に関するユーティリティ関数

これを使ってメインループを書き換える:

#include "color.h"
#include "vec3.h"

#include <iostream>

int main() {
  const int image_width = 256;
  const int image_height = 256;

  std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(double(i)/(image_width-1),
                        double(j)/(image_height-1),
                        0.25);
      write_color(std::cout, pixel_color);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.7 [main.cc] 最初の PPM ファイルを出力するプログラムの最終形

レイ・簡単なカメラ・背景

レイを表すクラス

どんなレイトレーサーにもレイを表すクラスとそのレイの色を計算する処理が存在する。レイを関数 \(\mathbf{P}(t) = \mathbf{A} + t \mathbf{b}\) と考えよう。\(\mathbf{P}\) は三次元空間に存在する直線上の点を表し、\(\mathbf{A}\) がレイの原点を、\(\mathbf{b}\) がレイの方向を意味する。レイのパラメータ \(t\) は実数 (double) であり、\(t\) を変えると \(\mathbf{P}(t)\) は三次元空間内の直線上を移動する。負の \(t\) も考えに入れれば直線上の全ての点が表され、\(t\) が正のとき \(P\) は \(\mathbf{A}\) の前方部分だけを移動する。この前方部分からなる半直線がレイである。

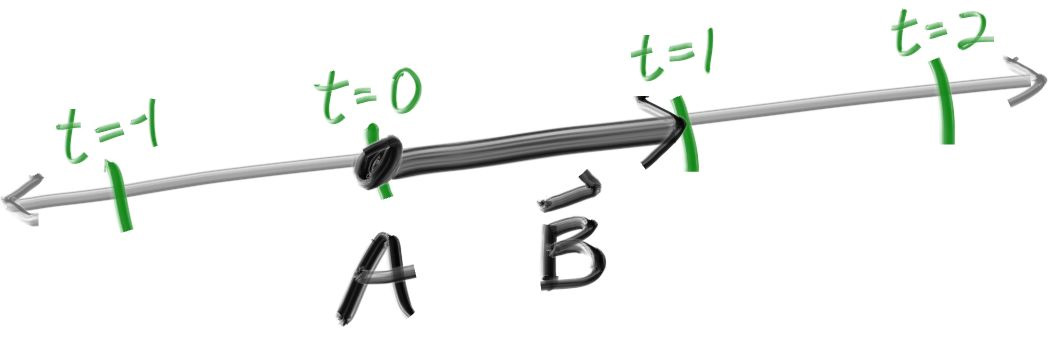
関数 \(\mathbf{P}(t)\) の実装はもう少し冗長に ray::at(t) と呼ぶことにする:

#ifndef RAY_H
#define RAY_H

#include "vec3.h"

class ray {
public:
  ray() {}
  ray(const point3& origin, const vec3& direction)
    : orig(origin), dir(direction) {}

  point3 origin() const  { return orig; }
  vec3 direction() const { return dir; }

  point3 at(double t) const {
    return orig + t*dir;
  }

public:
  point3 orig;
  vec3 dir;
};

#endif

リスト 1.8 [rah.h] ray クラス

レイの射出

これでレイトレーサーを作る準備が整った。レイトレーサーの核にあるのは「各ピクセルを通過するレイを放ち、視点からレイの方向を見たときの色を計算する」という処理である。この処理はさらに次の三つの処理に分けられる:

視点からピクセルへのレイを計算する
レイが交わるオブジェクトを求める
レイとオブジェクトの交点の色を計算する

私がレイトレーサーを開発するときは、必ず最初に簡単なカメラのコードを書いて実行できるところまで持っていくようにしている。さらに背景の色 (単純なグラデーション) を簡単に計算する ray_color(ray) 関数も作る。

私は \(x\) と \(y\) を本当によく取り違えるので、正方形の画像にレンダリングするとデバッグが大変になる。そこでレンダリングは正方形でない画像に行うことにする。画像のアスペクト比はたいていのディスプレイと同じ \(16:9\) としよう。

レンダリングする画像の解像度とは別に、仮想的なビューポートの形と位置を決めておく必要もある。通常の正方形のピクセルを使うとすれば、ビューポートのアスペクト比はレンダリングする画像と同じとなる。さらに高さを二単位と定めればビューポートの形が決まる。また射影平面と射影点の間の距離を一単位と定める。この距離は焦点距離 (focal length) と呼ばれるが、これは後で登場する集束距離 (focus distance) とは異なることに注意してほしい。

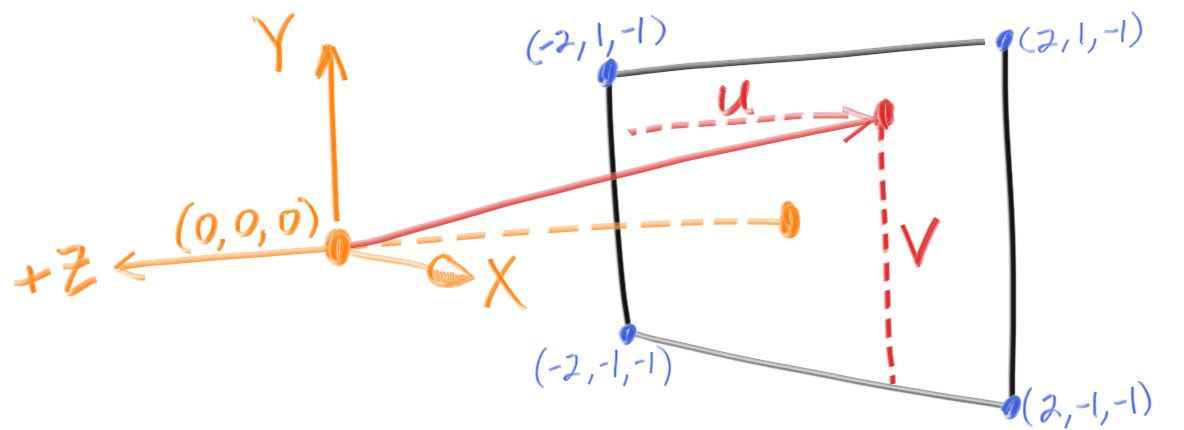
"目" (カメラの中心) は \((0, 0, 0)\) として、\(y\) 軸正方向は上、\(x\) 軸正方向は右とする。さらに座標を右手座標系とするために、スクリーンは \(z\) 座標が負になるように配置する。スクリーンの左下の点から走査を始め、スクリーンの辺に沿った二つのオフセットベクトル u と v を使ってレイがスクリーンと交わる点を管理する。実装ではレイの方向ベクトルを単位長としていない点に注意してほしい。こうした方がコードが単純になり、実行も多少高速になる。

次に示すコードではレイ r がピクセルのほぼ中心を通っている。後でアンチエイリアシングを追加するので、ここでは正確さを気にしない。

#include "ray.h"

#include <iostream>

color ray_color(const ray& r) {
  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);

  std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";

  auto viewport_height = 2.0;
  auto viewport_width = aspect_ratio * viewport_height;
  auto focal_length = 1.0;

  auto origin = point3(0, 0, 0);
  auto horizontal = vec3(viewport_width, 0, 0);
  auto vertical = vec3(0, viewport_height, 0);
  auto lower_left_corner =
    origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      auto u = double(i) / (image_width-1);
      auto v = double(j) / (image_height-1);
      ray r(origin, lower_left_corner + u*horizontal + v*vertical - origin);
      color pixel_color = ray_color(r);
      write_color(std::cout, pixel_color);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.9 [main.cc] 青と白のグラデーションをレンダリングするコード

ray_color(ray) 関数はまずレイの方向ベクトルを正規化し、正規化したベクトルの \(y\) 成分 (\(-1.0 \lt y \lt 1.0\)) を使って白と青を線形に混ぜ合わせる。正規化した後の \(y\) を考えているから、グラデーションは垂直方向だけではなく水平方向にも表れることが分かるだろう。

図 1.5:

正規化されたレイの \(y\) 成分から計算された青から白へのグラデーション

その後 \(y\) を \(0.0 \leq t \leq 1.0\) にスケールする簡単な処理を行う。続いて \(t = 1.0\) のときには青が、\(t = 0.0\) のときには白が、その間のときには二つが混ざった色が計算されるような処理を行う。これは二つの量の線形ブレンド (linear blend) あるいは線形補間 (linear interpolation) と呼ばれる処理であり、略して lerp と呼ばれる。lerp は必ず \[ {\footnotesize \text{補間された値}} = (1-t)\cdot {\footnotesize \text{始まりの値}} + t\cdot {\footnotesize \text{終わりの値}} \] という形をしており、\(t\) は \(0\) から \(1\) の値を取る。lerp によって上の画像が得られる。

球のレンダリング

レイトレーサーにオブジェクトを追加しよう。球とレイの交差判定は非常に簡単に行えるので、レイトレーサーに最初に追加されるオブジェクトは球であることが多い。

レイと球の衝突判定

原点中心で半径が \(R\) の球は \(x^{2} + y^{2} + z^{2} = R^{2}\) と表されることを思い出そう。つまり点 \((x, y, z)\) がこの球上にあるなら \(x^{2} + y^{2} + z^{2} = R^{2}\) が成立する。もし点 \((x, y, z)\) が球の内側にあるなら\(x^{2} + y^{2} + z^{2} \lt R^{2}\) が成り立ち、点 \((x, y, z)\) が球の外側にあるなら \(x^{2} + y^{2} + z^{2} > R^{2}\) が成り立つ。

球の中心が \((C_{x}, C_{y}, C_{z})\) なら、方程式は少し汚くなって \[ (x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 = r^2 \] となる。

グラフィックスでは、数式がベクトルを使って表され、x, y, z といった添え字が vec3 クラスの中に隠れている状態が望ましい。球の中心 \(\mathbf{C} = (C_{x}, C_{y}, C_{z})\) から点 \(\mathbf{P} = (x, y, z)\) へのベクトルは \((\mathbf{P} - \mathbf{C})\) と表せるから、 \[ (\mathbf{P} - \mathbf{C}) \cdot (\mathbf{P} - \mathbf{C}) = (x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 \] が成り立つ。よってベクトルを使った球の方程式は \[ (\mathbf{P} - \mathbf{C}) \cdot (\mathbf{P} - \mathbf{C}) = r^2 \] と書ける。

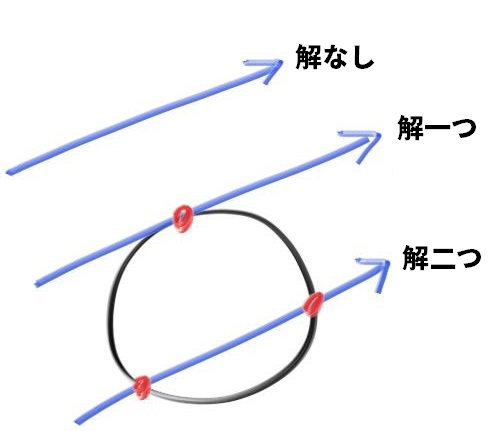
これは「ある点 \(\mathbf{P}\) がこの方程式を満たすなら、その点は球上にある」と読める。さてレイ \(\mathbf{P}(t) = \textbf{A} + t \textbf{b}\) が球と交わるかを調べたい。もしレイが球と交わるなら、ある \(t\) で \(\textbf{P}(t)\) が球の方程式を満たす。つまり次の条件を満たす \(t\) が存在するかを調べればよい: \[ (\mathbf{P}(t) - \mathbf{C}) \cdot (\mathbf{P}(t) - \mathbf{C}) = r^2 \] \(\mathbf{P}(t)\) に定義の式を代入すれば \[ (\mathbf{A} + t \mathbf{b} - \mathbf{C}) \cdot (\mathbf{A} + t \mathbf{b} - \mathbf{C}) = r^2 \] となる。後はベクトルの公式が使える。この等式を展開して項をまとめれば \[ t^2 \mathbf{b} \cdot \mathbf{b} + 2t \mathbf{b} \cdot (\mathbf{A}-\mathbf{C}) + (\mathbf{A}-\mathbf{C}) \cdot (\mathbf{A}-\mathbf{C}) - r^2 = 0 \] となる。この等式中のベクトルと \(r\) は全て既知の定数だから、これは未知の \(t\) に関する二次方程式となる。高校の数学で習ったように、この方程式の解 \(t\) を表す式には根号が含まれる。根号中の式が正・\(0\)・負となる場合に応じて、実数解の個数は二つ・一つ・解なしとなる。こういったグラフィックスにおける代数方程式には幾何学的な意味があることが多く、今考えている問題では次のようになる:

最初のレイトレーシング画像

この数式をプログラムにハードコードして正しいことを確かめよう。\(z\) 軸上の点 \(z = -1\) に置かれた小さな球とレイが交わるときにピクセルを赤くする:

bool hit_sphere(const point3& center, double radius, const ray& r) {
  vec3 oc = r.origin() - center;
  auto a = dot(r.direction(), r.direction());
  auto b = 2.0 * dot(oc, r.direction());
  auto c = dot(oc, oc) - radius*radius;
  auto discriminant = b*b - 4*a*c;
  return (discriminant > 0);
}


color ray_color(const ray& r) {
  if (hit_sphere(point3(0,0,-1), 0.5, r))
    return color(1, 0, 0);
  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.10 [main.cc] 赤い球のレンダリング

次の画像が得られる:

足りない機能は山ほどある ──シェーディングも反射もないし、オブジェクトは一つだけだ。しかし私たちは大きな一歩を踏み出した！一つ注意しておくと、このプログラムではレイが \(t \lt 0\) で交わる場合にもピクセルを赤くしている。そのため球の中心を \(z = +1\) としても同じ画像が得られてしまう。もちろんこれは正しくない！次はこういった問題を修正する。

法線と複数オブジェクト

法線を使ったシェーディング

まずシェーディングのために法線を計算しよう。法線とは物体とレイの交点を通って物体表面と垂直なベクトルのことを言う。法線に関して決めておくべき設計事項が二つある。一つ目は法線を単位長とするかどうかである。単位長にしておけばシェーディングが楽になるので、法線は単位長と定める。ただしコードでこれを明示的に確認することはしない。これによって軽微なバグが生まれる可能性もあるので、これは (他の様々な設計判断と同じく) 個人的な好みだと思ってほしい。さて球の場合には、外向きの法線は交点 \(p\) から中心 \(c\) を引いたベクトル \(p - c\) と同じ向きを持つ。球を地球だと考えれば、これは地球の中心からあなたへのベクトルが真上を向くことを意味する。

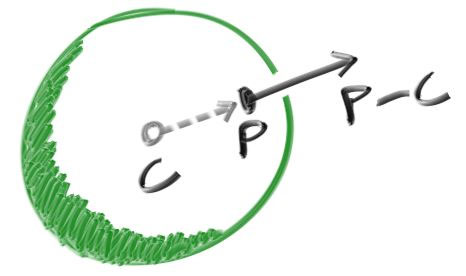
以上の説明をコードにしてシェーディングを行おう。まだ球以外には光も何もないから、法線をカラーマップとして可視化する。法線を可視化するのによく使われるのが、法線の \(x\), \(y\), \(z\) 成分をそれぞれ \(0\) から \(1\) の区間にマップして、それを \(r\), \(g\), \(b\) として読むというテクニックだ (このとき法線 \(\textbf{n}\) が単位ベクトルで、各成分が \(-1\) から \(1\) の値を持つとすると実装が簡単で理解もしやすい)。法線を扱うためにはレイが当たったかどうかに加えて交点の位置に関する情報も必要になるから、一番近くの (\(t\) が小さい方の) 交点を考えることにする。これで \(\textbf{n}\) の計算・可視化が可能になる:

double hit_sphere(const point3& center, double radius, const ray& r) {
  vec3 oc = r.origin() - center;
  auto a = dot(r.direction(), r.direction());
  auto b = 2.0 * dot(oc, r.direction());
  auto c = dot(oc, oc) - radius*radius;
  auto discriminant = b*b - 4*a*c;
  if (discriminant < 0) {
    return -1.0;
  } else {
    return (-b - sqrt(discriminant) ) / (2.0*a);
  }
}

color ray_color(const ray& r) {
  auto t = hit_sphere(point3(0,0,-1), 0.5, r);
  if (t > 0.0) {
    vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));
    return 0.5*color(N.x()+1, N.y()+1, N.z()+1);
  }
  vec3 unit_direction = unit_vector(r.direction());
  t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.11 [main.cc] 球の法線のレンダリング

次の画像が得られる:

レイと球の衝突判定の簡略化

レイと球の方程式を解く部分をもう一度考えよう:

vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius*radius;
auto discriminant = b*b - 4*a*c;

リスト 1.12 [main.cc] レイと球の衝突判定 (改良前)

まず、同じベクトル同士の内積はベクトルの長さの二乗に等しい。

次に、b に \(2\) が掛けられているが、\(b = 2h\) とすると \[ \begin{aligned} \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} & = \frac{-2h \pm \sqrt{(2h)^2 - 4ac}}{2a} \\ & = \frac{-2h \pm 2\sqrt{h^2 - ac}}{2a} \\ & = \frac{-h \pm \sqrt{h^2 - ac}}{a} \end{aligned} \] が成り立つ。

以上の観察を使えば、球の衝突判定コードを簡略化できる:

vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;

if (discriminant < 0) {
  return -1.0;
} else {
  return (-half_b - sqrt(discriminant) ) / a;
}

リスト 1.13 [main.cc] レイと球の衝突判定 (改良後)

レイが衝突するオブジェクトの抽象化

複数の球を配置する方法を考えよう。球の配列を使いたくなるかもしれないが、ここではレイが衝突しうる物体を表す抽象クラスを用意すると非常に美しく問題を解決できる。この抽象クラスの名前は決めづらい ── object も悪くないが、「オブジェクト指向」という言葉と衝突する。surface もよく使われるが、おそらく立体的な物体をレンダリングすることもある。メンバー関数を強調すれば hittable となる。どれも完璧ではないが、ここでは hittable を使うことにしよう。

抽象クラス hittable はレイを受け取って自身と交わるかを判定する関数 hit を持つ。たいていのレイトレーサーの hit 関数はレイとは別に有効な \(t\) の値を表す \(t_{\text{min}}\) と \(t_{\text{max}}\) を受け取り、\(t_{\text{min}} \lt t \lt t_{\text{max}}\) のときに限って「交わる」ようにしている。最初のレイでは必ず \(t_{\text{min}} = 0\) かつ \(t_{\text{max}} = \infty\) だが、今後 \(t_{\text{min}}\) と \(t_{\text{max}}\) を持っておくとコードが簡単に書ける場合がある。これとは別の設計上の問題として、レイが交わる場合の法線などの計算を hit 関数で行うかどうかがある。探索の結果レイがもっとカメラに近い物体に交わっていることが分かり、必要となるのは一番近くにある法線だけとなるかもしれない。ここでは簡単な方法を選び、様々なデータを hit 関数で計算して hit_record 構造体に収めることにする。こうして完成する抽象クラスを示す:

#ifndef HITTABLE_H
#define HITTABLE_H

#include "ray.h"

struct hit_record {
  point3 p;
  vec3 normal;
  double t;
};

class hittable {
public:
  virtual ~hittable() {}
  virtual bool hit(
    const ray& r, double t_min, double t_max, hit_record& rec
  ) const = 0;
};

#endif

リスト 1.14 [hittable.h] hittable クラス

そして球を表すクラスはこうなる:

#ifndef SPHERE_H
#define SPHERE_H

#include "hittable.h"
#include "vec3.h"

class sphere: public hittable {
public:
  sphere() {}
  sphere(point3 cen, double r) : center(cen), radius(r) {}

  virtual bool hit(
    const ray& r, double tmin, double tmax, hit_record& rec
  ) const;

public:
  point3 center;
  double radius;
};

bool sphere::hit(
  const ray& r, double t_min, double t_max, hit_record& rec
) const {
  vec3 oc = r.origin() - center;
  auto a = r.direction().length_squared();
  auto half_b = dot(oc, r.direction());
  auto c = oc.length_squared() - radius*radius;
  auto discriminant = half_b*half_b - a*c;

  if (discriminant > 0) {
    auto root = sqrt(discriminant);
    auto temp = (-half_b - root)/a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      rec.normal = (rec.p - center) / radius;
      return true;
    }
    temp = (-half_b + root) / a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      rec.normal = (rec.p - center) / radius;
      return true;
    }
  }
  return false;
}

#endif

リスト 1.15 [sphere.h] sphere クラス

法線の向き

法線に関してもう一つ、その向き (常に外を向くのか、それとも場合によっては内を向くのか) を決めておく必要がある。今の実装では法線が中心から交点の方向であり、常に外を向く。そのため外側から交わるレイと法線は逆向きとなり、内側から交わるレイと法線は同方向となる。こうではなくて、法線を常にレイと逆方向にする設計も考えられる。この設計ではレイが外側から交わるとき法線は外向きとなり、レイが内側から交わるなら法線は内向きとなる。

レイが物体のどちらか側からやってきたかに関する情報を今後使うことになるので、法線の向きの扱いを統一しておく必要がある。例えば両面印刷の紙のように裏と表でレンダリングが異なるオブジェクトや、ガラス球のように内側と外側を持つオブジェクトでこの情報が使われる。

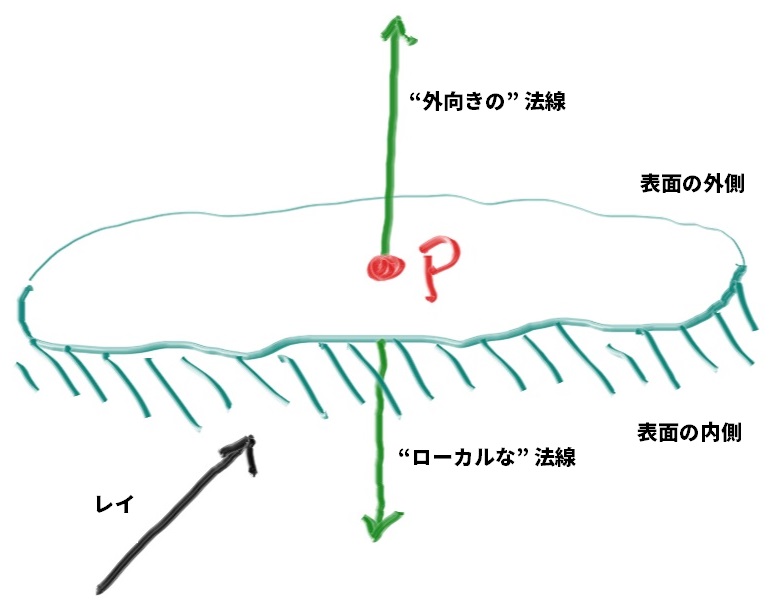
法線は常に外を向くと決めれば、レイが物体のどちら側にあるのかを色を計算するときに調べることになる。これはレイと法線を比較すれば分かる。つまりレイと法線が同じ方向を向いているならレイは物体の内部にあり、レイと法線が逆方向を向いているならレイはオブジェクトの外側にある。二つのベクトルの向きは内積を使えば判定でき、内積が正ならレイは物体の内部にある:

if (dot(ray_direction, outward_normal) > 0.0) {
  // レイは球の内側にある
  ...
} else {
  // レイは球の外側にある
  ...
}

リスト 1.16 [sphere.h] レイと法線の向きを調べる

法線が常にレイと逆方向を向くと決めれば、内積を使って物体とレイの位置関係を調べる方法は使えない。代わりにその情報を保存することになる:

bool front_face;
if (dot(ray_direction, outward_normal) > 0.0) {
  // レイは球の内側にある
  normal = -outward_normal;
  front_face = false;
} else {
  // レイは球の外側にある
  normal = outward_normal;
  front_face = true;
}

リスト 1.17 [sphere.h] 物体のレイの位置関係を保存する

法線が物体の "外側" を向くようにすることもできるし、レイと逆方向を向くようにすることもできる。法線の向きをジオメトリとの衝突判定時に決めたいのか、それとも色を計算するときに決めたいのかに応じて選ぶことになる。本書ではジオメトリよりマテリアルの種類が多くなるので、コードが少なくなるように法線をジオメトリとの衝突判定時に計算する方法を取る。これは好みに過ぎないので、他の文献を当たれば両方の実装が見つかるだろう。

hit_record 構造体にブール値 front_face を追加し、さらに法線の向きを計算する関数 set_face_normal も加える:

#ifndef HITTABLE_H
#define HITTABLE_H

#include "ray.h"

struct hit_record {
  point3 p;
  vec3 normal;
  bool front_face;

  inline void set_face_normal(const ray& r, const vec3& outward_normal) {
    front_face = dot(r.direction(), outward_normal) < 0;
    normal = front_face ? outward_normal :-outward_normal;
  }
};

...

リスト 1.18 [hittable.h] 法線の向きの計算を加えた hit_record クラス

そして sphere クラスに法線の向きの計算を追加する:

bool sphere::hit(
  const ray& r, double t_min, double t_max, hit_record& rec
) const {
  vec3 oc = r.origin() - center;
  auto a = r.direction().length_squared();
  auto half_b = dot(oc, r.direction());
  auto c = oc.length_squared() - radius*radius;
  auto discriminant = half_b*half_b - a*c;

  if (discriminant > 0) {
    auto root = sqrt(discriminant);
    auto temp = (-half_b - root)/a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      vec3 outward_normal = (rec.p - center) / radius;
      rec.set_face_normal(r, outward_normal);
      return true;
    }
    temp = (-half_b + root) / a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      vec3 outward_normal = (rec.p - center) / radius;
      rec.set_face_normal(r, outward_normal);
      return true;
    }
  }
  return false;
}

リスト 1.19 [sphere.h] 法線の向きの計算を加えた sphere::hit 関数

オブジェクトのリスト

hittable というレイが衝突しうるオブジェクトを表す一般的なクラスが手に入ったので、hittable のリストを保持するクラスも作ることができる:

#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H

#include "hittable.h"

#include <memory>
#include <vector>

using std::shared_ptr;
using std::make_shared;

class hittable_list: public hittable {
public:
  hittable_list() {}
  hittable_list(shared_ptr<hittable> object) { add(object); }

  void clear() { objects.clear(); }
  void add(shared_ptr<hittable> object) { objects.push_back(object); }

  virtual bool hit(
    const ray& r, double tmin, double tmax, hit_record& rec
  ) const;

public:
  std::vector<shared_ptr<hittable>> objects;
};

bool hittable_list::hit(
  const ray& r, double t_min, double t_max, hit_record& rec
) const {
  hit_record temp_rec;
  bool hit_anything = false;
  auto closest_so_far = t_max;

  for (const auto& object : objects) {
    if (object->hit(r, t_min, closest_so_far, temp_rec)) {
      hit_anything = true;
      closest_so_far = temp_rec.t;
      rec = temp_rec;
    }
  }

  return hit_anything;
}

#endif

リスト 1.20 [hitabble_list.h] hittable_list クラス

C++ に特有の機能

hittable_list クラスには C++ を普段使わないプログラマーには見慣れないであろう機能が二つある: vector と shared_ptr だ。

shared_ptr は共有ポインタであり、新しくアロケートされたオブジェクトを使って初期化する。使用例を示す:

shared_ptr<double> double_ptr = make_shared<double>(0.37);
shared_ptr<vec3>   vec3_ptr   = make_shared<vec3>(1.4142, 2.7182, 1.6180);
shared_ptr<sphere> sphere_ptr = make_shared<sphere>(point3(0,0,0), 1.0);

リスト 21: shared_ptr を使ったアロケートの例

make_shared<thing>(thing_constructor_params) はコンストラクタの引数として thing_constructor_params を使って thing の新しいインスタンスをアロケート・初期化し、shared_ptr<thing> を返す。

make_shared<type>() の返り値の型は機械的に推論できるから、上の例は C++ の型指定子 auto を使って簡単に書くことができる:

auto double_ptr = make_shared<double>(0.37);
auto vec3_ptr   = make_shared<vec3>(1.4142, 2.7182, 1.6180);
auto sphere_ptr = make_shared<sphere>(point3(0,0,0), 1.0);

リスト 22: auto を使った shared_ptr の使用例

これからは共有ポインタを使っていく。共有ポインタを使えば複数のジオメトリが同一のインスタンスを共有でき、メモリ管理が自動的で分かりやすくなる。例えばたくさんの球が同じテクスチャマップマテリアルを使うといったことが可能になる。

std::shared_ptr は <memory> ヘッダーでインクルードできる。

もう一つ見慣れないかもしれない C++ の機能が std::vector である。これは任意の型の値を線形に並べたコレクションを表す一般的な型であり、上の例では hittable を指すポインタの集まりに使っている。std::vector は要素が増えると自動的にメモリを確保する。上の例では objects.push_back(object) が std::vector 型のメンバー変数 objects の最後に値を追加している。

std::vector は <vector> ヘッダーでインクルードできる。

またリスト 1.20 の using std::shared_ptr と using std::make_shared は、std ライブラリの shared_ptr と make_shared をこれから使うことをコンパイラに伝えている。こうすると std:: と付けなくてもこれらの型と関数を参照できるようになる。

数学定数とユーティリティ関数

数学定数を一つのヘッダーファイルにまとめて定義しておくと便利である。いま必要なのは無限大だけだが、後で円周率 \(\pi\) も入れることになる。\(\pi\) の標準的でポータブルな定義はないので、自分で定義する。メインのヘッダーファイル rtweekend.h を作って、定数やユーティリティ関数はここに入れる:

#ifndef RTWEEKEND_H
#define RTWEEKEND_H

#include <cmath>
#include <cstdlib>
#include <limits>
#include <memory>


// using
using std::shared_ptr;
using std::make_shared;
using std::sqrt;

// 定数
const double infinity = std::numeric_limits<double>::infinity();
const double pi = 3.1415926535897932385;

// ユーティリティ関数
inline double degrees_to_radians(double degrees) {
  return degrees * pi / 180;
}

// 共通ヘッダー
#include "ray.h"
#include "vec3.h"

#endif

リスト 1.23 [rtweekend.h] 共通ヘッダー rtweekend.h

メイン関数も書き換える:

#include "rtweekend.h"

#include "hittable_list.h"
#include "sphere.h"

#include <iostream>

color ray_color(const ray& r, const hittable& world) {
  hit_record rec;
  if (world.hit(r, 0, infinity, rec)) {
    return 0.5 * (rec.normal + color(1,1,1));
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);

  std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

  auto viewport_height = 2.0;
  auto viewport_width = aspect_ratio * viewport_height;
  auto focal_length = 1.0;

  auto origin = point3(0, 0, 0);
  auto horizontal = vec3(viewport_width, 0, 0);
  auto vertical = vec3(0, viewport_height, 0);
  auto lower_left_corner =
    origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);

  hittable_list world;
  world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
  world.add(make_shared<sphere>(point3(0,-100.5,-1), 100));

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      auto u = double(i) / (image_width-1);
      auto v = double(j) / (image_height-1);
      ray r(origin, lower_left_corner + u*horizontal + v*vertical);

      color pixel_color = ray_color(r, world);

      write_color(std::cout, pixel_color);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.24 [main.cc] hittable を使ったメイン関数

このプログラムを実行すると、球の位置と法線を可視化した画像が得られる。これはモデルの特徴や欠陥を確認するのに役立つことが多い。

アンチエイリアシング

現実のカメラで撮った写真では、物体の周りがギザギザに見えることはない。これは物体の縁のピクセルにおいて前景と背景が混ざるためだ。各ピクセルに複数のサンプルを放って平均値を計算すれば、これと同じ効果を得られる。なお、この本ではランダムサンプリングの層化 (stratification) は実装しない。これは議論を呼ぶ設計だが、私が書くレイトレーサーではいつもこうしている。層化が欠かせないレイトレーサーもあるが、いま私たちが書いている一般的なパストレーサーでは層化で得られるものは少なく、ただコードが汚くなってしまう。また後で機能を足せるようにカメラを抽象化するクラスもここで作成する。

乱数関数

まず実数の乱数を生成する関数が必要になる。一様な乱数を返す関数では \(0 \leq r \lt 1\) の区間の実数を返すのが慣習となっている。\(1\) 未満なのが重要で、この事実を利用する場面もある。

簡単なアプローチは <cstdlib> にある関数 rand() を使うものだ。この関数は \(0\) から RAND_MAX の間の整数をランダムに返すから、\(0\) から \(1\) の間の実数乱数は次のコードで得られる。これは rtweekend.h に足しておく:

#include <cstdlib>
...

inline double random_double() {
  // [0,1) の実数乱数を返す
  return rand() / (RAND_MAX + 1.0);
}

inline double random_double(double min, double max) {
  // [min,max) の実数乱数を返す
  return min + (max-min)*random_double();
}

リスト 1.25 [rtweekend.h] random_double() 関数

長い間 C++ は標準の乱数生成器を持っていなかったが、新しいバージョンで <random> ヘッダーがこれを解決した (ただ専門家に言わせるとこれでも不十分らしい)。C++ の乱数生成関数を使う場合には次のようにする:

#include <random>

inline double random_double() {
  static std::uniform_real_distribution<double> distribution(0.0, 1.0);
  static std::mt19937 generator;
  return generator(distribution);
}

リスト 1.26 [rtweekend.h] <random> を使った random_double() の実装

複数のサンプルを使ったピクセルの描画

各ピクセルに対して複数のサンプルを生成し、各サンプルを通るレイを射出し、各レイの色の平均を求めよう:

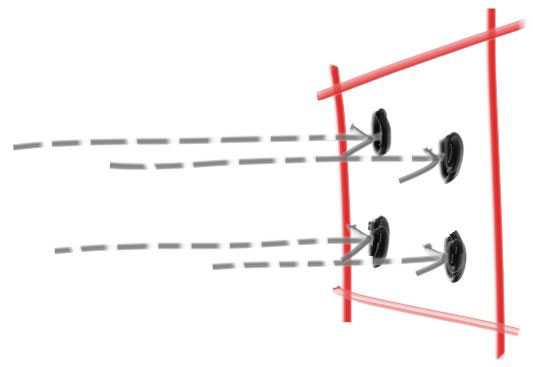
それから仮想的なカメラの管理とシーンのサンプリングに関連する処理を行う camera クラスも作る。次のクラスにはこれまでと同じ軸に固定されたカメラが実装されている:

#ifndef CAMERA_H
#define CAMERA_H

#include "rtweekend.h"

class camera {
public:
  camera() {
    auto aspect_ratio = 16.0 / 9.0;
    auto viewport_height = 2.0;
    auto viewport_width = aspect_ratio * viewport_height;
    auto focal_length = 1.0;

    origin = point3(0, 0, 0);
    horizontal = vec3(viewport_width, 0.0, 0.0);
    vertical = vec3(0.0, viewport_height, 0.0);
    lower_left_corner =
      origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
  }

  ray get_ray(double u, double v) const {
    return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
  }

private:
  point3 origin;
  point3 lower_left_corner;
  vec3 horizontal;
  vec3 vertical;
};
#endif

リスト 1.27 [camera.h] camera クラス

続いて複数のサンプルを使った色の計算を行うよう write_color() 関数を更新する。色をサンプル数で割ってから足すのではなくて、色を足してから最後にサンプル数で割って計算を減らすようにする。また x を [min,max] の範囲で切り捨てる関数 clamp(x, min, max) が必要になるので、ユーティリティ関数として rtweekend.h に追加する。

inline double clamp(double x, double min, double max) {
  if (x < min) return min;
  if (x > max) return max;
  return x;
}

リスト 1.28 [rtweekend.h] clamp() 関数

void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
  auto r = pixel_color.x();
  auto g = pixel_color.y();
  auto b = pixel_color.z();

  // 色の和をサンプル数で割る
  auto scale = 1.0 / samples_per_pixel;
  r *= scale;
  g *= scale;
  b *= scale;

  // 各成分を [0,255] に変換して出力する
  out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}

リスト 1.29 [color.h] マルチサンプルの write_color() 関数

メイン関数も同様に変更する:

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);
  const int samples_per_pixel = 100;

  std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";

  hittable_list world;
  world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
  world.add(make_shared<sphere>(point3(0,-100.5,-1), 100));

  camera cam;

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(0, 0, 0);
      for (int s = 0; s < samples_per_pixel; ++s) {
        auto u = (i + random_double()) / (image_width-1);
        auto v = (j + random_double()) / (image_height-1);
        ray r = cam.get_ray(u, v);
        pixel_color += ray_color(r, world);
      }
      write_color(std::cout, pixel_color, samples_per_pixel);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.30 [main.cc] マルチサンプルを使ったレンダリング

生成される画像を拡大すると、前景と背景にまたがる部分が大きく変化していることが分かる:

拡散マテリアル

複数のオブジェクトと各ピクセルに対する複数のレイがサポートできたので、これで現実的な見た目のマテリアルを作る準備が整った。まず拡散マテリアル (diffuse material) から始める (拡散マテリアルは非光沢マテリアル (matte material) とも呼ばれる)。ジオメトリとマテリアルの実装に関して、両者を分離する方法と両者を結び付ける方法がある。分離すると一つのマテリアルを複数のジオメトリに割り当てる使い方 (およびその逆) が可能になるが、結び付けるとプロシージャルなオブジェクトが扱いやすくなる。私たちは (他の多くのレンダラと同様) ジオメトリとマテリアルを分離する方法を使うが、その制限は意識しておくべきだ。

単純な拡散マテリアル

拡散マテリアルを持つ物体は周囲からの光をそのまま反射するのではなく、マテリアルに固有の色でその光を変化させる。また拡散表面で反射した光は方向がランダムになる。例えば二つの拡散マテリアルの間に三つのレイを放つと、それぞれがランダムに反射する (散乱する) ことになる:

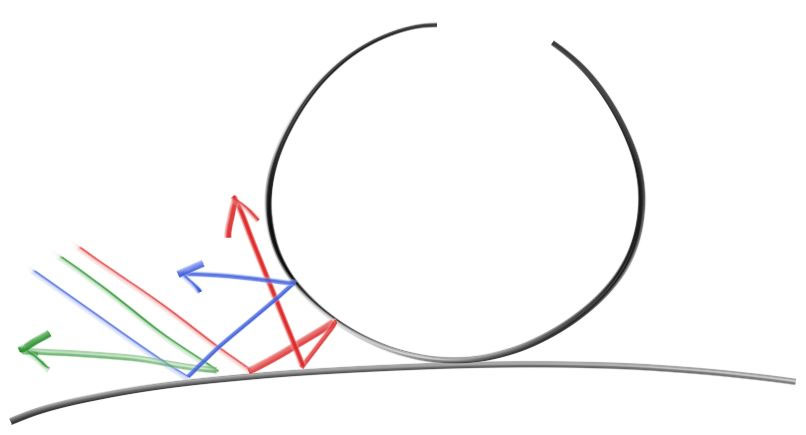
光は反射せずに吸収される可能性もある。表面が黒いならそれだけ吸収される光の量も増える (だから黒いのだ！)。実は反射光の方向を何らかの意味でランダムに設定するアルゴリズムを使えば、それだけで非光沢らしい見た目が得られる。これから説明するのは理想的な拡散表面を近似する簡単なアルゴリズムの一つである (私はこれを数学的に理想的なランバーティアン (Lambertian) を近似するための怠惰なハックとして使っていた)。

(この本を読んだ Vassillen Chizhov はこの手法が本当に怠惰なハックに過ぎず、ランバーティアンの近似として不正確なことを証明した。理想的なランバーティアンの正しい定式化は難しいものではなく、この節の最後に示してある)

レイと物体表面の交点 \(\mathbf{P}\) に接する単位球は二つある。法線を \(\mathbf{n}\) とすると、二つの球の中心は \(\textbf{P} + \textbf{n}\) および \(\textbf{P} - \textbf{n}\) と表せる。中心が \(\textbf{P} - \textbf{n}\) の球は物体の内側にあり、中心が \(\textbf{P} + \textbf{n}\) の球は物体の外側にある。物体から見てレイの始点と同じ方向にある球を選び、その球の中にランダムな点 \(\textbf{S}\) を取る。そして交点 \(\textbf{P}\) から \(\textbf{S}\) に向かって飛ばしたレイを散乱レイとして採用する (このレイは \(\mathbf{S}-\mathbf{P}\) を向く)。

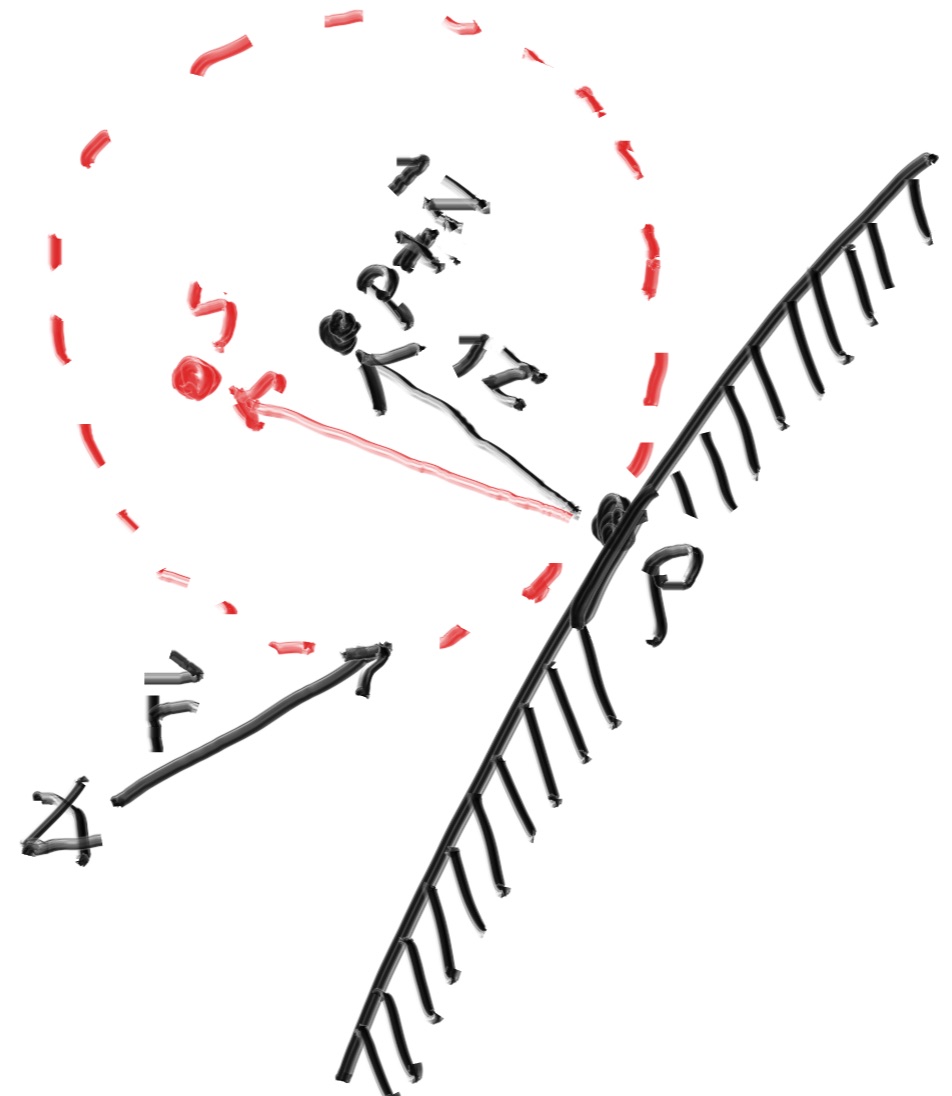
このアルゴリズムの実装では単位球の中にランダムな点を取る処理が必要になる。ここでは棄却法 (rejection method) と呼ばれる最も簡単なアルゴリズムを使う: x, y, z を \(-1\) から \(+1\) の範囲でランダムに取り、点 \((x, y, z)\) が単位球の内部にあるならそれを採用する。単位球の外側にあるなら棄却し、同じ処理をもう一度行う。

class vec3 {
public:
  ...
  inline static vec3 random() {
    return vec3(random_double(), random_double(), random_double());
  }

  inline static vec3 random(double min, double max) {
    return vec3(random_double(min,max),
                random_double(min,max),
                random_double(min,max));
  }

リスト 1.31 [vec3.h] ランダムな vec3 を計算するユーティリティ関数

vec3 random_in_unit_sphere() {
  while (true) {
    auto p = vec3::random(-1,1);
    if (p.length_squared() >= 1) continue;
    return p;
  }
}

リスト 1.32 [vec3.h] random_in_unit_sphere() 関数

レイが物体と衝突したら散乱レイとしてランダムなベクトルを生成し、そのレイの色をさらに計算するよう ray_color() 関数を書き換える:

color ray_color(const ray& r, const hittable& world) {
  hit_record rec;

  if (world.hit(r, 0, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_in_unit_sphere();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.33 [main.cc] ランダムな散乱レイを使った ray_color()

子レイの数を制限する

ここで生じうる問題が一つある。ray_color 関数が再帰的なことに注目してほしい。再帰呼び出しがいつ終わるのかと言えば、レイが何にも当たらないときだ。しかしそれまでの反射回数がとても多くなって、スタックを使い切ってしまう可能性がある。このケースに対処するために、再帰呼び出しの最大回数を制限しておこう。最大の深さまで行ったレイからの寄与はゼロとする:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_in_unit_sphere();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

...

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);
  const int samples_per_pixel = 100;
  const int max_depth = 50;

  ...
  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(0, 0, 0);
      for (int s = 0; s < samples_per_pixel; ++s) {
        auto u = (i + random_double()) / (image_width-1);
        auto v = (j + random_double()) / (image_height-1);
        ray r = cam.get_ray(u, v);
        pixel_color += ray_color(r, world, max_depth);
      }
      write_color(std::cout, pixel_color, samples_per_pixel);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.34 [main.cc] 再帰の深さに制限を付けた ray_color()

次の画像が得られる。球の下に影ができている (暗くて影がよく分からなくてもすぐに直すので気にしなくてよい)。

ガンマ補正による明るさの調整

球は反射ごとにエネルギーを半分だけしか吸収していないにもかかわらず、この画像はとても暗い。光の \(50\) %は反射されており、球は非常に明るく (現実世界であれば明るい灰色に) 見えるのが正しい。この画像が間違った色に見えるのは、ほぼ全ての画像ビューアが読み込む画像を「ガンマ補正 (gamma correction) 」されたものとして扱うことに原因がある。つまり \(0\) から \(1\) の値をバイトとして書き込む前に、特別な変換を施さなければならない。ガンマ補正が必要な理由はもちろん存在するが、ここではただ必要なのだと理解しておこう。ここでは \(\gamma = 2\) のガンマ変換を利用する。これは色の各成分を \(1/\gamma = 1/2\) 乗する処理であり、平方根を取ればよい:

void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
  auto r = pixel_color.x();
  auto g = pixel_color.y();
  auto b = pixel_color.z();

  // 色の合計をサンプルの数で割り、gamma = 2.0 のガンマ補正を行う
  auto scale = 1.0 / samples_per_pixel;
  r = sqrt(scale * r);
  g = sqrt(scale * g);
  b = sqrt(scale * b);

  // 各成分を [0,255] に変換して出力する
  out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}

リスト 1.35 [color.h] ガンマ補正を追加した write_color()

これで狙い通りの明るい画像が得られる:

シャドウアクネを消す

気付きにくいが、実はこの画像にもまだバグがある。散乱レイと球の交点は正確に \(t = 0\) ではなく、浮動小数の誤差によって \(t=-0.0000001\) あるいは \(t=0.0000001\) といった値になる。そのためレイと球の交点を判定するときには \(0\) に非常に近い交点を無視する必要がある:

if (world.hit(r, 0.001, infinity, rec)) {

リスト 1.36 [main.cc] 下限付きの散乱レイの計算

これでシャドウアクネ (shadow acne) の問題が解決できる。本当にこう呼ばれている²。

完全なランバート反射

先ほど示した棄却法は法線に接する単位球に含まれるランダムな点を生成する。この点が交点が中心で法線が天頂を指す半球上の点を指すベクトルを表しているとすれば、法線ベクトルに近い方向のベクトルは高い確率で、水平線に使い方向のベクトルは低い確率で生成される。棄却法によって生成されるベクトルと法線の角度を \(\phi\) とすると、角度が \(\phi\) のベクトルが生成される確率は \(\cos^{3} \phi\) に比例する。現実でも斜めの方向から入射した光は大きく広がってその点の色への影響が小さくなるので、これは現実的な挙動だと言える。

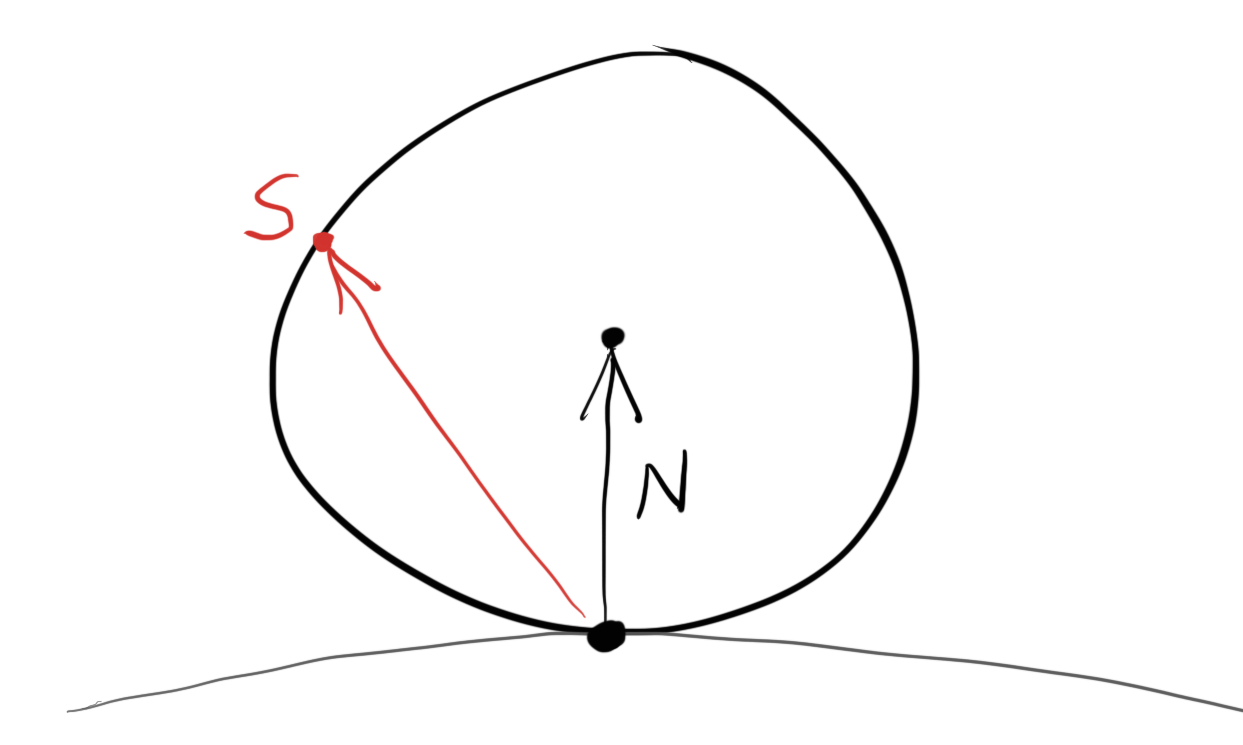
しかし拡散反射で通常使われるのはランバート分布であり、この分布では前述の確率が \(\cos \phi\) に比例する。つまり完全なランバート分布に従うマテリアルは法線に近い方向にレイを多く散乱させるが、その分布はもっと一様分布に近い。実は法線に接する単位球上の点を選ぶと、散乱レイがこの分布を満たすようになる。単位球上の点をランダムに選ぶには、緯度と高さをそれぞれランダムに選んでから座標を組み立てればよい:

vec3 random_unit_vector() {
  auto a = random_double(0, 2*pi);
  auto z = random_double(-1, 1);
  auto r = sqrt(1 - z*z);
  return vec3(r*cos(a), r*sin(a), z);
}

リスト 1.37 [vec3.h] random_unit_vector() 関数

現在使っている random_in_unit_sphere() 関数をこの random_unit_vector() 関数と取り換える:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0.001, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_unit_vector();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.38 [main.cc] 拡散レイの計算を変更した ray_color

次の画像が得られる:

拡散マテリアルを持った球が二つあるだけなので何が変わったのか分かりにくいが、二つの重要な違いに気が付くだろう:

変更後のレンダリングでは影が薄くなっている
変更後のレンダリングでは球が明るくなっている

レイがより一様に散乱するようになり、法線方向に散乱するレイが減ったのがこの原因である。つまり拡散マテリアルに入射したレイの中でカメラに向かうものの割合が増加した。また小さな球と大きな球に挟まれる部分に入射したレイが法線方向に反射して小さな球に当たる確率が減少するので、影は薄くなる。

拡散マテリアルの異なる定式化

拡散マテリアルとして最初に示したハック (単位球内のランダムな点を使うもの) が理想的なランバーティアン拡散マテリアルの近似として間違っていることが証明されるまでには長い時間がかかり、それまで誰も声を上げなかった。間違いが長い間残り続けたのは、間違いを正すのに次の二つが求められるためである:

確率分布が正しくないことを数学的に証明する。
\(\cos \phi\) という分布とレンダリング結果の正しさを納得する。

日常生活で目にする物体で完全な拡散マテリアルの性質を持つものはほとんどない。そのためそういった物体が理想的な環境でどう見えるかについて、私たちの直観はあまり役に立たない。

拡散マテリアルについて理解を深めるために、これまでのものより理解しやすく簡単な拡散レイの計算方法を示す。これまでに示した二つの方法はランダムなベクトルを生成していたが、このベクトルを法線で移動させる理由はあまり明らかでなかったかもしれない。

より理解しやすい計算方法とは、法線との角度に関係なく全ての方向に向かって一様にレイが散乱すると考えるものである。初期のレイトレーシングの論文はこの方法を使って拡散反射を計算していた (後になってランバーティアンが採用された)。

vec3 random_in_hemisphere(const vec3& normal) {
  vec3 in_unit_sphere = random_in_unit_sphere();
  if (dot(in_unit_sphere, normal) > 0.0)
    return in_unit_sphere; // in_unit_sphere は normal と同じ半球にある
  else
    return -in_unit_sphere;
}

リスト 1.39 [vec3.h] random_in_hemisphere() 関数

これを ray_color() 関数に組み込む:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0.001, infinity, rec)) {
    point3 target = rec.p + random_in_hemisphere(rec.normal);
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.40 [vec3.h] ray_color() 関数の変更部分

次の画像が得られる:

本を読み進めるとシーンはもっと複雑になる。そういったシーンをここで示した異なる拡散マテリアルを使ってレンダリングし、その結果を比較するとよい。興味深いシーンには多くの拡散マテリアルが含まれるから、異なる拡散マテリアルが持つシーン全体のライティングへの影響について多くのことが学べるだろう。

金属マテリアル

マテリアルを表す抽象クラス

異なるオブジェクトに異なるマテリアルを持たせようとすると、設計の変更が必要になる。一つの選択肢として、たくさんのパラメータを持つ一般的なマテリアルを用意して、マテリアルの種類に応じて使わないパラメータには \(0\) を設定する方法がある。これは悪くないアプローチだが、他にもマテリアルの振る舞いをカプセル化する抽象マテリアルクラスを作るという方法もある。私は後者の方法を気に入っている。今書いているプログラムでは、マテリアルは次の二つの処理を行う:

レイが散乱するか吸収されるかを判定する。
散乱するなら、散乱レイと減衰を求める。

ここから次の抽象クラスが導かれる:

#ifndef MATERIAL_H
#define MATERIAL_H

class material {
public:
  virtual ~material() {}
  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const = 0;
};

#endif

リスト 1.41 [material.h] material クラス

レイとオブジェクトの衝突を表すデータ構造

hit_record 構造体は scatter 関数に渡す変数が増えたときに関数の引数を増やさなくて済むように導入されている。好みの問題なので、引数を使ってもよい。hittable と material を定義するにはお互いがお互いを知っておく必要があり、一種の循環参照が生じている。C++ ではコンパイラに向かってクラスの存在を示しておけば問題は起きない。次のコードの class material; がそれに当たる。

#ifndef HITTABLE_H
#define HITTABLE_H

#include "rtweekend.h"
#include "ray.h"

class material;

struct hit_record {
  point3 p;
  vec3 normal;
  shared_ptr<material> mat_ptr;
  double t;
  bool front_face;

  inline void set_face_normal(const ray& r, const vec3& outward_normal) {
    front_face = dot(r.direction(), outward_normal) < 0;
    normal = front_face ? outward_normal : -outward_normal;
  }
};
...

リスト 1.42 [hittable.h] material を追加した hit_record

物体表面とレイの相互作用を処理するのが matrial::scatter 関数であり、この関数への引数はまとめて hit_record 構造体として表される。レイが物体 (例えば球) に当たると hit_record のマテリアルを表すポインタ mat_ptr に球の持つマテリアル (初期化時に main() で割り当てたもの) が代入される。hit_record が ray_color() に戻ると mat_ptr のメンバー関数が呼び出され、散乱レイが (その有無を含めて) 計算される。

実装では sphere クラスにマテリアルの参照を追加し、sphere::hit() 関数でこの参照を hit_record に追加する。ハイライトされた行に変更を示す:

class sphere: public hittable {
public:
  sphere() {}
  sphere(point3 cen, double r, shared_ptr<material> m)
    : center(cen), radius(r), mat_ptr(m) {}

  virtual bool hit(
    const ray& r, double tmin, double tmax, hit_record& rec
  ) const;

public:
  point3 center;
  double radius;
  shared_ptr<material> mat_ptr;
};

bool sphere::hit(
  const ray& r, double t_min, double t_max, hit_record& rec
) const {
  vec3 oc = r.origin() - center;
  auto a = r.direction().length_squared();
  auto half_b = dot(oc, r.direction());
  auto c = oc.length_squared() - radius*radius;
  auto discriminant = half_b*half_b - a*c;

  if (discriminant > 0) {
    auto root = sqrt(discriminant);
    auto temp = (-half_b - root)/a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      vec3 outward_normal = (rec.p - center) / radius;
      rec.set_face_normal(r, outward_normal);
      rec.mat_ptr = mat_ptr;
      return true;
    }
    temp = (-half_b + root) / a;
    if (temp < t_max && temp > t_min) {
      rec.t = temp;
      rec.p = r.at(rec.t);
      vec3 outward_normal = (rec.p - center) / radius;
      rec.set_face_normal(r, outward_normal);
      rec.mat_ptr = mat_ptr;
      return true;
    }
  }
  return false;
}

リスト 1.43 [sphere.h] マテリアルを追加したレイと球の衝突判定

ランバーティアンの実装

material を使って前節で実装したランバーティアン (拡散) マテリアルを実装する方法は二つある。一つはレイが必ず散乱してそのときの散乱が反射率 \(R\) だと考える方法で、もう一つはレイが確率 \(R\) で減衰なしに散乱し、それ以外のときは吸収されると考える方法である。どちらでも構わないし、二つを混ぜることもできる。前者の方法を実装した簡単なクラスを次に示す:

class lambertian : public material {
public:
  lambertian(const color& a) : albedo(a) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    vec3 scatter_direction = rec.normal + random_unit_vector();
    scattered = ray(rec.p, scatter_direction);
    attenuation = albedo;
    return true;
  }

public:
  color albedo;
};

リスト 1.44 [sphere.h] lambertian マテリアルクラス

なお適当な確率 p で減衰が albedo/p の散乱レイを生成してもこれと同じ挙動となる。

光の鏡面反射

滑らかな金属では、レイがランダムに散乱することはない。さて数学の時間だ: レイは金属鏡面でどのように反射するだろうか？ここではベクトルが私たちの友達になる:

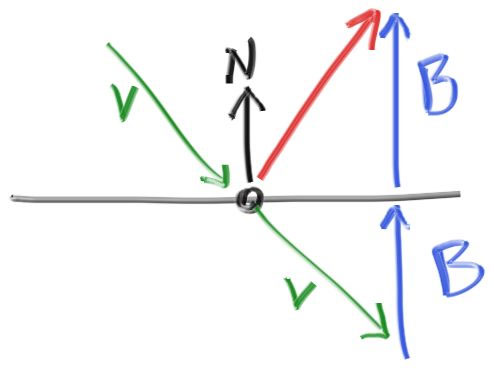
赤で示した反射レイは \(\mathbf{v} + 2\mathbf{b}\) と表される。今の実装では \(\textbf{n}\) は単位ベクトルだが、\(\textbf{v}\) はそうでない可能性がある。よって \(\textbf{b}\) の大きさは \(\mathbf{v} \cdot \mathbf{n}\) と表せる。また \(\textbf{v}\) は物体に向かうベクトルだから、マイナスが必要になる。以上より次のコードが得られる:

vec3 reflect(const vec3& v, const vec3& n) {
  return v - 2*dot(v,n)*n;
}

リスト 1.45 [vec3.h] vec3 の reflect 関数

金属マテリアルはこの公式を使ってレイを反射させる:

class metal : public material {
public:
  metal(const color& a) : albedo(a) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
    scattered = ray(rec.p, reflected);
    attenuation = albedo;
    return (dot(scattered.direction(), rec.normal) > 0);
  }

public:
  color albedo;
};

リスト 1.46 [material.h] metal クラスと反射レイの計算

material を使うよう ray_color() 関数を変更する必要がある:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0.001, infinity, rec)) {
    ray scattered;
    color attenuation;
    if (rec.mat_ptr->scatter(r, rec, attenuation, scattered))
      return attenuation * ray_color(scattered, world, depth-1);
    return color(0,0,0);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.47 [main.cc] 反射レイと減衰を使ったレイの色の計算

金属球を使ったシーン

シーンに金属球を追加しよう:

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);
  const int samples_per_pixel = 100;
  const int max_depth = 50;

  std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";


  hittable_list world;

  world.add(make_shared<sphere>(
    point3(0,0,-1), 0.5, make_shared<lambertian>(color(0.7, 0.3, 0.3))));
  world.add(make_shared<sphere>(
    point3(0,-100.5,-1), 100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
  world.add(make_shared<sphere>(
    point3(1,0,-1), 0.5, make_shared<metal>(color(.8,.6,.2))));
  world.add(make_shared<sphere>(
    point3(-1,0,-1), 0.5, make_shared<metal>(color(.8,.8,.8))));

  camera cam;

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(0, 0, 0);
      for (int s = 0; s < samples_per_pixel; ++s) {
        auto u = (i + random_double()) / (image_width-1);
        auto v = (j + random_double()) / (image_height-1);
        ray r = cam.get_ray(u, v);
        pixel_color += ray_color(r, world, max_depth);
      }
      write_color(std::cout, pixel_color, samples_per_pixel);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.48 [main.cc] 金属球を配置したシーン

レンダリングされる画像を示す:

ぼやけた反射

鏡面反射したレイの端点を中心とする小さな球を考えれば、反射レイの方向をランダムに変化させることができる:

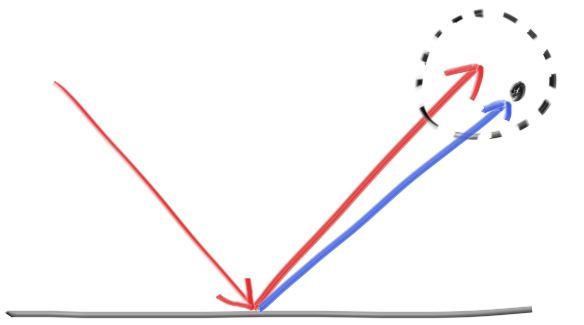
球が大きければそれだけ反射は大きくぼやける。この球の半径を「ぼやけ (fuzziness)」としてマテリアルのパラメータに追加するのが自然だろう (ぼやけが \(0\) なら反射は全くぶれない)。ただしここで、ぼやけが大きい表面にほぼ水平の角度で入射したレイが表面の下に散乱する可能性があることに注意が必要となる。こういったレイは表面に吸収されたとみなすことにする。

class metal : public material {
public:
  metal(const color& a, double f) : albedo(a), fuzz(f < 1 ? f : 1) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
    scattered = ray(rec.p, reflected + fuzz*random_in_unit_sphere());
    attenuation = albedo;
    return (dot(scattered.direction(), rec.normal) > 0);
  }

public:
  color albedo;
  double fuzz;
};

リスト 1.49 [material.h] fuzziness を追加した metal

ぼやけを \(0.3\) および \(1.0\) としたレンダリング結果を示す:

誘電体マテリアル

水・ガラス・ダイアモンドといった透明な材質を誘電体 (dielectric) と呼ぶ。こういった物体に衝突したレイは反射レイと屈折レイ (透過レイ) に分かれる。このレイトレーサーでは衝突ごとに反射と屈折をランダムに選び、反射レイと屈折レイのどちらか一方だけを散乱レイとして生成するものとする。

屈折

屈折レイのデバッグは本当に難しい。次の画像はこの本のために実際に書いたプログラムで得られたものだ。二つのガラス球が配置されたシーンをレンダリングしているのだが、これは正しいだろうか？

現実のガラス球も奇妙な見た目をしているが、この画像のように見えることはない。正しいガラス球の内部では上下が反転し、変な黒い環はできない。画像の中心周辺にレイを送れば、それだけで何かが間違っていると分かる (この方法が利用できることは多い)。また屈折レイをデバッグするときは、反射レイを無くして全てのレイを屈折させるようにするとよい。

スネルの法則

屈折はスネルの法則 (Snell's law) で表される: \[ \eta \cdot \sin\theta = \eta' \cdot \sin\theta' \] \(\theta\) と \(\theta'\) は法線からの角度であり、\(\eta\)エータと \(\eta'\)エータプライムは媒質の屈折率を表す (屈折率は空気なら \(1.0\), ガラスなら \(1.3–1.7\), ダイアモンドなら \(2.4\) 程度である)。屈折を表す図を示す:

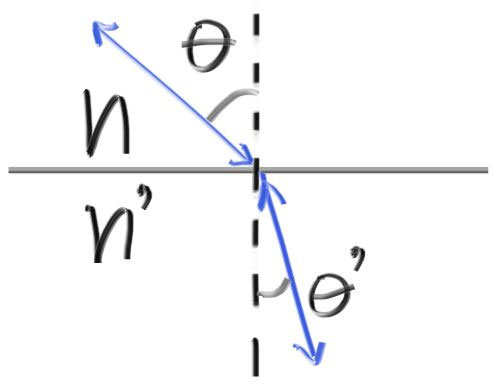
屈折後の角度 \(\sin \theta'\) は \[ \sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta \] と表せる。これを使って屈折後のレイのベクトルを求めよう。入射レイと屈折レイを \(\textbf{R},\ \) \(\textbf{R}'\) として、法線を \(\textbf{n}'\) とする (全て単位ベクトル)。\(\textbf{R}'\) を \(\textbf{n}'\) と平行な成分 \(R_{\parallel}\) と垂直な成分 \(R_{\bot}\) に分けると \[ \mathbf{R}' = \mathbf{R}'_{\parallel} + \mathbf{R}'_{\bot} \] が成り立つ。幾何的な関係を使って \(\mathbf{R}'_{\parallel}\) と \(\mathbf{R}'_{\bot}\) を求めると \[ \begin{aligned} \mathbf{R'}_{\parallel} & = \frac{\eta}{\eta'} (\mathbf{R} + \cos\theta \mathbf{n}) \\ \mathbf{R'}_{\bot} & = -\sqrt{1 - |\mathbf{R'}_{\parallel}|^2} \mathbf{n} \end{aligned} \] となる。導出は示さないが、可能なら自分で確認してみよ。これ以降この式の導出が必要になることはない。

さらに \(\cos\theta\) をベクトルで表す必要がある。よく知られているように、二つのベクトルの積はそれらがなす角度のコサインを使って表せる: \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta \] さらに \(\textbf{a}\) と \(\textbf{b}\) が単位ベクトルなら \[ \mathbf{a} \cdot \mathbf{b} = \cos\theta \] が成り立つ。

\(\textbf{R}\) と \(\textbf{n}\) は単位ベクトルだから、\(\mathbf{R}'_{\parallel}\) を既知の記号だけを使って表せる: \[ \mathbf{R'}_{\parallel} = \frac{\eta}{\eta'} (\mathbf{R} + (\mathbf{-R} \cdot \mathbf{n}) \mathbf{n}) \]

以上の考察を使えば \(\textbf{R}'\) を計算する関数が得られる:

vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {
  auto cos_theta = dot(-uv, n);
  vec3 r_out_parallel =  etai_over_etat * (uv + cos_theta*n);
  vec3 r_out_perp = -sqrt(1.0 - r_out_parallel.length_squared()) * n;
  return r_out_parallel + r_out_perp;
}

リスト 1.50 [vec3.h] refract 関数

この関数を使って常に屈折が起こる誘電体マテリアルを実装しよう:

class dielectric : public material {
public:
  dielectric(double ri) : ref_idx(ri) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    attenuation = color(1.0, 1.0, 1.0);
    double etai_over_etat;
    if (rec.front_face) {
      etai_over_etat = 1.0 / ref_idx;
    } else {
      etai_over_etat = ref_idx;
    }

    vec3 unit_direction = unit_vector(r_in.direction());
    vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
    scattered = ray(rec.p, refracted);
    return true;
  }

  double ref_idx;
};

リスト 1.51 [material.h] 常に屈折する dielectric マテリアル

この dielectric を使うと次の画像が得られる:

全反射

何かが明らかにおかしい。問題が起こっているのはレイが屈折率の高い媒質から屈折率の低い媒質に抜けていくときで、このときスネルの法則に解がなくなって屈折が起こらなくなる。スネルの法則によると \[ \sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta \] だから、ガラスの内部 (\(\eta = 1.5\)) から空気 (\(\eta' = 1.0\)) へレイが抜けるとき \[ \sin\theta' = \frac{1.5}{1.0} \cdot \sin\theta \] が成り立つ。\(\sin\theta'\) の値は \(1\) より大きくならないから、 \[ \frac{1.5}{1.0} \cdot \sin\theta > 1.0 \] のとき等式が意味を持たなくなり、解がなくなる。解がないとき屈折は起こらず、レイは反射する:

if (etai_over_etat * sin_theta > 1.0) {
  // 必ず反射する
  ...
}
else {
  // 反射または屈折する
  ...
}

リスト 1.52 [material.h] レイが屈折する可能性を判定する

条件 \(\dfrac{\eta}{\eta'} \sin \theta > 1\) が成り立つときに全ての光が反射されるこの現象を全反射 (total internal reflection) と呼ぶ ("internal" と付いているのは、光が媒質内から空気中に向かうときに起こることが多いためだ)。水中から水面を見上げると視界の端が鏡のように見えるのは全反射が起きるためである。

コード中で sin_theta を計算するときには、三角関数に関する恒等式 \[ \sin \theta = \sqrt{1 - \cos^{2} \theta} \] そして \[ \cos\theta = \mathbf{R} \cdot \mathbf{n} \] が利用できる。

double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if(etai_over_etat * sin_theta > 1.0) {
  // 必ず反射する
  ...
}
else {
  // 反射または屈折する
  ...
}

リスト 1.53 [material.h] レイが屈折する可能性を判定する

可能な場合に必ず屈折する誘電体マテリアルは次のように書ける:

class dielectric : public material {
public:
  dielectric(double ri) : ref_idx(ri) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    attenuation = color(1.0, 1.0, 1.0);
    double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);

    vec3 unit_direction = unit_vector(r_in.direction());
    double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
    double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
    if (etai_over_etat * sin_theta > 1.0 ) {
      vec3 reflected = reflect(unit_direction, rec.normal);
      scattered = ray(rec.p, reflected);
      return true;
    }

    vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
    scattered = ray(rec.p, refracted);
    return true;
  }

public:
  double ref_idx;
};

リスト 1.54 [material.h] 屈折を加えた dielectric クラス

減衰 (attenuation) は常に \(1\) である ──ガラス球は光を吸収しない。このマテリアルをシーンに追加しよう:

world.add(make_shared<sphere>(
  point3(0,0,-1), 0.5, make_shared<lambertian>(color(0.1, 0.2, 0.5))));
world.add(make_shared<sphere>(
  point3(0,-100.5,-1), 100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
world.add(make_shared<sphere>(
  point3(1,0,-1), 0.5, make_shared<metal>(color(.8, .6, .2), 0.0)));
world.add(make_shared<sphere>(
  point3(-1,0,-1), 0.5, make_shared<dielectric>(1.5)));

リスト 1.55 [main.cc] シーンに誘電体の球を加える

次の画像が得られる:

シュリックの近似

現実のガラスの反射率は角度によって異なる ──窓を水平に近い角度から見ると、まるで鏡のように見える。この現象を記述する複雑な数式もあるが、ほとんど誰もが次の近似を使っている。これは非常に簡単かつ正確な多項式近似であり、Christophe Schlick によって提案された:

double schlick(double cosine, double ref_idx) {
  auto r0 = (1-ref_idx) / (1+ref_idx);
  r0 = r0*r0;
  return r0 + (1-r0)*pow((1 - cosine),5);
}

リスト 1.56 [material.h] シュリックの近似

これで誘電体マテリアルが完成する:

class dielectric : public material {
public:
  dielectric(double ri) : ref_idx(ri) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
  ) const {
    attenuation = color(1.0, 1.0, 1.0);
    double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);

    vec3 unit_direction = unit_vector(r_in.direction());
    double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
    double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
    if (etai_over_etat * sin_theta > 1.0 ) {
      vec3 reflected = reflect(unit_direction, rec.normal);
      scattered = ray(rec.p, reflected);
      return true;
    }
    double reflect_prob = schlick(cos_theta, etai_over_etat);
    if (random_double() < reflect_prob) {
      vec3 reflected = reflect(unit_direction, rec.normal);
      scattered = ray(rec.p, reflected);
      return true;
    }
    vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
    scattered = ray(rec.p, refracted);
    return true;
  }

public:
  double ref_idx;
};

リスト 1.57 [material.h] 完成した誘電体マテリアル

中空ガラス球のモデリング

誘電体球の半径を負に設定すると、ジオメトリは変わらず法線だけが反転する。これを使うと中空の球を作ることができる:

world.add(make_shared<sphere>(
  point3( 0,      0, -1),   0.5, make_shared<lambertian>(color(0.1, 0.2, 0.5))));
world.add(make_shared<sphere>(
  point3( 0, -100.5, -1),   100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
world.add(make_shared<sphere>(
  point3( 1,      0, -1),   0.5, make_shared<metal>(color(0.8, 0.6, 0.2), 0.3)));
world.add(make_shared<sphere>(
  point3(-1,      0, -1),   0.5, make_shared<dielectric>(1.5)));
world.add(make_shared<sphere>(
  point3(-1,      0, -1), -0.45, make_shared<dielectric>(1.5)));

リスト 1.58 [main.cc] シーンに中空のガラス球を追加する

次の画像が得られる:

カメラの移動

誘電体と並んでカメラもデバッグが難しい。私はカメラを実装するとき必ずインクリメンタルに進めることにしている。まずは視野角 (field of view, fov) を実装しよう。私たちがレンダリングしている画像は正方形でないから、視野角は垂直または水平方向の角度で指定できる。私は必ず垂直方向の角度で指定する。それから視野角は弧度法で表し、コンストラクタでラジアンに変換する ──この辺は好みの問題だ。

カメラの視野

これまでのプログラムでは、原点にあるカメラから放たれるレイは平面 \(z = -1\) 上の点に向かっていた。レイが向かう点が \(z = -2\) のような他の平面上にあったとしても、平面までの距離と平面の高さの比が一定であればレイは変化しない。この平面の高さは下図の \(h\) である:

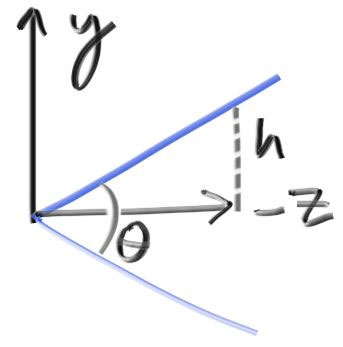
つまり \(h = \tan \dfrac{\theta}{2} \) が成り立つ。これをカメラのコードに組み込むと次のようになる:

class camera {
public:
  camera(
    double vfov, // 垂直方向の視野角 (弧度法)
    double aspect_ratio
  ) {
    auto theta = degrees_to_radians(vfov);
    auto h = tan(theta/2);
    auto viewport_height = 2.0 * h;
    auto viewport_width = aspect_ratio * viewport_height;

    auto focal_length = 1.0;

    origin = point3(0, 0, 0);
    horizontal = vec3(viewport_width, 0.0, 0.0);
    vertical = vec3(0.0, viewport_height, 0.0);
    lower_left_corner =
      origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
  }

  ray get_ray(double u, double v) const {
    return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
  }

private:
  point3 origin;
  point3 lower_left_corner;
  vec3 horizontal;
  vec3 vertical;
};

リスト 1.59 [camera.h] 視野角 (fov) が調節可能なカメラ

カメラを cam(90, double(image_width)/image_height) として、次の二つの球をシーンに加える:

auto R = cos(pi/4);
hittable_list world;
world.add(make_shared<sphere>(
  point3(-R, 0, -1), R, make_shared<lambertian>(color(0, 0, 1))));
world.add(make_shared<sphere>(
  point3( R, 0, -1), R, make_shared<lambertian>(color(1, 0, 0))));

リスト 1.60 [main.cc] 広角なカメラを使うシーン

レンダリングすると次の画像が得られる:

カメラの移動と回転

視点を自由に動かすために、まず視点を定める点の名前を定めよう。カメラの位置を lookfrom として、注視する点を lookat とする (最後まで実装できたら、こうする代わりに視線の方向を定義してもよい)。

さらにカメラのロール (横方向の傾き) を指定する必要がある。これは lookat と lookfrom を結ぶ軸に関する回転であり、人間で言えば同じものを見つめながら鼻を中心に顔を回転させるのに相当する。ここで必要なのはカメラの「上」を指すベクトルを指定する方法である。この「上」ベクトルはカメラを通って視線ベクトルと垂直な平面上に存在する。

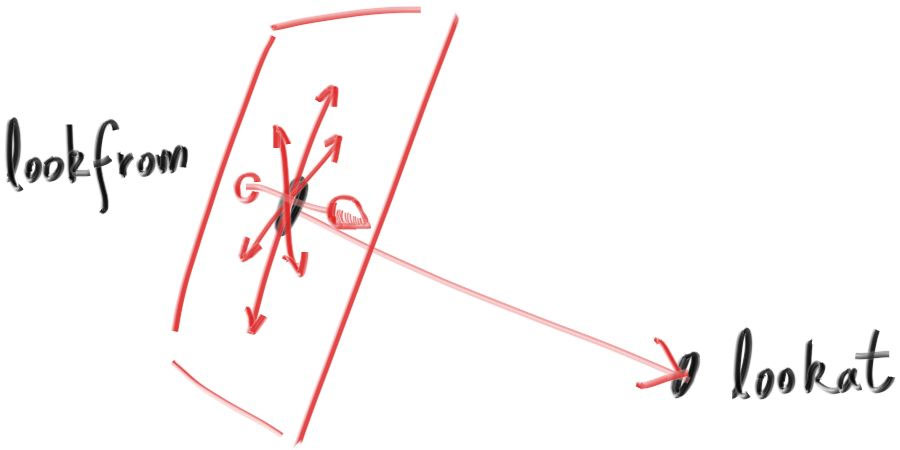
上ベクトルがこの平面上になくても射影すればよいので、上ベクトルは任意のベクトルで表せる。よく使われる名前を借りて、このベクトルを vup (view up) と呼ぶことにする。lookfrom, lookat, vup の三つのベクトルがあれば、何度か外積を使うことでカメラの位置と向きを表す正規直交基底 \((u, v, w)\) を計算できる。

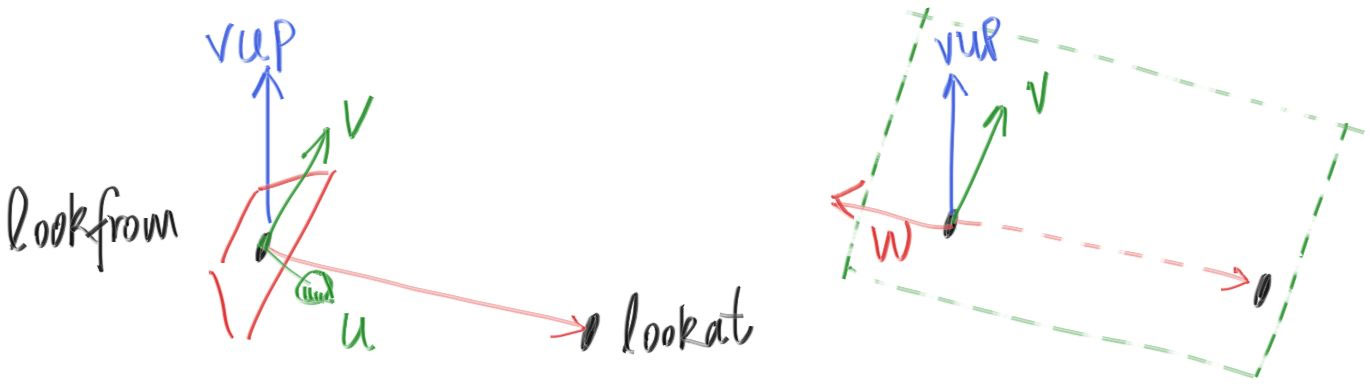
vup, v, w は全て同一平面上に存在する。また以前の固定されたカメラが \(-\text{Z}\) 方向を向いていたのと同様に、このカメラは \(-\text{w}\) 方向を向く。それから vup にはシーン全体の上方向を表す \((0, 1, 0)\) を使うことができる。絶対にこうしなければならない理由はないが、こうしておくとカメラが常に水平になるので便利である。カメラの角度で遊び始めるまではこうしておくことを勧める。

class camera {
public:
  camera(
    point3 lookfrom,
    point3 lookat,
    vec3   vup,
    double vfov, // 垂直方向の視野角 (弧度法)
    double aspect_ratio
  ) {
    auto theta = degrees_to_radians(vfov);
    auto h = tan(theta/2);
    auto viewport_height = 2.0 * h;
    auto viewport_width = aspect_ratio * viewport_height;


    auto w = unit_vector(lookfrom - lookat);
    auto u = unit_vector(cross(vup, w));
    auto v = cross(w, u);

    origin = lookfrom;
    horizontal = viewport_width * u;
    vertical = viewport_height * v;
    lower_left_corner = origin - horizontal/2 - vertical/2 - w;
  }

  ray get_ray(double u, double v) const {
    return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
  }

private:
  point3 origin;
  point3 lower_left_corner;
  vec3 horizontal;
  vec3 vertical;
};

リスト 1.61 [camera.h] 移動と回転が可能なカメラ

これにより視点の変更が可能になる:

camera cam(point3(-2,2,1), point3(0,0,-1), vec3(0,1,0), 90, aspect_ratio);

リスト 1.62 [main.cc] 視点のパラメータ

レンダリングすると次の画像となる:

視野角を変えてみよう:

camera cam(point3(-2,2,1), point3(0,0,-1), vup, 20, aspect_ratio);

リスト 1.63 [main.cc] 視野角の変更

こうなる:

焦点ぼけ

最後に焦点ぼけ (defocus blur) を実装する。普通はこれを被写体深度差 (depth of field) と呼ぶので、「焦点ぼけ」という言葉は友達とだけ使うようにしよう。

現実のカメラで焦点ぼけが生じるのは、光を集めるために (ピンホールではなく) 大きな穴を使っているためである。この穴をそのまま使うと全ての像がぼやけるが、この穴にレンズを設置すれば特定の距離にある平面上の物体にフォーカスを合わせることができる。言い換えると、この距離にある点から放たれレンズを通る任意のレイは画像センサー上の一点に集まる。

フォーカスの合う平面と射影点 (レンズ) の距離を集束距離 (focus distance) と呼ぶ。集束距離は焦点距離 (focal length) とは異なる。焦点距離は射影点から画像平面までの距離を表す。

現実のカメラはレンズとフィルム (センサー) の距離を変化させることで集束距離を調節する。カメラのピントを変えたときにレンズが動くのはこのためである (スマートフォンのカメラでは逆にセンサーが動く)。写真を撮るとき実際に光を集めるレンズの大きさを口径 (apature) と呼ぶ。物理的なカメラでは光が足りないときに口径を大きくするが、そうすると焦点ぼけが大きくなる。私たちが作っている仮想的なカメラには完璧なセンサーがあるので、光が足りなくなることはない。つまり口径を考えるのは焦点ぼけが欲しいときだけである。

薄レンズ近似

現実のカメラではいくつものレンズが複雑に組み合わさっている。センサー・レンズ・口径を正確にシミュレートすることも当然できる。そうすればレイをどこに放つべきかが分かり、計算結果を反転させれば画像が得られる (像はフィルム上に反転して現れる)。しかしグラフィックスプログラマーはたいていの場合次に示す薄いレンズを使った単純な近似 (薄レンズ近似, thin lens approximation) を使う:

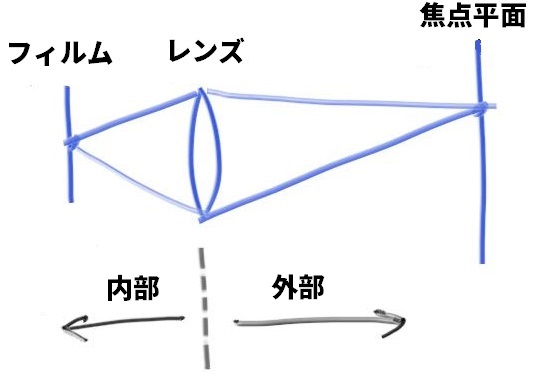
さらにカメラの内部は何もシミュレートする必要がない。カメラ外部の画像をレンダリングしているのだから、カメラの内部を考えてもコードが不必要に複雑になるだけだ。その代わりレイをレンズから放ち、レイの目標を完全にフォーカスが合う焦点平面 (focus_dist だけ離れた平面) 上の点とする。

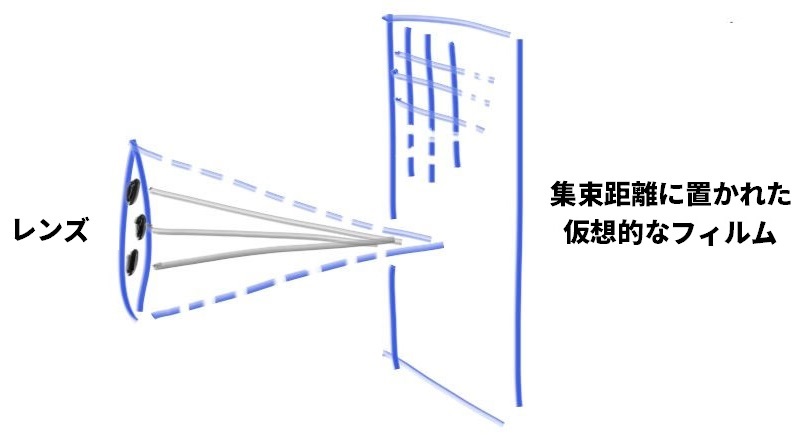
サンプルレイの生成

口径を考えない場合には全てのレイが lookfrom から放たれる。焦点ぼけを再現するには、レイを lookfrom を中心とした円盤から放てばよい。この円盤の半径を大きくすると、それだけ焦点ぼけも大きくなる。これまでに実装したカメラでは全てのレイが円盤の中心を始点とするので、この焦点円盤の半径が \(0\) だとみなせる (つまり焦点ぼけは存在しない)。

vec3 random_in_unit_disk() {
  while (true) {
    auto p = vec3(random_double(-1,1), random_double(-1,1), 0);
    if (p.length_squared() >= 1) continue;
    return p;
  }
}

リスト 1.64 [vec3.h] 単位円盤上にランダムな点を生成する関数

class camera {
public:
  camera(
    point3 lookfrom,
    point3 lookat,
    vec3   vup,
    double vfov,  // 垂直方向の視野角 (弧度法)
    double aspect_ratio,
    double aperture,
    double focus_dist
  ) {
    auto theta = degrees_to_radians(vfov);
    auto h = tan(theta/2);
    auto viewport_height = 2.0 * h;
    auto viewport_width = aspect_ratio * viewport_height;

    w = unit_vector(lookfrom - lookat);
    u = unit_vector(cross(vup, w));
    v = cross(w, u);

    origin = lookfrom;
    horizontal = focus_dist * viewport_width * u;
    vertical = focus_dist * viewport_height * v;
    lower_left_corner = origin - horizontal/2 - vertical/2 - focus_dist*w;

    lens_radius = aperture / 2;
  }

  ray get_ray(double s, double t) const {
    vec3 rd = lens_radius * random_in_unit_disk();
    vec3 offset = u * rd.x() + v * rd.y();

    return ray(
      origin + offset,
      lower_left_corner + s*horizontal + t*vertical - origin - offset
    );
  }

private:
  point3 origin;
  point3 lower_left_corner;
  vec3 horizontal;
  vec3 vertical;
  vec3 u, v, w;
  double lens_radius;
};

リスト 1.65 [camera.h] 被写体深度差 (pov) を設定可能なカメラ

大口径の画像を生成しよう:

point3 lookfrom(3,3,2);
point3 lookat(0,0,-1);
vec3 vup(0,1,0);
auto dist_to_focus = (lookfrom-lookat).length();
auto aperture = 2.0;

camera cam(lookfrom, lookat, vup, 20, aspect_ratio, aperture, dist_to_focus);

リスト 1.66 [camera.h] カメラのパラメータ

次の画像が得られる:

次は？

最後のシーン

この本のカバーにある画像を生成しよう ──ランダムな球をたくさん配置する:

hittable_list random_scene() {
  hittable_list world;

  auto ground_material = make_shared<lambertian>(color(0.5, 0.5, 0.5));
  world.add(make_shared<sphere>(point3(0,-1000,0), 1000, ground_material));

  for (int a = -11; a < 11; a++) {
    for (int b = -11; b < 11; b++) {
      auto choose_mat = random_double();
      point3 center(a + 0.9*random_double(), 0.2, b + 0.9*random_double());

      if ((center - vec3(4, 0.2, 0)).length() > 0.9) {
        shared_ptr<material> sphere_material;
        if (choose_mat < 0.8) {
          // diffuse
          auto albedo = color::random() * color::random();
          sphere_material = make_shared<lambertian>(albedo);
          world.add(make_shared<sphere>(center, 0.2, sphere_material));
        } else if (choose_mat < 0.95) {
          // metal
          auto albedo = color::random(0.5, 1);
          auto fuzz = random_double(0, 0.5);
          sphere_material = make_shared<metal>(albedo, fuzz);
          world.add(make_shared<sphere>(center, 0.2, sphere_material));
        } else {
          // glass
          sphere_material = make_shared<dielectric>(1.5);
          world.add(make_shared<sphere>(center, 0.2, sphere_material));
        }
      }
    }
  }

  auto material1 = make_shared<dielectric>(1.5);
  world.add(make_shared<sphere>(point3(0, 1, 0), 1.0, material1));
  auto material2 = make_shared<lambertian>(color(0.4, 0.2, 0.1));
  world.add(make_shared<sphere>(point3(-4, 1, 0), 1.0, material2));
  auto material3 = make_shared<metal>(color(0.7, 0.6, 0.5), 0.0);
  world.add(make_shared<sphere>(point3(4, 1, 0), 1.0, material3));

  return world;
}

int main() {
  ...
  auto world = random_scene();

  point3 lookfrom(13,2,3);
  point3 lookat(0,0,0);
  vec3 vup(0,1,0);
  auto dist_to_focus = 10.0;
  auto aperture = 0.1;
  camera cam(lookfrom, lookat, vup, 20, aspect_ratio, aperture, dist_to_focus);
  ...
}

リスト 1.67 [main.cc] 最後のシーン

次の画像が得られる:

ガラス球に影が落ちておらず浮いて見えることに気が付いたかもしれない。これはバグではない ──ガラス球を日常生活で目にすることはあまりないと思うが、実際に見ると変な感じがする。特に曇りの日に見ると、本当に浮かんで見える。ガラス球と大きな球に挟まれる点に達したレイは上にあるガラス球に遮られることなく空に到達できるので、ガラス球の下に影はできない。

次のステップ

これでクールなレイトレーサーの完成だ！次は何をしようか？

ライト ── シャドウレイを光源に向けて放って陽に影を付けることもできるし、オブジェクトを発光させて陰に影を付けることもできる。オブジェクトを発光させる場合には、発光しているオブジェクトに多くの散乱レイを放ってから重みを減らして調整する処理をすると効率良く計算できる。私は後者のアプローチを気に入っているマイノリティである。
三角形 ── 多くのクールなモデルは三角形から構成される。モデルの I/O は骨が折れる作業で、ほとんど全員が他人のコードに頼っている。
サーフェステクスチャ ── 壁紙のように画像を張り付ける機能である。実装はとても簡単で、勉強になる。
ソリッドテクスチャ ── Ken Perlin がコードをオンラインに示している。Andrew Kensler のブログには非常にクールな情報がある。
ボリュームレンダリング ── クールな機能だが、ソフトウェアとしてのレンダラのアーキテクチャが試される。ボリュームに hittable のインターフェースを持たせ、密度に応じて交点を確率的に計算するというのが私がよく使うアプローチだ。レンダリングのコードはボリュームが存在していることさえ知る必要がない。
並列化 ── 同じコードを異なるランダムシードを使って \(N\) 個のコアで一つずつ実行し、生成される \(N\) 個の画像の平均を計算する方法がある。平均の計算では \(N/2\) 個の組から \(N/4\) 個の画像を得る階層的な方法が利用できる。このように並列化を行うと、コアが数千個であってもほぼそのまま動作する。

楽しんで！クールな画像ができたらぜひ私に見せてほしい！

謝辞

初稿

Dave Hart
Jean Buckley

ウェブリリース

Berna Kabadayı
Lorenzo Mancini
Lori Whippler Hollasch
Ronald Wotzlaw

訂正・改善

Aaryaman Vasishta
Andrew Kensler
Apoorva Joshi
Aras Pranckevičius
Becker
Ben Kerl
Benjamin Summerton
Bennett Hardwick
Dan Drummond
David Chambers
David Hart
Eric Haines
Fabio Sancinetti
Filipe Scur
Frank He
Gerrit Wessendorf
Grue Debry
Ingo Wald
Jason Stone
Jean Buckley
Joey Cho
Lorenzo Mancini
Marcus Ottosson
Matthew Heimlich
Nakata Daisuke
Paul Melis
Phil Cristensen
Ronald Wotzlaw
Shaun P. Lee
Tatsuya Ogawa
Thiago Ize
Vahan Sosoyan
ZeHao Chen

ツール

図の作成に利用した Limnu のチームに感謝する。

このシリーズ³は Morgan McGuire による素晴らしい無料ライブラリ Markdeep を使って執筆された。ブラウザからソースを閲覧すれば、どのように書かれたかを確認できる。

訳注: Computer Graphics: Principles and Practice の第一版には邦訳 (コンピュータグラフィックス理論と実践, 佐藤義雄監訳, オーム社) がある。他の本に邦訳はない。^[return]
訳注: 「アクネ (acne)」は「にきび」のこと。^[return]
訳注: 英語版のこと。^[return]

週末レイトレーシング 第一週 (翻訳)

はじめに

画像の出力

PPM フォーマット

画像ファイルの作成

進捗インジケータの追加

vec3 クラス

vec3 の変数とメソッド

vec3 のユーティリティ関数

色に関するユーティリティ関数

レイ・簡単なカメラ・背景

レイを表すクラス

レイの射出

球のレンダリング

レイと球の衝突判定

最初のレイトレーシング画像

法線と複数オブジェクト

法線を使ったシェーディング

レイと球の衝突判定の簡略化

レイが衝突するオブジェクトの抽象化

法線の向き

オブジェクトのリスト

C++ に特有の機能

数学定数とユーティリティ関数

アンチエイリアシング

乱数関数

複数のサンプルを使ったピクセルの描画

拡散マテリアル

単純な拡散マテリアル

子レイの数を制限する

ガンマ補正による明るさの調整

シャドウアクネを消す

完全なランバート反射

拡散マテリアルの異なる定式化

金属マテリアル

マテリアルを表す抽象クラス

レイとオブジェクトの衝突を表すデータ構造

ランバーティアンの実装

光の鏡面反射

金属球を使ったシーン

ぼやけた反射

誘電体マテリアル

屈折

スネルの法則

全反射

シュリックの近似

中空ガラス球のモデリング

カメラの移動

カメラの視野

カメラの移動と回転

焦点ぼけ

薄レンズ近似

サンプルレイの生成

次は？

最後のシーン

次のステップ

謝辞

初稿

ウェブリリース

訂正・改善

ツール

週末レイトレーシング第一週 (翻訳)

`vec3` クラス

`vec3` の変数とメソッド

`vec3` のユーティリティ関数