ランダムな方向の生成
まず何らかの分布に沿った方向 (単位球上の点) をランダムに生成する方法を見つけよう。簡単のため \(z\) 軸を法線方向として、\(\theta\) を法線から測った角度とする。軸を回転させる方法は次節で説明する。考える分布は \(z\) 軸周りの回転に関して対称な分布だけとする。このとき \(p(\text{direction}) = f(\theta)\) が成り立つ。大学レベルの微積分を学んだことがあるなら、球座標で \(dA = \sin(\theta) \cdot d\theta \cdot d\phi\) が成り立つことを知っているだろう。もし学んだことがないなら、この等式を受け入れた上で次に進んでほしい。将来大学で微積分の講義を取れば理解できる。
方向を引数に取る PDF \(p(\text{direction}) = f(\theta)\) が与えられたとして、\(\theta\) および \(\phi\) に関する一次元の PDF をそれぞれ \(a(\phi)\), \(b(\theta)\) とする。このとき \[ \begin{aligned} a(\phi) & = \frac{1}{2\pi} \quad ({\footnotesize \text{一定}}) \\ b(\theta) & = 2\pi f(\theta)\sin \theta \end{aligned} \] が成り立つ。
一次元モンテカルロ積分で説明したように、\([0, 1]\) の一様乱数 \(r_{1}\) に対して \[ r_1 = \int_{0}^{\phi} a(t)\, dt = \int_{0}^{\phi} \frac{1}{2\pi}\, dt = \frac{\phi}{2\pi} \] が成り立つとき、\(r_{1}\) の PDF は \(a(\phi) = 1/2\pi\) となる。\(\phi\) について解けば \[ \phi = 2 \pi \cdot r_1 \] を得る。
同様に \(r_{2}\) を \([0, 1]\) の一様乱数とすれば、\(\theta\) の PDF が \(b(\theta) = 2\pi f(\theta) \sin \theta\) なら \[ r_2 = \int_{0}^{\theta} 2 \pi f(t) \sin t\, dt \] が成り立つ。ここで \(t\) はダミー変数を表す。\(f\) として異なる関数をいくつか考えよう。まず球上に一様な確率密度を考える。単位球の表面積は \(4\pi\) だから、一様分布では \(p(\text{direction}) = 1/4\pi\) となる。よって \[ \begin{aligned} r_2 & = \int_{0}^{\theta} 2 \pi \frac{1}{4\pi} \sin t \,dt \\ & = \int_{0}^{\theta} \frac{1}{2} \sin t \,dt \\ & = \frac{-\cos\theta}{2} - \frac{-\cos0}{2} \\ & = \frac{1 - \cos\theta}{2} \end{aligned} \] であり、\(\cos\theta\) について解けば \[ \cos(\theta) = 1 - 2 r_2 \] を得る。\(\theta\) より先に \(\cos \theta\) が求まる場合が多いから、この式を \(\theta\) について解く必要はない。\(\arccos\) が呼び出されるのも避けたい。
方向 \((\theta, \phi)\) に向かう単位ベクトルを生成するには、次の式を使ってデカルト座標系に変換する必要がある: \[ \begin{aligned} x & = \cos\phi \cdot \sin\theta \\ y & = \sin\phi \cdot \sin\theta \\ z & = \cos\theta \end{aligned} \] これと恒等式 \(\cos^{2} x + \sin^{2} x = 1\) を使えば、二つの一様乱数 \(r_{1}, r_{2}\) を使った表現が求まる: \[ \begin{aligned} x & = \cos(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} \\ y & = \sin(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} \\ z & = 1 - 2 r_2 \end{aligned} \] \((1 - 2 r_2)^2 = 1 - 4r_2 + 4r_2^2\) を使って簡略化すれば \[ \begin{aligned} x & = \cos(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} \\ y & = \sin(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} \\ z & = 1 - 2 r_2 \end{aligned} \] となる。
この式を使って点を生成しよう:
int main() {
for (int i = 0; i < 200; i++) {
auto r1 = random_double();
auto r2 = random_double();
auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
auto z = 1 - 2*r2;
std::cout << x << " " << y << " " << z << '\n';
}
}
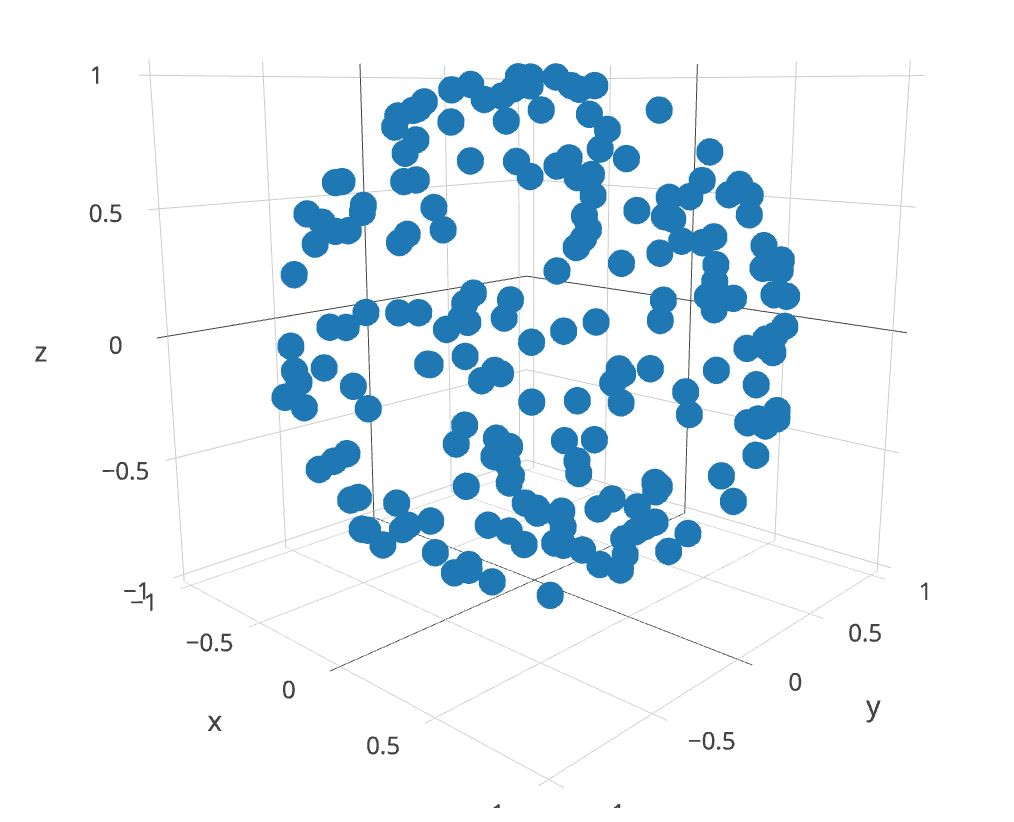
sphere_plot.cc] 単位球上の一様ランダムな点
plotly (三次元散布図のプロットをサポートする優れたサイト) を使えば、データを無料でプロットできる1。plot.ly では図を回転できるので、本当に一様に見えるかどうかを確認するとよい。
半球上の一様サンプリング
次は半球上の一様サンプリングを導出しよう。半球に渡って一様な密度関数は \(p(\text{direction}) = 1/2\pi\) だから、上で示した関係の定数部分が変わって \[ \cos \theta = 1 - r_2 \] となる。確認しておくと、左辺の \(\cos \theta\) は \(1\) から \(0\) の値を取り、このとき \(\theta\) は \(0\) から \(\pi/2\) の値を取るので矛盾はない。これを使って \(\cos^{3} \theta\) の半球に関する積分を計算しよう (\(\cos^{3} \theta\) は積分が解析的に計算できる適当な関数として選んだ)。手で積分を行うと \[ \begin{aligned} \int \cos^3 \theta dA & = \int_{0}^{2 \pi} \int_{0}^{\pi /2} \cos^3 \theta \sin \theta\, d\theta d\phi \\ & = 2 \pi \int_{0}^{\pi/2} \cos^3 \theta \sin \theta \, d\theta = \frac{\pi}{2} \end{aligned} \] となる。
この積分を重点サンプリングを使ったモンテカルロ積分で求める。\(p(\text{direction}) = 1/2\pi\) だから、平均すべき値は \(f/p = \cos^3 \theta / (1/2\pi)\) である。この正しさを確かめるプログラムを示す:
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto r1 = random_double();
auto r2 = random_double();
auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
auto z = 1 - r2;
sum += z*z*z / (1.0/(2.0*pi));
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "Pi/2 = " << pi/2 << '\n';
std::cout << "Estimate = " << sum/N << '\n';
}
cos_cubed.cc] \(\cos^{3} x\) の積分
次は \(p(\text{directions}) = \cos \theta / \pi\) となる方向を生成する方法を考える。これまでと同様に考えれば \[ r_2 = \int_{0}^{\theta} 2 \pi \frac{\cos(t)}{\pi} \sin t \, d\theta = 1 - \cos^2 \theta \] だから、 \[ \cos \theta = \sqrt{1 - r_2} \] となる。簡単な変形により次を得る: \[ \begin{aligned} z & = \cos\theta = \sqrt{1 - r_2} \\ x & = \cos\phi \sin\theta = \cos(2 \pi r_1) \sqrt{1 - z^2} = \cos(2 \pi r_1) \sqrt{r_2} \\ y & = \sin\phi \sin\theta = \sin(2 \pi r_1) \sqrt{1 - z^2} = \sin(2 \pi r_1) \sqrt{r_2} \end{aligned} \]
このランダムなベクトル \((x, y, z)\) を生成する関数を作っておく:
#include "rtweekend.h"
#include <iostream>
#include <math.h>
inline vec3 random_cosine_direction() {
auto r1 = random_double();
auto r2 = random_double();
auto z = sqrt(1-r2);
auto phi = 2*pi*r1;
auto x = cos(phi)*sqrt(r2);
auto y = sin(phi)*sqrt(r2);
return vec3(x, y, z);
}
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto v = random_cosine_direction();
sum += v.z()*v.z()*v.z() / (v.z()/pi);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "Pi/2 = " << pi/2 << '\n';
std::cout << "Estimate = " << sum/N << '\n';
}
cos_density.cc] コサイン密度関数を使った積分
この他の密度関数は後で必要になったときに考える。次節ではランダムなベクトルを物体表面の法線ベクトルの方向に傾ける方法を説明する。
-
訳注: ブラウザから使うにはアカウント登録が必要。jupyter notebook などを自分で用意すればアカウント登録無しに使える。[return]