直接的なライトのサンプリング

ほぼ一様に方向をサンプルする方法の問題は、ライトが存在する方向と他の重要でない方向が同程度にしかサンプルされないことである。シャドウレイを使って直接光の計算を特別扱いすることもできるが、ここではライトのある方向へ多くレイを放つようにする。ここで実装するアーキテクチャは後で任意の方向へレイを多く送れるようにするのに使われる。

ライトに向かうランダムな方向を選ぶのは非常に簡単で、ライト上の点をランダムに選び、その点に向かう方向を選べばよい。ただモンテカルロ積分を行うには、その方向の PDF \(p(\text{direction})\) を知る必要がある。PDF はいくつだろうか？

ライトの PDF

面積 \(A\) のライト上の点を一様ランダムに選択すると、ライト上の任意の点の PDF は \(1/A\) となる。方向を定義する単位球上におけるこのライトの面積を求めよう。幸い、単純な対応関係が存在する。

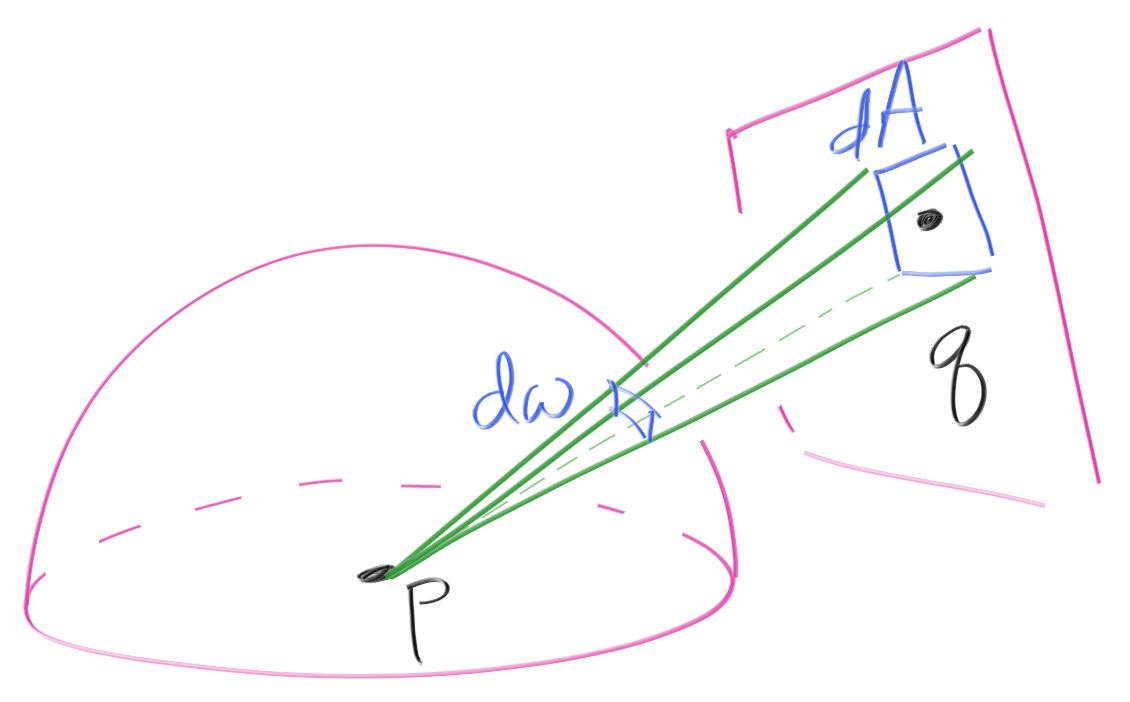
ライト上に小面積 \(dA\) を取り、その内部の点を適当に \(q\) とする。このとき一様ランダムに選択したライト上の点がこの小面積内にある確率は \(dA/A\) である。また求めようとしている PDF \(p(\text{direction})\) において単位球上の小面積 \(dw\) をサンプルする確率は \(p(\text{direction}) \cdot dw\) と表せる。さらに \(dw\) と \(dA\) の間には次の幾何学的な関係がある: \[ dw = \frac{dA \cdot \cos \alpha}{\text{distance}^2(p,q)} \] ここで \(\alpha\) は \(\text{direction}\) とライトの法線がなす角度を表す。\(dw\) と \(dA\) から点が選ばれる確率が同じだから \[ p(\text{direction}) \cdot dw = p(\text{direction}) \cdot \frac{dA \cdot \cos \alpha}{\text{distance}^2(p,q)} = \frac{dA}{A} \] つまり \[ p(\text{direction}) = \frac{\text{distance}^2(p,q)}{\cos \alpha \cdot A} \] が成り立つ。

ライトのサンプリング

ray_color 関数にライトのサンプリングを追加しよう。まずは数式と考え方の正しさを確認するために、ライトのサンプリングを関数の中にハードコードする:

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(rec.u, rec.v, rec.p);
  double pdf;
  color albedo;
  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf))
    return emitted;

  auto on_light = vec3(random_double(213,343), 554, random_double(227,332));
  auto to_light = on_light - rec.p;
  auto distance_squared = to_light.length_squared();
  to_light = unit_vector(to_light);

  if (dot(to_light, rec.normal) < 0)
    return emitted;

  double light_area = (343-213)*(332-227);
  auto light_cosine = fabs(to_light.y());
  if (light_cosine < 0.000001)
    return emitted;

  pdf = distance_squared / (light_cosine * light_area);
  scattered = ray(rec.p, to_light, r.time());

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1) / pdf;
}

リスト 3.20 [main.cc] ライトだけをサンプルする ray_color 関数

\(10\) サンプル/ピクセルでレンダリングすると次の画像が得られる:

これは光源だけをサンプルして得られる画像であり、正しく動いているように見える。

ライトの向き

天井のライト付近にあるノイズのような白点は、ライトが両面を照らしていてライトと天井の間に隙間があるために生じている。ライトは下方向だけを照らすのが正しいだろうから、diffuse_light のメンバー関数 emitted の引数に hit_record を追加してこれを処理する:

virtual color emitted(
  const hit_record& rec,
  double u, double v,
  const point3& p
) const {
  if (rec.front_face)
    return emit->value(u, v, p);
  else
    return color(0,0,0);
}

リスト 3.21 [material.h] 向きを考慮した material::emitted 関数

それからライトを反転させて法線が \(-y\) 方向を向くようにする必要もある。このために任意の hittable から法線が反転させる flip_face を作成する:

class flip_face : public hittable {
public:
  flip_face(shared_ptr<hittable> p) : ptr(p) {}

  virtual bool hit(
    const ray& r, double t_min, double t_max, hit_record& rec
  ) const {
    if (!ptr->hit(r, t_min, t_max, rec))
      return false;

    rec.front_face = !rec.front_face;
    return true;
  }

  virtual bool bounding_box(double t0, double t1, aabb& output_box) const {
    return ptr->bounding_box(t0, t1, output_box);
  }

public:
  shared_ptr<hittable> ptr;
}

リスト 3.21a [hittable.h] flip_face クラス

これを使ってライトを反転させる:

hittable_list cornell_box(camera& cam, double aspect) {
  ...
  world.add(
    make_shared<flip_face>(make_shared<xz_rect>(213, 343, 227, 332, 554, light))
  );
  ...
}

リスト 3.21b [main.h] コーネルボックスのライトの向きを反転させる

次の画像が得られる: