ボリュームレンダリング

レイトレーサーにぜひ追加したいのがフォグ (煙・霧) だ。これはボリューム (volume) あるいは関与媒質 (participating media) とも呼ばれる。またオブジェクト内部の濃い霧として表面下散乱 (subsuraface scattering) も追加しておきたい。こういった概念は物体の表面と大きく異なる代物なので、普通に実装するとソフトウェアのアーキテクチャがうんと複雑になる。しかしここでは、ボリュームをランダムな表面とみなすテクニックが使える。つまり煙が存在する領域を確率的に衝突する表面を持った物体で置き換えるのである。どういうことかはコードを見ればより理解できるだろう。

定数密度媒質

ここでは密度が定数の媒質だけを考える。この媒質中を進むレイは途中で散乱する可能性もあるし、散乱せずに突き抜ける可能性もある (下図)。媒質の透明度が高いと (煙が薄いと) 図中央のような突き抜けるレイが増える。またレイが媒質中を通る長さもレイが散乱する可能性に影響する。

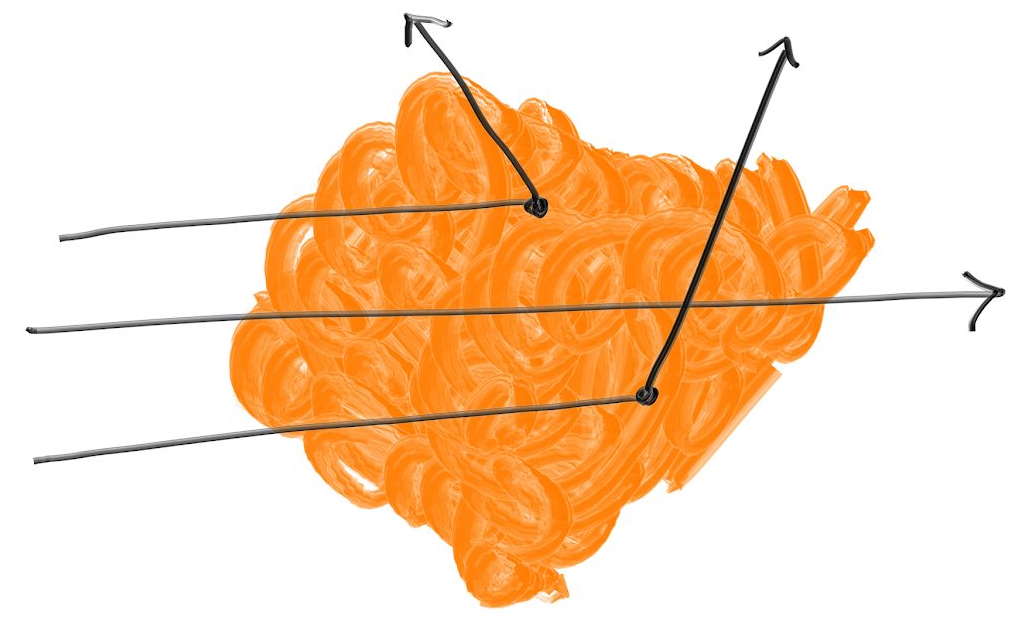
媒質中を進むレイは任意の点で散乱する可能性があり、媒質が濃いとそれだけ散乱しやすくなる。レイが小さい距離 \(\Delta L\) を進むときに散乱する確率は \[ {\footnotesize \text{散乱する確率}} = C \cdot \Delta L \] と表せる。ここで \(C\) は媒質の光学的密度に比例する。この微分方程式を全ての点で考えることで、乱数を散乱が起こる距離に結び付けることができる ¹。この距離が媒質の外側ならレイは媒質と「衝突」しない。密度が定数の媒質に対しては \(C\) と境界の情報があればこの計算が行える。境界には別の hittable を使うとすれば、次のクラスが書ける:

class constant_medium : public hittable {
public:
  constant_medium(shared_ptr<hittable> b, double d, shared_ptr<texture> a)
    : boundary(b), neg_inv_density(-1/d) {
    phase_function = make_shared<isotropic>(a);
  }

  virtual bool hit(
    const ray& r, double t_min, double t_max, hit_record& rec
  ) const;

  virtual bool bounding_box(double t0, double t1, aabb& output_box) const {
    return boundary->bounding_box(t0, t1, output_box);
  }

public:
  shared_ptr<hittable> boundary;
  shared_ptr<material> phase_function;
  double neg_inv_density;
};

リスト 2.65 [constant_medium.h] constant_medium クラス

等方性 (isotropic) テクスチャの scatter 関数は方向を一様ランダムに選ぶ:

class isotropic : public material {
public:
  isotropic(shared_ptr<texture> a) : albedo(a) {}

  virtual bool scatter(
    const ray& r_in,
    const hit_record& rec,
    color& attenuation,
    ray& scattered
  ) const {
    scattered = ray(rec.p, random_in_unit_sphere(), r_in.time());
    attenuation = albedo->value(rec.u, rec.v, rec.p);
    return true;
  }

public:
  shared_ptr<texture> albedo;
};

リスト 2.66 [material.h] isotropic クラス

そして hit 関数はこれだ:

bool constant_medium::hit(
  const ray& r, double t_min, double t_max, hit_record& rec
) const {
  // デバッグ中には低い確率でサンプルの様子を出力する。
  // enableDebug を true にすると有効になる。
  const bool enableDebug = false;
  const bool debugging = enableDebug && random_double() < 0.00001;

  hit_record rec1, rec2;

  if (!boundary->hit(r, -infinity, infinity, rec1))
    return false;

  if (!boundary->hit(r, rec1.t+0.0001, infinity, rec2))
    return false;

  if (debugging) std::cerr << "\nt0=" << rec1.t << ", t1=" << rec2.t << '\n';

  if (rec1.t < t_min) rec1.t = t_min;
  if (rec2.t > t_max) rec2.t = t_max;

  if (rec1.t >= rec2.t)
    return false;

  if (rec1.t < 0)
    rec1.t = 0;

  const auto ray_length = r.direction().length();
  const auto distance_inside_boundary = (rec2.t - rec1.t) * ray_length;
  const auto hit_distance = neg_inv_density * log(random_double());

  if (hit_distance > distance_inside_boundary)
    return false;

  rec.t = rec1.t + hit_distance / ray_length;
  rec.p = r.at(rec.t);

  if (debugging) {
    std::cerr << "hit_distance = " <<  hit_distance << '\n'
          << "rec.t = " <<  rec.t << '\n'
          << "rec.p = " <<  rec.p << '\n';
  }

  rec.normal = vec3(1,0,0); // どんな値でもよい
  rec.front_face = true;    // 同じくどんな値でもよい
  rec.mat_ptr = phase_function;

  return true;
}

リスト 2.67 [constant_medium.h] constant_medium::hit 関数

この関数はレイの始点が媒質の中にある場合にも正しい必要があるので、境界が関係する処理は慎重に行う必要がある。雲の中ではレイが何度も跳ね返るので、視点が媒質の中にあるレイは珍しいものではない。

このコードでは一度媒質に入ってから出たレイは二度と媒質に入らないことが仮定されている。言い換えると、境界の形状は凸である必要がある。この実装は直方体や球といった境界に対しては正しく動くが、穴を含むトーラスのような境界ではうまく動かない。任意の形状を扱える実装も可能だが、これは読者への練習問題とする。

煙がかった直方体のレンダリング

コーネルボックスの直方体を煙と霧 (暗いボリュームと明るいボリューム) に変えて、収束を速めるためにライトを大きく (さらに明るさで白飛びしないように暗く) する:

hittable_list cornell_smoke() {
  hittable_list objects;

  auto red   = make_shared<lambertian>(make_shared<solid_color>(.65, .05, .05));
  auto white = make_shared<lambertian>(make_shared<solid_color>(.73, .73, .73));
  auto green = make_shared<lambertian>(make_shared<solid_color>(.12, .45, .15));
  auto light = make_shared<diffuse_light>(make_shared<solid_color>(7, 7, 7));

  objects.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
  objects.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
  objects.add(make_shared<xz_rect>(113, 443, 127, 432, 554, light));
  objects.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
  objects.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
  objects.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

  shared_ptr<hittable> box1 =
    make_shared<box>(point3(0,0,0), point3(165,330,165), white);
  box1 = make_shared<rotate_y>(box1,  15);
  box1 = make_shared<translate>(box1, vec3(265,0,295));

  shared_ptr<hittable> box2 =
    make_shared<box>(point3(0,0,0), point3(165,165,165), white);
  box2 = make_shared<rotate_y>(box2, -18);
  box2 = make_shared<translate>(box2, vec3(130,0,65));

  objects.add(
    make_shared<constant_medium>(box1, 0.01, make_shared<solid_color>(0,0,0))
  );
  objects.add(
    make_shared<constant_medium>(box2, 0.01, make_shared<solid_color>(1,1,1))
  );

  return objects;
}

リスト 2.68 [main.cc] 煙を使ったコーネルボックス

次の画像が得られる:

訳注: レイが媒質中を散乱せずに \(L = n\Delta L\) だけ進み、その直後に散乱する確率を \(p(L)\) とする。このとき \(p(L) \propto \left(1 - C\Delta L\right)^{n} = \left(1 - C\Delta L\right)^{\frac{L}{\Delta L}}\) が成り立ち、\(\Delta L \to 0\) つまり \(n \to \infty\) のとき \(p(L) \to k e^{-CL}\) となる (\(k\) は定数)。確率を全区間で積分すれば \(1\) だから \[\int_{0}^{\infty} p(L) \, dL = \int_{0}^{\infty} ke^{-CL} \, dL = \frac{k}{C} = 1\] であり、\(k = C\) が分かる。\([0,1]\) の一様乱数 \(r\) に対して \[r = \int_{0}^{x} p(x)\,dx = \int_{0}^{x} Ce^{-Cx} \,dx = 1 - e^{-Cx} \] が成り立つとき \(x\) の確率密度関数は \(p(x)\) となる。よってこの等式を \(x\) について解いた \[x = -\frac{1}{C}\log(1 - r)\] という関係を使えばレイが散乱するまでの「ランダムな」長さを計算できる。^[return]