レイ・簡単なカメラ・背景

レイを表すクラス

どんなレイトレーサーにもレイを表すクラスとそのレイの色を計算する処理が存在する。レイを関数 \(\mathbf{P}(t) = \mathbf{A} + t \mathbf{b}\) と考えよう。\(\mathbf{P}\) は三次元空間に存在する直線上の点を表し、\(\mathbf{A}\) がレイの原点を、\(\mathbf{b}\) がレイの方向を意味する。レイのパラメータ \(t\) は実数 (double) であり、\(t\) を変えると \(\mathbf{P}(t)\) は三次元空間内の直線上を移動する。負の \(t\) も考えに入れれば直線上の全ての点が表され、\(t\) が正のとき \(P\) は \(\mathbf{A}\) の前方部分だけを移動する。この前方部分からなる半直線がレイである。

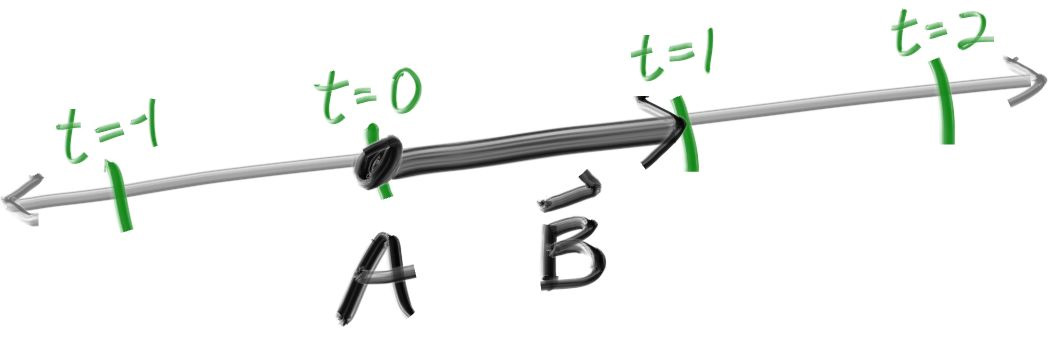
関数 \(\mathbf{P}(t)\) の実装はもう少し冗長に ray::at(t) と呼ぶことにする:

#ifndef RAY_H
#define RAY_H

#include "vec3.h"

class ray {
public:
  ray() {}
  ray(const point3& origin, const vec3& direction)
    : orig(origin), dir(direction) {}

  point3 origin() const  { return orig; }
  vec3 direction() const { return dir; }

  point3 at(double t) const {
    return orig + t*dir;
  }

public:
  point3 orig;
  vec3 dir;
};

#endif

レイの射出

これでレイトレーサーを作る準備が整った。レイトレーサーの核にあるのは「各ピクセルを通過するレイを放ち、視点からレイの方向を見たときの色を計算する」という処理である。この処理はさらに次の三つの処理に分けられる:

1. 視点からピクセルへのレイを計算する
2. レイが交わるオブジェクトを求める
3. レイとオブジェクトの交点の色を計算する

私がレイトレーサーを開発するときは、必ず最初に簡単なカメラのコードを書いて実行できるところまで持っていくようにしている。さらに背景の色 (単純なグラデーション) を簡単に計算する ray_color(ray) 関数も作る。

私は \(x\) と \(y\) を本当によく取り違えるので、正方形の画像にレンダリングするとデバッグが大変になる。そこでレンダリングは正方形でない画像に行うことにする。画像のアスペクト比はたいていのディスプレイと同じ \(16:9\) としよう。

レンダリングする画像の解像度とは別に、仮想的なビューポートの形と位置を決めておく必要もある。通常の正方形のピクセルを使うとすれば、ビューポートのアスペクト比はレンダリングする画像と同じとなる。さらに高さを二単位と定めればビューポートの形が決まる。また射影平面と射影点の間の距離を一単位と定める。この距離は焦点距離 (focal length) と呼ばれるが、これは後で登場する集束距離 (focus distance) とは異なることに注意してほしい。

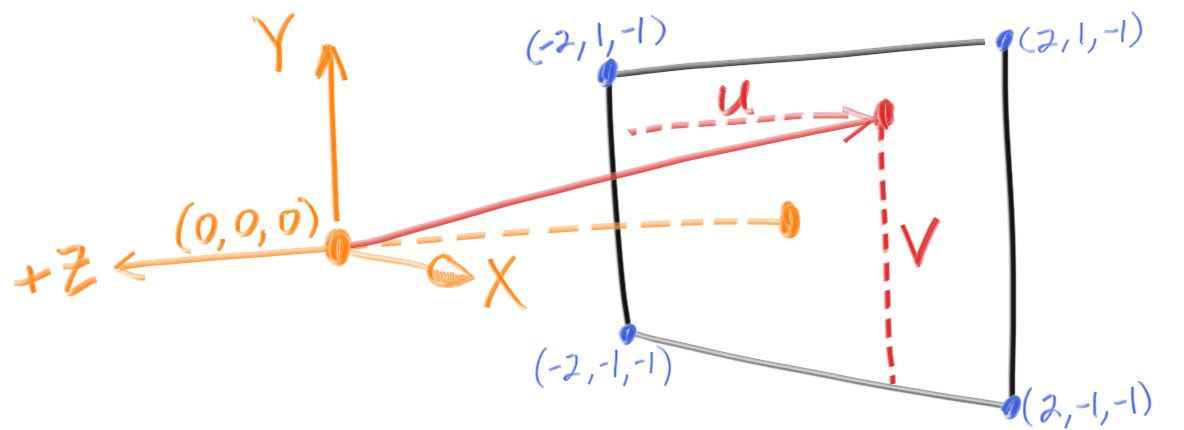
"目" (カメラの中心) は \((0, 0, 0)\) として、\(y\) 軸正方向は上、\(x\) 軸正方向は右とする。さらに座標を右手座標系とするために、スクリーンは \(z\) 座標が負になるように配置する。スクリーンの左下の点から走査を始め、スクリーンの辺に沿った二つのオフセットベクトル u と v を使ってレイがスクリーンと交わる点を管理する。実装ではレイの方向ベクトルを単位長としていない点に注意してほしい。こうした方がコードが単純になり、実行も多少高速になる。

次に示すコードではレイ r がピクセルのほぼ中心を通っている。後でアンチエイリアシングを追加するので、ここでは正確さを気にしない。

#include "ray.h"

#include <iostream>

color ray_color(const ray& r) {
  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);

  std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";

  auto viewport_height = 2.0;
  auto viewport_width = aspect_ratio * viewport_height;
  auto focal_length = 1.0;

  auto origin = point3(0, 0, 0);
  auto horizontal = vec3(viewport_width, 0, 0);
  auto vertical = vec3(0, viewport_height, 0);
  auto lower_left_corner =
    origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      auto u = double(i) / (image_width-1);
      auto v = double(j) / (image_height-1);
      ray r(origin, lower_left_corner + u*horizontal + v*vertical - origin);
      color pixel_color = ray_color(r);
      write_color(std::cout, pixel_color);
    }
  }

  std::cerr << "\nDone.\n";
}

ray_color(ray) 関数はまずレイの方向ベクトルを正規化し、正規化したベクトルの \(y\) 成分 (\(-1.0 \lt y \lt 1.0\)) を使って白と青を線形に混ぜ合わせる。正規化した後の \(y\) を考えているから、グラデーションは垂直方向だけではなく水平方向にも表れることが分かるだろう。

その後 \(y\) を \(0.0 \leq t \leq 1.0\) にスケールする簡単な処理を行う。続いて \(t = 1.0\) のときには青が、\(t = 0.0\) のときには白が、その間のときには二つが混ざった色が計算されるような処理を行う。これは二つの量の線形ブレンド (linear blend) あるいは線形補間 (linear interpolation) と呼ばれる処理であり、略して lerp と呼ばれる。lerp は必ず \[ {\footnotesize \text{補間された値}} = (1-t)\cdot {\footnotesize \text{始まりの値}} + t\cdot {\footnotesize \text{終わりの値}} \] という形をしており、\(t\) は \(0\) から \(1\) の値を取る。lerp によって上の画像が得られる。