一次元モンテカルロ積分
積分は突き詰めれば面積や体積の計算だから、第二節の内容は積分を使って最高に理解しにくく表現できる。しかしときには、積分を使って問題を定式化するのが最も自然で見通しが良くなる場合もある。レンダリングではそうなることが多い。
\(x^{2}\) の積分
古典的な積分を考えよう: \[ I = \int_{0}^{2} x^2 \, dx \] 情報科学っぽい記法を使うと \[ I = \text{area}( x^2, 0, 2 ) \] となる。これは次のように変形できる: \[ I = 2 \cdot \text{average}(x^2, 0, 2) \]
ここからモンテカルロ法を使った次のアプローチが分かる。直接積分を計算して求まる正確な値は \(I = 8/3\) であり、この近似値が計算される。
#include "rtweekend.h"
#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto x = random_double(0,2);
sum += x*x;
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "I = " << 2 * sum/N << '\n';
}
integrate_x_sq.cc] \(x^{2}\) の積分
この方法は解析的に積分できない \(\log \sin x\) のような関数の積分にも利用できる。グラフィックスでは値を求めることはできるが陽に書くことができない関数、あるいは確率的にしか値を計算できない関数がよく登場する。これまでの二巻で実装した ray_color() 関数がそうである ──任意のレイに対するこの関数の値を表す式は存在しないが、任意のレイに対する値を確率的に近似することはできる。
これまで行き当たりばったりに書いてきた私たちのプログラムが持つ問題の一つが、ライトが小さいときのノイズが非常に大きいことだ。これはプログラムで使われている一様なサンプリングが非常に低い頻度でしか光源をサンプルしないためである。光源がサンプルされるのは散乱したレイが光源に向かうときだけだが、光源が小さかったり遠くにあったりするとこれは起こりにくい。光源に向かうレイを多くサンプルすればこの問題の影響を和らげることができるが、そうするとシーンが不正確に明るくなる。多くサンプルした部分のレイからの寄与を低く勘定すれば結果を正確にできるのだが、さてどれくらい低くすればよいのだろうか? この質問に答えるには、確率密度関数 (probability density function) という概念が必要になる。
確率密度関数
確率密度関数とは何だろうか? これはヒストグラム (度数分布表) を連続にしたものと言える。ヒストグラムの Wikipedia には次の図が載っている1:
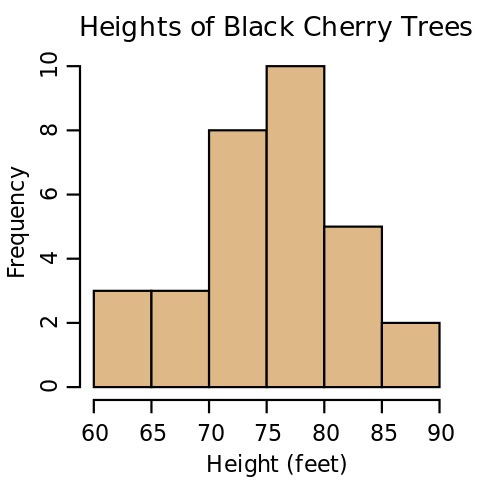
さらに多くの木の高さを調べるヒストグラムは高くなり、ビン (縦棒) を小さく分けて幅を狭くするとヒストグラムは低くなる。ヒストグラムの \(y\) 方向の高さを割合あるいはパーセンテージに正規化すると、離散の確率密度関数が得られる。ビンの数を無限大にすれば連続な連続なヒストグラムとなるが、そのままでは全てのビンの高さがゼロになってしまうので正規化できない。ビンの数で高さが変わらないように連続ヒストグラムを調整したのが確率密度関数である。木の高さのヒストグラムを表す密度関数では、 \[ H {\footnotesize \text{ から }} H' {\footnotesize \text{のビンの高さ}} = \frac{{\footnotesize \text{高さが }} H {\footnotesize \text{ から }} H' {\footnotesize \text{ の木の数}}}{H-H'} \] が成り立つ。この式が木の高さの統計的に推定していると解釈することもできる: \[ {\footnotesize \text{ランダムな木の高さが }} H {\footnotesize \text{ と }} H' {\footnotesize \text{の間にある確率}} = {\footnotesize \text{ビンの高さ}}\cdot(H-H') \] 複数のビンの区間に収まる確率はそれぞれの確率を足せば求まる。
つまり、確率密度関数 (probability density function, PDF) は割合を表すヒストグラムを連続にしたものである。
PDF の構築
理解を深めるために、PDF を作って先ほどの積分で利用してみよう。\(0\) から \(2\) の値を取る乱数 \(r\) があって、\(r\) の値が \(x\) となる確率が \(x\) 自身に比例する状況を考える。このとき PDF \(p(r)\) は次の形となるはずだが、この高さはいくつだろうか?
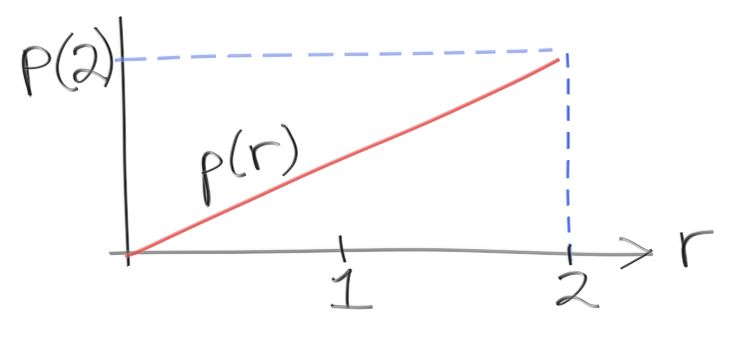
\(r = 2\) おける高さ \(p(2)\) を求めたい。ここで使うのは、ヒストグラムと同様に PDF の積分 (高さの和) が「乱数 \(r\) がとある区間に存在する確率」となる事実である: \[ x_0 \lt r \lt x_1 {\footnotesize \text{ となる確率}} = \text{area}(p(r), x_0, x_1) \] \(r\) が存在しうる区間全体を考えれば確率は \(1\) になる。さらに \(p(r)\) が \(r\) に比例するので、定数 \(C\) を使って \(p(r) = C x\) と表せる。ここから \[ \text{area}(Cr, 0, 2) = \int_{0}^{2} C r dr = \frac{Cr^2}{2} \biggr|_{r=2}^{r=0} = \frac{C \cdot 2^2}{2} - \frac{C \cdot 0^2}{2} = 2C = 1 \] が分かる。すなわち \(p(r) = r/2\) である。
では、この PDF \(p(r) = r/2\) に沿った乱数を生成するにはどうすればよいだろうか? この問題では逆関数法 (inverse method) と呼ばれるトリックが使える。あと一息だから、頑張れ!
\(0\) と \(1\) の間の一様変数を d = random_double() として、ここから PDF が \(p(r) = r/2\) となる乱数 \(e = f(d)\) を作りたい。例として \(e = f(d) = d^{2}\) としてみよう。\(0\) と \(1\) の間の数を二乗すると \(0\) に近づくから、二乗結果の分布は \(0\) に向かってよる。つまり \(e\) の PDF は一様ではなく、\(0\) 付近で大きく \(1\) 付近で小さくなる。この観察を一般的に定式化するには、次の累積分布関数 (cumulative distribution function, CDF) \(P(x)\) という概念が必要になる: \[ P(x) = \text{area}(p, -\infty, x) = \int_{-\infty}^{x} P(x)\, dx \] \(p(x)\) が定義されていない \(x\) では \(p(x) = 0\) とみなす。つまり乱数がその \(x\) となる確率は \(0\) である。先ほどの PDF \(p(r) = r/2\) の CDF \(P(x)\) は \[ \begin{cases} P(x) = 0 & (x \lt 0) \\ P(x) = \dfrac{x^2}{4} & (0 \lt x \lt 2) \\ P(x) = 1 & (2 \lt x) \\ \end{cases} \] となる。
\(d\) から \(e\) を計算する方法を考えているのに、どうして \(x\) や \(r\) が出てくるのだろうか? この二つの関数はダミー変数であり、プログラムにおける関数の引数に相当する。さて \(x = 1.0\) のときの \(P\) を計算すると \[ P(1.0) = \frac{1}{4} \] となる。これは「今考えている PDF に沿って生成した乱数が \(1\) より小さくなる確率は \(25\) % である」ことを意味している。ここから様々な非一様乱数の生成で使われる賢い観察が得られる。私たちが探しているのは関数 \(f\) であって \(f(\text{random\_double()})\) の返り値が PDF \(p(r) = r/2\) に従うものである。この関数が何なのかは分からないが、この関数からの返り値の \(25\) % は \(1\) より小さくなることは分かっている。よって \(f\) が単調増加と仮定すれば \(f(0.25) = 1.0\) が成り立つ。この議論を一般化すると任意の点に対する \(f\) と \(P\) の関係が得られる: \[ f(P(x)) = x \] すなわち \(f\) は \(P\) と逆の処理を行う。よって \[ f(x) = P^{-1}(x) \] である。この \(-1\) は「逆関数」を表す。分かりにくい記法だが、これが標準なので仕方がない。最初の問題に結論を出そう。もし確率密度関数 \(p\) と累積分布関数 \(P\) が既知なら、\(P\) の逆関数が求めるべき乱数を与える: \[ e = P^{-1} (\text{random\_double}()) \]
考えていた例 \(p(x) = x/2\) に対する \(P\) は上に示した通り \[ y = \frac{x^2}{4} \] である。\(y\) を使って \(x\) を表せば逆関数が求まる: \[ x = \sqrt{4y} \] よって密度関数に \(p(x) = x/2\) を持つ乱数 \(e\) は次の式で生成できると分かる: \[ e = \sqrt{4\cdot\text{random\_double}()} \] \(e\) の値域が \(p\) と同じく \(0\) から \(2\) である点に注目してほしい。また \(\text{random\_double}\) を \(1/4\) とすれば \(e = 1\) となり、以前の結果と一致する。
ではこのサンプル方法を使って最初の積分を計算してみよう: \[ I = \int_{0}^{2} x^2 \, dx \] \(x\) の PDF が一様でないことを考慮して、多くサンプルした部分には少ない重みを付ける必要がある。サンプルの量は PDF によって表されるので、重みは PDF の逆数の定数倍とすればよい。実は PDF の性質から PDF の逆数そのものが正しい重みだと証明できる。
inline double pdf(double x) {
return 0.5*x;
}
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto x = sqrt(random_double(0,4));
while (x == 0.0) {
// PDF が 0.5*x の乱数で x が 0 になる確率は 0
x = sqrt(random_double(0,4));
}
sum += x*x / pdf(x);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "I = " << sum/N << '\n';
}
integrate_x_sq.cc] PDF を使った \(x^{2}\) の積分 (バージョン 2)
pdf(x) で割るときにゼロ除算が発生しないよう x が 0 の場合を除外しているが、これは乱数の性質を考えてもおかしなことではない。pdf(x) が 0 となるような x はそもそも生成されてはいけないので、除外して考えるのが理にかなっている。
重点サンプリング
上のプログラムは被積分関数が大きくなる部分から多くサンプルしているので、ノイズが減って収束が速まる。分布の中で重要 (important) な部分にサンプルを寄せているということで、慎重に選んだ一様でない PDF に従うサンプルを使うこの方法を重点サンプリング (importence sampling) と呼ぶ。
同じコードで一様なサンプルを使うとすれば、PDF は \([0, 2]\) の範囲で値 \(1/2\) を取る関数となる。このとき x = random_double(0,2) であり、次のようになる:
inline double pdf(double x) {
return 0.5;
}
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto x = random_double(0,2);
sum += x*x / pdf(x);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "I = " << sum/N << '\n';
}
integrate_x_sq.cc] \(x^{2}\) の積分 (バージョン 3)
以前のコードにあった 2*sum/N の 2 が消えた点に注目してほしい ──この部分は PDF に移動した。重点サンプリングは収束を加速させるが、その効果は非常に大きいというわけではない。またこの積分では、被積分関数と完全に一致する PDF を使うこともできる: \[ p(x) = \frac{3}{8}x^2 \] とすれば \[ P(x) = \frac{x^3}{8} \] であり、 \[ P^{-1}(x) = 8x^\frac{1}{3} \] となる。こうした完璧な重点サンプリングが可能なのは答えが最初から分かっているとき (\(p\) を解析的に積分して \(P\) が求まるとき) に限られるが、コードが正しく動くことを確かめるのにはちょうどよいだろう。この場合には \(1\) サンプルだけで正確な値が求まる:
inline double pdf(double x) {
return 3*x*x/8;
}
int main() {
int N = 1;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto x = pow(random_double(0,8), 1./3.);
sum += x*x / pdf(x);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "I = " << sum/N << '\n';
}
integrate_x_sq.cc] \(x^{2}\) の積分 (バージョン 4)
重点サンプリングはモンテカルロレイトレーサーの基礎となる概念なので、その方法をここにまとめておく:
- 区間 \([a, b]\) における \(f(x)\) の積分を考える。
- \([a, b]\) で \(0\) にならない PDF \(p\) を見つける。
- PDF が \(p\) の乱数 \(r\) を大量に生成し、それらに関する \(\dfrac{f(r)}{p(r)}\) の平均を求める。
PDF \(p\) をどのように選んでも近似値は正しい値に収束するが、\(p\) が \(f\) の近似として優れていればそれだけ収束も速くなる。