インスタンス
普通コーネルボックスには二つの立方体があって、どちらも壁に対して角度が付いている。まず六個の長方形を使って辺が軸に平行な直方体を作ろう。
class box: public hittable {
public:
box() {}
box(const point3& p0, const point3& p1, shared_ptr<material> ptr);
virtual bool hit(const ray& r, double t0, double t1, hit_record& rec) const;
virtual bool bounding_box(double t0, double t1, aabb& output_box) const {
output_box = aabb(box_min, box_max);
return true;
}
public:
point3 box_min;
point3 box_max;
hittable_list sides;
};
box::box(const point3& p0, const point3& p1, shared_ptr<material> ptr) {
box_min = p0;
box_max = p1;
sides.add(make_shared<xy_rect>(p0.x(), p1.x(), p0.y(), p1.y(), p1.z(), ptr));
sides.add(make_shared<xy_rect>(p0.x(), p1.x(), p0.y(), p1.y(), p0.z(), ptr));
sides.add(make_shared<xz_rect>(p0.x(), p1.x(), p0.z(), p1.z(), p1.y(), ptr));
sides.add(make_shared<xz_rect>(p0.x(), p1.x(), p0.z(), p1.z(), p0.y(), ptr));
sides.add(make_shared<yz_rect>(p0.y(), p1.y(), p0.z(), p1.z(), p1.x(), ptr));
sides.add(make_shared<yz_rect>(p0.y(), p1.y(), p0.z(), p1.z(), p0.x(), ptr));
}
bool box::hit(const ray& r, double t0, double t1, hit_record& rec) const {
return sides.hit(r, t0, t1, rec);
}
box.h] box クラス
続いてシーンに二つの直方体を追加する。まだ角度は付いていない。
objects.add(make_shared<box>(point3(130, 0, 65), point3(295, 165, 230), white));
objects.add(make_shared<box>(point3(265, 0, 295), point3(430, 330, 460), white));
main.cc] box をシーンに追加する
次の画像が得られる:

さらに立方体を回転させれば真のコーネルボックスとなる。レイトレーシングではオブジェクトの回転や移動を実装するのにインスタンス (instance) という考え方を使うことが多い。インスタンスとはある幾何形状を移動あるいは回転させて得られる幾何形状のことである。レイトレーシングでは物体の移動がレイの移動で済むので、インスタンスの取り扱いが非常に簡単になる。例えば下図のピンクの四角を \(x\) 軸正方向に \(2\) だけ移動したインスタンスと黒いレイの衝突を判定したいとする。このとき実際に移動させた黒い四角を使うこともできるし、\(x\) 軸正方向に \(-2\) だけ移動させたピンク色のレイを使うこともできる。レイトレーシングで使うのは後者である。
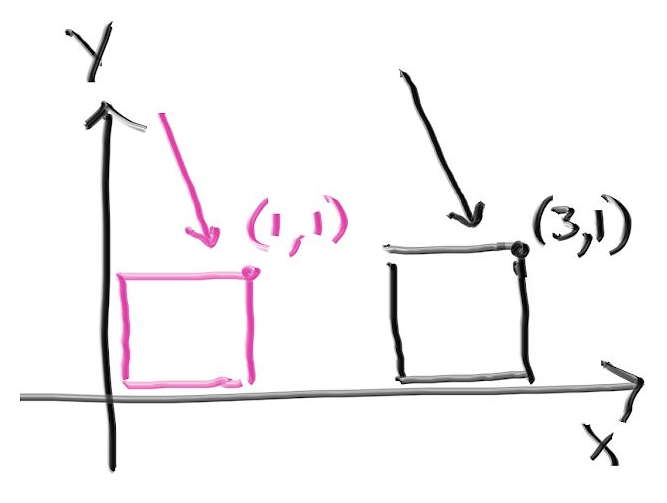
インスタンスの移動
物体を動かすと考えても座標を変えると考えてもどちらでも構わない。hittable を動かしてできる移動 (translation) インスタンスのコードは次の通りである:
class translate : public hittable {
public:
translate(shared_ptr<hittable> p, const vec3& displacement)
: ptr(p), offset(displacement) {}
virtual bool hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const;
virtual bool bounding_box(double t0, double t1, aabb& output_box) const;
public:
shared_ptr<hittable> ptr;
vec3 offset;
};
bool translate::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
ray moved_r(r.origin() - offset, r.direction(), r.time());
if (!ptr->hit(moved_r, t_min, t_max, rec))
return false;
rec.p += offset;
rec.set_face_normal(moved_r, rec.normal);
return true;
}
bool translate::bounding_box(double t0, double t1, aabb& output_box) const {
if (!ptr->bounding_box(t0, t1, output_box))
return false;
output_box = aabb(
output_box.min() + offset,
output_box.max() + offset);
return true;
}
hittable.h] translation クラス
インスタンスの回転
回転 (rotation) を理解して公式を導出するのは移動ほど簡単ではない。グラフィックスでは \(x\), \(y\), \(z\) 軸周りの回転を順に考えるのが一般的である。この三つの回転はある意味で「軸に平行」となる。最初に \(z\) 軸周りの回転を考える。\(x\) 座標と \(y\) 座標だけが変化し、その変化量には \(z\) 座標が関係しない。
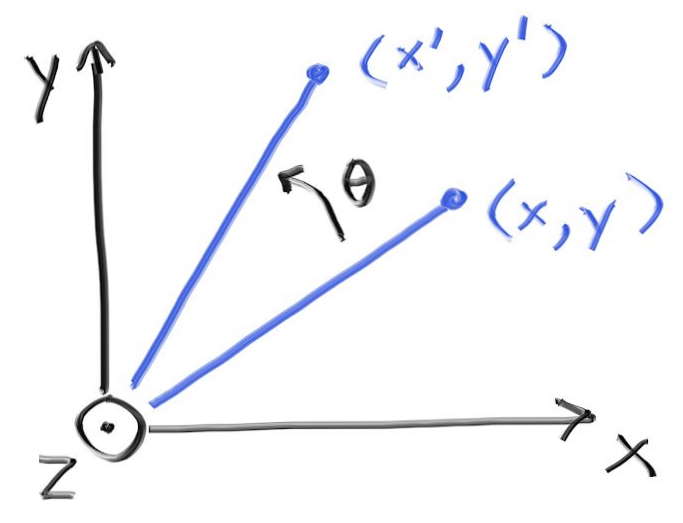
この回転を表す式の導出には三角関数の基本的な性質を用いる。ここでは説明しないが、グラフィックスの教科書あるいは講義ノートに必ず載っている。\(z\) 軸周りの反時計回りの回転を表す式は多少複雑で、次のようになる: \[ \begin{aligned} x' & = \cos \theta \cdot x - \sin \theta \cdot y \\ y' & = \sin \theta \cdot x + \cos \theta \cdot y \end{aligned} \] この式は任意の \(\theta\) で成り立ち、場合分けが必要ないのが素晴らしい。この逆変換は幾何学的に逆の操作つまり \(-\theta\) の回転であり、\(\cos \theta = \cos(-\theta)\) と \(\sin(-\theta) = -\sin \theta\) を使えば簡単に求まる。
同様に \(y\) 軸周りの回転 (コーネルボックスで使う回転) は \[ \begin{aligned} x' & = \hphantom{-} \cos \theta \cdot x + \sin \theta \cdot z \\ z' & = -\sin \theta \cdot x + \cos \theta \cdot z \end{aligned} \] であり、\(x\) 軸周りの回転は \[ \begin{aligned} y' & = \cos \theta \cdot y - \sin \theta \cdot z \\ z' & = \sin \theta \cdot y + \cos \theta \cdot z \end{aligned} \] となる。
移動の場合と異なり、回転では曲面の法線も変化する。そのため衝突を検出したときに法線の方向を変更しなければならないが、幸い回転では法線にも同じ式を利用できる。ただし拡大を伴う場合には法線の変換が複雑になるので注意がいる。https://in1weekend.blogspot.com/ に参考ページを載せておいた。
\(y\) 軸周りの回転インスタンスのクラスは次の通りである:
class rotate_y : public hittable {
public:
rotate_y(shared_ptr<hittable> p, double angle);
virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const;
virtual bool bounding_box(double t0, double t1, aabb& output_box) const {
output_box = bbox;
return hasbox;
}
public:
shared_ptr<hittable> ptr;
double sin_theta;
double cos_theta;
bool hasbox;
aabb bbox;
};
hittable.h] rotate_y クラス
コンストラクタを示す:
rotate_y::rotate_y(shared_ptr<hittable> p, double angle) : ptr(p) {
auto radians = degrees_to_radians(angle);
sin_theta = sin(radians);
cos_theta = cos(radians);
hasbox = ptr->bounding_box(0, 1, bbox);
point3 min( infinity, infinity, infinity);
point3 max(-infinity, -infinity, -infinity);
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
auto x = i*bbox.max().x() + (1-i)*bbox.min().x();
auto y = j*bbox.max().y() + (1-j)*bbox.min().y();
auto z = k*bbox.max().z() + (1-k)*bbox.min().z();
auto newx = cos_theta*x + sin_theta*z;
auto newz = -sin_theta*x + cos_theta*z;
vec3 tester(newx, y, newz);
for (int c = 0; c < 3; c++) {
min[c] = fmin(min[c], tester[c]);
max[c] = fmax(max[c], tester[c]);
}
}
}
}
bbox = aabb(min, max);
}
hittable.h] rotate_y のコンストラクタ
hit 関数は次のようにできる:
bool rotate_y::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
auto origin = r.origin();
auto direction = r.direction();
origin[0] = cos_theta*r.origin()[0] - sin_theta*r.origin()[2];
origin[2] = sin_theta*r.origin()[0] + cos_theta*r.origin()[2];
direction[0] = cos_theta*r.direction()[0] - sin_theta*r.direction()[2];
direction[2] = sin_theta*r.direction()[0] + cos_theta*r.direction()[2];
ray rotated_r(origin, direction, r.time());
if (!ptr->hit(rotated_r, t_min, t_max, rec))
return false;
auto p = rec.p;
auto normal = rec.normal;
p[0] = cos_theta*rec.p[0] + sin_theta*rec.p[2];
p[2] = -sin_theta*rec.p[0] + cos_theta*rec.p[2];
normal[0] = cos_theta*rec.normal[0] + sin_theta*rec.normal[2];
normal[2] = -sin_theta*rec.normal[0] + cos_theta*rec.normal[2];
rec.p = p;
rec.set_face_normal(rotated_r, normal);
return true;
}
hittable.h] rotate_y::hit 関数
コーネルボックスを変更しよう:
shared_ptr<hittable> box1 =
make_shared<box>(point3(0, 0, 0), point3(165, 330, 165), white);
box1 = make_shared<rotate_y>(box1, 15);
box1 = make_shared<translate>(box1, vec3(265,0,295));
objects.add(box1);
shared_ptr<hittable> box2 =
make_shared<box>(point3(0,0,0), point3(165,165,165), white);
box2 = make_shared<rotate_y>(box2, -18);
box2 = make_shared<translate>(box2, vec3(130,0,65));
objects.add(box2);
main.cc] 直方体を \(y\) 軸周りに回転させたコーネルボックス
次の画像が得られる:
