法線と複数オブジェクト
法線を使ったシェーディング
まずシェーディングのために法線を計算しよう。法線とは物体とレイの交点を通って物体表面と垂直なベクトルのことを言う。法線に関して決めておくべき設計事項が二つある。一つ目は法線を単位長とするかどうかである。単位長にしておけばシェーディングが楽になるので、法線は単位長と定める。ただしコードでこれを明示的に確認することはしない。これによって軽微なバグが生まれる可能性もあるので、これは (他の様々な設計判断と同じく) 個人的な好みだと思ってほしい。さて球の場合には、外向きの法線は交点 \(p\) から中心 \(c\) を引いたベクトル \(p - c\) と同じ向きを持つ。球を地球だと考えれば、これは地球の中心からあなたへのベクトルが真上を向くことを意味する。
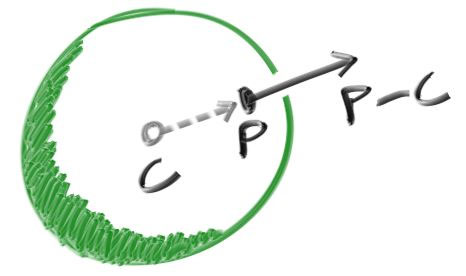
以上の説明をコードにしてシェーディングを行おう。まだ球以外には光も何もないから、法線をカラーマップとして可視化する。法線を可視化するのによく使われるのが、法線の \(x\), \(y\), \(z\) 成分をそれぞれ \(0\) から \(1\) の区間にマップして、それを \(r\), \(g\), \(b\) として読むというテクニックだ (このとき法線 \(\textbf{n}\) が単位ベクトルで、各成分が \(-1\) から \(1\) の値を持つとすると実装が簡単で理解もしやすい)。法線を扱うためにはレイが当たったかどうかに加えて交点の位置に関する情報も必要になるから、一番近くの (\(t\) が小さい方の) 交点を考えることにする。これで \(\textbf{n}\) の計算・可視化が可能になる:
double hit_sphere(const point3& center, double radius, const ray& r) {
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius*radius;
auto discriminant = b*b - 4*a*c;
if (discriminant < 0) {
return -1.0;
} else {
return (-b - sqrt(discriminant) ) / (2.0*a);
}
}
color ray_color(const ray& r) {
auto t = hit_sphere(point3(0,0,-1), 0.5, r);
if (t > 0.0) {
vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));
return 0.5*color(N.x()+1, N.y()+1, N.z()+1);
}
vec3 unit_direction = unit_vector(r.direction());
t = 0.5*(unit_direction.y() + 1.0);
return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}
main.cc] 球の法線のレンダリング
次の画像が得られる:

レイと球の衝突判定の簡略化
レイと球の方程式を解く部分をもう一度考えよう:
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius*radius;
auto discriminant = b*b - 4*a*c;
main.cc] レイと球の衝突判定 (改良前)
まず、同じベクトル同士の内積はベクトルの長さの二乗に等しい。
次に、b に \(2\) が掛けられているが、\(b = 2h\) とすると \[ \begin{aligned} \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} & = \frac{-2h \pm \sqrt{(2h)^2 - 4ac}}{2a} \\ & = \frac{-2h \pm 2\sqrt{h^2 - ac}}{2a} \\ & = \frac{-h \pm \sqrt{h^2 - ac}}{a} \end{aligned} \] が成り立つ。
以上の観察を使えば、球の衝突判定コードを簡略化できる:
vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;
if (discriminant < 0) {
return -1.0;
} else {
return (-half_b - sqrt(discriminant) ) / a;
}
main.cc] レイと球の衝突判定 (改良後)
レイが衝突するオブジェクトの抽象化
複数の球を配置する方法を考えよう。球の配列を使いたくなるかもしれないが、ここではレイが衝突しうる物体を表す抽象クラスを用意すると非常に美しく問題を解決できる。この抽象クラスの名前は決めづらい ── object も悪くないが、「オブジェクト指向」という言葉と衝突する。surface もよく使われるが、おそらく立体的な物体をレンダリングすることもある。メンバー関数を強調すれば hittable となる。どれも完璧ではないが、ここでは hittable を使うことにしよう。
抽象クラス hittable はレイを受け取って自身と交わるかを判定する関数 hit を持つ。たいていのレイトレーサーの hit 関数はレイとは別に有効な \(t\) の値を表す \(t_{\text{min}}\) と \(t_{\text{max}}\) を受け取り、\(t_{\text{min}} \lt t \lt t_{\text{max}}\) のときに限って「交わる」ようにしている。最初のレイでは必ず \(t_{\text{min}} = 0\) かつ \(t_{\text{max}} = \infty\) だが、今後 \(t_{\text{min}}\) と \(t_{\text{max}}\) を持っておくとコードが簡単に書ける場合がある。これとは別の設計上の問題として、レイが交わる場合の法線などの計算を hit 関数で行うかどうかがある。探索の結果レイがもっとカメラに近い物体に交わっていることが分かり、必要となるのは一番近くにある法線だけとなるかもしれない。ここでは簡単な方法を選び、様々なデータを hit 関数で計算して hit_record 構造体に収めることにする。こうして完成する抽象クラスを示す:
#ifndef HITTABLE_H
#define HITTABLE_H
#include "ray.h"
struct hit_record {
point3 p;
vec3 normal;
double t;
};
class hittable {
public:
virtual ~hittable() {}
virtual bool hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const = 0;
};
#endif
hittable.h] hittable クラス
そして球を表すクラスはこうなる:
#ifndef SPHERE_H
#define SPHERE_H
#include "hittable.h"
#include "vec3.h"
class sphere: public hittable {
public:
sphere() {}
sphere(point3 cen, double r) : center(cen), radius(r) {}
virtual bool hit(
const ray& r, double tmin, double tmax, hit_record& rec
) const;
public:
point3 center;
double radius;
};
bool sphere::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;
if (discriminant > 0) {
auto root = sqrt(discriminant);
auto temp = (-half_b - root)/a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;
return true;
}
temp = (-half_b + root) / a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;
return true;
}
}
return false;
}
#endif
sphere.h] sphere クラス
法線の向き
法線に関してもう一つ、その向き (常に外を向くのか、それとも場合によっては内を向くのか) を決めておく必要がある。今の実装では法線が中心から交点の方向であり、常に外を向く。そのため外側から交わるレイと法線は逆向きとなり、内側から交わるレイと法線は同方向となる。こうではなくて、法線を常にレイと逆方向にする設計も考えられる。この設計ではレイが外側から交わるとき法線は外向きとなり、レイが内側から交わるなら法線は内向きとなる。
レイが物体のどちらか側からやってきたかに関する情報を今後使うことになるので、法線の向きの扱いを統一しておく必要がある。例えば両面印刷の紙のように裏と表でレンダリングが異なるオブジェクトや、ガラス球のように内側と外側を持つオブジェクトでこの情報が使われる。
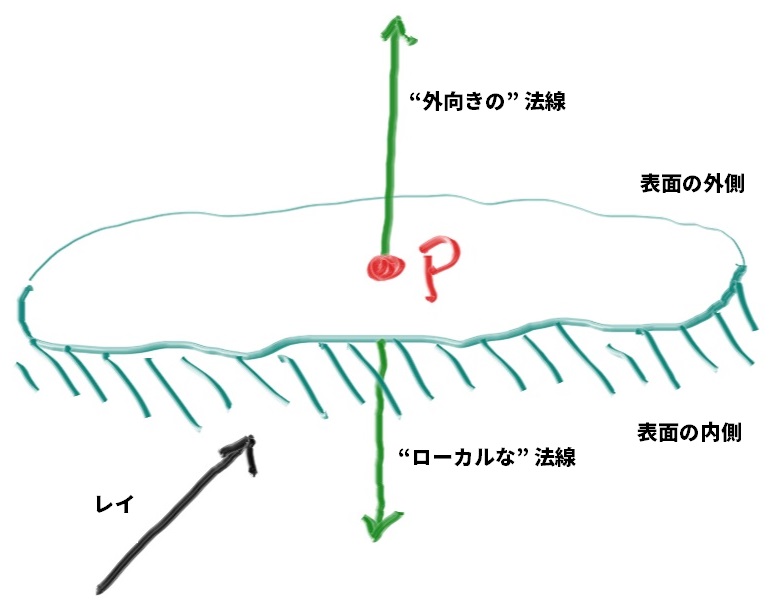
法線は常に外を向くと決めれば、レイが物体のどちら側にあるのかを色を計算するときに調べることになる。これはレイと法線を比較すれば分かる。つまりレイと法線が同じ方向を向いているならレイは物体の内部にあり、レイと法線が逆方向を向いているならレイはオブジェクトの外側にある。二つのベクトルの向きは内積を使えば判定でき、内積が正ならレイは物体の内部にある:
if (dot(ray_direction, outward_normal) > 0.0) {
// レイは球の内側にある
...
} else {
// レイは球の外側にある
...
}
sphere.h] レイと法線の向きを調べる
法線が常にレイと逆方向を向くと決めれば、内積を使って物体とレイの位置関係を調べる方法は使えない。代わりにその情報を保存することになる:
bool front_face;
if (dot(ray_direction, outward_normal) > 0.0) {
// レイは球の内側にある
normal = -outward_normal;
front_face = false;
} else {
// レイは球の外側にある
normal = outward_normal;
front_face = true;
}
sphere.h] 物体のレイの位置関係を保存する
法線が物体の "外側" を向くようにすることもできるし、レイと逆方向を向くようにすることもできる。法線の向きをジオメトリとの衝突判定時に決めたいのか、それとも色を計算するときに決めたいのかに応じて選ぶことになる。本書ではジオメトリよりマテリアルの種類が多くなるので、コードが少なくなるように法線をジオメトリとの衝突判定時に計算する方法を取る。これは好みに過ぎないので、他の文献を当たれば両方の実装が見つかるだろう。
hit_record 構造体にブール値 front_face を追加し、さらに法線の向きを計算する関数 set_face_normal も加える:
#ifndef HITTABLE_H
#define HITTABLE_H
#include "ray.h"
struct hit_record {
point3 p;
vec3 normal;
bool front_face;
inline void set_face_normal(const ray& r, const vec3& outward_normal) {
front_face = dot(r.direction(), outward_normal) < 0;
normal = front_face ? outward_normal :-outward_normal;
}
};
...
hittable.h] 法線の向きの計算を加えた hit_record クラス
そして sphere クラスに法線の向きの計算を追加する:
bool sphere::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;
if (discriminant > 0) {
auto root = sqrt(discriminant);
auto temp = (-half_b - root)/a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
vec3 outward_normal = (rec.p - center) / radius;
rec.set_face_normal(r, outward_normal);
return true;
}
temp = (-half_b + root) / a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
vec3 outward_normal = (rec.p - center) / radius;
rec.set_face_normal(r, outward_normal);
return true;
}
}
return false;
}
sphere.h] 法線の向きの計算を加えた sphere::hit 関数
オブジェクトのリスト
hittable というレイが衝突しうるオブジェクトを表す一般的なクラスが手に入ったので、hittable のリストを保持するクラスも作ることができる:
#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H
#include "hittable.h"
#include <memory>
#include <vector>
using std::shared_ptr;
using std::make_shared;
class hittable_list: public hittable {
public:
hittable_list() {}
hittable_list(shared_ptr<hittable> object) { add(object); }
void clear() { objects.clear(); }
void add(shared_ptr<hittable> object) { objects.push_back(object); }
virtual bool hit(
const ray& r, double tmin, double tmax, hit_record& rec
) const;
public:
std::vector<shared_ptr<hittable>> objects;
};
bool hittable_list::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
hit_record temp_rec;
bool hit_anything = false;
auto closest_so_far = t_max;
for (const auto& object : objects) {
if (object->hit(r, t_min, closest_so_far, temp_rec)) {
hit_anything = true;
closest_so_far = temp_rec.t;
rec = temp_rec;
}
}
return hit_anything;
}
#endif
hitabble_list.h] hittable_list クラス
C++ に特有の機能
hittable_list クラスには C++ を普段使わないプログラマーには見慣れないであろう機能が二つある: vector と shared_ptr だ。
shared_ptr は共有ポインタであり、新しくアロケートされたオブジェクトを使って初期化する。使用例を示す:
shared_ptr<double> double_ptr = make_shared<double>(0.37);
shared_ptr<vec3> vec3_ptr = make_shared<vec3>(1.4142, 2.7182, 1.6180);
shared_ptr<sphere> sphere_ptr = make_shared<sphere>(point3(0,0,0), 1.0);
shared_ptr を使ったアロケートの例
make_shared<thing>(thing_constructor_params) はコンストラクタの引数として thing_constructor_params を使って thing の新しいインスタンスをアロケート・初期化し、shared_ptr<thing> を返す。
make_shared<type>() の返り値の型は機械的に推論できるから、上の例は C++ の型指定子 auto を使って簡単に書くことができる:
auto double_ptr = make_shared<double>(0.37);
auto vec3_ptr = make_shared<vec3>(1.4142, 2.7182, 1.6180);
auto sphere_ptr = make_shared<sphere>(point3(0,0,0), 1.0);
auto を使った shared_ptr の使用例
これからは共有ポインタを使っていく。共有ポインタを使えば複数のジオメトリが同一のインスタンスを共有でき、メモリ管理が自動的で分かりやすくなる。例えばたくさんの球が同じテクスチャマップマテリアルを使うといったことが可能になる。
std::shared_ptr は <memory> ヘッダーでインクルードできる。
もう一つ見慣れないかもしれない C++ の機能が std::vector である。これは任意の型の値を線形に並べたコレクションを表す一般的な型であり、上の例では hittable を指すポインタの集まりに使っている。std::vector は要素が増えると自動的にメモリを確保する。上の例では objects.push_back(object) が std::vector 型のメンバー変数 objects の最後に値を追加している。
std::vector は <vector> ヘッダーでインクルードできる。
また リスト 1.20 の using std::shared_ptr と using std::make_shared は、std ライブラリの shared_ptr と make_shared をこれから使うことをコンパイラに伝えている。こうすると std:: と付けなくてもこれらの型と関数を参照できるようになる。
数学定数とユーティリティ関数
数学定数を一つのヘッダーファイルにまとめて定義しておくと便利である。いま必要なのは無限大だけだが、後で円周率 \(\pi\) も入れることになる。\(\pi\) の標準的でポータブルな定義はないので、自分で定義する。メインのヘッダーファイル rtweekend.h を作って、定数やユーティリティ関数はここに入れる:
#ifndef RTWEEKEND_H
#define RTWEEKEND_H
#include <cmath>
#include <cstdlib>
#include <limits>
#include <memory>
// using
using std::shared_ptr;
using std::make_shared;
using std::sqrt;
// 定数
const double infinity = std::numeric_limits<double>::infinity();
const double pi = 3.1415926535897932385;
// ユーティリティ関数
inline double degrees_to_radians(double degrees) {
return degrees * pi / 180;
}
// 共通ヘッダー
#include "ray.h"
#include "vec3.h"
#endif
rtweekend.h] 共通ヘッダー rtweekend.h
メイン関数も書き換える:
#include "rtweekend.h"
#include "hittable_list.h"
#include "sphere.h"
#include <iostream>
color ray_color(const ray& r, const hittable& world) {
hit_record rec;
if (world.hit(r, 0, infinity, rec)) {
return 0.5 * (rec.normal + color(1,1,1));
}
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5*(unit_direction.y() + 1.0);
return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}
int main() {
const auto aspect_ratio = 16.0 / 9.0;
const int image_width = 384;
const int image_height = static_cast<int>(image_width / aspect_ratio);
std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";
auto viewport_height = 2.0;
auto viewport_width = aspect_ratio * viewport_height;
auto focal_length = 1.0;
auto origin = point3(0, 0, 0);
auto horizontal = vec3(viewport_width, 0, 0);
auto vertical = vec3(0, viewport_height, 0);
auto lower_left_corner =
origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
hittable_list world;
world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
world.add(make_shared<sphere>(point3(0,-100.5,-1), 100));
for (int j = image_height-1; j >= 0; --j) {
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
auto u = double(i) / (image_width-1);
auto v = double(j) / (image_height-1);
ray r(origin, lower_left_corner + u*horizontal + v*vertical);
color pixel_color = ray_color(r, world);
write_color(std::cout, pixel_color);
}
}
std::cerr << "\nDone.\n";
}
main.cc] hittable を使ったメイン関数

このプログラムを実行すると、球の位置と法線を可視化した画像が得られる。これはモデルの特徴や欠陥を確認するのに役立つことが多い。