球のレンダリング

レイトレーサーにオブジェクトを追加しよう。球とレイの交差判定は非常に簡単に行えるので、レイトレーサーに最初に追加されるオブジェクトは球であることが多い。

レイと球の衝突判定

原点中心で半径が \(R\) の球は \(x^{2} + y^{2} + z^{2} = R^{2}\) と表されることを思い出そう。つまり点 \((x, y, z)\) がこの球上にあるなら \(x^{2} + y^{2} + z^{2} = R^{2}\) が成立する。もし点 \((x, y, z)\) が球の内側にあるなら\(x^{2} + y^{2} + z^{2} \lt R^{2}\) が成り立ち、点 \((x, y, z)\) が球の外側にあるなら \(x^{2} + y^{2} + z^{2} > R^{2}\) が成り立つ。

球の中心が \((C_{x}, C_{y}, C_{z})\) なら、方程式は少し汚くなって \[ (x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 = r^2 \] となる。

グラフィックスでは、数式がベクトルを使って表され、x, y, z といった添え字が vec3 クラスの中に隠れている状態が望ましい。球の中心 \(\mathbf{C} = (C_{x}, C_{y}, C_{z})\) から点 \(\mathbf{P} = (x, y, z)\) へのベクトルは \((\mathbf{P} - \mathbf{C})\) と表せるから、 \[ (\mathbf{P} - \mathbf{C}) \cdot (\mathbf{P} - \mathbf{C}) = (x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 \] が成り立つ。よってベクトルを使った球の方程式は \[ (\mathbf{P} - \mathbf{C}) \cdot (\mathbf{P} - \mathbf{C}) = r^2 \] と書ける。

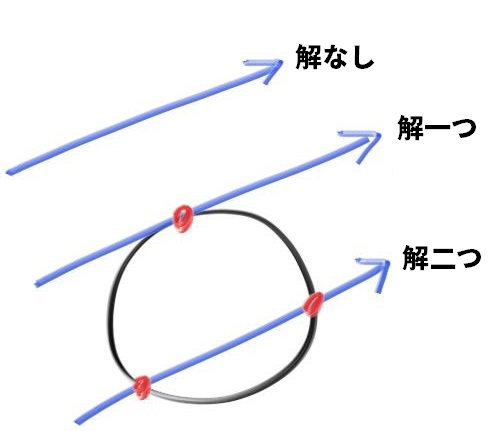
これは「ある点 \(\mathbf{P}\) がこの方程式を満たすなら、その点は球上にある」と読める。さてレイ \(\mathbf{P}(t) = \textbf{A} + t \textbf{b}\) が球と交わるかを調べたい。もしレイが球と交わるなら、ある \(t\) で \(\textbf{P}(t)\) が球の方程式を満たす。つまり次の条件を満たす \(t\) が存在するかを調べればよい: \[ (\mathbf{P}(t) - \mathbf{C}) \cdot (\mathbf{P}(t) - \mathbf{C}) = r^2 \] \(\mathbf{P}(t)\) に定義の式を代入すれば \[ (\mathbf{A} + t \mathbf{b} - \mathbf{C}) \cdot (\mathbf{A} + t \mathbf{b} - \mathbf{C}) = r^2 \] となる。後はベクトルの公式が使える。この等式を展開して項をまとめれば \[ t^2 \mathbf{b} \cdot \mathbf{b} + 2t \mathbf{b} \cdot (\mathbf{A}-\mathbf{C}) + (\mathbf{A}-\mathbf{C}) \cdot (\mathbf{A}-\mathbf{C}) - r^2 = 0 \] となる。この等式中のベクトルと \(r\) は全て既知の定数だから、これは未知の \(t\) に関する二次方程式となる。高校の数学で習ったように、この方程式の解 \(t\) を表す式には根号が含まれる。根号中の式が正・\(0\)・負となる場合に応じて、実数解の個数は二つ・一つ・解なしとなる。こういったグラフィックスにおける代数方程式には幾何学的な意味があることが多く、今考えている問題では次のようになる:

最初のレイトレーシング画像

この数式をプログラムにハードコードして正しいことを確かめよう。\(z\) 軸上の点 \(z = -1\) に置かれた小さな球とレイが交わるときにピクセルを赤くする:

bool hit_sphere(const point3& center, double radius, const ray& r) {
  vec3 oc = r.origin() - center;
  auto a = dot(r.direction(), r.direction());
  auto b = 2.0 * dot(oc, r.direction());
  auto c = dot(oc, oc) - radius*radius;
  auto discriminant = b*b - 4*a*c;
  return (discriminant > 0);
}


color ray_color(const ray& r) {
  if (hit_sphere(point3(0,0,-1), 0.5, r))
    return color(1, 0, 0);
  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

次の画像が得られる:

足りない機能は山ほどある ──シェーディングも反射もないし、オブジェクトは一つだけだ。しかし私たちは大きな一歩を踏み出した！ 一つ注意しておくと、このプログラムではレイが \(t \lt 0\) で交わる場合にもピクセルを赤くしている。そのため球の中心を \(z = +1\) としても同じ画像が得られてしまう。もちろんこれは正しくない！ 次はこういった問題を修正する。