誘電体マテリアル
水・ガラス・ダイアモンドといった透明な材質を誘電体 (dielectric) と呼ぶ。こういった物体に衝突したレイは反射レイと屈折レイ (透過レイ) に分かれる。このレイトレーサーでは衝突ごとに反射と屈折をランダムに選び、反射レイと屈折レイのどちらか一方だけを散乱レイとして生成するものとする。
屈折
屈折レイのデバッグは本当に難しい。次の画像はこの本のために実際に書いたプログラムで得られたものだ。二つのガラス球が配置されたシーンをレンダリングしているのだが、これは正しいだろうか?

現実のガラス球も奇妙な見た目をしているが、この画像のように見えることはない。正しいガラス球の内部では上下が反転し、変な黒い環はできない。画像の中心周辺にレイを送れば、それだけで何かが間違っていると分かる (この方法が利用できることは多い)。また屈折レイをデバッグするときは、反射レイを無くして全てのレイを屈折させるようにするとよい。
スネルの法則
屈折はスネルの法則 (Snell's law) で表される: \[ \eta \cdot \sin\theta = \eta' \cdot \sin\theta' \] \(\theta\) と \(\theta'\) は法線からの角度であり、\(\eta\) と \(\eta'\) は媒質の屈折率を表す (屈折率は空気なら \(1.0\), ガラスなら \(1.3–1.7\), ダイアモンドなら \(2.4\) 程度である)。屈折を表す図を示す:
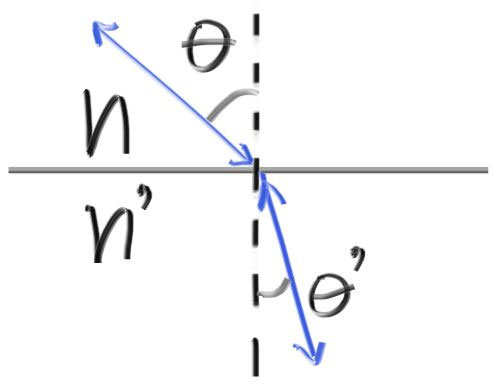
屈折後の角度 \(\sin \theta'\) は \[ \sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta \] と表せる。これを使って屈折後のレイのベクトルを求めよう。入射レイと屈折レイを \(\textbf{R},\ \) \(\textbf{R}'\) として、法線を \(\textbf{n}'\) とする (全て単位ベクトル)。\(\textbf{R}'\) を \(\textbf{n}'\) と平行な成分 \(R_{\parallel}\) と垂直な成分 \(R_{\bot}\) に分けると \[ \mathbf{R}' = \mathbf{R}'_{\parallel} + \mathbf{R}'_{\bot} \] が成り立つ。幾何的な関係を使って \(\mathbf{R}'_{\parallel}\) と \(\mathbf{R}'_{\bot}\) を求めると \[ \begin{aligned} \mathbf{R'}_{\parallel} & = \frac{\eta}{\eta'} (\mathbf{R} + \cos\theta \mathbf{n}) \\ \mathbf{R'}_{\bot} & = -\sqrt{1 - |\mathbf{R'}_{\parallel}|^2} \mathbf{n} \end{aligned} \] となる。導出は示さないが、可能なら自分で確認してみよ。これ以降この式の導出が必要になることはない。
さらに \(\cos\theta\) をベクトルで表す必要がある。よく知られているように、二つのベクトルの積はそれらがなす角度のコサインを使って表せる: \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta \] さらに \(\textbf{a}\) と \(\textbf{b}\) が単位ベクトルなら \[ \mathbf{a} \cdot \mathbf{b} = \cos\theta \] が成り立つ。
\(\textbf{R}\) と \(\textbf{n}\) は単位ベクトルだから、\(\mathbf{R}'_{\parallel}\) を既知の記号だけを使って表せる: \[ \mathbf{R'}_{\parallel} = \frac{\eta}{\eta'} (\mathbf{R} + (\mathbf{-R} \cdot \mathbf{n}) \mathbf{n}) \]
以上の考察を使えば \(\textbf{R}'\) を計算する関数が得られる:
vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {
auto cos_theta = dot(-uv, n);
vec3 r_out_parallel = etai_over_etat * (uv + cos_theta*n);
vec3 r_out_perp = -sqrt(1.0 - r_out_parallel.length_squared()) * n;
return r_out_parallel + r_out_perp;
}
vec3.h] refract 関数
この関数を使って常に屈折が起こる誘電体マテリアルを実装しよう:
class dielectric : public material {
public:
dielectric(double ri) : ref_idx(ri) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const {
attenuation = color(1.0, 1.0, 1.0);
double etai_over_etat;
if (rec.front_face) {
etai_over_etat = 1.0 / ref_idx;
} else {
etai_over_etat = ref_idx;
}
vec3 unit_direction = unit_vector(r_in.direction());
vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
scattered = ray(rec.p, refracted);
return true;
}
double ref_idx;
};
material.h] 常に屈折する dielectric マテリアル
この dielectric を使うと次の画像が得られる:

全反射
何かが明らかにおかしい。問題が起こっているのはレイが屈折率の高い媒質から屈折率の低い媒質に抜けていくときで、このときスネルの法則に解がなくなって屈折が起こらなくなる。スネルの法則によると \[ \sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta \] だから、ガラスの内部 (\(\eta = 1.5\)) から空気 (\(\eta' = 1.0\)) へレイが抜けるとき \[ \sin\theta' = \frac{1.5}{1.0} \cdot \sin\theta \] が成り立つ。\(\sin\theta'\) の値は \(1\) より大きくならないから、 \[ \frac{1.5}{1.0} \cdot \sin\theta > 1.0 \] のとき等式が意味を持たなくなり、解がなくなる。解がないとき屈折は起こらず、レイは反射する:
if (etai_over_etat * sin_theta > 1.0) {
// 必ず反射する
...
}
else {
// 反射または屈折する
...
}
material.h] レイが屈折する可能性を判定する
条件 \(\dfrac{\eta}{\eta'} \sin \theta > 1\) が成り立つときに全ての光が反射されるこの現象を全反射 (total internal reflection) と呼ぶ ("internal" と付いているのは、光が媒質内から空気中に向かうときに起こることが多いためだ)。水中から水面を見上げると視界の端が鏡のように見えるのは全反射が起きるためである。
コード中で sin_theta を計算するときには、三角関数に関する恒等式 \[ \sin \theta = \sqrt{1 - \cos^{2} \theta} \] そして \[ \cos\theta = \mathbf{R} \cdot \mathbf{n} \] が利用できる。
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if(etai_over_etat * sin_theta > 1.0) {
// 必ず反射する
...
}
else {
// 反射または屈折する
...
}
material.h] レイが屈折する可能性を判定する
可能な場合に必ず屈折する誘電体マテリアルは次のように書ける:
class dielectric : public material {
public:
dielectric(double ri) : ref_idx(ri) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const {
attenuation = color(1.0, 1.0, 1.0);
double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if (etai_over_etat * sin_theta > 1.0 ) {
vec3 reflected = reflect(unit_direction, rec.normal);
scattered = ray(rec.p, reflected);
return true;
}
vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
scattered = ray(rec.p, refracted);
return true;
}
public:
double ref_idx;
};
material.h] 屈折を加えた dielectric クラス
減衰 (attenuation) は常に \(1\) である ──ガラス球は光を吸収しない。このマテリアルをシーンに追加しよう:
world.add(make_shared<sphere>(
point3(0,0,-1), 0.5, make_shared<lambertian>(color(0.1, 0.2, 0.5))));
world.add(make_shared<sphere>(
point3(0,-100.5,-1), 100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
world.add(make_shared<sphere>(
point3(1,0,-1), 0.5, make_shared<metal>(color(.8, .6, .2), 0.0)));
world.add(make_shared<sphere>(
point3(-1,0,-1), 0.5, make_shared<dielectric>(1.5)));
main.cc] シーンに誘電体の球を加える
次の画像が得られる:

シュリックの近似
現実のガラスの反射率は角度によって異なる ──窓を水平に近い角度から見ると、まるで鏡のように見える。この現象を記述する複雑な数式もあるが、ほとんど誰もが次の近似を使っている。これは非常に簡単かつ正確な多項式近似であり、Christophe Schlick によって提案された:
double schlick(double cosine, double ref_idx) {
auto r0 = (1-ref_idx) / (1+ref_idx);
r0 = r0*r0;
return r0 + (1-r0)*pow((1 - cosine),5);
}
material.h] シュリックの近似
これで誘電体マテリアルが完成する:
class dielectric : public material {
public:
dielectric(double ri) : ref_idx(ri) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const {
attenuation = color(1.0, 1.0, 1.0);
double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if (etai_over_etat * sin_theta > 1.0 ) {
vec3 reflected = reflect(unit_direction, rec.normal);
scattered = ray(rec.p, reflected);
return true;
}
double reflect_prob = schlick(cos_theta, etai_over_etat);
if (random_double() < reflect_prob) {
vec3 reflected = reflect(unit_direction, rec.normal);
scattered = ray(rec.p, reflected);
return true;
}
vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
scattered = ray(rec.p, refracted);
return true;
}
public:
double ref_idx;
};
material.h] 完成した誘電体マテリアル
中空ガラス球のモデリング
誘電体球の半径を負に設定すると、ジオメトリは変わらず法線だけが反転する。これを使うと中空の球を作ることができる:
world.add(make_shared<sphere>(
point3( 0, 0, -1), 0.5, make_shared<lambertian>(color(0.1, 0.2, 0.5))));
world.add(make_shared<sphere>(
point3( 0, -100.5, -1), 100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
world.add(make_shared<sphere>(
point3( 1, 0, -1), 0.5, make_shared<metal>(color(0.8, 0.6, 0.2), 0.3)));
world.add(make_shared<sphere>(
point3(-1, 0, -1), 0.5, make_shared<dielectric>(1.5)));
world.add(make_shared<sphere>(
point3(-1, 0, -1), -0.45, make_shared<dielectric>(1.5)));
main.cc] シーンに中空のガラス球を追加する
次の画像が得られる:
