拡散マテリアル

複数のオブジェクトと各ピクセルに対する複数のレイがサポートできたので、これで現実的な見た目のマテリアルを作る準備が整った。まず拡散マテリアル (diffuse material) から始める (拡散マテリアルは非光沢マテリアル (matte material) とも呼ばれる)。ジオメトリとマテリアルの実装に関して、両者を分離する方法と両者を結び付ける方法がある。分離すると一つのマテリアルを複数のジオメトリに割り当てる使い方 (およびその逆) が可能になるが、結び付けるとプロシージャルなオブジェクトが扱いやすくなる。私たちは (他の多くのレンダラと同様) ジオメトリとマテリアルを分離する方法を使うが、その制限は意識しておくべきだ。

単純な拡散マテリアル

拡散マテリアルを持つ物体は周囲からの光をそのまま反射するのではなく、マテリアルに固有の色でその光を変化させる。また拡散表面で反射した光は方向がランダムになる。例えば二つの拡散マテリアルの間に三つのレイを放つと、それぞれがランダムに反射する (散乱する) ことになる:

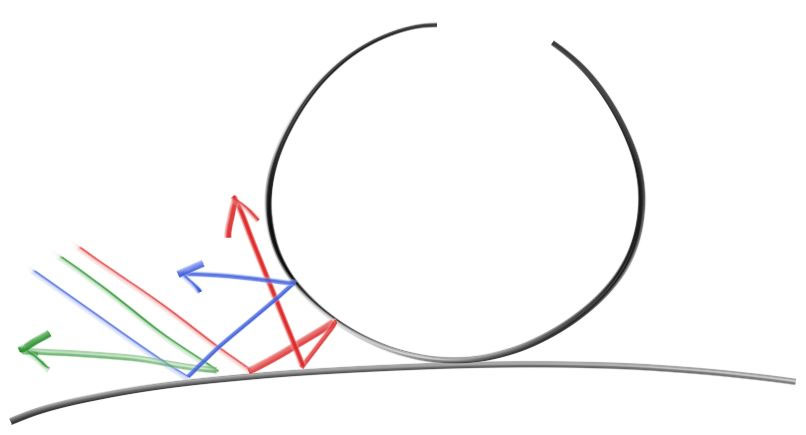
光は反射せずに吸収される可能性もある。表面が黒いならそれだけ吸収される光の量も増える (だから黒いのだ！)。実は反射光の方向を何らかの意味でランダムに設定するアルゴリズムを使えば、それだけで非光沢らしい見た目が得られる。これから説明するのは理想的な拡散表面を近似する簡単なアルゴリズムの一つである (私はこれを数学的に理想的なランバーティアン (Lambertian) を近似するための怠惰なハックとして使っていた)。

(この本を読んだ Vassillen Chizhov はこの手法が本当に怠惰なハックに過ぎず、ランバーティアンの近似として不正確なことを証明した。理想的なランバーティアンの正しい定式化は難しいものではなく、この節の最後に示してある)

レイと物体表面の交点 \(\mathbf{P}\) に接する単位球は二つある。法線を \(\mathbf{n}\) とすると、二つの球の中心は \(\textbf{P} + \textbf{n}\) および \(\textbf{P} - \textbf{n}\) と表せる。中心が \(\textbf{P} - \textbf{n}\) の球は物体の内側にあり、中心が \(\textbf{P} + \textbf{n}\) の球は物体の外側にある。物体から見てレイの始点と同じ方向にある球を選び、その球の中にランダムな点 \(\textbf{S}\) を取る。そして交点 \(\textbf{P}\) から \(\textbf{S}\) に向かって飛ばしたレイを散乱レイとして採用する (このレイは \(\mathbf{S}-\mathbf{P}\) を向く)。

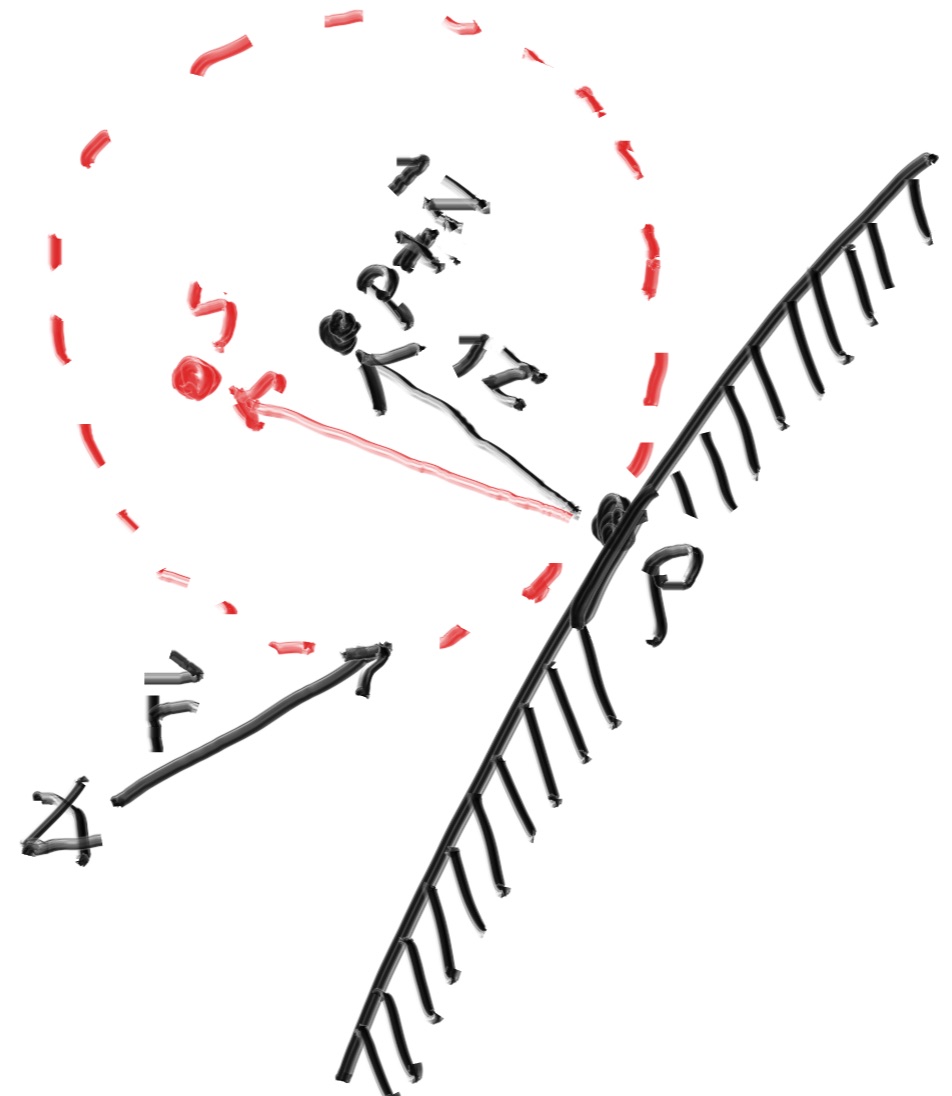
このアルゴリズムの実装では単位球の中にランダムな点を取る処理が必要になる。ここでは棄却法 (rejection method) と呼ばれる最も簡単なアルゴリズムを使う: x, y, z を \(-1\) から \(+1\) の範囲でランダムに取り、点 \((x, y, z)\) が単位球の内部にあるならそれを採用する。単位球の外側にあるなら棄却し、同じ処理をもう一度行う。

class vec3 {
public:
  ...
  inline static vec3 random() {
    return vec3(random_double(), random_double(), random_double());
  }

  inline static vec3 random(double min, double max) {
    return vec3(random_double(min,max),
                random_double(min,max),
                random_double(min,max));
  }

リスト 1.31 [vec3.h] ランダムな vec3 を計算するユーティリティ関数

vec3 random_in_unit_sphere() {
  while (true) {
    auto p = vec3::random(-1,1);
    if (p.length_squared() >= 1) continue;
    return p;
  }
}

リスト 1.32 [vec3.h] random_in_unit_sphere() 関数

レイが物体と衝突したら散乱レイとしてランダムなベクトルを生成し、そのレイの色をさらに計算するよう ray_color() 関数を書き換える:

color ray_color(const ray& r, const hittable& world) {
  hit_record rec;

  if (world.hit(r, 0, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_in_unit_sphere();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.33 [main.cc] ランダムな散乱レイを使った ray_color()

子レイの数を制限する

ここで生じうる問題が一つある。ray_color 関数が再帰的なことに注目してほしい。再帰呼び出しがいつ終わるのかと言えば、レイが何にも当たらないときだ。しかしそれまでの反射回数がとても多くなって、スタックを使い切ってしまう可能性がある。このケースに対処するために、再帰呼び出しの最大回数を制限しておこう。最大の深さまで行ったレイからの寄与はゼロとする:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_in_unit_sphere();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

...

int main() {
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 384;
  const int image_height = static_cast<int>(image_width / aspect_ratio);
  const int samples_per_pixel = 100;
  const int max_depth = 50;

  ...
  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(0, 0, 0);
      for (int s = 0; s < samples_per_pixel; ++s) {
        auto u = (i + random_double()) / (image_width-1);
        auto v = (j + random_double()) / (image_height-1);
        ray r = cam.get_ray(u, v);
        pixel_color += ray_color(r, world, max_depth);
      }
      write_color(std::cout, pixel_color, samples_per_pixel);
    }
  }

  std::cerr << "\nDone.\n";
}

リスト 1.34 [main.cc] 再帰の深さに制限を付けた ray_color()

次の画像が得られる。球の下に影ができている (暗くて影がよく分からなくてもすぐに直すので気にしなくてよい)。

ガンマ補正による明るさの調整

球は反射ごとにエネルギーを半分だけしか吸収していないにもかかわらず、この画像はとても暗い。光の \(50\) %は反射されており、球は非常に明るく (現実世界であれば明るい灰色に) 見えるのが正しい。この画像が間違った色に見えるのは、ほぼ全ての画像ビューアが読み込む画像を「ガンマ補正 (gamma correction) 」されたものとして扱うことに原因がある。つまり \(0\) から \(1\) の値をバイトとして書き込む前に、特別な変換を施さなければならない。ガンマ補正が必要な理由はもちろん存在するが、ここではただ必要なのだと理解しておこう。ここでは \(\gamma = 2\) のガンマ変換を利用する。これは色の各成分を \(1/\gamma = 1/2\) 乗する処理であり、平方根を取ればよい:

void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
  auto r = pixel_color.x();
  auto g = pixel_color.y();
  auto b = pixel_color.z();

  // 色の合計をサンプルの数で割り、gamma = 2.0 のガンマ補正を行う
  auto scale = 1.0 / samples_per_pixel;
  r = sqrt(scale * r);
  g = sqrt(scale * g);
  b = sqrt(scale * b);

  // 各成分を [0,255] に変換して出力する
  out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
      << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}

リスト 1.35 [color.h] ガンマ補正を追加した write_color()

これで狙い通りの明るい画像が得られる:

シャドウアクネを消す

気付きにくいが、実はこの画像にもまだバグがある。散乱レイと球の交点は正確に \(t = 0\) ではなく、浮動小数の誤差によって \(t=-0.0000001\) あるいは \(t=0.0000001\) といった値になる。そのためレイと球の交点を判定するときには \(0\) に非常に近い交点を無視する必要がある:

if (world.hit(r, 0.001, infinity, rec)) {

リスト 1.36 [main.cc] 下限付きの散乱レイの計算

これでシャドウアクネ (shadow acne) の問題が解決できる。本当にこう呼ばれている¹。

完全なランバート反射

先ほど示した棄却法は法線に接する単位球に含まれるランダムな点を生成する。この点が交点が中心で法線が天頂を指す半球上の点を指すベクトルを表しているとすれば、法線ベクトルに近い方向のベクトルは高い確率で、水平線に使い方向のベクトルは低い確率で生成される。棄却法によって生成されるベクトルと法線の角度を \(\phi\) とすると、角度が \(\phi\) のベクトルが生成される確率は \(\cos^{3} \phi\) に比例する。現実でも斜めの方向から入射した光は大きく広がってその点の色への影響が小さくなるので、これは現実的な挙動だと言える。

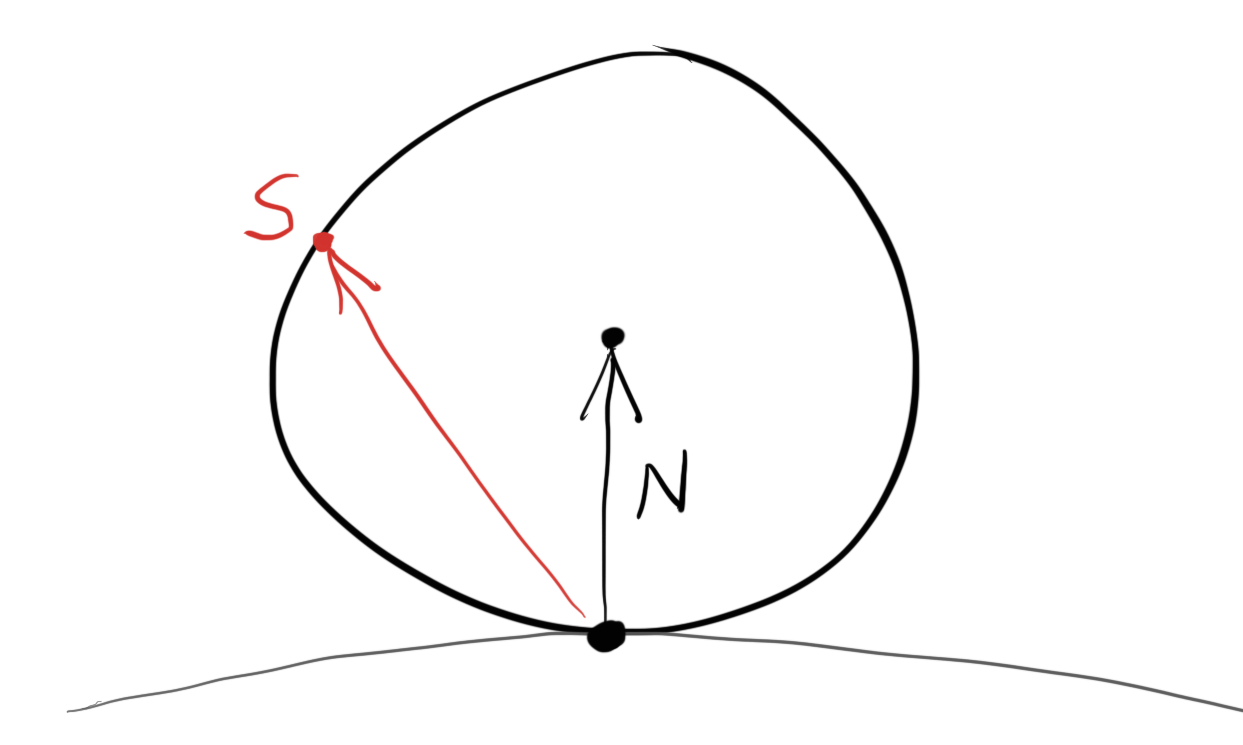
しかし拡散反射で通常使われるのはランバート分布であり、この分布では前述の確率が \(\cos \phi\) に比例する。つまり完全なランバート分布に従うマテリアルは法線に近い方向にレイを多く散乱させるが、その分布はもっと一様分布に近い。実は法線に接する単位球上の点を選ぶと、散乱レイがこの分布を満たすようになる。単位球上の点をランダムに選ぶには、緯度と高さをそれぞれランダムに選んでから座標を組み立てればよい:

vec3 random_unit_vector() {
  auto a = random_double(0, 2*pi);
  auto z = random_double(-1, 1);
  auto r = sqrt(1 - z*z);
  return vec3(r*cos(a), r*sin(a), z);
}

リスト 1.37 [vec3.h] random_unit_vector() 関数

現在使っている random_in_unit_sphere() 関数をこの random_unit_vector() 関数と取り換える:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0.001, infinity, rec)) {
    point3 target = rec.p + rec.normal + random_unit_vector();
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.38 [main.cc] 拡散レイの計算を変更した ray_color

次の画像が得られる:

拡散マテリアルを持った球が二つあるだけなので何が変わったのか分かりにくいが、二つの重要な違いに気が付くだろう:

変更後のレンダリングでは影が薄くなっている
変更後のレンダリングでは球が明るくなっている

レイがより一様に散乱するようになり、法線方向に散乱するレイが減ったのがこの原因である。つまり拡散マテリアルに入射したレイの中でカメラに向かうものの割合が増加した。また小さな球と大きな球に挟まれる部分に入射したレイが法線方向に反射して小さな球に当たる確率が減少するので、影は薄くなる。

拡散マテリアルの異なる定式化

拡散マテリアルとして最初に示したハック (単位球内のランダムな点を使うもの) が理想的なランバーティアン拡散マテリアルの近似として間違っていることが証明されるまでには長い時間がかかり、それまで誰も声を上げなかった。間違いが長い間残り続けたのは、間違いを正すのに次の二つが求められるためである:

確率分布が正しくないことを数学的に証明する。
\(\cos \phi\) という分布とレンダリング結果の正しさを納得する。

日常生活で目にする物体で完全な拡散マテリアルの性質を持つものはほとんどない。そのためそういった物体が理想的な環境でどう見えるかについて、私たちの直観はあまり役に立たない。

拡散マテリアルについて理解を深めるために、これまでのものより理解しやすく簡単な拡散レイの計算方法を示す。これまでに示した二つの方法はランダムなベクトルを生成していたが、このベクトルを法線で移動させる理由はあまり明らかでなかったかもしれない。

より理解しやすい計算方法とは、法線との角度に関係なく全ての方向に向かって一様にレイが散乱すると考えるものである。初期のレイトレーシングの論文はこの方法を使って拡散反射を計算していた (後になってランバーティアンが採用された)。

vec3 random_in_hemisphere(const vec3& normal) {
  vec3 in_unit_sphere = random_in_unit_sphere();
  if (dot(in_unit_sphere, normal) > 0.0)
    return in_unit_sphere; // in_unit_sphere は normal と同じ半球にある
  else
    return -in_unit_sphere;
}

リスト 1.39 [vec3.h] random_in_hemisphere() 関数

これを ray_color() 関数に組み込む:

color ray_color(const ray& r, const hittable& world, int depth) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  if (world.hit(r, 0.001, infinity, rec)) {
    point3 target = rec.p + random_in_hemisphere(rec.normal);
    return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
  }

  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5*(unit_direction.y() + 1.0);
  return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

リスト 1.40 [vec3.h] ray_color() 関数の変更部分

次の画像が得られる:

本を読み進めるとシーンはもっと複雑になる。そういったシーンをここで示した異なる拡散マテリアルを使ってレンダリングし、その結果を比較するとよい。興味深いシーンには多くの拡散マテリアルが含まれるから、異なる拡散マテリアルが持つシーン全体のライティングへの影響について多くのことが学べるだろう。

訳注: 「アクネ (acne)」は「にきび」のこと。^[return]