包含立体階層
この節で説明するのは私たちが作っているレイトレーサーの中で格段に難しく入り組んだ部分である。これを実装すればコードの実行が速くなるのでここで取り上げる。さらにここで hittable をリファクタリングしておけば、後で長方形と直方体を簡単に追加できるようになる。
レイとオブジェクトの衝突判定はレイトレーサーの実行時間におけるボトルネックの一つであり、実行時間はオブジェクトの数に対して線形に増加する。しかしレンダリングでは同じモデルに対する探索が繰り返されるので、二分探索の考え方を応用すれば探索を対数時間にできるに違いない。モデルに放たれるレイの数は数百万ときには数億に達するから、モデルのソートのような処理でレイとの衝突判定の処理時間を劣線形1にできれば非常に大きな高速化となる。モデルのソートには大きく分けて二つの方法がある。一つは空間を分割するもので、もう一つはオブジェクトを分割するものである。後者の方がずっと簡単に実装でき、たいていのモデルに対しては前者と同程度に高速となる。
基本的なアイデア
3D オブジェクトの集合の包含立体 (bounding volume) とは、集合内の全てのオブジェクトを含む (包む) 立体 のことを言う。例えば \(10\) 個のオブジェクトの包含球 (bonding sphere) が計算できているなら、包含球と交わらない任意のレイは \(10\) 個のオブジェクトのどれとも交わらない。逆にレイが包含球と交わるなら、そのレイは \(10\) 個のオブジェクトのどれかと交わる可能性がある。つまり包含立体を使うコードは必ず次の形をしている:
if (レイが包含立体と交わる)
return レイが包含立体内のオブジェクトと交わるかどうか
else
return false
スクリーンや空間ではなくオブジェクトを分割しているのが鍵である。またオブジェクト一つごとにちょうど一つの包含立体を考えるが、異なるオブジェクトの包含立体同士は重なる場合もある。
包含立体階層
劣線形性を達成するには、包含立体の階層を考える必要がある。例えばオブジェクトの集合を二つ (赤と青) に分け、その上で二つの集合それぞれの包含立体 (直方体) を考える。このとき次の図のような状況となる:
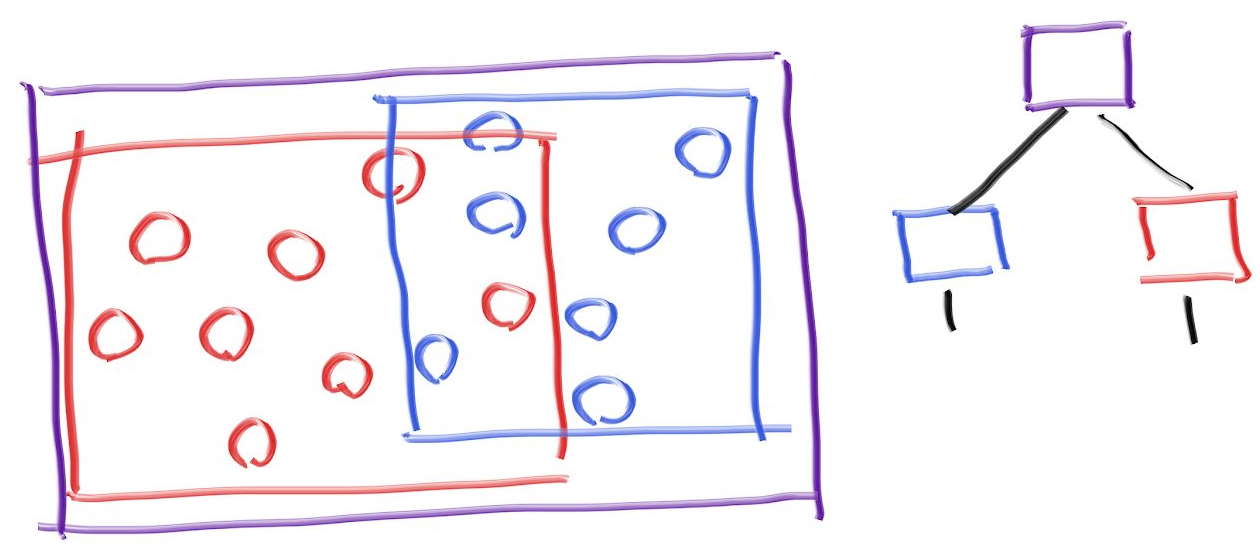
紫の包含立体には青と赤の包含立体が含まれるが、この二つは重なり得る。また青と赤の包含立体は両方とも紫の中にあるだけで、順序付いていない。図にある木では青を右の子として、赤を左の子として書いているが、この方向に意味は無い。この包含立体階層を使うコードは次のようになる:
if (紫と交わる)
hit0 = 青に含まれるオブジェクトと交わる
hit1 = 赤に含まれるオブジェクトと交わる
if (hit0 or hit1)
return (true, 近い方の交点の情報)
return false
軸平行包含直方体
以上のアイデアを実装するには、包含立体とレイの衝突判定とオブジェクトの良い分割処理が必要になる (悪い分割も存在する)。包含立体とレイの衝突判定は高速である必要があり、さらに包含立体は小さくなければならない。現実で扱う多くのモデルでは辺が軸に平行な直方体が包含立体として他の選択肢よりも優れている。ただし変わったモデルを扱うときには他の選択肢もあることを思い出せるようにしておくべきである。
正確に「辺が軸に平行な包含直角平行六面体」と呼んだのでは長すぎるので、これからは軸平行包含直方体 (axis-aligned bounding box, AABB) と呼ぶ。レイと AABB の衝突判定にはどんな方法を使っても構わない。また知りたいのは衝突するかどうかだけであり、描画するオブジェクトとの衝突判定のように衝突点やそこでの法線といった情報は必要ない。
レイと AABB の衝突判定には「スラブ」を使った方法が使われることが多い2。この方法は \(n\) 次元の AABB が \(n\) 個の軸に平行な区間の和集合として表せるという観察を利用する。区間とは二つの端点に挟まれた点の集合であり、例えば「\(3 \lt x \lt 5\) を満たす \(x\)」あるいは「\((3, 6)\)に含まれる \(x\)」は区間を定義する。二次元では、\(x\) の区間と \(y\) の区間が 2D の AABB (長方形) を構成する:
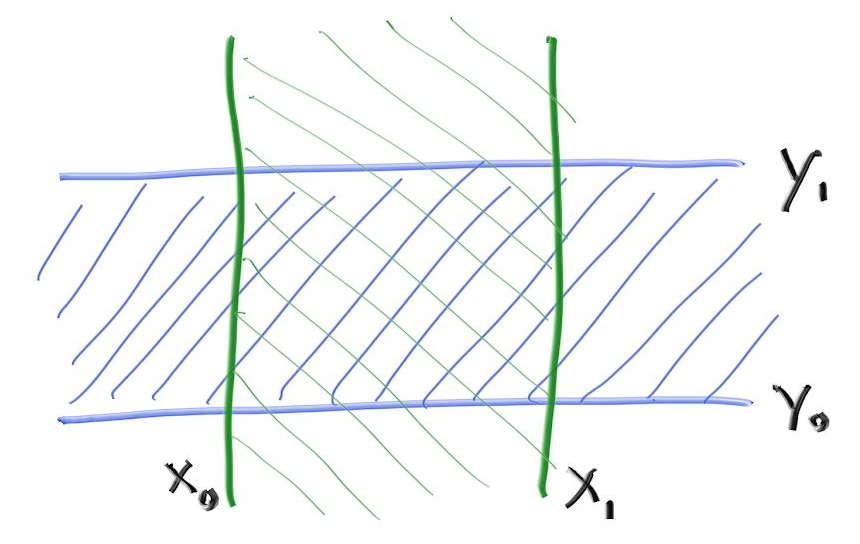
レイと区間の衝突を判定するには、まずレイが区間の境界 (スラブ) と交わるかを調べる。二次元の例であれば、レイがスラブと交わるときのレイのパラメータは \(t_{0}\) および \(t_{1}\) と表せる (スラブと平行なレイでは \(t_{0}\) と \(t_{1}\) は定義されない)。
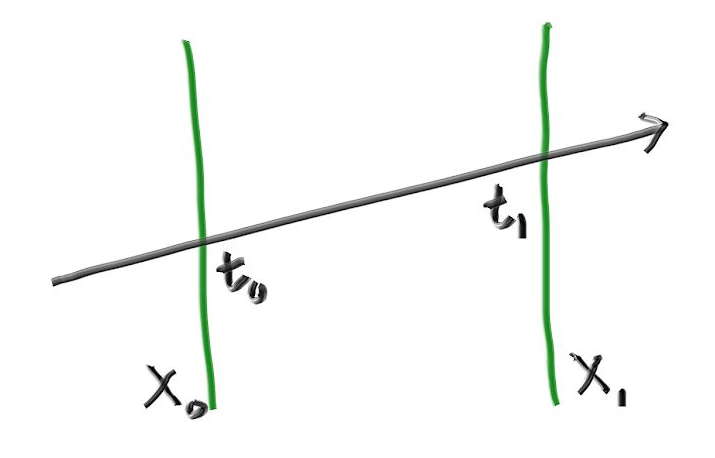
三次元では区間の境界が平面になり、その方程式は \(x = x_{0}\) および \(x = x_{1}\) と表せる (\(x\) の区間の場合)。この平面とレイはどこで交わるだろうか? レイは実数 \(t\) を受け取って位置 \(\textbf{P}(t)\) を返す関数 \[ \mathbf{P}(t) = \mathbf{A} + t \mathbf{b} \] と考えることができ、この等式は \(x\), \(y\), \(z\) 座標のそれぞれで成り立つ。例えば \(x\) 座標では \(x(t) = A_{x} + t b_{x}\) となる。よってこのレイが平面 \(x = x_{0}\) と交わるときの \(t\) で次の等式が成り立つ: \[ x_0 = A_x + t_0 b_x \] したがって交点における \(t = t_{0}\) で \[ t_0 = \frac{x_0 - A_x}{b_x} \] だと分かる。\(x_{1}\) についても同様に \[ t_1 = \frac{x_1 - A_x}{b_x} \] を得る。この一次元の結果を使って衝突を判定するときに鍵となるのが、座標ごとの \(t\) の区間が重なるなら例と AABB が衝突するという事実である。例えば次の二次元の例では、レイと長方形が衝突するときに限って緑と青の区間が重なる:
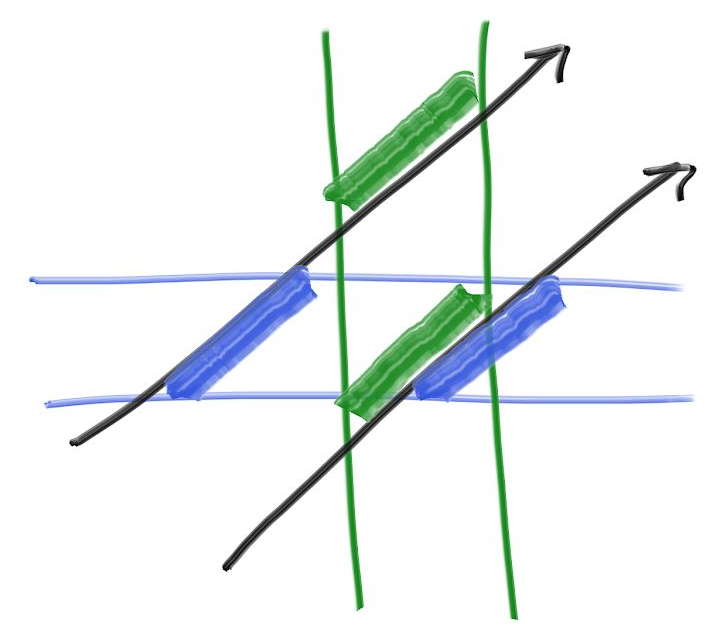
AABB を使ったレイの衝突判定
次の疑似コードはレイがスラブを通る \(t\) の値を求め、座標ごとの \(t\) の区間が重なるかを判定する:
compute (tx0, tx1)
compute (ty0, ty1)
return overlap?( (tx0, tx1), (ty0, ty1))
これは素晴らしく簡単である。この方法は三次元でも同じように使えるというのが、多くの人々から AABB が選ばれる理由となっている:
compute (tx0, tx1)
compute (ty0, ty1)
compute (tz0, tz1)
return overlap?( (tx0, tx1), (ty0, ty1), (tz0, tz1))
このスラブを使った方法にはいくつか注意点があるから、一見したほどには美しくないかもしれない。第一に、\(x\) 軸負方向に進むレイに対して上記の方法で区間 \(t_{x_{0}}, t_{x_{1}}\) を計算すると、\((7, 3)\) のように反転した区間が手に入る可能性がある。第二に、除算で無限大が生じる可能性がある。さらに、レイの始点がスラブの境界上にあると計算結果に NaN が生じる可能性がある。様々なレイトレーサーは様々な方法で AABB に関する問題に対処している (さらに SIMD などのベクトル化から生まれる問題もある。ベクトル化を使ってさらなる高速化を行いたいなら、Ingo Wald による論文が最初に読むものとして優れている)。今の私たちのプログラムでは、この部分はそれなりに速くしておけば大きなボトルネックになることはない。というわけで、できるだけ単純に実装しよう。そうするのが最も高速な場合もよくあるのだから! まず区間を表す式に注目する: \[ \begin{aligned} t_{x_{0}} & = \frac{x_0 - A_x}{b_x} \\ t_{x_{1}} & = \frac{x_1 - A_x}{b_x} \end{aligned} \] ここで問題なのが、何の変哲もない普通のレイでも \(b_{x} = 0\) となって \(0\) 除算が発生することがあり得る点である。そういったレイはスラブの外側にあるかもしれないし、内側にあるかもしれない。また IEEE 浮動小数点数の \(0\) には \(\pm\) の符号がある。ただここで、\(b_{x} = 0\) となるレイが \(x_{0}\) から \(x_{1}\) の間にないなら \(t_{x_{0}}\) と \(t_{x_{1}}\) は両方とも \(\infty\) となるか両方とも \(-\infty\) のなるかのどちらかであるという事実が利用できる。つまり \(\min\) と \(\max\) を使って \(t_{x_{0}}\) と \(t_{x_{1}}\) を求めれば、どんな場合にも正しい区間が計算される: \[ \begin{aligned} t_{x_{0}} & = \min \left( \frac{x_0 - A_x}{b_x}, \frac{x_1 - A_x}{b_x} \right) \\ t_{x_{1}} & = \max \left( \frac{x_0 - A_x}{b_x}, \frac{x_1 - A_x}{b_x} \right) \end{aligned} \]
もう一つ問題なのが \(b_{x} = 0\) かつ「\(x_{0} - A_{x} = 0\) または \(x_{1} - A_{x} = 0\)」となるときである。このとき NaN となってしまう。ただこの場合にはレイが交わるとしても交わらないとしても大きな問題はない。後でもう一度触れる。
続いて重なりを判定する関数を考えよう。区間が反転していない (一つ目の値が二つ目の値より小さい) として、区間が重なるとき true を返すとする。区間 \(d, D\) と \(e, E\) が重なるかを調べ、重なる場合には共通する区間 \(f, F\) を計算する関数は次のように書ける:
bool overlap(d, D, e, E, f, F)
f = max(d, e)
F = min(D, E)
return (f < F)
入力に NaN が含まれるとき、この関数は false を返す。つまり AABB と水平に近い角度で衝突するレイを扱うには、AABB を本来よりも少しだけ大きく取る必要がある (レイトレーサーではどんな可能性もいずれ起こるので、こうしなければならない)。三つの次元をループで扱うようにして、さらに区間 \(t_{\text{min}}, t_{\text{max}}\) を関数の引数として渡すようにすれば次のコードを得る:
#include "rtweekend.h"
class aabb {
public:
aabb() {}
aabb(const point3& a, const point3& b) { _min = a; _max = b;}
point3 min() const {return _min; }
point3 max() const {return _max; }
bool hit(const ray& r, double tmin, double tmax) const {
for (int a = 0; a < 3; a++) {
auto t0 = fmin((_min[a] - r.origin()[a]) / r.direction()[a],
(_max[a] - r.origin()[a]) / r.direction()[a]);
auto t1 = fmax((_min[a] - r.origin()[a]) / r.direction()[a],
(_max[a] - r.origin()[a]) / r.direction()[a]);
tmin = fmax(t0, tmin);
tmax = fmin(t1, tmax);
if (tmax <= tmin)
return false;
}
return true;
}
point3 _min;
point3 _max;
};
aabb.h] aabb クラス
AABB の衝突判定の最適化
この衝突判定法をレビューしたピクサーの Anrew Kensler は実験を行い、次のコードを提案した。これはコンパイラに関わらず非常に高速なので、私はこちらを使うようにしている:
inline bool aabb::hit(const ray& r, double tmin, double tmax) const {
for (int a = 0; a < 3; a++) {
auto invD = 1.0f / r.direction()[a];
auto t0 = (min()[a] - r.origin()[a]) * invD;
auto t1 = (max()[a] - r.origin()[a]) * invD;
if (invD < 0.0f)
std::swap(t0, t1);
tmin = t0 > tmin ? t0 : tmin;
tmax = t1 < tmax ? t1 : tmax;
if (tmax <= tmin)
return false;
}
return true;
}
aabb.h] AABB の衝突判定 (最適化後)
AABB の構築
続いて hittable 全体に対する AABB を計算する関数が必要になる。計算するのはシーンに含まれる全てのプリミティブに関する AABB の階層であり、球などの個々のプリミティブが葉となる。無限に広がる平面のように AABB を持たないプリミティブもあるので、この関数は AABB が構築できたかを表す bool 値を返す。また移動するオブジェクトに関しては、その AABB が time0 から time1 まで全ての時刻におけるオブジェクトを含むことになる。
class hittable {
public:
virtual bool hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const = 0;
virtual bool bounding_box(double t0, double t1, aabb& output_box) const = 0;
};
hittable.h] hittable クラスに AABB を追加する
球の bounding_box 関数は簡単に書ける:
bool sphere::bounding_box(double t0, double t1, aabb& output_box) const {
output_box = aabb(center - vec3(radius, radius, radius),
center + vec3(radius, radius, radius));
return true;
}
sphere.h] sphere::bounding_box 関数
moving_sphere ではまず \(t_{0}\) における AABB と \(t_{1}\) における AABB 計算し、二つの AABB を含む AABB をさらに計算すればよい:
bool moving_sphere::bounding_box(double t0, double t1, aabb& output_box) const {
aabb box0(center(t0) - vec3(radius, radius, radius),
center(t0) + vec3(radius, radius, radius));
aabb box1(center(t1) - vec3(radius, radius, radius),
center(t1) + vec3(radius, radius, radius));
output_box = surrounding_box(box0, box1);
return true;
}
moving_sphere.h] moving_sphere::bounding_box 関数
二つの AABB の AABB を計算する surrouding_box 関数は次のように書ける:
aabb surrounding_box(aabb box0, aabb box1) {
point3 small(fmin(box0.min().x(), box1.min().x()),
fmin(box0.min().y(), box1.min().y()),
fmin(box0.min().z(), box1.min().z()));
point3 big(fmax(box0.max().x(), box1.max().x()),
fmax(box0.max().y(), box1.max().y()),
fmax(box0.max().z(), box1.max().z()));
return aabb(small,big);
}
aabb.h] AABB の AABB
オブジェクトリストの AABB の計算
リストの AABB は作成時に計算することもできるし、bounding_box を呼び出したときその場で計算することもできる。通常 bounding_box は BVH を構築するときに一度だけ呼ばれるので、私はその場で AABB を計算させる方法を取る:
bool hittable_list::bounding_box(double t0, double t1, aabb& output_box) const {
if (objects.empty()) return false;
aabb temp_box;
bool first_box = true;
for (const auto& object : objects) {
if (!object->bounding_box(t0, t1, temp_box)) return false;
output_box = first_box ? temp_box : surrounding_box(output_box, temp_box);
first_box = false;
}
return true;
}
hittable_list.h] hittable_list::bounding_box 関数
BVH を表すクラス
BVH は ── hittable のリストと同様に── hittable となる。BVH は他の hittable を保持するコンテナに過ぎないが、「このレイと交わるか?」という質問には答えることができる。BVH を設計するときの選択肢として、木とノードを表すクラスをそれぞれ作る方法と、ノードを表すクラスだけを作って木をノードとして表す方法がある。私は可能な限りクラスを一つだけ使った設計を使うようにしている。BVH を表すクラスを示す:
class bvh_node : public hittable {
public:
bvh_node();
bvh_node(hittable_list& list, double time0, double time1)
: bvh_node(list.objects, 0, list.objects.size(), time0, time1)
{}
bvh_node(
std::vector<shared_ptr<hittable>>& objects,
size_t start, size_t end, double time0, double time1);
virtual bool hit(
const ray& r, double tmin, double tmax, hit_record& rec
) const;
virtual bool bounding_box(double t0, double t1, aabb& output_box) const;
public:
shared_ptr<hittable> left;
shared_ptr<hittable> right;
aabb box;
};
bool bvh_node::bounding_box(double t0, double t1, aabb& output_box) const {
output_box = box;
return true;
}
bvh.h] 包含立体階層 (BVH)
子へのポインタが一般的な hittable となっている点に注目してほしい。子は bvh_node にも sphere にも他の hittable にもなれる。
bvh_node の hit 関数は非常に簡単である: そのノードが持つ AABB と交わるか調べ、もし交わるなら子に詳細を調べさせればよい:
bool bvh_node::hit(
const ray& r, double t_min, double t_max, hit_record& rec
) const {
if (!box.hit(r, t_min, t_max))
return false;
bool hit_left = left->hit(r, t_min, t_max, rec);
bool hit_right = right->hit(r, t_min, hit_left ? rec.t : t_max, rec);
return hit_left || hit_right;
}
bvh.h] bvh_node::hit 関数
BVH の分割
効率化のためのデータ構造で最も複雑になるのはその構築であり、BVH も例外ではない。BVH の構築は bvh_node のコンストラクタで行う。ただ BVH で素晴らしいのが、bvh_node に渡されるオブジェクトの集合を二つに分けさえすれば hit 関数が正しく動く点である。もちろん二つの子の AABB が親の AABB より小さくなる分割が望ましいが、分割の質が関係するのは実行速度だけで正しさは関係しない。ここでは単純さと効率の妥協点となるアルゴリズムとして、各ノードで一つの軸に沿ってオブジェクトを分割する方法を採用する。つまり
- ランダムに軸を選ぶ。
- プリミティブを (
std::sortで) ソートする - オブジェクトを半分ずつ子に入れ、子を再帰的に分割する。
という操作を行う。
受け取ったリストが持つ要素が二つだけなら、左および右の子に一つずつ要素を設定して再帰を終える。走査アルゴリズムは高速である必要があり、ヌルポインタをチェックしている暇はないので、要素が一つの場合には二つの子に同じオブジェクトを入れる。要素が三つのときを明示的に処理して再帰をなくしたとしてもあまり高速にならないだろう。いずれにせよこのメソッドは後で高速化する可能性が高い。
#include <algorithm>
...
inline int random_int(int min, int max) {
// {min, min+1, ..., max} から整数をランダムに返す
return min + rand() % (max - min + 1);
}
bvh_node::bvh_node(
std::vector<shared_ptr<hittable>>& objects,
size_t start, size_t end, double time0, double time1
) {
int axis = random_int(0,2);
auto comparator = (axis == 0) ? box_x_compare
: (axis == 1) ? box_y_compare
: box_z_compare;
size_t object_span = end - start;
if (object_span == 1) {
left = right = objects[start];
} else if (object_span == 2) {
if (comparator(objects[start], objects[start+1])) {
left = objects[start];
right = objects[start+1];
} else {
left = objects[start+1];
right = objects[start];
}
} else {
std::sort(objects.begin() + start, objects.begin() + end, comparator);
auto mid = start + object_span/2;
left = make_shared<bvh_node>(objects, start, mid, time0, time1);
right = make_shared<bvh_node>(objects, mid, end, time0, time1);
}
aabb box_left, box_right;
if ( !left->bounding_box (time0, time1, box_left)
|| !right->bounding_box(time0, time1, box_right))
std::cerr << "No bounding box in bvh_node constructor.\n";
box = surrounding_box(box_left, box_right);
}
bvh.h] BVH の構築
AABB の存在を確認しているのは、無限に広がる平面のように AABB が存在しないオブジェクトが存在するためである。今の段階ではそういったオブジェクトを実装していないから、明示的に追加するまでこのエラーは起こらない。
AABB の比較関数
次に std::sort() が使う AABB の比較関数を実装する必要がある。二つの AABB を引数で表される軸で比較する一般的な関数を作れば、軸に関する比較はこの一般的な関数を使って書ける:
inline bool box_compare(
const shared_ptr<hittable> a, const shared_ptr<hittable> b, int axis
) {
aabb box_a;
aabb box_b;
if (!a->bounding_box(0,0, box_a) || !b->bounding_box(0,0, box_b))
std::cerr << "No bounding box in bvh_node constructor.\n";
return box_a.min().e[axis] < box_b.min().e[axis];
}
bool box_x_compare (
const shared_ptr<hittable> a, const shared_ptr<hittable> b
) {
return box_compare(a, b, 0);
}
bool box_y_compare (
const shared_ptr<hittable> a, const shared_ptr<hittable> b
) {
return box_compare(a, b, 1);
}
bool box_z_compare (
const shared_ptr<hittable> a, const shared_ptr<hittable> b
) {
return box_compare(a, b, 2);
}
bvh.h] AABB の比較関数