週末レイトレーシング 余生 (翻訳)

はじめに

『週末レイトレーシング 第一週』と『週末レイトレーシング 第二週』で、あなたは「本物の」レイトレーサーを作成した。

この巻はレイトレーシングに関連するキャリアに興味を持っている読者を想定し、非常に本格的なレイトレーサーを作成するために必要な数学について解説する。最後まで読み切れば、映画やプロダクトデザインで使われる本物の商用レイトレーサーをいじって遊べるようになるだろう。この短いシリーズで触れられないトピックはたくさんある。モンテカルロレンダリングを行うプログラムを書く方法はいくつもあるが、ここで説明するのは一つだけだ。ライトに向かってレイを多く飛ばす方法を取る代わりにシャドウレイは考えず、双方向パストレーシング・メトロポリス法・フォトンマッピングにも触れていない。ただ私はこういった手法を研究する分野で使われる言葉を使って話をする。この本はそういった言葉に深く触れるための本であり、初めて触れる人でも読めるように書かれている。他の文献で勉強するための概念・数学の知識・専門用語の使い方を学ぶことができるだろう。

これまでと同様に、発展的な文献やリンクは https://in1weekend.blogspot.com/ にまとめてある。

このプロジェクトに手を貸してくれた全ての人に感謝する。名前は巻末の謝辞にある。

簡単なモンテカルロプログラム

モンテカルロ法 (Monte Carlo Method, MC) を使う最も簡単なプログラムから始めよう。モンテカルロ法を使うと真の値の統計的な近似値を計算でき、近似値は実行時間を長くすればそれだけ正確になる。誤差はあるが時間をかければ正確になる値を簡単なプログラムで求められるという基本的な特性が MC の全てである。グラフィックスのように極限まで正確な値が必要とされない分野においてモンテカルロ法は特に有用となる。

円周率の計算

例として \(\pi\) の近似値を計算してみよう。古典的な方法としてビュフォンの針を使うものがあるが、ここに示す方法はその変種と言える。正方形に内接する円を考える:

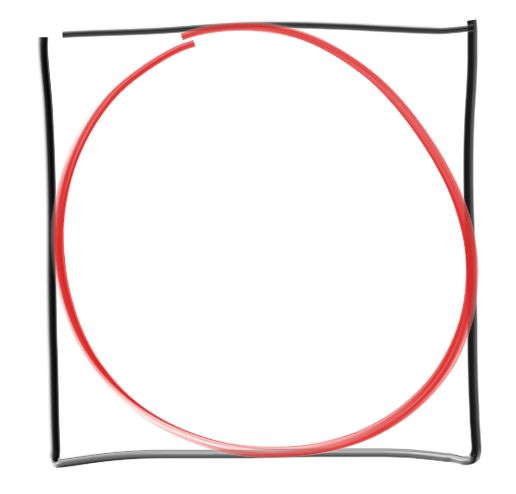
この正方形の中にランダムな点をたくさん打つとする。このときランダムな点が円の中に入る確率は円の面積に比例する。正確に言えば、その確率は円の面積と正方形の面積の比に等しくなる。つまり \[ \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4} \] であり、\(r\) に関係しない。\(r\) は計算しやすいように決められるので、\(r = 1\) と定める。さらに中心を原点とすれば、次のプログラムが書ける:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
  int N = 1000;
  int inside_circle = 0;
  for (int i = 0; i < N; i++) {
    auto x = random_double(-1,1);
    auto y = random_double(-1,1);
    if (x*x + y*y < 1)
      inside_circle++;
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "Estimate of Pi = " << 4*double(inside_circle) / N << '\n';
}

このプログラムが計算する \(\pi\) の近似値はコンピューターの種類やランダムシードによって異なる。私のマシンでは Estimate of Pi = 3.0880000000 という結果になった。

収束の確認

収束の様子が分かりやすいように、実行を止めずに近似値を計算し続けるようにしておこう:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
  int inside_circle = 0;
  int runs = 0;
  std::cout << std::fixed << std::setprecision(12);
  while (true) {
    runs++;
    auto x = random_double(-1,1);
    auto y = random_double(-1,1);
    if (x*x + y*y < 1)
      inside_circle++;

    if (runs % 100000 == 0)
      std::cout << "Estimate of Pi = "
            << 4*double(inside_circle) / runs
            << '\n';
  }
}

サンプルの層化 (振動)

近似値は最初 \(\pi\) に素早く近づくが、その後はゆっくりとしか近づかない。つまり後に加えられるサンプルはそれまでのサンプルよりも低い寄与しか持たず、収穫逓減の法則 (Law of Diminishing Returns) が働いている。これはモンテカルロ法の持つ厄介な性質だが、サンプルを層化 (stratifying) することで改善できる。「サンプルを振動 (jittering) させる」と表現される場合もあるこのテクニックでは、ランダムなサンプルを一つずつ取るのではなく、格子状に分けた小領域の全てでサンプルを一度に取る:

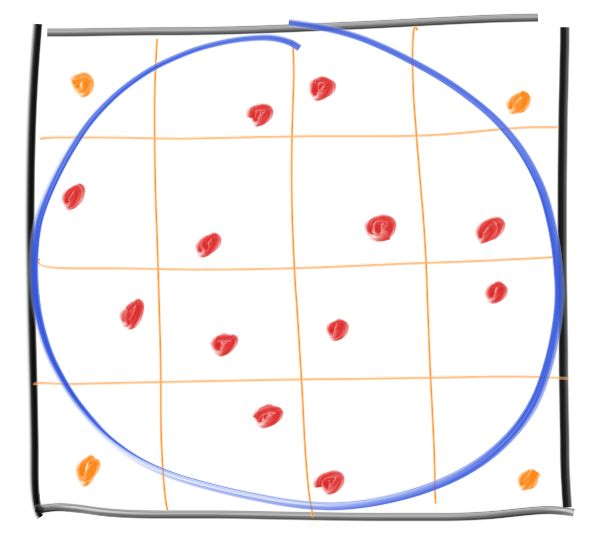
層化サンプリングは格子を使うので、サンプル数をあらかじめ決めておかなくてはならない。サンプル数を十億として、二つの方法を比べよう:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
  int inside_circle = 0;
  int inside_circle_stratified = 0;
  int sqrt_N = 10000;
  for (int i = 0; i < sqrt_N; i++) {
    for (int j = 0; j < sqrt_N; j++) {
      auto x = random_double(-1,1);
      auto y = random_double(-1,1);
      if (x*x + y*y < 1)
        inside_circle++;
      x = 2*((i + random_double()) / sqrt_N) - 1;
      y = 2*((j + random_double()) / sqrt_N) - 1;
      if (x*x + y*y < 1)
        inside_circle_stratified++;
    }
  }

  auto N = static_cast<double>(sqrt_N) * sqrt_N;
  std::cout << std::fixed << std::setprecision(12);
  std::cout
    << "Regular Estimate of Pi = "
    << 4*double(inside_circle) / N << '\n'
    << "Stratified Estimate of Pi = "
    << 4*double(inside_circle_stratified) / N << '\n';
}

私のマシンでは次の結果が得られた:

Regular Estimate of Pi = 3.14151480
Stratified Estimate of Pi = 3.14158948

興味深いことに、層化したサンプルを使う方法は正確な近似が得られるだけではなく、収束の速さも優れている！ しかし残念ながらこの利点は問題の次元が増えると薄れてしまう (例えば三次元の球で同じ計算を行うと改善は小さくなる)。この現象は次元の呪い (Curse of Dimensionality) と呼ばれる。この本ではサンプルの層化をレイトレーサーに追加しないが、反射やシャドウを一度だけ考えるときや厳密に二次元の問題を考えるときには層化を必ず利用するべきである。

一次元モンテカルロ積分

積分は突き詰めれば面積や体積の計算だから、第二節の内容は積分を使って最高に理解しにくく表現できる。しかしときには、積分を使って問題を定式化するのが最も自然で見通しが良くなる場合もある。レンダリングではそうなることが多い。

\(x^{2}\) の積分

古典的な積分を考えよう: \[ I = \int_{0}^{2} x^2 \, dx \] 情報科学っぽい記法を使うと \[ I = \text{area}( x^2, 0, 2 ) \] となる。これは次のように変形できる: \[ I = 2 \cdot \text{average}(x^2, 0, 2) \]

ここからモンテカルロ法を使った次のアプローチが分かる。直接積分を計算して求まる正確な値は \(I = 8/3\) であり、この近似値が計算される。

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto x = random_double(0,2);
    sum += x*x;
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << 2 * sum/N << '\n';
}

この方法は解析的に積分できない \(\log \sin x\) のような関数の積分にも利用できる。グラフィックスでは値を求めることはできるが陽に書くことができない関数、あるいは確率的にしか値を計算できない関数がよく登場する。これまでの二巻で実装した ray_color() 関数がそうである ──任意のレイに対するこの関数の値を表す式は存在しないが、任意のレイに対する値を確率的に近似することはできる。

これまで行き当たりばったりに書いてきた私たちのプログラムが持つ問題の一つが、ライトが小さいときのノイズが非常に大きいことだ。これはプログラムで使われている一様なサンプリングが非常に低い頻度でしか光源をサンプルしないためである。光源がサンプルされるのは散乱したレイが光源に向かうときだけだが、光源が小さかったり遠くにあったりするとこれは起こりにくい。光源に向かうレイを多くサンプルすればこの問題の影響を和らげることができるが、そうするとシーンが不正確に明るくなる。多くサンプルした部分のレイからの寄与を低く勘定すれば結果を正確にできるのだが、さてどれくらい低くすればよいのだろうか？ この質問に答えるには、確率密度関数 (probability density function) という概念が必要になる。

確率密度関数

確率密度関数とは何だろうか？ これはヒストグラム (度数分布表) を連続にしたものと言える。ヒストグラムの Wikipedia には次の図が載っている¹:

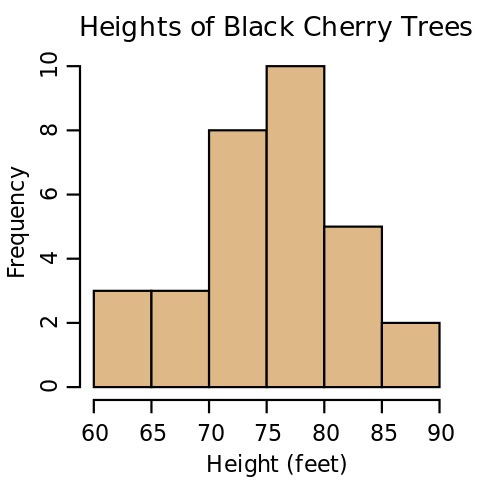
さらに多くの木の高さを調べるヒストグラムは高くなり、ビン (縦棒) を小さく分けて幅を狭くするとヒストグラムは低くなる。ヒストグラムの \(y\) 方向の高さを割合あるいはパーセンテージに正規化すると、離散の確率密度関数が得られる。ビンの数を無限大にすれば連続な連続なヒストグラムとなるが、そのままでは全てのビンの高さがゼロになってしまうので正規化できない。ビンの数で高さが変わらないように連続ヒストグラムを調整したのが確率密度関数である。木の高さのヒストグラムを表す密度関数では、 \[ H {\footnotesize \text{ から }} H' {\footnotesize \text{のビンの高さ}} = \frac{{\footnotesize \text{高さが }} H {\footnotesize \text{ から }} H' {\footnotesize \text{ の木の数}}}{H-H'} \] が成り立つ。この式が木の高さの統計的に推定していると解釈することもできる: \[ {\footnotesize \text{ランダムな木の高さが }} H {\footnotesize \text{ と }} H' {\footnotesize \text{の間にある確率}} = {\footnotesize \text{ビンの高さ}}\cdot(H-H') \] 複数のビンの区間に収まる確率はそれぞれの確率を足せば求まる。

つまり、確率密度関数 (probability density function, PDF) は割合を表すヒストグラムを連続にしたものである。

PDF の構築

理解を深めるために、PDF を作って先ほどの積分で利用してみよう。\(0\) から \(2\) の値を取る乱数 \(r\) があって、\(r\) の値が \(x\) となる確率が \(x\) 自身に比例する状況を考える。このとき PDF \(p(r)\) は次の形となるはずだが、この高さはいくつだろうか？

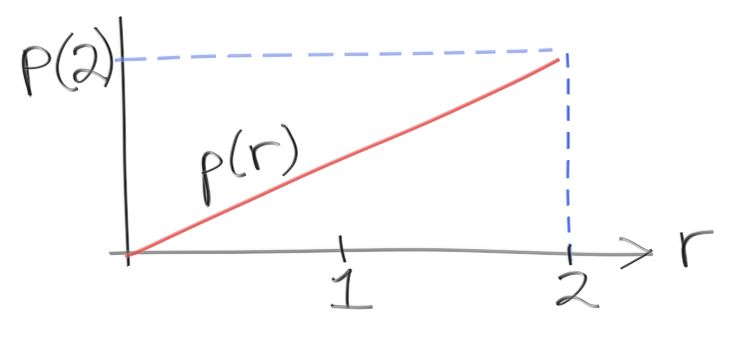
\(r = 2\) おける高さ \(p(2)\) を求めたい。ここで使うのは、ヒストグラムと同様に PDF の積分 (高さの和) が「乱数 \(r\) がとある区間に存在する確率」となる事実である: \[ x_0 \lt r \lt x_1 {\footnotesize \text{ となる確率}} = \text{area}(p(r), x_0, x_1) \] \(r\) が存在しうる区間全体を考えれば確率は \(1\) になる。さらに \(p(r)\) が \(r\) に比例するので、定数 \(C\) を使って \(p(r) = C x\) と表せる。ここから \[ \text{area}(Cr, 0, 2) = \int_{0}^{2} C r dr = \frac{Cr^2}{2} \biggr|_{r=2}^{r=0} = \frac{C \cdot 2^2}{2} - \frac{C \cdot 0^2}{2} = 2C = 1 \] が分かる。すなわち \(p(r) = r/2\) である。

では、この PDF \(p(r) = r/2\) に沿った乱数を生成するにはどうすればよいだろうか？ この問題では逆関数法 (inverse method) と呼ばれるトリックが使える。あと一息だから、頑張れ！

\(0\) と \(1\) の間の一様変数を d = random_double() として、ここから PDF が \(p(r) = r/2\) となる乱数 \(e = f(d)\) を作りたい。例として \(e = f(d) = d^{2}\) としてみよう。\(0\) と \(1\) の間の数を二乗すると \(0\) に近づくから、二乗結果の分布は \(0\) に向かってよる。つまり \(e\) の PDF は一様ではなく、\(0\) 付近で大きく \(1\) 付近で小さくなる。この観察を一般的に定式化するには、次の累積分布関数 (cumulative distribution function, CDF) \(P(x)\) という概念が必要になる: \[ P(x) = \text{area}(p, -\infty, x) = \int_{-\infty}^{x} P(x)\, dx \] \(p(x)\) が定義されていない \(x\) では \(p(x) = 0\) とみなす。つまり乱数がその \(x\) となる確率は \(0\) である。先ほどの PDF \(p(r) = r/2\) の CDF \(P(x)\) は \[ \begin{cases} P(x) = 0 & (x \lt 0) \\ P(x) = \dfrac{x^2}{4} & (0 \lt x \lt 2) \\ P(x) = 1 & (2 \lt x) \\ \end{cases} \] となる。

\(d\) から \(e\) を計算する方法を考えているのに、どうして \(x\) や \(r\) が出てくるのだろうか？ この二つの関数はダミー変数であり、プログラムにおける関数の引数に相当する。さて \(x = 1.0\) のときの \(P\) を計算すると \[ P(1.0) = \frac{1}{4} \] となる。これは「今考えている PDF に沿って生成した乱数が \(1\) より小さくなる確率は \(25\) % である」ことを意味している。ここから様々な非一様乱数の生成で使われる賢い観察が得られる。私たちが探しているのは関数 \(f\) であって \(f(\text{random\_double()})\) の返り値が PDF \(p(r) = r/2\) に従うものである。この関数が何なのかは分からないが、この関数からの返り値の \(25\) % は \(1\) より小さくなることは分かっている。よって \(f\) が単調増加と仮定すれば \(f(0.25) = 1.0\) が成り立つ。この議論を一般化すると任意の点に対する \(f\) と \(P\) の関係が得られる: \[ f(P(x)) = x \] すなわち \(f\) は \(P\) と逆の処理を行う。よって \[ f(x) = P^{-1}(x) \] である。この \(-1\) は「逆関数」を表す。分かりにくい記法だが、これが標準なので仕方がない。最初の問題に結論を出そう。もし確率密度関数 \(p\) と累積分布関数 \(P\) が既知なら、\(P\) の逆関数が求めるべき乱数を与える: \[ e = P^{-1} (\text{random\_double}()) \]

考えていた例 \(p(x) = x/2\) に対する \(P\) は上に示した通り \[ y = \frac{x^2}{4} \] である。\(y\) を使って \(x\) を表せば逆関数が求まる: \[ x = \sqrt{4y} \] よって密度関数に \(p(x) = x/2\) を持つ乱数 \(e\) は次の式で生成できると分かる: \[ e = \sqrt{4\cdot\text{random\_double}()} \] \(e\) の値域が \(p\) と同じく \(0\) から \(2\) である点に注目してほしい。また \(\text{random\_double}\) を \(1/4\) とすれば \(e = 1\) となり、以前の結果と一致する。

ではこのサンプル方法を使って最初の積分を計算してみよう: \[ I = \int_{0}^{2} x^2 \, dx \] \(x\) の PDF が一様でないことを考慮して、多くサンプルした部分には少ない重みを付ける必要がある。サンプルの量は PDF によって表されるので、重みは PDF の逆数の定数倍とすればよい。実は PDF の性質から PDF の逆数そのものが正しい重みだと証明できる。

inline double pdf(double x) {
  return 0.5*x;
}

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto x = sqrt(random_double(0,4));
    while (x == 0.0) {
      // PDF が 0.5*x の乱数で x が 0 になる確率は 0
      x = sqrt(random_double(0,4));
    }
    sum += x*x / pdf(x);
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << sum/N << '\n';
}

pdf(x) で割るときにゼロ除算が発生しないよう x が 0 の場合を除外しているが、これは乱数の性質を考えてもおかしなことではない。pdf(x) が 0 となるような x はそもそも生成されてはいけないので、除外して考えるのが理にかなっている。

重点サンプリング

上のプログラムは被積分関数が大きくなる部分から多くサンプルしているので、ノイズが減って収束が速まる。分布の中で重要 (important) な部分にサンプルを寄せているということで、慎重に選んだ一様でない PDF に従うサンプルを使うこの方法を重点サンプリング (importence sampling) と呼ぶ。

同じコードで一様なサンプルを使うとすれば、PDF は \([0, 2]\) の範囲で値 \(1/2\) を取る関数となる。このとき x = random_double(0,2) であり、次のようになる:

inline double pdf(double x) {
  return 0.5;
}

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto x = random_double(0,2);
    sum += x*x / pdf(x);
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << sum/N << '\n';
}

以前のコードにあった 2*sum/N の 2 が消えた点に注目してほしい ──この部分は PDF に移動した。重点サンプリングは収束を加速させるが、その効果は非常に大きいというわけではない。またこの積分では、被積分関数と完全に一致する PDF を使うこともできる: \[ p(x) = \frac{3}{8}x^2 \] とすれば \[ P(x) = \frac{x^3}{8} \] であり、 \[ P^{-1}(x) = 8x^\frac{1}{3} \] となる。こうした完璧な重点サンプリングが可能なのは答えが最初から分かっているとき (\(p\) を解析的に積分して \(P\) が求まるとき) に限られるが、コードが正しく動くことを確かめるのにはちょうどよいだろう。この場合には \(1\) サンプルだけで正確な値が求まる:

inline double pdf(double x) {
  return 3*x*x/8;
}

int main() {
  int N = 1;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto x = pow(random_double(0,8), 1./3.);
    sum += x*x / pdf(x);
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << sum/N << '\n';
}

重点サンプリングはモンテカルロレイトレーサーの基礎となる概念なので、その方法をここにまとめておく:

1. 区間 \([a, b]\) における \(f(x)\) の積分を考える。
2. \([a, b]\) で \(0\) にならない PDF \(p\) を見つける。
3. PDF が \(p\) の乱数 \(r\) を大量に生成し、それらに関する \(\dfrac{f(r)}{p(r)}\) の平均を求める。

PDF \(p\) をどのように選んでも近似値は正しい値に収束するが、\(p\) が \(f\) の近似として優れていればそれだけ収束も速くなる。

球上の点を使ったモンテカルロ積分

私たちのレイトレーサーには方向をランダムに選ぶ処理があり、方向は単位球上の点として表される。前節で説明したモンテカルロ積分をここでも利用できるが、そのためには二次元の PDF が必要になる。

全ての方向に関する次の関数の積分を求めたいとする²: \[ \int \cos^2 \theta \] モンテカルロ積分では \(\cos^{2} \theta / p(\text{direction})\) をサンプルすることになる。この式における \(p(\text{direction})\) について考えよう。極座標で \(\text{direction}\) を表すと \((\theta, \phi)\) を使った \(p\) の式が手に入るが、どんな表現であれ PDF は全体に渡る積分が \(1\) で、その値 \(p(\text{direction})\) は方向 \(\text{direction}\) がサンプルされる相対確率を表さなければならない。

単位球上の点を一様ランダムに選択する関数をこれまでに実装した:

vec3 random_unit_vector() {
  auto a = random_double(0, 2*pi);
  auto z = random_double(-1, 1);
  auto r = sqrt(1 - z*z);
  return vec3(r*cos(a), r*sin(a), z);
}

この関数から得られる点に対する PDF はどう表せるだろうか？ 単位球上の任意の点が得られる確率が一定で、全体に渡る積分は \(1\) になるから、PDF は常に \(1/({\footnotesize \text{面積}}) = 1/4\pi\) となる。被積分関数が \(\cos^{2} \theta\) で \(\theta\) は \(z\) 軸との角度を表すので、考えていた積分は次のように計算できる:

inline double pdf(const vec3& p) {
  return 1 / (4*pi);
}

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    vec3 d = random_unit_vector();
    auto cosine_squared = d.z()*d.z();
    sum += cosine_squared / pdf(d);
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << sum/N << '\n';
}

解析解は \(\frac{4}{3} \pi\) であり (積分法を覚えているなら計算してみよ)、上のコードはこの近似値を計算する。これで重点サンプリングをレイトレーシングに適用する準備が整った！

積分や確率が単位球上に渡るものである点が、ここで重要となる。"方向" は単位球上の面積として測られ、方向、立体角 (solid angle)、面積といった言葉で表される ──立体角と呼ばれることが最も多い。もしこの言葉を理解できるなら、素晴らしい！ もしよく理解できないなら、私と同じように方向を指すベクトルの束が貫く単位球上の領域の面積を考えるとよい。立体角 \(\omega\) は単位球上に射影した領域の面積 \(A\) と等しい。

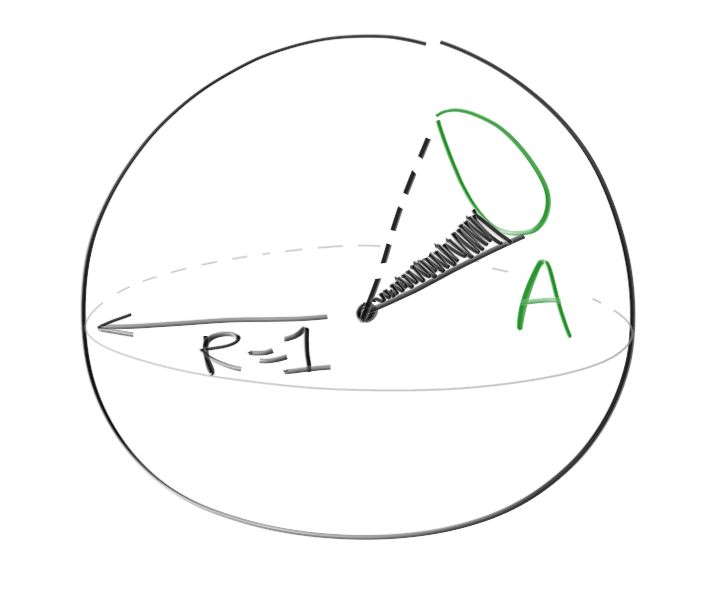
次は私たちが解こうとしている光輸送方程式 (light transport equation) を考えよう。

光の散乱

この節ではプログラムを書かずに、次節で行うライティング処理の大きな変更に向けて用語や概念を説明する。

アルベド

これまでに作ったプログラムは物体表面やボリュームでレイを散乱させていた。これは光と物体表面の間の相互作用を説明するのによく使われるモデルであり、確率を使って自然に実装できる。これまでのプログラムにはライトが吸収されるかどうかを判断する確率がある:

• 光が散乱する確率: \(A\)
• 光が吸収される確率: \(1 - A\)

この \(A\) をアルベド (albedo) と呼ぶ (albedo はラテン語で「白さ」を意味する)。アルベドは分野によっては正確な定義を持つ専門用語だが、どの場合でも何らかの反射率 (reflectance) を表している。アルベド (反射率) は光の色と入射方向によって変化する: 第一巻でガラスを実装したときには、シュリックの近似を使って反射率を計算した。

散乱

多くの物理ベースレンダラでは、光の色を表すのに RGB ではなく複数の波長の集まりが使われる。長い波長の光、中くらいの波長の光、短い波長の光を特定の割合で組み合わせたものが R, G, B だとみなせば、今のプログラムでも同じように考えることができる。

光が散乱するとき、散乱レイの方向の分布は立体角を引数に取る PDF として表せる。この分布をこれから散乱 PDF (scattering PDF) と呼び、\(s(\text{direction})\) と表す。散乱 PDF は入射するレイの入射角 (incident direction) によっても変化する。入射方向による散乱 PDF の変化は、水面から反射する光を見るとよく分かる ──遠くを見て視点の角度 (入射角) が水平に近づくと、水面は鏡のように見える³。

以上の記号を使えば、物体表面の色は次のように表せる⁴: \[ \text{Color} = \int A \cdot s(\text{direction}) \cdot \text{color}(\text{direction}) \] \(A\) と \(s(\text{direction})\) は視点の方向および散乱位置 (物体表面またはボリューム内部における位置) に依存するので、出力の色はこの二つの値によって変化する。

散乱 PDF

モンテカルロ積分の基礎公式に当てはめると、次の統計的推定値が得られる: \[ \text{Color} = \frac{A \cdot s(\text{direction}) \cdot \text{color}(\text{direction})}{p(\text{direction})} \] ここで \(p(\text{direction})\) は "ランダム" に生成した方向 \(\text{direction}\) の PDF である。

これまでランバート表面では \(p(\text{direction})\) がコサイン密度となる特別な場合として暗黙の内にこの式を実装していた。\(\theta\) を物体表面の法線と散乱レイの角度とすると、ランバート表面では \(s(\text{direction})\) が \(\cos \theta\) に比例する。PDF の積分は \(1\) になる必要があることを思い出そう。\(\cos \theta \lt 0\) のときは \(s(\text{direction}) = 0\) であり、半球に関する \(\cos \theta\) の積分は次に示すように \(\pi\) となる。

積分を求めるには、球面座標で成り立つ次の等式を使う⁵: \[ dA = \sin \theta\, d\theta d\phi \] ここから \[ \cos \theta \text{ の単位半球上に渡る面積分} = \int_{0}^{2 \pi} \int_{0}^{\pi / 2} \cos \theta \sin \theta\, d\theta d\phi = 2 \pi \frac{1}{2} = \pi \] を得る。つまりランバート表面における散乱 PDF は \[ s(\text{direction}) = \frac{\cos \theta}{\pi} \] である。

散乱 PDF と等しい PDF を使ってサンプルを行うとすれば \[ p(\text{direction}) = s(\text{direction}) = \frac{\cos \theta}{\pi} \] であり、分母と分子が打ち消し合う。そして \[ \text{Color} = A \cdot \text{color}(\text{direction}) \] が得られる。これは最初に実装した ray_color() 関数にあった式そのものだ！ ただここでは、値の大きい方向 (例えばライト方向) へ多くのレイを飛ばせるようこの議論を一般化する必要がある。

以上の議論は標準的ではない。物体表面とボリュームの両方に適用できる数式が欲しかったのでこの議論を使った。他のやり方だと複雑なコードが生まれてしまう。

レイトレーシングに関する標準的な文献では、反射は双方向反射率分布関数 (bidirectional reflectance distribution function, BRDF) によって記述される。この関数は本書の記号を使って簡単に表せる: \[ \text{BRDF} = \frac{A \cdot s(\text{direction})}{\cos\theta} \]

例えばランバート表面では \(\text{BRDF} = A / \pi\) となる。本書で使う記号と \(\text{BRDF}\) の変換は難しくない。

関与媒質 (ボリューム) を考えるときにはアルベドを散乱アルベド (scattering albedo) と呼び、散乱 PDF を位相関数 (phase function) と呼ぶことが多い。

重点サンプリング付きマテリアル

ここからいくつかの節を使って、画像のノイズを減らすためにレイを光源に向かって多く放つようプログラムを改変する。光源へ多くレイを放つときの PDF を \(p_{\text{light}}(\text{direction})\) として、\(s(\text{direction})\) が大きい部分へ多くレイを放つときの PDF を \(p_{\text{surface}}(\text{direction})\) とする。PDF に関して便利なのが、複数の PDF の線形和を取って確率密度を混ぜることで別の PDF を作れることだ。例えば一番簡単な線形和 \[ p(\text{direction}) = \frac{1}{2}\cdotp p_{\text{light}}(\text{direction}) + \frac{1}{2}\cdot p_{\text{surface}}(\text{direction}) \] は PDF である。重みが正で積分が \(1\) である限り、複数 PDF を組み合わせてできる関数は PDF となる。PDF はどんなものでも構わないことを思い出そう: 任意の PDF を使ったモンテカルロ積分は真の値に収束する。よって問題は \(s(\text{direction}) \cdot \text{color}(\text{direction})\) が大きい部分の PDF を大きくする方法である。拡散表面では、これは \(\text{color}(\text{direction})\) が高い部分を推定する問題となる。

鏡面では \(s(\text{direction})\) が特定の方向の周りでのみ非常に大きくなるので、拡散表面より \(s(\text{direction})\) がずっと重要になる。実は多くのレンダラは鏡面を特殊ケースとしており、\(s/p\) を陰に計算して済ませている ──現在の私たちのコードもこうしている。

コーネルボックス

少しリファクタリングをして、ランバーティアンでないマテリアルを取り除こう。コーネルボックスのシーンを使って、モデルを生成する関数の中でカメラも生成する:

hittable_list cornell_box(camera& cam, double aspect) {
  hittable_list world;

  auto red   = make_shared<lambertian>(make_shared<solid_color>(.65, .05, .05));
  auto white = make_shared<lambertian>(make_shared<solid_color>(.73, .73, .73));
  auto green = make_shared<lambertian>(make_shared<solid_color>(.12, .45, .15));
  auto light = make_shared<diffuse_light>(make_shared<solid_color>(15, 15, 15));

  world.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
  world.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
  world.add(make_shared<xz_rect>(213, 343, 227, 332, 554, light));
  world.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
  world.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
  world.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

  shared_ptr<hittable> box1 =
    make_shared<box>(point3(0,0,0), point3(165,330,165), white);
  box1 = make_shared<rotate_y>(box1, 15);
  box1 = make_shared<translate>(box1, vec3(265,0,295));
  world.add(box1);

  shared_ptr<hittable> box2 =
    make_shared<box>(point3(0,0,0), point3(165,165,165), white);
  box2 = make_shared<rotate_y>(box2, -18);
  box2 = make_shared<translate>(box2, vec3(130,0,65));
  world.add(box2);

  point3 lookfrom(278, 278, -800);
  point3 lookat(278, 278, 0);
  vec3 vup(0, 1, 0);
  auto dist_to_focus = 10.0;
  auto aperture = 0.0;
  auto vfov = 40.0;
  auto t0 = 0.0;
  auto t1 = 1.0;

  cam = camera(
    lookfrom, lookat, vup, vfov, aspect, aperture, dist_to_focus, t0, t1
  );

  return world;
}

解像度を 500 × 500 として 1 ピクセルに 500 本のレイを放つと、私の Macbook (1 コア使用) では次の画像が 10 分で得られた:

このノイズを減らすのが目標である。これからライトに向けてレイを多く放つ PDF を構築することでこれを達成する。

まず、明示的に PDF のサンプルと正規化を行うようコードを変更する。モンテカルロ積分の基本を思い出そう: \(\displaystyle \int f(x) \approx f(r)/p(r)\) である。lambertian マテリアルでは今までと同じように \(p(\text{direction}) = \cos \theta / \pi\) としてサンプルを行うことにする。

基底クラス material に重点サンプリングを追加する:

class material {
public:

  virtual bool scatter(
    const ray& r_in,
    const hit_record& rec,
    color& albedo,
    ray& scattered,
    double& pdf
  ) const {
    return false;
  }

  virtual double scattering_pdf(
    const ray& r_in, const hit_record& rec, const ray& scattered
  ) const {
    return 0;
  }

  virtual color emitted(double u, double v, const point3& p) const {
    return color(0,0,0);
  }
};

lambertian クラスは次のようになる:

class lambertian : public material {
public:
  lambertian(shared_ptr<texture> a) : albedo(a) {}

  virtual bool scatter(
    const ray& r_in,
    const hit_record& rec,
    color& alb,
    ray& scattered,
    double& pdf
  ) const {
    point3 target = rec.p + rec.normal + random_unit_vector();
    scattered = ray(rec.p, unit_vector(target-rec.p), r_in.time());
    alb = albedo->value(rec.u, rec.v, rec.p);
    pdf = dot(rec.normal, scattered.direction()) / pi;
    return true;
  }

  double scattering_pdf(
    const ray& r_in, const hit_record& rec, const ray& scattered
  ) const {
    auto cosine = dot(rec.normal, unit_vector(scattered.direction()));
    return cosine < 0 ? 0 : cosine/pi;
  }

public:
  shared_ptr<texture> albedo;
};

ray_color 関数にも少しだけ変更が加わる:

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(rec.u, rec.v, rec.p);
  double pdf;
  color albedo;

  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf))
    return emitted;

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1) / pdf;
}

レンダリングされる画像は変わらないはずである。

ランダムな半球サンプリング

ここで実験として、異なるサンプリング戦略を試してみよう。第一巻で示した、物体表面の半球上を一様ランダムにサンプルする方法を使う。このとき \(p(\text{direction}) = \frac{1}{2}\pi\) であり、scatter 関数は次のようになる:

bool scatter(
  const ray& r_in,
  const hit_record& rec,
  color& alb,
  ray& scattered,
  double& pdf
) const {
  vec3 direction = random_in_hemisphere(rec.normal);
  scattered = ray(rec.p, unit_vector(direction), r_in.time());
  alb = albedo->value(rec.u, rec.v, rec.p);
  pdf = 0.5 / pi;
  return true;
}

これまでと同じ画像が得られるが、ノイズの付き方が変わる。

ノイズを減らすために、もう少し理論を説明する。

ランダムな方向の生成

まず何らかの分布に沿った方向 (単位球上の点) をランダムに生成する方法を見つけよう。簡単のため \(z\) 軸を法線方向として、\(\theta\) を法線から測った角度とする。軸を回転させる方法は次節で説明する。考える分布は \(z\) 軸周りの回転に関して対称な分布だけとする。このとき \(p(\text{direction}) = f(\theta)\) が成り立つ。大学レベルの微積分を学んだことがあるなら、球座標で \(dA = \sin(\theta) \cdot d\theta \cdot d\phi\) が成り立つことを知っているだろう。もし学んだことがないなら、この等式を受け入れた上で次に進んでほしい。将来大学で微積分の講義を取れば理解できる。

方向を引数に取る PDF \(p(\text{direction}) = f(\theta)\) が与えられたとして、\(\theta\) および \(\phi\) に関する一次元の PDF をそれぞれ \(a(\phi)\), \(b(\theta)\) とする。このとき \[ \begin{aligned} a(\phi) & = \frac{1}{2\pi} \quad ({\footnotesize \text{一定}}) \\ b(\theta) & = 2\pi f(\theta)\sin \theta \end{aligned} \] が成り立つ。

一次元モンテカルロ積分で説明したように、\([0, 1]\) の一様乱数 \(r_{1}\) に対して \[ r_1 = \int_{0}^{\phi} a(t)\, dt = \int_{0}^{\phi} \frac{1}{2\pi}\, dt = \frac{\phi}{2\pi} \] が成り立つとき、\(r_{1}\) の PDF は \(a(\phi) = 1/2\pi\) となる。\(\phi\) について解けば \[ \phi = 2 \pi \cdot r_1 \] を得る。

同様に \(r_{2}\) を \([0, 1]\) の一様乱数とすれば、\(\theta\) の PDF が \(b(\theta) = 2\pi f(\theta) \sin \theta\) なら \[ r_2 = \int_{0}^{\theta} 2 \pi f(t) \sin t\, dt \] が成り立つ。ここで \(t\) はダミー変数を表す。\(f\) として異なる関数をいくつか考えよう。まず球上に一様な確率密度を考える。単位球の表面積は \(4\pi\) だから、一様分布では \(p(\text{direction}) = 1/4\pi\) となる。よって \[ \begin{aligned} r_2 & = \int_{0}^{\theta} 2 \pi \frac{1}{4\pi} \sin t \,dt \\ & = \int_{0}^{\theta} \frac{1}{2} \sin t \,dt \\ & = \frac{-\cos\theta}{2} - \frac{-\cos0}{2} \\ & = \frac{1 - \cos\theta}{2} \end{aligned} \] であり、\(\cos\theta\) について解けば \[ \cos(\theta) = 1 - 2 r_2 \] を得る。\(\theta\) より先に \(\cos \theta\) が求まる場合が多いから、この式を \(\theta\) について解く必要はない。\(\arccos\) が呼び出されるのも避けたい。

方向 \((\theta, \phi)\) に向かう単位ベクトルを生成するには、次の式を使ってデカルト座標系に変換する必要がある: \[ \begin{aligned} x & = \cos\phi \cdot \sin\theta \\ y & = \sin\phi \cdot \sin\theta \\ z & = \cos\theta \end{aligned} \] これと恒等式 \(\cos^{2} x + \sin^{2} x = 1\) を使えば、二つの一様乱数 \(r_{1}, r_{2}\) を使った表現が求まる: \[ \begin{aligned} x & = \cos(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} \\ y & = \sin(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} \\ z & = 1 - 2 r_2 \end{aligned} \] \((1 - 2 r_2)^2 = 1 - 4r_2 + 4r_2^2\) を使って簡略化すれば \[ \begin{aligned} x & = \cos(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} \\ y & = \sin(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} \\ z & = 1 - 2 r_2 \end{aligned} \] となる。

この式を使って点を生成しよう:

int main() {
  for (int i = 0; i < 200; i++) {
    auto r1 = random_double();
    auto r2 = random_double();
    auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
    auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
    auto z = 1 - 2*r2;
    std::cout << x << " " << y << " " << z << '\n';
  }
}

plotly (三次元散布図のプロットをサポートする優れたサイト) を使えば、データを無料でプロットできる⁶。plot.ly では図を回転できるので、本当に一様に見えるかどうかを確認するとよい。

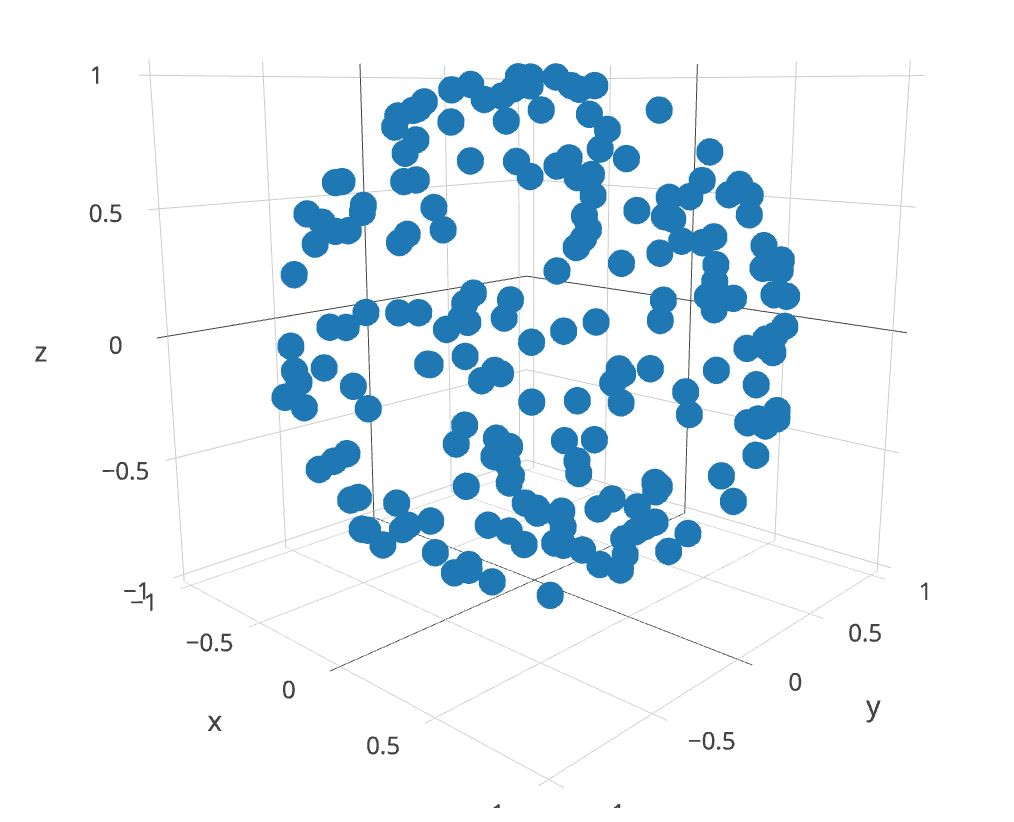
半球上の一様サンプリング

次は半球上の一様サンプリングを導出しよう。半球に渡って一様な密度関数は \(p(\text{direction}) = 1/2\pi\) だから、上で示した関係の定数部分が変わって \[ \cos \theta = 1 - r_2 \] となる。確認しておくと、左辺の \(\cos \theta\) は \(1\) から \(0\) の値を取り、このとき \(\theta\) は \(0\) から \(\pi/2\) の値を取るので矛盾はない。これを使って \(\cos^{3} \theta\) の半球に関する積分を計算しよう (\(\cos^{3} \theta\) は積分が解析的に計算できる適当な関数として選んだ)。手で積分を行うと \[ \begin{aligned} \int \cos^3 \theta dA & = \int_{0}^{2 \pi} \int_{0}^{\pi /2} \cos^3 \theta \sin \theta\, d\theta d\phi \\ & = 2 \pi \int_{0}^{\pi/2} \cos^3 \theta \sin \theta \, d\theta = \frac{\pi}{2} \end{aligned} \] となる。

この積分を重点サンプリングを使ったモンテカルロ積分で求める。\(p(\text{direction}) = 1/2\pi\) だから、平均すべき値は \(f/p = \cos^3 \theta / (1/2\pi)\) である。この正しさを確かめるプログラムを示す:

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto r1 = random_double();
    auto r2 = random_double();
    auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
    auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
    auto z = 1 - r2;
    sum += z*z*z / (1.0/(2.0*pi));
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "Pi/2   = " << pi/2 << '\n';
  std::cout << "Estimate = " << sum/N << '\n';
}

次は \(p(\text{directions}) = \cos \theta / \pi\) となる方向を生成する方法を考える。これまでと同様に考えれば \[ r_2 = \int_{0}^{\theta} 2 \pi \frac{\cos(t)}{\pi} \sin t \, d\theta = 1 - \cos^2 \theta \] だから、 \[ \cos \theta = \sqrt{1 - r_2} \] となる。簡単な変形により次を得る: \[ \begin{aligned} z & = \cos\theta = \sqrt{1 - r_2} \\ x & = \cos\phi \sin\theta = \cos(2 \pi r_1) \sqrt{1 - z^2} = \cos(2 \pi r_1) \sqrt{r_2} \\ y & = \sin\phi \sin\theta = \sin(2 \pi r_1) \sqrt{1 - z^2} = \sin(2 \pi r_1) \sqrt{r_2} \end{aligned} \]

このランダムなベクトル \((x, y, z)\) を生成する関数を作っておく:

#include "rtweekend.h"

#include <iostream>
#include <math.h>

inline vec3 random_cosine_direction() {
  auto r1 = random_double();
  auto r2 = random_double();
  auto z = sqrt(1-r2);

  auto phi = 2*pi*r1;
  auto x = cos(phi)*sqrt(r2);
  auto y = sin(phi)*sqrt(r2);

  return vec3(x, y, z);
}

int main() {
  int N = 1000000;

  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    auto v = random_cosine_direction();
    sum += v.z()*v.z()*v.z() / (v.z()/pi);
  }

  std::cout << std::fixed << std::setprecision(12);
  std::cout << "Pi/2   = " << pi/2 << '\n';
  std::cout << "Estimate = " << sum/N << '\n';
}

この他の密度関数は後で必要になったときに考える。次節ではランダムなベクトルを物体表面の法線ベクトルの方向に傾ける方法を説明する。

正規直交基底

前節では \(z\) 軸を基準にランダムな方向を生成する方法を導出した。次は物体表面の法線を基準に同じことを行いたい。

相対座標

互いに直交する三つの単位ベクトルの集合を正規直交基底 (orthonormal basis) と呼ぶ。例えばデカルト座標系の \(x\), \(y\), \(z\) 軸方向の単位ベクトルからなる集合は ONB である。私はよく忘れてしまうのだが、現実世界における物体の位置と傾きを決めるには、基準となる ONB がどこかに必要となる。同様に仮想空間にある物体の位置と傾きを記述するには ONB をどこかに配置しなければならない。写真とはカメラから見たシーンの相対的な位置と傾きを写したものであり、カメラとシーンが同じ座標系で表されている限りどんな座標系でも問題はない。

原点を \(\textbf{O}\) として、デカルト座標系の単位ベクトルを \(\textbf{x}\), \(\textbf{y}\), \(\textbf{z}\) とする。私たちが「位置 \((3, -2, 7)\)」 と言うとき本当に意味しているのは、 \[ {\footnotesize \text{位置}} = \mathbf{O} + 3\mathbf{x} - 2\mathbf{y} + 7\mathbf{z} \] である。原点 \(\textbf{O}'\) と基底ベクトル \(\textbf{u}\), \(\textbf{v}\), \(\textbf{w}\) を使ってこの位置を表すのであれば、 \[ {\footnotesize \text{位置}} = \mathbf{O}' + u\mathbf{u} + v\mathbf{v} + w\mathbf{w} \] となるように実数 \((u, v, w)\) を選ぶことになる。

正規直交基底の構築

グラフィックス入門の講義を取ると、座標系や 4×4 の座標変換行列についての説明に長い時間が費やされる。これを無視してはいけない。グラフィックスで重要な概念なのだから！ しかし今の私たちにはこの概念は必要ない。今考えているのは法線 \(\textbf{n}\) を基準とした特定の分布に従うランダムな方向の生成である。方向は基準となる原点を持たないので、原点を考える必要ない。ただし \(\textbf{n}\) に直交して互いに直行する二つの余接ベクトルは必要になる。

モデルによっては各面の余接ベクトルが一つ以上保存されている場合もある。モデルの余接ベクトルが一つしかない場合には、ONB の計算に少し手間がかかる。長さが \(0\) より大きく \(\textbf{n}\) と平行でない適当なベクトルを \(\textbf{a}\) とすれば、\(\textbf{n}\) と垂直で互いに直交する二つのベクトル \(\textbf{s}\), \(\textbf{t}\) は次の式から得られる: \[ \begin{aligned} \mathbf{t} & = \text{unit\_vector}(\mathbf{a} \times \mathbf{n}) \\ \mathbf{s} & = \mathbf{t} \times \mathbf{n} \end{aligned} \]

このやり方は間違っていないが、モデルを読み込んでも \(\textbf{a}\) は得られない点が問題となる。よく考えずに適当な \(\textbf{a}\) を選ぶと、\(\textbf{n}\) に平行な \(\textbf{a}\) を選んでしまう可能性がある。これに対処するためによく使われるのが、if を使って \(\textbf{n}\) がある軸に平行かどうかを判定し、もし平行でなければその軸を \(\textbf{a}\) として採用するという方法である:

if absolute(n.x > 0.9)
  a ← (0, 1, 0)
else
  a ← (1, 0, 0)

ONB \(\textbf{s}\), \(\textbf{t}\), \(\textbf{n}\) が計算できたら、次に \(z\) 軸を基準にしたランダムな方向ベクトル \(\text{random}(x,y,z)\) を生成する。すると法線 \(\textbf{n}\) を基準にしたランダムな方向ベクトルは \[ x \mathbf{s} + y \mathbf{t} + z \mathbf{n} \] と表せる。

カメラからレイを得るときにも同じような数式を使ったことに気が付くかもしれない。あの処理はカメラの座標系への座標変形とみなすことができる。

ONB を表すクラス

ONB のためにクラスを作るべきだろうか、それともユーティリティ関数で十分だろうか？ 私には分からない。ただクラスがユーティリティ関数よりずっと複雑になることはなさそうなので、クラスを作る:

class onb {
public:
  onb() {}
  inline vec3 operator[](int i) const { return axis[i]; }

  vec3 u() const { return axis[0]; }
  vec3 v() const { return axis[1]; }
  vec3 w() const { return axis[2]; }

  vec3 local(double a, double b, double c) const {
    return a*u() + b*v() + c*w();
  }

  vec3 local(const vec3& a) const {
    return a.x()*u() + a.y()*v() + a.z()*w();
  }

  void build_from_w(const vec3&);

public:
  vec3 axis[3];
};

void onb::build_from_w(const vec3& n) {
  axis[2] = unit_vector(n);
  vec3 a = (fabs(w().x()) > 0.9) ? vec3(0,1,0) : vec3(1,0,0);
  axis[1] = unit_vector(cross(w(), a));
  axis[0] = cross(w(), v());
}

これを使って lambertian マテリアルを描き直そう:

bool scatter(
  const ray& r_in,
  const hit_record& rec,
  color& alb,
  ray& scattered,
  double& pdf
) const {
  onb uvw;
  uvw.build_from_w(rec.normal);
  vec3 direction = uvw.local(random_cosine_direction());
  scattered = ray(rec.p, unit_vector(direction), r_in.time());
  alb = albedo->value(rec.u, rec.v, rec.p);
  pdf = dot(uvw.w(), scattered.direction()) / pi;
  return true;
}

次の画像が得られる:

これでようやく、ライトに向けてサンプルを多く飛ばす準備が整った。

直接的なライトのサンプリング

ほぼ一様に方向をサンプルする方法の問題は、ライトが存在する方向と他の重要でない方向が同程度にしかサンプルされないことである。シャドウレイを使って直接光の計算を特別扱いすることもできるが、ここではライトのある方向へ多くレイを放つようにする。ここで実装するアーキテクチャは後で任意の方向へレイを多く送れるようにするのに使われる。

ライトに向かうランダムな方向を選ぶのは非常に簡単で、ライト上の点をランダムに選び、その点に向かう方向を選べばよい。ただモンテカルロ積分を行うには、その方向の PDF \(p(\text{direction})\) を知る必要がある。PDF はいくつだろうか？

ライトの PDF

面積 \(A\) のライト上の点を一様ランダムに選択すると、ライト上の任意の点の PDF は \(1/A\) となる。方向を定義する単位球上におけるこのライトの面積を求めよう。幸い、単純な対応関係が存在する。

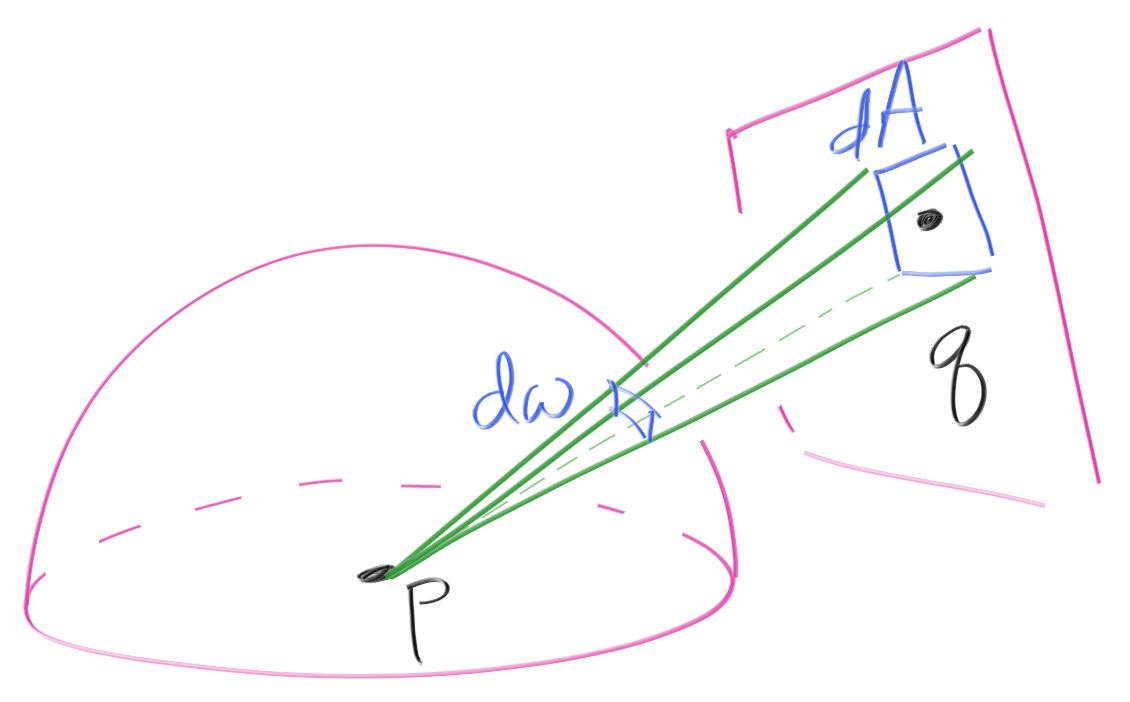
ライト上に小面積 \(dA\) を取り、その内部の点を適当に \(q\) とする。このとき一様ランダムに選択したライト上の点がこの小面積内にある確率は \(dA/A\) である。また求めようとしている PDF \(p(\text{direction})\) において単位球上の小面積 \(dw\) をサンプルする確率は \(p(\text{direction}) \cdot dw\) と表せる。さらに \(dw\) と \(dA\) の間には次の幾何学的な関係がある: \[ dw = \frac{dA \cdot \cos \alpha}{\text{distance}^2(p,q)} \] ここで \(\alpha\) は \(\text{direction}\) とライトの法線がなす角度を表す。\(dw\) と \(dA\) から点が選ばれる確率が同じだから \[ p(\text{direction}) \cdot dw = p(\text{direction}) \cdot \frac{dA \cdot \cos \alpha}{\text{distance}^2(p,q)} = \frac{dA}{A} \] つまり \[ p(\text{direction}) = \frac{\text{distance}^2(p,q)}{\cos \alpha \cdot A} \] が成り立つ。

ライトのサンプリング

ray_color 関数にライトのサンプリングを追加しよう。まずは数式と考え方の正しさを確認するために、ライトのサンプリングを関数の中にハードコードする:

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(rec.u, rec.v, rec.p);
  double pdf;
  color albedo;
  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf))
    return emitted;

  auto on_light = vec3(random_double(213,343), 554, random_double(227,332));
  auto to_light = on_light - rec.p;
  auto distance_squared = to_light.length_squared();
  to_light = unit_vector(to_light);

  if (dot(to_light, rec.normal) < 0)
    return emitted;

  double light_area = (343-213)*(332-227);
  auto light_cosine = fabs(to_light.y());
  if (light_cosine < 0.000001)
    return emitted;

  pdf = distance_squared / (light_cosine * light_area);
  scattered = ray(rec.p, to_light, r.time());

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1) / pdf;
}

\(10\) サンプル/ピクセルでレンダリングすると次の画像が得られる:

これは光源だけをサンプルして得られる画像であり、正しく動いているように見える。

ライトの向き

天井のライト付近にあるノイズのような白点は、ライトが両面を照らしていてライトと天井の間に隙間があるために生じている。ライトは下方向だけを照らすのが正しいだろうから、diffuse_light のメンバー関数 emitted の引数に hit_record を追加してこれを処理する:

virtual color emitted(
  const hit_record& rec,
  double u, double v,
  const point3& p
) const {
  if (rec.front_face)
    return emit->value(u, v, p);
  else
    return color(0,0,0);
}

それからライトを反転させて法線が \(-y\) 方向を向くようにする必要もある。このために任意の hittable から法線が反転させる flip_face を作成する:

class flip_face : public hittable {
public:
  flip_face(shared_ptr<hittable> p) : ptr(p) {}

  virtual bool hit(
    const ray& r, double t_min, double t_max, hit_record& rec
  ) const {
    if (!ptr->hit(r, t_min, t_max, rec))
      return false;

    rec.front_face = !rec.front_face;
    return true;
  }

  virtual bool bounding_box(double t0, double t1, aabb& output_box) const {
    return ptr->bounding_box(t0, t1, output_box);
  }

public:
  shared_ptr<hittable> ptr;
}

これを使ってライトを反転させる:

hittable_list cornell_box(camera& cam, double aspect) {
  ...
  world.add(
    make_shared<flip_face>(make_shared<xz_rect>(213, 343, 227, 332, 554, light))
  );
  ...
}

次の画像が得られる:

混合密度

\(\cos \theta\) となる PDF とライトをサンプルする PDF の両方が手に入った。次はこの二つを組み合わせた PDF が作りたい。

ライティングと反射の平均

確率論では複数の密度関数を混ぜて混合密度 (mixture density) を作るテクニックがよく使われる。例えば二つの密度関数の平均を取れば混合密度となる: \[ p_{\text{mixture}}(\text{direction}) = \frac{1}{2} p_{\text{reflection}}(\text{direction}) + \frac{1}{2} p_{\text{light}}(\text{direction}) \]

これを実装する方法を考える。非常に重要な細かい問題があるので、実装は意外なほど難しくなる。まずランダムな方向の選択は簡単に行える:

if (random_double() < 0.5)
  pdf_reflection に従って方向を選択する
else
  pdf_light に従って方向を選択する

\(p_{\text{mixture}}\) の計算にはさらに慎重な議論が必要になる。上のコードが選択する方向が両方の PDF から得られる可能性もあるので、\(p_{\text{reflection}}\) と \(p_{\text{light}}\) の両方を計算しなければならない。例えば \(p_{\text{reflection}}\) を使って生成した方向がライトを向いている可能性がある。

ここまでを振り返ると、PDF にはサポートすべき関数が二つあることが分かる:

1. 与えられた方向に対する PDF の値を求める。
2. 分布に従うランダムな方向を生成する。

具体的な関数の処理は \(p_{\text{reflection}}\) や \(p_{\text{light}}\) および二つの混合密度の間で異なる。これはクラスの継承が発明された理由そのものだ！ 抽象クラスで正確に何が必要になるかは分からないので、最小限のインターフェースを作って上手く行くことを願うという貪欲なアプローチを私は取る。このアプローチで作った PDF クラスを示す:

class pdf {
public:
  virtual ~pdf() {}

  virtual double value(const vec3& direction) const = 0;
  virtual vec3 generate() const = 0;
};

この設計で大丈夫かどうかは \(p_{\text{reflection}}\) や \(p_{\text{light}}\) を子クラスとして実装すれば明らかになる。ライトのサンプルでは hittable が今までにないクエリに答える必要があるので、インターフェースを新しく追加する必要があるだろう。そのときは AABB と同じように、親の hittable クラスにメンバー関数を追加して子クラスの実装を省けないかを最初に考える。

まずコサイン密度を実装しよう:

inline vec3 random_cosine_direction() {
  auto r1 = random_double();
  auto r2 = random_double();
  auto z = sqrt(1-r2);

  auto phi = 2*pi*r1;
  auto x = cos(phi)*sqrt(r2);
  auto y = sin(phi)*sqrt(r2);

  return vec3(x, y, z);
}

class cosine_pdf : public pdf {
public:
  cosine_pdf(const vec3& w) { uvw.build_from_w(w); }

  virtual double value(const vec3& direction) const {
    auto cosine = dot(unit_vector(direction), uvw.w());
    return (cosine <= 0) ? 0 : cosine/pi;
  }

  virtual vec3 generate() const {
    return uvw.local(random_cosine_direction());
  }

public:
  onb uvw;
};

ray_color() 関数を次のように変更すればこのクラスを試せる。pdf クラスをコードに組み込むのに加えて、名前の衝突を避けるためにローカル変数 pdf の名前を変える必要がある。

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(r, rec, rec.u, rec.v, rec.p);
  double pdf_val;
  color albedo;
  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf_val))
    return emitted;

  cosine_pdf p(rec.normal);
  scattered = ray(rec.p, p.generate(), r.time());
  pdf_val = p.value(scattered.direction());

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1)
          / pdf_val;
}

このプログラムからは今までと同じ結果が得られる。何が起こったかというと、リファクタリングによって pdf が計算される場所が移動したのである。

物体に向けてレイをサンプルする

続いて hittable に向かうレイのサンプルを実装しよう。例えばライトが hittable となる。

class hittable_pdf : public pdf {
public:
  hittable_pdf(shared_ptr<hittable> p, const point3& origin)
    : ptr(p), o(origin) {}

  virtual double value(const vec3& direction) const {
    return ptr->pdf_value(o, direction);
  }

  virtual vec3 generate() const {
    return ptr->random(o);
  }

public:
  shared_ptr<hittable> ptr;
  point3 o;
};

このクラスはまだ実装していない hittable クラスの関数を二つ使っている。hittable の子クラス全てで実装するのを避けるために、hittable クラスにダミー関数を二つ追加する:

class hittable {
public:
  virtual bool hit(
    const ray& r, double t_min, double t_max, hit_record& rec
  ) const = 0;

  virtual bool bounding_box(double t0, double t1, aabb& output_box) const = 0;

  virtual double pdf_value(const point3& o, const vec3& v) const {
    return 0.0;
  }

  virtual vec3 random(const vec3& o) const {
    return vec3(1, 0, 0);
  }
};

この関数を xz_rect で実装する:

class xz_rect: public hittable {
public:
  ...
  virtual double pdf_value(const point3& origin, const vec3& v) const {
    hit_record rec;
    if (!this->hit(ray(origin, v), 0.001, infinity, rec))
      return 0;

    auto area = (x1-x0)*(z1-z0);
    auto distance_squared = rec.t * rec.t * v.length_squared();
    auto cosine = fabs(dot(v, rec.normal) / v.length());

    return distance_squared / (cosine * area);
  }

  virtual vec3 random(const point3& origin) const {
    auto random_point = point3(random_double(x0,x1), k, random_double(z0,z1));
    return random_point - origin;
  }
  ...
}

そして ray_color() も変更する:

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(r, rec, rec.u, rec.v, rec.p);
  double pdf_val;
  color albedo;
  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf_val))
    return emitted;

  shared_ptr<hittable> light_shape =
    make_shared<xz_rect>(213, 343, 227, 332, 554, nullptr);
  hittable_pdf p(light_shape, rec.p);

  scattered = ray(rec.p, p.generate(), r.time());
  pdf_val = p.value(scattered.direction());

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1)
          / pdf_val;
}

\(10\) サンプル/ピクセルでレンダリングすると次の画像が得られる:

混合 PDF クラス

次はコサインとライトの混合密度を使ったサンプリングを行う。混合密度を表すクラスは簡単に書ける:

class mixture_pdf : public pdf {
public:
  mixture_pdf(shared_ptr<pdf> p0, shared_ptr<pdf> p1) {
    p[0] = p0;
    p[1] = p1;
  }

  virtual double value(const vec3& direction) const {
    return 0.5 * p[0]->value(direction) + 0.5 *p[1]->value(direction);
  }

  virtual vec3 generate() const {
    if (random_double() < 0.5)
      return p[0]->generate();
    else
      return p[1]->generate();
  }

public:
  shared_ptr<pdf> p[2];
};

これを ray_color() に組み込む:

color ray_color(
  const ray& r, const color& background, const hittable& world, int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  ray scattered;
  color attenuation;
  color emitted = rec.mat_ptr->emitted(r, rec, rec.u, rec.v, rec.p);
  double pdf_val;
  color albedo;
  if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf_val))
    return emitted;

  shared_ptr<hittable> light_ptr =
    make_shared<xz_rect>(213, 343, 227, 332, 554, nullptr);
  auto p0 = make_shared<hittable_pdf>(light_shape, rec.p);
  auto p1 = make_shared<cosine_pdf>(rec.normal);
  mixture_pdf p(p0, p1);

  scattered = ray(rec.p, p.generate(), r.time());
  pdf_val = p.value(scattered.direction());

  return emitted
     + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
          * ray_color(scattered, background, world, depth-1)
          / pdf_val;
}

\(1000\) サンプル/ピクセルとしてレンダリングすれば次の画像が得られる:

レイトレーサーのアーキテクチャについて

この節ではコードを書かない。現在の私たちは交差点に立っていて、アーキテクチャに関する決断を下さなければならない。混合密度を使ったアプローチを取ると、レイトレーシングでよく使われるシャドウレイが使えなくなる。一方で光源に限らずドアの下の明るい隙間や窓といった明るくなると思われる場所を自由にサンプルできるので、私はこのアプローチを気に入っている。しかし多くのレイトレーサーは処理を分け、ライトに向かう一つ以上の終端レイ (シャドウレイ) と物体表面の反射分布に従う一つのレイを生成する。シャドウレイを選択して収束の速さのためにシーンの柔軟性を犠牲にすることもできた。これは個人的な好みである。

これ以外にもコードに関して問題がいくつかある。

まず PDF の構築が ray_color() 関数にハードコードされている。クリーンアップすべきであり、ライトに関する情報を ray_color() 関数に引数として渡す方法が考えられる。BVH の構築と違ってサンプルの数に限りが無いので、PDF の構築ではメモリリークに気を付けなければならない。

次に鏡面反射レイ (を使うガラスと金属) はもはやサポートされない。散乱レイの PDF をデルタ関数とすれば数式上は上手く行くが、それを浮動小数点を使って実装すれば悪夢となる。鏡面反射を別にして処理することもできるし、表面の粗さは \(0\) にならないと決めて NaN が発生しない鏡面反射に非常に近い PDF を実装することもできる。私はどちらを選んでもよいと思っている (両方とも試したが、どちらにも利点があった)。ただ今までに滑らかな金属とガラスのコードを実装したので、ここでは f()/p() の計算を行わない完全鏡面マテリアルを追加する方法を取る。

さらに背景関数を扱う設計も欠いており、環境マップや複雑な機能を持つ背景を追加できない。環境マップは HDR となっている (RGB が \(0\) から \(255\) の整数で表され \(0\) から \(1\) の小数と解釈されるのではなく、最初から float で表される) 場合もある。なお出力はこれまでも HDR だった: 最後に切り捨てていただけである。

最後に、私たちのレンダラは RGB を使っているが、より物理ベースな ──自動車メーカーが使うような── レンダラでは、多くの場合スペクトルカラーが要求される。偏光さえ必要になる場合もある。映画用のレンダラでは RGB が必要だろう。両方のモードで動作するハイブリッドなレンダラを作ることもできるが、当然それは難しい。ここでは RGB のまま進み、本の終わりでもう一度この問題に触れる。

PDF の管理方法の整理

今の ray_color() 関数には二つの PDF がハードコードされている:

1. ライトの形状が関係する p0()
2. 法線と物体表面の種類が関係する p1()

p0() についてはライト (および多くサンプルしたい hittable) に関する情報を ray_color() 関数に渡し、p1() については material に PDF を尋ねるようにできる。さらに鏡面ベクトルの存在は hit 関数か material クラスが答えるようにする。

拡散反射と鏡面反射

ぜひ表現できるようにしておきたいマテリアルの一つが、ニスを塗った木材のような部分的には理想的な鏡面反射をして部分的には拡散反射をするマテリアルである。マテリアルで鏡面反射レイと拡散反射レイの二つを同時に生成するレンダラもある。ただ私は場合分けが好きではないので、マテリアルで反射と拡散をランダムに選ぶようにする。このアプローチでは PDF を慎重に計算しなければならず、さらに拡散と鏡面に応じて ray_color() の処理を切り替える必要がある。幸い拡散の場合には pdf_value() を呼べば PDF を計算できるので、特別な処理はいらない。

matrial の設計を変更して、関数の引数を struct にまとめるとしよう。hittable の hit_record と同様である:

struct scatter_record {
  ray specular_ray;
  bool is_specular;
  color attenuation;
  shared_ptr<pdf> pdf_ptr;
};

class material {
public:
  virtual ~material() {}

  virtual color emitted(
    const ray& r_in, const hit_record& rec, double u, double v, const point3& p
  ) const {
    return color(0,0,0);
  }

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, scatter_record& srec
  ) const {
    return false;
  }

  virtual double scattering_pdf(
    const ray& r_in, const hit_record& rec, const ray& scattered
  ) const {
    return 0;
  }
};

lambertian マテリアルは簡単になる:

class lambertian : public material {
public:
  lambertian(shared_ptr<texture> a) : albedo(a) {}

  bool scatter(
    const ray& r_in, const hit_record& rec, scatter_record& srec
  ) const {
    srec.is_specular = false;
    srec.attenuation = albedo->value(rec.u, rec.v, rec.p);
    srec.pdf_ptr = make_shared<cosine_pdf>(rec.normal);
    return true;
  }

  double scattering_pdf(
    const ray& r_in, const hit_record& rec, const ray& scattered
  ) const {
    auto cosine = dot(rec.normal, unit_vector(scattered.direction()));
    return cosine < 0 ? 0 : cosine/pi;
  }

public:
  shared_ptr<texture> albedo;
};

ray_color() にも変更が必要になる。

color ray_color(
  const ray& r,
  const color& background,
  const hittable& world,
  shared_ptr<hittable> lights,
  int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  scatter_record srec;
  color emitted = rec.mat_ptr->emitted(r, rec, rec.u, rec.v, rec.p);
  if (!rec.mat_ptr->scatter(r, rec, srec))
    return emitted;

  auto light_ptr = make_shared<hittable_pdf>(lights, rec.p);
  mixture_pdf p(light_ptr, srec.pdf_ptr);

  ray scattered = ray(rec.p, p.generate(), r.time());
  auto pdf_val = p.value(scattered.direction());

  return emitted
    + srec.attenuation * rec.mat_ptr->scattering_pdf(r, rec, scattered)
               * ray_color(scattered, background, world, lights, depth-1)
               / pdf_val;
}

ライトに関する情報は main で直接与える:

int main() {
  ...
  camera camera;
  hittable_list world = cornell_box(camera, aspect_ratio);
  shared_ptr<hittable> light =
    make_shared<xz_rect>(213, 343, 227, 332, 554, nullptr);

  for (int j = image_height-1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
      color pixel_color(0, 0, 0);
      for (int s = 0; s < samples_per_pixel; ++s) {
        auto u = (i + random_double()) / (image_width-1);
        auto v = (j + random_double()) / (image_height-1);
        ray r = camera.get_ray(u, v);
        pixel_color += ray_color(r, background, world, light, max_depth);
      }
      write_color(std::cout, pixel_color, samples_per_pixel);
    }
  }
}

鏡面反射の計算

鏡面反射をするマテリアルは今まで放っておいてきた。また法線を変化させるインスタンスについても何もしていない。しかし scatter_record を使った設計は全体的に整っているので、いずれも修復すればそのまま使える。ここには鏡面マテリアルを直す方法だけを示す。metal は簡単に直せる:

class metal : public material {
public:
  metal(const color& a, double f) : albedo(a), fuzz(f < 1 ? f : 1) {}

  virtual bool scatter(
    const ray& r_in, const hit_record& rec, scatter_record& srec
  ) const {
    vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
    srec.specular_ray = ray(rec.p, reflected+fuzz*random_in_unit_sphere());
    srec.attenuation = albedo;
    srec.is_specular = true;
    srec.pdf_ptr = 0;
    return true;
  }

public:
  color albedo;
  double fuzz;
};

fuzz の値が大きいと、このマテリアルは理想的な鏡面反射とは異なる反射レイを生成する。しかし陰的な (PDF を使わない) サンプリングがあるので、このマテリアル以前と同様に正しく動作する。

ray_color() では陰的にサンプルされたレイを生成するケースを追加するだけでよい:

color ray_color(
  const ray& r,
  const color& background,
  const hittable& world,
  shared_ptr<hittable> lights,
  int depth
) {
  hit_record rec;

  // 反射回数が一定よりも多くなったら、その時点で追跡をやめる
  if (depth <= 0)
    return color(0,0,0);

  // レイがどのオブジェクトとも交わらないなら、背景色を返す
  if (!world.hit(r, 0.001, infinity, rec))
    return background;

  scatter_record srec;
  color emitted = rec.mat_ptr->emitted(r, rec, rec.u, rec.v, rec.p);
  if (!rec.mat_ptr->scatter(r, rec, srec))
    return emitted;

  if (srec.is_specular) {
    return srec.attenuation
       * ray_color(srec.specular_ray, background, world, lights, depth-1);
  }

  shared_ptr<pdf> light_ptr = make_shared<hittable_pdf>(lights, rec.p);
  mixture_pdf p(light_ptr, srec.pdf_ptr);

  ray scattered = ray(rec.p, p.generate(), r.time());
  auto pdf_val = p.value(scattered.direction());
  delete srec.pdf_ptr;

  return emitted + srec.attenuation
           * rec.mat_ptr->scattering_pdf(r, rec, scattered)
           * ray_color(scattered, background, world, lights, depth-1)
           / pdf_val;
}

コーネルボックスの直方体のマテリアルを metal に変更しよう:

hittable_list cornell_box(camera& cam, double aspect) {
  hittable_list world;

  auto red   = make_shared<lambertian>(make_shared<solid_color>(.65, .05, .05));
  auto white = make_shared<lambertian>(make_shared<solid_color>(.73, .73, .73));
  auto green = make_shared<lambertian>(make_shared<solid_color>(.12, .45, .15));
  auto light = make_shared<diffuse_light>(make_shared<solid_color>(15, 15, 15));

  world.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
  world.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
  world.add(make_shared<flip_face>(
    make_shared<xz_rect>(213, 343, 227, 332, 554, light))
  );
  world.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
  world.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
  world.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

  shared_ptr<material> aluminum =
    make_shared<metal>(color(0.8, 0.85, 0.88), 0.0);
  shared_ptr<hittable> box1 =
    make_shared<box>(point3(0,0,0), point3(165,330,165), aluminum);
  box1 = make_shared<rotate_y>(box1, 15);
  box1 = make_shared<translate>(box1, vec3(265,0,295));
  world.add(box1);

  shared_ptr<hittable> box2 =
    make_shared<box>(point3(0,0,0), point3(165,165,165), white);
  box2 = make_shared<rotate_y>(box2, -18);
  box2 = make_shared<translate>(box2, vec3(130,0,65));
  world.add(box2);

  point3 lookfrom(278, 278, -800);
  point3 lookat(278, 278, 0);
  vec3 vup(0, 1, 0);
  auto dist_to_focus = 10.0;
  auto aperture = 0.0;
  auto vfov = 40.0;
  auto t0 = 0.0;
  auto t1 = 1.0;

  cam = camera(
    lookfrom, lookat, vup, vfov, aspect, aperture, dist_to_focus, t0, t1
  );

  return world;
}