簡単なモンテカルロプログラム

モンテカルロ法 (Monte Carlo Method, MC) を使う最も簡単なプログラムから始めよう。モンテカルロ法を使うと真の値の統計的な近似値を計算でき、近似値は実行時間を長くすればそれだけ正確になる。誤差はあるが時間をかければ正確になる値を簡単なプログラムで求められるという基本的な特性が MC の全てである。グラフィックスのように極限まで正確な値が必要とされない分野においてモンテカルロ法は特に有用となる。

円周率の計算

例として \(\pi\) の近似値を計算してみよう。古典的な方法としてビュフォンの針を使うものがあるが、ここに示す方法はその変種と言える。正方形に内接する円を考える:

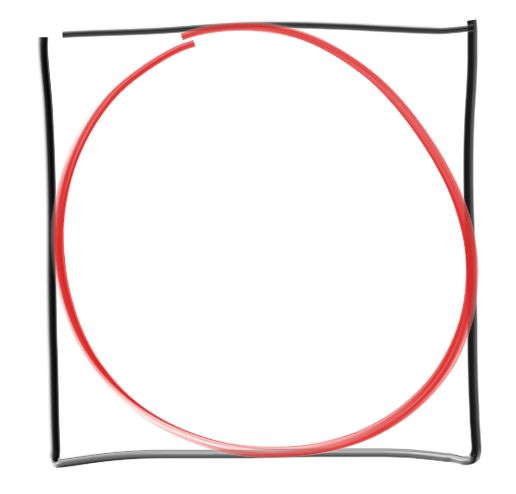
この正方形の中にランダムな点をたくさん打つとする。このときランダムな点が円の中に入る確率は円の面積に比例する。正確に言えば、その確率は円の面積と正方形の面積の比に等しくなる。つまり \[ \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4} \] であり、\(r\) に関係しない。\(r\) は計算しやすいように決められるので、\(r = 1\) と定める。さらに中心を原点とすれば、次のプログラムが書ける:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
  int N = 1000;
  int inside_circle = 0;
  for (int i = 0; i < N; i++) {
    auto x = random_double(-1,1);
    auto y = random_double(-1,1);
    if (x*x + y*y < 1)
      inside_circle++;
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "Estimate of Pi = " << 4*double(inside_circle) / N << '\n';
}

リスト 3.1 [pi.cc] \(\pi\) の近似

このプログラムが計算する \(\pi\) の近似値はコンピューターの種類やランダムシードによって異なる。私のマシンでは Estimate of Pi = 3.0880000000 という結果になった。

収束の確認

収束の様子が分かりやすいように、実行を止めずに近似値を計算し続けるようにしておこう:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main() {
  int inside_circle = 0;
  int runs = 0;
  std::cout << std::fixed << std::setprecision(12);
  while (true) {
    runs++;
    auto x = random_double(-1,1);
    auto y = random_double(-1,1);
    if (x*x + y*y < 1)
      inside_circle++;

    if (runs % 100000 == 0)
      std::cout << "Estimate of Pi = "
            << 4*double(inside_circle) / runs
            << '\n';
  }
}

リスト 3.2 [pi.cc] \(\pi\) の近似 (バージョン 2)

サンプルの層化 (振動)

近似値は最初 \(\pi\) に素早く近づくが、その後はゆっくりとしか近づかない。つまり後に加えられるサンプルはそれまでのサンプルよりも低い寄与しか持たず、収穫逓減の法則 (Law of Diminishing Returns) が働いている。これはモンテカルロ法の持つ厄介な性質だが、サンプルを層化 (stratifying) することで改善できる。「サンプルを振動 (jittering) させる」と表現される場合もあるこのテクニックでは、ランダムなサンプルを一つずつ取るのではなく、格子状に分けた小領域の全てでサンプルを一度に取る:

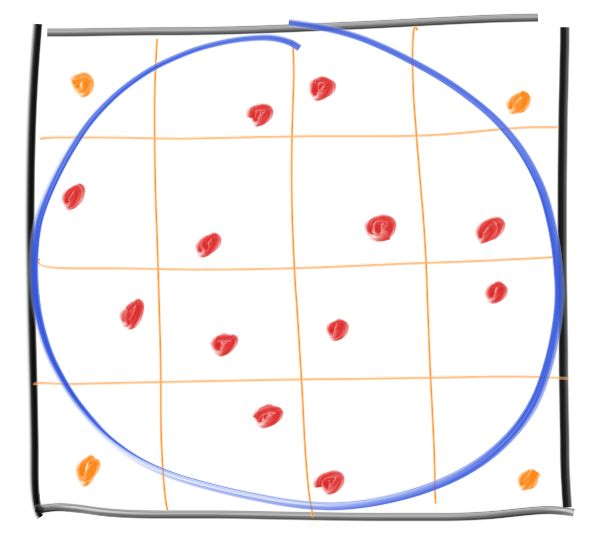
層化サンプリングは格子を使うので、サンプル数をあらかじめ決めておかなくてはならない。サンプル数を十億として、二つの方法を比べよう:

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
  int inside_circle = 0;
  int inside_circle_stratified = 0;
  int sqrt_N = 10000;
  for (int i = 0; i < sqrt_N; i++) {
    for (int j = 0; j < sqrt_N; j++) {
      auto x = random_double(-1,1);
      auto y = random_double(-1,1);
      if (x*x + y*y < 1)
        inside_circle++;
      x = 2*((i + random_double()) / sqrt_N) - 1;
      y = 2*((j + random_double()) / sqrt_N) - 1;
      if (x*x + y*y < 1)
        inside_circle_stratified++;
    }
  }

  auto N = static_cast<double>(sqrt_N) * sqrt_N;
  std::cout << std::fixed << std::setprecision(12);
  std::cout
    << "Regular Estimate of Pi = "
    << 4*double(inside_circle) / N << '\n'
    << "Stratified Estimate of Pi = "
    << 4*double(inside_circle_stratified) / N << '\n';
}

リスト 3.3 [pi.cc] \(\pi\) の近似 (バージョン 3)

私のマシンでは次の結果が得られた:

Regular Estimate of Pi = 3.14151480
Stratified Estimate of Pi = 3.14158948

興味深いことに、層化したサンプルを使う方法は正確な近似が得られるだけではなく、収束の速さも優れている！しかし残念ながらこの利点は問題の次元が増えると薄れてしまう (例えば三次元の球で同じ計算を行うと改善は小さくなる)。この現象は次元の呪い (Curse of Dimensionality) と呼ばれる。この本ではサンプルの層化をレイトレーサーに追加しないが、反射やシャドウを一度だけ考えるときや厳密に二次元の問題を考えるときには層化を必ず利用するべきである。