球上の点を使ったモンテカルロ積分

私たちのレイトレーサーには方向をランダムに選ぶ処理があり、方向は単位球上の点として表される。前節で説明したモンテカルロ積分をここでも利用できるが、そのためには二次元の PDF が必要になる。

全ての方向に関する次の関数の積分を求めたいとする¹: \[ \int \cos^2 \theta \] モンテカルロ積分では \(\cos^{2} \theta / p(\text{direction})\) をサンプルすることになる。この式における \(p(\text{direction})\) について考えよう。極座標で \(\text{direction}\) を表すと \((\theta, \phi)\) を使った \(p\) の式が手に入るが、どんな表現であれ PDF は全体に渡る積分が \(1\) で、その値 \(p(\text{direction})\) は方向 \(\text{direction}\) がサンプルされる相対確率を表さなければならない。

単位球上の点を一様ランダムに選択する関数をこれまでに実装した:

vec3 random_unit_vector() {
  auto a = random_double(0, 2*pi);
  auto z = random_double(-1, 1);
  auto r = sqrt(1 - z*z);
  return vec3(r*cos(a), r*sin(a), z);
}

この関数から得られる点に対する PDF はどう表せるだろうか？ 単位球上の任意の点が得られる確率が一定で、全体に渡る積分は \(1\) になるから、PDF は常に \(1/({\footnotesize \text{面積}}) = 1/4\pi\) となる。被積分関数が \(\cos^{2} \theta\) で \(\theta\) は \(z\) 軸との角度を表すので、考えていた積分は次のように計算できる:

inline double pdf(const vec3& p) {
  return 1 / (4*pi);
}

int main() {
  int N = 1000000;
  auto sum = 0.0;
  for (int i = 0; i < N; i++) {
    vec3 d = random_unit_vector();
    auto cosine_squared = d.z()*d.z();
    sum += cosine_squared / pdf(d);
  }
  std::cout << std::fixed << std::setprecision(12);
  std::cout << "I = " << sum/N << '\n';
}

解析解は \(\frac{4}{3} \pi\) であり (積分法を覚えているなら計算してみよ)、上のコードはこの近似値を計算する。これで重点サンプリングをレイトレーシングに適用する準備が整った！

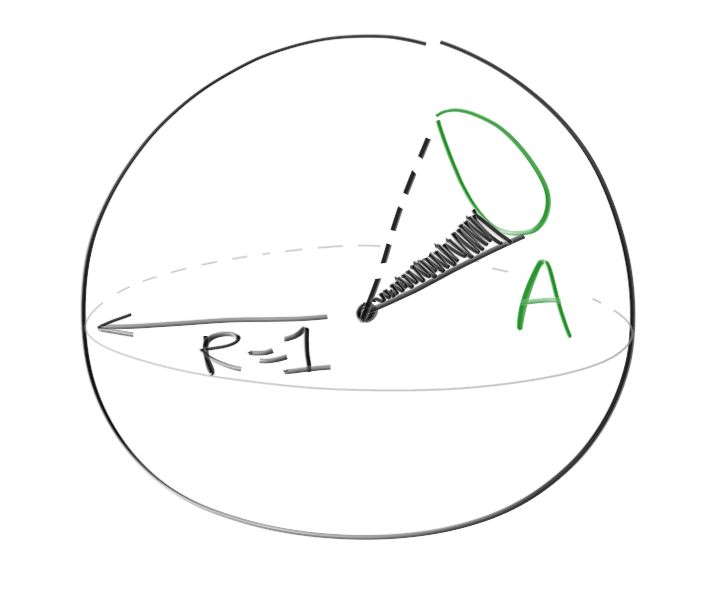
積分や確率が単位球上に渡るものである点が、ここで重要となる。"方向" は単位球上の面積として測られ、方向、立体角 (solid angle)、面積といった言葉で表される ──立体角と呼ばれることが最も多い。もしこの言葉を理解できるなら、素晴らしい！ もしよく理解できないなら、私と同じように方向を指すベクトルの束が貫く単位球上の領域の面積を考えるとよい。立体角 \(\omega\) は単位球上に射影した領域の面積 \(A\) と等しい。

次は私たちが解こうとしている光輸送方程式 (light transport equation) を考えよう。

1. 訳注: 数式の最後に微小量が付いておらず、この積分は厳密な意味での数式でないことに注意。^[return]