X. 微分の幾何学的な意味

微分係数の持つ幾何学的な意味を考えると、有用な事実が明らかになる。

まず、\(x^{2},\ \) \(\sqrt{x},\ \) \(ax + b\) といった \(x\) の関数は曲線としてプロットできる。この曲線を描く方法は今の学生なら誰でも知っている。

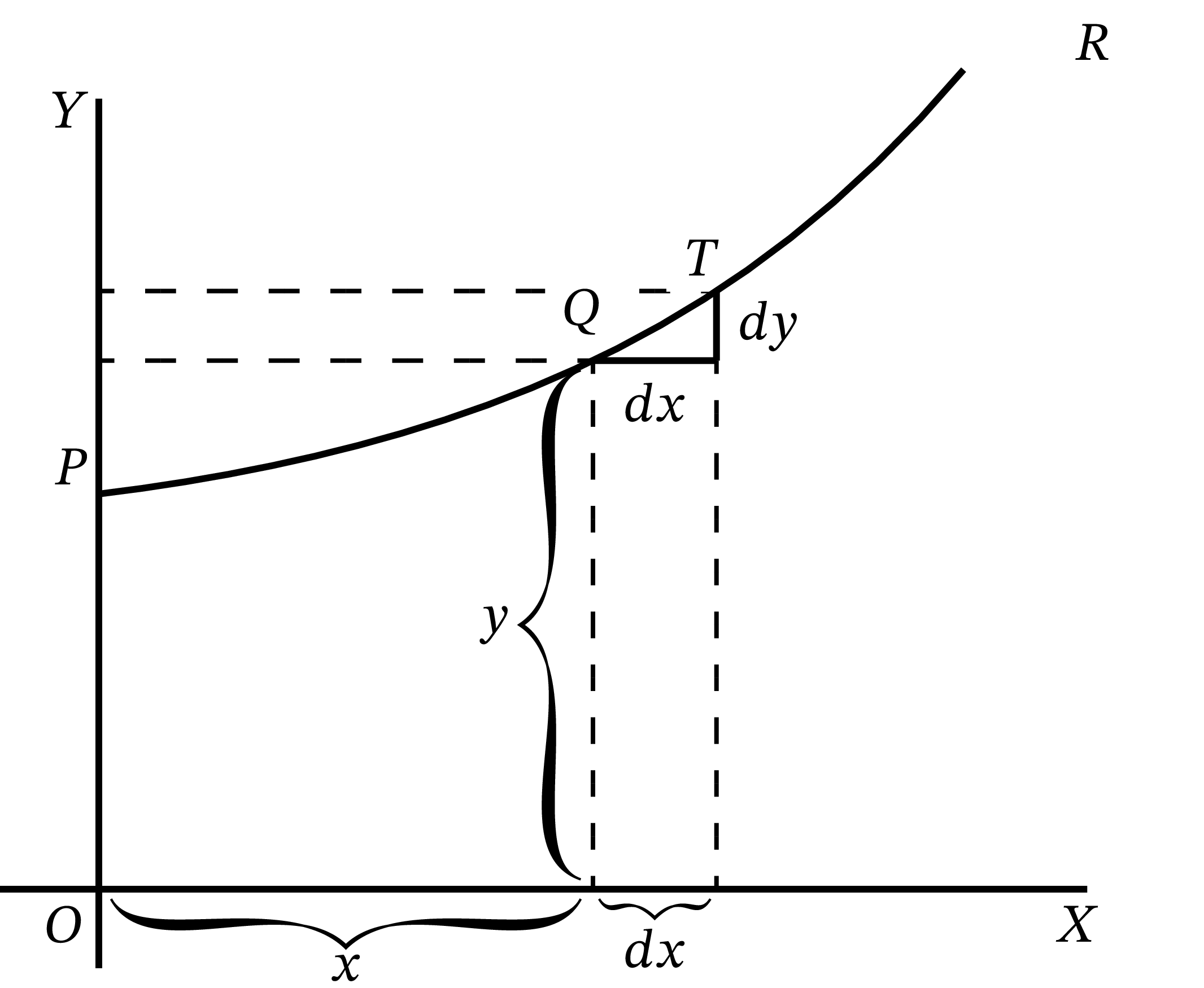
\(OX\) と \(OY\) を軸としてプロットしたとある曲線の一部が図 7 の \(PQR\) として表されている。この曲線上の適当な点 \(Q\) を取り、\(Q\) の横座標と縦座標をそれぞれ \(x\) と \(y\) とする。この状況では \(x\) が変化すると \(y\) も変化する。\(x\) を小さな値 \(dx\) だけ右に移動させれば \(y\) も動くが、その変化は上方向であり、大きさは \(dy\) という小さな値として表せる (今考えている図中の曲線は \(x\) と共に上昇する曲線なためである)。このとき \(dy\) と \(dx\) の比は二点 \(Q\) と \(T\) の間における曲線の傾きに近い値だとみなせる。ただ図からも分かるように、実際には \(Q\) から \(T\) の間で曲線は様々な傾きを持つ。しかし、もし \(Q\) と \(T\) が非常に近くて曲線の \(Q\) から \(T\) の部分が事実上直線とみなせるのであれば、比 \(\dfrac{dy}{dx}\) は曲線 \(QT\) の (唯一の) 傾きに等しいと言うことができる。この部分のどちらの端で作られる直線 \(QT\) も曲線とは \(QT\) でのみ交わるから、\(QT\) が無限に小さいとき直線 \(QT\) と曲線の交点は事実上一つだけとなる。すなわちこの直線は曲線の接線 (tangent) である。

こうして見つかる曲線の接線は明らかに \(QT\) と同じ傾きを持つ。つまり点 \(Q\) で \(\dfrac{dy}{dx}\) が存在するなら、その値は \(Q\) における曲線の接線の傾きと等しくなる。

「曲線の傾き」とただ言っただけでは意味が正確に定まらない。曲線はたくさんの傾きを持つ ──曲線上の全ての部分で異なる傾きが存在する── ためである。一方で「この点における曲線の傾き」と言った場合には一つの値が定まる。それはその点を含む非常に小さい曲線の一部分の傾きであり、「その点における曲線の接線の傾き」に等しい。

\(dx\) が右向きの小さな変位であり、\(dy\) が上方向への小さな変位であることを確認してほしい。この二つの変位は考えうる限り短く ──無限に短く── 取らなければならないが、図では有限の長さで書かざるをえない。本当に無限小として書けば何も見えなくなってしまう。

これから \(\bm{\dfrac{dy}{dx}}\) が任意の点における曲線の傾きを表す例を見ていく。

図 8 のように特定の点で曲線の傾きが \(45^{\circ}\) だとする。このとき対応する \(dy\) と \(dx\) は等しく、\(\dfrac{dy}{dx} = 1\) が成り立つ。

曲線の傾きが \(45^{\circ}\) より急な場合 (図 9) には、\(\dfrac{dy}{dx}\) の値が \(1\) より大きくなる。逆に \(45^{\circ}\) より緩やかな場合 (図 10) には、\(\dfrac{dy}{dx}\) の値は \(1\) より小さくなる。また水平な直線上の任意の点や曲線が水平となる点では \(dy = 0\) だから、\(\dfrac{dy}{dx} = 0\) が成り立つ。

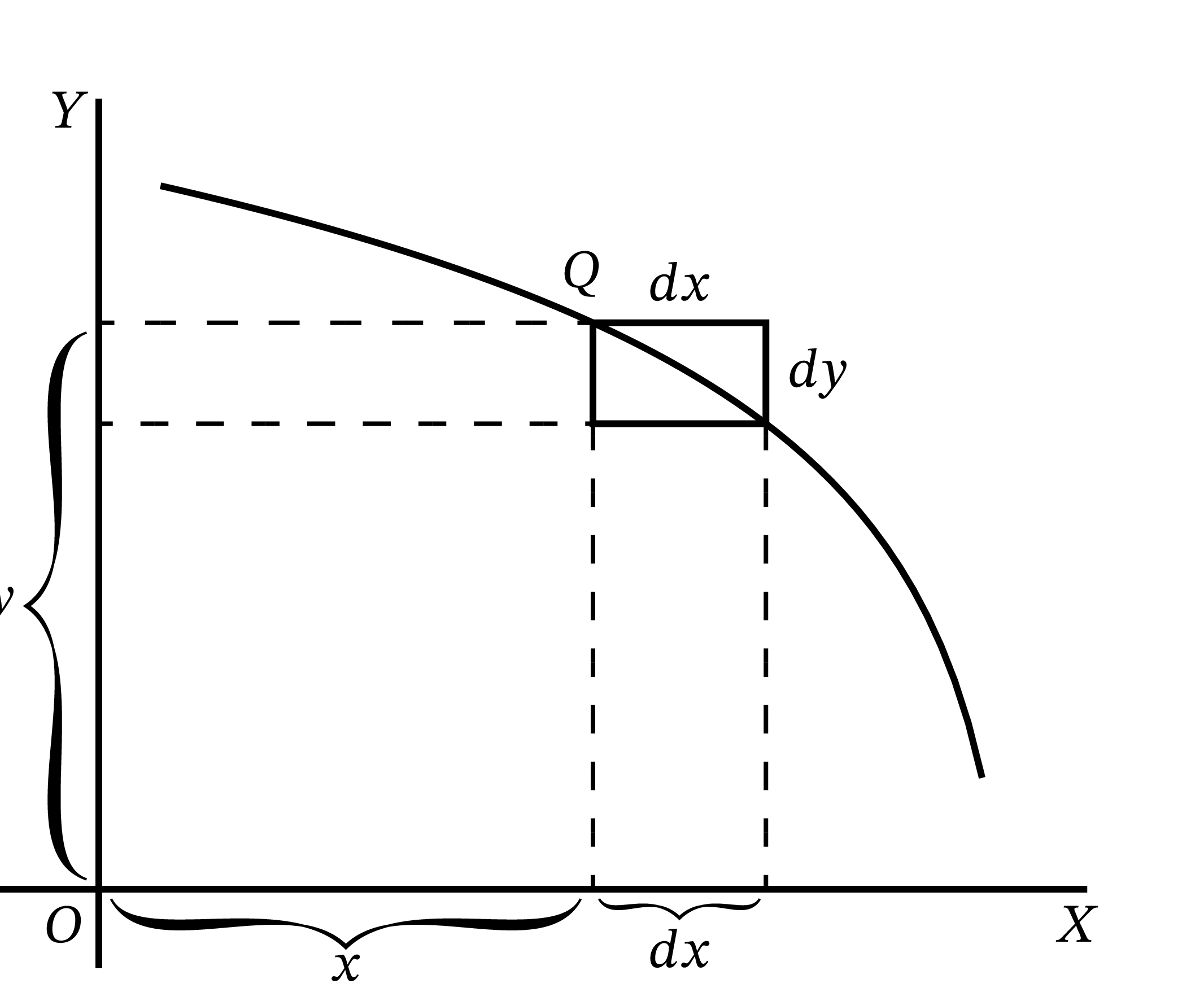
図 11 のように曲線が下向きなら、\(dy\) は下方向への変位となる。つまり \(dy\) は負であり、\(\dfrac{dy}{dx}\) の値も負となる。

図 12 のように “曲線” が直線なら、\(\dfrac{dy}{dx}\) の値は直線上の全ての点で同じになる。言い換えると、直線の傾きは一定である。

曲線を右に進むと傾きが急になるなら、\(\dfrac{dy}{dx}\) の値は曲線が急になるにつれて大きくなる。このような曲線の例を図 13 に示す。

曲線を右に進むと傾きが緩くなっていくなら、\(\dfrac{dy}{dx}\) の値は傾きが緩やかになるにつれて小さくなる。このような曲線の例を図 14 に示す。

図 15 のように最初は下降し、ある点からは上昇する曲線を考える。このとき曲線は凹型であり、\(\dfrac{dy}{dx}\) の値は最初は負で、曲線が底を付く点で \(0\) となり、その点より右では正の値を取りながら大きさを増していく。このような場合、\(y\) は極小値 (mimima) を取ると言う。\(y\) の極小値が \(y\) が取る全ての値の中の最小値である必要はなく、極小値はその値が凹型の底に対応することしか意味しない。例えば図 28 では \(y\) が \(1\) である点が凹型の底に対応する一方で、\(y\) が \(1\) よりも小さい値を取る場所が存在する。極小値の条件は、その点の両側で \(y\) が増加することである。

注意 ── \(y\) が極小値となる \(x\) では \(\dfrac{dy}{dx} = 0\) が成り立つ。

曲線が最初は増加し、ある点からは下降する場合を考える (図 16)。このとき \(\dfrac{dy}{dx}\) は最初は正で、曲線が頂上に達する点で \(0\) になり、それからの曲線が下降する部分では負となる。このとき \(y\) は極大値 (maxima) を取ると言う。ただし \(y\) の極大値が \(y\) の最大値であるとは限らない。例えば図 28 の曲線では \(y\) に極大値 \(\dfrac{7}{3}\) が存在するものの、これは他の曲線上の点を考えたときの \(y\) の最大値ではない。

注意 ── \(y\) が極大値となる \(x\) では \(\dfrac{dy}{dx} = 0\) が成り立つ。

図 17 の形をした曲線では、\(\dfrac{dy}{dx}\) の値は常に正となる。しかしそれでも傾きが最小となる点は存在する。その点で \(\dfrac{dy}{dx}\) は最小、つまり曲線上の任意の点における \(\dfrac{dy}{dx}\) よりも小さくなる。

曲線が図 18 のような形をしているなら、\(\dfrac{dy}{dx}\) は上の部分では負で、下の部分では正となる。曲線の鼻先に当たる点では曲線が垂直になるので、\(\dfrac{dy}{dx}\) は無限に大きくなる。

\(\dfrac{dy}{dx}\) の値がその点における曲線の傾きを表すことがこれで理解できた。では微分の方法を知っている関数を使ってこれを実際に確認してみよう。

\(\text{(1)}\) 最も簡単なケースとして次の関数を考える: \[ y = x + b \]

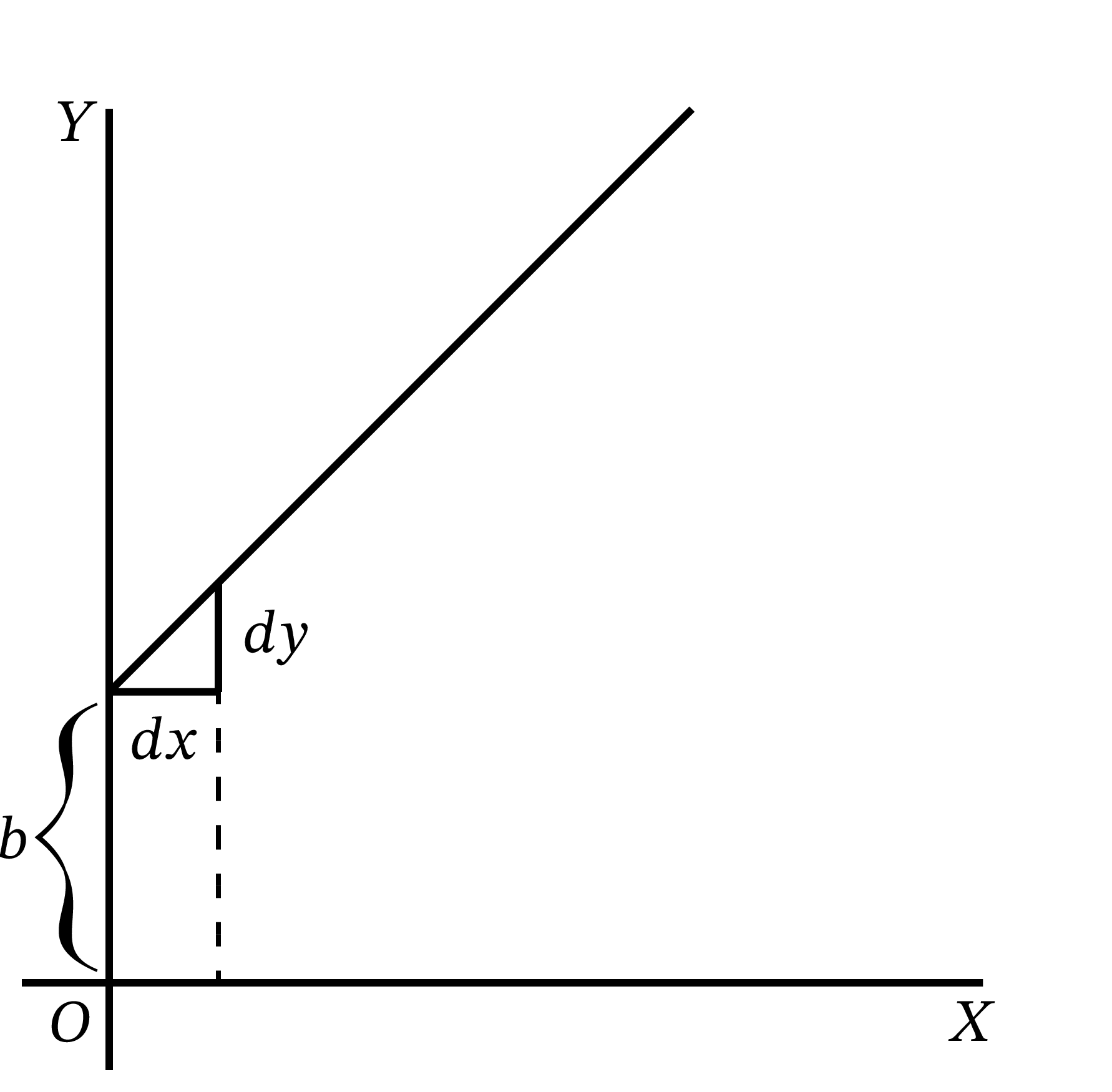
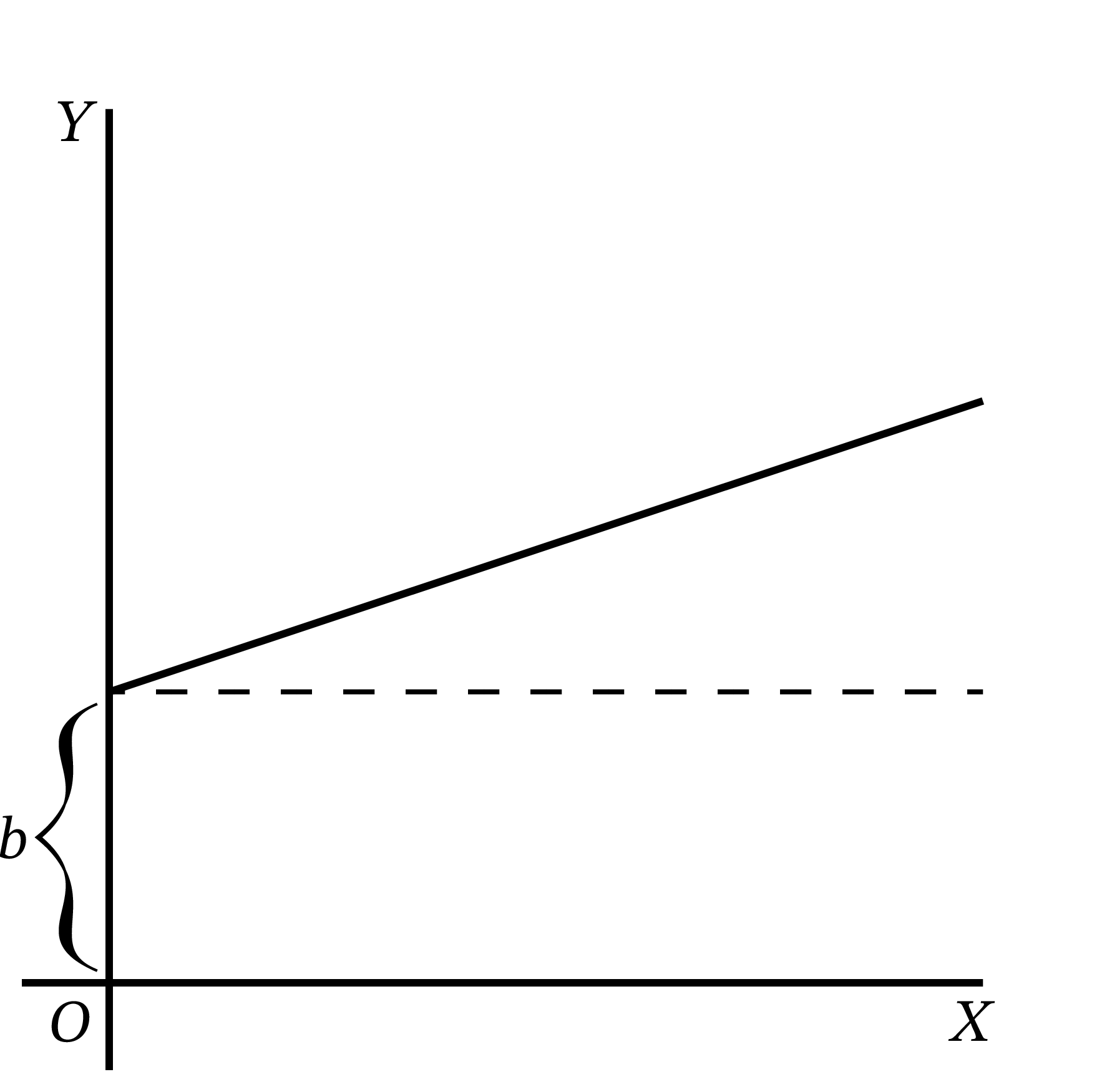
この関数を \(x\) 軸と \(y\) 軸のスケールが同じ図にプロットすると図 19 のようになる。\(x = 0\) に対応する \(y\) 座標は \(y = b\) であり、この “曲線” と \(y\) 軸は高さ \(b\) の点で交わる。曲線はこの点から \(45^{\circ}\) の角度で右上に上っていき、\(x\) が増加すると \(y\) は同じだけ増加する。

\(y = x + b\) を前に学んだ方法で微分すれば \(\dfrac{dy}{dx} = 1\) を得る。

つまりこの直線は右方向に \(dx\) だけ移動すると同じだけ上方向に \(dy\) だけ移動するような傾きを持っている。傾きは一定であり、直線のどこでも傾きは変わらない。

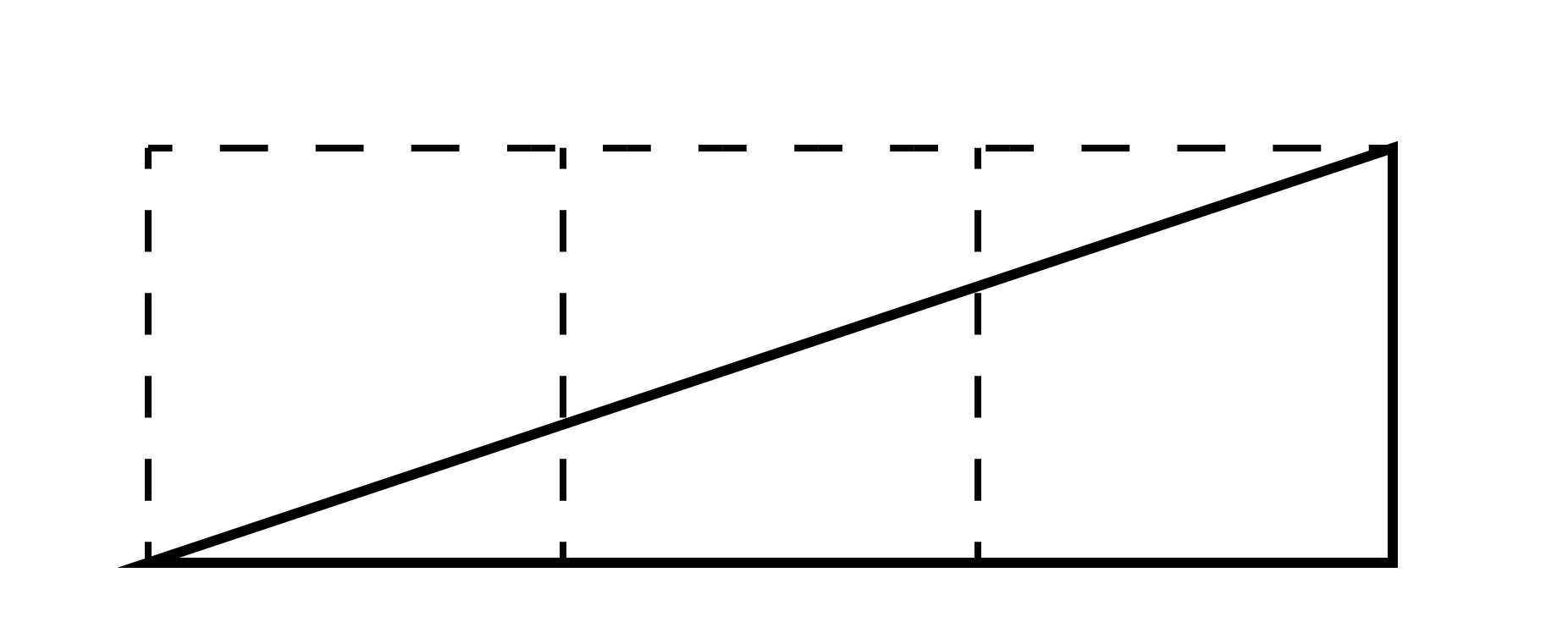
\(\text{(2)}\) 次の例を考える: \[ y = ax + b \] 一つ前の例と同じように、この曲線も \(y\) 軸上の高さ \(b\) の点を通る。ここでは曲線を描く前に微分で傾きを求めてみよう。微分は \(\dfrac{dy}{dx} = a\) だから傾きは一定で、直線が水平方向となす角度のタンジェントは \(a\) となる。例えば \(a\) が \(\dfrac{1}{3}\) なら、\(dx\) は \(dy\) の三倍に等しい (図 21)。この曲線の全体図を図 20 に示す。

\(\text{(3)}\) 次の例はもう少し難しい: \[ y= ax^{2} + b \]

この曲線と \(y\) 軸の交点は原点から高さ \(b\) の点であり、これは変わらない。

では微分してみよう [もし微分の方法を覚えていないなら第五章を読み返すとよい。あるいは読み返さずとも、微分を計算してみよ]。すると次が分かる: \[ \frac{dy}{dx} = 2ax \]

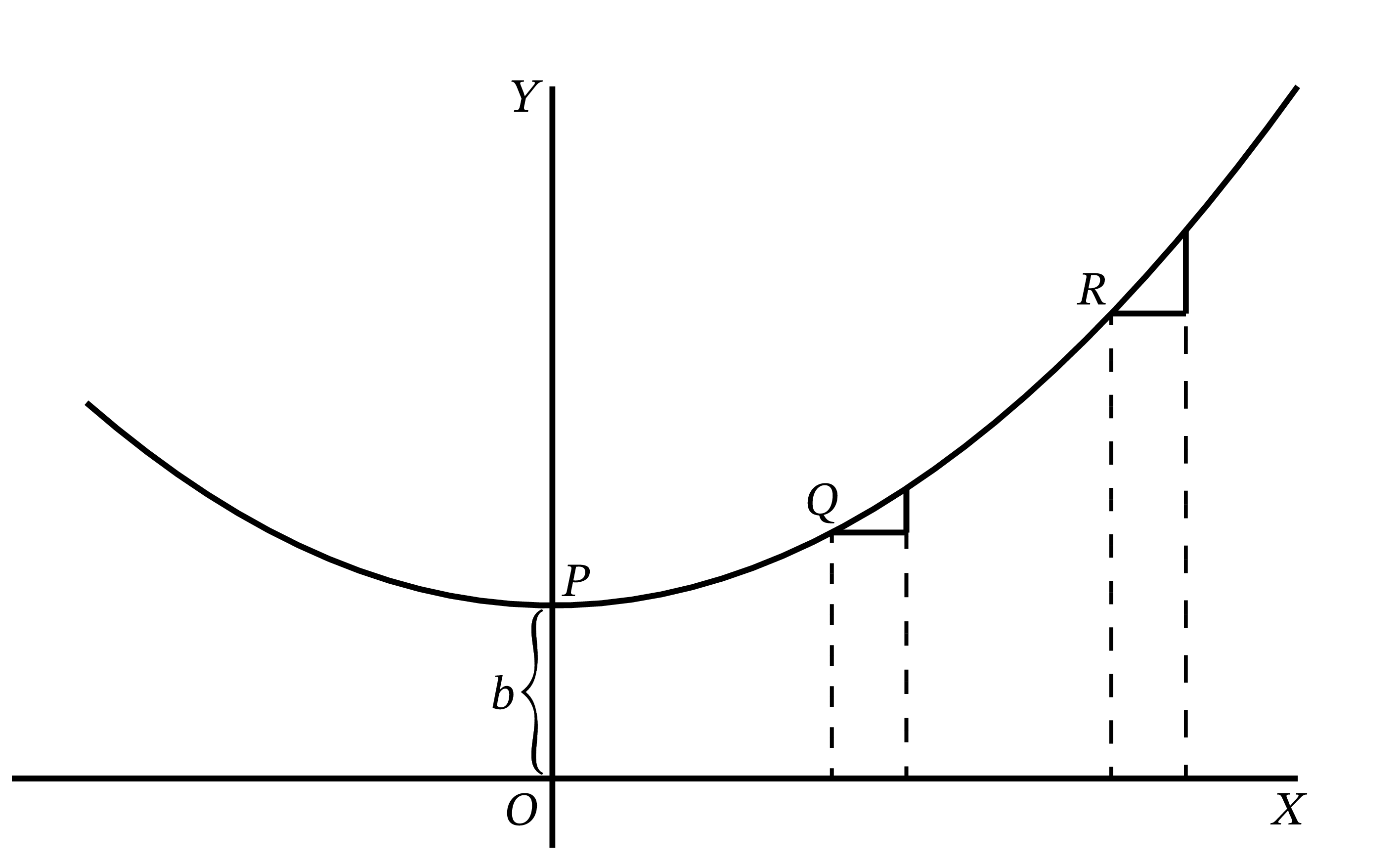
微分の結果からは曲線の傾きが一定でないことが分かる: 曲線は \(x\) が増すにつれて急になる。また \(x = 0\) の点 \(P\) では傾きは \(0\) に等しい ──つまり曲線は水平である (図 22)。\(P\) より左の \(x\) が負になる部分では \(\dfrac{dy}{dx}\) も負なので、曲線を左から右にたどると図のように下へ向かう。

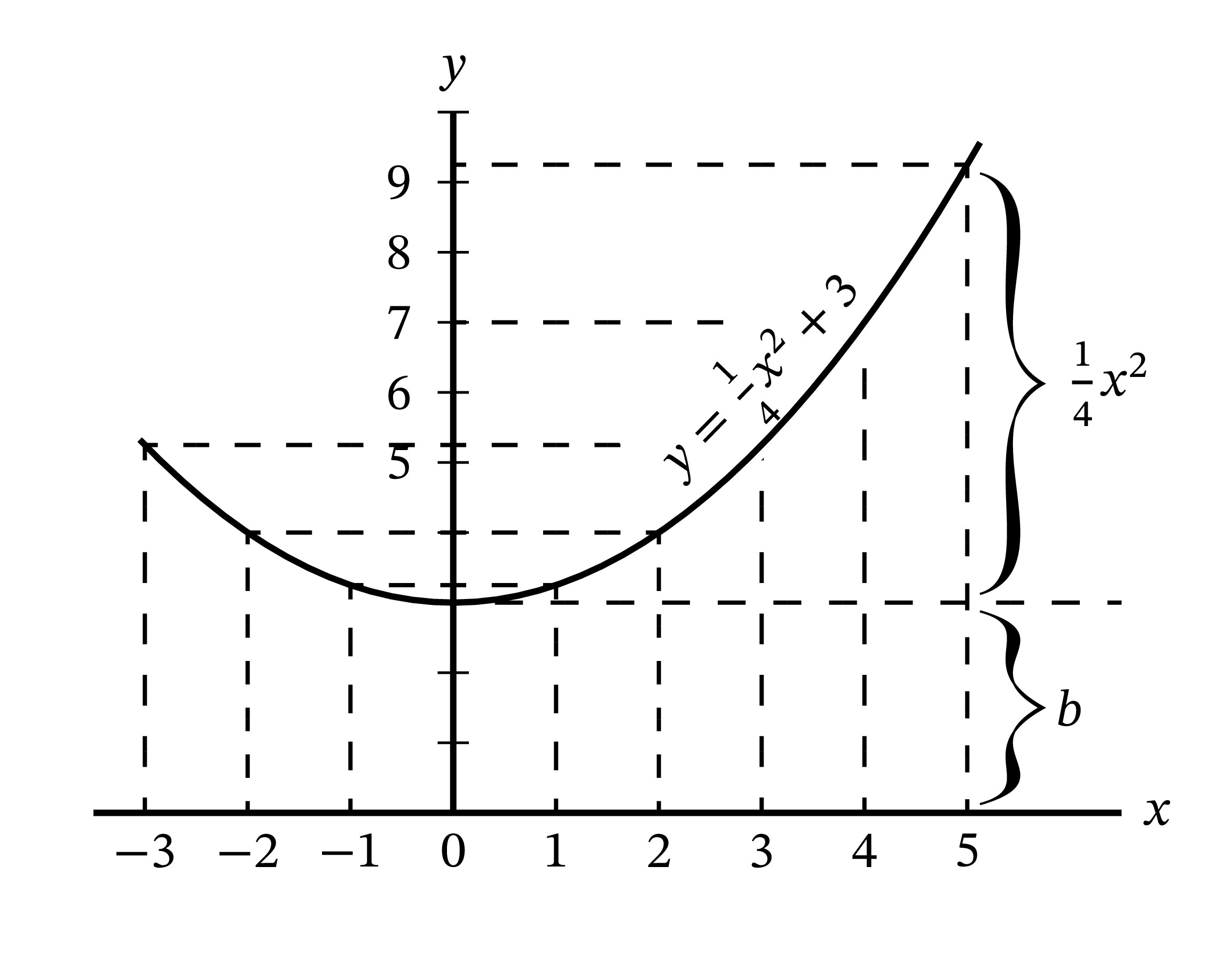
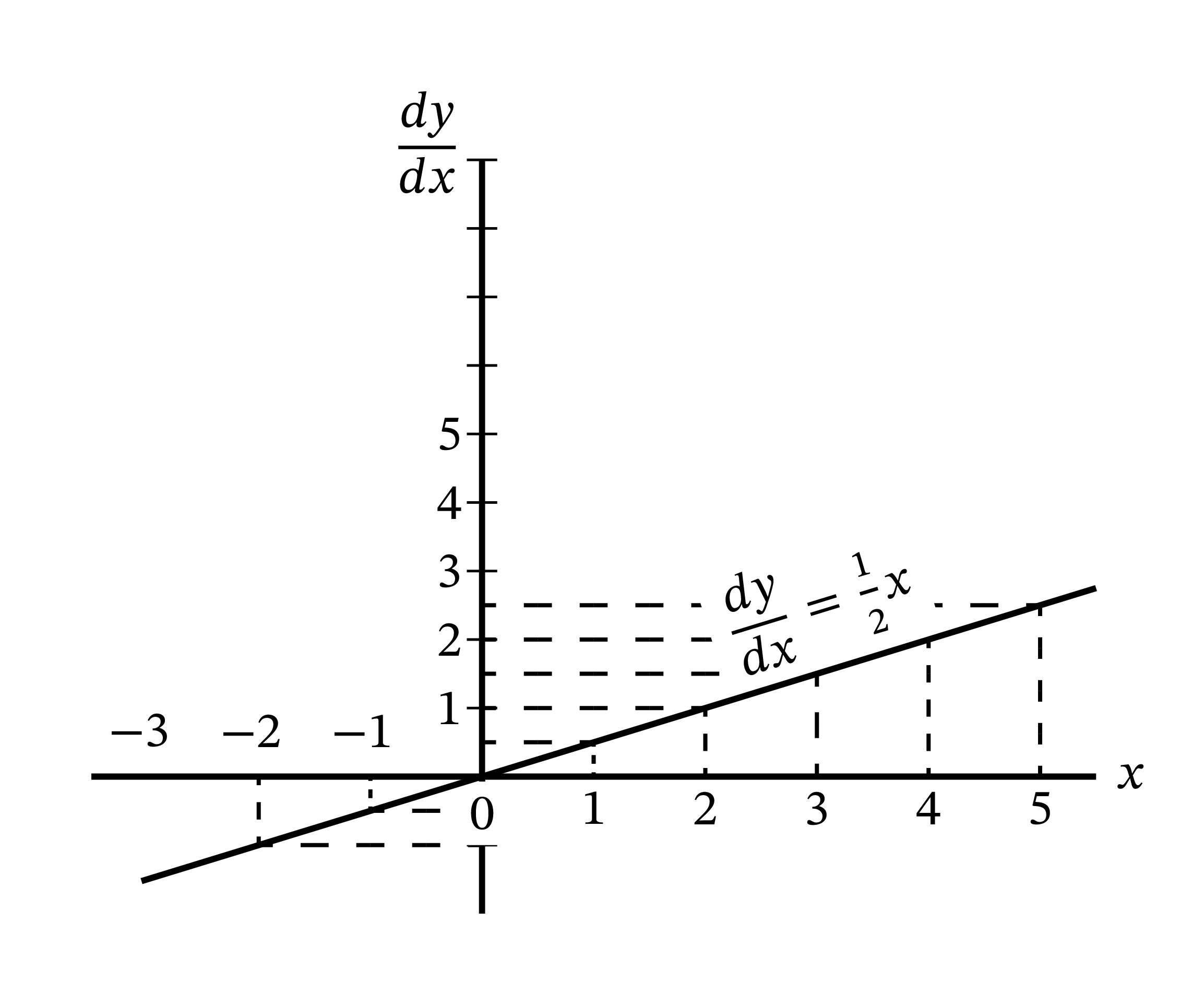
この事実を次の具体例を使って確認しよう: \[ y = \frac{1}{4}x^{2} + 3 \] これを微分すれば \[ \dfrac{dy}{dx} = \frac{1}{2}x \] となる。\(x\) として \(0\) から \(5\) までの値を取って、対応する \(y\) と \(\dfrac{dy}{dx}\) の値をこの二つの式を使って計算した結果を次の表にまとめる: \[ \begin{array}{c|cccccc} x & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline \vphantom{\Large \dfrac{dy}{dx}} y & 3 & \dfrac{13}{4} & 4 & \dfrac{21}{4} & 7 & \dfrac{37}{4} \\ \hline \vphantom{\Large \dfrac{dy}{dx}} \dfrac{dy}{dx} & 0 & \dfrac{1}{2} & 1 & \dfrac{3}{2} & 2 & \dfrac{5}{2} \\ \end{array} \] \(y\) と \(\dfrac{dy}{dx}\) のプロットを図 23 と図 24 に示す。値を計算した \(x\) に対応する点のそれぞれにおいて、二番目のグラフの \(y\) 座標の値は一つ目のグラフの傾きに比例している。

曲線が図 25 のように尖った点を持つ場合、その点で曲線の傾きが上向きから下向きに突然変化する。簡単に分かるように、このとき \(\dfrac{dy}{dx}\) が負の値から正の値に急に変化する。

次の例はここまでに示した事実を利用すると解ける問題である。

\(\text{(4)}\) 次の曲線に \(x = -1\) の点で引いた接線の傾きを求めよ: \[ y = \frac{1}{2x} + 3 \] さらにこの接線と曲線 \(y = 2x^{2} + 2\) がなす角度を求めよ。

接線の傾きは接点における曲線の傾きであり、これは接点での \(\dfrac{dy}{dx}\) の値に等しい。今の例では \(\dfrac{dy}{dx} = \dfrac{1}{2x^{2}}\) より \(x = -1\) では \(\dfrac{dx}{dy} = -\dfrac{1}{2}\) で、これがこの点における曲線の接線の傾きとなる。接線はもちろん直線だから、\(y = ax + b\) という方程式で表せる。この直線では \(\dfrac{dy}{dx} = a\) だから \(a = -\dfrac{1}{2}\) が分かる。さらに最初の曲線で \(x = -1\) とすると \(y = \dfrac{1}{2(-1)} + 3 = \dfrac{5}{2}\) を得る。接線がこの点 \(\left(-1, \dfrac{5}{2}\right)\) を通るとき、その座標は次の接線の方程式を満たす: \[ y = -\dfrac{1}{2} x + b \] つまり \(\dfrac{5}{2} = -\dfrac{1}{2} \times (-1) + b\) であり、ここから \(b = 2\) が分かる。よって接線の方程式は \(y = -\dfrac{1}{2} x + 2\) である。

二つの曲線の交点は両方の曲線上に存在し、その交点の座標は両方の曲線の方程式を満たす。つまり曲線の方程式を並べた連立方程式の解が交点の座標となる。今の例であれば、接線と曲線 \(y = 2x^{2} + 2\) の交点の座標は連立方程式 \[ \begin{cases} y = 2x^{2} + 2 \\ y = -\dfrac{1}{2} x + 2 \end{cases} \] の解となる。これを変形すれば \[ \begin{aligned} 2x^{2} + 2 &= -\frac{1}{2} x + 2 \\ x\left(2x + \frac{1}{2}\right) &= 0 \end{aligned} \] だから、この方程式の解は \(x = 0\) と \(x = -\dfrac{1}{4}\) である。曲線 \(y = 2x^{2} + 2\) の任意の点における傾きは \[ \dfrac{dy}{dx} = 4x \] であり、\(x = 0\) での曲線の傾きは \(0\) と分かる。つまりこの点で曲線は水平となる。\(x = -\dfrac{1}{4}\) では \(\dfrac{dy}{dx} = -1\) だから、この点における曲線の傾きは負であり、曲線が \(x\) 軸正方向となす角度 \(\theta\) は \(\tan \theta = 1\) を満たす。つまりこの曲線は \(x = - \dfrac{1}{4}\) で \(x\) 軸正方向から \(45^{\circ}\) 下を向く。

最初に考えていた接線の傾きは \(-\dfrac{1}{2}\) だった。つまり接線は \(x\) 軸正方向より右下を向いており、その角度 \(\phi\) は \(\tan \phi = \dfrac{1}{2}\) を満たす。この角度はおよそ \(26^{\circ}~34'\) である。よって接線と曲線 \(y = 2x^{2} + 2\) は一つ目の交点では \(26^{\circ}~34'\) の角度で交わり、二つ目の交点では \(45^{\circ} - 26^{\circ}~34' = 18^{\circ}~26'\) の角度で交わる。

\(\text{(5)}\) 座標が \(x = 2,\ \) \(y = -1\) である点を通り曲線 \(y = x^{2} - 5x + 6\) に接するように直線を引く。直線と曲線の交点の座標を求めよ。

曲線の \(\dfrac{dy}{dx}\) は \(2x - 5\) であり、この式の接点における値が接線の傾きと一致する必要がある。

直線の方程式を \(y = ax + b\) とすれば、この方程式は \(x = 2,\ \) \(y = -1\) で満たされる。よって \(-1 = x \times 2 + b\) が成り立つ。さらに交点における傾きについての考察から \(\dfrac{dy}{dx} = a = 2x - 5\) も成り立つ。

直線と曲線の交点の \(x\) 座標と \(y\) 座標は、傾きに関する方程式と座標に関する方程式を両方とも満たす必要がある。

以上より、\(a\) と \(b\) に関する次の四つの等式が分かる: \[ \left\{ \begin{array}{rlc} y & = x^{2} - 5x + 6 & \text{(i)} \\ y & = ax + b & \text{(ii)} \\ -1 & = 2a + b & \text{(iii)} \\ a & = 2x - 5 & \text{(iv)} \end{array} \right. \]

\(\text{(i)}\) と \(\text{(ii)}\) から \(x^{2} - 5x + 6 = ax+b\) が分かる。

\(a\) と \(b\) に \(x\) を使った式を代入すれば \[ x^{2} - 5x + 6 = (2x - 5)x - 1 - 2(2x - 5) \] であり、整理すれば \(x^{2} - 4x + 3 = 0\) を得る。この解は \(x = 3\) と \(x = 1\) だから、それぞれ \(\text{(i)}\) に代入すれば \(y = 0\) と \(y = 2\) を得る。よって交点はそれぞれ \(x = 1,\ \) \(y = 2\) と \(x = 3,\ \) \(y = 0\) である。

注意 ──曲線を扱う練習問題の全てにおいて、曲線を実際にプロットして自分が導いた結果を確認することを強く勧める。

練習問題 VIII

解答はここにある。

\(\text{(1)}\) 曲線 \(y = \dfrac{3}{4} x^{2} - 5\) をプロットし、適当な \(x\) の値について曲線の傾きの角度を計測せよ。

方程式を微分して傾きを求める式を求めよ。三角関数の数表を使って、計算した値と計測した値が矛盾しないことを確かめよ。

\(\text{(2)}\) 曲線 \[ y = 0.12x^{3} - 2 \] の \(x\) 座標が \(2\) の点における傾きを求めよ。

\(\text{(3)}\) 曲線 \(y = (x - a)(x - b)\) を考える。この曲線上の \(\dfrac{dy}{dx} = 0\) が成り立つ点の \(x\) 座標が \(\dfrac{1}{2} (a + b)\) だと示せ。

\(\text{(4)}\) 方程式 \(y = x^{3} + 3x\) に対する \(\dfrac{dx}{dy}\) を求めよ。\(x = 0,\ \) \(\dfrac{1}{2},\ \) \(1,\ \) \(2\) の点における \(\dfrac{dy}{dx}\) の値を計算せよ。

\(\text{(5)}\) 方程式 \(x^{2} + y^{2} = 4\) で表される曲線について、傾きが \(1\) となる点の \(x\) 座標を求めよ。

\(\text{(6)}\) 方程式が \(\dfrac{x^{2} }{3^{2}} + \dfrac{y^{2}}{2^{2}} = 1\) であるような曲線について、任意の点における傾きを求めよ。\(x = 0\) と \(x = 1\) における傾きを数値的に計算せよ。

\(\text{(7)}\) 曲線 \(y = 5 - 2x + 0.5x^{3}\) の接線の方程式を、定数 \(m,\ n\) を使って \(y = mx + n\) の形で表せ。接点の \(x\) 座標が \(2\) になるような \(m\) と \(n\) の値を求めよ。

\(\text{(8)}\) 二つの曲線 \[ y = 3.5x^{2} + 2, \quad y = x^{2} - 5x + 9.5 \] はどんな角度で交わるか？

\(\text{(9)}\) 曲線 \(y = ± \sqrt{25-x^{2}}\) に \(x = 3\) と \(x = 4\) で接線を引く (接点の \(y\) 座標は正とする)。この二つの接線の交点と交わる角度を求めよ。

\(\text{(10)}\) 直線 \(y = 2x - b\) と曲線 \(y = 3x^{2} + 2\) がある点で接している。接点の座標および \(b\) の値は何か？