XIX. 積分を使った面積の計算
積分の応用の一つに、曲線で囲まれる領域の面積の計算がある。例を使ってこれを説明しよう。
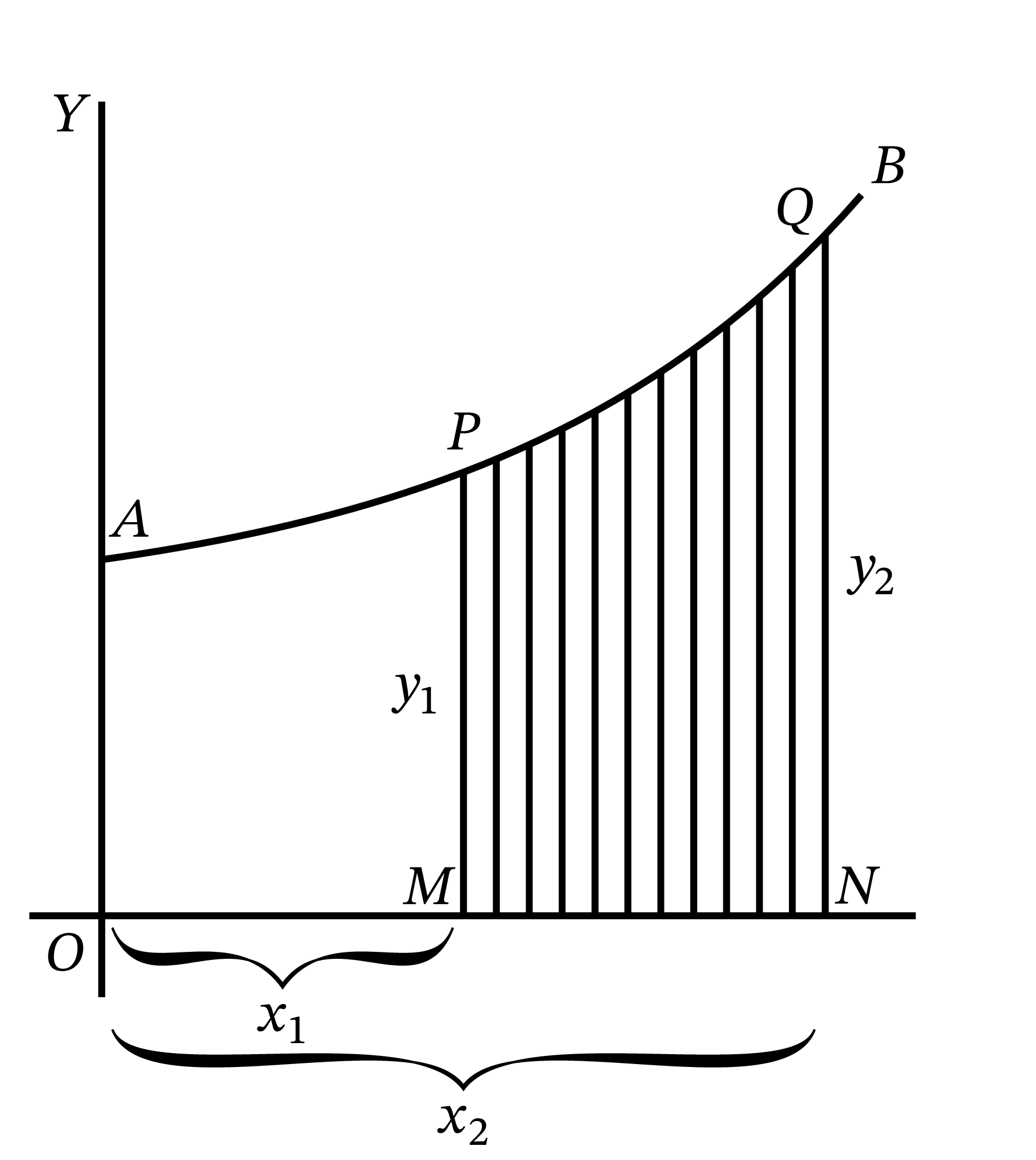
曲線を \(AB\) として、その方程式が分かっているとする。つまりこの曲線の \(y\) 座標を表す \(x\) の関数が既知だと仮定する。曲線 \(AB\) の \(P\) から \(Q\) の部分を考える。
\(P\) から\(x\) 軸に垂線 \(PM\) を下ろし、同様に \(Q\) から垂線 \(QN\) を下ろす。さらに \(OM = x_{1}\) および \(ON = x_{2}\) とする。このとき \(PQ\) の下部に領域 \(PQNM\) が定まる。問題は領域 \(\bm{PQNM}\) の面積の計算である。
この問題を解く鍵は、領域全体を小さな短冊状の小領域に分割することにある。分割された小領域の幅は \(dx\) であり、\(dx\) を小さく取ればそれだけ \(x_{1}\) と \(x_{2}\) の間にある小領域の数が増える。このとき領域全体の面積はもちろん小領域の面積の和に等しい。つまり細い小領域の面積を表す式を見つけることができれば、それを積分を使って足し上げることで求めたい面積が計算できる。小領域の一つに注目すると、この領域の端は二つの垂直な直線で、底辺は長さ \(dx\) の直線、そして上部は少しだけ曲がった曲線となっている。この領域を左図に示す。その平均の高さを \(y\) とすると、底辺の幅は \(dx\) より領域の面積は \(y\, dx\) となる (\(dx\) が十分小さいとき、上部の曲線は直線と見分けがつかなくなる)。幅 \(dx\) は好きなだけ小さく取れるので、平均の高さが中間の点の高さと実質等しくなるように \(dx\) を取ればよい。すると領域全体の面積を \(S\) に対して小領域一つの面積はその一部分 \(dS\) だから、 \[ {\footnotesize \text{小領域一つの面積}} = dS = y \, dx \] が成り立つ。全ての小領域を足せば \[ S\ {\footnotesize \text{全体の面積}} = \int dS = \int y\, dx \] となる。
つまり曲線の \(y\) 座標を表す \(x\) の関数が分かっているなら、\(y \cdot dx\) の積分の計算によって \(S\) が求まる。
例えば曲線 \(y = b + ax^{2}\) の面積を求めよと言われたときには、今説明した式に代入して \(\displaystyle \int (b + ax^{2})\, dx\) を計算することになる。
これは素晴らしい結果である。しかし少し考えれば分かるように、計算はこれで終わりではない。今考えているのは曲線全体の下にある面積ではなく \(PM\) と \(QN\) で区切られる区間の面積だから、この区間を考えに入れる必要がある。
ここで区間の間の積分という新しい概念を導入する。この積分では、\(x\) を変化させるときに \(x_{1}\) より小さい (\(OM\) より左側の) \(x\) と \(x_{2}\) より大きい (\(OM\) より右側の) \(x\) を考えない。積分が二つの端によって制限されるとき、小さい方の端を下端 (lower limit) と呼び、大きい方の端を上端 (upper limit) と呼ぶ。こういった区間を持つ積分を定積分 (definite integral) と呼び、区間を持たない積分を不定積分 (indefinite integral) と呼んで区別する。
積分区間は積分記号の上と下に書く。例えば \[ \int_{x=x_1}^{x=x_2} y \cdot dx \] は「下端 \(x_{1}\) から上端 \(x_{2}\) までの \(y \cdot dx\) の積分を求めよ」を意味する。これを省略して \[ \int^{x_2}_{x_1} y \cdot dx \] と書く場合もある。
ではこのような命令を受けたときに、どうすれば区間の付いた積分を求められるだろうか?
図 52 をもう一度考える。\(x = 0\) に対応する \(A\) から \(x = x_{2}\) に対応する \(Q\) までの広い領域 \(AQNO\) の面積が求まったとする。さらに \(x = 0\) に対応する \(A\) から \(x = x_{1}\) に対応する \(P\) までの領域 \(APMO\) の面積が分かれば、求めるべき領域 \(PQNM\) の面積は二つの面積の差となる。ここから定積分の計算方法が分かる: 定積分は上端で計算した積分と下端で計算した積分の差に等しい。
最初の問題に戻ろう。まず不定積分 \[ \int y\, dx \] を求める。図 52 では曲線の方程式が \(y = b + ax^{2}\) だから、不定積分 \[ \int (b + ax^{2})\, dx \] を求める必要がある。
前章の方法を使ってこれを計算すれば \[ bx + \frac{a}{3} x^{3} + C \] を得る。この式が \(0\) から \(x\) までの部分の面積を任意の \(x\) に対して与える。
よって積分の上端 \(x_{2}\) までの領域の面積は \[ bx_2 + \frac{a}{3} x_2^{3} + C \] であり、積分の下端 \(x_{1}\) までの領域の面積は \[ bx_1 + \frac{a}{3} x_1^{3} + C \] となる。二つの面積の差を求めれば \(S\) が求まる: \[ S = b(x_2 - x_1) + \frac{a}{3}(x_2^{3} - x_1^{3}) \]
答はこれで求まった。数値的な値を求めてみよう。\(b = 10,\ \) \(a = 0.06\) とすれば、\(x_1 = 6\) から \(x_2 = 8\) までの領域の面積 \(S\) は \[ \begin{aligned} 10(8 - 6) + \frac{0.06}{3} (8^{3} - 6^{3}) &= 20 + 0.02(512 - 216) \\ &= 20 + 0.02 \times 296 \\ &= 20 + 5.92 \\ &= 25.92 \end{aligned} \] と計算できる。
区間を明示する記法で積分を表せば \[ \int^{x=x_2}_{x=x_1} y\, dx = y_2 - y_1 \] となる。ここで \(y_{2}\) は \(x_{2}\) における \(y\, dx\) の積分値であり、\(y_{1}\) は \(x_{1}\) における積分値を意味する。
区間を持つ積分の値を計算するには区間の両端における積分の値の差を求めればよいと分かった。また積分定数 \(C\) が差を求めるときに消えていることにも注目するとよい。
例

\(\text{(1)}\) 定積分に慣れるために、答が最初から分かっている場合を考えよう。図 53 の三角形は底辺が \(x = 12\) で高さが \(y = 4\) だから、積分を使わなくても面積は \(24\) と分かる。
この三角形の斜辺を “曲線” とみなせば、その方程式は \[ y = \frac{x}{3} \] となる。そして三角形を表す領域の面積は \[ \int^{x=12}_{x=0} y \cdot dx = \int^{x=12}_{x=0} \frac{x}{3} \cdot dx \] と表される。\(\dfrac{x}{3}\, dx\) を積分し、その結果を鍵括弧で囲んで上下に積分区間を書く記法を使えば \[ \begin{aligned} {\footnotesize \text{三角形の面積}} &= \left[ \frac{1}{3} \cdot \frac{1}{2} x^{2} + C \right]^{x=12}_{x=0} \\ &= \left[ \frac{x^{2}}{6} + C \right]^{x=12}_{x=0} \\ &= \left[ \frac{12^{2}}{6} \right] - \left[ \frac{0^{2}}{6} \right] \\ &= \frac{144}{6} = 24 \ \cdots \ \textbf{\small (答)} \end{aligned} \] と計算できる。
この意外とも言える計算テクニックの正しさを実際に確かめよう。方眼紙 (目が細かいものがよい) を取り、方程式 \[ y = \frac{x}{3} \] のグラフをプロットする。プロットする値は \[ \begin{array}{c|cccccc} x & 0 & 3 & 6 & 9 & 12 \\ \hline y & 0 & 1 & 2 & 3 & 4 \\ \end{array} \] であり、図 54 のようになる。
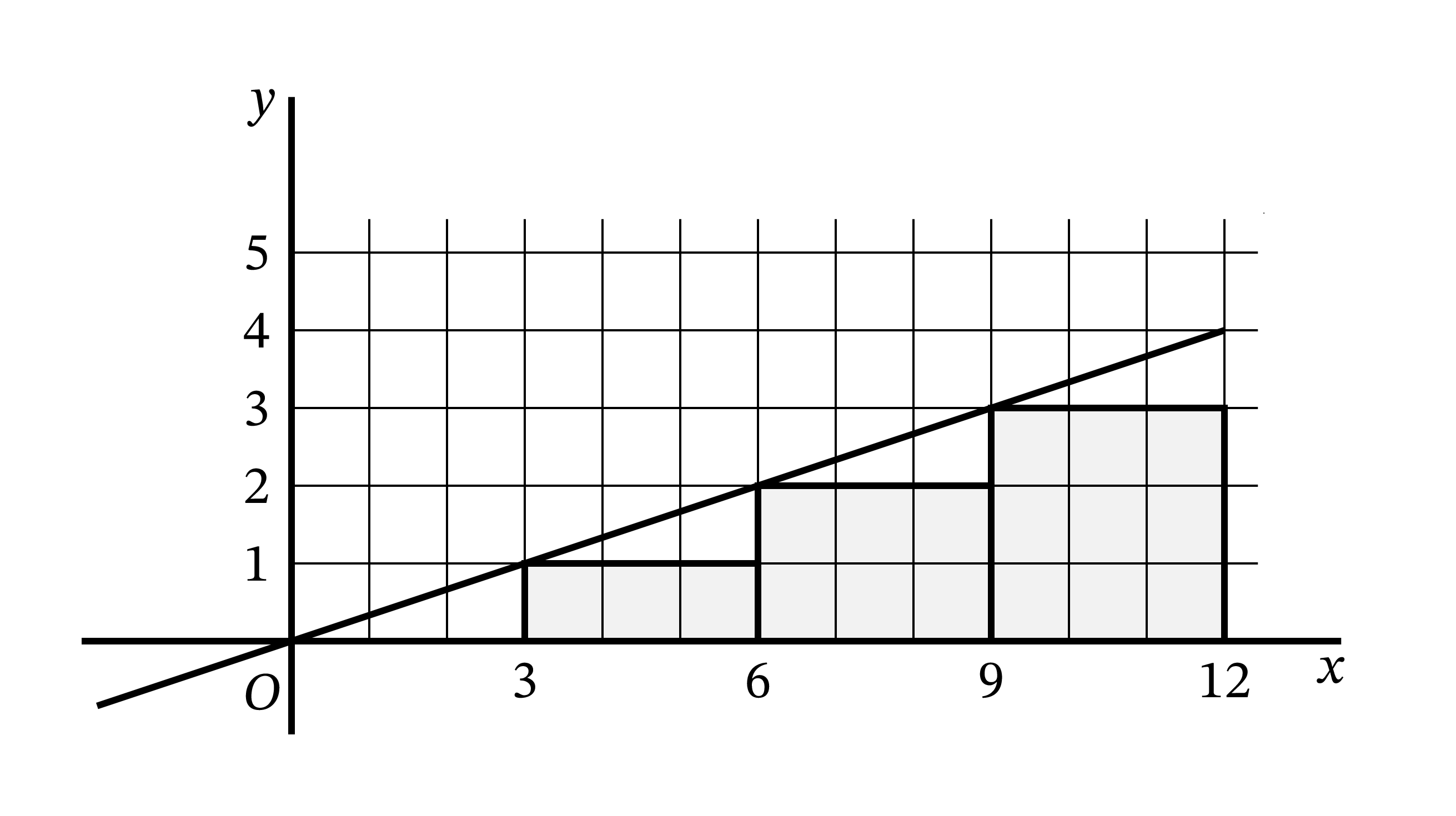
領域の面積を求めるために、\(x = 0\) から \(x = 12\) の間で曲線の下にある正方形の数を数えてみよ。正方形は \(18\) 個あり、その他に正方形 \(\dfrac{3}{2}\) 個分の三角形が四つある。よって全体の面積は \(24\) であり、これは下端 \(x = 0\) から上端 \(x = 12\) までの \(\dfrac{x}{3}\, dx\) の積分と等しい。
さらに練習問題として、\(x = 3\) から \(x = 15\) を積分区間としたときの積分値が \(36\) であることを示せ。
\(\text{(2)}\) 曲線 \(y = \dfrac{b}{x + a}\) の \(x = 0\) から \(x = x_{1}\) の領域 (図 55) の面積を求めよ。 \[ \begin{aligned} {\footnotesize \text{面積}} &= \int^{x=x_1}_{x=0} y \cdot dx \\ &= \int^{x=x_1}_{x=0} \frac{b}{x+a}\, dx \\ &= b \bigl[\log_e(x + a) + C \bigr]^{x_1} _{0}\\ &= b \bigl[\log_e(x_1 + a) - \log_e(0 + a)\bigr] \\ &= b \log_e \frac{x_1 + a}{a} \ \cdots \ \textbf{\small (答)} \end{aligned} \]
注意 ──定積分の計算では、積分定数 \(C\) が引き算で必ず消える。
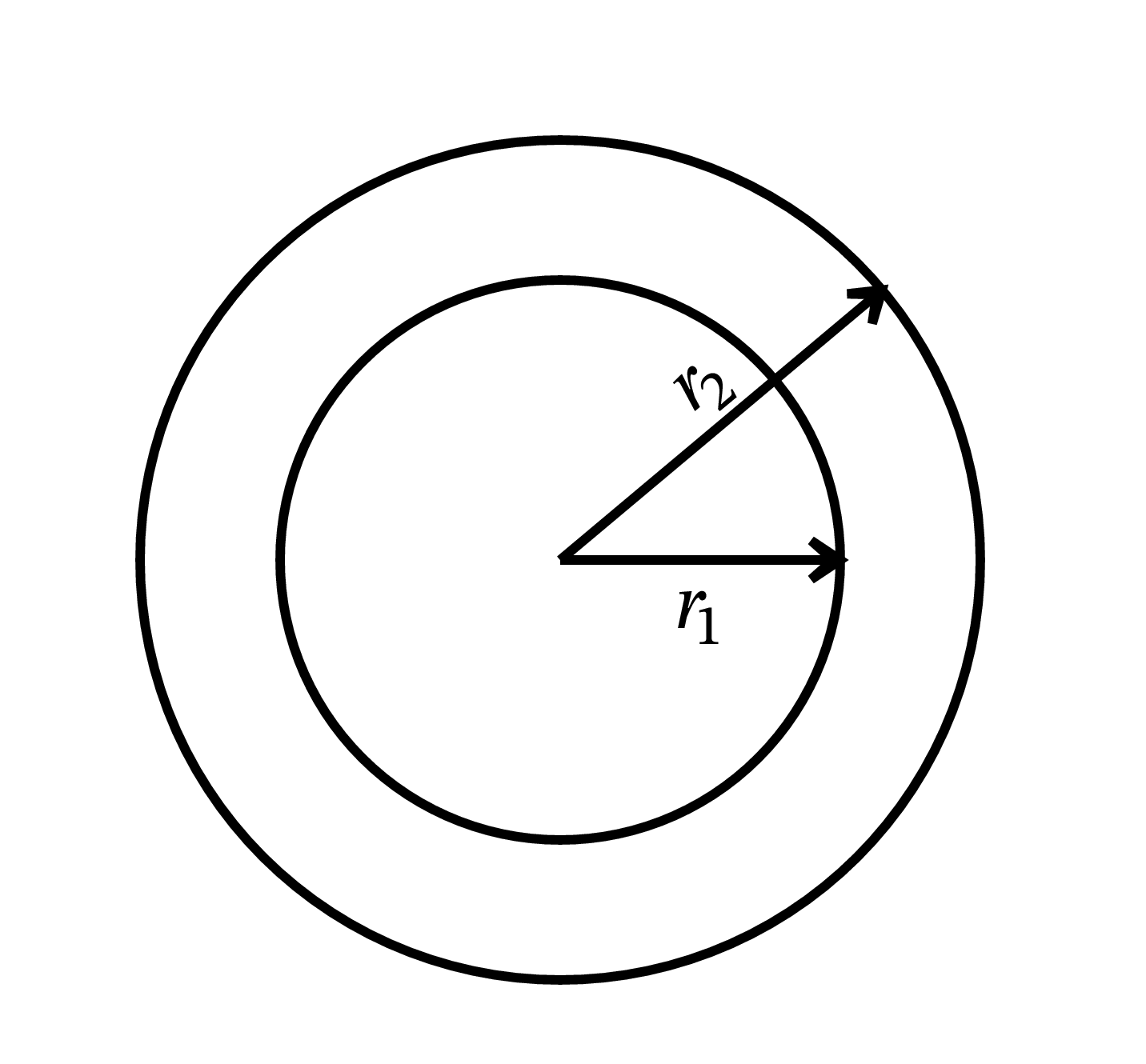
大きな部分から小さな部分を引くという操作は積分以外でも使われることがある。例えば外側の半径が \(r_{2}\) で内側の半径が \(r_{1}\) の環 (図 56) の面積を求める問題を考える。円の面積の公式を使えば外側の円の面積が \(\pi r_{2}^{2}\) で内側の円の面積が \(\pi r_{2}^{2}\) だと分かるので、和の面積この二つの値の差 \(\pi(r_2^{2} - r_1^{2})\) だと計算できる。ちなみにこの式は \[ \pi(r_2 + r_1)(r_2 - r_1) = {\footnotesize \text{和の平均半径}} \times {\footnotesize \text{和の幅}} \] と変形でき、後で回転体ときにはこの式を利用する。
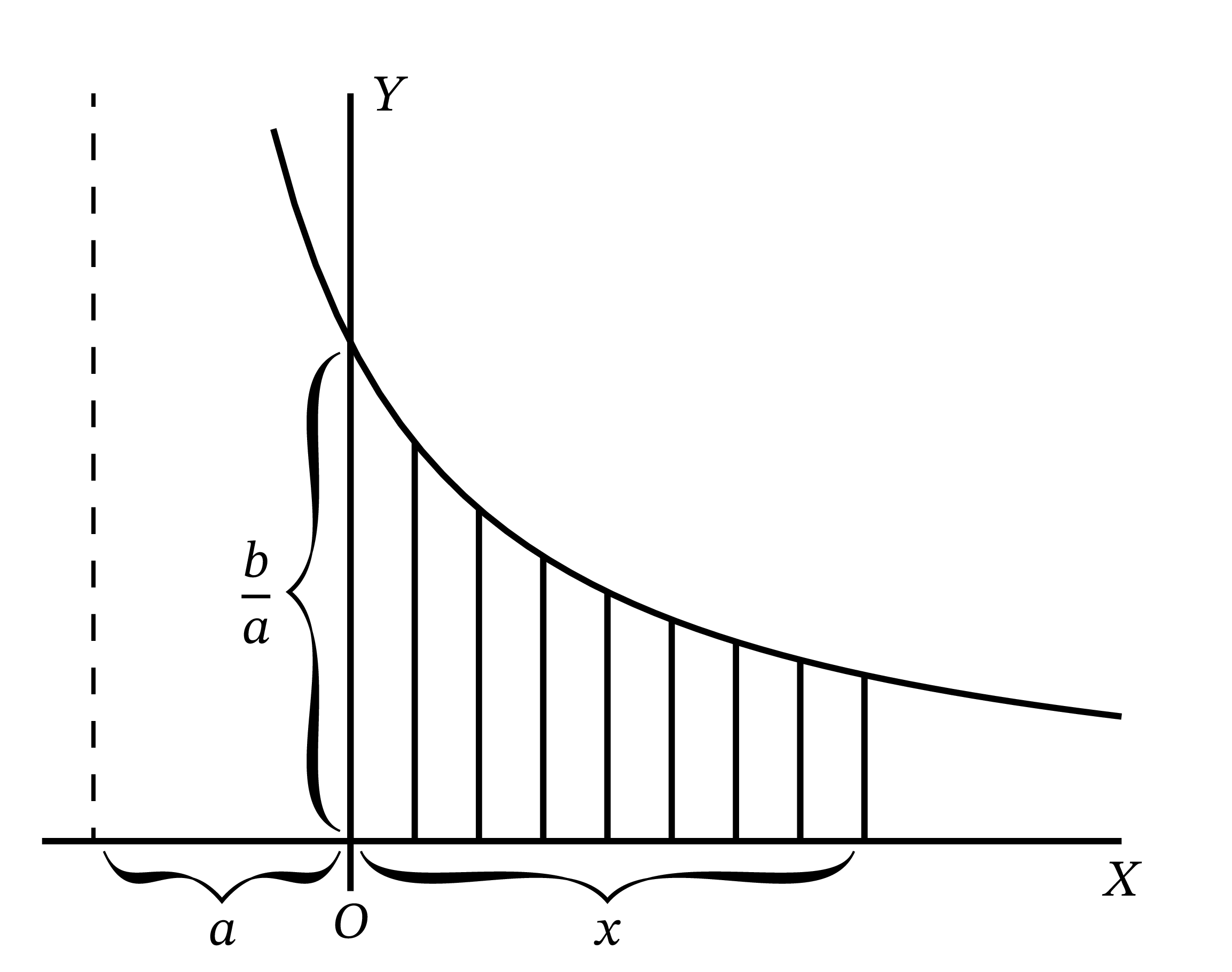
\(\text{(3)}\) 続いて減衰曲線を考える。方程式が \[ y = be^{-x} \] で表される曲線 (図 57) について、\(x = 0\) から \(x = a\) までの領域の面積を求めよう。 \[ {\footnotesize \text{面積}} = b\int^{x=a} _{x=0} e^{-x} \cdot dx \] だから、積分を計算して \[ \begin{aligned} \quad {\footnotesize \text{面積}} &= b\left[-e^{-x}\right]^a _0 \\ &= b\bigl[-e^{-a} - (-e^{-0})\bigr] \\ &= b(1-e^{-a}) \end{aligned} \] と分かる。
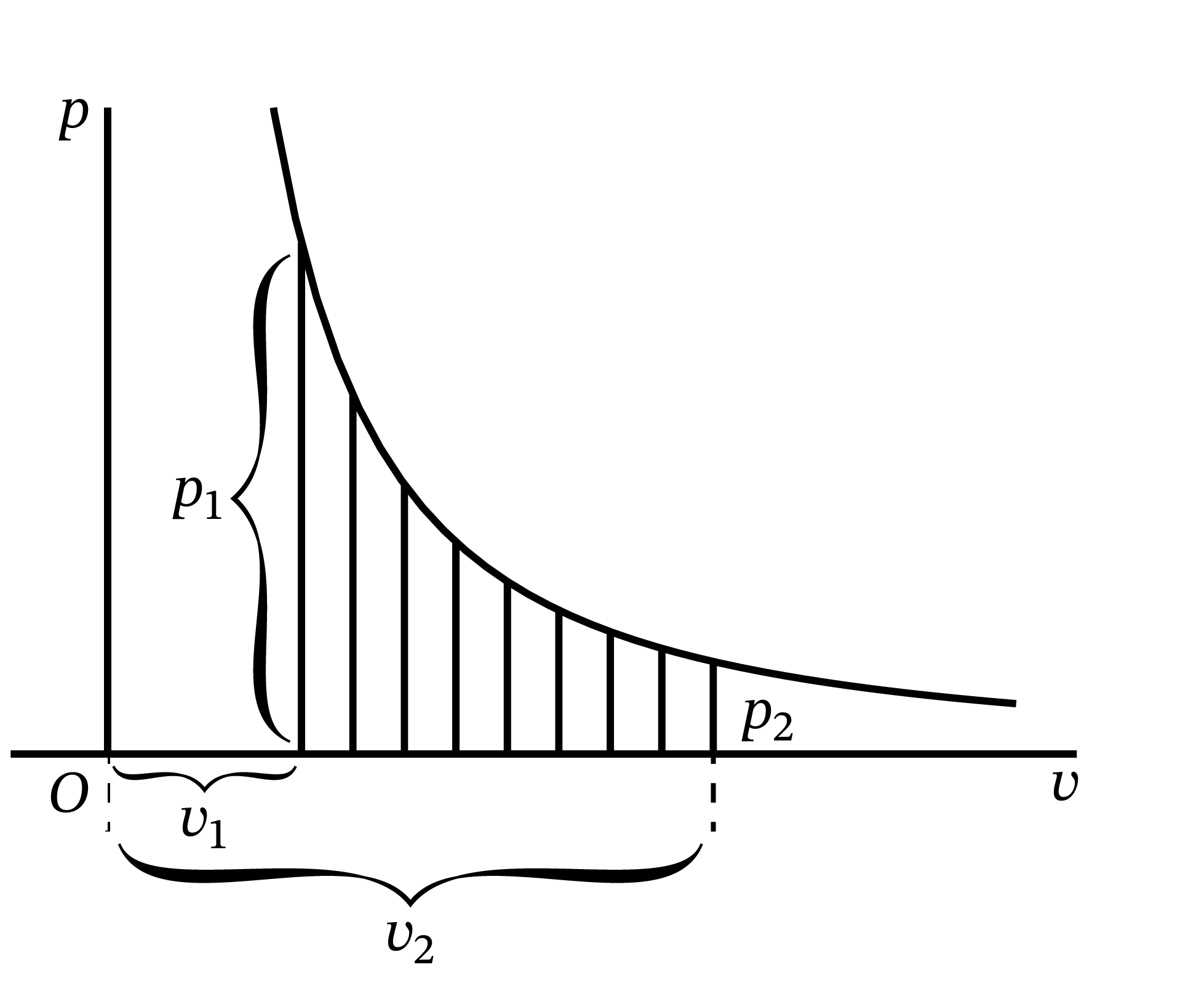
\(\text{(4)}\) 次の例は理想気体の断熱曲線を考える。\(p\) を圧力、\(v\) と体積、\(n\) を定数 \(1.42\) とすると、関係 \(pv^n = c\) が成り立つ (図 58)。
体積 \(v = v_{2}\) から \(v = v_{1}\) の間で曲線の下側にある領域の面積を求めよ (これは気体を瞬間的に圧縮したときに働く仕事に等しい)。
仮定から \[ \begin{aligned} {\footnotesize \text{面積}} &= \int^{v=v_2}_{v=v_1} cv^{-n} \cdot dv \\ &= c\left[\frac{1}{1-n} v^{1-n} \right]^{v_2} _{v_1} \\ &= c \frac{1}{1-n} (v_2^{1-n} - v_1^{1-n}) \\ &= \frac{-c}{0.42}\left(\frac{1}{v_2^{0.42}} - \frac{1}{v_1^{0.42}}\right) \end{aligned} \] が分かる。
練習問題
半径 \(R\) の円を \(A\) とする。\(A\) の面積が \(\pi R^{2}\) に等しいことを証明せよ。

中心が \(A\) と同じ環を考える (図 59)。この環は中心から \(r\) だけ離れた点を通り、幅は \(dr\) で非常に細い。円全体はこういった細い環が集まって出来ていると考えられるので、\(A\) の面積は中心から外側までの環の面積の積分によって計算できる。つまり \(r = 0\) から \(r = R\) まで環の面積を積分すればよい。
続いて環の面積 \(dA\) を表す式を求める。環を幅 \(dr\) の細い道だと考えれば、その長さは半径 \(r\) の円周と等しい。よってその面積は \[ dA = 2 \pi r\, dr \] となる。ここから円全体の面積が \[ A = \int dA = \int^{r=R}_{r=0} 2 \pi r \cdot dr = 2 \pi \int^{r=R}_{r=0} r \cdot dr \] だと分かる。\(r \cdot dr\) の不定積分は \(\dfrac{1}{2} r^{2}\) より \[ \begin{aligned} A &= 2 \pi \left[\frac{1}{2} r^{2} \right]^{r=R}_{r=0} \\ &= 2 \pi \left[\frac{1}{2} R^{2} - \frac{1}{2}(0)^{2}\right] \\ &= \pi R^{2} \end{aligned} \] を得る。
練習問題
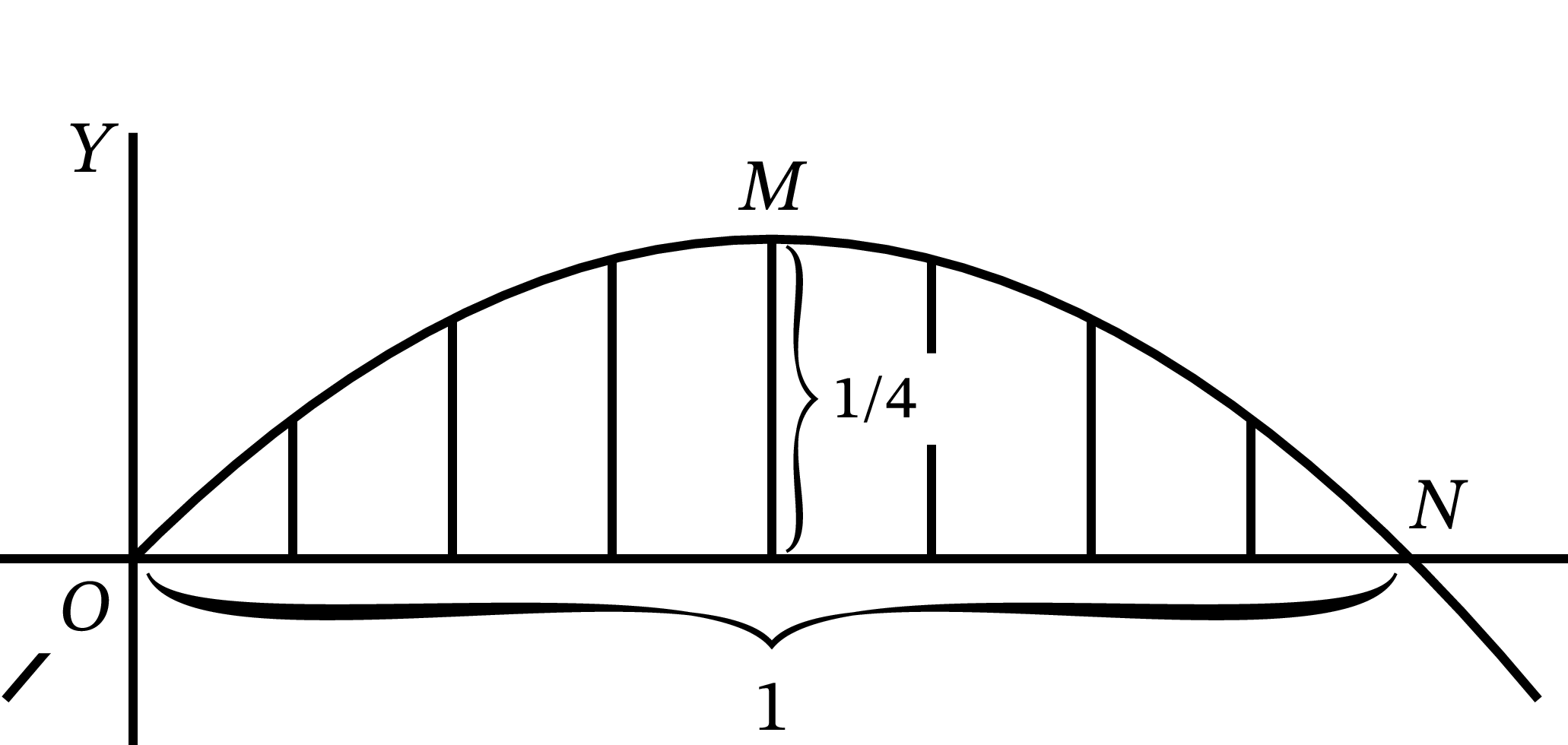
曲線 \(y = x - x^{2}\) の正の部分における \(y\) 座標の平均値を求める問題を考える。この曲線を 図 60 に示す。領域 \(OMN\) の面積を求め、それを底辺 \(ON\) の長さで割ればよい。ただし領域の面積を考える前に、底辺の長さを計算して積分区間を求める必要がある。\(N\) は \(y\) 座標が \(0\) となる点だから、\(y = 0\) となる \(x\) の値を求めればよい。明らかに \(x = 0\) のとき \(y = 0\) だから、考えている曲線は \(O\) を通る。さらに \(x = 1\) のときも \(y = 0\) だから、点 \(N\) の \(x\) 座標は \(1\) だと分かる。
よって考えている領域の面積は次のように計算できる: \[ \begin{aligned} {\footnotesize \text{面積}} &= \int^{x=1}_{x=0} (x-x^{2})\, dx \\ &= \left[\frac{1}{2} x^{2} - \frac{1}{3} x^{3} \right]^{1}_{0} \\ &= \left[\frac{1}{2} - \frac{1}{3} \right] - [0-0] \\ &= \frac{1}{6} \end{aligned} \] 底辺の長さは \(1\) だから、\(y\) 座標の平均値は \(\dfrac{1}{6}\) と求まる。
[注意 ──この曲線が極大が極大となる点の \(y\) 座標を求める問題は微分の練習問題としてちょうどよいだろう。答は平均値よりも高くなるはずである]
一般的な曲線の \(x = 0\) から \(x = x_{1}\) の部分の \(y\) 座標の平均値は \[ y\ {\footnotesize \text{の平均値}} = \frac{1}{x_1} \int^{x=x_1}_{x=0} y \cdot dx \] と表せる。
回転体の表面積も同じ方法で計算できる。
例: 曲線 \(y = x^{2} - 5\) を \(x\) 軸に関して回転させたとき、曲線の \(x = 0\) から \(x = 6\) の部分に対応する回転体の表面積を求めよ。
曲線上のある点の \(y\) 座標が \(a\) のとき、その点は回転体の側面において周りの長さが \(2 \pi y\) で幅が \(dx\) の環に対応する。この環の面積は \(2\pi y\, dx\) だから、積分によって全体の面積が計算できる: \[ \begin{aligned} 2\pi \int^{x=6}_{x=0} y\, dx &= 2\pi \int^{x=6}_{x=0} (x^{2}-5)\, dx \\ &= 2\pi \left[\frac{x^{3}}{3} - 5x\right]^{6}_0 \\ &= 6.28 \times 42=263.76 \end{aligned} \]
極座標で表される曲線の面積
領域の境界の方程式が \(r\) と \(\theta\) の関数として表されるとする。ここで \(r\) は極 (pole) と呼ばれる固定点 \(O\) からの距離を表し、\(\theta\) は正の水平方向 \(OX\) との角度を表す (図 61)。これまで説明してきた方法を少し変えれば、この場合にも面積の計算が行える。領域を短冊状に切る代わりに、図中 \(OAB\) で表される小さな三角形に切ることを考える。この三角形は \(O\) の角度が \(d\theta\) であり、\(OA\) と \(OB\) は (\(d \theta\) が小さいとき) ほぼ等しい。三角形全ての面積の和を求めれば、その値が領域の面積となる。
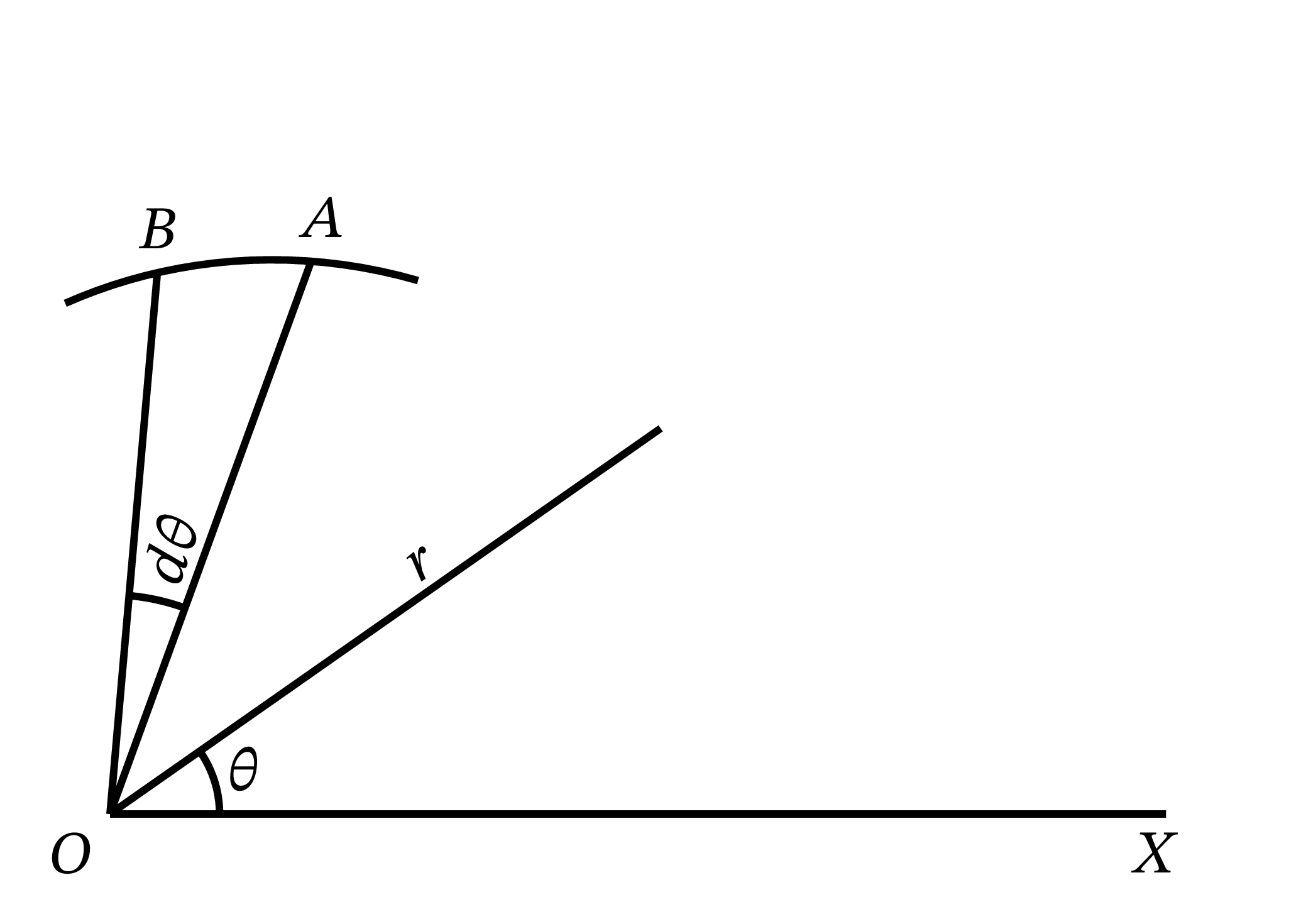
小さな三角形の面積は近似的に \(\dfrac{AB}{2}×r = \dfrac{r\, d\theta}{2}×r\) に等しい。よって角度 \(\theta_{1}\) と \(\theta_{2}\) に対応する二つの \(r\) で挟まれる部分の面積は \[ \frac{1}{2} \int^{\theta=\theta_2}_{\theta=\theta_1} r^{2}\, d\theta \] で与えられる。
例
\(\text{(1)}\) 半径 \(a\) の円の角度 \(1\) ラジアンに対応する扇形の面積を求めよ。
円を表す極方程式はもちろん \(r = a\) だから、求める面積は \[ \frac{1}{2} \int^{\theta=\theta_2}_{\theta=\theta_1} a^{2}\, d\theta = \frac{a^{2}}{2} \int^{\theta=1}_{\theta=0} d\theta = \frac{a^{2}}{2} \] となる。
\(\text{(2)}\) 極方程式 \(r = a(1 + \cos \theta)\) で表される曲線を四等分した領域の面積を求めよ。この曲線はパスカルの蝸牛形 (Pascal's Snail) と呼ばれる。 \[ \begin{aligned} {\footnotesize \text{面積}} &= \frac{1}{2} \int^{\theta=\frac{\pi}{2}}_{\theta=0} a^{2}(1+\cos \theta)^{2}\, d\theta \\ &= \frac{a^{2}}{2} \int^{\theta=\frac{\pi}{2}}_{\theta=0} (1+2 \cos \theta + \cos^{2} \theta)\, d\theta \\ &= \frac{a^{2}}{2} \left[\theta + 2 \sin \theta + \frac{\theta}{2} + \frac{\sin 2 \theta}{4} \right]^{\frac{\pi}{2}}_{0} \\ &= \frac{a^{2}(3\pi+8)}{8} \end{aligned} \]
積分を使った体積の計算
ここまで小さく切った領域に対して行ってきた議論は、もちろん小さく切った空間に対しても適用できる。小さな面積を全て足すことで対象の領域全体の面積を求めたのと同じように、小さな空間を全て足すことで対象の空間全体の体積を計算できる。
例
\(\text{(1)}\) 半径 \(r\) の球の体積を求めよ。
球を 図 59 の形に切ってできる薄い球殻の体積は \(4 \pi x^{2}\, dx\) だから、球を構成する中心が同じ球殻を全て足せば \[ {\footnotesize \text{球の体積}} = \int^{x=r}_{x=0} 4\pi x^{2}\, dx = 4\pi \left[\frac{x^{3}}{3} \right]^r_0 = \frac{4}{3} \pi r^{3} \] が分かる。

球の体積は次のように求めることもできる。球を 図 62 のように厚さ \(dx\) で \(y\) 軸と平行に切ると、一切れの体積は \(\pi y^{2}\, dx\) となる。\(x\) と \(y\) の間には \[ y^{2} = r^{2} - x^{2} \] という関係があるから、体積は次のように求められる: \[ \begin{aligned} {\footnotesize \text{球の体積}} &= 2 \int^{x=r}_{x=0} \pi(r^{2}-x^{2})\, dx \\ &= 2 \pi \left[ \int^{x=r}_{x=0} r^{2}\, dx - \int^{x=r}_{x=0} x^{2}\, dx \right] \\ &= 2 \pi \left[r^{2}x - \frac{x^{3}}{3} \right]^r_0 = \frac{4\pi}{3} r^{3} \end{aligned} \]
\(\text{(2)}\) 曲線 \(y^{2} = 6x\) を \(x\) 軸に関して回転させて得られる立体の \(x = 0\) から \(x = 4\) に対応する部分の体積を求めよ。
回転体を \(y\) 軸と平行な平面で分割すれば、一切れの体積は \(\pi y^{2}\, dx\) である。よって \[ \begin{aligned} {\footnotesize \text{体積}} &= \int^{x=4}_{x=0} \pi y^{2}\, dx = 6\pi \int^{x=4}_{x=0} x\, dx \\ &= 6\pi \left[ \frac{x^{2}}{2} \right]^{4}_0 = 48\pi = 150.8 \end{aligned} \] が分かる。
二次平均
物理の諸分野、特に交流に関する理論では、変動する値の二次平均 (quadratic mean) と呼ばれる値の計算が必要になる。二次平均とは考えている区間における変数の二乗の平方根を取った値であり、RMSや実効値 (virtual value) と呼ばれることもある。RMS は「平方根・平均・二乗 (root, mean, square)」の頭文字であり、実効値はフランス語で valeur efficance と言う。考えている関数を \(y\) とすると、\(x = 0\) から \(x = l\) における \(y\) の二次平均は \[ \sqrt[2] {\frac{1}{l} \int^l_0 y^{2}\, dx} \] と表される。
例
\(\text{(1)}\) 関数 \(y = ax\) の二次平均を求める (図 63)。

二乗の積分は \(\displaystyle \int^l_0 a^{2} x^{2}\, dx = \frac{1}{3} a^{2} l^{3}\) となる。これを \(l\) で割って平方根を取れば、 \[ {\footnotesize \text{二次平均}} = \frac{1}{\sqrt 3}\, al \] が分かる。
同じ関数の算術平均は \(\dfrac{1}{2}al\) であり、二次平均と算術平均の比は \(\dfrac{2}{\sqrt 3}=1.155\) となる。この比を波形率 (form factor) と呼ぶ。
\(\text{(2)}\) 関数 \(y = x^a\) の二次平均を求める。
二乗の積分は \(\displaystyle \int^{x=l}_{x=0} x^{2a}\, dx = \dfrac{l^{2a+1}}{2a+1}\) である。よって \[ {\footnotesize \text{二次平均}} = \sqrt{\dfrac{l^{2a}}{2a+1}} \] が分かる。
\(\text{(3)}\) 関数 \(y = a^{\frac{x}{2}}\) の二次平均を求める。
二乗の積分は \(\displaystyle \int^{x=l}_{x=0} (a^{\frac{x}{2}})^{2}\, dx = \displaystyle \int^{x=l}_{x=0} a^x\, dx\) であり、これは \[ \left[ \frac{a^x}{\log_e a} \right]^{x=l}_{x=0} = \dfrac{a^l-1}{\log_e a} \] と計算できる。よって二次平均は \(\sqrt[2] {\dfrac{a^l - 1}{l \log_e a}}\) である。
練習問題 XVIII
解答はここにある。
\(\text{(1)}\) 曲線 \(y = x^{2}+x-5\) の \(x = 0\) から \(x = 6\) の部分の面積と二次平均を求めよ。
\(\text{(2)}\) 放物線 \(y = 2a \sqrt{x}\) の \(x = 0\) から \(x = a\) の部分の面積を求めよ。この面積が区間の端における曲線上の点からなる長方形の面積の \(\dfrac{2}{3}\) に等しいことを示せ。
\(\text{(3)}\) サイン曲線の \(0\) から \(\pi\) の部分について、その面積と \(y\) 座標の平均値を求めよ。
\(\text{(4)}\) 曲線 \(y = \sin^{x} x\) の正の部分の面積と \(y\) 座標の平均値を求めよ。
\(\text{(5)}\) 曲線 \(y = x^{2} ± x^{\frac{5}{2}}\) の \(x = 0\) から \(x = 1\) の部分にある二つの枝で囲まれる部分の面積を求めよ。さらに曲線の下の枝の正の部分の面積を求めよ (曲線の概形は 図 30 を参照)。
\(\text{(6)}\) 底面の半径が \(r\) で高さが \(h\) の円錐の体積を求めよ。
\(\text{(7)}\) 曲線 \(y = x^{3}-\log_e x\) の \(x = 0\) から \(x = 1\) の部分の面積を求めよ。
\(\text{(8)}\) \(y = \sqrt{1+x^{2}}\) を \(x\) 軸に関して回転させて得られる立体の、\(x = 0\) から \(x = 4\) の部分の体積を求めよ。
\(\text{(9)}\) サイン曲線の \(0\) から \(\pi\) の部分を \(x\) 軸に関して回転させて得られる立体の体積と表面積を求めよ。
\(\text{(10)}\) 曲線 \(xy = a\) の \(x = 1\) から \(x = a\) の部分の \(y\) 座標の平均値と面積を求めよ。
\(\text{(11)}\) 関数 \(y = \sin x\) の \(0\) から \(\pi\) における二次平均が \(\dfrac{\sqrt{2}}{2}\) だと示せ。同じ区間における算術平均を求め、実行率が \(1.11\) だと確認せよ。
\(\text{(12)}\) 関数 \(x^{2} + 3x + 2\) の \(x = 0\) から \(x = 3\) における算術平均と二次平均を求めよ。
\(\text{(13)}\) 関数 \(y=A_1 \sin x + A_3 \sin 3x\) の算術平均と二次平均を求めよ。
\(\text{(14)}\) 方程式 \(y = 3.42e^{0.21x}\) が表す曲線の \(x = 2\) から \(x = 8\) の部分と \(x\) 軸が囲む領域の面積を求めよ。さらに同じ区間における \(y\) 座標の二次平均を求めよ。
\(\text{(15)}\) 極座標上のとある領域を取り、その二倍の面積を持つ円を書く。この円の半径が領域上の全ての点に関する \(r\) の二次平均に等しいことを示せ。
\(\text{(16)}\) 曲線 \(y = ±\dfrac{x}{6}\sqrt{x(10 - x)}\) を \(x\) 軸に関して回転させて得られる立体の体積を求めよ。