XII. 曲線の曲がり具合
微分の反復の話に戻ろう。微分を二回以上行う理由は何だろうか? 変化する量が位置と時間なら、位置を時間で二回微分すると加速度が得られることは知っている。また関数を曲線として幾何学的に表現した場合には、\(\dfrac{dy}{dx}\) は曲線の傾きを意味する。では \(\dfrac{d^{2} y}{dx^{2}}\) の幾何学的な意味は何だろうか? この値は (単位量の \(x\) あたりの) 傾きの変化率であり、一言で言えば、曲線の曲がり具合を表す。
まず 図 31 のように傾きが一定の直線を考える。この場合 \(\dfrac{dy}{dx}\) は定数であり、\(\dfrac{d\left(\dfrac{dy}{dx}\right)}{dx} = \dfrac{d^{2}y}{dx^{2}}\) は \(0\) となる。
次に 図 32 のように右に進むと傾きが大きくなる場合を考える。このとき \(\dfrac{dy}{dx}\) が右に進むにつれて大きくなるから、\(\dfrac{d^{2}y}{dx^{2}}\) は正となる。
また曲線を右に進むと傾きが小さくなる 図 33 や 図 14 のような場合であれば傾きは正の値から \(0\) に向かうので、(曲線は上に進むにもかかわらず) \(\dfrac{d^{2}y}{dx^{2}}\) は負となる。

では秘密をもう一つ教えよう ──前章で説明した「\(0\) と等号で結ぶ」方法の結果が極小値なのか極大値を判定する方法である: 一度微分した式 (\(0\) と等号で結ぶ式) をもう一度微分し、二次微分係数の符号を見ればよい。もし \(\dfrac{d^{2}y}{dx^{2}}\) が正なら、対応する \(y\) の値は極小値となる。反対に \(\dfrac{d^{2}y}{dx^{2}}\) が負なら、対応する \(y\) の値は極大値となる。これがルールである。
この理由を理解するのは難しくない。図 15 や 図 34 のように極小値を持つ曲線を考えよう。極小値を取る点を \(M\) とすると、曲線は \(M\) を底とした凹面となる。\(M\) より左側では傾きは下向き (負) で、\(M\) より右側では傾きは上向き (正) となる。ここから \(M\) における傾きの変化率 \(\dfrac{d^{2}y}{dx^{2}}\) は正だと分かる。\(x\) が増加するとき傾きも負から正に増加するためである。
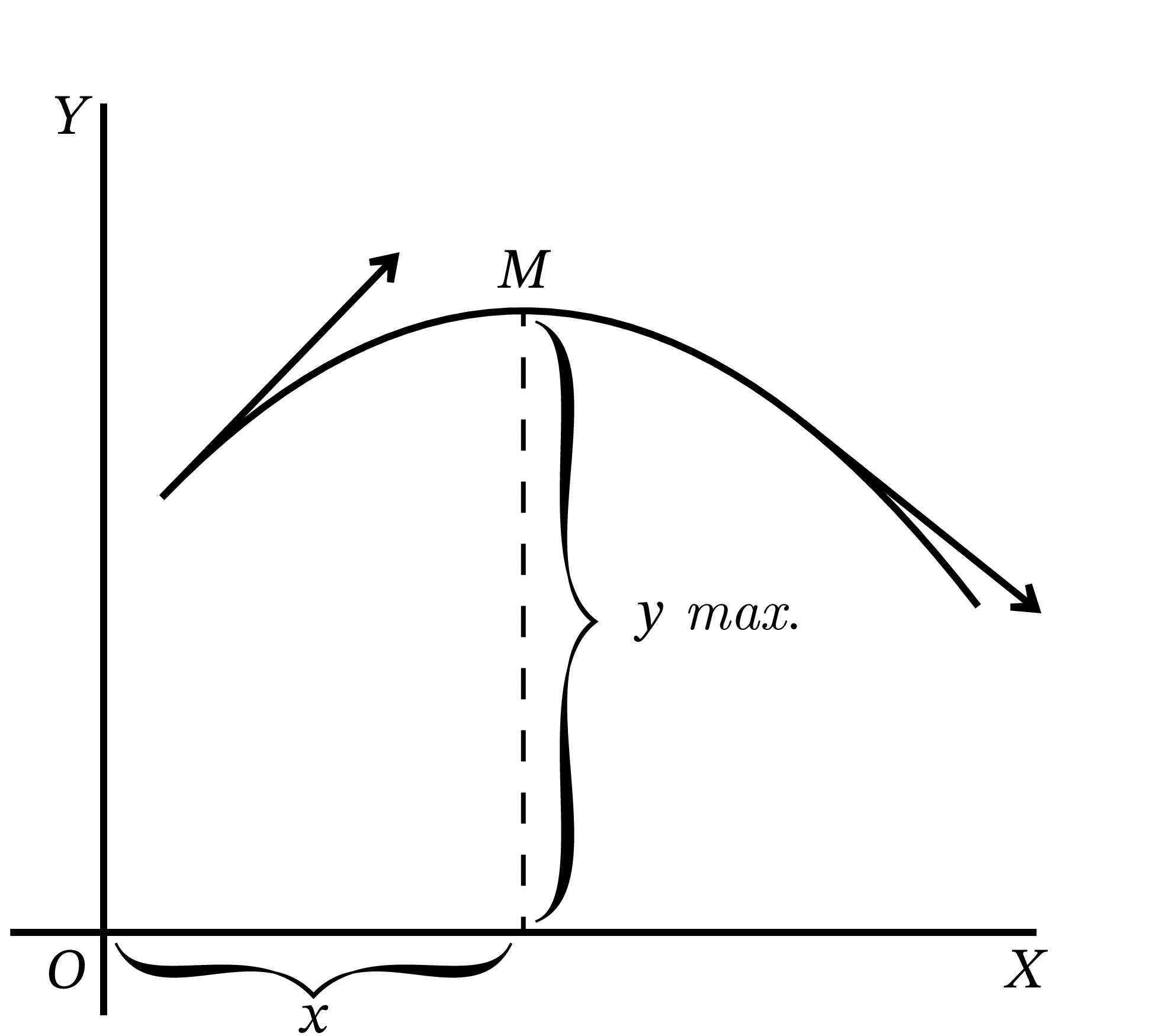
同様に曲線が 図 16 や 図 35 のように極大値を持つ場合には、曲線は極大点 \(M\) を頂点とした凸型になる。点が左から右に \(M\) を通過するとき、曲線の傾きは上向き (正) から下向き (負) に変化する。つまり「傾きの傾き」\(\dfrac{d^{2}y}{dx^{2}}\) は負となる。
前章の最後に示した例に戻って、今説明した方法で極大値と極小値が判定できるかどうかを確認してみよ。ここにもいくつか例を示す。
\(\text{(1)}\) 次の関数が極大または極小となる点を求めよ: \[ \text{(a)}\ y = 4x^{2} - 9x - 6, \quad \text{(b)}\ y = 6 + 9x - 4x^{2} \] その点が極大値と極小値のどちらに対応するのか答えよ。
\(\text{(a)}\) \(\dfrac{dy}{dx} = 8x-9=0\) より \(x = \dfrac{9}{8}\) で、このとき \(y = -11.065\) となる。\(\dfrac{d^{2}y}{dx^{2}} = 8 > 0\) よりこの点は極小値である。
\(\text{(b)}\) \(\dfrac{dy}{dx} = 9 - 8x = 0\) より \(x = \dfrac{9}{8}\) で、このとき \(y = +11.065\) となる。\(\dfrac{d^{2}y}{dx^{2}} = -8\) が \(0\) より小さいのでこの点は極大値である。
\(\text{(2)}\) 関数 \(y = x^{3}-3x+16\) の極大値と極小値を求めよ。
\(\dfrac{dy}{dx} = 3x^{2} - 3 = 0,\ \) \(x^{2} = 1\) より \(x = ±1\) を得る。また \(\dfrac{d^{2}y}{dx^{2}}= 6x\) より二次導関数は \(x = 1\) のとき正で \(x = -1\) のとき負となる。よって \(x = 1\) の \(y = 14\) は極小値で \(x = -1\) の \(y = 18\) は極大値である。
\(\text{(3)}\) \(y=\dfrac{x-1}{x^{2}+2}\) の極大値と極小値を求めよ。
\[ \frac{dy}{dx} = \frac{(x^{2}+2) \times 1 - (x-1) \times 2x}{(x^{2}+2)^{2}} = \frac{2x - x^{2} + 2}{(x^{2} + 2)^{2}} = 0 \] となるとき \(x^{2} - 2x - 2 = 0\) であり、この根は \(x = +2.73,\ \) \(-0.73\) である。
また \[ \begin{aligned} \dfrac{d^{2}y}{dx^{2}} &= - \frac{(x^{2} + 2)^{2} \times (2x-2) - (x^{2} - 2x - 2)(4x^{3} + 8x)}{(x^{2} + 2)^{4}} \\ &= - \frac{2x^{5} - 6x^{4} - 8x^{3} - 8x^{2} - 24x + 8}{(x^{2} + 2)^{4}} \end{aligned} \] の分母は常に正だから、分子の符号を確認すれば極大と極小のどちらかが分かる。
\(x = 2.73\) を代入すれば分子は負だから、\(y = 0.183\) で極大値となる。
\(x = -0.73\) を代入すれば分子は正だから、\(y = -0.683\) で極小値となる。
\(\text{(4)}\) ある工場で一週間に \(P\) 個の製品を生産するのにかかるコスト \(C\) は正の定数 \(a,\ \) \(b,\ \) \(c,\ \) \(d\) を使って \(C = aP + \dfrac{b}{c+P} + d\) と表される。コストが最小となる生産量はいくつか?
極大値もしくは極小値で \(\dfrac{dC}{dP} = a - \dfrac{b}{(c+P)^{2}} = 0\) が成り立つ。このとき \(a = \dfrac{b}{(c+P)^{2}}\) すなわち \(P = ±\sqrt{\dfrac{b}{a}} - c\) である。
生産量は負にならないから \(P=+\sqrt{\dfrac{b}{a}} - c\) が分かる。また \[ \frac{d^{2}C}{dP^{2}} = + \frac{b(2c + 2P)}{(c + P)^{4}} \] は全ての \(P\) に対して正だから、\(P = +\sqrt{\dfrac{b}{a}} - c\) は極小値に対応する。
\(\text{(5)}\) ある建物にとある種類の照明が \(N\) 個あり、それらを \(C\) 時間点けておく一時間当たりのコストは \[ C = N\left(\frac{C_l}{t} + \frac{EPC_e}{1000}\right) \] と表される。ここで \(E\) は照明効率 (ワット毎燭)、\(P\) は照明の明るさ (燭)、\(t\) は証明の平均寿命 (時間)、\(C_{l}\) は照明を交換するコスト (ペンス)、\(C_{e}\) は \(1000\) ワット毎時あたりのコストをそれぞれ表す。
さらに照明の平均寿命と照明効率が \(t = mE^{n}\) という関係で近似的に結ばれているとする。\(m,\ \) \(n\) は定数であり、照明の種類によって決まる。
照明コストが最小となる照明効率を求めよ。
問題の設定から、\(C\) を表す式と極大または極小のための条件は \[ \begin{aligned} C &= N\left(\frac{C_l}{m} E^{-n} + \frac{PC_e}{1000} E\right) \\ \dfrac{dC}{dE} &= \frac{PC_e}{1000} - \frac{nC_l}{m} E^{-(n+1)} = 0 \end{aligned} \] だと分かる。よって \[ E^{n+1} = \frac{1000 \times nC_l}{mPC_e}, \quad E = \sqrt[n+1]{\frac{1000 \times nC_l}{mPC_e}} \] を得る。
これが極小値になるのは次の式から分かる: \[ \frac{d^{2}C}{dE^{2}} = (n + 1) \frac{nC_l}{m} E^{-(n+2)} \] これは正の \(E\) に対して正である。
とある \(16\) 燭の照明では、\(C_{l} = 16\) ペンス、\(C_{e} = 5\) ペンス、\(m = 10\) および \(n = 3.6\) と分かっている。このとき \[ E = \sqrt[4.6]{\frac{1000 \times 3.6 \times 17}{10 \times 16 \times 5}} = 2.6\ {\footnotesize \text{ワット毎燭}} \] となる。
練習問題 X
それぞれの例について関数のグラフを描いてみるとよい。解答はここにある。
\(\text{(1)}\) 関数 \[ y = x^{3} + x^{2} - 10x + 8 \] の極大値と極小値を求めよ。
\(\text{(2)}\) \(y = \dfrac{b}{a}x - cx^{2}\) に対する \(\dfrac{dy}{dx}\) と \(\dfrac{d^{2}y}{dx^{2}}\) を求め、\(y\) が極大または極小となる \(x\) の値を求めよ。さらに極大値と極小値のどちらか答えよ。
\(\text{(3)}\) 次の曲線に極大値と極小値がいくつあるか求めよ: \[ y = 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} \] 同様に次の関数についても求めよ: \[ y = 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} \]
\(\text{(4)}\) 次の関数の極大値と極小値を求めよ: \[ y = 2x + 1 + \frac{5}{x^{2}} \]
\(\text{(5)}\) 次の関数の極大値と極小値を求めよ: \[ y = \frac{3}{x^{2} + x + 1} \]
\(\text{(6)}\) 次の関数の極大値と極小値を求めよ: \[ y = \frac{5x}{2 + x^{2}} \]
\(\text{(7)}\) 次の関数の極大値と極小値を求めよ: \[ y = \frac{3x}{x^{2} - 3} + \frac{x}{2} + 5 \]
\(\text{(8)}\) \(N\) を二つに分けて、一方の二乗の三倍ともう一方の二乗の二倍の和が最小になるようにしたい。どう分けるべきか答えよ。
\(\text{(9)}\) とある発電機の出力 \(x\) と効率 \(u\) の間には次の関係がある: \[ u = \frac{x}{a + bx + cx^{2}} \] \(a,\ b,\ c\) は定数を表す。\(a\) は主に鉄の電力消費が関係し、\(c\) は主に銅の部品の抵抗が関係する。効率が最大となる出力を求めよ。
\(\text{(10)}\) とある船に搭載されている蒸気機関が消費する石炭の量は \(y = 0.3 + 0.001v^{3}\) と表される。ここで \(y\) は一時間あたりに燃やされる石炭の重量 (トン) であり、\(v\) は速度 (海里毎時) である。一時間当たりの船員の賃金・船舶の権利・船の損傷の修復コストが全て合わせて \(1\) トンの石炭と等しいとき、\(1000\) 海里の航海のコストを最小化する速度はいくらか? 石炭の値段が一トン当たり \(10\) シリングのとき、航海の最小コストは全部でいくらか?
\(\text{(11)}\) 次の関数の極大値と極小値を求めよ: \[ y = ±\frac{x}{6}\sqrt{x(10-x)} \]
\(\text{(12)}\) 次の関数の極大値と極小値を求めよ: \[ y = 4x^{3} - x^{2} - 2x + 1 \]