III. 相対的な増加速度

微積分では増加する数値とその増加の速さをひたすら考え続けることになる。数値には定数 (constant) と変数 (variable) の二つがある。変わらないとみなされる数値を定数と呼び、\(a,\ \) \(b,\ \) \(c\) といったアルファベットの最初の文字を使って表す。これに対して増加する (数学者の言葉を使えば「変動する」) とみなされる数値を変数と呼び、\(x,\ \) \(y,\ \) \(z,\ \) \(u,\ \) \(v,\ \) \(w\) といったアルファベットの最後にある文字を使って表す。変数は \(t\) で表されることもある。

さらに多くの場合では一つ以上の変数を同時に扱って、片方の変数がもう一方の変数にどう影響するかを考えることになる。例えば投射体の最高高度がそこに達するまでの時間にどのように関係しているかを考えたり、面積が一定の長方形の高さを増やすと幅がどれだけ減るかを調べたり、梯子の角度を変えると届く高さがどれだけ変わるかを求めたりする。

互いに依存する二つの変数が与えられたとする。互いに依存するとは、一方の変数を変化させるともう一方の変数も変化することを意味する。いずれかの変数を \(x\) と書き、\(x\) に依存するもう一つの変数を \(y\) と書く。

\(x\) に小さな数 \(dx\) を加えて \(x\) を変化させる (ところを想像する) と、\(x\) は \(x + dx\) になる。\(x\) が置き換わったので \(y\) も置き換わり、\(y + dy\) となる。ここで \(dy\) は負になる可能性もあれば正になる可能性もある。さらに \(dy\) と \(dx\) は (特別なケースを除いて) 異なる値となる。

二つの例

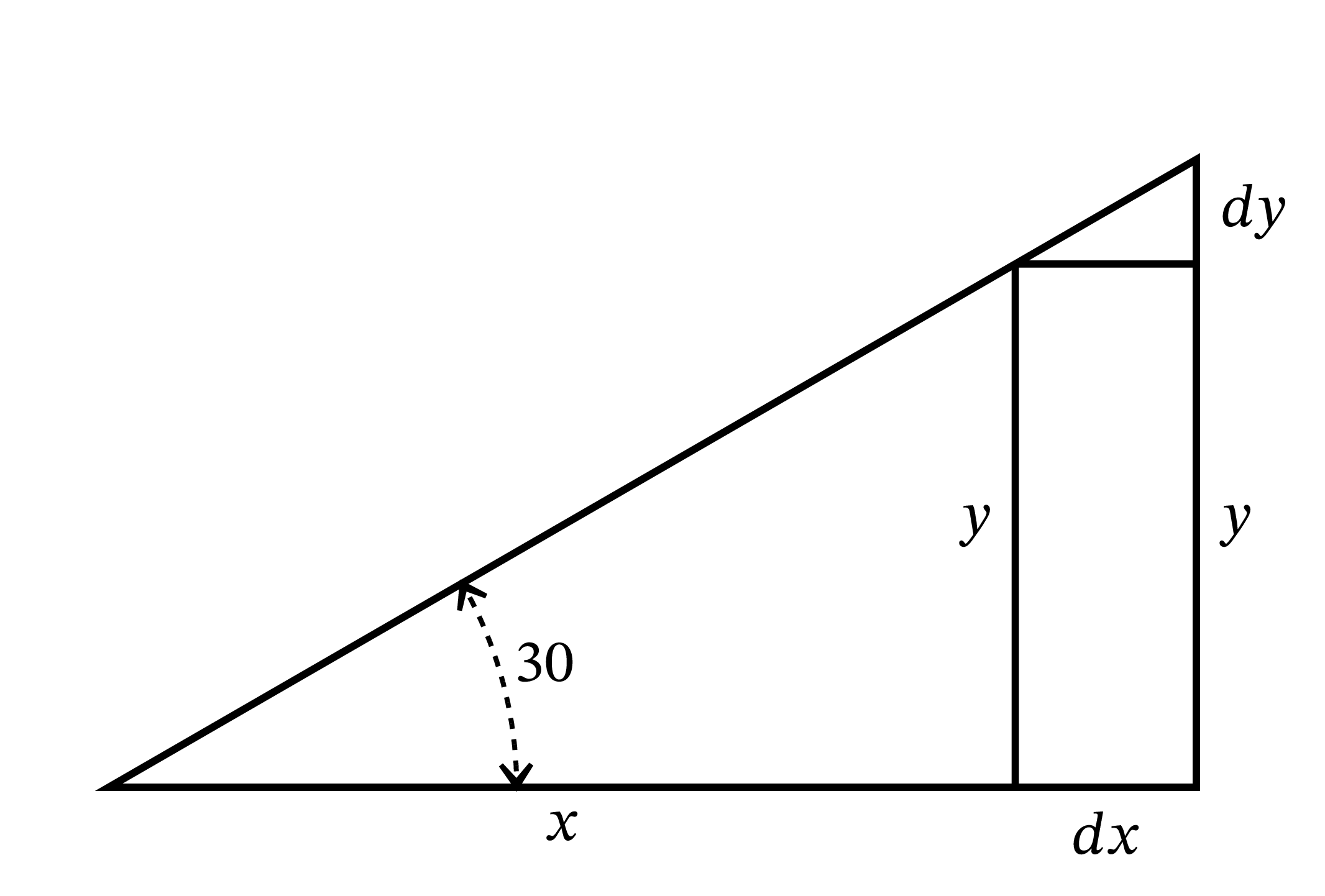
\(\text{(1)}\) 斜辺の傾きが \(30^{\circ}\) で固定された直角三角形を考え、底辺の長さと高さをそれぞれ \(x,\ y\) とする (図 4)。角度を一定に保ったまま三角形を大きくして、底辺の長さが \(x + dx\) に、高さが \(y + dy\) になったとする。つまり \(x\) を増加させた結果 \(y\) が増加したとする。図中の小さな三角形の高さは \(dy\) で底辺の長さは \(dx\) であり、元の三角形と相似である。よって \(\dfrac{dy}{dx}\) は \(\dfrac{y}{x}\) と等しい。斜辺の傾きは \(30^{\circ}\) だから、 \[ \frac{dy}{dx} = \frac{1}{\sqrt{3}} = \frac{1}{1.73} \] が成り立つ。

\(\text{(2)}\) 図 5 のように立てかけた梯子を考える。下端から壁までの距離を \(x\) として、梯子の長さは \(AB\) で固定されているとする。さらに \(y\) を梯子の高さとすれば、明らかに \(y\) は \(x\) に依存する。簡単に分かるように、下端 \(A\) を壁から遠ざかる方向に引っ張ると、上端 \(B\) は下に移動する。この様子を科学的な言葉で表してみよう。\(x\) を \(x + dx\) に増加させると、\(y\) は \(y - dy\) となる。つまり \(x\) が正の増加を受けると、その結果生じる \(y\) の増加は負となる。

\(y\) の増加はどれくらいだろうか？梯子がとても長くて、下端 \(A\) が壁から \(19\) インチの場所にあるとき上端 \(B\) は地面からちょうど \(15\) フィートの場所にあるとする。このとき下端を \(1\) インチ引っ張ると上端はどれだけ下に動くだろうか？まず全ての数値をインチに変換しよう: \(x = 19\) インチで、\(y = 180\) インチである。\(dx\) で表される \(x\) の増分は \(1\) インチだから、\(x + dx = 20\) インチとなる。

\(y\) はどれだけ減少するだろうか？新しい高さは \(y - dy\) であり、ユークリッド I. 47 の方法で新しい高さを計算すれば \(dy\) を求められる。梯子の長さは \[ \sqrt{ (180)^2 + (19)^2 } = 181 {\footnotesize \text{ インチ}} \] だから、新しい高さ \(y - dy\) は \[ \begin{aligned} (y - dy)^2 &= (181)^2 - (20)^2 = 32761 - 400 = 32361, \\ y - dy &= \sqrt{32361} = 179.89 {\footnotesize \text{ インチ}} \end{aligned} \] となる。\(y\) は \(180\) だから、\(dy\) は \(180 - 179.89 = 0.11\) インチと分かる。

つまり増加量 \(dx\) を \(1\) インチとすると、減少量 \(dy\) は \(0.11\) インチとなることが判明した。

このとき \(dy\) と \(dx\) の比は \[ \frac{dy}{dx} = - \frac{0.11}{1} \] となる。

また (一つの特殊な場合を除いて) \(dy\) が \(dx\) と異なる値になることも簡単に分かる。

微積分ではとある興味深い値を求めて求めて求め続けることになる。その値とは、\(\bm{dx}\) と \(\bm{dy}\) が無限に小さくなるときの \(\bm{dx}\) に対する \(\bm{dy}\) の比である。

比 \(\dfrac{dy}{dx}\) が求められるのは \(y\) と \(x\) の間に関係があるときに限ることを注意しておく。例えば一つ目の例では、三角形の底辺の長さ \(x\) が増加するとき高さ \(y\) も増加する。また二つ目の例では、地面から梯子の下端までの距離 \(x\) を増やすと、それに応じて梯子が届く高さ \(y\) は減少する (\(y\) が減少する速度は最初ゆっくりだが、\(x\) が大きくなるにつれて速くなる)。この二つの例では \(x\)と \(y\) の間の関係は完全に固定されており、数学的に表すこともできる。具体的にはそれぞれ \(\dfrac{y}{x} = \tan 30^{\circ}\) と \(x^{2} + y^{2} = l^{2}\) であり (梯子の長さを \(l\) とする)、\(\dfrac{dy}{dx}\) は上で見たような意味を持つ。

\(x\) が前と同じように壁から梯子の下端までの距離を表すとする。ただし \(y\) が梯子の届く高さではなくて、壁の高さ、壁に含まれるレンガブロックの数、あるいは壁ができてからの年数を表すとする。すると \(x\) が大きくなっても当然 \(y\) は変化しない。\(\dfrac{dy}{dx}\) は意味を持たないし、式で表すこともできない。\(dx,\ \) \(dy,\ \) \(dz\) といった微分小を使うときには、必ず \(x,\ \) \(y,\ \) \(z\) の間に何らかの関係が存在する。この関係を \(x,\ \) \(y,\ \) \(z\) の関数 (function) と呼ぶ。上の二つの例における \(\dfrac{y}{x} = \tan 30^{\circ}\) と \(x^{2} + y^{2} = l^{2}\) はどちらも \(x\) と \(y\) の関数である。こういった式は \(x\) を使って \(y\) を表す方法と \(y\) を使って \(x\) を表す方法を陰に示している (つまり、求めるのは簡単にではないにせよそのための情報を持っている) ので、\(x\) と \(y\) の陰関数 (implicit function) と呼ばれる。

この二つの関数はそれぞれ次のように変形できる: \[ \begin{aligned} y &= x \tan 30^{\circ} \quad {\footnotesize \text{および}} \quad x = \frac{y}{\tan 30^{\circ}} \\ y &= \sqrt{l^2 - x^2} \quad {\footnotesize \text{および}} \quad x = \sqrt{l^2 - y^2} \end{aligned} \] これらの式は \(x\) を使って \(y\) を、そして \(y\) を使って \(x\) を陽に (簡単に求められる形で) 表している。こういった式をそれぞれ \(x\) または \(y\) の陽関数 (explicit function) と呼ぶ。例えば \(x^{2} + 3 = 2y - 7\) は \(x\) と \(y\) の陰関数だが、これを \(y = \dfrac{x^2 + 10}{2}\) と書けば \(x\) の陽関数となり、\(x = \sqrt{2y - 10}\) と書けば \(y\) の陽関数となる。\(x,\ \) \(y,\ \) \(z,\ \dots\) の陽関数と言った場合には、それは \(x,\ \) \(y,\ \) \(z,\ \dots\) の一つあるいは全てを同時に変化させたときに変化する値を意味する。陽関数の値は式に含まれる変数の値に従って決まるので、従属変数 (dependent variable) と呼ばれる。その他の変数は関数が取る値から値が求まらないので、独立変数 (independent variable) と呼ばれる。例えば \(u = x^{2} \sin \theta\) では \(x\) と \(\theta\) が独立変数で、\(u\) が従属変数となる。

\(x,\ \) \(y,\ \) \(z\) といった変数の間に何らかの関係が存在する、つまり \(x\) と \(y\) と \(z\) のいずれかを変化させると他の変数も変化することが分かっていても、その関係が具体的に分かっていなかったり、分かっていても簡単に表現できなかったりする場合がある。このとき \(x,\ \) \(y,\ \) \(z\) の関数の存在を \(F(x, y, z)\) という記号で表す。\(F(x, y, z)\) は陰関数を使った記法であり、陽関数を使って表す場合には \(x = F(y, z),\ \) \(y = F(x, z),\ \) \(z = F(x, y)\) と表記する。\(F\) ではなく \(f\) や \(\phi\) を使うこともあるが、意味は変わらない。つまり \(y = F(x),\ \) \(y = f(x),\ \) \(y = \phi(x)\) などと書かれていたら、それは \(y\) の値が \(x\) の値に依存しており、どのように依存しているかは明示されていないことを意味する。

比 \(\dfrac{dy}{dx}\) を \(x\) に関する \(y\) の微分係数 (differential coefficient) と呼ぶ。とても単純なものにしては厳かで科学的な名前が付いているが、この名前に怖じ気付くことはない。非常に簡単なものに長くて発音しにくい名前をわざわざ付けているのだと思えばよい。そうして気を楽にしてから、比 \(\dfrac{dy}{dx}\) という簡単な式について次章でさらに考える。

学校で習った代数では、\(x\) とか \(y\) とか呼ばれる変数の値を求めたり、二つある変数を同時に求めたりした。この本では別の値を求める方法を学ぶ。新しい獲物は \(\dfrac{dy}{dx}\) である。\(\dfrac{dy}{dx}\) の値を求める手続きを微分 (differentiation) と呼ぶ。ここで微分係数における \(dy\) と \(dx\) は無限に小さいという事実を意識しておく必要がある。微分係数の真の値は、\(dy\) と \(dx\) の両方が無限に小さくなる極限を考えたときに \(\dfrac{dy}{dx}\) が向かう値である。

では次章で \(\dfrac{dy}{dx}\) を求める方法を学ぼう。

微分記号の読み方

\(dx\) は \(d\) に \(x\) を乗じたものだと学生は誤って考えがちだが、これは全くの間違いである。\(d\) は \(x\) の係数ではなく、「...の小要素」あるいは「...の小部分」を意味する。そのため \(dx\) の発音は「ディーエックス」となる。

読者に微分記号の読み方を教えられる人がいない可能性もあるので、ここで簡単に読み方を示しておく。微分係数 \(\dfrac{dy}{dx}\) は「ディーワイ・ディーエックス」あるいは「ディーワイ・バイ・ディーエックス」と読む。同様に \(\dfrac{du}{dt}\) は「ディーユー・ディーティー」あるいは「ディーユー・バイ・ディーティー」と読む。

この本では後に二次微分係数についても触れる。二次微分係数は次の形をしている: \[ \dfrac{d^2 y}{dx^2} \] これは「ディーツーワイ・ディーエックスにじょう」と読み、\(x\) に関して \(y\) を微分する操作を二回行うことを表す (あるいはあなたにそう命令する)。

関数が微分されていることを表すために関数の記号にアクセントを付ける場合もある。\(y\) が \(x\) の何らかの関数であることを表すのに \(y = F(x)\) という表記があるが (上の説明を参照)、このとき \(\dfrac{d(F(x))}{dx}\) を \(F'(x)\) と書く。同様に \(F''(x)\) は元の関数 \(F(x)\) が二回微分されていることを表す。