V. 定数の微分

ここまでは等式中の \(x\) の増加を考え、\(x\) が増やされた結果として \(y\) も値を変えて増加するものとしてきた。普通は \(x\) を私たちが変えられる量だとして、\(x\) の変動という原因によって \(y\) の変動という結果が起こると考える。つまり \(y\) の値が \(x\) の値に依存しているみなす。\(x\) も \(y\) も変数ではあるが、私たちが値を変えられるのは \(x\) だけであり、\(y\) は “従属” 変数である。前章では独立に起こる \(x\) の変動によって引き起こされる \(y\) の変動の比率を求める規則を導いた。

次のステップとして、定数を持つ式を微分したときに何が起こるかを調べよう。定数とは \(x\) や \(y\) の値が変わっても値を変えない数値である。

定数が足される場合

\(x\) の関数に定数が足されているという簡単な場合を考えよう。具体的な例として \[ y = x^{3}+5 \] を取る。以前と同じく \(x\) が \(x + dx\) に増加するとき \(y\) が \(y + dy\) に増加すると仮定すれば \[ \begin{aligned} y + dy &= (x + dx)^{3} + 5 \\ &= x^{3} + 3x^{2}\, dx + 3x(dx)^{2} + (dx)^{3} + 5 \end{aligned} \] を得る。高次の微小量を無視すれば、この式は \[ y + dy = x^{3} + 3x^{2}\cdot dx + 5 \] となる。元の等式 \(y = x^{3} + 5\) を引けば、次の式が残る: \[ \begin{aligned} dy &= 3x^{2}\, dx \\ \frac{dy}{dx} &= 3x^{2} \end{aligned} \] \(5\) は全く消えてしまった。\(y\) に \(5\) が足されても \(x\) の増加量は変わらないので、定数が足されていても微分係数は変わらない。\(5\) を \(7\) や \(700\) など好きな数としても、微分係数は変化しない。つまり \(a,\ \) \(b,\ \) \(c\) といった文字で表される任意の定数を微分すると \(0\) になる。

足される定数が \(-5\) や \(-b\) のような負の値を持っていたとしても、同じ理由で微分係数は変わらない。

定数が掛けられる場合

この場合を考えるために単純な例 \(y = 7x^{2}\) を考える。前章と同様にすれば \[ \begin{aligned} y + dy &= 7(x+dx)^{2} \\ &= 7\{x^{2} + 2x\cdot dx + (dx)^{2}\} \\ &= 7x^{2} + 14x\cdot dx + 7(dx)^{2} \end{aligned} \] を得る。元の等式 \(y = 7x^{2}\) を引いて最後の項を取り除けば \[ \begin{aligned} dy & = 14x\cdot dx \\ \frac{dy}{dx} & = 14x \end{aligned} \] となる。

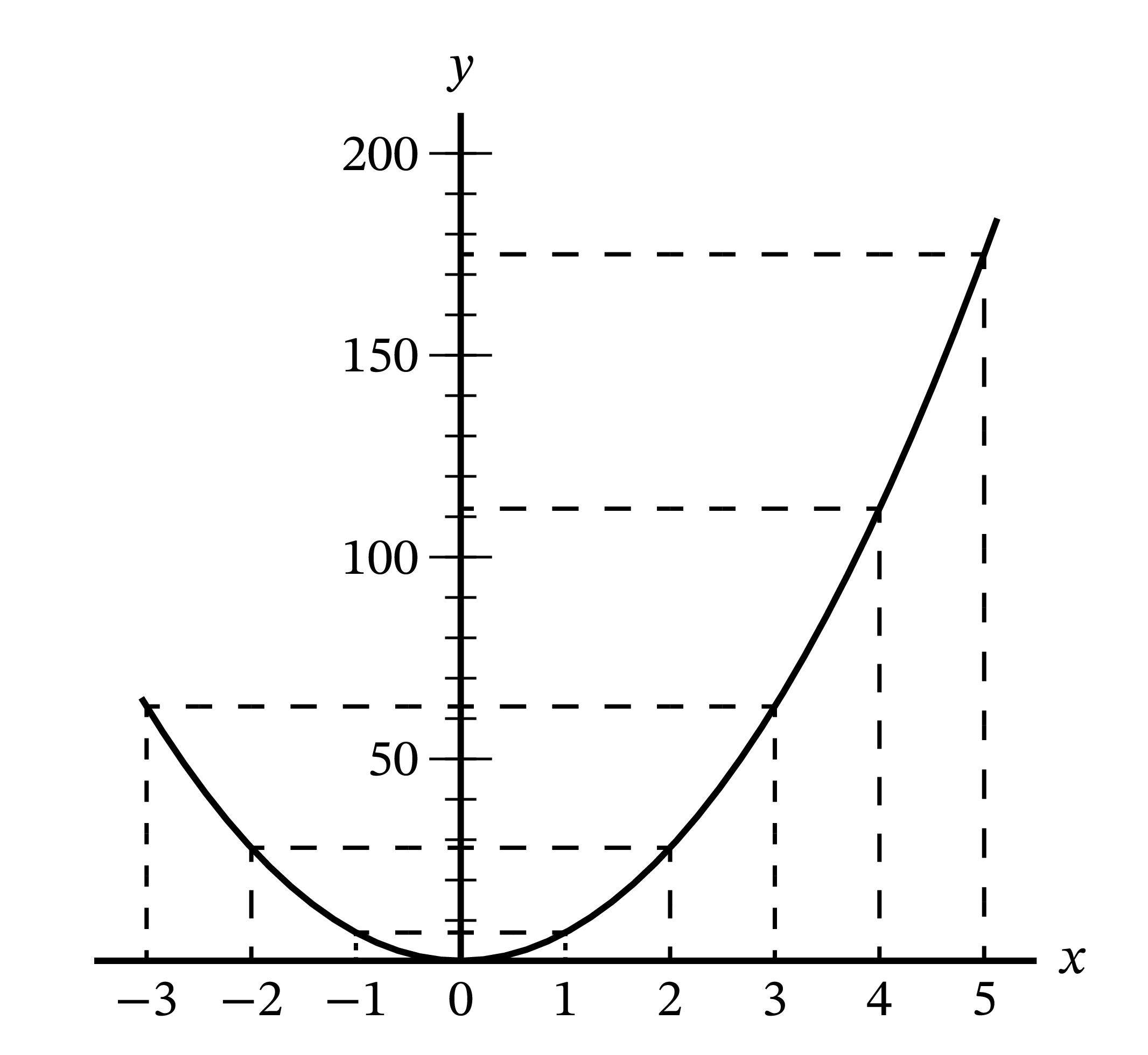
この結果を理解するために、\(y = 7x^{2}\) と \(\dfrac{dy}{dx} = 14x\) のグラフを描いてみよう。\(0,\ \) \(1,\ \) \(2,\ \) \(3\) といった \(x\) の値を考え、対応する \(y\) と \(\dfrac{dy}{dx}\) の値を計算し、グラフにプロットする。

計算した値を次の表にまとめる: \[ \begin{array}{c|rrrrrrrrr} x & 0 & 1 & 2 & 3 & 4 & 5 & -1 & -2 & -3 \\ \hline y & 0 & 7 & 28 & 63 & 112 & 175 & 7 & 28 & 63 \\ \hline \vphantom{\Large \dfrac{dy}{dx}} \dfrac{dy}{dx} & 0 & 14 & 28 & 42 & 56 & 70 & -14 & -28 & -42 \\ \end{array} \]

この値をプロットすると 図 6 と 図 6a に示す二つの曲線が得られる。

二つの図を注意深く観察すると、関数の微分係数を表す曲線 (図 6a) の \(y\) 座標が、\(x\) 座標が同じ点における 図 6 の曲線の傾きと同じように増減していることが分かる。例えば原点の左側では元の曲線の傾きは負であり (つまり左から右に進むとき曲線は下に進んでおり)、この領域における微分係数を表す曲線の \(y\) 座標は負となっている。

前に説明したように、\(x^{2}\) を微分すると \(2x\) になる。つまり \(7x^{2}\) の微分係数は \(x^{2}\) の微分係数を \(7\) 倍すれば得られる。あるいは \(8x^{2}\) なら、\(x^{2}\) の微分係数を \(8\) 倍すれば微分係数が得られる。つまり \(y = ax^{2}\) のとき \[ \frac{dy}{dx} = a \times 2x \] が成り立つ。

また \(y = ax^{n}\) なら \(\dfrac{dy}{dx} = a×nx^{n-1}\) となる。つまり関数に定数を掛けると、その微分係数にも同じ数が掛けられる。定数の除算でも同じことが成り立つ。というのも、上述の例における \(7\) を \(\dfrac{1}{7}\) にすれば微分の結果に \(\dfrac{1}{7}\) が掛かるからである。

例

解説付きの例をさらにいくつか見れば、簡単な代数式に対する微分を完璧に習得し、章末の練習問題を自力で解けるようになるだろう。

\(\text{(1)}\) \(y = \dfrac{x^{5}}{7} - \dfrac{3}{5}\) を微分せよ。

\(-\dfrac{3}{5}\) は足された定数だから、微分すると消える。よって直ちに \[ \begin{aligned} \frac{dy}{dx} & = \frac{1}{7} \times 5 \times x^{5-1} \\ & = \frac{5}{7} x^{4} \end{aligned} \] を得る。

\(\text{(2)}\) \(y = a\sqrt{x} - \dfrac{1}{2}\sqrt{a}\) を微分せよ。

定数 \(\dfrac{1}{2}\sqrt{a}\) は微分すると \(0\) になる。また \(a\sqrt{x}\) を指数を使った形で書けば \(ax^{\frac{1}{2}}\) だから、 \[ \frac{dy}{dx} = a \times \frac{1}{2} \times x^{\frac{1}{2}-1} = \frac{a}{2} \times x^{-\frac{1}{2}} \] となる。よって \[ \frac{dy}{dx} = \frac{a}{2\sqrt{x}} \] である。

\(\text{(3)}\) \(ay + bx = by - ax + (x+y)\sqrt{a^{2} - b^{2}}\) とする。\(x\) に関する \(y\) の微分係数を求めよ。

こういった種類の式を一般的に微分するには、これまでに説明したよりも少し高度な知識が必要になる。ただどんなときでも、式を簡単な形に変形できないかを確認するべきである。

つまり与えられた式を \(x\) だけに関する式を使った \(y = \cdots\) という形に変形できないかを最初に考える。

上の式を変形すると \[ (a-b)y + (a + b)x = (x+y) \sqrt{a^{2} - b^{2}} \] となる。これを二乗すれば \[ (a-b)^{2} y^{2} + (a + b)^{2} x^{2} + 2(a+b)(a-b)xy = (x^{2}+y^{2}+2xy)(a^{2}-b^{2}) \] であり、整理すると \[ (a-b)^{2}y^{2} + (a+b)^{2} x^{2} = x^{2}(a^{2} - b^{2}) + y^{2}(a^{2} - b^{2}) \] \[ [(a-b)^{2} - (a^{2} - b^{2})]y^{2} = [(a^{2} - b^{2}) - (a+b)^{2}]x^{2} \] \[ 2b(b-a)y^{2} = -2b(b+a)x^{2} \] を得る。ここから \[ y = \sqrt{\frac{a+b}{a-b}} x, \quad \frac{dy}{dx} = \sqrt{\frac{a+b}{a-b}} \] が分かる。

\(\text{(4)}\) 半径が \(r\) で高さが \(h\) の円柱の体積 \(V\) は等式 \(V = \pi r^{2} h\) で与えられる。\(r = 5.5\) インチおよび \(h = 20\) インチのときの半径に対する体積の変化率を求めよ。また \(r = h\) と仮定したときに、半径が \(1\) インチだけ大きくなったときに体積が \(400\) 立方インチだけ大きくなるような円柱の寸法を求めよ。

\(r\) に関する \(V\) の変化率は次の式で与えられる: \[ \frac{dV}{dr} = 2 \pi r h \]

これに \(r = 5.5\) インチと \(h = 20\) インチを代入すれば \(690.8\) となる。これは半径が \(1\) インチ増えると体積が \(690.8\) 立方インチ増えることを意味するが、この事実は簡単に確認できる: \(r = 5\) と \(r = 6\) としたときの体積はそれぞれ \(1570\) 立方インチと \(2260.8\) 立方インチであり、\(2260.8 - 1570 = 690.8\) が成り立つ。

同様に \(r = h\) なら \(\dfrac{dV}{dr} = 2\pi r^{2}\) であり、これが \(400\) に等しいなら \[ r = h = \sqrt{\dfrac{400}{2\pi}} = 7.98\, {\footnotesize\text{インチ}} \] が分かる。

\(\text{(5)}\) フェリー¹の輻射高温計の指す目盛りの値 \(\theta\) は、測定している物体の摂氏温度 \(t\) との間に次の関係がある: \[ \dfrac{\theta}{\theta_1} = \left(\dfrac{t}{t_1}\right)^{4} \] ここで \(\theta_{1}\) は既知の温度 \(t_{1}\) における物体の測定結果である。

\(800^{\circ}\text{\small C},\ \) \(1000^{\circ}\text{\small C},\ \) \(1200^{\circ}\text{\small C}\) における輻射高温計の感度を比較せよ。\(1000^{\circ}\text{\small C}\) における目盛りの値を \(25\) とする。

求めるべき感度はこれらの温度における目盛りの変化率、つまり \(\dfrac{d\theta}{dt}\) である。上の等式は \[ \theta = \dfrac{\theta_1}{t_1^{4}} t^{4} = \dfrac{25t^{4}}{1000^{4}} \] と変形できるから \[ \dfrac{d\theta}{dt} = \dfrac{100t^{3}}{1000^{4}} = \dfrac{t^{3}}{10{,}000{,}000{,}000} \] を得る。

\(t = 800,\ 1000,\ 1200\) のとき、それぞれ \(\dfrac{d\theta}{dt} = 0.0512,\ \) \(0.1,\ \) \(0.1728\) となる。

つまり温度が \(800^{\circ}\text{\small C}\) から \(1000^{\circ}\text{\small C}\) になると感度はおよそ半分となり、\(1200^{\circ}\text{\small C}\) になるとさらに \(50{\footnotesize \text{\%}}\) 以上減少する。

練習問題 II

解答はここにある。

\(\text{(12)}\) 鉄の棒の温度 \(T\) における長さ \(L\) は \(L = l_t\bigl[1 + 0.000012(T-t)\bigr]\) で与えられる。ここで \(l_{t}\) は温度が \(t\) のときの長さを表す。鉄の棒を変形させてタイヤを作るとき、タイヤの半径 \(D\) の温度に対する変化率を求めよ。最終的なタイヤの温度を \(T\) とする。

1. 訳注: シャルル・フェリー (1865–1935) はフランスの物理学者で、輻射高温計をはじめとした様々な測定器具を発明した。^[return]

2. 訳注: 燭 (candlepower) はかつて利用されていた明るさの単位。^[return]