XV. サインとコサインの取り扱い
角度はギリシャ文字で表される。本書では角度を表す変数として \(\theta\) (シータ) を使う。
関数 \[ y= \sin \theta \] の微分を考えよう。

調べるべきは \(\dfrac{d(\sin \theta)}{d \theta}\) の値である。つまり \(\theta\) を変化させたときサインの増分と角度の増分の比を考えて、変化がどちらも無限に小さい場合のこの比を求めたい。図 43 では円の半径が \(1\) で、高さ \(y\) が \(\sin \theta\) となっている。\(\theta\) が少し (角度の小要素 \(d \theta\)) だけ大きくなったとき、\(\sin \theta\) も少しだけ大きくなる。\(y\) の変位を \(dy\) とすれば、新しい高さは \(y + dy\) となる。新しい角度は \(\theta + d \theta\) だから、これを等式として表せば \[ y + dy = \sin(\theta + d \theta) \] となる。最初の等式を引けば \[ dy = \sin(\theta + d \theta)- \sin \theta \] を得る。
右辺は二つのサインの差であり、この変形方法は三角法の教科書に載っている。つまり \(M\) と \(N\) が異なる角度のとき \[ \sin M - \sin N = 2 \cos\frac{M+N}{2}\cdot\sin\frac{M-N}{2} \] が成り立つ。
今の例では \(M = \theta + d \theta\) および \(N = \theta\) だから、 \[ \begin{aligned} dy &= 2 \cos\frac{\theta + d\theta + \theta}{2} \cdot \sin\frac{\theta + d\theta - \theta}{2} \\ &= 2\cos \left(\theta + \frac{1}{2}d\theta\right) \cdot \sin\frac{1}{2} d\theta \end{aligned} \] となる。
ここで \(d \theta\) を無限に小さくした極限を考えるとき、\(\theta\) と比較したときの \(\dfrac{1}{2} d \theta\) は無視できる。さらに \(\sin\dfrac{1}{2} d \theta\) は \(\dfrac{1}{2} d \theta\) と等しいとみなせる1。すると \[ \begin{aligned} dy &= 2 \cos \theta \times \frac{1}{2} d \theta \\ &= \cos \theta \cdot d \theta \end{aligned} \] となり、最終的な答えが得られる: \[ \dfrac{dy}{d \theta} = \cos \theta \]
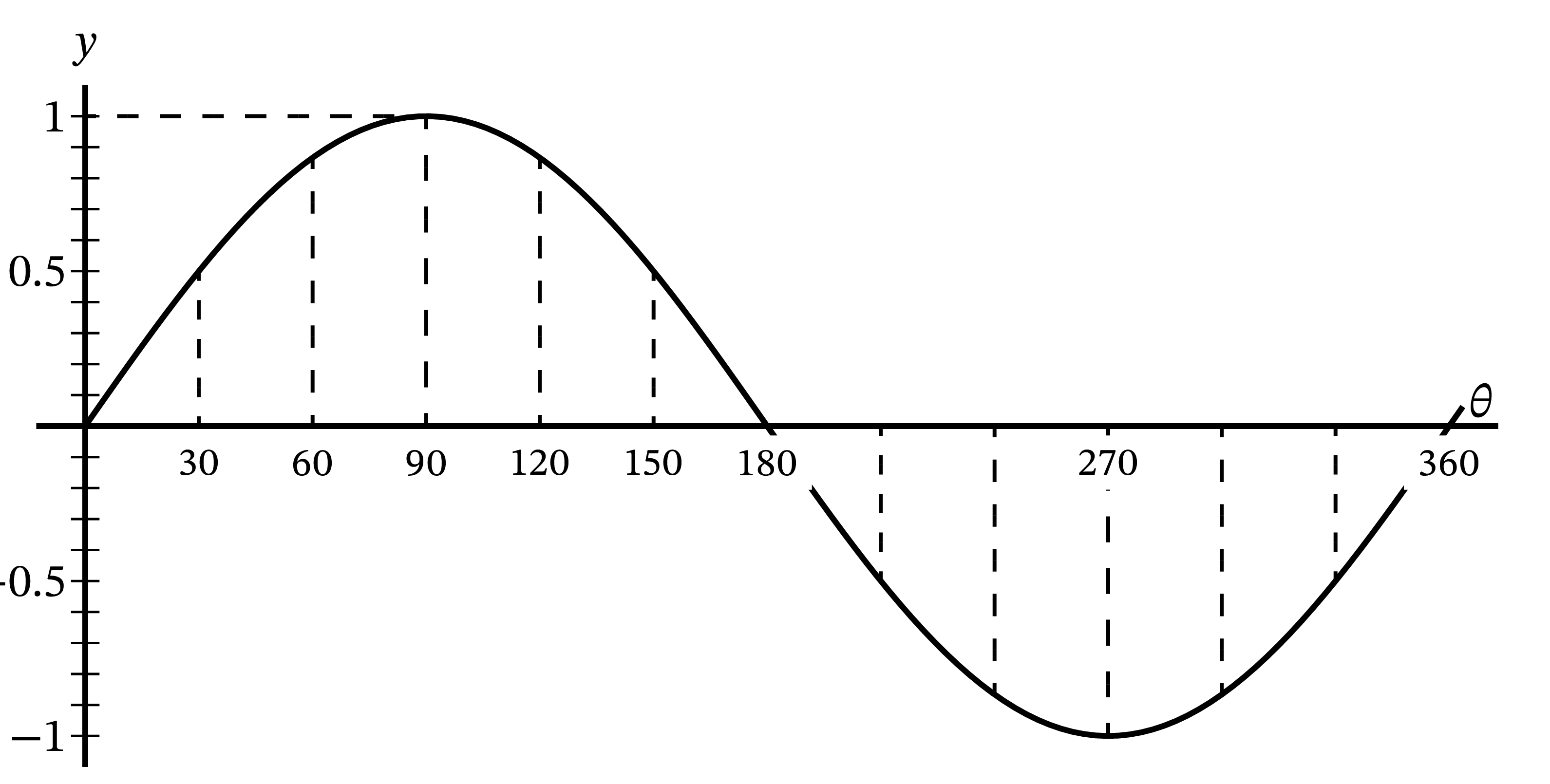
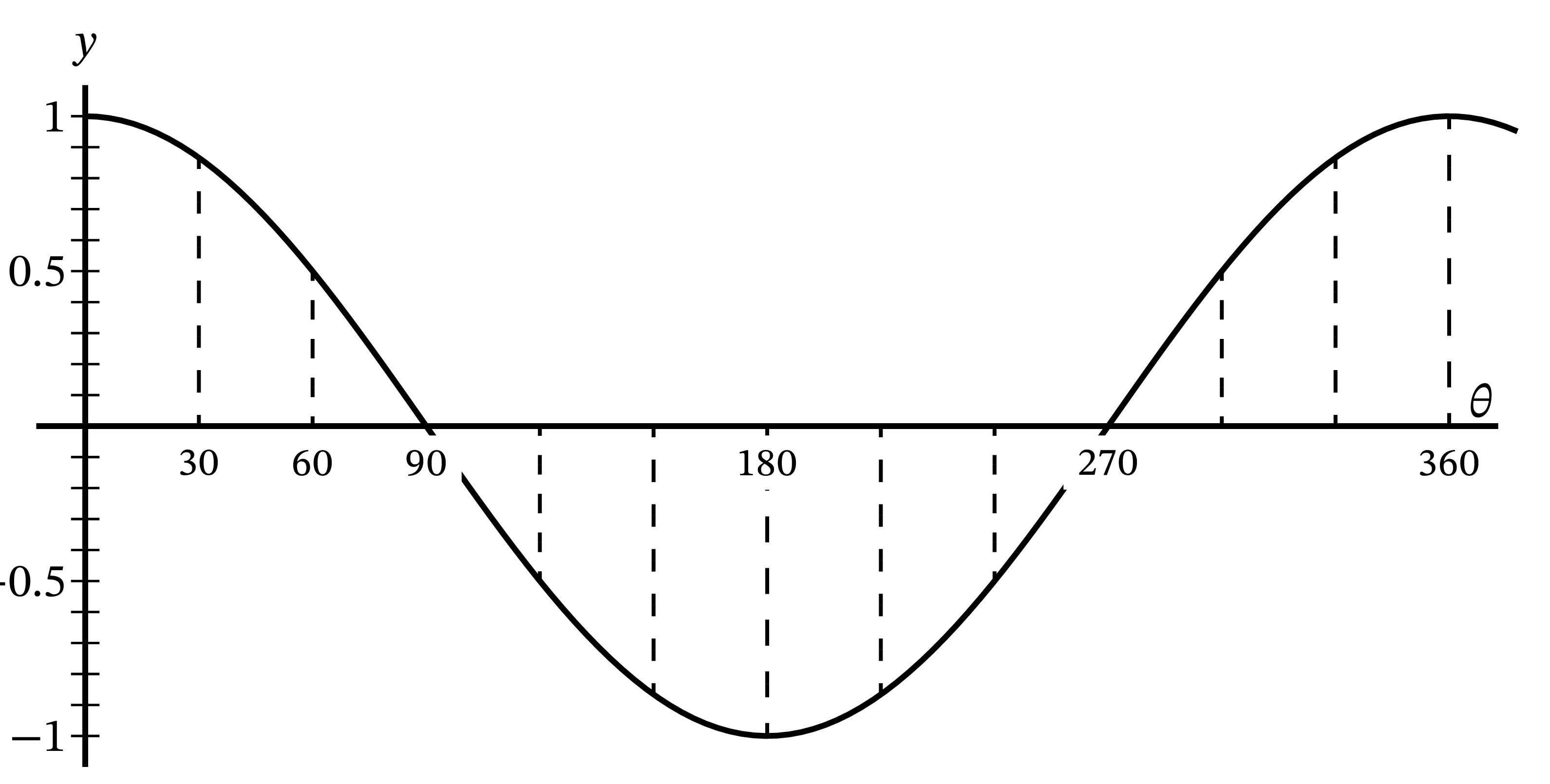
図 44 と 図 45 に \(y=\sin \theta\) と \(\dfrac{dy}{d\theta}=\cos\theta\) が表す曲線を示す。
続いてコサインを考えよう。
\(y = \cos \theta\) とする。\(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) だから、 \[ \begin{aligned} dy &= d\left(\sin\left(\frac{\pi}{2} - \theta\right)\right) \\ &= \cos\left(\frac{\pi}{2} - \theta\right) \times d(-\theta) \\ &= \cos\left(\frac{\pi}{2} - \theta\right) \times (-d\theta) \\ \frac{dy}{d\theta} &= -\cos\left(\frac{\pi}{2} - \theta\right) \end{aligned} \] が分かる。これでコサインの微分が求まった: \[ \frac{dy}{d\theta} = -\sin \theta \]
最後にタンジェントを考える。 \[ \begin{aligned} y &= \tan \theta \\ dy &= \tan(\theta + d\theta) - \tan\theta \end{aligned} \] とする。三角法の教科書に載っているように \[ \tan(\theta + d\theta) = \frac{\tan\theta + \tan d\theta} {1 - \tan\theta\cdot\tan d\theta} \] だから、次を得る: \[ \begin{aligned} dy &= \frac{\tan\theta + \tan d\theta} {1-\tan\theta\cdot\tan d\theta} - \tan\theta \\ &= \frac{(1 + \tan^{2}\theta)\tan d\theta} {1-\tan\theta\cdot\tan d\theta} \end{aligned} \]
\(d\theta\) が無限に小さいとき \(\tan d\theta\) は \(d\theta\) に等しくなり2、\(\tan\theta \cdot d\theta\) は \(1\) と比べたとき無視できるほどに小さい値となる。よってこの式は \[ dy = \frac{(1+\tan^{2} \theta)\, d\theta}{1} \] と変形できる。従って次が分かる: \[ \begin{aligned} \frac{dy}{d\theta} & = 1 + \tan^{2}\theta \\ & = \sec^{2} \theta \end{aligned} \]
以上の結果をまとめる: \[ \def\arraystretch{1.5} \begin{array}{c|rrc} y & \sin \theta & \cos \theta & \tan \theta \\ \hline \dfrac{dy}{d\theta}\vphantom{\Large \dfrac{dy}{d\theta}} & \cos \theta & -\sin \theta & \sec^{2} \theta \end{array} \]
単振動や波運動といった工学と物理の問題では時間の経過と共に増加する角度を扱う場合がある。角度の周期 (period) を \(T\) とすれば、\(T\) の間に角度は円を一周する。一周の角度は \(2\pi\) ラジアン \(= 360^{\circ}\) だから、時刻 \(t\) における角度は \[ \theta = 2\pi\frac{t}{T}\ {\footnotesize \text{ラジアン}} = 360\frac{t}{T}\ {\footnotesize \text{度}} \] と表せる。
一秒間あたりの周期の数を周波数 (frequency) と呼ぶ。周波数を \(n\) とすれば \(n = \dfrac{1}{T}\) が成り立ち、 \[ \theta = 2\pi nt \] と書ける。このとき \[ y = \sin 2\pi nt \] となる。
この関係においてサインの値が時間と共にどのように変化するかを知りたい場合には、\(\theta\) ではなく \(t\) に関する微分を求める必要がある。第九章で説明したテクニックが利用できる。つまり \[ \frac{dy}{dt} = \frac{dy}{d\theta} \cdot \frac{d\theta}{dt} \] で \(\dfrac{d\theta}{dt}\) は明らかに \(2 \pi n\) だから、 \[ \begin{aligned} \frac{dy}{dt} &= \cos \theta \times 2\pi n \\ &= 2\pi n \cdot \cos 2\pi nt \\ \end{aligned} \] が分かる。同様に \[ \frac{d(\cos 2\pi nt)}{dt} = -2\pi n \cdot \sin 2\pi nt \] が成り立つ。
サインとコサインの二次導関数
\(\sin \theta\) を \(\theta\) で微分すると \(\cos \theta\) になることを見た。さらに \(\cos \theta\) を \(\theta\) で微分すると \(-\sin \theta\) となる。これは数式で \[ \frac{d^{2}(\sin \theta)}{d\theta^{2}} = -\sin \theta \] と表せる。
つまりサインは二回微分すると符号が反転して元の関数に戻るという興味深い性質を持つ。
コサインでも同じ結果が得られる。\(\cos\theta\) を微分すると \(-\sin \theta\) となり、\(-\sin\theta\) を微分すると \(-\cos\theta\) となる。数式で表せば \[ \frac{d^{2}(\cos\theta)}{d\theta^{2}} = -\cos\theta \] が成り立つ。
サインとコサインは二回微分すると (符号が反転して) 元に戻る唯一の関数である。
例
ここまでの知識を使えば、さらに複雑な形をした式を微分できる。
\(\text{(1)}\) \(y = \arcsin x\)
サインが \(x\) であるような角度を \(y\) とすれば \(x = \sin y\) が成り立つ。このとき \[ \frac{dx}{dy} = \cos y \] であり、逆関数を使って元の関数を微分すれば \[ \frac{dy}{dx} = \frac{1}{\;\dfrac{dx}{dy}\;} = \frac{1}{\cos y} \] が分かる。さらに \[ \cos y = \sqrt{1-\sin^{2} y}=\sqrt{1-x^{2}} \] より \[ \frac{dy}{dx} = \frac{1}{\sqrt{1-x^{2}}} \] という意外な結果が得られる。
\(\text{(2)}\) \(y = \cos^{3} \theta\)
この式は \(y=(\cos \theta)^{3}\) を表す。
\(\cos \theta = v\) とすれば \(y = v^{3}\) および \(\dfrac{dy}{dv} = 3v^{2}\) が成り立つ。ここから \[ \begin{aligned} \frac{dv}{d\theta} &= -\sin\theta \\ \frac{dy}{d\theta} &= \frac{dy}{dv} \times \frac{dv}{d\theta} = -3 \cos^{2} \theta \sin\theta \end{aligned} \] が分かる。
\(\text{(3)}\) \(y = \sin(x + a)\)
\(x + a = v\) とすれば \(y = \sin v\) だから \[ \frac{dy}{dv}=\cos v, \qquad \frac{dv}{dx}=1, \quad \frac{dy}{dx}=\cos(x+a) \] を得る。
\(\text{(4)}\) \(y=\log_e \sin \theta\)
\(\sin\theta=v\) とすれば \(y=\log_e v\) であり、次が分かる: \[ \begin{aligned} \frac{dy}{dv} &= \frac{1}{v},\quad \frac{dv}{d\theta}=\cos\theta, \\ \frac{dy}{d\theta} &= \frac{1}{\sin\theta} \times \cos\theta = \cot\theta \end{aligned} \]
\(\text{(5)}\) \(y = \cot\theta = \dfrac{\cos\theta}{\sin\theta}\) \[ \begin{aligned} \frac{dy}{d\theta} & = \frac{-\sin^{2}\theta - \cos^{2} \theta}{\sin^{2} \theta} \\ & = -(1+\cot^{2} \theta) \\ & = -\cosec^{2} \theta \end{aligned} \]
\(\text{(6)}\) \(y=\tan 3\theta\)
\(3\theta = v\) とすれば \(y = \tan v\) と \(\dfrac{dy}{dv}=\sec^{2} v\) が成り立つ。ここから \[ \frac{dv}{d\theta}=3, \quad \frac{dy}{d\theta}=3 \sec^{2} 3\theta \] が分かる。
\(\text{(7)}\) \(y = \sqrt{1+3\tan^{2}\theta}\)
この式は \(y=(1+3 \tan^{2} \theta)^{\frac{1}{2}}\) に等しい。\(3 \tan^{2}\theta=v\) とすれば \[ \begin{aligned} y &= (1+v)^{\frac{1}{2}},\quad \frac{dy}{dv} = \frac{1}{2\sqrt{1+v}}, \\ \frac{dv}{d\theta} &= 6\tan\theta \sec^{2} \theta \\ \end{aligned} \] が分かる。\(v = 3\tan^{2}\theta\) の微分では、\(\tan \theta = u\) とすれば \[ v = 3u^{2};\quad \frac{dv}{du} = 6u,\quad \frac{du}{d\theta} = \sec^{2} \theta \] となることを利用する。ここから \[ \frac{dv}{d\theta} = 6 (\tan \theta \sec^{2} \theta) \] が分かり、最終的な結果 \[ \frac{dy}{d\theta} = \frac{6\tan\theta \sec^{2}\theta}{2\sqrt{1 + 3\tan^{2}\theta}} \] が得られる。
\(\text{(8)}\) \(y = \sin x \cos x\) \[ \begin{aligned} \frac{dy}{dx} &= \sin x(-\sin x) + \cos x \times \cos x \\ &= \cos^{2} x - \sin^{2} x \end{aligned} \]
練習問題 XIV
解答はここにある。
\(\text{(1)}\) 次の関数を微分せよ: \[ \begin{aligned} \text{(i)} && y &= A \sin\left(\theta - \frac{\pi}{2}\right) \\ \text{(ii)} && y &= \sin^{2} \theta, \quad y = \sin 2\theta \\ \text{(iii)} && y &= \sin^{3} \theta, \quad y = \sin 3\theta \end{aligned} \]
\(\text{(2)}\) \(\sin\theta \times \cos\theta\) が極大となる \(\theta\) を求めよ。
\(\text{(3)}\) \(y = \dfrac{1}{2\pi} \cos 2\pi nt\) を微分せよ。
\(\text{(4)}\) \(y = \sin a^x\) に対する \(\dfrac{dy}{dx}\) を求めよ。
\(\text{(5)}\) \(y = \log_e \cos x\) を微分せよ。
\(\text{(6)}\) \(y=18.2 \sin(x+26^{\circ})\) を微分せよ。
\(\text{(7)}\) 曲線 \(y = 100 \sin(\theta-15^{\circ})\) をプロットせよ。\(\theta = 75^{\circ}\) における曲線の傾きが最大値の半分だと示せ。
\(\text{(8)}\) \(y = \sin \theta\cdot\sin 2\theta\) とする。\(\dfrac{dy}{d\theta}\) を求めよ。
\(\text{(9)}\) \(y=a\cdot\tan^m(\theta^n)\) とする。\(\theta\) に関する \(y\) の微分係数を求めよ。
\(\text{(10)}\) \(y = e^x \sin^{2} x\) を微分せよ。
\(\text{(11)}\) 練習問題 XIII の問題 4 にある三つの関数を微分し、微分係数を比較せよ。\(x\) が小さいとき、\(x\) が非常に大きいとき、\(x\) が \(30\) 程度のときのそれぞれについて、微分係数が等しいか、ほぼ等しいか、全く異なるかを答えよ。
\(\text{(12)}\) 次の式を微分せよ: \[ \begin{aligned} \text{(i)}\quad y &= \sec x & \text{(ii)}\quad y &= \arccos x \\ \text{(iii)}\quad y &= \arctan x & \text{(iv)}\quad y &= \operatorname{arcsec} x \\ \text{(v)}\quad y &= \tan x \times \sqrt{3 \sec x} && \end{aligned} \]
\(\text{(13)}\) \(y = \sin(2\theta + 3)^{2.3}\) を微分せよ。
\(\text{(14)}\) \(y=\theta^{3}+3 \sin(\theta+3)-3^{\sin \theta} - 3^\theta\) を微分せよ。
\(\text{(15)}\) \(y=\theta \cos \theta\) の極大値または極小値を求めよ。