VI. 和・差・積・商の微分
ここまでで \(x^{2} + c\) や \(ax^{4}\) といった簡単な代数関数を微分する方法を学んだ。次に取り組むのは二つ以上の関数の和を微分する方法である。
例えば \[ y = (x^{2}+c) + (ax^{4}+b) \] のとき、\(\dfrac{dy}{dx}\) はどうなるだろうか? この新しい種類の問題にどう取り掛かるべきだろうか?
この問題は非常に簡単である: それぞれの関数を個別に微分すれば答が得られる。つまり \[ \dfrac{dy}{dx} = 2x + 4ax^{3} \ \cdots \ \textbf{\small (答)} \] となる。
この正しさを少しでも疑問に思うなら、より一般的な場合を第一原理から計算しなけらばならない。その方法をここに示す。
\(y = u + v\) とする。\(u\) は適当な \(x\) の関数で、\(v\) も適当な \(x\) の関数である。このとき \(x\) が \(x + dx\) に増加すると \(y\) は \(y + dy\) に増加し、\(u\) は \(u + du\) に、\(v\) は \(v + dv\) に増加する。ここから \[ y+dy = u+du + v+dv \] が分かる。元の等式 \(y = u + v\) を引けば \[ dy = du+dv \] となる。両辺を \(dx\) で割れば次を得る: \[ \dfrac{dy}{dx} = \dfrac{du}{dx} + \dfrac{dv}{dx} \]
これで考えていた手続きの正しさが分かる。関数の和を微分するには、関数をそれぞれ個別に微分し、その結果を足せばよい。本章の最初に示した例にこの手続きを適用すれば \[ \begin{aligned} \frac{dy}{dx} & = \frac{d(x^{2}+c)}{dx} + \frac{d(ax^{4}+b)}{dx} \\ & = 2x + 4ax^{3}&& \end{aligned} \] となって予告通りの結果が得られる (前に説明した記法を使った)。
\(x\) の関数が \(u,\ \) \(v,\ \) \(w\) の三つで \[ y = u+v+w \] なら、次の関係が成り立つ: \[ \frac{dy}{dx} = \frac{du}{dx} + \frac{dv}{dx} + \frac{dw}{dx} \]
差の微分については簡単に分かる。考えている関数 \(v\) にマイナスが付いているなら、その微分係数にもマイナスが付く。つまり \[ y = u - v \] を微分すれば \[ \frac{dy}{dx} = \frac{du}{dx} - \frac{dv}{dx} \] となる。
一方で積の微分の問題はそう簡単にはいかない。次の関数を微分せよと言われたとしよう: \[ y = (x^{2}+c) \times (ax^{4}+b) \] どうすればよいだろうか? 結果が \(2x \times 4ax^{3}\) でないことは確かである。これは \(c \times ax^{4}\) と \(x^{2} \times b\) を考えに入れていない。
この問題を解く方法は二つある。
一つ目の方法: 積を最初に求め、展開してから微分する。
まず \(x^{2} + c\) と \(ax^{4} + b\) を掛けて \(ax^{6} + acx^{4} + bx^{2} + bc\) を得る。これを微分すれば答が求まる: \[ \dfrac{dy}{dx} = 6ax^{5} + 4acx^{3} + 2bx \]
二つ目の方法: 第一原理に戻って \[ y = u \times v \] を考える。\(u\) は \(x\) の関数で、\(v\) も \(x\) の関数とする。\(x\) が \(x + dx\) に増加すると、\(y\) は \(y + dx\) に、\(u\) は \(u + du\) に、\(v\) は \(v + dv\) になり、次の等式が成り立つ: \[ \begin{aligned} y + dy &= (u + du) \times (v + dv) \\ &= u \cdot v + u \cdot dv + v \cdot du + du \cdot dv \end{aligned} \] \(du \cdot dv\) は二次の微小量だから、\(dx\) の極限を考えるときには無視できる。よって \[ y + dy = u \cdot v + u \cdot dv + v \cdot du \] となる。さらに元の等式 \(y = y \cdot v\) を引けば \[ dy = u \cdot dv + v \cdot du \] を得る。最後に両辺を \(dx\) で割れば結果が得られる: \[ \dfrac{dy}{dx} = u\, \dfrac{dv}{dx} + v\, \dfrac{du}{dx} \]
この結果から微分の手順が得られる: 二つの関数の積を微分するには、それぞれの関数をもう一方の微分係数と掛け、その二つの積を足す。
この手続きはこう言い換えることもできる。まず \(u\) を定数とみなして \(v\) を微分し、次に \(v\) を定数とみなして \(v\) を微分する。こうして得られる二つの項の和が全体の微分係数 \(\dfrac{dy}{dx}\) となる。
ではこの規則を先ほどの例に適用しよう。微分する式は \[ (x^{2} + c) \times (ax^{4} + b) \] だから、\((x^{2} + c) = u\) そして \((ax^{4} + b) = v\) とする。
このとき、ちょうどいま示した一般的な規則から \[ \begin{alignedat}{2} \dfrac{dy}{dx} &= (x^{2} + c)\, \frac{d(ax^{4} + b)}{dx} &&+ (ax^{4} + b)\, \frac{d(x^{2} + c)}{dx} \\ &= (x^{2} + c)\, 4ax^{3} &&+ (ax^{4} + b)\, 2x \\ &= 4ax^{5} + 4acx^{3} &&+ 2ax^{5} + 2bx \\ &= 6ax^{5} + 4acx^{3} &&+ 2bx \end{alignedat} \] が分かる。これは前に求めた結果と等しい。
最後に商の微分を考える。
例として \(y = \dfrac{bx^{5} + c}{x^{2} + a}\) を考える。\(bx^{5} + c\) と \(x^{2} + a\) には共通因数が存在せず分子は分母で割り切れないので、最初に割り算を行うことはできない。そのため第一原理に戻って一般的な規則を見つけるのが唯一の選択肢となる。そこで \[ y = \frac{u}{v} \] とする。ここで \(u\) と \(v\) はどちらも独立変数 \(x\) の関数を表す。\(x\) が \(x + dx\) になるとき \(y\) は \(y + dy\) になり、\(u\) は \(u + du\) に、\(v\) は \(v + dv\) になる。そして \[ y + dy = \dfrac{u + du}{v + dv} \] が成り立つ。続いて多項式の割り算を行う。結果を次に示す:
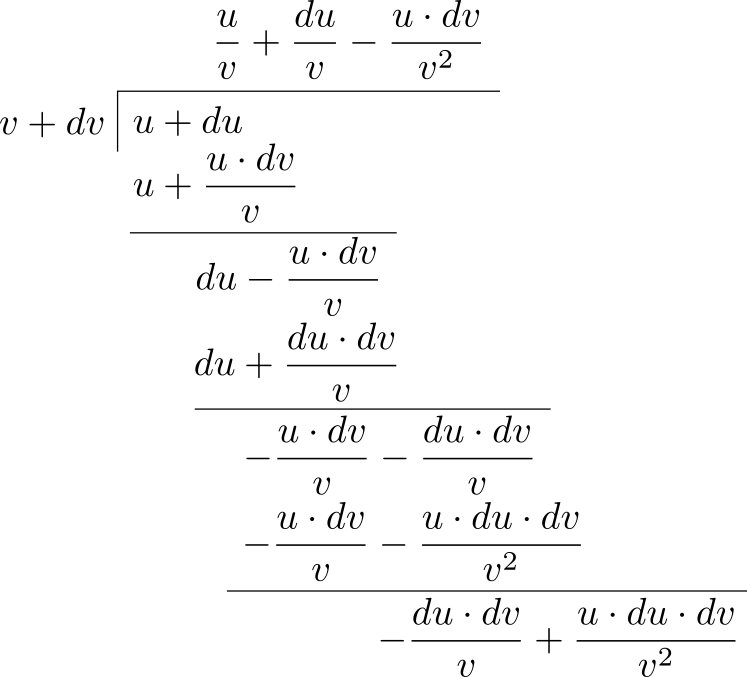
余りの項はどちらも二次の微小量なので、無視できる。さらにこれ以上割り算を進めてもこれより小さい値しか生じないので、割り算はここで終了する。
つまり \[ y + dy = \dfrac{u}{v} + \dfrac{du}{v} - \dfrac{u\cdot dv}{v^{2}} \] であり、これを書き換えれば \[ y + dy = \dfrac{u}{v} + \dfrac{v\cdot du - u\cdot dv}{v^{2}} \] となる。元の等式 \(y = \dfrac{u}{v}\) を引けば \[ dy = \dfrac{v\cdot du - u\cdot dv}{v^{2}} \] が残る。したがって次を得る: \[ \dfrac{dy}{dx} = \dfrac{v\, \dfrac{du}{dx} - u\, \dfrac{dv}{dx}}{v^{2}} \]
以上をまとめると二つの関数の商を微分する手順が得られる: 分母の微分係数に分子を掛け、分子の微分係数に分母を掛ける。前者から後者を引き、その結果を分子の二乗で割ると商の微分係数となる。
最初に示した例 \(y = \dfrac{bx^{5} + c}{x^{2} + a}\) に戻ろう。この場合 \[ bx^{5} + c = u, \quad x^{2} + a = v \] だから、 \[ \begin{aligned} \frac{dy}{dx} &= \frac{(x^{2} + a)\, \dfrac{d(bx^{5} + c)}{dx} - (bx^{5} + c)\, \dfrac{d(x^{2} + a)}{dx}}{(x^{2} + a)^{2}} \\ &= \frac{(x^{2} + a)(5bx^{4}) - (bx^{5} + c)(2x)}{(x^{2} + a)^{2}} \\ &= \frac{3bx^{6} + 5abx^{4} - 2cx}{(x^{2} + a)^{2}} \ \cdots \ \textbf{\small (答)} \end{aligned} \] となる。
商の微分は面倒な計算が必要になることが多いが、手順が分からないという意味で難しくなることはない。
解説付きの例をさらにいくつか示す。
\(\text{(1)}\) \(y = \dfrac{a}{b^{2}} x^{3} - \dfrac{a^{2}}{b} x + \dfrac{a^{2}}{b^{2}}\) を微分せよ。
\(\dfrac{a^{2}}{b^{2}}\) は定数だから、微分すると消える。よって \[ \frac{dy}{dx} = \frac{a}{b^{2}} \times 3 \times x^{3-1} - \frac{a^{2}}{b} \times 1 \times x^{1-1} \] となる。ここで \(x^{1-1} = x^{0} = 1\) だから、 \[ \frac{dy}{dx} = \frac{3a}{b^{2}} x^{2} - \frac{a^{2}}{b} \] が答となる。
\(\text{(2)}\) \(y = 2a\sqrt{bx^{3}} - \dfrac{3b \sqrt[3]{a}}{x} - 2\sqrt{ab}\) を微分せよ。
\(x\) の部分を指数を使った形に書き直すと \[ y = 2a\sqrt{b} x^{\frac{3}{2}} - 3b \sqrt[3]{a} x^{-1} - 2\sqrt{ab} \] となる。よって \[ \frac{dy}{dx} = 2a\sqrt{b} \times \frac{3}{2} \times x^{\frac{3}{2}-1} - 3b\sqrt[3]{a} \times (-1) \times x^{-1-1} \] つまり \[ \frac{dy}{dx} = 3a\sqrt{bx} + \frac{3b\sqrt[3]{a}}{x^{2}} \] である。
\(\text{(3)}\) \(z = 1.8 \sqrt[3]{\dfrac{1}{\theta^{2}}} - \dfrac{4.4}{\sqrt[5]{\theta}} - 27^{\circ}\) を微分せよ。
与えられた式は \(z= 1.8\, \theta^{-\frac{2}{3}} - 4.4\, \theta^{-\frac{1}{5}} - 27^{\circ}\) と書ける。
微分すると \(27^{\circ}\) は消えて、 \[ \frac{dz}{d\theta} = 1.8 \times -\frac{2}{3} \times \theta^{-\frac{2}{3}-1} - 4.4 \times \left(-\frac{1}{5}\right)\theta^{-\frac{1}{5}-1} \] となる。これをさらに変形すれば次を得る: \[ \frac{dz}{d\theta} = -1.2\, \theta^{-\frac{5}{3}} + 0.88\, \theta^{-\frac{6}{5}} = \frac{0.88}{\sqrt[5]{\theta^{6}}} - \frac{1.2}{\sqrt[3]{\theta^{5}}} \]
\(\text{(4)}\) \(v = (3t^{2} - 1.2 t + 1)^{3}\) を微分せよ。
この式を直接微分する方法を第九章で説明するが、今までの知識を使っても微分できる。
三乗を展開すると \[ v = 27t^{6} - 32.4t^{5} + 39.96t^{4} - 23.328t^{3} - 13.32t^{2} - 3.6t + 1 \] となり、ここから \[ \frac{dv}{dt} = 162t^{5} - 162t^{4} + 159.84t^{3} - 69.984t^{2} + 26.64t - 3.6 \] が分かる。
\(\text{(5)}\) \(y = (2x - 3)(x + 1)^{2}\) を微分せよ。
\[ \begin{aligned} \frac{dy}{dx} &= (2x - 3)\, \frac{d\left[(x + 1)(x + 1)\right]}{dx} + (x + 1)^{2}\, \frac{d(2x - 3)}{dx} \\ &= (2x - 3) \left[(x + 1)\, \frac{d(x + 1)}{dx}\right. + \left.(x + 1)\, \frac{d(x + 1)}{dx}\right] \\ &\quad + (x + 1)^{2}\, \frac{d(2x - 3)}{dx} \\ & = 2(x + 1)\left[(2x - 3) + (x + 1)\right] \\ & = 2(x + 1)(3x - 2) \end{aligned} \] あるいはもっと単純に、積を計算してから微分してもよい。
\(\text{(6)}\) \(y = 0.5 x^{3}(x-3)\) を微分せよ。
\[ \begin{aligned} \frac{dy}{dx} &= 0.5\left[x^{3} \frac{d(x-3)}{dx} + (x-3) \frac{d(x^{3})}{dx}\right] \\ &= 0.5\left[x^{3} + (x-3) \times 3x^{2}\right] = 2x^{3} - 4.5x^{2} \end{aligned} \] 前問と同じことがこの問題でも言える。
\(\text{(7)}\) \(w = \left(\theta + \dfrac{1}{\theta}\right) \left(\sqrt{\theta} + \dfrac{1}{\sqrt{\theta}}\right)\) を微分せよ。
与えられた式を変形すると \[ w = (\theta + \theta^{-1})(\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}}) \] となる。よって \[ \begin{aligned} \frac{dw}{d\theta} &= (\theta + \theta^{-1}) \frac{d(\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}})}{d\theta} + (\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}}) \frac{d(\theta+\theta^{-1})}{d\theta} \\ &= (\theta + \theta^{-1})\left(\frac{1}{2}\theta^{-\frac{1}{2}} - \frac{1}{2}\theta^{-\frac{3}{2}}\right) + (\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}})(1 - \theta^{-2}) \\ &= \frac{1}{2}(\theta^{ \frac{1}{2}} + \theta^{-\frac{3}{2}} - \theta^{-\frac{1}{2}} - \theta^{-\frac{5}{2}}) + (\theta^{ \frac{1}{2}} + \theta^{-\frac{1}{2}} - \theta^{-\frac{3}{2}} - \theta^{-\frac{5}{2}}) \\ &= \frac{3}{2} \left(\sqrt{\theta} - \frac{1}{\sqrt{\theta^{5}}}\right) + \frac{1}{2} \left(\frac{1}{\sqrt{\theta}} - \frac{1}{\sqrt{\theta^{3}}}\right) \end{aligned} \] が分かる。
ここでも二つの因数の積を先に求めてから微分をしたほうが簡単に微分を求められる。ただし積を最初に計算する方法が常に使えるとは限らない。例えば 第十六章の例 (8) では、積の微分規則を必ず使わなければならない。
\(\text{(8)}\) \(y =\dfrac{a}{1 + a\sqrt{x} + a^{2}x}\) を微分せよ。
\[ \begin{aligned} \frac{dy}{dx} &= \frac{(1 + ax^{\frac{1}{2}} + a^{2}x) \times 0 - a\dfrac{d(1 + ax^{\frac{1}{2}} + a^{2}x)}{dx}} {(1 + a\sqrt{x} + a^{2}x)^{2}} \\ &= - \frac{a(\frac{1}{2}ax^{-\frac{1}{2}} + a^{2})} {(1 + ax^{\frac{1}{2}} + a^{2}x)^{2}} \end{aligned} \]
\(\text{(9)}\) \(y = \dfrac{x^{2}}{x^{2} + 1}\) を微分せよ。
\[ \dfrac{dy}{dx} = \dfrac{(x^{2} + 1)\, 2x - x^{2} \times 2x}{(x^{2} + 1)^{2}} = \dfrac{2x}{(x^{2} + 1)^{2}} \]
\(\text{(10)}\) \(y = \dfrac{a + \sqrt{x}}{a - \sqrt{x}}\) を微分せよ。
指数を使った形に書き直せば \(y = \dfrac{a + x^{\frac{1}{2}}}{a - x^{\frac{1}{2}}}\) だから \[ \begin{aligned} \frac{dy}{dx} & = \frac{(a - x^{\frac{1}{2}})( \frac{1}{2} x^{-\frac{1}{2}}) - (a + x^{\frac{1}{2}})(-\frac{1}{2} x^{-\frac{1}{2}})} {(a - x^{\frac{1}{2}})^{2}} \\ & = \frac{ a - x^{\frac{1}{2}} + a + x^{\frac{1}{2}}} {2(a - x^{\frac{1}{2}})^{2}\, x^{\frac{1}{2}}} \\ & = \frac{a}{(a - \sqrt{x})^{2}\, \sqrt{x}} \end{aligned} \] となる。
\(\text{(11)}\) \(\theta = \dfrac{1 - a \sqrt[3]{t^{2}}}{1 + a \sqrt[2]{t^{3}}}\) を微分せよ。
与えられた式は \(\theta = \dfrac{1 - at^{\frac{2}{3}}}{1 + at^{\frac{3}{2}}}\) である。よって \[ \begin{aligned} \frac{d\theta}{dt} &= \frac{(1 + at^{\frac{3}{2}}) (-\frac{2}{3} at^{-\frac{1}{3}}) - (1 - at^{\frac{2}{3}}) \times \frac{3}{2} at^{\frac{1}{2}}} {(1 + at^{\frac{3}{2}})^{2}} \\ &= \frac{5a^{2} \sqrt[6]{t^{7}} - \dfrac{4a}{\sqrt[3]{t}} - 9a \sqrt[2]{t}} {6(1 + a \sqrt[2]{t^{3}})^{2}} \end{aligned} \] が分かる。
\(\text{(12)}\) 錐台を逆さにした形の容器がある。底面は一辺の長さが \(200\) フィートの正方形で、側面と垂直方向の角度は \(45^{\circ}\) である。水深が \(1\) フィート変化したときの水量の変化量を表す式を求めよ。その式を使って、\(24\) 時間で水深が \(14\) フィートから \(10\) フィートに変化したときの一時間当たりの水量の変化量を (ガロンで) 求めよ1。
錐台の上下の底面の面積を \(A,\ \) \(a\) として、高さを \(H\) とする。このとき錐台の体積 \(V\) は \(V = \dfrac{H}{3} (A + a + \sqrt{Aa} )\) と表せる。容器の側面の傾きが \(45^{\circ}\) だから、水深が \(h\) のとき、水面の正方形の一辺の長さは \(200 + 2h\) となる。よってそのときの水量は \[ \dfrac{h}{3} [200^{2} + (200 + 2h)^{2} + 200(200 + 2h)] = 40{,}000h + 400h^{2} + \dfrac{4h^{3}}{3} \] である。よって水深が \(1\) フィート変化するごとに体積は \(\dfrac{dV}{dh} = 40{,}000 + 800h + 4h^{2}\) 立方フィートだけ変化する。\(14\) フィートと \(10\) フィートの平均は \(12\) フィートだから、\(h = 12\) として \(\dfrac{dV}{dh} = 50{,}176\) 立方フィートを得る。
この水深 \(4\) フィート分の変化が \(24\) 時間で起こったなら、一時間当たりの水量の変化量は \(\dfrac{4 \times 50{,}176 \times 6.25}{24} = 52{,}267\) ガロンとなる。
\(\text{(13)}\) デュロン2は温度 \(t^{\circ}\text{\small C}\) の飽和蒸気の絶対圧 \(P\) が \(P = \left( \dfrac{40 + t}{140} \right)^{5}\) 気圧と表せることを発見した (\(t\) は \(80^{\circ}\text{\small C}\) より大きいとする)。\(100^{\circ}\text{\small C}\) における圧力の変化率を求めよ。
二項定理を使って分子を展開すると \[ P = \frac{1}{140^{5}} (40^{5} + 5×40^{4} t + 10 \times 40^{3} t^{2} + 10 \times 40^{2} t^{3} + 5 \times 40t^{4} + t^{5}) \] となり、ここから \[ \dfrac{dP}{dt} = \dfrac{1}{537{,}824 \times 10^{5}} (5 \times 40^{4} + 20 \times 40^{3} t + 30 \times 40^{2} t^{2} + 20 \times 40t^{3} + 5t^{4}) \] が分かる。この式で \(t = 100\) とすれば、摂氏温度の変化 \(1\) 度あたりの気圧の変化が \(0.036\) 気圧だと分かる。
練習問題 III
解答はここにある。
\(\text{(1)}\) 次の関数を微分せよ:
\(\text{(2)}\) \(w = at - \dfrac{1}{2}bt^{2}\) とする。\(\dfrac{dw}{dt}\) を求めよ。
\(\text{(3)}\) 次の関数の微分係数を求めよ: \[ y = (x + \sqrt{-1}) \times (x - \sqrt{-1}) \]
\(\text{(4)}\) 次の関数を微分せよ: \[ y = (197x - 34x^{2}) \times (7 + 22x - 83x^{3}) \]
\(\text{(5)}\) \(x = (y + 3) \times (y + 5)\) とする。\(\dfrac{dx}{dy}\) を求めよ。
\(\text{(6)}\) \(y = 1.3709x \times (112.6 + 45.202x^{2})\) を微分せよ。
次の関数の微分係数を求めよ:
\(\text{(11)}\) 白熱電球のフィラメントの温度 \(t\) と電球に流れる電流 \(C\) の間には次の関係がある: \[ C = a + bt + ct^{2} \] 温度の変化に対する電流の変化を与える式を求めよ。
\(\text{(12)}\) 電線の電気抵抗 \(R\) と温度 \(t\) の間の関係として、次の式が提案されている。温度 \(0^{\circ}\text{\small C}\) における電気抵抗を \(R_{0}\) として、\(a,\ \) \(b,\ \) \(c\) は定数を表す。 \[ \begin{aligned} R &= R_0(1 + at + bt^{2}) \\ R &= R_0(1 + at + b\sqrt{t}) \\ R &= R_0(1 + at + bt^{2})^{-1} \end{aligned} \] それぞれの式について、温度を変化させたときの電気抵抗の変化率を求めよ。
\(\text{(13)}\) ある種類の電池の起電力 \(E\) は、温度 \(t\) に応じて次のように変化することが分かった: \[ E = 1.4340 \bigl[1 - 0.000814(t-15) + 0.000007(t-15)^{2}\bigr] \, {\footnotesize\text{ボルト}} \] \(15^{\circ}\text{\small C},\ \) \(20^{\circ}\text{\small C},\ \) \(25^{\circ}\text{\small C}\) における \(1^{\circ}\text{\small C}\) 当たりの起電力の変化をそれぞれ求めよ。
\(\text{(14)}\) \(i\) の電流が流れる長さ \(l\) のアーク放電を保持するのに必要な起電力 \(E\) を表す次の式は、エアトン女史3によって発見された: \[ E = a + bl + \frac{c + kl}{i} \] \(a,\ \) \(b,\ \) \(c,\ \) \(d\) は定数である。アークの長さおよび電流の大きさに対する起電力の変化を表す式をそれぞれ求めよ。