II. 微小量の次元
これから微積分では、小さな量 (微小量) であって小ささの次元が違うものを扱う必要がある。
また小さな量をあまりにも小さいという理由で無視できるのはどんな状況かも理解する必要がある。全ては相対的な小ささにかかっている。
一般的な規則を示す前に、身近な例を考えよう。一時間は \(60\) 分であり、一日は \(24\) 時間、一週間は \(7\) 日である。よって一日は \(1440\) 分で、一週間は \(10080\) 分となる。
明らかに、一週間全体と比較した一分は非常に小さい。そもそも私たちの先祖は一時間と比べたときにこの時間が非常に小さいということで、一時間の小さな部分 (具体的には六十分の一) を「分 (minute)」と呼んだのだった1。彼らは時間をもっと小さく分ける必要が生じたとき一分をさらに \(60\) 個に分け、それをエリザベス女王の時代には「第二の分 (second minute)」と呼んだ (つまりこの時間の単位は二次の小ささを持つ)。この二次の小ささを持つ時間の長さを現在の私たちは「秒 (second)」と呼んでいる2。しかしそう呼ばれている理由を知っている人は少ない。
一日と比べれば一分でさえ小さいのだから、一日と比べた一秒はなんと小さいことか!
別の例として、ソブリンと比較したときのファージングを考えよう3。\(1\) ソブリンは \(1\) ファージングの \(\frac{1}{1000}\) の価値しかない。ソブリンと比べれば、ファージングはほんの少しの価値しかないと言えるだろう。つまり \(1\) ファージングは小さい量である。しかしファージングを \(1000\) ポンドと比べたらどうだろうか。\(1000\) ポンドという大きな金額と比較したときの \(1\) ファージングは、\(1\) ソブリンと比較したときの \(\frac{1}{1000}\) ファージングと同じ価値しか持たない。大富豪にとっては金のソブリンさえ取るに足らない量に過ぎない。
「比較的小さい」とみなす部分への分割比率を適当に固定すれば、異なる小ささの次元を持つ分割を簡単に作ることができる。例えば時間を考えるときには \(\frac{1}{60}\) が小さい部分となるなので、\(\frac{1}{60}\) の \(\frac{1}{60}\) (小さい部分の小さい部分) が二次の小ささを持つ小さい量 (二次の微小量) となる4。
あるいは \(\frac{1}{100}\) (\(1{\footnotesize \text{\%}}\)) を小さい部分の比率として選んだとすれば、\(\frac{1}{10000}\) (\(1{\footnotesize \text{\%}}\) の \(1{\footnotesize \text{\%}}\)) が二次の微小量となる。また \(1{\footnotesize \text{\%}}\) の \(1{\footnotesize \text{\%}}\) の \(1{\footnotesize \text{\%}}\) は \(\frac{1}{1000000}\) だから、\(\frac{1}{1000000}\) は三次の微小量となる。
最後に非常に細かい分割が必要で、\(\frac{1}{1{,}000{,}000}\) が“小さい”とみなされる状況を考えよう。例えば最高級の時計は一年で三十秒もズレないから、\(1051200\) 分でズレが \(1\) 分以下となる精度で時を刻む必要がある。この場合は一次の微小量を \(\frac{1}{1{,}000{,}000}\) として、\(\frac{1}{1{,}000{,}000}\) の \(\frac{1}{1{,}000{,}000}\) つまり \(\frac{1}{1{,}000{,}000{,}000{,}000}\) を二次の微小量とみなすことになる。そして比較して考えているときには二次の小ささを持つ量を全く無視して構わない。
この例から分かるように、最初に考える小さい量が小さければ小さいほど、対応する二次の微小量が小さくなる。よって一次の小ささを十分小さく取れば、二次や三次の (そして三次より高次の) 微小量を無視できる。
しかし小さい数であっても、式の中で大きな数が掛けられると小さくなくなることがある点には気を付けなければならない。ファージングも数千を掛ければ大きな価値を持つ。
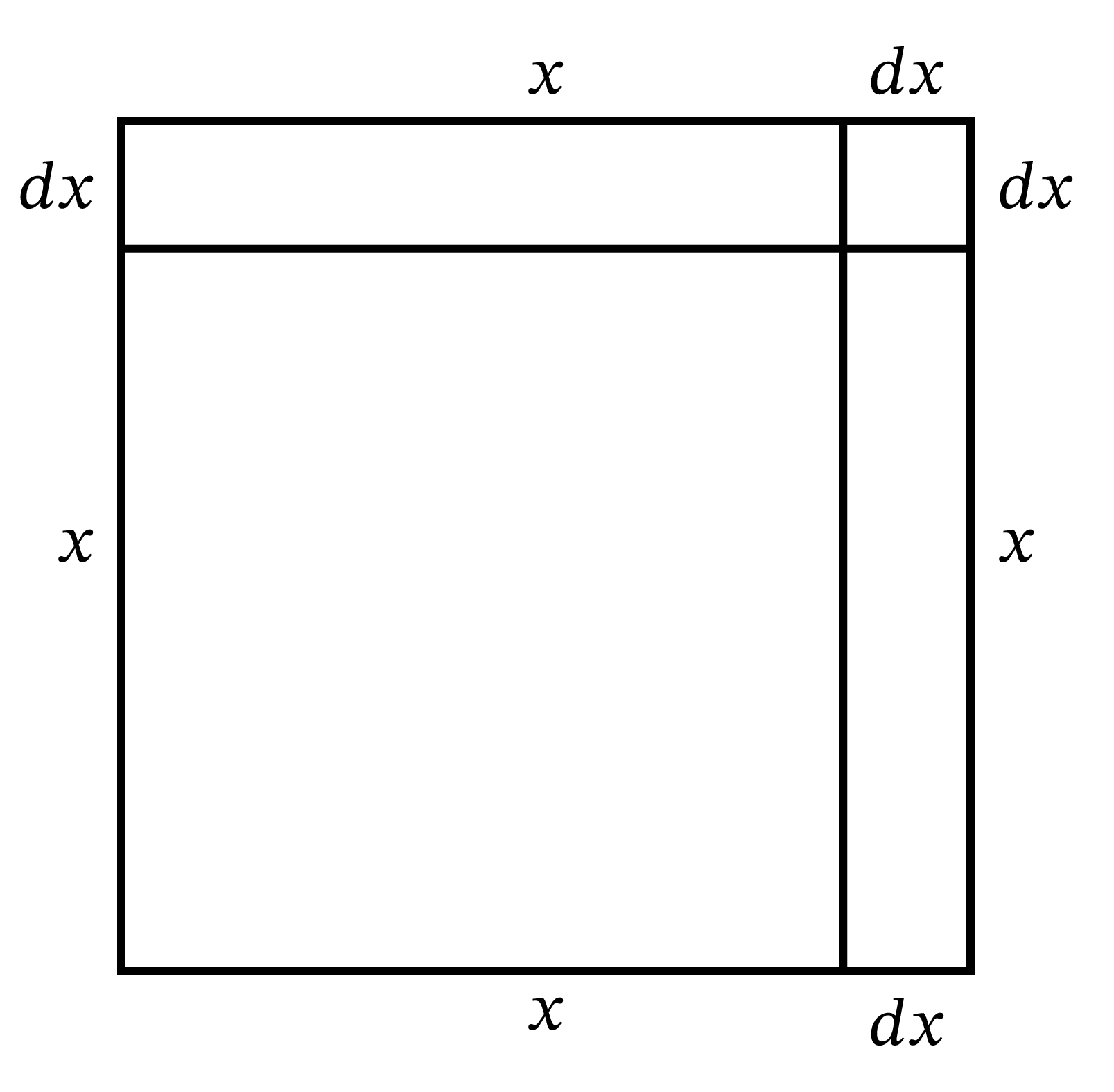
さて微積分では、\(dx\) で \(x\) の小さな部分を表す。\(dx,\ \) \(du,\ \) \(dy\) といった式を \(x,\ \) \(y,\ \) \(z\) の微分小 (differential) と呼ぶ (それぞれ「ディーエックス」「ディーユー」「ディーワイ」と読む)。\(dx\) が非常に小さい \(x\) の部分で \(x\) と比べたとき小さいとする。このとき \(x \cdot dx,\ \) \(x^2\, dx,\ \) \(a^x\, dx\) はどれも一次の微小量なので無視できないが、\(dx \times dx\) は二次の小ささをもつ量であり、無視できる。
非常に単純な例を使ってこれを説明しよう。
ある量 \(x\) が少しだけ増加して \(x + dx\) になったとする。ここで \(dx\) が増えた分の小さな量を表す。\(x + dx\) を二乗すると \(x^{2} + 2x \cdot dx + (dx)^{2}\) となる。二つ目の項 \(2x \cdot dx\) は一次の小ささを持つ量なので、無視することはできない。しかし三つ目の項 \((dx)^{2}\) は二次の小ささを持ち、\(x\) の小さな部分の小さな部分を表す。例えば \(dx\) が \(x\) の \(\frac{1}{60}\) の大きさなら二番目の項は \(x\) の \(\frac{2}{60}\) となり、三番目の項は \(x\) の \(\frac{1}{3600}\) となる。つまり最後の項は他の項よりもずっと小さい。もっと極端に \(dx\) が \(x\) の \(\frac{1}{1000}\) だとすれば、二番目の項は \(x^{2}\) の \(\frac{2}{1000}\) となり、三番目の項は \(x\) のわずか \(\frac{1}{1{,}000{,}000}\) となる。よって三番目の項は無視できる。
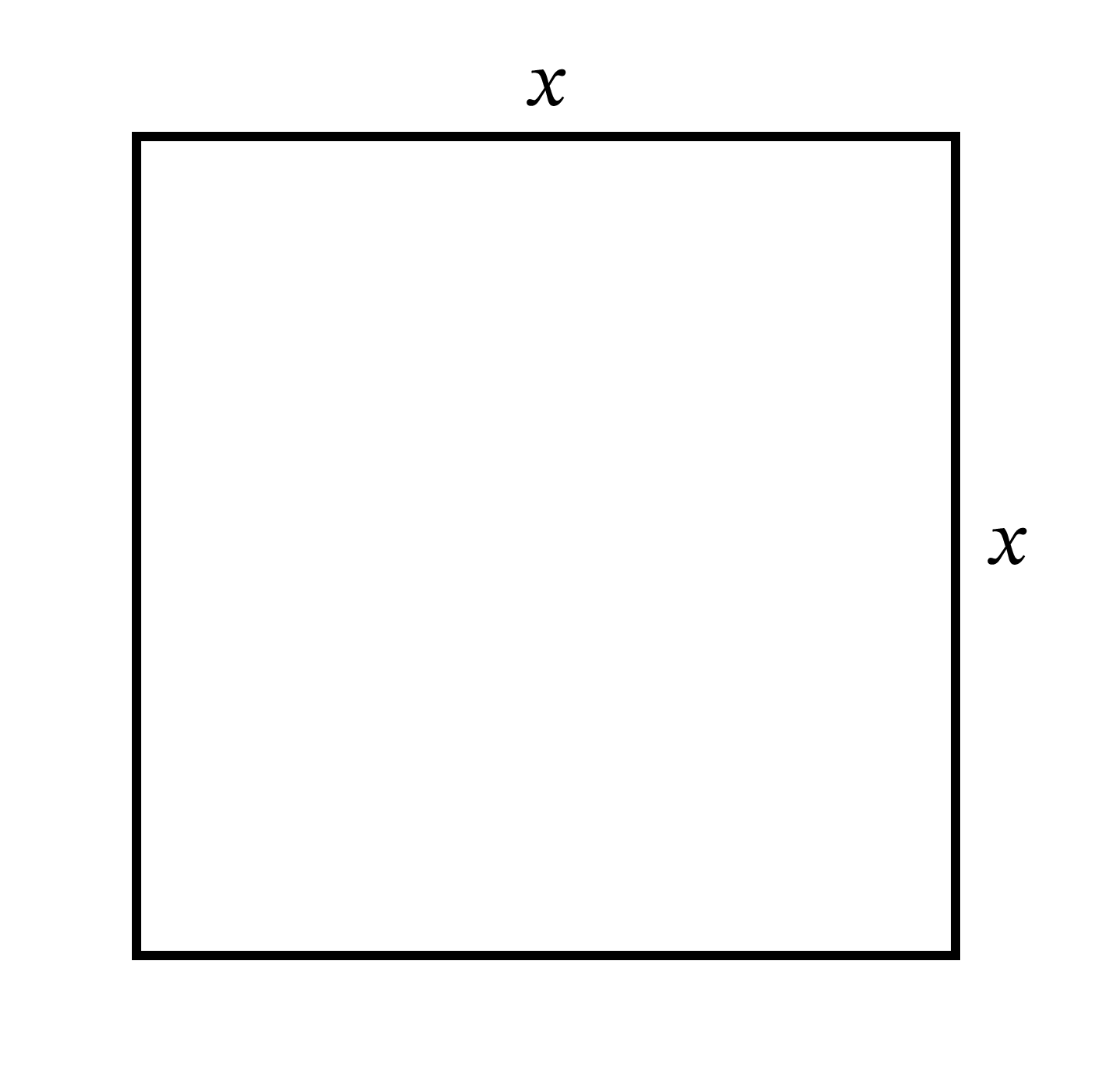
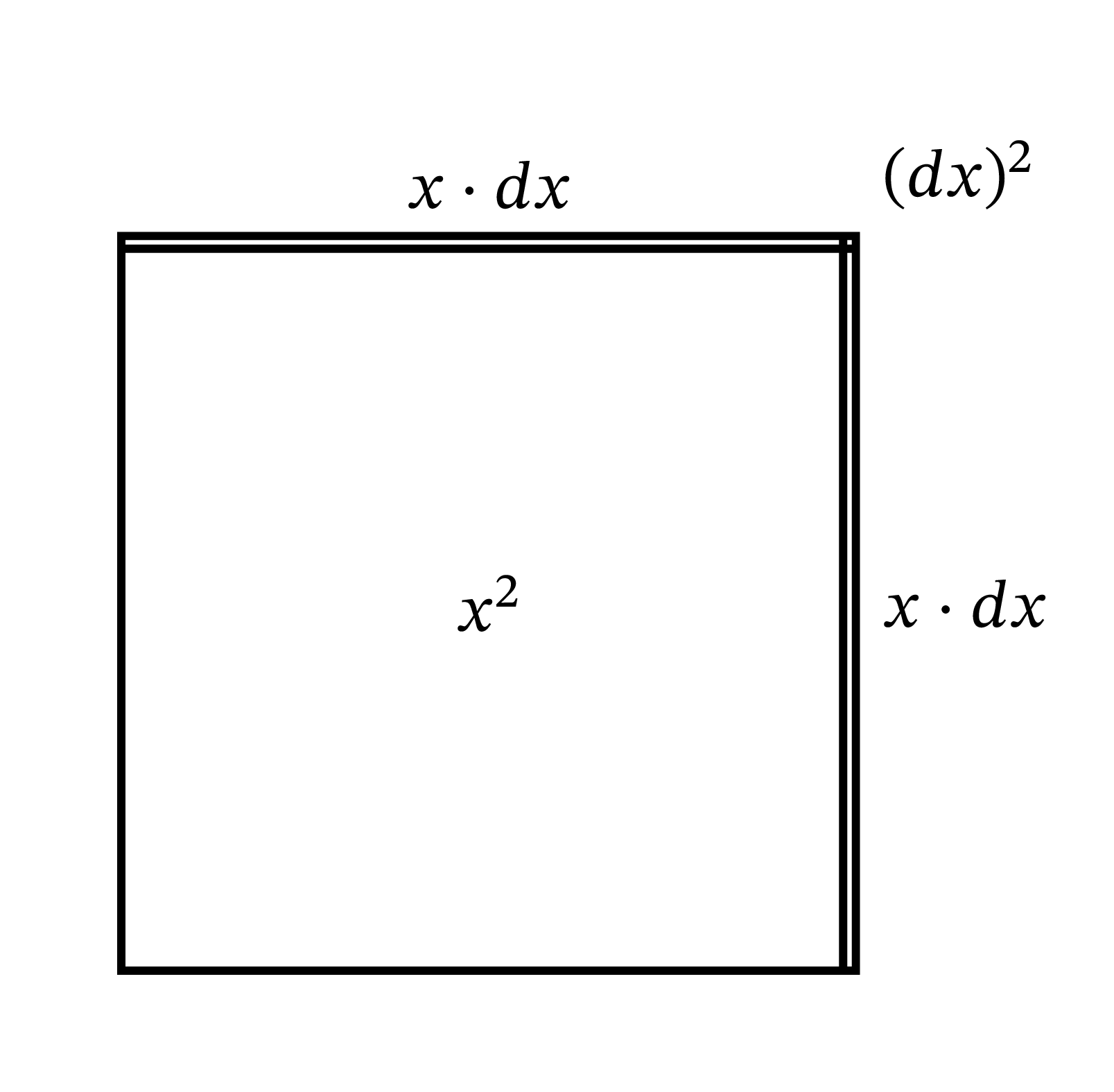
この事実は幾何学的にも説明できる。正方形を描き (図 1)、一辺の長さを \(x\) とおく。この正方形が両方向に \(dx\) だけ大きくなったとする。大きくなった後の正方形の面積は、元の正方形の面積 \(x^{2}\)、上と右にある二つの長方形の面積の和 \(2x \cdot dx\)、右上にある小さな正方形の面積 \((dx)^{2}\) からなる。図 2 では \(dx\) を \(x\) のかなり大きな部分として ──およそ \(\frac{1}{5}\) として── 取っている。この値を \(\frac{1}{100}\) ──鋭いペン先で書いた線の幅ほど── まで小さくしたところを想像してほしい。このとき右上の正方形の面積は \(x^{2}\) のわずか \(\frac{1}{10{,}000}\) に過ぎず、結果に全く影響しない。さらにこの例からは、増加量 \(dx\) が小さいときに限って \((dx)^{2}\) が無視できることも分かる。
別の比喩を使って説明しよう。
富豪が秘書に向かって「私に入ってくるお金の一定の割合を君に渡そう」と伝え、秘書も自分の息子に向かって同じように「私がもらったお金の一定の割合を君に渡そう」と伝えたとする。この割合がどちらも \(\frac{1}{100}\) だとすれば、富豪の収入が週に \(1000\) ポンドのとき、秘書は \(10\) ポンド、少年は \(2\) シリングもらうことになる。\(1000\) ポンドと比べると \(10\) ポンドは小さな金額だが、\(2\) シリングというのはさらに増して小さい金額であり、これは二次の微小量である。ではもし割合が \(\frac{1}{100}\) ではなくて \(\frac{1}{1000}\) になったら、この差はどうなるだろうか? このとき富豪が \(1000\) ポンドを得たとしても秘書は \(1\) ポンドしか得られず、少年にいたっては \(1\) ファージングも得ることができない!
優れた作家ディーン・スウィフトはかつてこう書いた5:
博物学者が観察するノミ、
その体を苦しめるもっと小さいノミがいる。
そのノミを噛むもっと小さいノミもいて、
これは無限に続くのみ。
牛は通常のサイズのノミ ──つまり一次の小ささを持つ生物── を気にするかもしれない。しかしノミに付いたノミを牛が気にすることはないだろう。全てのノミに付いている全てのノミを集めたとしても、牛にとってみれば何でもない量にしかならない。