XI. 極大値と極小値

微分という手続きの重要な応用の一つが、微分対象の関数が極大または極小となる条件の導出である。工学の問題ではコストを最小化する条件や効率を最大化する条件を知りたい場合が多いので、関数が極大または極小となる条件の導出方法は大きな価値を持つ。

最初は次の具体的な例から始めよう: \[ y = x^{2} - 4x + 7 \]

いくつかの \(x\) の値に対応する \(y\) の値を求めれば、この方程式が表す曲線に極小値が存在することが分かる: \[ \begin{array}{c|cccccc} x & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline y & 7 & 4 & 3 & 4 & 7 & 12 \\ \end{array} \]

この値をプロットした 図 26 からは、\(y\) が \(3\) で \(x\) が \(2\) のとき \(y\) が極小値となるようだと分かる。しかし \(y\) が極小値となる \(x\) が \(\dfrac{9}{4}\) でも \(\dfrac{7}{4}\) でもなく \(2\) であることは、どうすれば確信できるだろうか？

もちろん代数的な式であれば好きなだけ多く点を計算してプロットできるから、そうすれば極大値または極小値と思しき値がいずれ見つかる。

別の例を考えよう: \[ y = 3x - x^{2} \]

値をいくつか計算すると \[ \begin{array}{c|rrrrrrr} x & -1 & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline y & -4 & 0 & 2 & 2 & 0 & -4 & -10 \\ \end{array} \] となる。

この値をプロットした図を 図 27 に示す。

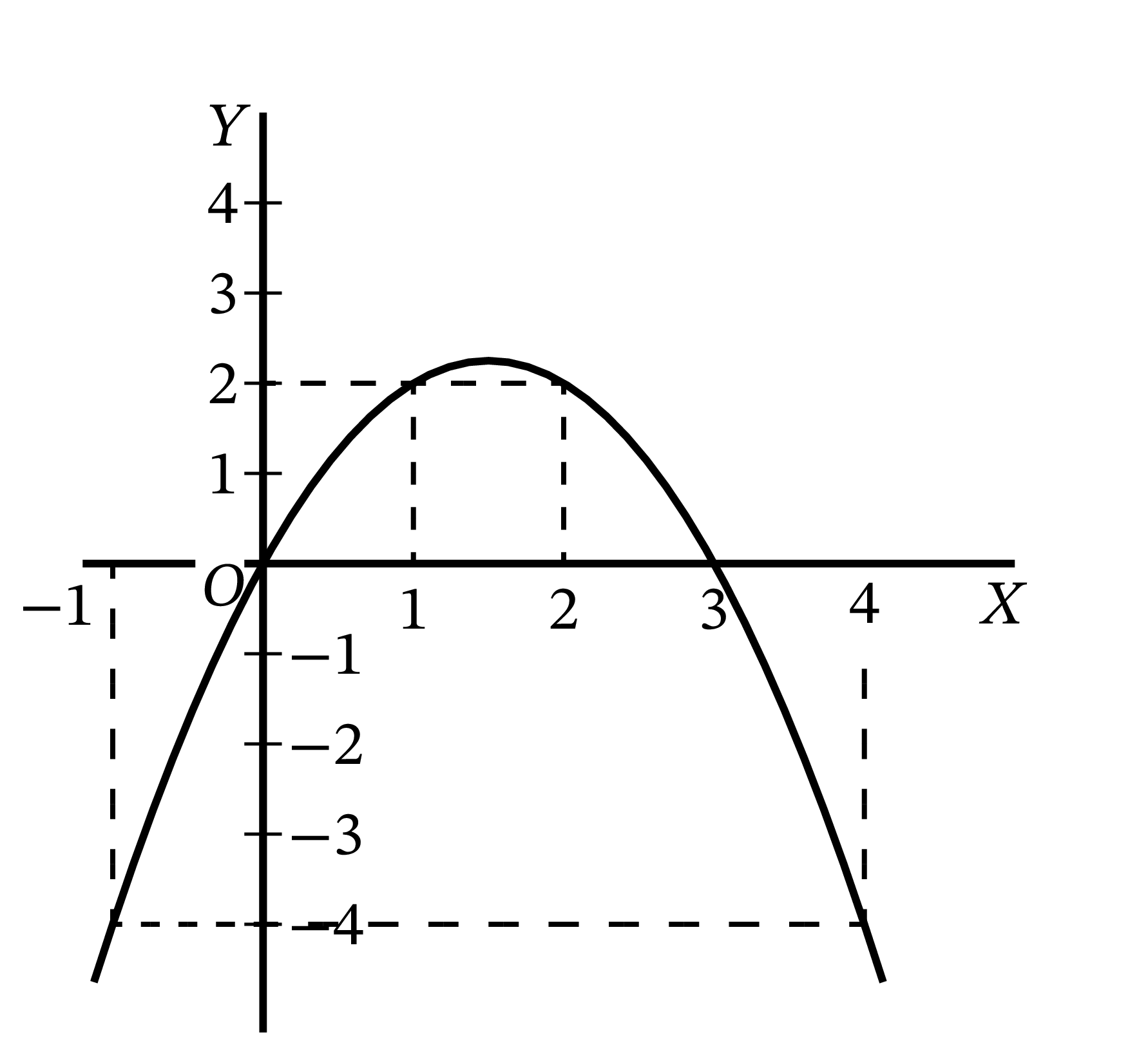
\(x = 1\) と \(x = 2\) の間に極大値 \(\dfrac{5}{2}\) があるように見えるが、ちょうどこの値が極大なのかは分からない。近くの値を試せば \(x = \dfrac{5}{4}\) なら \(y = 2.1875,\ \)\(x = \dfrac{3}{2}\) なら \(y = 2.25,\ \) \(x = 1.6\) なら \(y = 2.24\) となる。\(x = \dfrac{3}{2}\) に対応する \(y = 2.25\) が真の極大値であることはどうすれば確信できるだろうか？

極大値や極小値を事前に予想することなく求める方法が存在するなど眉唾な話に思えるかもしれない。その方法に関係するのが微分である。図 14 と 図 15 に関する説明で前に触れたように、曲線の高さが極大または極小となる点で \(\dfrac{dy}{dx} = 0\) が成り立つ。この事実が考えている手続きの手がかりとなる。目の前に方程式があり、\(y\) が極大値 (または極小値) となる \(x\) の値を求めたいとする。そのときはまず微分せよ、それから \(\dfrac{dy}{dx}\) を \(\bm{0}\) と等しいとせよ、そして方程式を \(\bm{x}\) について解け。こうして求まる \(x\) の値を元の方程式に代入すれば求めるべき \(y\) の値が得られる。この手続きは「 \(0\) と等号で結ぶ (equating to zero)」方法と呼ばれる。

この手続きの単純さを理解するために、この章の最初で示した次の例を考える: \[ y = x^{2} - 4x + 7 \] 方程式を微分すれば \[ \dfrac{dy}{dx} = 2x - 4 \] を得る。\(\dfrac{dy}{dx}\) を \(0\) と等号で結べば \[ 2x - 4 = 0 \] であり、この方程式を \(x\) について解けば \[ \begin{aligned} 2x &= 4 \\ x &= 2 \end{aligned} \] が分かる。これで極大値または極小値が起こるのが \(x = 2\) だと分かった。

元の方程式に \(x = 2\) を代入すれば \[ \begin{aligned} y &= 2^{2} - (4×2) + 7 \\ &= 4 - 8 + 7 \\ &= 3 \end{aligned} \] となる。

ここで 図 26 を見返せば、\(y\) は \(x = 2\) で極小値を取ると分かる。その極小値は \(y = 3\) である。

二番目の例を試してみよう (図 27)。考える方程式は \[ y = 3x - x^{2} \] であり、微分すれば \[ \frac{dy}{dx} = 3 - 2x \] となる。\(\dfrac{dy}{dx}\) を \(0\) と等号で結べば \[ 3 - 2x = 0 \] だから、ここから \[ x = \frac{3}{2} \] が分かる。この \(x\) を最初の方程式に代入すれば \[ \begin{aligned} y &= \frac{9}{2} - \left(\frac{3}{2} \times \frac{3}{2}\right) \\ &= \frac{9}{4} \end{aligned} \] となる。曲線上の点の座標をいくら求めても確かなことは分からなかった問題にも、この手続きを使えば正確な解答が得られる。

次の例に進む前に注意しておくべきことが二つある。まず \(\dfrac{dy}{dx}\) と \(0\) を等号で結べと言われたとき、(思慮深い読者は)そんなことをしていいのかと疑問に思ったかもしれない。曲線の傾きが上向きか下向きかに応じて \(\dfrac{dy}{dx}\) は異なる部分で異なる値を持つのに、突然 \[ \frac{dy}{dx} = 0 \] と書けと言われたからである。これは道理が通っておらず、正しいはずがないと不思議に思うことだろう。ここでは “方程式” と “条件を表す方程式” の違いを理解する必要がある。方程式を常に成り立つものだと思って扱うことも多いが、ときには必ず成り立つわけではなく、特定の条件が成り立つときに限って成り立つとして方程式を扱うこともある。そのような場合には最初に方程式を書いて、それから方程式を成り立たせる条件を見つけることになる。今の例では傾きが上向きでも下向きでもなくなる点の \(x\) 座標、つまり \(\dfrac{dx}{dy} = 0\) という条件を満たす \(x\) の値を探している。\(\dfrac{dy}{dx} = 0\) と書いたとしても、この等式は \(\dfrac{dy}{dx}\) が常に \(0\) と等しいとは主張していない。そうではなくて、\(\dfrac{dy}{dx}\) が \(0\) になるときの \(x\) の条件として等式を書いているのである。

二つ目の注意点は読者の多くが気付いているであろう次の点である: 先ほどから大きく宣伝されている「\(0\) と等号で結ぶ」この方法は、見つかった \(x\) が \(y\) の極大値と極小値のどちらを与えるのかを示さない。その通りである。これは間違っているということではない。求めるべき \(x\) はこの方法で見つかるが、対応する \(y\) が極大と極小のどちらなのかは自分で求める必要があるというだけである。もちろん曲線をプロットすればすぐに分かる。

例えば次の方程式を考えよう: \[ y = 4x + \frac{1}{x} \] この方程式が表す曲線を思い描く前に、まず微分して \(0\) と等号で結ぶ: \[ \frac{dy}{dx} = 4 - x^{-2} = 4 - \frac{1}{x^{2}} = 0 \] すると \[ x = \frac{1}{2} \] となる。これを元の方程式に代入すれば、 \[ y = 4 \] が極大値または極小値になると分かる。どちらだろうか？ 二次微分係数を使ってこれを判定する方法を第十一章で学ぶが、ここでは \(x = \dfrac{1}{2}\) から少し離れた \(x\) の値をいくつか試せば十分である。それらの値が \(y = 4\) と比べて小さいか大きいかを見ればよい。

極大値と極小値に関する簡単な問題をもう一つ示す。与えられた数を二つに分けて、その積が最大になるようにせよと言われたとする。\(0\) と等号で結ぶ方法を知らなかったらどうしていただろうか？ たくさんの選択肢を手当たり次第に試すという方法を使ったことだろう。もし \(60\) が与えられた数なら、\(60\) を二つに分けて積を求める。すると \(50\) と \(10\) の積は \(500,\ \) \(52\) と \(8\) の積は \(416,\ \) \(40\) と \(20\) の積は \(800,\ \) \(45\) と \(15\) の積は \(675,\ \) \(30\) と \(30\) の積は \(900\) となる。ここからは \(900\) が最大に思える。分け方を少し変えると、\(31\) と \(29\) の積は \(899\)、\(32\) と \(29\) の積は \(896\) となって小さくなる。よって与えられた数を等しく分けると積が最大になるようだと予想できる。

微積分を使えば何が分かるかを見よう。分ける数を \(n\) とする。すると分けた数の一つを \(x\) とすれば、もう一つは \(n - x\) となる。二つの積は \(x (n - x)\) つまり \(nx - x^{2}\) だから、\(y = nx-x^{2}\) とおく。微分して \(0\) と等号で結んだ \[ \dfrac{dy}{dx} = n - 2x = 0 \] を \(x\) について解けば \[ \dfrac{n}{2} = x \] となる。ここから \(n\) がどんな数であっても、二つの等しい数に分けたときにその積が最大になることが正確に分かる。さらに最大の積が \(\dfrac{1}{4} n^{2}\) だとも分かる。

この非常に便利な法則は因数が二つより多くても成り立つ。例えば \(m + n + p\) が定数なら、\(m \times n \times p\) は \(m = n = p\) で最大となる。

判定法の確認

ここまでで学んだ知識を適用できる例を簡単に確認しよう。関数 \[ y = x^{2} - x \] が極大値または極小値を持つか、もし持つならそれは極大値と極小値のどちらかを考える。

微分すれば \[ \qquad \quad \frac{dy}{dx} = 2x - 1 \] となり、\(0\) と等号で結べば \[ \begin{aligned} 2x - 1 &= 0 \\ x &= \frac{1}{2} \end{aligned} \] が分かる。つまり \(x\) が \(\dfrac{1}{2}\) のとき、\(y\) は極大値または極小値になる。\(x = \dfrac{1}{2}\) を元の方程式に代入すると \[ \begin{aligned} y &= \left(\frac{1}{2}\right)^{2} - \frac{1}{2} \\ y &= -\frac{1}{4} \end{aligned} \] を得る。

これは極大値と極小値のどちらだろうか？ \(x\) に \(\dfrac{1}{2}\) より少しだけ大きい値、例えば \( 0.6\) を代入すると \[ y = (0.6)^{2} - 0.6 = 0.36 - 0.6 = -0.24 \] となる。これは \(-0.25\) より大きいから、\(y = -0.25\) は極小値である。

自分で曲線を描き、この正しさを確認してみよ。

例題

極大値と極小値を両方持つ曲線はとても興味深い例となる。方程式 \[ y = \frac{1}{3} x^{3} - 2x^{2} + 3x + 1 \] が表す曲線がそういった曲線の例である。

微分すれば \[ \dfrac{dy}{dx} = x^{2} - 4x +3 \] を得る。\(0\) と等号で結べば、二次方程式 \[ x^{2} - 4x +3 = 0 \] となる。この二次方程式を解くと二つの解 \[ \begin{cases} x = 3 \\ x = 1 \end{cases} \] が得られる。

\(x = 3\) のとき \(y = 1\) で、\(x = 1\) のとき \(y = \dfrac{7}{3}\) となる。一つ目が極小値に対応し、二つ目が極大値に対応する。

下の表に示すように最初の方程式を使って通る点を計算すれば、曲線全体をプロットできる (図 28)。 \[ \def\arraystretch{2.25} \begin{array}{c|cccccccc} x & -1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\[5pt] \hline y & - \dfrac{13}{3} & 1 & \dfrac{7}{3} & \dfrac{5}{3} & 1 & \dfrac{7}{3} & \dfrac{23}{3} & 19 \rule{0pt}{27pt} \\ \end{array} \]

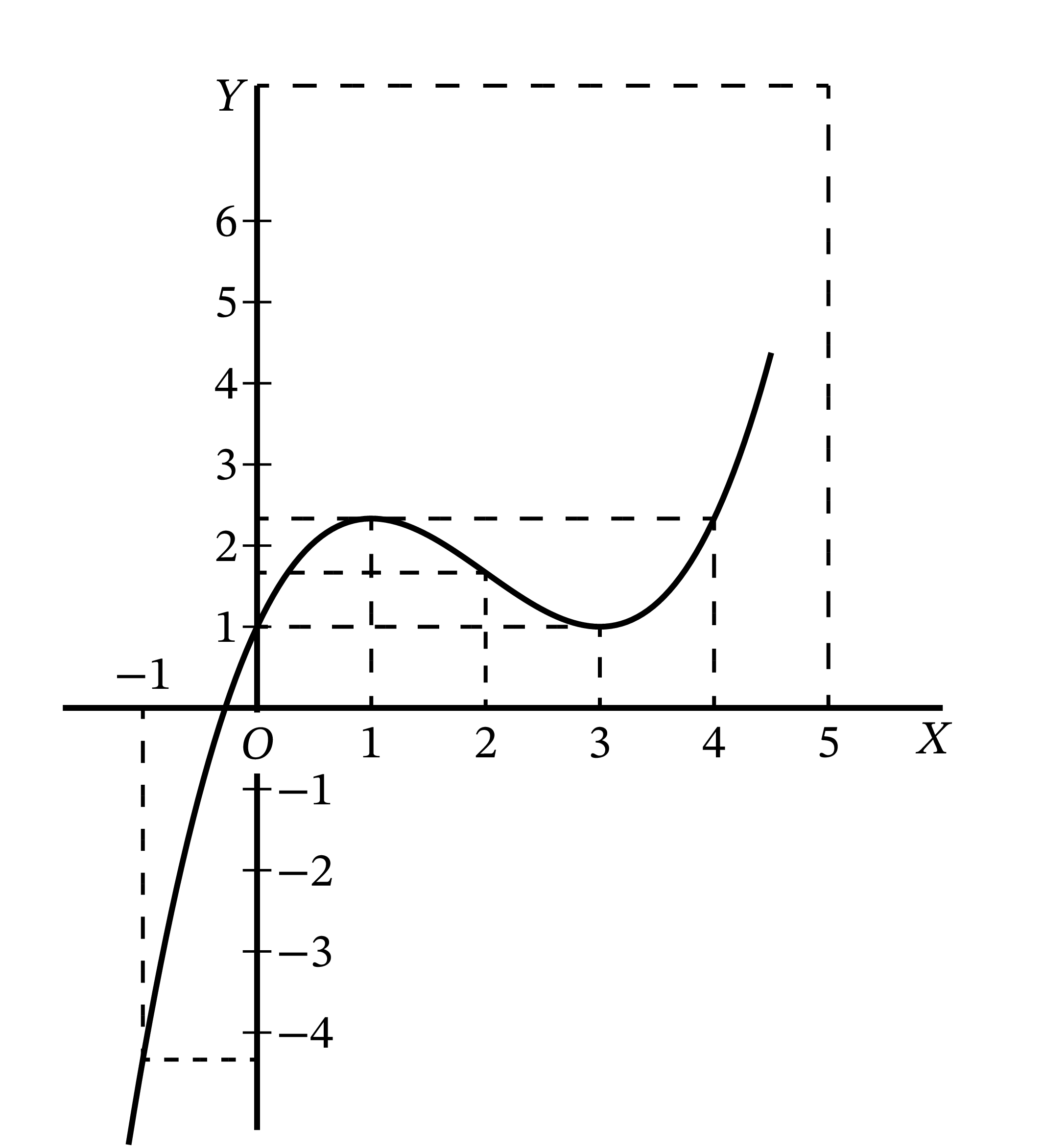
極大値と極小値に関する例をもう一つ示す。

中心が点 \(C\) で半径が \(r\) の円を考える。図 29 のように \(C\) の座標を \(x = a,\ \) \(y = b\) とすれば、円の方程式は \[ (y-b)^{2} + (x-a)^{2} = r^{2} \] となる。これを変形すると次を得る: \[ y = \sqrt{r^{2}-(x-a)^{2}} + b \]

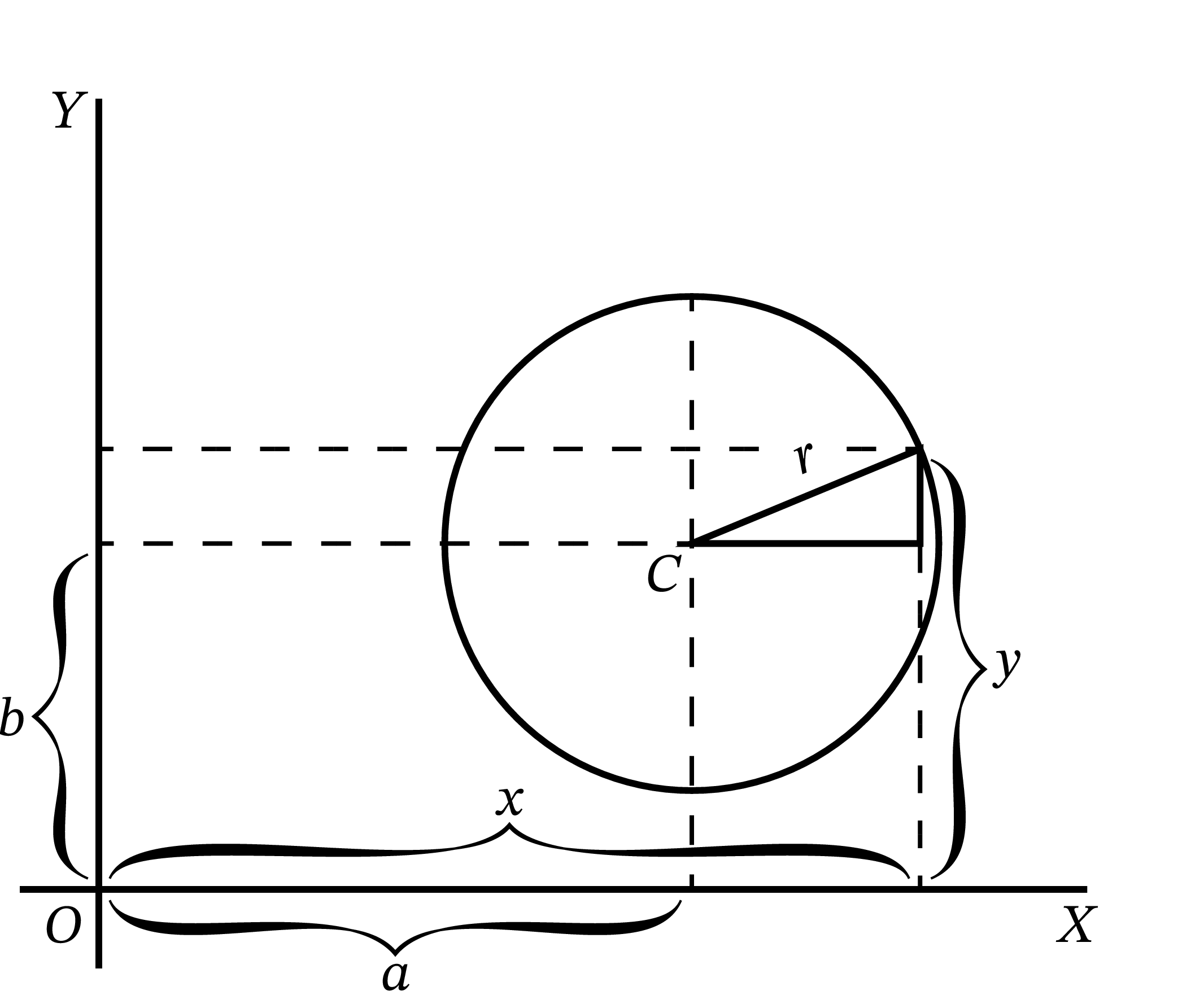
図からは \(y\) が極大値 \(b + r\) と極小値 \(b - r\) を \(x = a\) で取ることが微分をせずともわかる。ただここでは幾何学ではなく微分の知識を使ってみよう。\(y\) が極大または極小となる \(x\) の値を求めたいなら、微分を \(0\) と等号で結ぶ方法を使えばよいのだった。\(y\) を微分すると \[ \begin{aligned} \frac{dy}{dx} &= \frac{1}{2} \frac{1}{\sqrt{r^{2}-(x-a)^{2}}} \times (2a-2x) \\ &= \frac{a-x}{\sqrt{r^{2}-(x-a)^{2}}} \end{aligned} \] だから、\(y\) が極大または極小となる条件は \[ \frac{a-x}{\sqrt{r^{2}-(x-a)^{2}}} = 0 \] である。

\(x\) にどんな値を代入しても分母が無限大になることはないから、この条件が成り立つのは \[ x = a \] の場合に限られる。これを元の方程式に代入すれば \[ y = \sqrt{r^{2}} + b \] となる。\(r^{2}\) の二乗根は \(+r\) と \(-r\) だから、\(y\) の値として次の二つを得る: \[ \begin{cases} y = b + r \\ y = b - r \end{cases} \] 一つ目の値が頂上に対応する極大値で、二つ目の値が底に対応する極小値である。

曲線が極大または極小となる場所が存在しない場合には、\(0\) と等式で結んで得られる方程式から矛盾した結果が導かれる。例えば \[ y = ax^{3} + bx + c \] とすると \[ \frac{dy}{dx} = 3ax^{2} + b \] であり、これを \(0\) と等式で結ぶと \(3ax^{2} + b = 0\) となる。ここから \[ x^{2} = \frac{-b}{3a},\quad x = \pm \sqrt{\frac{-b}{3a}} \] が分かるので、\(a\) と \(b\) の符号が同じとき \(y\) に極大値と極小値は存在しない。

例題をさらにいくつか説明すれば、微積分の中で最も興味深く最も有用なこの手法を完全にマスターできるだろう。

\(\text{(1)}\) 半径 \(R\) の円に内接する長方形の面積が最大のとき、その辺の長さはいくつか？

一つの辺の長さを \(x\) とすると \[ {\footnotesize \text{もう一辺の長さ}} = \sqrt{({\footnotesize \text{対角線の長さ}})^{2} - x^{2}} \] が成り立つ。対角線の長さは円の直径 \(2R\) だから、これは \(\sqrt{4R^{2} - x^{2}}\) に等しい。

よって長方形の面積は \(S = x\sqrt{4R^{2} - x^{2}}\) となる。そして \[ \frac{dS}{dx} = x \times \dfrac{d\left(\sqrt{4R^{2} - x^{2}}\,\right)}{dx} + \sqrt{4R^{2} - x^{2}} \times \dfrac{d(x)}{dx} \] が成り立つ。

\(\sqrt{4R^{2}-x^{2}}\) を微分する方法を忘れている読者に向けてヒントを示す: \(4R^{2}-x^{2} = w\) そして \(y = \sqrt{w}\) とおいて、\(\dfrac{dy}{dw}\) と \(\dfrac{dw}{dx}\) を求めるところから始める。もしどうしても自分で解けなかったら、第九章を読み直すとよい。

微分を計算すると \[ \begin{aligned} \dfrac{dS}{dx} &= x \times -\dfrac{x}{\sqrt{4R^{2} - x^{2}}} + \sqrt{4R^{2} - x^{2}} \\ &= \dfrac{4R^{2} - 2x^{2}}{\sqrt{4R^{2} - x^{2}}} \end{aligned} \] を得る。

極大値または極小値では \[ \dfrac{4R^{2} - 2x^{2}}{\sqrt{4R^{2} - x^{2}}} = 0 \] が成り立つ。よって \(4R^{2} - 2x^{2} = 0\) つまり \(x = R\sqrt{2}\) である。

もう一方の辺の長さは \(\sqrt{4R^{2} - 2R^{2}} = R\sqrt{2}\) となるから、二つの辺は長さが等しい。この長方形は正方形であり、面積の極大値に対応する。この正方形の一辺を対角線に持つ正方形の一辺の長さは半径に等しい。

\(\text{(2)}\) 側面の長さが \(l\) の円錐容器の中で容量が最大のものの半径はいくつか？

側面の長さが \(l\) の容器の半径を \(R\) として高さを \(H\) とすれば、\(H = \sqrt{l^{2} - R^{2}}\) が成り立つ。よって体積 \(V\) は \[ V = \pi R^{2} \times \dfrac{H}{3} = \pi R^{2} \times \dfrac{\sqrt{l^{2} - R^{2}}}{3} \] と表せる。

前問と同様に議論を進めれば、 \[ \begin{aligned} \dfrac{dV}{dR} &= \pi R^{2} \times -\dfrac{R}{3\sqrt{l^{2} - R^{2}}} + \dfrac{2\pi R}{3} \sqrt{l^{2} - R^{2}} \\ &= \dfrac{2\pi R(l^{2} - R^{2}) - \pi R^{3}}{3\sqrt{l^{2} - R^{2}}} = 0 \end{aligned} \] が極大値または極小値のために必要だと分かる。

ここから \(2\pi R(l^{2} - R^{2}) - \pi R^{2} = 0\) すなわち \(R = l\sqrt{\dfrac{2}{3}}\) を得る。このとき明らかに \(V\) は極大値を取る。

\(\text{(3)}\) 次の関数の極大値と極小値を求めよ: \[ y = \dfrac{x}{4-x} + \dfrac{4-x}{x} \]

極大値または極小値のための条件は \[ \dfrac{dy}{dx} = \dfrac{(4-x)-(-x)}{(4-x)^{2}} + \dfrac{-x - (4-x)}{x^{2}} = 0 \] である。ここから \[ \begin{aligned} \dfrac{4}{(4-x)^{2}} - \dfrac{4}{x^{2}} &= 0 \\ x &= 2 \end{aligned} \] を得る。

条件を満たす値は一つだけだから、極大値または極小値が一つだけ存在する。\(x = 2\) およびその周りの \(y\) の値を計算すれば \[ \begin{aligned} \quad x &= 2 \phantom{.5} \quad {\footnotesize \text{のとき}} \quad y = 2 \\ \quad x &= 1.5 \quad {\footnotesize \text{のとき}} \quad y = 2.27 \\ \quad x &= 2.5 \quad {\footnotesize \text{のとき}} \quad y = 2.27 \end{aligned} \] だから、これは極小値である (グラフを描いてみるとよい)。

\(\text{(4)}\) 関数 \(y = \sqrt{1+x} + \sqrt{1-x}\) の極大値と極小値を求めよ (この関数もグラフを描いてみるとよい)。

微分すれば \[ \dfrac{dy}{dx} = \dfrac{1}{2\sqrt{1+x}} - \dfrac{1}{2\sqrt{1-x}} = 0 \] が極大または極小のための条件だと分かる (微分の方法は第九章の例 \(\text{(1)}\) を参照)。

よって \(\sqrt{1+x} = \sqrt{1-x}\) つまり \(x = 0\) が唯一の解となる。\(x = 0\) では \(y = 2\) である。

\(x=±0.5\) では \(y= 1.932\) だから、\(y = 2\) は極大値と分かる。

\(\text{(5)}\) 次の関数の極大値と極大値を求めよ: \[ y = \dfrac{x^{2}-5}{2x-4} \]

極大値または極小値の条件は \[ \dfrac{dy}{dx} = \dfrac{(2x-4) \times 2x - (x^{2}-5)2}{(2x-4)^{2}} = 0 \] である。変形すれば \[ \dfrac{2x^{2} - 8x + 10}{(2x - 4)^{2}} = 0 \] つまり \(x^{2} - 4x + 5 = 0\) となる。この解は \[ x = \frac{5}{2} ± \sqrt{-1} \] と求まる。

解が複素数なので、\(\dfrac{dy}{dx} = 0\) となる \(x\) は存在しない。よってこの関数は極大値と極小値を持たない。

\(\text{(6)}\) 次の関数の極大値と極小値を求めよ: \[ (y-x^{2})^{2} = x^{5} \]

この関数は \(y = x^{2} ± x^{\frac{5}{2}}\) と書ける。極大値または極小値の条件は \[ \dfrac{dy}{dx} = 2x ± \frac{5}{2} x^{\frac{3}{2}} = 0 \] であり、変形すると \(x \left(2 ± \dfrac{5}{2} x^{\frac{1}{2}}\right) = 0\) となる。よって \(2 ± \dfrac{5}{2} x^{\frac{1}{2}} = 0\) つまり \(x = \dfrac{16}{25}\) と \(x = 0\) が条件を満たし、この問題には二つ答がある。

まず \(x = 0\) の場合を考える。\(x = -0.5\) では \(y = 0.25 ± \sqrt[2]{-(0.5)^{5}}\) となり、\(x = +0.5\) では \(y = 0.25 ± \sqrt[2]{(0.5)^{5}}\) となる。つまり \(x = 0\) の片側では \(y\) が虚数となり、グラフ上に描ける \(y\) の値は存在しない。曲線はもう一方の側にのみ存在する (図 30)。

グラフを描くと、曲線が極小値が存在するかのように原点に向かうことが分かる。しかし曲線は原点より左側には進まず、来た方向に戻っていく (“尖端” が作られる)。よって \(\dfrac{dy}{dx} = 0\) という条件が成立するにもかかわらず \(x = 0\) は極小値にも極大値にもならない。極値を判定するときには候補の値の両側で値の確認が必要なことをこの例は示している。

次に \(x = \dfrac{16}{25} = 0.64\) の場合を考える。\(x = 0.64\) なら \(y = 0.7373\) および \(y = 0.0819\) で、\(x = 0.6\) なら \(y\) は \(0.6389\) および \(0.0811\) になり、\(x = 0.7\) なら \(0.8996\) および \(0.0804\) になる。

ここから曲線には二つの枝があることが分かる。上の枝は極大にならないが、下の枝は極大になる。

\(\text{(7)}\) 高さが半径の二倍の円柱が形を保ったまま膨張している。つまり任意の時点における円柱は元の円柱と相似である。最初の半径が \(r\) インチで一秒ごとに底面の面積が \(20\) 平方インチ増えるとき、体積の変化率はいくらか？

問題の設定から \[ \begin{aligned} {\footnotesize \text{面積}} &= S = 2(\pi r^{2})+ 2 \pi r \times 2r = 6 \pi r^{2} \\ {\footnotesize \text{体積}} &= V = \pi r^{2} \times 2r=2 \pi r^{3} \\ \frac{dS}{dr} &= 12\pi r,\quad \frac{dV}{dr}=6 \pi r^{2} \\ dS &= 12\pi r\, dr=20,\quad dr=\frac{20}{12 \pi r} \\ dV &= 6\pi r^{2}\, dr = 6 \pi r^{2} \times \frac{20}{12 \pi r} = 10r \end{aligned} \] が分かる。よって体積の変化率は \(10r\) 立方インチである。

これ以外の例を自分で作ってみよ。興味深い例がこれほどたくさん作れる理論は他にそうない。

練習問題 IX

解答はここにある。

\(\text{(1)}\) \(y = \dfrac{x^{2}}{x + 1}\) とする。\(x\) がどんな値のとき \(y\) は極大または極小となるか？

\(\text{(2)}\) 方程式 \(y = \dfrac{x}{a^{2}+x^{2}}\) において、\(y\) を極大にする \(x\) の値は何か？

\(\text{(3)}\) 長さ \(p\) の線分を \(4\) つに分割して長方形を作る。この長方形の面積が最大となるのは全ての辺が長さが \(\dfrac{1}{4}p\) のときだと示せ。

\(\text{(4)}\) 長さ \(30\) インチのひもの両端をつなぎ、三か所を固定して三角形を作る。このひもから作れる三角形の面積の最大値はいくつか？

\(\text{(5)}\) 方程式 \[ y = \frac{10}{x} + \frac{10}{8-x} \] に対応する曲線をプロットし、\(\dfrac{dy}{dx}\) を求めよ。さらに \(y\) を極小とする \(x\) の値を求め、\(y\) の極小値を計算せよ。

\(\text{(6)}\) \(y = x^{5} - 5x\) とする。\(y\) を極大または極小にする \(x\) の値を求めよ。

\(\text{(7)}\) 与えられた四角形に内接する最小の四角形は何か？

\(\text{(8)}\) 高さが半径と等しい円錐が与えられる。この円錐に内接する円柱の中で、\(\text{(a)}\) 体積最大 \(\text{(b)}\) 側面積最大 \(\text{(c)}\) 表面積最大のものをそれぞれ求めよ。

\(\text{(9)}\) 球に内接する円柱の中で \(\text{(a)}\) 体積最大 \(\text{(b)}\) 側面積最大 \(\text{(c)}\) 表面積最大のものをそれぞれ求めよ。

\(\text{(10)}\) 丸い風船が膨らんでいる。半径が \(r\) フィートのときの体積の増加率が毎秒 \(4\) 立方フィートなら、表面積の増加率はいくらか？

\(\text{(11)}\) 与えられた球に内接する円錐で体積が最大のものを求めよ。

\(\text{(12)}\) \(N\) 個のボルタ電池を並列につないだバッテリーが生み出す電流 \(C\) は \[ C=\dfrac{n×E}{R+\dfrac{rn^{2}}{N}} \] と表せる。ここで \(E,\ \) \(R,\ \) \(r\) は定数であり、\(n\) は直列に繋がった電池の数を表す。電流が最大になる \(n\) と \(N\) の比を求めよ。