XIV. 真の複利と組織的成長の法則
ある量が増加していて、一定期間の増加量がその量自身に比例している場合を考える。これは金利が一定の口座に預けた資金の増え方と似ている: 預けている金額が多ければ多いほど、一定期間における金利も大きくなる。
金利の計算方法は二つある。専門用語で一つは単利 (simple interest) と呼ばれ、もう一つは複利 (compound interest) と呼ばれる。単利では金利の計算に利用される金額がいつでも一定だが、複利ではこの金額が金利で増える。そのため複利の口座に資金を長く預けると金利が増えていく。
\(\text{(1)}\) 単利: 具体的な例を考えよう。預金が \(100\) ポンドで、一年ごとに \(10\) パーセントの金利が得られるとする。金利を毎年引き出して固定資産を買う (あるいは金庫に移す) ものとすれば、\(10\) 年間で \(10\) ポンドの金利を \(10\) 回、合計で \(100\) ポンド受け取ることになる。つまり全て合わせれば \(200\) ポンドであり、\(10\) 年間で預金が倍になる。金利が \(5\) パーセントなら \(20\) 年で預金が倍になり、金利が \(2\) パーセントなら \(50\) 年で預金が倍になる。簡単に分かるように、金利が預金の \(\dfrac{1}{n}\) である単利では \(n\) 年間で預金が倍になる。
つまり元の預金が \(y\) で年ごとの金利が \(\dfrac{y}{n}\) なら、\(n\) 年後の預金は \[ y + n\dfrac{y}{n} = 2y \] と表せる。
\(\text{(2)}\) 複利: 単利の例と同じく最初に \(100\) ポンド持っていて、金利が一年ごとに \(10{\footnotesize \text{\%}}\) だとする。すると一年目の終わりに預金は \(110\) ポンドとなり、二年目の金利は \(110\) ポンドの \(10{\footnotesize \text{\%}}\) つまり \(11\) ポンドとなる。三年目が始まる時点での預金は \(121\) ポンド、その年の終わりの金利は \(12.2\) ポンドであり、四年目は \(133.2\) ポンドの預金で始まる。以下同様であり、簡単な計算によって \(10\) 年目の終わりの預金が \(259.37\) ポンドだと分かる。一年の終わりごとに \(1\) ポンドごとに \(0.1\) ポンドの利息が得られるので、預金は \(\dfrac{11}{10}\) となる。そのため預金は十年間で \(\left(\dfrac{11}{10}\right)^{10} = 2.59374\) 倍になる。この計算を記号を使って表そう。最初の預金を \(y_{0}\) として、預金が \(\dfrac{1}{n}\) だけ増加するという操作を \(n\) 回行ったとする。最終的な預金を \(y_{n}\) とすれば \[ y_n = y_0\left(1 + \frac{1}{n}\right)^n \] が成り立つ。
しかしこの金利の計算方法にはある意味で不公平な部分がある: 最初の一年が終わらなくとも預金が \(100\) ポンドから増加していると主張できなくもない。例えば半年後には預金は少なくとも \(105\) ポンドまで増えているはずだから、残りの半年の金利はこの \(105\) ポンドを使って計算すべきだと言うことができる。この場合には半年ごとに \(5{\footnotesize \text{\%}}\) の金利が得られるから、預金が \(\dfrac{21}{20}\) に増える操作が \(20\) 回行われる。この方法で \(10\) 年が経過すると、預金は \(265.3\) ポンドに増える: \[ 100 \left(1 + \frac{1}{20}\right)^{20} = 265.3 \]
しかしこうしても、まだ公平でないと言うかもしれない。最初の一か月で預金は増加しているにもかかわらず、半年ごとに金利を計算する方法ではその間預金が変わらないことを仮定しているからである。一年を \(10\) 等分して、それぞれで \(1{\footnotesize \text{\%}}\) の金利が得られるとしよう。すると十年間で預金は \(100\) 回増加するから \[ y_n = 100 \left( 1 + \frac{1}{100} \right)^{100} = 270.48 \] となる。
こうしても最終的な値ではない。十年を \(1000\) 等分したとしよう。このとき一年の \(\dfrac{1}{100}\) が一つの単位となり、この期間ごとに \(\dfrac{1}{10}{\footnotesize \text{\%}}\) が預金に追加される。よって \[ y_n = 100 \left( 1 + \frac{1}{1000} \right)^{1000} = 271.69 \] となる。
さらに細かく分けよう。十年を \(10000\) 等分すれば、一年の \(\dfrac{1}{1000}\) ごとに \(1{\footnotesize \text{\%}}\) の \(\dfrac{1}{100}\) だけ金利が得られる。このとき \[ y_n = 100 \left( 1 + \frac{1}{10{,}000} \right)^{10{,}000} \] であり、計算すればこれは \(271.81\) だと分かる。
ここまでで明らかなように、私たちが計算しようとしている真の複利には \(\left(1 + \dfrac{1}{n}\right)^n\) の極限が関係する。\(\left(1 + \dfrac{1}{n}\right)^n\) は \(2\) より大きく、\(n\) が大きくなるにつれてとある極限値に限りなく近づいていく。\(n\) を大きくしたときに \(\left(1 + \dfrac{1}{n}\right)^n\) が近づく値は \[ 2.71828\cdots \] であり、この値は絶対に忘れてはいけない。

ここまでの議論を図を使って説明してみよう。図 36 の \(OP\) が最初の量を表し、\(OT\) が量が増加する期間を表す。\(OT\) は \(10\) 等分されており、それぞれが \(OT\) の \(\dfrac{1}{10}\) である。このグラフでは \(\dfrac{dy}{dx}\) は一定で、ステップごとに \(OP\) の \(\dfrac{1}{10}\) だけ増える。つまり \(OT\) 全体で高さは倍になる。もしステップごとの増加を半分にしたとしても、一ステップごとの増分が半分になるだけで \(OT\) で高さが倍になるという事実は変わらない。もちろん \(OP\) の高さの \(\dfrac{1}{n}\) だけ増える \(n\) 個のステップを考えたとしても同様となる。これは単利の場合に対応し、最初の \(OP\) の高さを \(1\) とすれば最後の高さは \(2\) となる。
「幾何的に」増加する量のグラフを 図 37 に示す。ここでは曲線上の点の \(y\) 座標は一つ前の点の \(y\) 座標の \(1 + \dfrac{1}{n} = \dfrac{n+1}{n}\) 倍となっている。ステップごとの高さの増加量が曲線のその点における \(y\) 座標の \(\dfrac{1}{n}\) なので、単利の場合とは違い増分は定数ではない。最初の \(OP\) の長さを \(1\) とすると、\(10\) ステップ先での高さは \(\left(1 + \dfrac{1}{10}\right)^{10} = 2.594\) となる。もし \(n\) を十分大きく (つまり \(\dfrac{1}{n}\) を十分小さく) すれば、最終的な値 \(\left(1 + \dfrac{1}{n}\right)^n\) は \(2.71828 \cdots\) まで大きくなる。

この不思議な値 \(2.7182818\cdots\) に対して、数学者はギリシャ文字 \(\varepsilon\) (イプシロン) を割り当てた。ギリシャ文字 \(\pi\) が \(3.141592 \cdots\) を表すことは中学生なら誰でも知っているが、イプシロンが \(2.7182818\cdots\) であることはもう少し高級な知識だろう。この数 \(\varepsilon\) は \(\pi\) よりもさらに重要である!
ではイプシロン \(\varepsilon\) とはどんな値だろうか?
単利で \(1\) が \(2\) に増加する間に、同じ金利の “真の” 複利で \(1\) を増加させたとする。このとき \(1\) が最終的に到達する値が \(\varepsilon\) である1。
任意の瞬間における増分がその量に比例する増加の仕方をここまで説明してきたが、専門家はこの増加を指して 「増加が指数的 (exponential) である」と言う。単位時間で \(1\) が \(2.718281\cdots\) となる増加率が指数的増加の基準となる。指数的増加は組織的増加 (organic growth) と言うこともできるだろう。単位時間当たりの成長速度が組織の大きさそのものに比例するなら、組織の大きさは指数的に増加する。
増加率の基準を \(100\) {\footnotesize \text{\%}}として、単位時間の基準を適当に固定したとする。このとき \(1\) を算術的に増加させると \(2\) となり、\(1\) を指数的に増加させると \(2.71828\cdots\) となる。
さらに \(\bm{e}\) について: \(n\) が無限に大きくなるときの \(\left(1 + \dfrac{1}{n}\right)^n\) の値がここまでの議論で登場した。対数表を使って計算した \(n = 2,\ \) \(5,\ \) \(10,\ \cdots\) \(10{,}000\) に対するこの式の値を示す: \[ \begin{alignedat}{2} &\left(1 + \frac{1}{2}\right)^{2} &&= 2.25 \\ &\left(1 + \frac{1}{5}\right)^{5} &&= 2.488 \\ &\left(1 + \frac{1}{10}\right)^{10} &&= 2.594 \\ &\left(1 + \frac{1}{20}\right)^{20} &&= 2.653 \\ &\left(1 + \frac{1}{100}\right)^{100} &&= 2.705 \\ &\left(1 + \frac{1}{1000}\right)^{1000} &&= 2.7169 \\ &\left(1 + \frac{1}{10{,}000}\right)^{10{,}000} &&= 2.7181 \end{alignedat} \]
実数 \(e\) は非常に重要なので、計算方法をもう一つ示しておく。
これから二項定理を使って \(\left(1 + \dfrac{1}{n}\right)^n\) をよく知られた形に展開する。二項定理によると \[ \begin{aligned} (a + b)^n &= a^n + n \dfrac{a^{n-1} b}{1!} + n(n - 1) \dfrac{a^{n-2} b^{2}}{2!} \\ & \hphantom{= a^{n} + } + n(n -1)(n - 2) \dfrac{a^{n-3} b^{3}}{3!} + \cdots \end{aligned} \] が成り立つ。\(a = 1\) と \(b = \dfrac{1}{n}\) を代入すれば \[ \begin{aligned} \left(1 + \dfrac{1}{n}\right)^n &= 1 + 1 + \dfrac{1}{2!} \left(\dfrac{n - 1}{n}\right) + \dfrac{1}{3!} \dfrac{(n - 1)(n - 2)}{n^{2}} \\ & \hphantom{= 1 + 1\quad } + \dfrac{1}{4!} \dfrac{(n - 1)(n - 2)(n - 3)}{n^{3}} + \cdots \end{aligned} \] を得る。この等式で \(n\) が数億や数兆といった無限に大きくなるとすれば、\(n - 1\) や \(n - 2\) あるいは \(n - 3\) はどれも \(n\) とほぼ等しくなる。よってこの等式は \[ e = 1 + 1 + \dfrac{1}{2!} + \dfrac{1}{3!} + \dfrac{1}{4!} + \cdots \] となる。この高速に収束する級数の項を好きなだけ取ることで、和を望むだけの精度で計算できる。第 \(10\) 項までの値を次に示す: \[ \begin{array}{c|c} {\footnotesize \text{項数}} & {\footnotesize \text{値}} \\ \hline 1 & 1.000000 \\ 2 & 1.000000 \\ 3 & 0.500000 \\ 4 & 0.166667 \\ 5 & 0.041667 \\ 6 & 0.008333 \\ 7 & 0.001389 \\ 8 & 0.000198 \\ 9 & 0.000025 \\ 10 & 0.000002 \\ \hline {\footnotesize \text{合計}} & 2.718281 \end{array} \]
同様に二項定理の手を借りて \(\left(1 + \dfrac{1}{n}\right)^{nx}\) を展開してみよう。この式は \(n\) が無限に大きいとき \(e^{x}\) に等しいから、 \[ \begin{aligned} e^x &= 1^{nx} + \frac{nx}{1!} 1^{nx-1} \left(\dfrac{1}{n}\right) + \frac{nx(nx - 1)}{2!} 1^{nx - 2} \left(\dfrac{1}{n}\right)^{2} \\ & \phantom{= 1^{nx}\ } + \frac{nx(nx - 1)(nx - 2)}{3!} 1^{nx-3} \left(\dfrac{1}{n}\right)^{3} + \cdots \\ &= 1 + x + \frac{1}{2!} \cdot \frac{n^{2}x^{2} - nx}{n^{2}} + \frac{1}{3!} \cdot \frac{n^{3}x^{3} - 3n^{2}x^{2} + 2nx}{n^{3}} + \cdots \\ &= 1 + x + \frac{1}{2!}\left(x^{2} -\frac{x}{n}\right) + \frac{1}{3!} \left(x^{3} - \dfrac{3x^{2}}{n} + \dfrac{2x}{n^{2}}\right) + \cdots \end{aligned} \] が分かる。\(n\) を無限に大きくすれば、この等式は次の形に単純化される: \[ e^x = 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \frac{x^{4}}{4!} + \cdots \] この級数を指数級数 (exponential series) と呼ぶ。
\(e\) が重要とされるのは、関数 \(e^{x}\) が微分しても値が変わらないという性質を持つことが大きな理由である。この性質を持つ \(x\) の関数は他に無い。言い換えると、\(e^{x}\) の微分係数は \(e^{x}\) に等しい。この事実は上の等式を \(x\) で微分すればすぐに分かる: \[ \begin{aligned} \frac{d(e^x)}{dx} & = 0 + 1 + \frac{2x}{1 \cdot 2} + \frac{3x^{2}}{1 \cdot 2 \cdot 3} + \frac{4x^{3}}{1 \cdot 2 \cdot 3 \cdot 4} + \frac{5x^{4}}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} + \cdots \\ & = 1 + x + \frac{x^{2}}{1 \cdot 2} + \frac{x^{3}}{1 \cdot 2 \cdot 3} + \frac{x^{4}}{1 \cdot 2 \cdot 3 \cdot 4} + \cdots \end{aligned} \] であり、これは微分する前の級数と等しい。
次にこれと逆の問題を解こう。つまり微分係数がそれ自身となるような \(x\) の関数を求めるのである。\(x\) のべきだけが関係する式であって微分しても変化しない関数はあるだろうか? そのような関数が存在すると仮定して、その関数が \[ \quad \quad \ y = A + Bx + Cx^{2} + Dx^{3} + Ex^{4} + \cdots \] だとする (\(A,\ \) \(B,\ \) \(C, \ldots\) は定数であり、これから求める)。この関数を微分すると \[ \dfrac{dy}{dx} = B + 2Cx + 3Dx^{2} + 4Ex^{3} + \cdots \] となる。この式が微分する前の式と等しいのだから、\(A = B\) が分かる。同様に \(C=\dfrac{B}{2}=\dfrac{A}{1\cdot 2},\ \) \(D = \dfrac{C}{3} = \dfrac{A}{1 \cdot 2 \cdot 3},\ \) \(E = \dfrac{D}{4} = \dfrac{A}{1 \cdot 2 \cdot 3 \cdot 4}\) も成り立つ必要がある。
よって条件を満たす関数は \[ y = A\left(1 + \dfrac{x}{1} + \dfrac{x^{2}}{1 \cdot 2} + \dfrac{x^{3}}{1 \cdot 2 \cdot 3} + \dfrac{x^{4}}{1 \cdot 2 \cdot 3 \cdot 4} + \cdots \right) \] だと分かる。簡単のため \(A = 1\) とすれば \[ y = 1 + \dfrac{x}{1} + \dfrac{x^{2}}{1 \cdot 2} + \dfrac{x^{3}}{1 \cdot 2 \cdot 3} + \dfrac{x^{4}}{1 \cdot 2 \cdot 3 \cdot 4} + \cdots \] を得る。この関数は何度微分しても同じ関数が得られる。
また \(A = 1\) である場合について級数の値を計算すると \[ \begin{aligned} x = 1 \quad {\footnotesize \text{のとき}} \quad y = \hphantom{(} 2.718281 \cdots \hphantom{)^{1}} & = e \\ x = 2 \quad {\footnotesize \text{のとき}} \quad y = (2.718281 \cdots)^{2} & = e^{2} \\ x = 3 \quad {\footnotesize \text{のとき}} \quad y = (2.718281 \cdots)^{3} & = e^{3} \end{aligned} \] となる。ここから \[ x = x\quad {\footnotesize \text{のとき}} \quad y = (2.718281\cdots)^x \quad = e^x \] であり、 \[ e^x = 1 + \dfrac{x}{1} + \dfrac{x^{2}}{1\cdot2} + \dfrac{x^{3}}{1\cdot 2\cdot 3} + \dfrac{x^{4}}{1\cdot 2\cdot 3\cdot 4} + \cdots \] だと判明する。
[指数の読み方: 教師が周りにいない人のために説明しておく。\(e^{x}\) は「イプシロンのエックスじょう」または「エクスポネンシャル・エックス」と読む。\(e^{pt}\) は「イプシロンのピー・ティーじょう」あるいは「エクスポネンシャル・ピー・ティー」と読む。同様に \(e^{-2}\) の読み方は「イプシロンのマイナスにじょう」あるいは「エクスポネンシャル・マイナスツー」であり、\(e^{-ax}\) の読み方は「イプシロンのマイナスエー・エックスじょう」あるいは「エクスポネンシャル・マイナスエー・エックス」である]
もちろん \(e^{y}\) を \(y\) に関して微分しても変化しない。また \(e^{ax}\) は \((e^a)^x\) と等しいから、\(e^{ax}\) を \(x\) に関して微分すると定数 \(a\) が前に出て \(a e^{ax}\) となる。
自然対数 (ネイピアの対数)
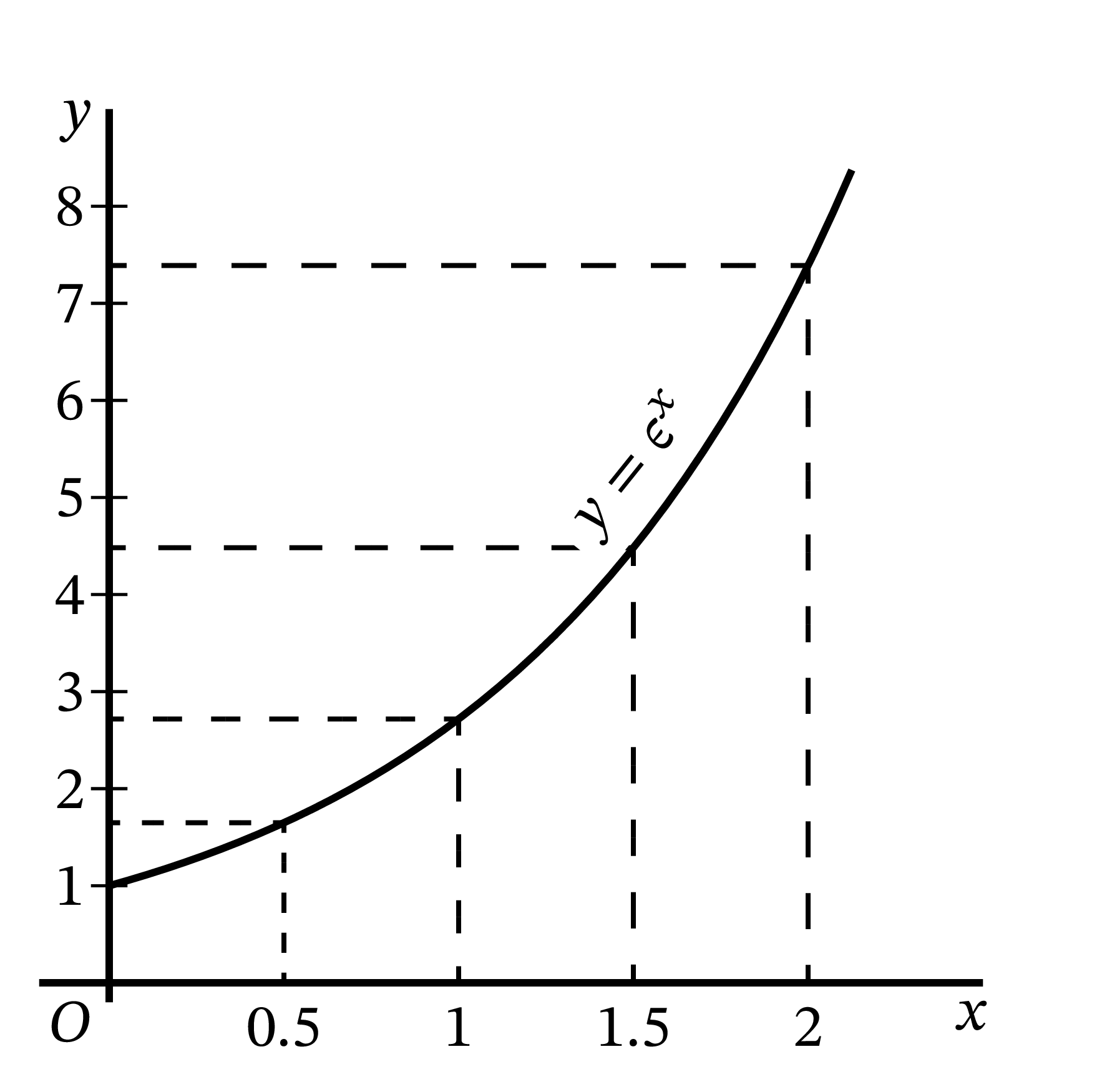
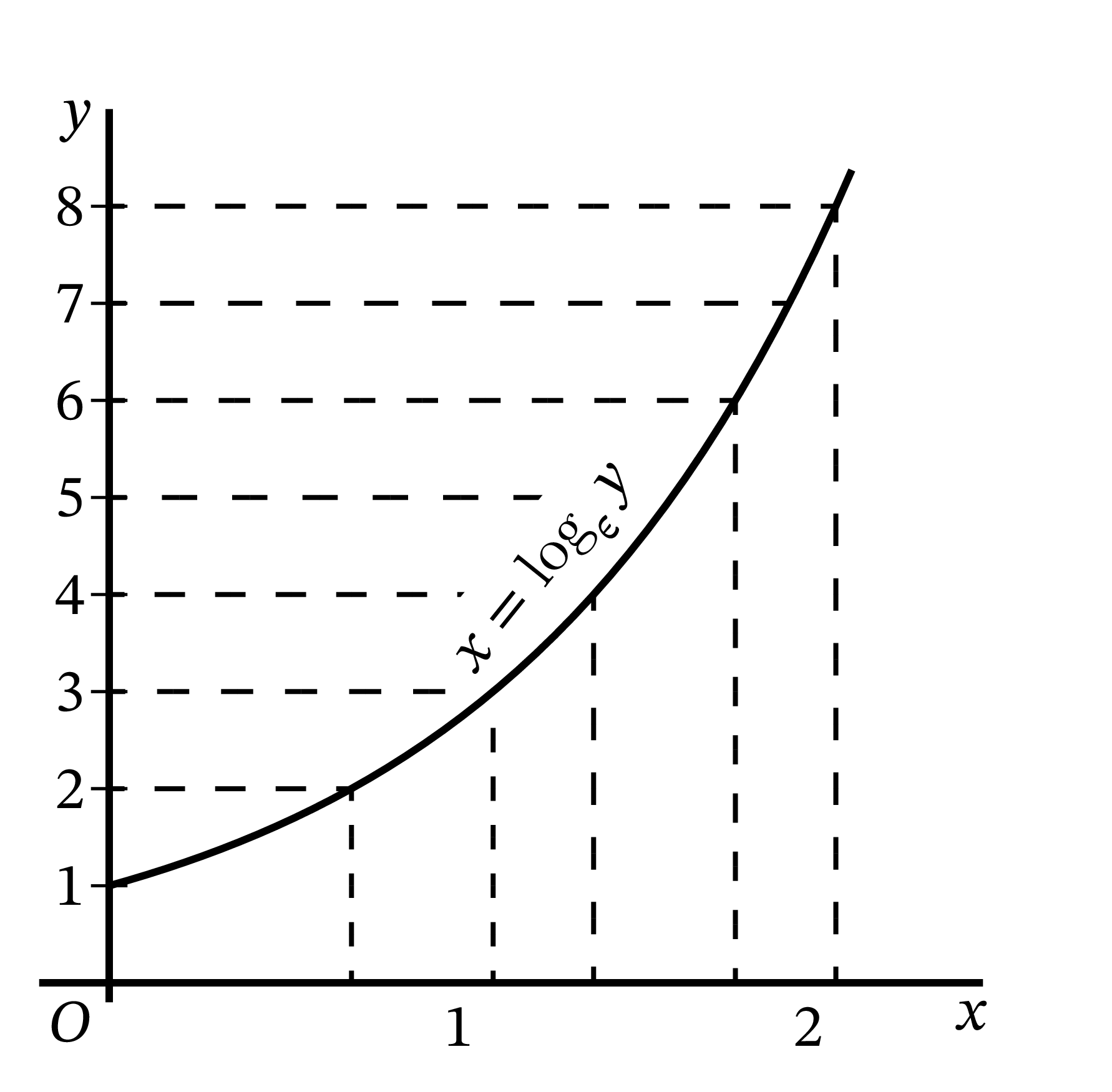
\(e\) が重要とされるのは、対数の発明で知られるネイピアが対数計算の底として \(e\) を使ったためでもある2。\(e^{x} = y\) のとき、\(x\) を底 \(e\) に関する \(y\) の対数 (logarithm) と呼ぶ。そして \[ y = e^{x} \] のとき \[ y = \log_{e} y \] と書く。この二つの方程式が表す曲線を 図 38 と 図 39 に示す。
いくつかの点で計算した関数の値を示す: \[ \begin{aligned} {\footnotesize \text{図 38}} \left\{ \begin{array}{c|cccccc} \hline x & 0 & 0.5 & 1 & 1.5 & 2 \\ \hline y & 1 & 1.65 & 2.71 & 4.50 & 7.39 \\ \hline \end{array} \right. \\ {\footnotesize \text{図 39}} \left\{ \begin{array}{c|cccccc} \hline y & 1 & 2 & 3 & 4 & 8 \\ \hline x & 0 & 0.69 & 1.10 & 1.39 & 2.08 \\ \hline \end{array} \right. \end{aligned} \]
計算してプロットした点は異なっているものの、二つの曲線が同一なことは図から明らかである。つまり二つの方程式は同じ関係を表している。
底に \(e\) ではなく \(10\) を用いる常用対数 (common logarithm) を使ってきた大勢の読者は \(e\) を底とした自然対数 (natural logarithm) に馴染みがないと思うので、少し説明しておく。対数を足すと積の対数となるという一般的な法則は底が \(e\) でも成り立つ。言い換えれば \[ \log_e a + \log_e b = \log_e ab \] である。次の指数法則も成り立つ: \[ n \times \log_e a = \log_e a^n \] しかし底が \(10\) でないので、\(100\) や \(1000\) を掛ける代わりに対数に \(2\) や \(3\) を足すという操作は行えない。また自然対数から常用対数への変換は \(0.4343\) を掛ければ行える。つまり \[ \log_{10} x = 0.4343 \times \log_{e} x \] が成り立つ。これを逆にすれば \[ \log_{e} x = 2.3026 \times \log_{10} x \] となる。
指数関数や対数関数を含む式
続いて指数関数や対数関数を含む式の微分に進もう。
次の関係を考える: \[ y = \log_e x \] これは次のように変形できる: \[ e^y = x \] \(e^{y}\) を \(y\) に関して微分しても変わらないから \[ \frac{dx}{dy} = e^y \] が成り立つ。これを元の等式に代入すれば \[ \frac{dy}{dx} = \frac{1}{\ \dfrac{dx}{dy}\ } = \frac{1}{e^y} = \frac{1}{x} \] を得る。
これは非常に興味深い結果である。この結果の表記を変えると \[ \frac{d(\log_e x)}{dx} = x^{-1} \] となる。\(x^{-1}\) は \(x\) のべきの微分結果としては表れないことを思い出してほしい。\(x\) のべきの微分規則は指数を乗じてから指数を \(1\) 減らすというものだった。例えば \(x^{3}\) を微分すれば \(3x^{2}\) となり、\(x^{2}\) を微分とすれば \(2x^{1}\) となる。しかし \(x^{0} = 1\) は定数なので、\(x^{0}\) を微分した結果に \(x^{-1}\) は表れない。\(\log_{e} x\) を微分すると \(\dfrac{1}{x}\) になるという興味深い事実は積分に関する章でもう一度触れる。
続いて次の式の微分を考える: \[ \begin{aligned} y &= \log_e(x+a) \\ {\footnotesize \text{つまり}}\quad e^y &= x+a \end{aligned} \] \(e^y\) の微分は \(e^y\) だから、二つ目の式より \(\dfrac{d(x+a)}{dy} = e^y\) が分かる。
したがって \[ \frac{dx}{dy} = e^y = x+a \] となる。逆関数の微分規則を使えば \[ \frac{dy}{dx} = \frac{1}{\;\dfrac{dx}{dy}\;} = \frac{1}{x+a} \] が分かる。
続いて次の式の微分を考える: \[ y = \log_{10} x \]
まず常用対数に \(0.4343\) を掛けて自然対数に変換する。すると \[ y = 0.4343 \log_e x \] となる。ここから \[ \frac{dy}{dx} = \frac{0.4343}{x} \] を得る。
次の例はこれまでより少しだけ難しい。次の式の微分である: \[ y = a^x \]
両辺の対数を取ると \[ \log_e y = x \log_e a \] であり、ここから \[ x = \frac{\log_e y}{\log_e a} = \frac{1}{\log_e a} \times \log_e y \] が分かる。
\(\dfrac{1}{\log_e a}\) は定数だから \[ \frac{dx}{dy} = \frac{1}{\log_e a} \times \frac{1}{y} = \frac{1}{a^x \times \log_e a} \] と計算でき、\(y\) に関する表記に戻せば \[ \frac{dy}{dx} = \frac{1}{\;\dfrac{dx}{dy}\;} = a^x \times \log_e a \] となる。さらに \[ \frac{dx}{dy} \times \frac{dy}{dx} = 1,\quad \frac{dx}{dy} = \frac{1}{y} \times \frac{1}{\log_e a} \] から \[ \frac{1}{y} \times \frac{dy}{dx} = \log_e a \] を得る。
これまでの例から分かるように、\(\log_{e} y\) が \(x\) の関数と等号で結ばれている場合には、\(\dfrac{1}{y}\, \dfrac{dy}{dx}\) と \(x\) の関数の微分が等号で結ばれる。つまり \(\log_e y = x \log_e a\) から直接 \[ \frac{1}{y}\, \frac{dy}{dx} = \log_e a \] すなわち \[ \frac{dy}{dx} = a^x \log_e a \] を結論できる。
さらに例題を見よう。
\(\text{(1)}\) \(y=e^{-ax}\)
\(-ax = z\) とすると \(y=e^z\) が成り立つことを使えば微分が計算できる: \[ \frac{dy}{dz} = e^z,\quad \frac{dz}{dx} = -a,\quad \frac{dy}{dx} = -ae^{-ax} \]
あるいは次のようにもできる: \[ \log_e y = -ax,\quad \frac{1}{y}\, \frac{dy}{dx} = -a,\quad \frac{dy}{dx} = -ay = -ae^{-ax} \]
\(\text{(2)}\) \(y=e^{\frac{x^{2}}{3}}\)
\(\dfrac{x^{2}}{3}=z\) とすれば \(y=e^z\) であり、ここから次が分かる: \[ \frac{dy}{dz} = e^z,\quad \frac{dz}{dx} = \frac{2x}{3},\quad \frac{dy}{dx} = \frac{2x}{3}\, e^{\frac{x^{2}}{3}} \]
あるいは次のようにもできる: \[ \log_e y = \frac{x^{2}}{3},\quad \frac{1}{y}\, \frac{dy}{dx} = \frac{2x}{3},\quad \frac{dy}{dx} = \frac{2x}{3}\, e^{\frac{x^{2}}{3}} \]
\(\text{(3)}\) \(y = e^{\frac{2x}{x+1}}\) \[ \begin{aligned} \log_e y &= \frac{2x}{x+1},\quad \frac{1}{y}\, \frac{dy}{dx} = \frac{2(x+1)-2x}{(x+1)^{2}} \\ \end{aligned} \] より \[ \frac{dy}{dx} = \frac{2}{(x+1)^{2}} e^{\frac{2x}{x+1}} \] となる。\(\dfrac{2x}{x+1} = z\) とする方法でこの答を確かめよ。
\(\text{(4)}\) \(y=e^{\sqrt{x^{2}+a}}\)
この等式は \(\log_e y=(x^{2}+a)^{\frac{1}{2}}\) とできる。よって \[ \frac{1}{y}\, \frac{dy}{dx} = \frac{x}{(x^{2}+a)^{\frac{1}{2}}},\quad \frac{dy}{dx} = \frac{x \times e^{\sqrt{x^{2}+a}}}{(x^{2}+a)^{\frac{1}{2}}} \] となる。途中の微分計算では、\((x^{2}+a)^{\frac{1}{2}} = u\) および \(x^{2} + a = v\) とすれば \(u=v^{\frac{1}{2}}\) だから \[ \frac{du}{dv} = \frac{1}{{2v}^{\frac{1}{2}}},\quad \frac{dv}{dx} = 2x,\quad \frac{du}{dx} = \frac{x}{(x^{2}+a)^{\frac{1}{2}}} \] となる事実を使う。
\(\sqrt{x^{2}+a}=z\) とする方法でこの答えを確かめよ。
\(\text{(5)}\) \(y=\log(a+x^{3})\)
\((a+x^{3})=z\) とすると \(y = \log_{e} z\) が成り立つ。よって \[ \frac{dy}{dz} = \frac{1}{z},\quad \frac{dz}{dx} = 3x^{2} \] が分かり、ここから \[ \frac{dy}{dx} = \frac{3x^{2}}{a+x^{3}} \] を得る。
\(\text{(6)}\) \(y=\log_e\{{3x^{2}+\sqrt{a+x^{2}}}\}\)
\(3x^{2} + \sqrt{a+x^{2}}=z\) とすれば \(y = \log_{e} z\) だから、次が分かる: \[ \begin{aligned} \frac{dy}{dz} &= \frac{1}{z}, \quad \frac{dz}{dx} = 6x + \frac{x}{\sqrt{x^{2}+a}} \\ \frac{dy}{dx} &= \frac{6x + \dfrac{x}{\sqrt{x^{2}+a}}}{3x^{2} + \sqrt{a+x^{2}}} = \frac{x(1 + 6\sqrt{x^{2}+a})}{(3x^{2} + \sqrt{x^{2}+a}) \sqrt{x^{2}+a}} \end{aligned} \]
\(\text{(7)}\) \(y=(x+3)^{2} \sqrt{x-2}\) \[ \log_e y = 2 \log_e(x+3)+ \frac{1}{2} \log_e(x-2) \qquad \qquad \] より \[ \begin{aligned} \frac{1}{y}\, \frac{dy}{dx} &= \frac{2}{(x+3)} + \frac{1}{2(x-2)} \\ \frac{dy}{dx} &= (x+3)^{2} \sqrt{x-2} \left\{\frac{2}{x+3} + \frac{1}{2(x-2)}\right\} \end{aligned} \] が分かる。
\(\text{(8)}\) \(y=(x^{2}+3)^{3}(x^{3}-2)^{\frac{2}{3}}\)
\[ \log_e y = 3 \log_e(x^{2}+3) + \frac{2}{3} \log_e(x^{3}-2) \] より \[ \frac{1}{y}\, \frac{dy}{dx} = 3 \frac{2x}{(x^{2}+3)} + \frac{2}{3} \frac{3x^{2}}{x^{3}-2} = \frac{6x}{x^{2}+3} + \frac{2x^{2}}{x^{3}-2} \] となる。\(u = \log_e(x^{2}+3)\) の微分の計算は次のようにする。\(x^{2} + 3 = z\) とすれば \(u=\log_e z\) だから \[ \frac{du}{dz} = \frac{1}{z},\quad \frac{dz}{dx} = 2x,\quad \frac{du}{dx} = \frac{2x}{x^{2}+3} \] が分かる。同様に \(v=\log_e(x^{3}-2)\) なら \(\dfrac{dv}{dx} = \dfrac{3x^{2}}{x^{3}-2}\) だと計算できるから \[ \frac{dy}{dx} = (x^{2}+3)^{3}(x^{3}-2)^{\frac{2}{3}} \left\{ \frac{6x}{x^{2}+3} + \frac{2x^{2}}{x^{3}-2} \right\} \] を得る。
\(\text{(9)}\) \(y = \dfrac{\sqrt[2]{x^{2} + a}}{\sqrt[3]{x^{3} - a}}\)
\[ \begin{aligned} \log_e y &= \frac{1}{2} \log_e(x^{2}+a) - \frac{1}{3} \log_e(x^{3}-a), \\ \frac{1}{y}\, \frac{dy}{dx} &= \frac{1}{2}\, \frac{2x}{x^{2}+a} - \frac{1}{3}\, \frac{3x^{2}}{x^{3}-a} = \frac{x}{x^{2}+a} - \frac{x^{2}}{x^{3}-a} \\ \end{aligned} \] より次が分かる: \[ \begin{aligned} \frac{dy}{dx} &= \frac{\sqrt[2]{x^{2}+a}}{\sqrt[3]{x^{3}-a}} \left\{ \frac{x}{x^{2}+a} - \frac{x^{2}}{x^{3}-a} \right\} \end{aligned} \]
\(\text{(10)}\) \(y = \dfrac{1}{\log_e x}\)
\[ \frac{dy}{dx} = \frac{\log_e x \times 0 - 1 \times \dfrac{1}{x}} {\log_e^{2} x} = -\frac{1}{x \log_e^{2}x} \]
\(\text{(11)}\) \(y = \sqrt[3]{\log_e x} = (\log_e x)^{\frac{1}{3}}\)
\(z = \log_e x\) とすれば \(y = z^{\frac{1}{3}}\) が成り立つ。よって \[ \frac{dy}{dz} = \frac{1}{3} z^{-\frac{2}{3}},\quad \frac{dz}{dx} = \frac{1}{x},\quad \frac{dy}{dx} = \frac{1}{3x \sqrt[3]{\log_e^{2} x}} \] を得る。
\(\text{(12)}\) \(y=\left(\dfrac{1}{a^x}\right)^{ax}\)
\[ \begin{aligned} \log_e y &= ax(\log_e 1 - \log_e a^x) = -ax \log_e a^x, \\ \frac{1}{y}\, \frac{dy}{dx} &= -ax \times a^x \log_e a - a \log_e a^x \end{aligned} \] より \[ \begin{aligned} \frac{dy}{dx} &= -\left(\frac{1}{a^x}\right)^{ax} (x \times a^{x+1} \log_e a + a \log_e a^x). \end{aligned} \] が分かる。
では次の練習問題を解いてみよ。
練習問題 XII
解答はここにある。
\(\text{(1)}\) \(y=b(e^{ax} -e^{-ax})\) を微分せよ。
\(\text{(2)}\) \(u=at^{2}+2\log_e t\) の \(t\) に関する微分係数を求めよ。
\(\text{(3)}\) \(y = n^{t}\) とする。\(\dfrac{d(\log_e y)}{dt}\) を求めよ。
\(\text{(4)}\) \(y=\dfrac{1}{b}\cdot\dfrac{a^{bx}}{\log_e a}\) なら \(\dfrac{dy}{dx}=a^{bx}\) だと示せ。
\(\text{(5)}\) \(w=pv^n\) とする。\(\dfrac{dw}{dv}\) を求めよ。
次の関数を微分せよ:
\(\text{(13)}\) ケルビン卿の発見によると、海底ケーブルを伝わる信号の速さは中心部の外径とそれを囲む銅線の半径の比に依存する。この比を \(y\) とすると、一分間あたりに送信できる信号の数 \(s\) は \[ s = ay^{2} \log_e \frac{1}{y} \] と表される。ここで \(a\) は定数であり、ケーブルの質と長さによって決まる。このとき \(s\) が \(y=1 ÷ \sqrt{e}\) で最大になることを示せ。
\(\text{(14)}\) 次の関数の極大値と極小値を求めよ: \[ y=x^{3}-\log_e x \]
\(\text{(15)}\) \(y=\log_e(axe^x)\) を微分せよ。
\(\text{(16)}\) \(y=(\log_e ax)^{3}\) を微分せよ。
対数曲線
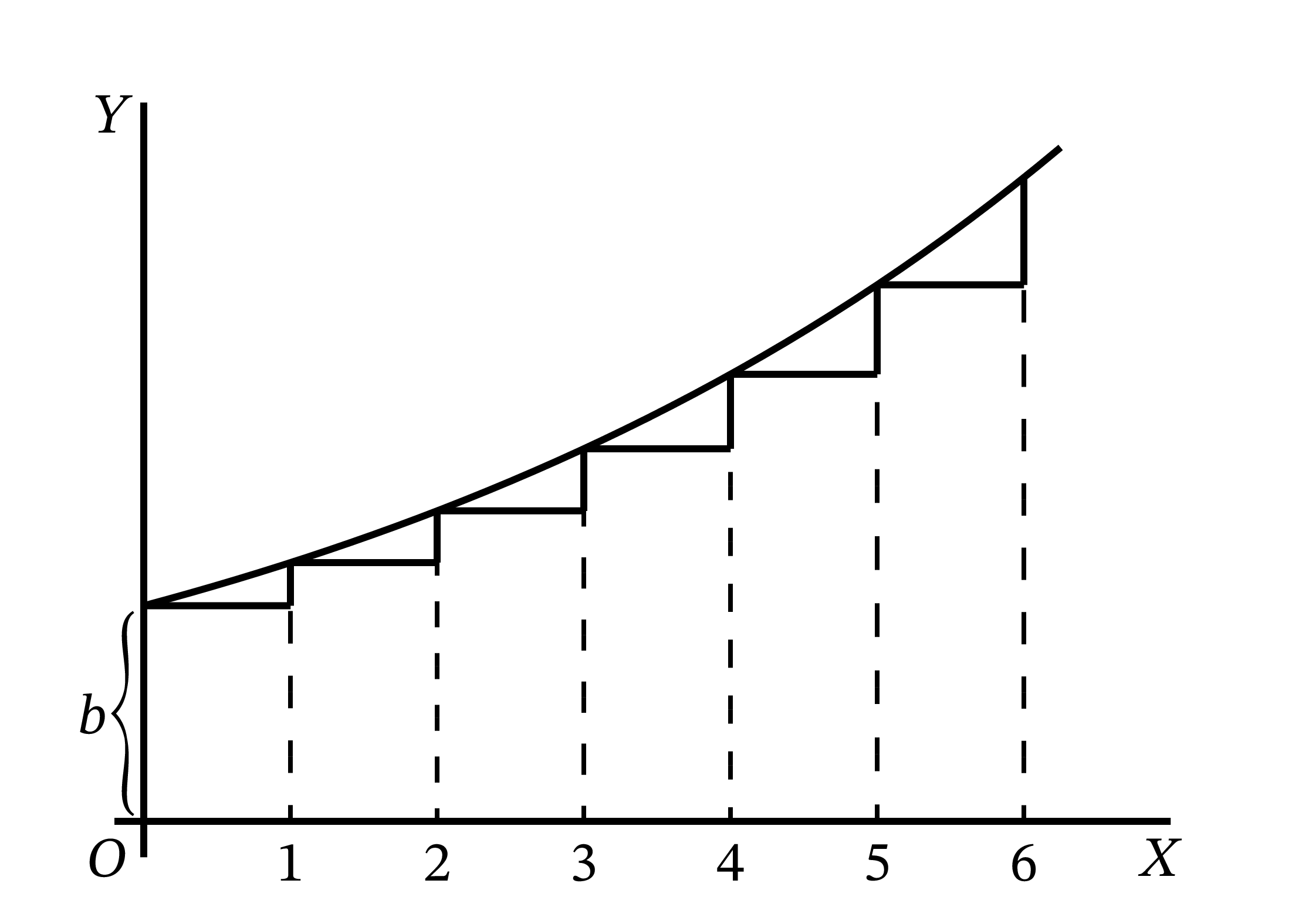
方程式 \(y = bp^{x}\) で表される、\(y\) 座標が幾何的に増加する曲線を考える。
\(x = 0\) を代入すれば、グラフの最初の高さが \(y\) だと分かる。さらに \[ \begin{aligned} x &= 1 \quad {\footnotesize \text{のとき}} & y &= bp \\ x &= 2 \quad {\footnotesize \text{のとき}} & y &= bp^{2} \\ x &= 3 \quad {\footnotesize \text{のとき}} & y &= bp^{3} \\ \end{aligned} \] も分かる。
つまり \(x\) 座標が整数の点を考えたとき、隣り合う二点の \(y\) 座標の比は \(p\) となる。図 40 では \(p\) を \(\dfrac{6}{5}\) としており、縦線を一つ右に移動するたびに \(y\) 座標は \(\dfrac{6}{5}\) になる。
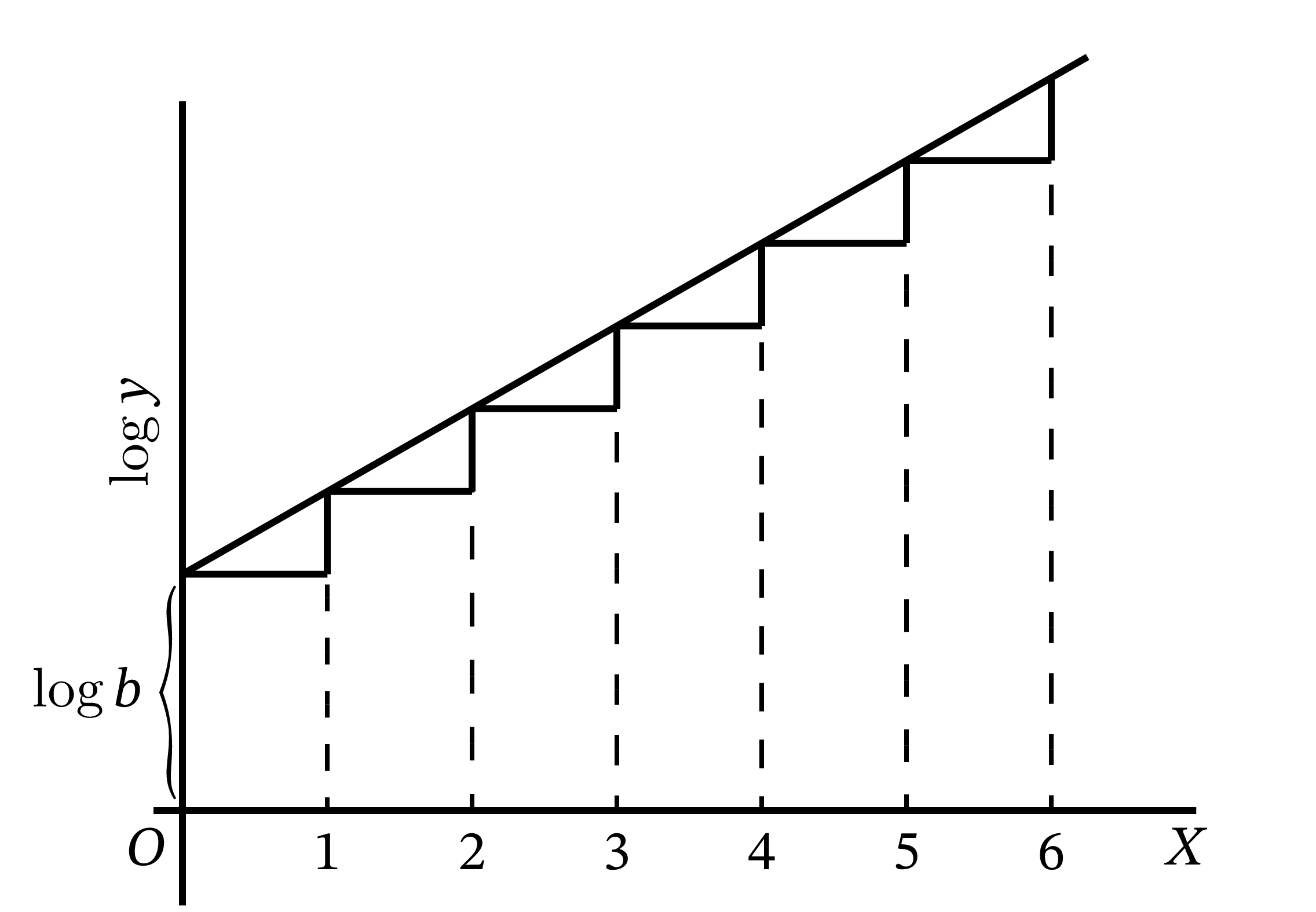
隣り合う点の \(y\) 座標が一定の比で結ばれているなら、\(y\) 座標の対数は一定の差で結ばれる。よって \(y\) 座標が \(\log_{e} y\) の点をプロットすると、傾きが常に一定の曲線、つまり直線となる (図 41)。この事実は次の等式からも分かる: \[ \begin{aligned} \log_e y &= \log_e b + x \cdot \log_e p \\ \log_e y &- \log_e b = x \cdot \log_e p \end{aligned} \] \(\log_{e} p\) はただの定数だから、\(\log_e p=a\) とできる。すると \[ \log_e \frac{y}{b}=ax \] となる。ここから最初の等式が次の形で表せると分かる: \[ y = be^{ax} \]
減衰曲線
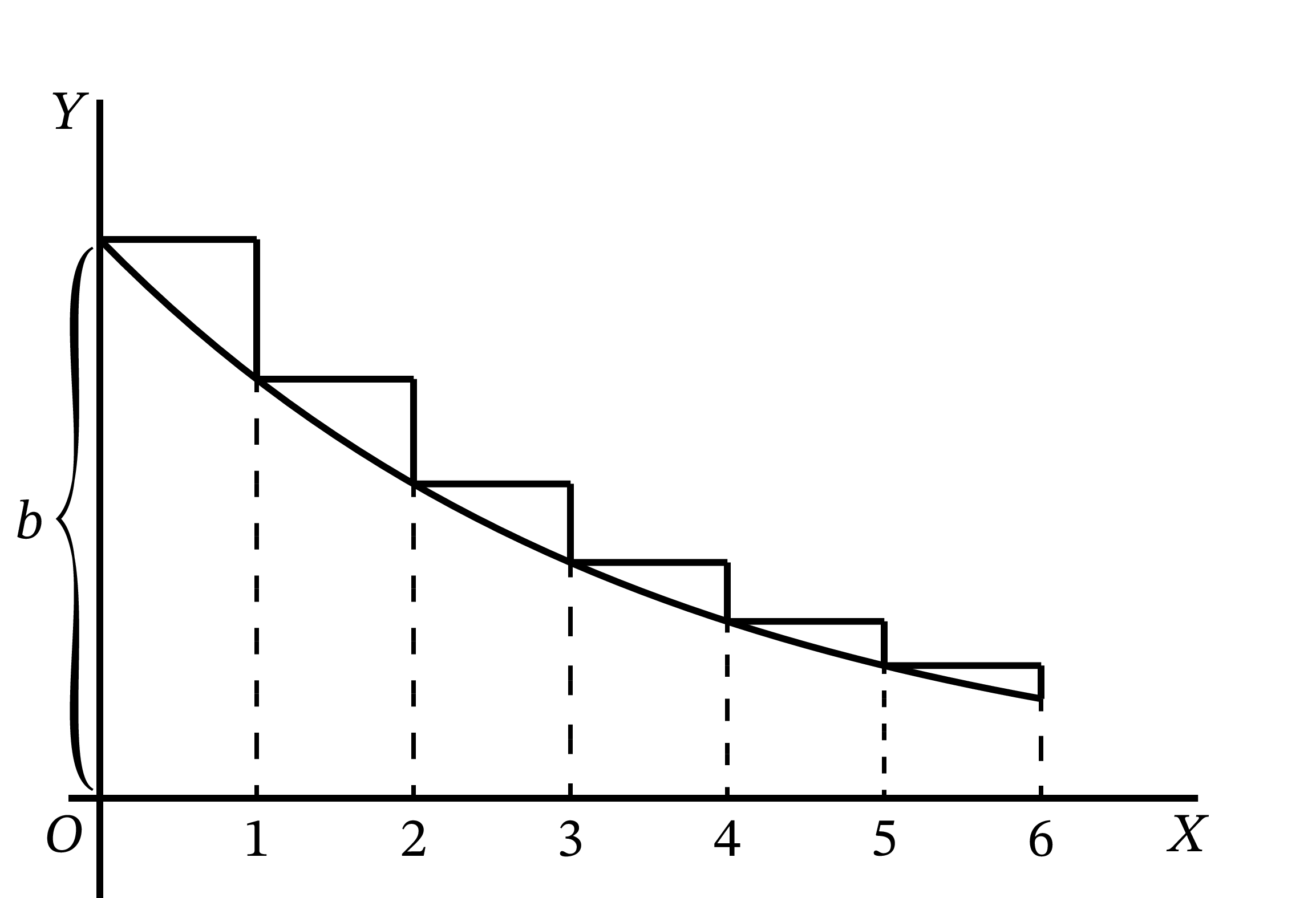
\(p\) を真分数 (\(1\) より小さい分数) とすると、曲線 \(y = bp^{x}\) は下を向く。隣り合う点の \(y\) 座標が一つ前の \(\dfrac{3}{4}\) となっている曲線を 図 42 に示す。
この場合でも方程式は \[ y = bp^x \] で変わらないものの、\(p\) が \(1\) より小さいので \(\log_{e} p\) は負になる。\(-a = \log_{e} p\) とすれば \(p = e^{-a}\) となり、この減衰曲線 (die-away curve) を表す方程式は \[ y = be^{-ax} \] と表される。
この式が重要なのは、独立変数を時間と解釈すると、実に様々な少しずつ量が減少する過程を表せるためである。例えば高温物体の冷却を表す方程式 (ニュートンの冷却の法則) は \[ \theta_t = \theta_0 e^{-at} \] と表せる。\(\theta_{0}\) は最初の時点における物体と周りの温度差を表し、\(\theta_{t}\) は \(t\) 秒が経過したときの温度差を表す。\(a\) は減衰定数 (constant of decrement) と呼ばれる定数であり、物体の表面積・伝導率・放射率などに依存する。
似た方程式 \[ Q_t=Q_0 e^{-at} \] は帯電体の電荷量を表す。電荷量は最初 \(Q_{0}\) であり、減衰定数は \(a\) である。\(a\) は物体の静電容量や漏電路の抵抗に依存する。
ばねを引っ張ったときに生まれる振動は時間と共に小さくなるが、その振幅の減衰も同じ方程式で表せる。
ある量の減少速度が量そのものに比例するなら、\(e^{-at}\) はその現象の減衰項 (die-away factor) として利用できる。これまでの言葉を使ってこの条件を言い換えれば「微分係数 \(\dfrac{dy}{dt}\) が常に \(y\) の定数倍である」となる。図 42 の曲線では任意の点で傾き \(\dfrac{dy}{dx}\) が高さ \(y\) に比例しており、\(y\) が大きくなるにつれて曲線は水平に近づく。数式で表せば \[ y = be^{-ax} \] つまり \[ \log_e y = \log_e b - ax \log_e e = \log_e b - ax \] であり、微分すれば \[ \begin{gathered} \frac{1}{y}\, \frac{dy}{dx} = -a \\ \frac{dy}{dx} = -ay \end{gathered} \] となる。つまり傾きは負で \(y\) に比例し、比例定数は \(a\) である。
同じ結果を得る変形をもう一つ示す。 \[ y = bp^x \] より \[ \frac{dy}{dx} = bp^x \times \log_e p \] が分かる。一方で \[ \log_{e} p = -a \] からは \[ \frac{dy}{dx} = y \times (-a) = -ay \] が得られる。
時定数: 減衰項 \(e^{-at}\) において、\(a\) の逆数を時定数 (time-constant) と呼び、\(T\) で表す。減衰項は時定数を使って \(e^{-\frac{t}{T}}\) と表せる。\(t = T\) とすれば減衰項は \(e^{-1}\) だから、時定数 \(T\) は初期値 (上の例における \(\theta_{0}\) や \(Q_{0}\)) が \(\dfrac{1}{e} = 0.3678\) 倍まで減少するのにかかる時間を表す。
\(e^{x}\) と \(e^{-x}\) は物理の様々な分野で必要となるが、数表には載っていないことが多い。いくつかの値を次に示しておく。
この数表の使用例として、高温の物体を冷却する実験を考える。最初 (\(t = 0\) のとき) 物体は周囲よりも \(72^{\circ}\) 高温で、冷却の時定数 (つまり温度が \(72^{\circ}\) の \(\dfrac{1}{e}\) になるのにかかる時間) が \(20\) 分だとする。このとき任意の時間 \(t\) における物体の温度を計算できる。例えば \(t\) が \(60\) 分なら \(\dfrac{t}{T} = 60 ÷ 20 = 3\) だから、\(e^{-3}\) の値に初期値 \(72^{\circ}\) を掛ければ温度が求まる。数表によると \(e^{-3} = 0.0498\) だから、\(60\) 分後の周囲との温度の差は \(72^{\circ} \times 0.0498 = 3.586^{\circ}\) と求まる。
例
\(\text{(1)}\) 導体に起電力を加えてから \(t\) 秒後の電流の大きさは \(C = \dfrac{E}{R}\left\{1 - e^{-\frac{Rt}{L}}\right\}\) と表される。
時定数は \(\dfrac{L}{R}\) である。
さらに \(E = 10,\ \) \(R = 1,\ \) \(L = 0.01\) とすれば、\(t\) が非常に大きいとき \(e^{-\frac{Rt}{L}}\) は \(0\) に等しく、\(C = \dfrac{E}{R} = 10\) となる。また時定数は \[ \frac{L}{R} = T = 0.01 \] であり、任意の時間における \(C\) の値は \[ C = 10 - 10e^{-\frac{t}{0.01}} \] と表される。つまり \(0.01\) 秒が経過すると、変動する項が初期値 \(10e^{-\frac{0}{0.01}} = 10\) の \(\dfrac{1}{e} = 0.3678\) 倍となる。
例えば \(t = 0.001\) 秒では \(\dfrac{t}{T} = 0.1\) であり、数表から \(e^{-0.1} = 0.9048\) と分かる。つまり \(0.001\) 秒経過後の変動項は \(0.9048 \times 10 = 9.048\) であり、電流は \(10 - 9.048 = 0.952\) アンペアとなる。
同様に \(0.1\) 秒が経過した時点では \[ \frac{t}{T} = 10, \quad e^{-10} = 0.000045 \] であり、変動する項は \(10 \times 0.000045 = 0.00045\) で電流は \(9.9995\) アンペアとなる。
\(\text{(2)}\) 光線が厚さ \(l\, {\footnotesize\text{cm}}\) の透明な媒質を通り抜けるとき、通過後の光の強さ \(I\) は \(I = I_{0}e^{-Kl}\) を満たす。ここで \(I_{0}\) は最初の光の強さであり、\(K\) は「吸収定数」を表す。
定数 \(K\) の値は通常実験で求める。例えば厚さ \(10\, {\footnotesize\text{cm}}\) の特定の媒質を通過した光線の強さを測定したところ、最初の \(18{\footnotesize \text{\%}}\) だったとする。この実験結果は \(82 = 100 \times e^{-K \times 10}\) つまり \(e^{-10K} = 0.82\) を意味する。数表を使えばほぼ \(10K = 0.20\) だと分かるから、\(K = 0.02\) が求まる。
光の強さを半分にする厚さを求めるには、\(50 = 100 \times e^{-0.02l}\) を満たす \(l\) の値を計算する必要がある。この条件を変形すれば \(0.5 = e^{-0.02l}\) だから、対数を取ることで \[ \log 0.5 = -0.02 \times l \times \log e \] が分かる。よって近似的に \[ l = \frac{-0.3010}{-0.02 \times 0.4343} = 34.7\, {\footnotesize\text{cm}} \] が求まる。
\(\text{(3)}\) 放射性物質のまだ遷移していない部分の質量 \(Q\) と初期質量 \(Q_{0}\) の間には \(Q = Q_{0} e^{-\lambda t}\) という関係がある。\(\lambda\) は定数で、\(t\) は遷移が始まってからの経過時間を表す。
“ラジウム A” と呼ばれる物質では、時間が秒で表されるとき \(\lambda = 3.85 \times 10^{-3}\) であることが実験で分かっている。物質の半分が遷移するのにかかる時間を求めよう。この時間を放射性物質の半減期 (half-life) と呼ぶ。
\(0.5 = e^{-0.00385t}\) となる \(t\) を求めればよいから、 \[ \log 0.5 = -0.00385t \times \log e \] より近似的に \(t = 3\) だと分かる。
練習問題 XIII
解答はここにある。
\(\text{(1)}\) \(b = 12,\ \) \(T = 8\) として曲線 \(b e^{-\frac{t}{T}}\) を \(t = 0\) から \(t = 20\) まで描け。
\(\text{(2)}\) とある高温の物体の温度が低下しており、周囲との温度差が半分になるまでの時間が \(24\) 分だという。時定数を求め、温度差が初期値の \(1{\footnotesize \text{\%}}\) となるまでの時間を求めよ。
\(\text{(3)}\) 曲線 \(y = 100(1 - e^{-2t})\) をプロットせよ。
\(\text{(4)}\) 次の三つの方程式は非常によく似た曲線を表す: \[ \begin{aligned} \text{(i)}\quad y &= \frac{ax}{x + b} \\ \text{(ii)}\quad y &= a(1 - e^{-\frac{x}{b}}) \\ \text{(iii)}\quad y &= \frac{a}{90^{\circ}} \arctan \left(\frac{x}{b}\right) \end{aligned} \] \(a = 100\, {\footnotesize\text{mm}}\) および \(b = 30\, {\footnotesize\text{mm}}\) として三つの曲線を描け。
\(\text{(5)}\) 次の関数のそれぞれについて、\(x\) に関する \(y\) の微分係数を求めよ: \[ (\textit{a})~y = x^x\quad (\textit{b})~y = (e^x)^x\quad (\textit{c})~y = e^{x^x} \]
\(\text{(6)}\) “トリウム A” と呼ばれる物質では \(\lambda = 5\) である。トリウム A の半減期を求めよ。半減期とは、遷移による減少が次式で表されるトリウム A の質量 \(Q\) が初期値 \(Q_{0}\) の半分になるまでの時間を言う: \[ Q = Q_0 e^{-\lambda t} \] \(t\) の単位は秒とする。
\(\text{(7)}\) 容量 \(K = 4 \times 10^{-6}\) ファラッドのコンデンサを \(V_{0} = 20\) ボルトで充電し、その後 \(10{,}000\) オームの抵抗を通じて放電する。放電を始めてから \(\text{(a)}\) \(0.1\) 秒後および \(\text{(b)}\) \(0.01\) 秒後の電圧 \(V\) を求めよ。電圧の減少は \(V = V_0 e^{-\frac{t}{KR}}\) という関係を満たすとする。
\(\text{(8)}\) 帯電した鉄球を絶縁して放置したところ、電荷 \(Q\) が \(10\) 分間で \(20\) 単位から \(16\) 単位まで減少した。電荷が \(Q = Q_{0} \times e^{-\mu t}\) と表されるとして、喪失係数 \(\mu\) を求めよ。\(Q_{0}\) は最初の電荷、\(t\) は経過秒数とする。電荷の半分が喪失するまでの時間を求めよ。
\(\text{(9)}\) 電話線を伝わる信号の減衰は \(i = i_0 e^{-\beta l}\) という関係から計算できる。\(i\) は \(t\) 秒後の電話信号の強さで、\(i_{0}\) はその初期値を表す。\(l\) は電話線の長さ (キロメートル) で、\(\beta\) は定数を表す。1910 年に敷設されたフランス–イギリス間の海底ケーブルでは \(\beta = 0.0114\) だと分かっている。このケーブルの両端 (\(40\) キロメートル) における減衰を求めよ。また元の信号の \(80{\footnotesize \text{\%}}\) が保たれる距離を求めよ (特に品質の高い通話のためにはこの数値が必要になる)。
\(\text{(10)}\) 高度 \(h\) キロメートルにおける大気圧 \(p\) は \(p = p_0 e^{-kh}\) で与えられる。\(p_{0}\) は海抜における大気圧 (\(760\) 水銀柱ミリメートル) を表す。
高度 \(10,\ \) \(20,\ \) \(50\) キロメートルにおける大気圧が \(199.2,\ \) \(42.2,\ \) \(0.32\) 水銀柱ミリメートルだとして、それぞれの値を使って \(k\) を計算し、平均からの誤差を求めよ。
\(\text{(11)}\) \(y = x^{x}\) の極大値または極小値を求めよ。
\(\text{(12)}\) \(y = x^{\frac{1}{x}}\) の極大値または極小値を求めよ。
\(\text{(13)}\) \(y = xa^{\frac{1}{x}}\) の極大値または極小値を求めよ。