XVII. 積分

\(\displaystyle \int\) という摩訶不思議な記号の意味は第一章で説明した。これは上下に伸ばした \(S\) であり、「...の和」あるいは「...という条件を満たす値の和」を意味する。\(\displaystyle \int\) は同じく和を表す記号 \(\sum\) と似ているが、数学の世界では一つ違いがある。\(\sum\) は有限の大きさを持つ値を有限個足し合わせた和を表すのに対して、積分の記号 \(\displaystyle \int\) は無限に小さい値を無限個足し合わせた和を表す。積分が足し上げる無限に小さい値とは考えている値の小部分であり、例えば \(\displaystyle \int dy = y\) や \(\displaystyle \int dx = x\) が成り立つ。

どんなものであれ全体は小さな部分に分けられること、そして分かれる部分が小さくなれば部分の個数が増えることは理解できると思う。例えば \(1\) インチの線分は長さ \(\dfrac{1}{10}\) インチの部分 \(10\) 個で構成されると考えることもできるし、\(\dfrac{1}{100}\) インチが \(100\) 個とも、\(\dfrac{1}{1{,}000{,}000}\) インチが \(1{,}000{,}000\) 個とも考えることができる。分割を限りなく細かくすれば、無限に小さい部分が無限個集まっていると考えることもできる。

「なるほど」とあなたは言うだろう。そして「で、そうして何の役に立つのか？ 全体を一つとして考えて何がいけないのか？」と続けるに違いない。そうする理由は、全体を考えては大きさを計算できず、小さな部分への分割を考えてから足すことで始めて計算が可能になる値が実に多く存在するためである。積分 (integration) という手続きを使うと、他の方法では直接計算できない和が計算可能になる。

まずは簡単な例をいくつか使って、小さな部分を足すという考え方に慣れよう。

次の級数を考える: \[ 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \cdots \] 級数の各項は一つ前の項の半分となっている。

項を無限に足したときの和はいくつだろうか？ この和が \(2\) になることは中学生なら誰でも知っている。\(1\) インチから始めて \(\dfrac{1}{2}\) インチを足し、\(\dfrac{1}{4}\) インチを足し、\(\dfrac{1}{8}\) インチを足すという処理をどこまで続けても \(2\) になることはないが、和と \(2\) は最後に足した数と同じだけ離れる。例えば \(1,\ \) \(\dfrac{1}{2},\ \) \(\dfrac{1}{4}\) を足した和 \(\dfrac{3}{4}\) は \(2\) と \(\dfrac{1}{4}\) だけ離れ、\(\dfrac{1}{64}\) まで続ければ \(\dfrac{1}{64}\) だけ離れる。項を無限に足せば和は \(2\) に無限に近づき、見分けがつかなくなる。実際十項も足せば \(2\) との差は \(\dfrac{1}{1024}\) インチとなり、肉眼では違いが分からない。第二十項まで取れば差はホイットワース¹の測定器具でも測れないほどになり、顕微鏡で見分けが付かなくなるには十八項で十分である！ 無限に続く足し算もそう難しいものではない。積分とは本当に無限に足した和であり、これから見るように積分を使わなければ無限に足した和を正確に計算できない場合がある。積分を使わずにそういった和を近似するとなれば関数の値をいくつも計算してさらに補間をしなければならないが、積分法があれば和を簡単に直接求めることができる。つまり積分の計算方法を学んでおいて損はない。

曲線とその傾き

まず曲線の傾きに関する前提知識を確認しよう。曲線を微分すると (任意の点における) 傾きを表す式が得られることはこれまでに説明した。では各点における傾きから曲線を復元するという逆の処理は可能だろうか？

第十章の例 \(\text{(2)}\) をもう一度考える。この例では傾きを持つ直線という最も単純な曲線を扱った。この曲線は \[ y = ax + b \] という方程式で表される。

\(b\) は \(x = 0\) に対応する点の高さを表し、\(a\) は直線の傾き \(\dfrac{dy}{dx}\) に等しいことを私たちは知っている。この曲線は一定の傾きを持ち、直線に沿った直角三角形 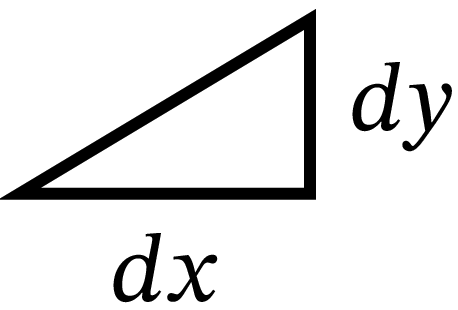をどこに作ったとしても底辺と高さの比が等しい。ここで \(dx\) と \(dy\) を有限の長さを持ち、\(dx\) の十倍が一インチだとすると、同じ形の三角形が十個得られる:

\(\dfrac{dy}{dx} = a\) という情報、つまりこの \(10\) 個の三角形から直線という “曲線” を復元するよう言われたら、何ができるだろうか？ このときには \(dx\) と \(dy\) を底辺と高さに持つ直角三角形を 図 48 のように端を合わせて並べることができる。すると傾きが \(\dfrac{dy}{dx} = a\) で一定なので、小さな三角形の斜辺全体が直線を構成する。\(dy\) と \(dx\) が有限の大きさを持つとしても無限に小さいとしても比は変わらず、\(dy\) の和 \(y\) と \(dx\) の和 \(x\) に対して \(\dfrac{y}{x} = a\) が必ず成り立つ。

ではこの傾きを持つ直線をどこに配置すべきだろうか？ \(x = 0\) で曲線が通るのは原点 \(O\) か、それとももっと上か？ 与えられたのは曲線の傾きに関する情報だけなので、この曲線が \(O\) のどれぐらい上 (あるいは下) を通るのかは示されていない。つまり \(x = 0\) における高さは決定できず、傾きが一定なことだけが分かる。そこで \(x = 0\) における高さを適当に \(C\) とおこう。すると直線の方程式は \[ y = ax + C \] となる。こう書けば \(x = 0\) における \(y\) の値が後から足される定数である点がはっきりする。

さらに難しい場合を次に考えよう。傾きが一定ではなく、\(x\) に比例して増えるとする。数式で表せば \[ \frac{dy}{dx} = ax \] である。具体的に \(a = \dfrac{1}{5}\) として \[ \frac{dy}{dx} = \frac{1}{5} x \] を考える。

まず異なる \(x\) における傾きを計算するところから始めよう。さらに前の例で示した傾きを表す三角形も描いておく:

\(x = 0\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 0.0 \quad\)

\(x = 1\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 0.2 \quad\)

\(x = 2\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 0.4 \quad\)

\(x = 3\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 0.6 \quad\)

\(x = 4\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 0.8 \quad\)

\(x = 5\quad {\footnotesize \text{のとき}} \quad\) \(\dfrac{dy}{dx} = 1.0 \quad\)

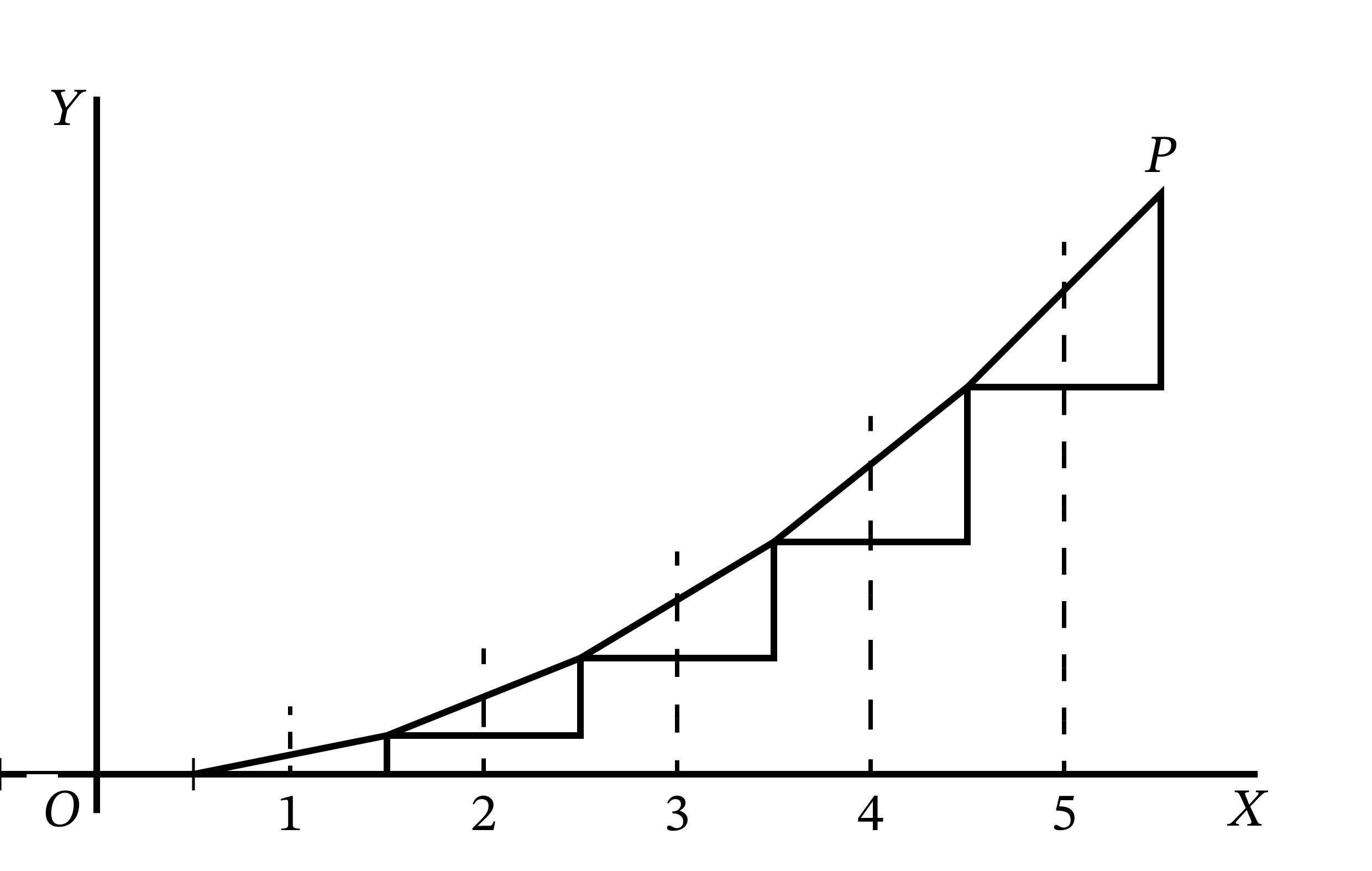
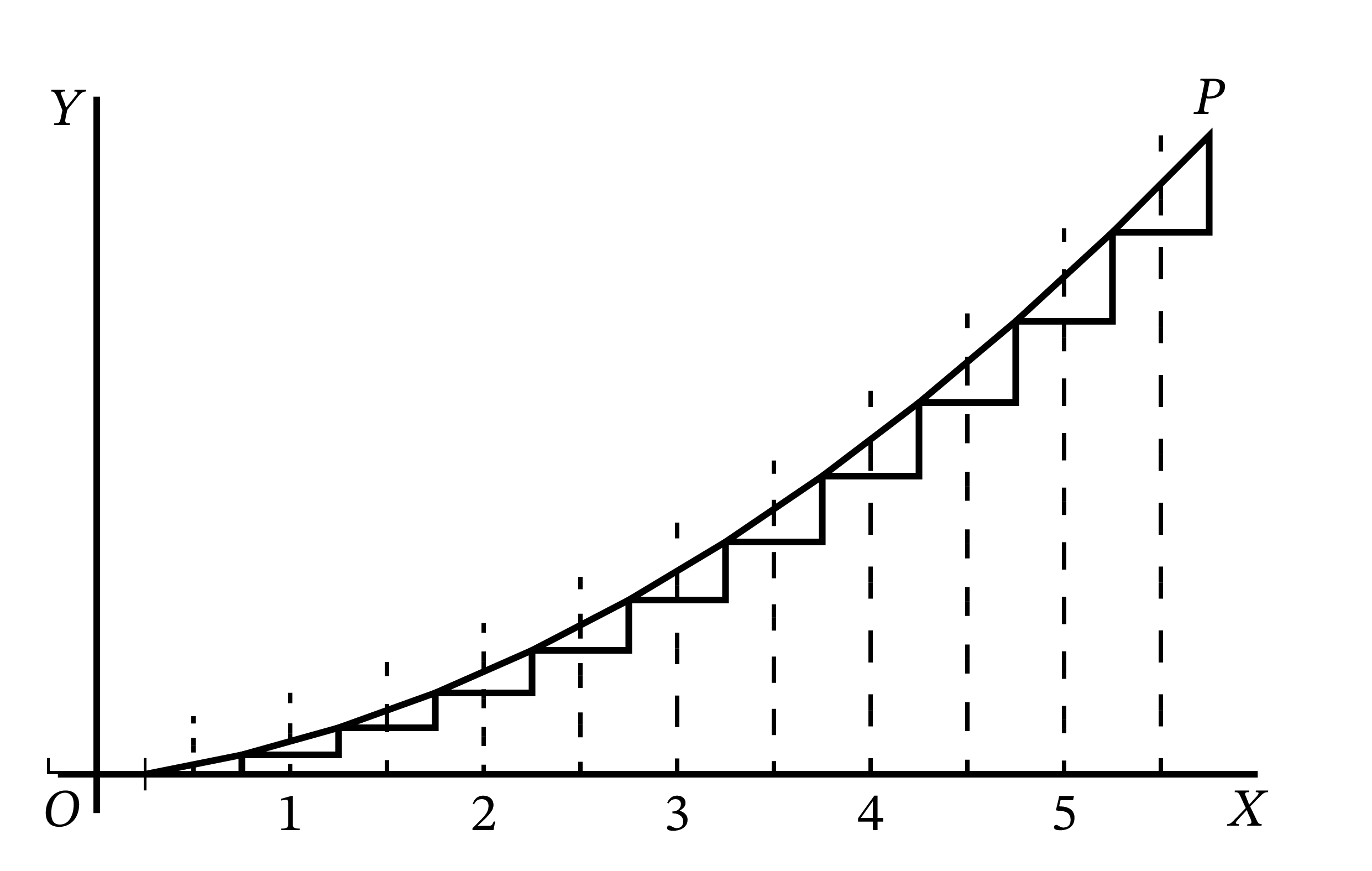
これらの三角形を底辺が \(x\) 軸と平行で斜辺同士がつながるように並べると 図 49 のようになる。三角形を並べて得られる曲線はもちろん滑らかでないが、求める曲線の近似となっている。横幅を半分にすると三角形の数は倍になり、さらに正確な近似曲線が得られる (図 50)。しかし正確な曲線を得るには、\(dx\) と \(dy\) を無限に小さく取って無限に多くの三角形を並べなければならない。

任意の \(x\) に対する \(y\) はいくらだろうか？ 曲線上の適当な点 \(P\) の高さ \(y\) を求めるには、その点までの \(dy\) を \(0\) からその高さまで全て足す必要がある。等式 \(\displaystyle \int dy = y\) がこの事実を表す。今の例では \(dy\) が任意の点で \(\dfrac{1}{5}x \cdot dx\) に等しいから、\(y = \displaystyle \int \frac{1}{5}x \cdot dx\) となる。

もし \(x\) が定数なら \(\displaystyle \int \frac{1}{5}x \cdot dx\) は \(\dfrac{1}{5}x \displaystyle \int dx = \dfrac{1}{5} x^2\) に等しい。しかし \(x\) は \(0\) から始まって \(P\) の \(x\) 座標 \(x\) まで増加するので、その平均値は \(\dfrac{1}{2}x\) である。よって \(\displaystyle \int \frac{1}{5} x\, dx = \frac{1}{10} x^{2}\) つまり \(y = \dfrac{1}{10}x^2\) が分かる。

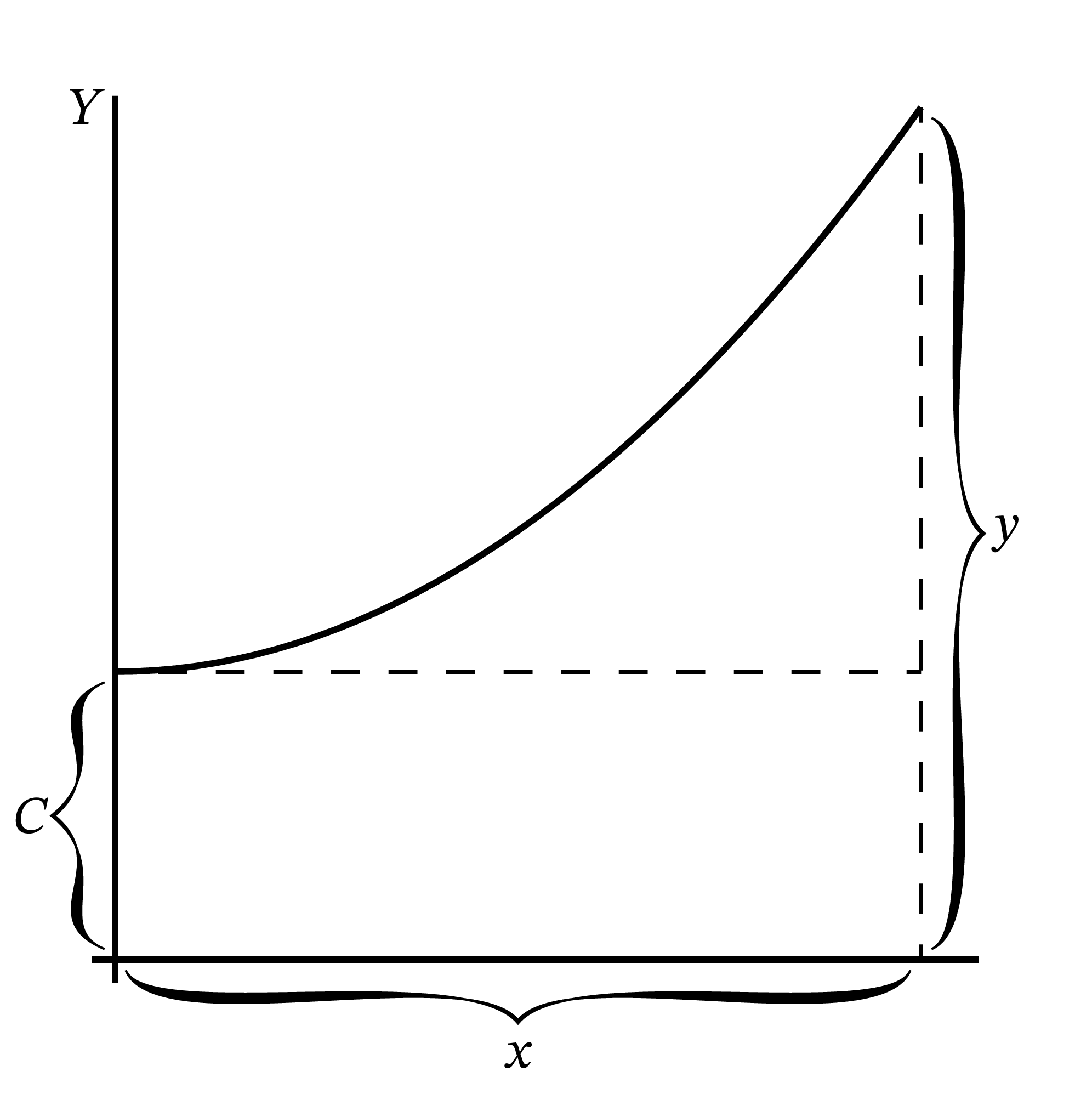
ただし一つ前の例と同じように、不定の定数 \(C\) を足す必要がある。曲線が \(x = 0\) で原点を通るとは言われていないためである。つまり 図 51 にある曲線を表す \[ y = \frac{1}{10}x^{2} + C \] が最終的な答となる。

練習問題 XVI

解答はここにある。

\(\text{(1)}\) \(\dfrac{2}{3} + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{12} + \dfrac{1}{24} + \cdots\) を全て足した和を求めよ。

\(\text{(2)}\) 級数 \(1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{5} - \dfrac{1}{6} + \dfrac{1}{7} + \cdots\) が収束すると示し、最初の \(8\) 項を取った和を求めよ。

\(\text{(3)}\) \(\log_e(1+x) = x - \dfrac{x^{2}}{2} + \dfrac{x^{3}}{3} - \dfrac{x^{4}}{4} + \cdots\) が成り立つ。この事実を使って \(\log_e 1.3\) を求めよ。

\(\text{(4)}\) この章で説明したのと同じ議論を使って、\(\dfrac{dy}{dx}\) が次の式で表されるときの \(y\) を求めよ: \[ \text{(a)}\ \frac{dy}{dx} = \frac{1}{4} x\quad \text{(b)}\ \frac{dy}{dx} = \cos x \]

\(\text{(5)}\) \(\dfrac{dy}{dx} = 2x + 3\) とする。\(y\) を求めよ。

1. 訳注: ジョセフ・ホイットワース (1803–1887) はイギリスの工学者・技術者で、ねじ規格の考案や精密測定器具の発明で知られる。^[return]