2.4 誤り検出

第 1 章で議論したように、電気的干渉や熱雑音などが原因でフレームにビット誤りが入り込むことがある。ビット誤りは稀であるものの、訂正処理を行うためにビット誤りを検出する何らかの仕組みが必要になる。その仕組みが無ければ、エンドユーザーは「先ほど正しくコンパイルできた C プログラムがネットワーク越しにコピーしただけで構文エラーが出るようになったのはなぜだ？」と頭を悩ませることになるだろう。

コンピューターシステムで発生するビット誤りに対処するテクニックには、少なくとも 1940 年代から続く長い歴史がある。重要なものにハミング符号 (Hamming code) とリード・ソロモン符号 (Reed-Solomon code) がある。この二つのテクニックはデータを磁気ディスクや磁気コアメモリに保存していた時代にパンチカードリーダーで使うために開発された。本節ではネットワークでよく利用される誤り検出テクニックをいくつか見る。

誤りの検出は問題の片側でしかない。もう片側には、検出された誤りを訂正する問題がある。メッセージの誤りを検出した受信側が取れるアプローチは大きく分けて二つある。まず、メッセージが破損したことを送信側に通知し、送信側にメッセージのコピーを再送するよう頼むアプローチがある。ビット誤りが稀なら、再送されたメッセージはまず間違いなく誤りを含まないだろう。次に、破損したメッセージを受け取った受信側が自力でメッセージを訂正できるような誤り検出アルゴリズムを使うアプローチがある。そういったアルゴリズムが利用するのは ECC (error-correcting codes, 誤り訂正符号) であり、本節で説明される。

転送中に発生するビット誤りを検出する最もよく知られた手法の一つに CRC (cyclic redundancy check, 巡回冗長検査) がある。CRC は本章で議論されるリンクレベルのプロトコルのほぼ全てで使われている。本節では基本的な CRC のアルゴリズムを説明する。ただ、CRC の説明に入る前に、CRC より単純なチェックサム (checksum) と呼ばれる誤り検出手法をまず説明する。チェックサムはインターネットアーキテクチャに含まれるいくつかのプロトコルで利用される。

全ての誤り検出手法の裏には「誤りが入り込んだかどうかの判定に利用できる冗長な情報をフレームに追加する」という考え方がある。極端なことを言えば、データの完全なコピーを二つ送れば誤りは減らせる: もし全く同じコピーが二つ受信側に届いたなら、両方とも正しい可能性が非常に高い。もし異なっていれば、どちらか (あるいは両方) に誤りが入り込んでいるので、破棄すべきだと分かる。ただし、この手法は二つの理由により誤り検出手法として望ましくない: まず、\(n\) ビットのメッセージに対して \(n\) ビットが余分に必要になる。次に、検出できない誤りが多い ── 二つのコピーの同じビットが破損すると検出できなくなる。一般に、誤りを検出する符号の目標は高い確率で誤りを検出しつつも冗長なビットをメッセージ本体に対して小さく抑えることである。

この単純な手法よりもずっと優れた手法が幸い存在するので、必要になる冗長なビットはメッセージに対して格段に少なくて済む。例えばイーサネットでは、12,000 ビット (1500 バイト) のデータがたった 32 ビットの CRC 符号 (CRC-32) しか必要としない。これから見るように、そういった符号は圧倒的大部分の誤りを検出できる。

誤り検出用に追加されるビットを「冗長なビット」と呼ぶのは、これらのビットがメッセージに新しい情報を追加しないためである。そうではなく、冗長なビットは事前に定められた曖昧さの無いアルゴリズムによってメッセージから導出される。送信側と受信側はこのアルゴリズムに関して知っている。送信側はメッセージに対してアルゴリズムを適用して冗長なビットを計算し、メッセージと冗長なビットの両方を送信する。受信側が受け取ったメッセージに同じアルゴリズムを適用すると、(誤りが無ければ) 送信側と同じ結果が得られる。受信側は冗長なビットの計算結果と受け取った結果を比較し、もし両者が一致すれば、転送中にメッセージに対して誤りは入り込んでいない (可能性が高い) と結論できる。もし両者が一致しなければ、メッセージと冗長なビットの少なくとも一方が破損していると分かるので、適切な操作を行う ── つまりメッセージを破棄するか、もし可能ならメッセージを訂正する。

この「追加のビット」に関する用語を定義しておく。通常はこれらのビットを誤り検出符号 (error-detecting code) と呼ぶ。さらに、この符号を作成するアルゴリズムが加算に基づいているときはチェックサム (checksum) とも呼ぶ。以降の説明から分かるように、チェックサムは名が体を表している: この値は誤りの有無を判定チェックするために存在し、加算サムを使ったアルゴリズムで計算される。嘆かわしいことに、「チェックサム」という言葉は誤って CRC を含んだ任意の誤り検出符号を指して使われる場合がある。混乱を招きかねないので、本節で説明されるような一般の符号のクラスを指すときは「誤り検出符号」を用い、加算を使って計算される誤り検出符号を指すときにだけ「チェックサム」を用いることを強く推奨する。

2.4.1 チェックサム

最初に紹介する誤り検出のアプローチは、インターネットチェックサムに代表されるアプローチである。インターネットチェックサムはリンクレベルでは用いられないものの、CRC と同様の機能を提供するので、ここで紹介する。

チェックサムの背後にある考え方は非常に易しい ── 転送されるワードを全て足し上げ、その和を転送するというものである。この和がチェックサムと呼ばれる。受信側は受け取ったデータに対して同じ計算を行い、その結果を受け取ったチェックサムと比較する。もしチェックサムを含めた転送データのどこかが破損していれば両者は一致しないので、受信側は誤りを検出できる。

チェックサムの基本的な考え方が分かれば、様々な異なるバージョンのアルゴリズムを考えられるだろう。インターネットプロトコルで用いられるインターネットチェックサム (Internet checksum) と呼ばれる方式は次のように動作する。チェックサムを計算するデータが 16 ビット整数の列だと仮定する。並んだ整数を 16 ビットの 1 の補数算術 (後述) で足し、結果の 1 の補数を取る。そうして手に入る 16 ビットの数値がチェックサムである。

1 の補数算術で負の整数 -x は x の 1 の補数として表現される。つまり、x の各ビットを反転させると -x となる。1 の補数で表された数値を加算するときは、最上位桁からの繰り上がりを最下位桁に足す必要がある。例として 4 ビット整数で表された -5 と -3 の 1 の補数算術における加算を考えよう。+5 は 0101 だから、-5 は 1010 と分かる。同様に +3 は 0011 だから、-3 は 1100 だと分かる。1010 と 1100 を足して最上位桁の繰り上がりを無視すると 0110 を得る。この加算では最上位桁で繰り上がりが起こるので、1 の補数算術の規則に従って結果に 1 を足すと 0111 となる。これは 1 の補数として表した -8 (1000 を反転すると得られる) であり、期待通りの結果が得られた。

インターネットチェックサムのアルゴリズムの単純な実装を次に示す。引数 count は 16 ビットを一単位とした buf の長さを表す。cksum 関数は buf が 16 ビット境界まで 0 で埋められていることを仮定している。

#include <stdint.h>

uint16_t
cksum(uint16_t *buf, int count) {
    register uint32_t sum = 0;

    while (count--) {
        sum += *buf++;
        if (sum & 0xFFFF0000) {
            /* 繰り上がりが起きたので、上位桁をクリアしてから 1 を足す */
            sum &= 0xFFFF;
            sum++;
        }
    }
    return ~(sum & 0xFFFF);
}

このコードでは、多くのマシンで使われる 2 の補数算術ではなく 1 の補数算術が計算で使われることを保証している。while ループの中の if 文がその処理である。繰り上がりによって sum の上位 16 ビットが 0 でなくなったときは、先述の例と同じように sum に 1 を足さなければならない。

最初に示したメッセージを反復する符号と比べると、このアルゴリズムは冗長なビットが少ない ── メッセージの長さに関わらず 16 ビット ── 割には良く動作する。一方で非常に優れた誤り検出だとは言えない。例えばワードを 1 増やす誤りとワードを 1 減らす誤りが同時に発生した場合、その二つの誤りは検出されない。保護が比較的 (CRC などと比べて) 弱いにもかかわらずチェックサムが利用されるのは、単純だからである: このアルゴリズムはソフトウェアで非常に簡単に実装できる。この形式のチェックサムで十分なことは経験からも示唆されている。ただし、チェックサムが「十分」な理由の一つは、このアルゴリズムがエンドツーエンドプロトコルの最終防衛ラインとして使われるからである。誤りの大部分はリンクレベルで CRC などのもっと強力な誤り検出アルゴリズムによって検出される。

2.4.2 巡回冗長検査 (CRC)

これまでの間に、誤り検出アルゴリズムの設計における主要な目標が冗長なビットを少しだけ使って誤りを検出できる確率を最大化することにあると理解できただろう。CRC (cyclic redundancy check, 巡回冗長検査) は非常に強力な数学的理論を利用してこの目標を達成する。例えば 32 ビットの CRC は数千バイトのメッセージに含まれるよくあるビット誤りに対する強力な保護を提供する。CRC の理論的基礎は有限体 (finite fields) と呼ばれる数学の分野にルーツを持つ。難しそうに聞こえるかもしれないが、基本的な考え方は簡単に理解できる。

まず、\(n+1\) ビットのメッセージが \(n\) 次多項式で表されると考えよう。\(n\) 次多項式とは最高次の項が \(x^{n}\) の定数倍であるような多項式である。\(n+1\) ビットのメッセージは多項式の各項の係数によって表され、最上位ビットが最高次の係数になるとする。例えば 8 ビットのメッセージ 10011010 は次の 7 次多項式 \(M(x)\) で表される:

\[ \begin{aligned} M(x) &= (1 \times x^7) + (0 \times x^6) + (0 \times x^5) + (1 \times x^4 ) \\ &\qquad \quad + (1 \times x^3) + (0 \times x^2) + (1 \times x^1) + (0 \times x^0) \\ &= x^7 + x^4 + x^3 + x^1 \end{aligned} \]

このとき、送信側と受信側は多項式をやり取りすると考えることができる。

CRC を使ってメッセージをやり取りするとき、送信側と受信側は生成多項式 (generator polynomial) と呼ばれる \(k\) 次多項式 \(C(x)\) を事前に決めておく。例えば \(k=3\) で \(C(x) = x^{3} + x^{2} + 1\) かもしれない。「\(C(x)\) はどうやって決めるのか？」という質問への答えは、実際にプログラムを書くケースのほとんどで「教科書に書いてあるのを見る」である。実は、これから議論するように、\(C(x)\) の選択は確実に検出できる誤りの種類に大きく影響する。様々な環境で非常に良い選択肢となる生成多項式がいくつか知られており、通常はプロトコルの設計の一環としてどれかが選択される。例えばイーサネット規格はよく知られた 32 次多項式を利用する。

送信側が \(n+1\) ビットのメッセージ \(M(x)\) を転送したいと思ったとき、実際には \(n+1\) ビットのメッセージに加えて \(k\) ビットの誤り検出符号が送信される。誤り検出符号を含めた送信されるビット全体を表す多項式を \(P(x)\) とする。このとき、\(k\) ビットの誤り検出符号は \(P(x)\) が \(C(x)\) でちょうど割り切れるように選択される: その方法は後述する。\(P(x)\) がリンクを通じて転送され、転送中に誤りが入り込まなければ、受信側は \(P(x)\) を \(C(x)\) で余りを出さずに割り切れる。一方で、もし転送中に \(P(x)\) に誤りが入り込んだなら、まず間違いなく受信側が受け取る多項式は \(C(x)\) で割り切れなくなる。つまり \(0\) でない余りは誤りが発生したことを示す。

多項式算術をよく知らないなら、次の事項を理解しておくといいだろう (整数の算術と大きくは変わらない)。ここで行おうとしているのは多項式の係数が \(0\) か \(1\) にしかならない特殊な多項式算術であり、「法が 2 の多項式算術 (polynomial arithmetic modulo 2)」と呼ばれる。本書はネットワークに関する本であり数学の教科書ではないので、CRC を考える上で重要なこの算術の特徴を証明無しに次に示す。どうか受け入れてほしい:

例えば、多項式 \(x^{3} + 1\) は \(x^{3} + x^{2} + 1\) で割ることができ、そのときの余りは係数の XOR を取ることで \(0 \times x^3 + 1 \times x^2 + 0 \times x^1 + 0 \times x^0 = x^2\) と求められる。対応するメッセージを考えると、「1001 は 1101 で割れて、余りは 0100」となる。二つのメッセージの XOR が余りとなることが分かるだろう。

多項式の除算の基本的な規則が分かれば、長いメッセージを処理するときに必要になる長い除算も行える。多項式の除算の例は解説の後に行う。

転送される多項式 \(P(x)\) は無加工のメッセージ \(M(x)\) から計算できる \(k\) ビットの誤り検出符号を持っており、生成多項式 \(C(x)\) で割り切れるという特徴を持っていたことを思い出そう。この多項式は次のように計算できる:

  1. \(M(x)\) に \(x^{k}\) を乗じる。つまり、\(k\) 個のゼロをメッセージの末尾に付け足す。ゼロが付け足されたメッセージを \(T(x)\) と呼ぶ。

  2. \(T(x)\) を \(C(x)\) で割り、余りを求める。

  3. その余りを \(T(x)\) から引く。

こうして得られるメッセージが \(C(x)\) で割り切れることは明らかに分かる。また、計算結果の先頭が無加工のメッセージ \(M(x)\) で、末尾 \(k\) ビットがステップ 2 で計算した余りであることもわかる。なぜならステップ 3 で余り (\(k\) ビット以下) を引くと、下位 \(k\) 桁でステップ 1 で付け足したゼロとの XOR が取られるからである。次の例を見ればさらによく理解できるだろう。

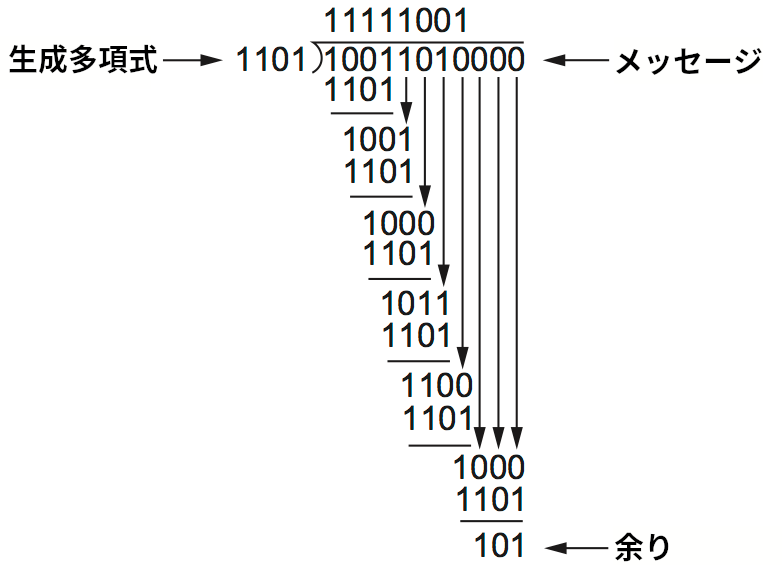
多項式の筆算を使った CRC の計算
図 32.
多項式の筆算を使った CRC の計算

では例として、メッセージ \(M(x) = x^7 + x^4 + x^3 + x^1\) (10011010) を生成多項式 \(C(x) = x^{3} + x^{2} + 1\) (1101) の CRC で転送するときの \(P(x)\) を求めてみよう。生成多項式の次数は 3 だから、\(M(x)\) に \(x^{3}\) を乗じて 10011010000 を得る。続いてこれを \(C(x)\) (1101) で割る。この計算の筆算を図 32 に示す。 最初にメッセージの上位 4 ビット 1001 と生成多項式 1101 の次数が一致するので、メッセージの上位 4 ビットを除数で割れることが分かる。この除算の余りは 1101 と 1001 の XOR を取ることで 100 と求まる。続いて、この余りが \(C(x)\) で割れるようになるまで桁をメッセージから降ろしていく。今のケースでは一つ桁を降ろした時点で 1001 となって \(C(x)\) で割れるようになる。そうしたら余りの計算をもう一度行う (新たな余りは 100 となる)。以上の処理を桁が降ろせなくなるまで続ける。なお、除算の商 (筆算でメッセージの上に書かれる数値) にはあまり意味がない ── CRC の計算には一番下に書かれる余りだけが関係する。

図 32 の一番下を見ると、除算の余りが 101 だと分かる。よってオリジナルのメッセージ 10011010000 から 101 を引けば \(C(x)\) で割り切れるメッセージ (つまり、送信すべきメッセージ) が得られる。法が 2 の多項式算術では減算が桁ごとの XOR に等しいので、10011010101 を送信することになる。上述したように、この値はオリジナルのメッセージに筆算で求まった余りを付け足したものである。受信側は受け取った多項式を \(C(x)\) で割り、もし余りが \(0\) なら誤りがないと結論付ける。もし余りが \(0\) でないなら、メッセージは破損しているので破棄しなければならない。なお一部の符号では、誤りが少数なら訂正できる場合がある。誤りの訂正が可能な符号を ECC (error-correcting codes, 誤り訂正符号) と呼ぶ。

続いて生成多項式 \(C(x)\) をどうやって定めるかを考えよう。簡単に言えば、生成多項式の選択では元のメッセージと誤りが入り込んだメッセージの両方が \(C(x)\) で割り切れる可能性をできるだけ低くするのが望ましい。転送されるメッセージを \(P(x)\) とするとき、入り込む誤りは別の多項式 \(E(x)\) の加算と考えることができる。このとき受信側は \(P(x) + E(x)\) を受け取る。誤りが検出されずに見過ごされるのは、唯一 \(P(x) + E(x)\) が \(C(x)\) で割り切れるときだけである。\(P(x)\) が \(C(x)\) で割り切れるのは知っているから、この条件は \(E(x)\) が \(C(x)\) で割り切れることに等しい。よって、よくある種類の誤りで \(E(x)\) が \(C(x)\) で割り切れないようにするのがポイントとなる。

よくある種類の誤りの一つが単一ビットの誤りである。\(i\) 桁目のビットだけを破損させる誤りは \(E(x) = x^{i}\) と表現できる。最初と最後の項 (つまり \(x^{k}\) の項と定数項) が非ゼロになるように \(C(x)\) を選べば、その \(C(x)\) は一つの項からなる \(E(x)\) のいずれも割り切れなくなる。よってそういった \(C(x)\) は単一ビットの誤りを検出できる。一般に、\(C(x)\) の特徴と検出できる誤りの種類に関して次の関係が証明できる:

リンクレベルで広く利用される \(C(x)\) として六つのバージョンが知られている。例えばイーサネットは CRC-32 を使っており、対応する \(C(x)\) は次のように定義される:

\[ \begin{aligned} \text{CRC-32:} \quad x^{32} + &x^{26} + x^{23} + x^{22} + x^{16} + x^{12} + x^{11}\\ & + x^{10} + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1 \end{aligned} \]

誤りの存在を検出するだけではなく誤りを訂正できる符号も存在すると前に述べた。誤り訂正符号の詳細を説明するには CRC より複雑な数学が必要になるので、ここでは説明しない。ただ、誤り検出符号と誤り訂正符号のメリットの比較はここで行う。

一見すると、どんなときでも誤り訂正符号の方が優れているように思える。誤りの検出しかできないと、誤りがあったときにメッセージを破棄して再送を頼まなければならない。再送で帯域が利用される上に、再送を待つ分レイテンシが増加する。しかし、誤り訂正符号にも欠点はある。それは、誤りの検出だけを行う符号と同じ強さを持つ (つまり、同じだけの誤りを訂正できる) 誤り訂正符号には一般に冗長なビットが多く必要になることである。言い換えると、誤り検出符号は誤りが発生したときに多くのビットを要求するのに対して、誤り訂正符号は常に多くのビットを要求する。このため、誤り訂正符号は次の条件が成り立つときに最も有用となる:

ネットワークにおける誤り訂正符号の利用を指して FEC (forward error correction, 前方誤り訂正) という言葉が使われることもある。誤りが起こるのを待って後から再送で誤りを直すのではなく、追加の情報を送ることで誤りの訂正を「事前に」行っているためにこう呼ばれる。FEC は IEEE 802.11 といった無線ネットワークで広く用いられる。

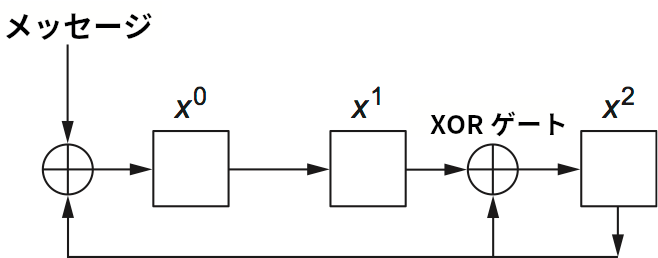
最後に、CRC のアルゴリズムは一見複雑に見えるものの、ハードウェアでは \(k\) ビットのシフトレジスタと XOR ゲートを使って簡単に実装できることを指摘しておく (\(k\) は生成多項式の次数)。例で用いた生成多項式 \(x^{3} + x^{2} + 1\) を使った CRC のハードウェア実装を図 33 に示す。メッセージは最上位桁から入力され、左から右にシフトされる。メッセージの末尾に付け足される \(k\) 個のゼロが入力されると計算は終了し、そのときレジスタには除算の余り ── つまり CRC の誤り検出符号がレジスタに残る (最上位桁が右)。XOR ゲートの位置は次のように決定される: シフトレジスタを左から右に \(0\) から \(k-1\) と名前を付け、生成多項式に \(x^{n}\) の項が存在するならレジスタ \(n\) の前に XOR ゲートを置く。図 33 では生成多項式が \(x^3 + x^2 + x^0\) なので、\(0\) と \(2\) のレジスタの前に XOR ゲートが存在している。

シフトレジスタを使った CRC の計算
図 33.
シフトレジスタを使った CRC の計算
広告
このページの文章はテキストゆれないくんを使って校正されました。